Abstract
Residential colleges are considering re-opening under uncertain futures regarding the COVID-19 pandemic. We consider repeat SARS-CoV-2 testing models for the purpose of containing outbreaks in the residential campus community. The goal of repeat testing is to detect and isolate new infections rapidly to block transmission that would otherwise occur both on and off campus. The models allow for specification of aspects including scheduled on-campus resident screening at a given frequency, test sensitivity that can depend on the time since infection, imported infections from off campus throughout the school term, and a lag from testing until student isolation due to laboratory turnaround and student relocation delay. For early- (late-) transmission of SARS-CoV-2 by age of infection, we find that weekly screening cannot reliably contain outbreaks with reproductive numbers above 1.4 (1.6) if more than one imported exposure per 10,000 students occurs daily. Screening every three days can contain outbreaks providing the reproductive number remains below 1.75 (2.3) if transmission happens earlier (later) with time from infection, but at the cost of increased false positive rates requiring more isolation quarters for students testing positive. Testing frequently while minimizing the delay from testing until isolation for those found positive are the most controllable levers for preventing large residential college outbreaks. A web app that implements model calculations is available to facilitate exploration and consideration of a variety of scenarios.
Keywords: SARS-CoV-2, COVID-19, Repeat testing, Residential college coronavirus screening, Epidemic model, Probability model
Highlights
Model accounts for test frequency, test specificity, dependence of test sensitivity on time since infection, laboratory turnaround and individual notification delays, imported infections from off campus, intensity and time dependence of transmissions, and initial infection conditions
Characterizes the probability distribution of the time from infection until detection and isolation
Compares random and regular testing schedules and analyzes the more realistic and also more efficient case of regular testing
Helps university planners match testing frequency with anticipated risk behaviors and reveals how the demand for isolation units evolves over time
Provides an online tool that implements model calculations
Introduction
Universities and colleges around the world, along with other businesses and institutions, have spent the past several months on lockdown on account of the COVID-19 pandemic. Students were sent home, classes and faculty meetings went on-line, and university buildings have remained eerily empty. With stay-at-home restrictions being relaxed if not rescinded, residential universities and colleges are planning to re-open, and perhaps the most prominent decision to be made is whether or not to invite students to return in person. Different schools are approaching this issue in different ways. Some colleges feel they have no choice but to allow students to return [10, 16], while others have opted for students to remain off-campus with instruction offered remotely via the internet [5, 24]. At the heart of this decision is the anticipated ability of colleges and universities to keep campuses free from student-driven SARS-CoV-2 outbreaks. While the details of infection control and social distancing represent important public health components on campus, increasingly institutions are considering whether testing students for SARS-CoV-2 offers additional protection against the spread of infection [1, 11, 32].
Coronavirus testing in the general population has been reserved largely for persons exhibiting symptoms with the goal of diagnosing individual cases, though testing of persons who have been in close contact with known COVID-19 cases is also recommended [6]. The argument behind such symptomatic testing prioritizes detecting and referring to medical care those at greatest risk for developing complications of infection while trying to prevent further transmission, especially when testing capacity is limited.
By contrast, asymptomatic testing for preventing SARS-CoV-2 infections is different than standard diagnostic testing. Usually when a patient is tested for the presence of some medical condition, it leads to a specific set of instructions for the benefit of the patient screened: a change in diet, the prescription of drugs, or a course of more intensive medical treatment such as radiation, chemotherapy, or surgery. With coronavirus, the purpose of asymptomatic testing is not to gain access to some treatment. Rather, those who test positive are instructed to isolate to prevent transmitting infection to others. The purpose of repeatedly screening students for SARS-CoV-2 is thus not for the screened patient’s individual health, but for the benefit of those who would have been in contact with an infectious person had the detection of an infection not occurred. Some have argued that repeat asymptomatic testing at the population level could control or even eliminate SARS-CoV-2 transmission [20]. Taipale et al. [31] presented model-based arguments to arrive at testing frequencies capable of eradicating the spread of the coronavirus at the population level, while [29] specialized these arguments to the case of the United Kingdom.
Returning to universities, it is well documented that contagious infections such as influenza, mumps, and sexually transmitted diseases spread readily in the residential college context [3, 9, 26], and there is no reason to expect that SARS-CoV-2 would not be transmitted as well. However, students themselves are not at great medical risk from COVID-19 complications resulting from infection with SARS-CoV-2. Indeed, many if not most students would experience mild to no symptoms of infection at all. However, absent testing, all such infected students would unknowingly pose risks to anyone with whom they are in contact, whether on campus or off. For residential colleges that are themselves isolated geographically, vulnerable workers and faculty (and some students with underlying health conditions to be sure) are the main beneficiaries of repeat student testing. For urban campuses centrally located within surrounding communities that contain many more vulnerable persons, the main beneficiary of screening students is that community itself. In this sense, beyond protecting the health of vulnerable workers, faculty and students, the main goal of repeatedly screening students on campus is to prevent them from unknowingly igniting transmission chains in the surrounding community.
The way screening programs work to impact the transmission of infection in this context has not been well studied or analyzed. This paper presents a first attempt to do so.1 The models we will describe were developed in support of Yale University’s planning to return students to campus, and Yale’s current community testing program relies heavily upon the recommendations of this work. The model development was prospective: in the absence of data describing prior university (or other institutional) repeat screening programs, we developed models based on biological and operational realism with attention to policy levers the university could exert: test frequency, delays in test reporting and notification, and overall infection control measures. Specifically, based on published epidemiological data, our models explicitly account for the timing of transmission since infection, and show directly how isolating infectious persons identified via repeat testing interrupts such transmission. The models also account for the differential ability of screening tests to detect infection depending upon the age of infection at the time of testing, and the delays associated with the time from sample collection until test results are reported and those testing positive are notified and isolated. The outbreak model includes imported infections from off campus in addition to internally generated infections due to contact between infectious and susceptible community members.
The goal of the analysis is to assess the ability of repeat testing programs to control outbreaks over the course of a fixed time horizon such as a college semester. Rather than attempting to simulate exhaustively the impact of each model feature on the resulting number of infections, our approach focused on characterizing the worst case inputs that would lead to acceptable levels of infections under different test frequencies, transmission timing and logistical delays. Also, rather than trying to detail the specifics of “who mixes with whom” contact patterns on campus, we relied on homogeneous mixing recognizing that such models tend to produce worse outbreaks than more heterogeneous contact models given the same epidemiological parameters [19, 21]. In particular, in structured “small world” contact networks that have been documented for at least one college population [35], it is known that the transmission of infections can behave as if population members were interacting at random [34]. Testing programs that can control infections under homogeneous mixing are thus likely to perform even better when heterogeneous contact patterns are taken into account, adding a layer of robustness to our analysis.
The remainder of the paper is organized as follows: we begin with a simple characterization of the early transmission dynamics associated with nascent outbreaks of SARS-CoV-2, and in Section 3 show how test frequency, sensitivity and reporting delay influence transmission via isolating those testing positive when test results are obtained. In Section 4 we incorporate this interruption of transmission directly into a dynamic model of an internally generated SARS-CoV-2 outbreak on campus, and we expand the model to include exposures to imported infections from off-campus due to students traveling, wandering about town to restaurants, bars or clubs, or due to visitors. We present the key performance measures by which to assess repeat screening focusing on the cumulative incidence of infection, the number of infections detected, and the number of students placed in isolation for given outbreak and screening scenarios (different reproductive numbers governing on-campus transmission, different imported exposure rates, different screening frequencies, different test sensitivity, specificity, and delay from testing until isolation for those testing positive). We consider numerous examples in Section 5 with a focus on which outbreaks can and cannot be brought under control. We discuss implications of our analysis in Section 6.
Age-of-infection dependent transmission
The model employed to analyze repeat screening follows [17] in presuming that at the beginning of an outbreak, a newly-infected index surrounded by otherwise uninfected students transmits infections according to a time-varying Poisson process with intensity λ(a), where a denotes the time from infection of the index (the age of infection). The reproductive number denoting the expected number of infections the index will transmit over all time then equals
| 1 |
and as is well known, an epidemic cannot be self-sustaining unless R0 > 1.
The transmission intensity λ(a) can be represented as
| 2 |
where
| 3 |
is the probability density function of the forward generation time [4, 8, 33]. This representation separates the strength of transmission (R0) from the timing of infectiousness (captured by f(a)), enabling flexible investigation of both.
Modeling transmission in this form generalizes many epidemic models commonly used. For example, S usceptible-I nfectious-R ecovered (SIR) models presume constant transmission at rate β during an exponentially distributed infectious period with mean 1/μ [2]. This can be captured by
| 4 |
with R0 =β /μ and f(a) = μe−μa. Similarly, modifications of S usceptible-E xposed-I nfectious-R ecovered (SEIR) models have been widely applied to model SARS-CoV-2 transmission [13, 22, 27]. In such models, newly infected but not yet infectious persons enter an exposed state for an exponentially distributed length of time with mean 1/μ1, after which they become infectious for an exponentially distributed duration of mean 1/μ2 during which transmission again occurs at constant rate β. Letting D1 and D2 denote the duration of time after infection spent in the exposed and infectious states, early transmission in this model can be captured by
| 5 |
where R0 =β /μ2 and
Beyond SIR and SEIR models, epidemiologists have approximated generation time distributions directly from contact tracing data, and several such studies have been conducted using early SARS-CoV-2 outbreak data from China (see [28] for a summary). The generation times are often presumed to follow gamma distributions, as the latter provide a flexible statistical model for the time between the onset of symptoms for infector/infectee pairs within a transmission chain (the serial interval), and the distribution of serial intervals is taken as an estimate of the unobservable times between infections (which is what the generation time density f(a) is meant to represent).
Modeling the impact of testing and isolation
Suppose that an infected student is isolated at age T days following infection, having been detected via repeat screening2. We model T as a random variable independent of the Poisson process of infections. Figure 1 shows the transmission rate λ(a) with the isolation age T represented by the vertical black line. The effect of isolation at T is to erase all infections that would have been transmitted beyond time T; this is illustrated as the shaded blue area in Fig. 1.
Fig. 1.

Impact of isolation. For a person isolated at a random time T after infection, the blue shaded area shows the expected number of further infections whose transmissions are prevented by the isolation, and the red area shows the expected number of further infections that escape isolation and are still transmitted
The sooner an infectious person is isolated (the smaller the value of T), the greater the number of infections that can be prevented, and the fewer the number of transmissions that escape isolation. Following the Poisson model, conditional on T, the expected number of transmissions that occur before isolation is . Thus, the expected number of infections that would escape isolation and still be transmitted, RT, is given by
| 6 |
here 1B denotes the indicator function taking the value 1 if the event B occurs and 0 otherwise. Defining λT(a) = λ(a)P{T > a} to be the effective transmission rate at age a taking account of the testing program, is the area under the curve λT. Clearly RT ≤ R0 as Pr{T > a}≤ 1, with the extent of the reduction in transmission depending on the distribution of T, which in turn depends upon testing characteristics such as the timing of repeat tests, test sensitivity, and the lag time from testing to isolation.
Perfect repeat testing
As a contrast to the regularly scheduled testing that is the subject of most of this paper, consider a perfect test that on average is administered to each student once every τ days but whose timing is random and memoryless with a constant hazard rate. This implies that T would follow an exponential distribution with mean τ, with
| 7 |
Alternatively, as a model of regularly scheduled testing, suppose that students are administered a perfect test literally once every τ days on a fixed schedule. For example, scheduled weekly testing would require each student to be tested once every seven days. One way to implement this would be for 1/7th of the students to be tested each Sunday, a different 1/7th each Monday, and so on such that each student has a specified day of the week (and time slot) for testing. For such a schedule in continuous time, T would follow a uniform distribution on (0,τ), and
| 8 |
From Eqs. 7 and 8, it is clear that regularly scheduled screening would be more effective than memoryless screening for all values of τ since 1 − a/τ < e−a/τ for a > 0. With memoryless screening, on average a newly infected person would not be detected and isolated until τ time units after infection, whereas with regularly scheduled screening, the mean time from infection to isolation would be just τ/2, while τ would be the maximum time from infection until isolation. This distinction is important, as expanding SIR or SEIR models to include testing by applying a constant testing rate to the infected population amounts to memoryless screening.
Imperfect repeat testing
Tests are not perfect, however. The specificity of a test refers to the conditional probability a test will deliver a negative result, given that the person tested is not infected. Poor specificity gives rise to false positive test results, which can be a serious issue when persons testing positive are subjected to isolation. We will return to test specificity in Section 4.2 below.
The sensitivity of a test is defined as the conditional probability of receiving a positive test result on an individual, given that the person tested is in fact infected. We denote the sensitivity of a screening test by σ. Memoryless random screening with a mean intertest period of τ also results in the time of detection being exponentially distributed, but now with mean τ/σ, inflating the time to detection by the factor 1/σ.
Regularly scheduled screening, with a deterministic separation of τ days between successive tests for a given individual, is more complicated. Let ⌊x⌋ denote the largest integer less than or equal to x (the floor function). Regularly scheduled screening with sensitivity σ yields
| 9 |
This follows because in each screening interval of duration τ, detection will occur with probability σ, which makes the number of testing intervals until the interval containing detection follow a geometric distribution with mean 1/σ. If detection occurs, the timing of detection within the interval will be uniformly distributed between 0 and τ. As a consequence, the expected time from infection to detection with scheduled imperfect screening once every τ days equals
| 10 |
Note this time is shorter than the mean time to detection with imperfect random screening by τ/2 days, which is the same difference in mean detection times for scheduled versus random screening with perfect testing (σ = 1).
Scheduled screening with age-of-infection-dependent sensitivity
Given both the shorter lags from infection to isolation and the ease of implementing scheduled versus random testing, we will narrow our focus to scheduled testing while increasing model realism. While we have included test sensitivity in our model, thus far we have presumed constant sensitivity that does not depend on the time since infection. This latter assumption is not realistic. For example, viral tests such as reverse transcriptase polymerase chain reaction (RT-PCR) cannot detect infections immediately after they occur, and indeed the ability of a test to detect the virus presumably behaves in a manner that is somewhat related to the ability of an infectious individual to transmit the virus [23]. To model the dependence of sensitivity on time since infection, we denote the sensitivity of a test administered at an age of a time units after infection by σ(a), where σ is called the sensitivity function of the test. For simplicity we assume here that the results of tests taken at different times after infection are mutually independent given the sensitivity function.3
Determining the survivor function Pr{T > a} from the sensitivity function σ(a) is best approached by first deriving the probability density function gT(a) for the isolation age T. In a scheduled repeat testing policy with screening interval τ, we want the probability that an individual who has been infected for a time units was not detected over the previous tests administered since becoming infected, but is tested and detected in the time slice (a,a + da). Owing to the independence of the infection, screening and detection processes, this probability is given by , where an empty product equals 1 by definition. In other words, the probability density function for the time T from infection until isolation is given by
| 11 |
and the survivor function Pr{T > a} then follows from integration as
| 12 |
Example: Step function sensitivity
One simple model of test sensitivity could be described by a silent window of duration w after infection during which it is not possible to detect the presence of infection, after which infection can be detected with constant sensitivity σ until time r, the reach of the test, beyond which the test becomes insensitive. In this case the test sensitivity would follow a step function over the time from infection, that is
| 13 |
The survivor distribution Pr{T > a} is a function of a ∧ r, the minimum of a and r, and can be thought of as scheduled screening beginning at time w after infection (for no detection is possible within the window period). Due to the independence of the infection and testing processes, Eq. 9 still applies, but to the number of days since expiration of the window period rather than to the age of infection, so that the survivor distribution of the time from infection until detection is given by
| 14 |
Accounting for the silent window w can substantially reduce the efficiency of repeat testing, as illustrated by the simple result in the case where the test reach r is infinite that the expected time from infection until detection increases by w days to
Example: Kucirka et al. [23]
An estimated sensitivity function of reverse-transcriptase polymerase chain reaction (RT-PCR) tests for SARS-CoV-2 is provided by [23], based on a Bayesian hierarchical model fit to data drawn from 7 previously published studies. Their sensitivity function is approximated by
| 15 |
where logistic(z) = ez/(1 + ez) is the logistic function. This function fits precisely with values obtained by Kucirka et al. [23] in the range 0 ≤ a ≤ 21, and then the cubic function of is extrapolated linearly on the logistic scale for a > 21.
Incorporating delay from testing to isolation
Finally, tests take time to process, as does informing students of their test result and ensuring the start of isolation. We refer to this additional delay as the isolation lag, denoted by ℓ, and note that the impact of incorporating this lag is to shift any 0-lag survivor distribution for the time from infection to isolation by ℓ days to account for the additional delay. Define Tℓ as the time from infection to isolation incorporating an isolation lag of ℓ, while T0 is the time from infection until isolation based on whatever screening interval τ or age-of-infection-dependent sensitivity σ(a) is being studied in the absence of isolation delay. Our final model for the survivor function for Tℓ, the time from infection until isolation accounting for the isolation lag, is given by
| 16 |
Illustrative examples
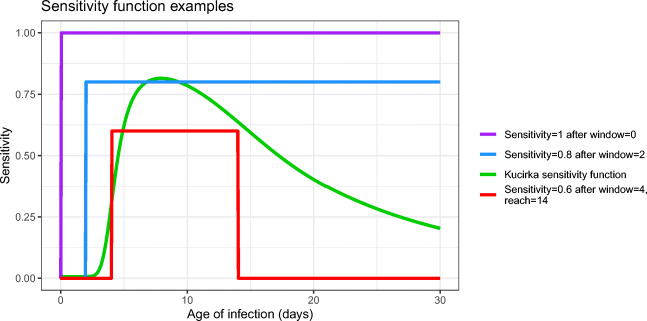
Figure 2 illustrates four examples of sensitivity functions:
perfect sensitivity (with no window of zero sensitivity)
a step function with sensitivity 0.8 [15] after a window of 2 days with zero sensitivity,
the [23] sensitivity function
a step function having a window of 4 days with zero sensitivity, followed by 10 days with sensitivity 0.6, after which the sensitivity returns to 0 (i.e. reach = 14 days).
Fig. 2.
Examples of test sensitivity functions
Applying these four tests with regular weekly screening and 1 day of isolation delay in all cases, the corresponding survivor functions are shown in Fig. 3. This figure shows how repeat testing is harmed by both imperfect testing (which forces multiple testing cycles to detect new infections), and an isolation lag (which shifts the survivor function one day to the right, increasing the time from detection to isolation).
Fig. 3.
Probability that the time from infection to isolation exceeds a. Here the isolation delay in all four scenarios was taken to be 1 day
Figure 4 plots the transmission function λ(a) corresponding to the forward generation time density implied by [25], which is a gamma distribution with a mean (standard deviation) of 8.86 (4.02) days, for an outbreak with R0 = 1.6. Also shown are the effective transmission curves found by multiplying by the four survivor functions of Fig. 3.
Fig. 4.
Transmission curves under different testing scenarios
The effect of repeat testing on blocking transmission is considerable, but harmed by imperfect sensitivity and isolation delay. One way to quantify this effect is to compute RT for each scenario; following Eq. 6, each RT is the area under the corresponding effective transmission curve. Starting with R0 = 1.6 in the absence of any screening, testing students each week with perfect sensitivity would result in RT = 0.26. Replacing perfect screening by a window of 2 days of zero sensitivity followed by sensitivity 0.8 increases RT to 0.69. Replacing the sensitivity function by that of [23] increases RT to 0.97. The fourth example sensitivity function with lower sensitivity, longer window of zero sensitivity, and finite test reach further increases RT to 1.11; the effect of the test reach is relatively minor though since it changes the survivor function at times a large enough so that λ(a) is relatively small. This shows that weekly screening helps reduce transmission, but is harmed by imperfect test sensitivity in ways that depend on the shape of the sensitivity function.
Dynamic transmission model
To expand this framework to a dynamic transmission model, we follow [18] with slightly different notation while incorporating the effect of repeat screening and define:
s(t) ≡ fraction of the population that is susceptible to infection at calendar time t;
π(t) = incidence of infection at time t;
λ(a) ≡ the transmission intensity as a function of age of infection introduced earlier;
T = the isolation age induced by repeat testing as discussed previously with distribution characterized by the survivor function Pr{T > a}
Thinking of time 0 as the start of the term when students arrive to campus, given initial conditions, the dynamic screening model can be written as:
| 17 |
| 18 |
for t > 0. Equation 17 sets SARS-CoV-2 incidence proportional to the fraction of the population that is susceptible and the infected population-weighted age-of-infection adjusted transmission intensity thinned by the effect of repeat testing and Eq. 18 depletes susceptibles with the incidence of infection. Note that the distribution of infectiousness over time from infection is implicitly accounted for in the definition of λ(a), thus there is no need for explicit removal of infectious persons from the population as they simply cease transmitting in accord with λ(a).
To specify initial conditions for the model we suppose each student is tested in an initial screening. Letting π0 denote the fraction of students who were infectious at time 0 but not detected by the initial screening, we assume that their ages of infection at time 0 are uniformly distributed over an interval [0,A], so that π(t) = π0/A for t ∈ [−A,0]. We choose A large enough so that it is a good approximation to consider students at time 0 with infections of age greater than A as no longer infectious. With this assumption there is no need to keep track of when infections of age greater than A at time 0 occurred, but rather it is enough to note their total number as reflected in the initial susceptibility s(0). Thus initial conditions are given by s(0) and π0.
Incorporating imported infections
Thus far the model has only considered the detection of internally generated infections due to a closed outbreak beginning with the initial conditions s(0) and π0. However, due to off-campus wanderings as well as visitors to campus, one can expect on-campus residents to be infected by external exposures. A screening policy must contain transmission generated by such imported infections in addition to internal transmission among college residents. Let v(t) denote the exposure rate of imported infections at time t per campus resident. The rate such exposures lead to actual infections presuming on-campus residents are exposed at random then equals v(t)s(t).
For example, if there are n on-campus residents, and on average one such resident has one imported exposure sufficient to transmit infection weekly (either by direct off-campus exposure or as the result of exposure to an infected visitor on-campus), then v(t) = 1/(7n) per day. If instead a single sufficient imported exposure happens on a daily basis, then v(t) = 1/n per day. We modify our model by including transmission from imported infections in the on-campus incidence rate, and thus modify (17) to
| 19 |
Note the dual role played by v(t): imported infections will contribute to on-campus incidence the same way infections acquired on-campus contribute over time, marking transmission from imported infections. But the persons who acquired these imported infections immediately deplete the on-campus susceptible population at their time of infection. Both effects are accounted for in Eq. 19; v(t)s(t) is the instantaneous contribution to incidence by imported exposures at time t, and via (18) immediately contribute to the depletion of susceptibles.
Performance measures: cumulative incidence, isolation, and undetected infections
The cumulative incidence c(h) of infections that occur over some planning horizon h is given by
| 20 |
Minimizing transmission is the most important goal of a repeat testing program, but it is not the only one. Administrators will also need to have an estimate of the number of students that screening will detect and isolate. Until this point in our discussion, we have focused on detecting actual infections, that is, true positives, but testing also produces false positive errors [15] that will land additional students in isolation. We now consider both true and false positives in determining the number of students who would require isolation over the planning horizon.
Let δTP(t) denote the true positive isolation rate, that is, the rate at which infected students are isolated accounting for scheduled screening frequency, test sensitivity, window and reporting lag at time t from the start of the planning horizon. This isolation rate is given by
| 21 |
where denotes the probability density function for the isolation age T for an infection that occurred at time u. This carries some dependence on u because in our model we assume that regular screening begins at time 0 so that an individual infected at time u < 0 is not tested for the first |u| units of time following infection. For u < 0 the density may be obtained by the general density (11) applied to a test sensitivity function that has been modified by multiplying it by the indicator function 1{a>|u|}, since we can think of not being tested for the first |u| time units after infection as equivalent to using a test that has sensitivity 0 for the first |u| time units. In our calculations we approximate δTP(t) by replacing the infinite upper limit of integration in Eq. 21 by A.
To model the false positive isolation rate δFP(t), we let ϕ denote the false positive rate of the test (which equals one minus the specificity) and continue to use the notation ℓ for the isolation lag and τ for the spacing of the regular tests. To become a false positive isolated in a time interval dt, a person needs to be susceptible and tested in the time interval dt − ℓ, which happens with probability s(t − ℓ)dt/τ, and receive a false positive error on the test with probability ϕ, so that
| 22 |
Students testing positive thus enter isolation at time t with total rate δ(t) = δTP(t) + δFP(t), and remain isolated for duration Δ. The fraction of the population in isolation at time t, ι(t), when the duration of isolation is equal to Δ (typically 14 days) thus equals
| 23 |
with corresponding formulas for true positive and false positive isolations, ιTP and ιFP, in terms of the functions δTP and δFP. We assume that false positive detections are not susceptible while in isolation but then they return to the susceptible pool and to regular testing once they leave isolation.
Finally, integrating (21) up to a given time yields the total fraction of the population that was infected and detected over the course of the outbreak up to that time. Comparing this result to the cumulative incidence in the population at that time yields the fraction of the population that was infected but not detected by that time, that is,
| 24 |
Controlling outbreaks via repeat testing and isolation
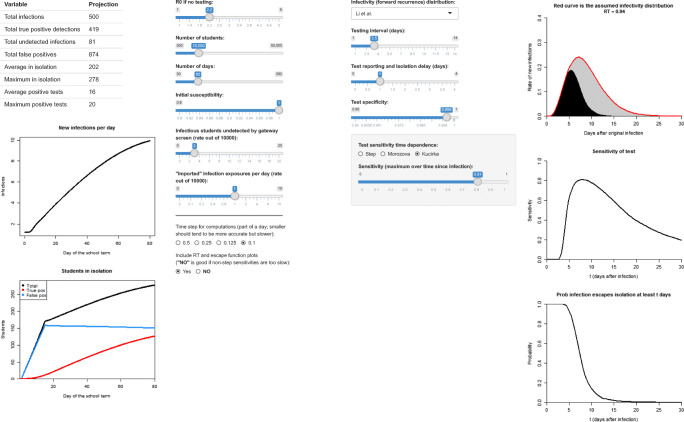
The models described throughout this paper have been implemented in a web app available at https://jtwchang.shinyapps.io/testing/. The app allows the user to select values from a wide range of model input parameters as illustrated in Fig. 5. The app also allows users to address the timing of transmission as implied by the forward generation time density f(a). We consider two different models for f(a). The first is the gamma distribution with mean 8.87 days and standard deviation 4.02 days, drawn from Li et al.’s [25] study of early transmission dynamics in Wuhan referred to earlier, which is widely cited as the first detailed analysis of early SARS-CoV-2 transmission. The second is also a gamma distribution but with mean (standard deviation) equal to 8.50 (6.07) days; this is based on parameter point estimates in the Bayesian meta-analysis conducted by Park et al. [28]. These two forward generation time densities are displayed in Fig. 6. Comparing these distributions, we see that while the Park et al. and Li et al. densities have similar means of 8.9 and 8.5 days, the standard deviation is smaller for the Li density, causing generation times to cluster closer to the mean which implies delayed transmission. The Park et al. density rises more steeply and peaks earlier, presenting an early transmission challenge.
Fig. 5.
A web app available at https://jtwchang.shinyapps.io/testing/ that implements the model and facilitates exploring a variety of scenarios
Fig. 6.

Two estimated generation time distributions found in published studies. We refer to these distributions as featuring relatively early transmission [28] and late transmission [25]
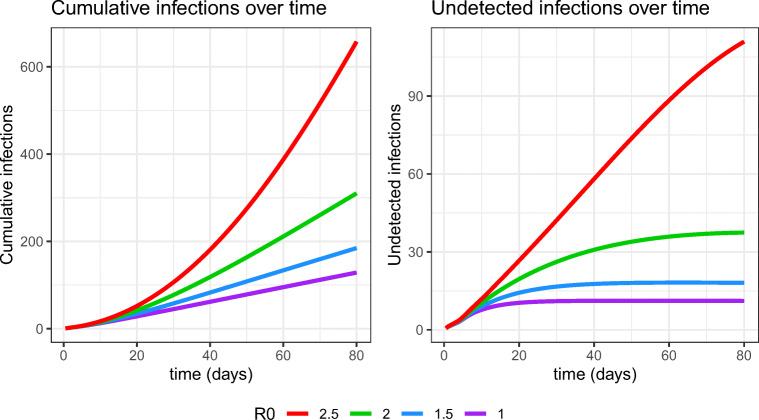
We illustrate the model with four testing scenarios over an 80 day period simulating an abbreviated fall term in a population of 10,000 students with reproductive numbers of 1.0, 1.5, 2.0, and 2.5 using the Li et al. [25] forward generation time distribution. We assume that testing takes place every three days, set v(t) = 1imported exposure per day, test specificity equals 99.8% [15], and test sensitivity follows the trajectory estimated by Kucirka et al. [23] discussed earlier. The outbreaks begin with three initially infectious students at the start of school (everyone else in the population is susceptible), and a 24 hour delay from testing to student isolation for students testing positive. The first plot in Fig. 7 shows the cumulative number of infections over time in these four scenarios. Cumulative infections at day 80 increase from 131, to 187, to 312, and then 658 as R0 increases from 1.0 to 2.5 in increments of 0.5, while the time averaged number of students isolated equals 102, 109, 124, and 162 in these same scenarios. There are about 90 false positives in isolation on average in all four scenarios. The nonlinear effect of R0 on these otherwise equivalent scenarios is notable. University preparations in the realms of social distancing and infection control are meant to lower R0, and if students comply with such directives, the likelihood of achieving a favorable epidemic outcome should increase. However, some are skeptical that students will comply with such directives [30], which could lead to higher reproductive numbers (and imported exposures) and worse epidemic outcomes, perhaps comparable to cruise ship transmission [36]. The second plot in Fig. 7 shows the number of undetected infected persons given by Eq. 24. Not all undetected infected persons are actually infectious; some will have been very recently infected so that their transmission intensity λ would still be very low. However, others will be infectious while escaping detection thus far, and as illustrated in the case R0 = 2.5 in the present example, a growing number of undetected infectious individuals could pose a threat not only to college residents, but to the surrounding community as well.
Fig. 7.
Cumulative infections and undetected infections over time in scenarios with testing every 3 days and fixed infectivity function, sensitivity function, and delays, as R0 varies
This model is flexible in allowing users to simulate many different testing scenarios, but it is perhaps most useful in identifying the limits of outbreak control for alternative repeat-testing policies. The proposed approach is to first identify an acceptable control level of infection within a defined time periord, such as 5% of the student population over the course of a semester. Such a control level could reflect the maximum number of infections university health systems can handle considering realistic testing (both collection and laboratory resources) and isolation capacity (residential space, human resources for monitoring, counseling and compliance). The control level could also reflect university concern with secondary transmission from students to vulnerable persons such as certain faculty, workers, or the residents of the surrounding community in which the university is embedded. The control level could even follow from a mortality goal such as ensuring the probability of zero COVID-19 fatalities is at least a specified value.
For a given repeat testing interval, one can use the app to determine the most challenging parameter values for which total infections remain within the previously stated control level. Repeating this for different testing frequencies thus helps determine the limits of control for each policy. While identifying appropriate control limits is the responsibility of university leadership as opposed to analysts, having the ability to show officials the limits of different control strategies enables senior decision makers to trade off infection outcomes against other important considerations including testing costs as well as intangibles such as the importance and value of residential education in the midst of a pandemic.
We illustrate by again considering a scenario where 10,000 students will be repeatedly tested over 80 days. We maintain the assumptions that there is one imported exposure per day, test specificity equals 99.8%, there are three initially infectious students, and a 24 hour delay from testing to student isolation. There are four transmission and detection scenarios considered, corresponding to using the late-transmission [25] or early-transmission [28] forward generation time density with either the Kucirka et al. [23] or step-function sensitivity, where the step-function presumes a two day non-detection window followed by constant 80% sensitivity [15]. For weekly screening and testing every three days, we determine the largest value of R0 (in increments of 0.05) such that total infections are held beneath 500 (or 5% of the population tested), and report total infections, average and maximum daily numbers of students isolated, and average daily positive tests.
Table 1 reports the maximal values of R0 for weekly screening that can keep infections below 5% of the population. The most pessimistic scenario -- early transmission and Kucirka et al. [23] sensitivity -- requires that R0 falls at 1.4 or below. The most optimistic scenario -- late transmission and the presumed step-function sensitivity -- keeps infections below 5% providing R0 falls below 2.25. The two intermediate scenarios contain infections below 5% of the population providing R0 is at most 1.6-1.8. While all four of these scenarios result in comparable numbers of infections and daily positive tests, note that both scenarios employing the step-function sensitivty on average isolate more students than the remaining scenarios. This is because of the high 80% test sensitivity that applies once the two-day non-detection window expires in the step-function scenarios. A greater number of infected students are detected as a consequence, leading to the larger number of students in isolation. CDC [7] recommends considering R0 to fall in the range from 2 to 3 in modeling studies, with 2.5 serving as their recommended base case value. Our analysis suggests that weekly testing could not contain infections below 5% for CDC’s base case reproductive number. However, the CDC recommendations are not specifically for residential college outbreaks, where one would hope that social distancing and infection control protocols would result in milder outbreaks with lower values of R0. On the other hand, conservative planning principles would suggest that hope is not enough, especially given recent evidence regarding outbreaks already occurring at residential colleges [12, 14]. The wide range of results reported in Table 1 suggests that while weekly screening could contain an otherwise large-scale outbreak under favorable conditions of late transmission and (relatively) early detection with 80% test sensitivity, overall weekly screening is not sufficiently robust to reliably contain outbreaks in the residential college setting.
Table 1.
Weekly screening results for an 80-day term for various scenarios described in the text
| Scenario | |||||
|---|---|---|---|---|---|
| (f(a), σ(a)) | Maximal R0 | Infections | Average Isolated | Maximum Isolated | Positive Tests/day |
| Li et al. | |||||
| Kucirka | 1.6 | 472 | 87 | 152 | 7 |
| Li et al. | |||||
| step-function | 2.25 | 465 | 93 | 155 | 8 |
| Park et al. | |||||
| Kucirka | 1.4 | 447 | 87 | 139 | 7 |
| Park et al. | |||||
| step-function | 1.8 | 456 | 99 | 156 | 8 |
Table 2 reports results for testing once every three days. The worst case scenario combining early transmission with Kucirka et al. [23] sensitivity can now contain outbreaks for any reproductive number lower than 1.75, while the optimistic scenario combining late transmission with step-function sensitivity could contain outbreaks with R0 as large as 4.8. The intermediate scenarios can keep infections below 5% of the population for reproductive numbers as large as 2.3-2.65. Of course, compared to weekly screening, the number of students isolated increases greatly due to the inevitable increase in false positives associated with more frequent testing. Testing students every three days is thus more robust than weekly screening in that the range of reproductive numbers for which infections can be kept below 5% is larger for all scenarios. Such improved performance comes at the expense of isolating many more students over the semester, in addition to the cost of the increased number of tests required.
Table 2.
Testing every three days
| Scenario | |||||
|---|---|---|---|---|---|
| (f(a), σ(a)) | Maximal R0 | Infections | Average Isolated | Maximum Isolated | Positive Tests/day |
| Li et al. | |||||
| Kucirka | 2.3 | 474 | 143 | 207 | 11 |
| Li et al. | |||||
| step-function | 4.8 | 491 | 150 | 206 | 12 |
| Park et al. | |||||
| Kucirka | 1.75 | 459 | 143 | 194 | 11 |
| Park et al. | |||||
| step-function | 2.65 | 499 | 153 | 197 | 12 |
Results when testing every 3 days replaces the weekly testing in the scenarios of Table 1
These examples illustrate how, other things being equal, more frequent screening enables adequate infection control to be achieved over wider ranges of values of R0. The examples also indicate that it is more difficult to contain scenarios where more transmission occurs earlier after infection (as with the Park et al. [28] generation time distribution) rather than later (as with Li et al. [25]). Another factor that can make infection control more difficult is the rate of imported exposures. Both Tables 1 and 2 presumed a single daily imported exposure over the modeled outbreaks; increasing this rate can make matters much worse. For example, for the Li et al. [25]/ Kucirka et al. [23] scenario when testing every 3 days shown in the first row of Table 2, if the rate of imported exposures were to increase from 1 to 2 out of 10000 students, the maximal R0 for which infections could be kept below 500 would decrease from 2.3 to 1.8. Another factor of key importance is the delay from testing until isolation for those receiving a positive test result. For example, again in the example of the first row of Table 2, if the delay from testing to isolation increased from 24 to 48 hours, the maximal R0 at which infections could be kept below 500 would drop from 2.3 to 1.9, and adding one more day to increase the delay to 72 hours would further reduce the maximal controllable R0 to 1.65. This shows that two additional days of post-test delay would render testing once every three days no more effective than weekly testing with one day of delay.
Discussion
With much of the world only now emerging from COVID-19 lockdowns, educational institutions are struggling with a fundamental question: absent a vaccine against SARS-CoV-2 or an effective treatment for COVID-19, is it safe to bring residential students back to campus? Presuming infections can enter the student population, and recognizing that many if not most such infections will be asymptomatic, the ability to detect and isolate infections as they occur is crucial to prevent large outbreaks among students on campus and ignited by students off campus. Testing itself is not a panacea; it is the isolation of infectious students that prevents transmission, and should isolation not follow the detection of infected students, repeat screening would be relegated to producing descriptive outbreak statistics rather than actively stopping outbreaks from happening. This article has shown how repeat testing interrupts transmission via the isolation of infectious students, and analyzed numerous transmission scenarios.
We hope that this model and its web-based implementation are useful in helping college officials assess and anticipate quantitative influences of key factors that affect the performance of repeat screening programs. In particular, with substantial uncertainty surrounding multiple model inputs, it is prudent to explore a range of plausible scenarios, and it quickly becomes clear that plausible scenarios exhibit a wide range of outcomes from well controlled to badly out of control. While uncertainty and imprecise knowledge of inputs to our model preclude precise projections of future results, we can draw insights from the modeling that can help inform planning and implementation. For example, delay from testing until isolation emerges as a key target for control as we see how much each day of delay is expected to degrade the infection control benefits that high-frequency repeat testing can bring.
This analysis suggests that administrators must proceed cautiously and with open eyes when designing residential college screening programs, for while repeat testing for SARS-CoV-2 infection can be a powerful tool for preventing infections and preserving public health in the residential college setting, it is not guaranteed to succeed. Even if students are tested once every three days, there are plausible transmission scenarios where the model projection has 5% or more of a student population becoming infected over the course of an abbreviated 80 day semester. Unlike engineering systems that are built conservatively to withstand multiple failures, the repeat testing system is necessarily fragile in that to succeed, all of the system components must work. Students must comply with infection control, social distancing, test scheduling and (if testing positive) isolation requirements for the repeat testing system to work effectively. The tests themselves must perform at or above expectation in terms of their ability to detect infected students. Isolation delay, including laboratory turnaround time, must be minimized as extra delay markedly degrades the ability of repeated testing to control outbreaks. While many of the factors involved are beyond control, college administrators should be able to implement systems that minimize isolation delay, both by contracting with testing laboratories to guarantee acceptable test turnaround times and by putting in place efficient communications and support mechanisms so that students who do test positive can be isolated as quickly as possible. Colleges can also effectively inform students what behaviors will be expected of them on campus while also clearly communicating the consequences of failing to comply with the adopted behavioral code. Finally, if a repeat testing and isolation program begins to lose control and infections are detected at higher rates than anticipated, colleges can shut down and confine students to quarters while ensuring that all those in need of medical attention receive it. The whole point of repeat screening is to avoid such an outcome, but nonetheless university administrators must be ready to close their residential colleges should repeat testing fail to contain the spread of SARS-CoV-2 on campus.
Footnotes
A university screening model by Paltiel, Zheng and Walensky appeared while the present article was in review; see https://jamanetwork.com/journals/jamanetworkopen/fullarticle/2768923
Isolation would typically last only two weeks, but incorporating this would modify our results only slightly while complicating the analysis; see [17] for details.
This independence assumption could be generalized, and in fact the only probabilities the current model would require are of the form Pr{Rt = Rt+τ = ⋯ = Rt+kτ = 0} where Rt is the result (1 for positive and 0 for negative) of a test at time t after infection for a given person.
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Change history
5/25/2021
A Correction to this paper has been published: 10.1007/s10729-021-09568-y
Contributor Information
Joseph T. Chang, Email: joseph.chang@yale.edu
Forrest W. Crawford, Email: forrest.crawford@yale.edu
Edward H. Kaplan, Email: edward.kaplan@yale.edu
References
- 1.Anderson N, Svriuga S (2020) Colleges push viral testing, other ideas for reopening in fall. But some worry about deepening the health crisis. Washington Post https://tinyurl.com/y8r2o6sy (accessed June 13, 2020)
- 2.Anderson RM, May RM (1991) Infectious diseases of humans: Dynamics and control. Oxford University Press, Oxford
- 3.Bauer-Wolf J (2019) Mumps outbreak at Temple University. Inside Higher-Ed https://tinyurl.com/yaha2vz8 (accessed June 13, 2020)
- 4.Britton T, Tomba GS (2019) Estimation in emerging epidemics: Biases and remedies. J R Soc Interface 16:20180670. 10.1098/rsif.2018.0670 (accessed April 15, 2020) [DOI] [PMC free article] [PubMed]
- 5.Castle S (2020) Cambridge University will hold its lectures online next year. https://tinyurl.com/yax8k4ou (accessed June 3, 2020)
- 6.CDC (2020a) COVID-19 Testing Overview. United States Centers for Disease Control and Prevention, https://www.cdc.gov/coronavirus/2019-ncov/symptoms-testing/testing.html (accessed September 22, 2020)
- 7.CDC (2020b) COVID-19 Pandemic Planning Scenarios. United States Centers for Disease Control and Prevention, https://www.cdc.gov/coronavirus/2019-ncov/hcp/planning-scenarios.html (accessed June 20, 2020)
- 8.Champredon D, Dushoff J (2015) Intrinsic and realized generation intervals in infectious-disease transmission. Proc R Soc B 282:20152026. 10.1098/rspb.2015.2026 (accessed May 28, 2020) [DOI] [PMC free article] [PubMed]
- 9.Costill D, Muoio D (2015) College campus outbreaks require timely, effective public health measures. Infectious Disease News https://tinyurl.com/y79ggfan (accessed June 13, 2020)
- 10.Daniels M (2020) Why failing to reopen Purdue University this fall would be an unacceptable breach of duty. Washington Post https://tinyurl.com/yblsjth3 (accessed June 6, 2020)
- 11.Diep F, Zahneis M (2020) Welcome to the socially distanced campus. Chronicle of Higher Education https://www.chronicle.com/article/Welcome-to-the-Socially/248850 (accessed June 6, 2020)
- 12.Ellis L (2020) At One Flagship, Coronavirus Cases Surge Even in the Midst of Summer. Chronicle of Higher Education https://www.chronicle.com/article/At-One-Flagship-Coronavirus/249054 (accessed July 3, 2020)
- 13.Ferguson N, Laydon D, Gemma N-G et al (2020) Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. Imperial College COVID-19 Response Team, https://tinyurl.com/tcdy42y (accessed April 11, 2020)
- 14.Fields A (2020) At least 80 UW students in fraternities test positive for coronavirus, a foreboding sign for college reopenings. Seattle Times https://tinyurl.com/y77epskr (accessed July 3, 2020)
- 15.Hanson KE, Caliendo AM, Arias CA, Englund JA, Lee MJ, Loe M, Patel R, El Alayli, Kalot MA, Falck-Ytter Y, Lavergne V, Morgan RL, Murad MH, Sultan S, Bhimraj A, Mustafa RA (2020) Infectious Diseases Society of America Guidelines on the Diagnosis of COVID-19. http://www.idsociety.org/COVID19guidelines/dx (accessed June 3, 2020) [DOI] [PMC free article] [PubMed]
- 16.Jenkins JI (2020) We’re reopening Notre Dame. It’s worth the risk. New York Times https://tinyurl.com/y7vmz3mp (accessed June 3, 2020)
- 17.Kaplan EH (2020a) Containing 2019-nCoV (Wuhan) coronavirus. Health Care Manag Sci 10.1007/s10729-020-09504-6 (accessed May 9, 2020) [DOI] [PMC free article] [PubMed]
- 18.Kaplan EH (2020b) COVID-19 Scratch Models to Support Local Decisions. Manufacturing and Services Operations Management 10.1287/msom.2020.0891 (accessed July 8, 2020)
- 19.Kaplan EH (1991) Mean-max bounds for worst-case endemic mixing models. Math Biosci 105(1):97–109. https://www.sciencedirect.com/science/article/abs/pii/002555649190050S [DOI] [PubMed]
- 20.Kaplan EH, Forman H (2020) Logistics of Aggressive Community Screening for Coronavirus 2019. JAMA Health Forum https://jamanetwork.com/channels/health-forum/fullarticle/2765693 (accessed September 22, 2020) [DOI] [PubMed]
- 21.Kaplan EH, Lee YS (1990) How bad can it get? bounding worst case endemic heterogenous mixing models of HIV/AIDS. Math Biosci 99(2):157–180. https://www.sciencedirect.com/science/article/abs/pii/002555649090002G (accessed September 22, 2020) [DOI] [PubMed]
- 22.Kissler S, Tedijanto C, Lipsitch M, Grad YH (2020) Social distancing strategies for curbing the COVID-19 epidemic. Harvard School of Public Health, March 2020 http://nrs.harvard.edu/urn-3:HUL.InstRepos:42638988 (accessed April 11, 2020)
- 23.Kucirka LM, Lauer SA, Laeyendecker O, Boon D, Lessler J (2020) Variation in false-negative rate of reverse transcriptase polymerase chain reaction–based SARS-CoV-2 tests by time since exposure. Annals of Internal Medicine 10.7326/M20-1495 (accessed June 13, 2020) [DOI] [PMC free article] [PubMed]
- 24.Laframboise K (2020) McGill University looks to take fall semester online amid coronavirus pandemic. https://tinyurl.com/ybkae6w3 (accessed June 2, 2020)
- 25.Li Q, Guan X, Wu P et al (2020b) Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N Engl J Med. 10.1056/NEJMoa2001316 (accessed April 15, 2020) [DOI] [PMC free article] [PubMed]
- 26.Mangan K (2019) Colleges face swine-flu challenge as number of sick students surges. Chronicle of Higher Education https://tinyurl.com/ybprqdqw (accessed June 13, 2020)
- 27.Morozova O, Li ZR, Crawford FW (2020) A model for COVID-19 transmission in Connecticut. https://tinyurl.com/ydyh623m (accessed June 13, 2020)
- 28.Park SW, Bolker BM, Champredon D, Earn DJD, Li M, Weitz JS, Grenfell BT, Dushoff J (2020) Reconciling early-outbreak estimates of the basic reproductive number and its uncertainty: framework and applications to the novel coronavirus (SARS-CoV-2) outbreak. J R Soc Interface 17:20200144. 10.1098/rsif.2020.0144 (accessed September 22, 2020) [DOI] [PMC free article] [PubMed]
- 29.Peto J, Carpenter J, Smith GD, Duffy S, Houlston R, Hunter DJ, McPherson K, Pearce N, Romer P, Sasieni P, Turnbull C (2020) Weekly COVID-19 testing with household quarantine and contact tracing is feasible and would probably end the epidemic. R Soc Open Sci 7:200915. 10.1098/rsos.200915 (accessed September 22, 2020) [DOI] [PMC free article] [PubMed]
- 30.Steinberg L. (2020) Expecting students to play it safe if colleges reopen is a fantasy. New York Times, https://www.nytimes.com/2020/06/15/opinion/coronavirus-college-safe.html (accessed June 29, 2020)
- 31.Taipale J, Romer P, Linnarsson S (2020) Population-scale testing can suppress the spread of COVID-19. 10.1101/2020.04.27.20078329v2.full.pdf (accessed September 22, 2020)
- 32.UCSD (2020) Return to Learn Program. University of California San Diego, https://coronavirus.ucsd.edu/return-to-learn/index.html (accessed Jun 13, 2020)
- 33.Wallinga J, Lipsitch M (2007) How generation intervals shape the relationship between growth rates and reproductive numbers. Proc R Soc B 274:599–604. 10.1098/rspb.2006.3754 (accessed May 29, 2020) [DOI] [PMC free article] [PubMed]
- 34.Watts DJ, Strogatz SH (1998) Collective dynamics of ‘small-world’ networks. Nature 393:440–442. 10.1038/30918 (accessed September 22, 2020) [DOI] [PubMed]
- 35.Weeden KA, Cornwell B (2020) The small-world network of college classes: implications for epidemic spread on a university campus. Sociol Sci 7:222–24. https://sociologicalscience.com/articles-v7-9-222/ (accessed September 22, 2020)
- 36.Zhang S, Diao MY, Yu W, Pei L, Lin Z, Che D (2020) Estimation of the reproductive number of novel coronavirus (COVID-19) and the probable outbreak size on the Diamond Princess cruise ship: A data-driven analysis. Int J Infect Diseases 93:201–204. https://tinyurl.com/ybt5vmux (accessed July 13, 2020) [DOI] [PMC free article] [PubMed]