Optimization and numerical evaluation of multi-compartment diffusion MRI using the spherical mean technique for practical multiple sclerosis imaging

Abstract

Background

The multi-compartment diffusion MRI using the spherical mean technique (SMT) has been suggested to enhance the pathological specificity to tissue injury in multiple sclerosis (MS) imaging, but its accuracy and precision have not been comprehensively evaluated.

Methods

A Cramer-Rao Lower Bound method was used to optimize an SMT protocol for MS imaging. Finite difference computer simulations of spins in packed cylinders were then performed to evaluate the influences of five realistic pathological features in MS lesions: axon diameter, axon density, free water fraction, axonal crossing, dispersion, and undulation.

Results

SMT derived metrics can be biased by some confounds of pathological variations, such as axon size and free water fraction. However, SMT in general provides valuable information to characterize pathological features in MS lesions with a clinically feasible protocol.

Conclusion

SMT may be used as a practical MS imaging method and should be further improved in clinical MS imaging.

1. INTRODUCTION

Neurodegeneration featured by irreversible axonal loss is a prominent feature of multiple sclerosis (MS) and a key determinant of patient disability [1]. Despite its cardinal biological importance, treatments preventing axonal injury or fostering its repair once it has occurred are still lacking [2]. A significant obstacle to the development of those therapies is the shortage of an in vivo imaging biomarker that can be used as a measure of outcome during proof-of-concept clinical trials assessing neurodegeneration and repair in patients with MS. Axial diffusivity (AD) derived from diffusion tensor imaging (DTI) has been used as a biometric of axonal integrity in several clinical studies [3]. While sensitive to neurodegenerative processes, the pathological specificity of AD remains limited due to its inability to discriminate signal from other pathologies like demyelination, edema, inflammation, and end stage cavitation [4,5], some or all of which may co-exist in MS lesional and non-lesional tissue [6,7].

To increase specificity, more sophisticated multi-compartment models relating acquired signal to physiopathology have been developed in MS imaging. These models generally include parameter estimation of axonal signal fraction which, though confounded by proton density and T1 and T2 relaxation effects, can be used as a surrogate to detect changes in axonal volume fraction; for this reason, we term the parameter apparent volume fraction. White matter tract integrity (WMTI) [8] uses kurtosis metrics to give useful estimates of intra- and extra-axonal diffusivities and apparent axonal volume fraction in parallel fibers and has shown interesting results in MS [9], but may fail in regions with crossing or dispersing fibers. Diffusion basis spectrum imaging (DBSI) [10] has been reported to resolve crossing fibers and fit multiple isotropic compartments (e.g., free water and restricted cells) simultaneously, but it has not been widely studied across different institutes [11]. The neurite orientation dispersion and density imaging (NODDI) [12] is a widely used method that may be useful for gleaning apparent isotropic and axonal volume fractions; however, by fixing diffusivity it may bias parameter estimates of apparent volume fraction where the diffusivity value is poorly assumed a priori. The spherical mean technique (SMT) [13] considers white matter (WM) as a two-compartment (intra- and extra-axonal) tissue and provides signal fraction and diffusion metrics per axon without confounds from fiber direction, crossing, or dispersion. This is particularly important for MS imaging because many WM voxels contain such complex fiber configurations, and fiber arrangements likely vary in MS lesions [14,15]. Fiber orientation-independent diffusion metrics could potentially provide more accurate estimates of axon integrity. For this reason, SMT has been successfully applied to characterize the brain [16] and spinal cord [17] of MS patients.

However, there remains a lack of validation of SMT in complex WM tissues. Although histology has been considered as a gold-standard for the validation of many MRI methods, there are experimental challenges that impede histological validation of MRI in brain tissue [18]. For example, chemical changes in the tissue during fixation can change the T1, T2, and diffusivity values, undermining postmortem tissue as a model of an in vivo state. Dehydration during the fixation processes can lead to structural changes in e.g. axon diameter and density as well as fractions of edema-induced free water. Additionally, the 3D phenomena of fiber crossings, dispersion, and undulation can be difficult to reconstruct accurately from 2D histology. Finally, it is difficult to control for the signal-to-noise ratio (SNR) to isolate the effects of noise on accuracy and precision in the final parameter maps.

Given these challenges, to assess a practical MS imaging method in lieu of histology, we performed numerical evaluation to isolate the effects of key histopathological changes which may occur in MS lesions: (i) free water induced by inflammation, (ii) fiber crossing, (iii) fiber dispersion which is reported to be altered in MS lesions [14,19], and (iv) fiber undulation [20]. By performing these assessments via simulation, we are able to selectively evaluate each phenomenon’s impact on the SMT output independent of other factors and with practical noise levels. We perform this analysis in three key steps: (i) to optimize an SMT protocol to maximize precision with a clinically feasible scan time, (ii) to perform numerical simulations in modeled tissues with realistic pathological features (e.g. with free water and fiber crossings) to synthesize diffusion MRI signals, and (iii) to fit the SMT model to synthesized signals with Rician noise at a clinically applicable SNR to evaluate the accuracy and precision of the SMT method. Although these simulations cannot replace histology as a gold standard, and more sophisticated histology methods [21,22] to overcome these challenges in future work may serve as such a standard, this study can give a better understanding of how the SMT fitting performs with varying geometric configurations which model common histopathological changes in MS lesions.

2. METHODS

2.1. Optimization

SMT assumes diffusion-weighted signals arise from two compartments in white matter as $\overline{S}=v_{ax}\overline{S_{ax}}+\left(1-v_{ax}\right)\overline{S_{ex}}$, where ν_ax is the apparent axonal volume fraction, $\overline{S_{ax}}=S_0\left[\sqrt{\pi }\text{erf}\left(\sqrt{b{D}_{ax}}\right)\right]/\left[2\sqrt{b{D}_{ax}}\right]$ and $\overline{S_{ex}}=S_0\text{exp}\left(-b{D}_{\perp ,ex}\right)\left[\sqrt{\pi }\text{erf}\left(\sqrt{b\left(D_{ax}-D_{\perp ,ex}\right)}\right)\right]/\left[2\sqrt{b\left(D_{ax}-D_{\perp ,ex}\right)}\right]$ are the mean intra- and extra-axonal diffusion signals per volume after taking the spherical average over all gradient directions, respectively [13]. SMT assumes the intra- and extra-axonal parallel diffusivities are the same as D_ax. If the long diffusion limit (i.e., tortuosity limit [23]) holds, the intra- and extra-axonal axial diffusivities are approximated as D_x and D_⊥,in ≈ 0, D_⊥,ex = (1 − ν_ax)D_ax, respectively. Therefore, two key parameters can be fit from SMT: ν_ax and D_ax. The data acquisition protocols used in previous SMT studies were not optimized so their data precision efficiency may be further improved. In this work, we first optimize an SMT protocol for clinical MS imaging. The appendix to this manuscript details this optimization. To summarize,

1. The optimization domain was b ∈ [0 10,000] s/mm² discretized in 10 s/mm² increments. These were split into 10 shells of 10 directions each to achieve 100 acquisitions – closely matching the clinically feasible scan time of the widely used NODDI protocol [12]. For simplicity, resulting shells within 100 s/mm² were averaged into one.

2. Because our previous studies suggest only ν_ax is a sensitive indicator of axon integrity and D_ax lacks contrast for sufficient CNR [16], the optimization objective is to maximize the precision of ν_ax estimates. We adopt a Cramer-Rao lower bound (CRLB) approach [24,25] to minimize the theoretical lower limit on parameter variance (i.e., the CRLB) as a surrogate for the true variance, which is much more computationally cumbersome to determine.

3. Four types of tissues are included in the optimization: normal white matter in healthy subjects (NWM), normal appearing white matter in MS patients (NAWM), T2-hyperintense lesions (T2-ls), and T1-hypointense chronic black-hole lesions (cBH). With clinical MS imaging as the targeted application, we use our previously published SMT results in MS patients [16] as the reference SMT values for these tissues (Table 1). The optimization calculates the CRLB for all tissues with a given protocol and chooses the protocol with the lowest variance of the least precise (i.e., worst-case) tissue [26]. Varying dispersion arrangements were also considered and, similar to varying the ν_ax and D_ax parameters, the least precise arrangement was used.

4. To validate the optimized SMT protocol, we compare it with other previously reported acquisition protocols shown in Table 2, all of which have approximately the same scan time.

Table 1.

Summarized results from previous SMT studies in MS [16] to inform optimization.

Tissue	vax [%]	Dax [μm2/ms]
NWM*	60.7	1.9
NAWM**	45.0	1.8
T2-lesion	36.5	1.7
cBH	24.1	1.7

^*Defined by ROIs in the internal capsula

^**Determined from ROIs contralateral to T2-lesions

Table 2.

Summarized SMT acquisition protocols tested for precision in optimization and simulation

Protocol	b(Ndirs) [s/mm2]
A	430(10)	990(10)	4230(80)
B	0(10)	530(10)	3790(80)
C	0(10)	711(32)	2855(64)
D	0(10)	1000(45)	2500(45)
E	0(4)	1000(32)	2000(32)	3000(32)

2.2. Computer simulations

A finite difference simulation method [27] was used and its specific implementation in simulating diffusion-weighted signals in nerves was reported in [28]. The cross-section of each fiber bundle was discretized as a 500×500 matrix with a spatial step dx = dy = 0.2 μm. The temporal step dt = 3 μs. The revised periodic boundary condition was used to count for water molecules diffusing in and out of the computation domain in all directions [26]. WM tissues were modeled consisting of one or more axonal fiber bundles with both intra- and extra-axonal spaces. For simplicity, each fiber bundle is modeled as parallel cylinders with a volume fraction of axons (AxV) and a distribution of axon diameters (AxD) with a mean value $(\overline{\text{AxD}})$. The intra-axonal diffusivity was 2.25 μm²/ms in the simulations, as found out in a previous brain WM study in vivo [29]. The extra-axonal diffusivity was 2 μm²/ms [28], consistent with recent findings that extra-axonal diffusivity is lower than that of intra-axonal space [30]. The diffusion-weighted experimental parameters were the same as those in the SMT imaging in MS patients [16]: echo time (TE) = 74 ms, repetition time (TR) = 13.5 seconds, δ = 21 ms, Δ = 31.8 ms, and b values varied in each acquisition protocol (see Table 2). Gradient directions were obtained using the approach suggested in [31].

During the progression of MS lesions, many tissue microstructure parameters may change, including the size, content, arrangement, and orientation of the fiber bundles. Therefore, six simulations were performed to mimic the underlying pathological variations in MS and their influences on SMT measurements. Only one histopathologic feature varies in each simulation so that we can evaluate the influences of each on the accuracy and precision of the SMT method to characterize the histopathological information in MS. Specifically,

1. Axon diameter: Although most axon diameters in the central nervous system are small (1–2 μm), there are reports of variations in axon diameters of 1–5 μm. We therefore simulated five different axon diameter distributions with $\overline{\text{AxD}}\in \left\{1.5,2.6,3.6,4.5,5.5\mu \text{m}\right\}$, all of which have a similar AxV of 69 – 72%. Note that SMT assumes the intra-axonal radial diffusivity is zero, so this simulation challenges this assumption, especially in larger axons.

2. Axon density: One clinically relevant histopathologic feature is the axon density, which is an indicator of axon integrity and a biomarker of tissue injury. We simulated seven different axonal volume fractions AxV∈ {10.6, 22.0, 31.6, 41.3, 51.7, 59.2, 69.4 %}, all of which have a similar $\overline{\text{AxD}}~1.5\mu \text{m}$, a typical mean axon diameter in the central nervous system.

3. Fractions of free water: MS is an inflammatory disease, wherein the free water content varies as a function of the degree of inflammation. We simulated five different signal fractions arising from free water ν_free ∈ {0, 20, 40, 60, 80 %}, all of which have $\overline{\text{AxD}}\approx 1.5\mu \text{m}$ and the relative intra-axonal volume fraction without free water is the same at 69.4%.

4. Axonal bundle crossing: Axonal fiber crossing is a well-known problem in the field of diffusion MRI. We simulated two crossing axonal bundles with an angle θ ∈ {0, 15, 30, 45, 60, 75, 90 °}, all of which have $\overline{\text{AxD}}\approx 1.5\mu \text{m}$ and the relative intra-axonal volume fraction of 69.4%.

5. Axonal bundle dispersion: It has been reported that axon orientations may disperse along a main direction [12,14]. We follow Zhang et al. [12] to assume the dispersed axon orientations obey a Watson distribution with ODI ∈ {1, 0.84, 0.50, 0.16, 0.04}, all of which have $\overline{\text{AxD}}\approx 1.5\mu \text{m}$ and relative intra-axonal volume fraction 69.4%.

6. Axonal bundle undulation: In addition to variations in the arrangement of multiple axonal fiber bundles, each fiber bundle may display curving or undulation [20]. We follow Nilsson et al. to assume a sinusoidal undulation with an axonal undulation length L = 12 μm, an undulation amplitude A ∈ {0, 2, 4, 6, 8 μm}, and a calculated tortuosity factor λ that can be determined from L and A using a complete elliptical integral of the second kind [20].

2.3. Data analysis

Random Rician noise was added to each set of noise-free simulated diffusion signals with SNR = 20, and then the noisy signals were analyzed using the publicly available SMT code (https://github.com/ekaden/smt). This process was repeated 1000 times. The fitting accuracy was evaluated using the absolute differences between the mean fits and the ground truth values, and fitting precision was evaluated using the coefficient of variance (COV), i.e., the standard deviation divided by the mean of 1000 fitted SMT metrics. Violin plots were used to visualize the results. Pearson correlation was used to evaluate the correlation of SMT derived apparent axon volume fractions with the ground-truth values.

3. RESULTS

3.1. Optimized SMT

Table 2 describes five possible SMT protocols for MS imaging: both A and B are optimized protocols, with A having 10 free shells and B having 9 free shells and 1 fixed at b = 0 mm/s²; C denotes the NODDI optimized protocol [12]; D is the protocol used in our previous MS studies [16]; and E is the original SMT protocol from Kaden et al [13] with reduced acquisitions to match the total scan time. Protocol A was chosen as our optimized SMT protocol because it shows higher precision in NAWM and T2-lesions, which can be more challenging to characterize than cBH; this protocol was also used to generate the simulation results shown below. Precision efficiency [26] – defined as $1/\sqrt{N_{\mathit{\text{dir}}}*\mathit{\text{CRLB}}/v_{\text{ax}}^2}$ to be independent of N_dir – was increased by 30% of our previously employed protocol [16] (Table 2, protocol D). Figure 1 depicts this metric for each protocol and each tissue of interest. In general we found that an axonal arrangement of many fibers with ODI = 1 had the least precision, and we therefore optimized over this. Of the four tissues in consideration, chronic black hole lesions (the smallest ν_ax) were generally the least precise and therefore the determining tissue for the overall optimization, with normal white matter (the largest ν_ax) also having low precision. We note that while we strictly valued precision in our choice to use Protocol A for simulation, a b = 0 mm/s² acquisition is necessary to take practical imaging considerations such as motion and distortion correction into account. Either implementing Protocol B or interleaving additional b = 0 mm/s² acquisitions (each costing scan time of one TR) into Protocol A would be advisable for in vivo scanning.

Figure 1.

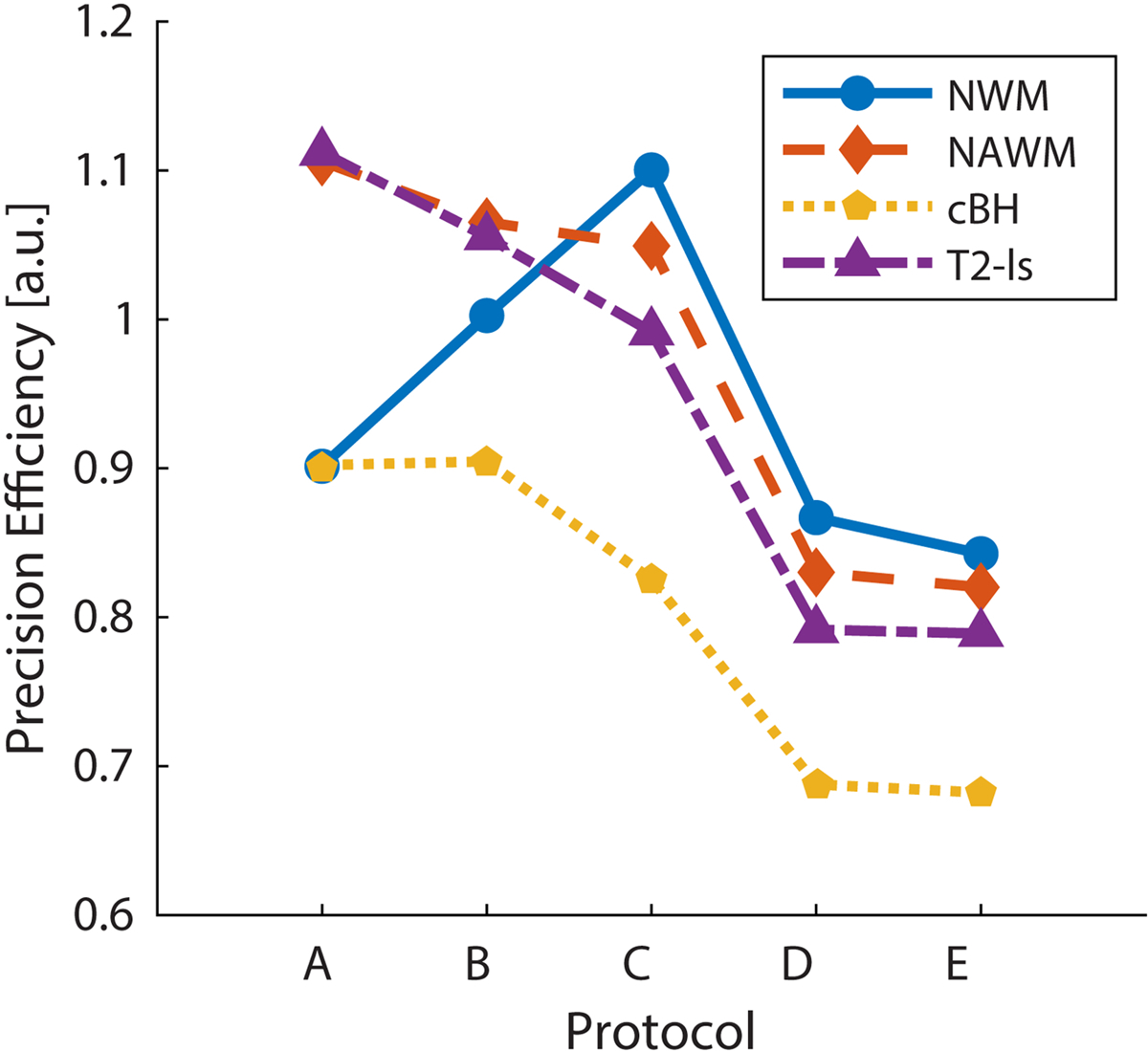
Comparison of the ν_ax precision efficiency of the SMT acquisition protocols for four types of tissues. The optimized protocols show higher precision per b-vector than the compared protocols for the highest variance tissue (cBH).

3.2. Influence of axon diameter

Figure 2 shows the influence of AxD distribution on SMT fitted metrics using Protocol A. For a physiologically relevant range of $\overline{\text{AxD}}$, SMT provides accurate fits of ν_ax from 2.6 to 4.5 μm (differences < 8% of the ground truth) but overestimates ν_ax by 16% of the true value for small $\overline{\text{AxD}}(1.5\mu \text{m})$ while underestimating ν_ax by −15% for large $\overline{\text{AxD}}(5.5\mu \text{m})$. Presumably, this is because at small mean AxD, extra-axonal diffusivity in some regions is highly restricted and close to zero. SMT uses zero transverse diffusion D_⊥ as a marker of thin axons, so it could misidentify some extra-axonal space as axonal spaces and hence overestimate ν_ax. Similarly, when AxD is very large, some intra-axonal D_⊥ is not zero so that the SMT fitting can misidentify parts of these large axons as extra-axonal space. This suggests the accuracy of SMT is dependent on the axon diameter. For D_ax fittings, although the accuracy is good (differences < 11% of the ground truth), the COV’s are > 25% for all mean AxD values. This is consistent with previous reports of SMT imaging in MS patients that D_ax is not a reliable indicator of MS lesions due to variations much larger than the measured contrast [16].

Figure 2.

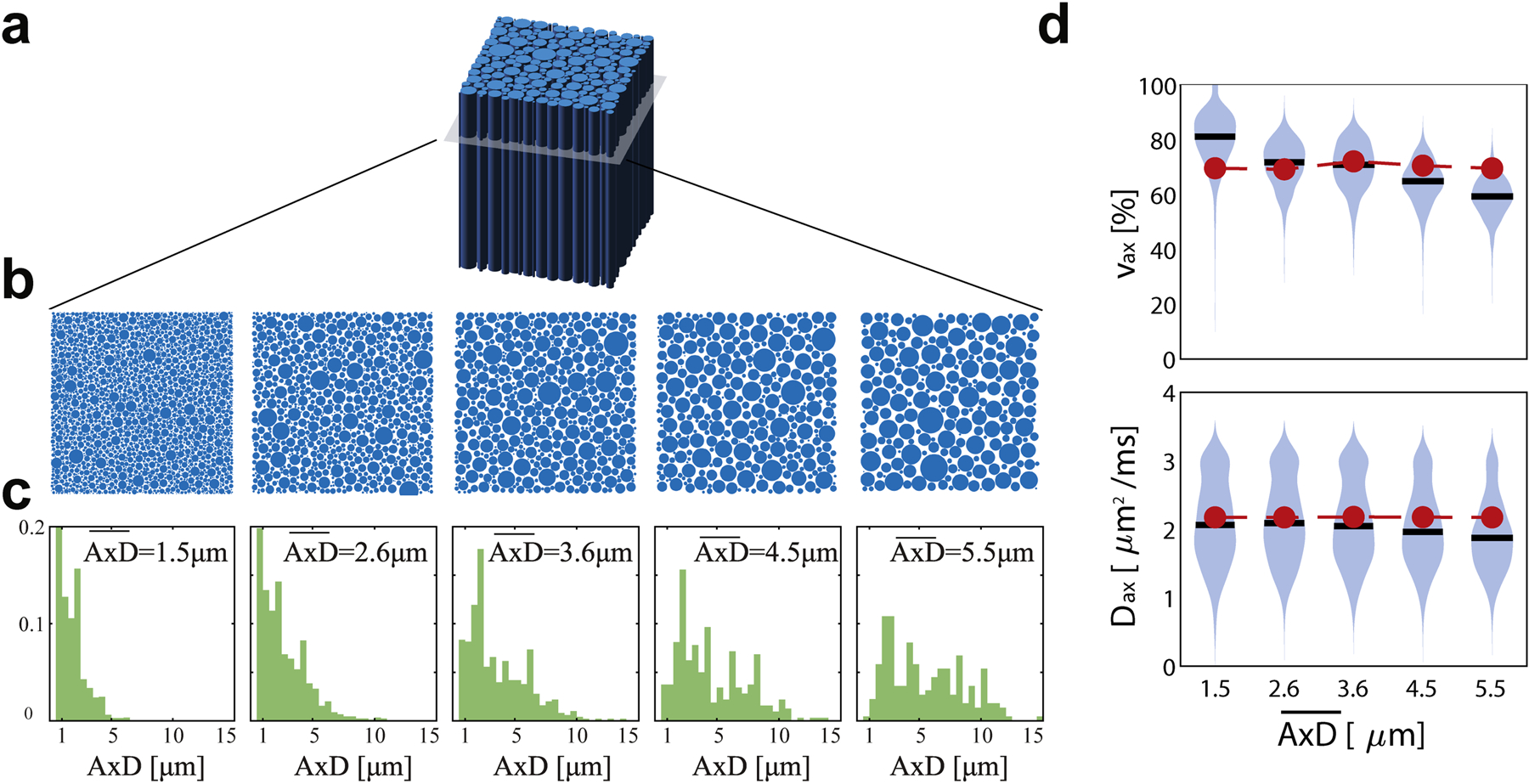
(a) Tissue was simulated as randomly packed parallel cylinders with varying axon diameter (AxD) distributions (b,c). Violin plots in (d) and (e) show estimations of ν_ax and D_ax with the mean values in black, distribution in blue, and ground truth in red.

3.3. Influence of axon volume fraction

Figure 3 describes the effect of AxV on the SMT parameters using Protocol A. ν_ax tends to have high precision (σ = 2 percentage points (pp)) for small values and lower precision (10 pp) for larger values. Correlation between estimated and true ν_ax is strong (Pearson r = 0.96, p < 0.01). Bias in ν_ax is most extreme for the AxV = 10.4 and 69.4% tissues, with differences of 5.1 and 12.6 pp (50% and 18% of the ground truths), respectively. The bias at low AxV mostly vanishes under Gaussian noise, suggesting that high SNR may be required for detecting changes in this regime. Similar to varying $\overline{\text{AxD}}$, D_ax estimations were generally accurate (bias = 16% for AxV = 10.4% and < 6% for all other AxV) but precision was poor (COV > 14%).

Figure 3.

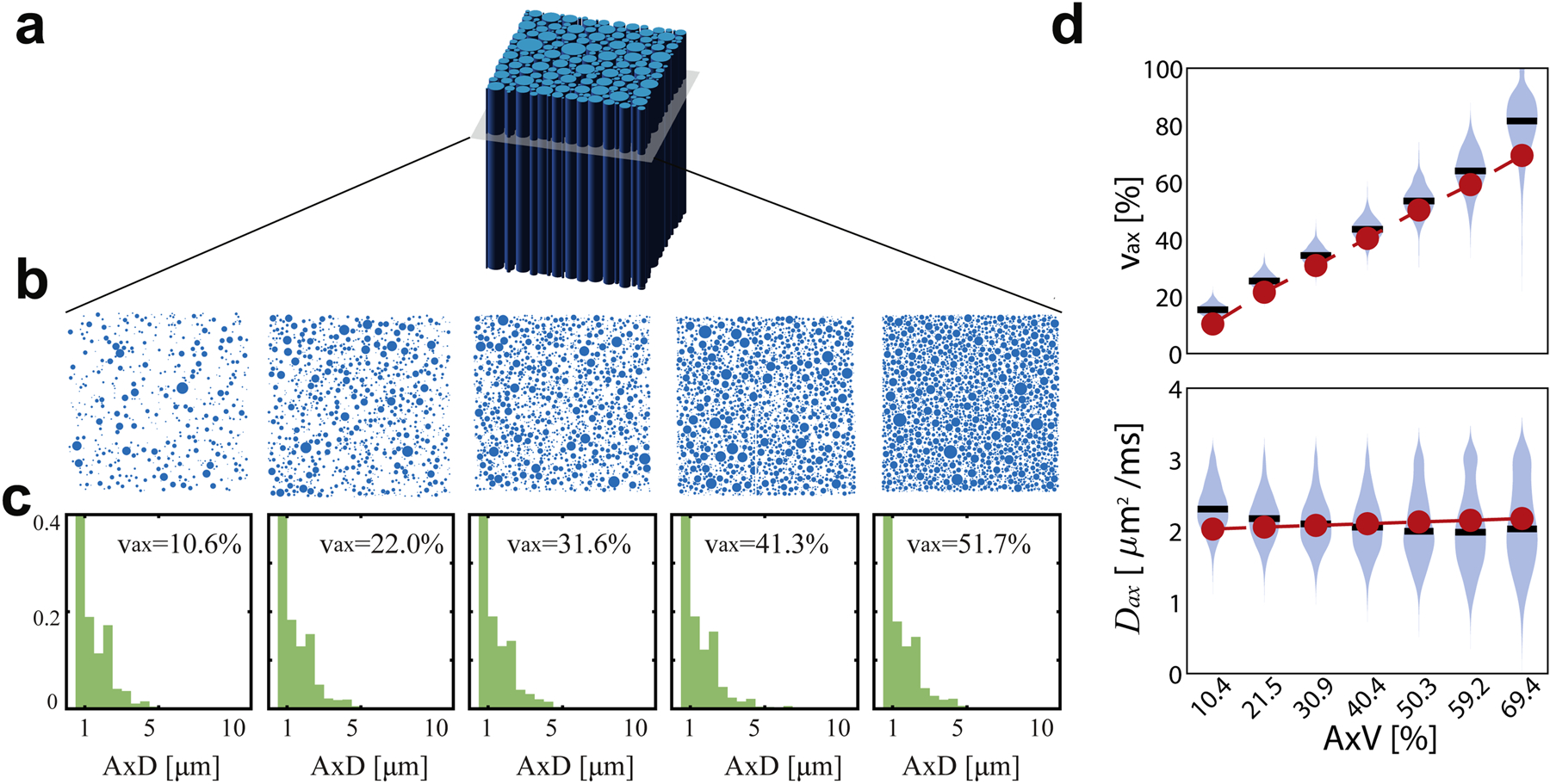
(a) Tissue was simulated as randomly packed parallel cylinders with varying axon volume fraction (AxV) (b,c). Violin plots in (d) and (e) show estimations of ν_ax and D_ax with the mean values in black, distribution in blue, and ground truth in red.

3.4. Influence of other histopathological features

Figure 4 shows a schematic of the geometries simulated and the fitted parameters under such conditions using Protocol A. The introduction of free water seems to provide the largest confound to estimates of ν_ax and D_ax, presumably due to the breakdown of the 2-compartment model when a third compartment is included with higher diffusivity. Biases are larger in this case, ranging from 11.6 to 16.8 pp in ν_ax and up to 0.37 μm²/ms in D_ax; interestingly, while deviating from the compartment-averaged ADC, mean D_ax is similar to the diffusivity of the added free water (3.07 μm²/ms).). Because of the low diffusion-weighted signal with high free water fraction, this tissue is particularly susceptible to Rician bias, which further increases the inaccuracy.

Figure 4.

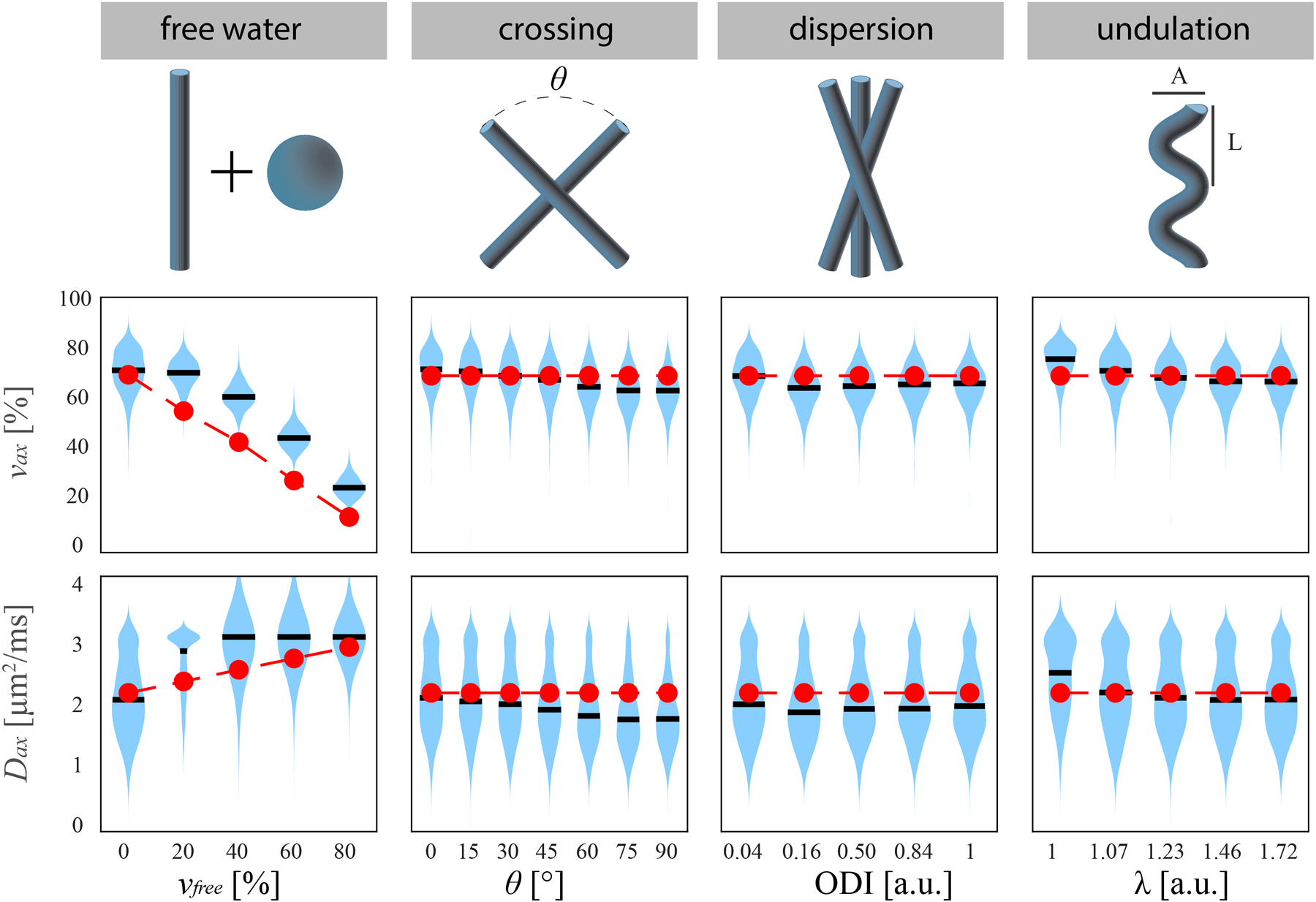
(top) Schematic of four neural geometries tested in simulation. (middle) ν_ax and (bottom) D_ax estimates from N=1000 trials each, with the mean values in black, distribution in blue, and ground truth in red.

Fiber crossing, axon dispersion, and undulation had no discernable effect on the precision and accuracy of ν_ax and D_ax. Comparing estimates to the single-direction case of AxV = 69.4% and AxD = 1.5 μm, no value of θ, ODI, or λ gives significantly different bias or COV than the single-direction case.

4. DISCUSSION

In this study, we use numerical simulations to compare SMT-derived metrics with known ground truth values to evaluate the accuracy and precision of SMT metrics. Different from histological validation, this approach is much easier to be carried out and, more importantly, the influences of individual histopathological features can be investigated separately. This assists a better interpretation of SMT metrics to characterize MS. A limitation of numerical validation is the simulated geometries used here as a simplified model of physiological tissue differ from in vivo structures. Cylinders representing axons have no wall thickness in our simulation, but myelination in vivo may differ between WM, NAWM, and lesions [32] and alter this geometry to affect diffusion results [33]. Axon diameter distributions were assumed to follow gamma distributions as reported by Horowitz et al. in a previous healthy human brain study [34], but the axon diameter distributions likely change in MS lesions. All of these assumptions may alter the extra-axonal signal contribution to affect ν_ax and D_ax estimation. Moreover, because SMT relies on the radial diffusivities to distinguish intra- and extra-axonal spaces, it can over- or under-estimate AxV with small or larger AxD, respectively. All of these suggested the limitation of SMT in MS imaging and may warrant future study with possibly improved modeling, as well as emphasizing the need for future histopathological validation studies to better understand how such in vivo effects influence SMT modeling.

In addition to axon diameters, this study introduces confounds to challenge the assumptions of the SMT signal model and evaluate its performance under more realistic situations. First, SMT assumes the extra-axonal diffusivity is a function of ν_ax and D_ax under the tortuosity limit [23]. While tortuosity models in general can handle differing intra- and extra-axonal diffusivities [35], SMT in particular assumes they are equal to improve precision; however, this is not necessarily true in reality. To allow for this limitation, the differing intra- and extra-axonal diffusivities in the simulations were chosen from previous reports [29] to mimic realistic tissues. Although the effect of this is not directly explored in this study, future studies to comprehensively evaluate the resulting bias may be useful. Additionally, the tortuosity assumption D_⊥,ex = (1 − ν_ax)D_ax breaks down with high fiber density, such that ν_ax may be overestimated in this regime (Figure 3). This assumption also does not capture dependence on packing arrangement [36,37], which may lead to further bias. While the implications of these biases on detection of lesions remain unknown, they may be mitigated due to the low axonal volume fraction in neurodegenerative lesions and high contrast relative to NWM and NAWM. Second, SMT assumes a two-compartment model but the free water induced by inflammation is usually modeled as a third compartment [10,12]. Despite the violation of the SMT assumptions, the two-compartment SMT model was still fit to the simulated data with free water in this study. This provides an opportunity to investigate the necessity to include more compartments in SMT. The results shown in Figure 3 and Figure 4 suggest that, despite some discrepancies in the estimation of ν_ax with free water, SMT-derived ν_ax can robustly characterize the variation of axon volume fractions with a broad range of histopathological features.

One limitation of the current study is that the differences between myelinated and unmyelinated axons are not considered in the computer simulations. Because myelin is invisible in diffusion MRI due to a short T₂ relaxation time, numerous previous simulation studies in diffusion MRI do not include myelin in the modeled tissues [20,27,38]. However, this assumption could be a disadvantage for SMT in MS imaging. For myelinated axons, myelin layers significantly restrict the water exchange between intra- and extra-axonal spaces. It is therefore plausible for the SMT model to assume two diffusion compartments (intra- and extra-axonal) without water exchange. However, demyelination is one of the characteristics of MS progression. The absence of myelin layers removes the barriers to exchange between intra- and extra-axonal compartments. Axon membranes are usually maintained in unmyelinated axons and they are the determinant of anisotropic water diffusion in nerves, indicating significant restriction to water diffusion [39]. It is likely that in late stages of a demyelinated axon, as the energy demand is no longer met and axons undergo degradation due to failure of transmembrane Na++/K+ pumps, the membrane permeability becomes high enough to break the SMT assumptions and lead to a bias in the estimation of SMT metrics. However, until this occurs, which may take several years, SMT may be considered a good indirect estimate of both myelinated and demyelinated axons. Future studies are required to evaluate the accuracy of SMT for imaging both myelinated and unmyelinated axons.

A main advantage of the SMT method is that, by theory, it is insensitive to axonal fiber orientations, which could improve the accuracy of the estimation of microstructure features. However, this advantage has not been validated to date. In the current study, we used computer simulations to confirm that SMT is immune to the fiber orientation with the presence of complex axonal fiber arrangements, such as crossing, dispersion, and undulation, all of which are usually seen in the central nervous system. Moreover, SMT uses off-the-shelf diffusion MRI sequence and is easy to be implemented in clinical imaging. This suggest SMT could be of a choice to characterize rotationally invariant axonal integrity in clinics.

5. CONCLUSIONS

SMT provides a clinically feasible in vivo probe which is sensitive to changes in neural tissue independent of fiber orientation but lacks validation in complex tissue structures. We provide numerical simulation results to (i) assess the accuracy and precision of SMT-derived parameters, (ii) demonstrate that SMT is insensitive to fiber orientation effects, and (iii) provide estimates of parameter bias induced by confounds such as inflammation. These results provide evidence that SMT may be used as a practical MS imaging method and should be further investigated in humans.

HIGHLIGHTS.

• An optimized SMT protocol was developed for clinical MS imaging

• The influences of realistic pathological features in MS lesions were investigated

• The accuracy and precision of SMT was comprehensively evaluated

• SMT provides valuable pathological information on axon integrity

6. Appendix

6.1. Optimization Design

To optimize over precision, we minimize the relative Cramer-Rao Lower Bound of ν_ax, which can be viewed as a surrogate for the CoV (coefficient of variation). This is calculated from the Fisher Information Matrix (FIM), defined as:

$$I_{ij}=-E\left(\frac{{\partial }^2\text{ln}p(x;\theta )}{\partial {\theta }_i\partial {\theta }_j}\right)$$

where p(x; θ) is the likelihood of a set of fitting parameters θ given a set of measurements x, and θ_i denotes the ith element of θ. To capture the heterogeneity of the individual acquisitions and to determine the expectation over a well-characterized probability distribution (namely, in this case, a Rician distribution), we consider the FIM of the direction-dependent acquisitions. For a set of acquisitions, this gives a likelihood function:

$$p(x;\theta )=\prod _i\frac{x_i}{{\sigma }^2}{I}_0\left(\frac{x_i{S}_i(\theta )}{{\sigma }^2}\right)e^{-\frac{x_i^2+S_i{(\theta )}^2}{2{\sigma }^2}}$$

Here S is the modeled noise-free signal (described below), I_n is the modified Bessel function of the first kind of order n, and i indexes the acquisition design parameters: b-value b and unit gradient direction g. Fixing the extra-axonal diffusivity to (1 − ν_ax)D_ax per the SMT model assumptions, the signal equation was used to calculate the relative CRLB on a superposition of fiber directions:

$$S_{b,g}=\frac{1}{N_f}\sum _{\mathit{\text{f}}\in \mathit{\text{F}}}{S}_0\left(v_{ax}{e}^{-b{\langle \mathit{\text{g}},\mathit{\text{f}}\rangle }^2{D}_{ax}}+\left(1-v_{ax}\right)e^{-b{\langle \mathit{\text{g}},\mathit{\text{f}}\rangle }^2{D}_{ax}}{e}^{-b{(1-\langle \mathit{\text{g}},\mathit{\text{f}}\rangle )}^2\left(1-v_{ax}\right)D_{ax}}\right)$$

where F is the length N_f set of equally-weighted fiber directions f. 10 shells with 10 uniformly spaced directions each were predetermined as inputs for g. The optimization argument comprised 10 b-values (one for each shell) constrained on the domain [0, 10,000] s/mm². The estimation parameters were θ = {S₀, ν_ax, D_ax}. The Fisher Information Matrix I(b; θ) was calculated from the signal as:

$$I{(b;\theta )}_{ij}=\frac{1}{{\sigma }^2}\sum _{b,g}^N\frac{\partial S_{b,g}}{{\theta }_i}\frac{\partial S_{b,g}}{{\theta }_j}R\left(S_{b,g},\sigma \right)$$

where N is the total number of measurements, θ_i ∈ θ, and R is a factor from expected value of the log-likelihood signal under a Rician distribution depending on “true” signal S and noise σ, evaluated as:

$$R(S,\sigma )=-\frac{S^2}{{\sigma }^2}+\frac{1}{{\sigma }^4}\underset{0}{\overset{\infty }{\int }}{x}^3\frac{I_1^2\left(\frac{xS}{{\sigma }^2}\right)}{I_0\left(\frac{xS}{{\sigma }^2}\right)}{e}^{-\frac{x^2+S^2}{2{\sigma }^2}}dx$$

The relative CRLB for parameter θ_i was then:

$$\mathit{\text{rCRLB}}\left(b;{\theta }_i\right)=I{(b;\theta )}_{ii}^{-1}/{\theta }_i^2$$

With k indexing the tissue type (e.g., NWM, NAWM), the rCRLB was calculated for each set of tissue parameters θ_k outlined in Table 1, determined from ref [16], and the maximum value (i.e., the worst precision) was used as the optimization objective. The optimal set of b-values b_opt across tissue types was:

$$b_{opt}=\underset{b}{\mathit{\text{argmin}}}\left\{\begin{array}{c}\mathit{\text{max}}\\ k\end{array}r\mathit{\text{CRLB}}\left(b;{\theta }_{k,i^{*}}\right)\right\}$$

where i* is the index corresponding to ν_ax. Finally, various axonal configurations F were considered, including:

• 1 fiber bundle, tested 3 times with orthogonal directions

• 2 fiber bundles of equal volume at 30, 60, and 90°

• 3, 4, 8, 16, and 32 fiber bundles of equal volume and uniformly spaced

b_opt was calculated separately for each F. Once again, we minimized the worst-case objective among these tissues to determine a globally optimal set of b-values, with results in Table 2.