Abstract
Purpose:
To develop and evaluate a deep adversarial learning-based image reconstruction approach for rapid and efficient MR parameter mapping.
Methods:
The proposed method provides an image reconstruction framework by combining the end-to-end convolutional neural network (CNN) mapping, adversarial learning, and MR physical models. The CNN performs direct image-to-parameter mapping by transforming a series of undersampled images directly into MR parameter maps. Adversarial learning is used to improve image sharpness and enable better texture restoration during the image-to-parameter conversion. An additional pathway concerning the MR signal model is added between the estimated parameter maps and undersampled k-space data to ensure the data consistency during network training. The proposed framework was evaluated on T2 mapping of the brain and the knee at an acceleration rate R=8 and was compared with other state-of-the-art reconstruction methods. Global and regional quantitative assessments were performed to demonstrate the reconstruction performance of the proposed method.
Results:
The proposed adversarial learning approach achieved accurate T2 mapping up to R=8 in brain and knee joint image datasets. Compared to conventional reconstruction approaches that exploit image sparsity and low-rankness, the proposed method yielded lower errors and higher similarity to the reference and better image sharpness in the T2 estimation. The quantitative metrics were normalized root mean square error of 3.6% for brain and 7.3% for knee, structural similarity index of 85.1% for brain and 83.2% for knee, and tenengrad measures of 9.2% for brain and 10.1% for the knee. The adversarial approach also achieved better performance for maintaining greater image texture and sharpness in comparison to the CNN approach without adversarial learning.
Conclusion:
The proposed framework by incorporating the efficient end-to-end CNN mapping, adversarial learning, and physical model enforced data consistency is a promising approach for rapid and efficient reconstruction of quantitative MR parameters.
Keywords: Deep Learning, MR Parameter Mapping, Convolutional Neural Network, Model-based Reconstruction, Generative Adversarial Network, Adversarial Learning
INTRODUCTION
Quantitative MR parameter mapping has been shown as valuable image biomarkers for assessing a variety of diseases(1). Traditional approaches for imaging MR parameters such as the spin-spin relaxation time (T2) usually require repeated acquisitions to capture a set of imaging contrast, followed by a pixel-wise curve fitting using an MR signal model. This leads to longer scan times compared to conventional contrast-weighted imaging and thus limits its widespread clinical use. As a result, the acceleration for parameter mapping has become a popular research direction in the MR research community.
There has been recent interest in using deep learning to accelerate MR acquisition and reconstruction (2–10). We have previously developed a deep learning reconstruction method, called Model-Augmented Neural neTwork with Incoherence Sampling (MANTIS) (11), for mapping T2 parameters using a rapid multi-echo spin-echo acquisition. MANTIS uses an efficient end-to-end CNN mapping (modified U-Net (12)) to directly convert a series of undersampled images into parametric maps (e.g., a T2 map and a proton density map I0 for T2 mapping) by exploiting the spatial-temporal information in undersampled images. In addition, a physical model characterizing the MR signal evolution is further incorporated into the learning framework to guide the image-to-parameter transform, so that the parameter maps can be robustly estimated directly from undersampled images.
A number of studies have also shown that when training a deep learning model for imaging applications, the implementation of a simple l1/l2-norm as a training loss could result in image blurring and loss of image details (13). This is also a potential challenge for the MANTIS framework. While MANTIS has demonstrated promising results for accelerated T2 mapping, the use of a simple training loss could limit the further acceleration of T2 mapping, particularly at high image resolution. Our study and others have recently demonstrated that the Generative Adversarial Network (GAN) (14) can improve image sharpness and better preserve image texture through the addition of an adversarial training process into deep learning-based MR reconstruction (15–18). The aim of this current study was thus to expand the MANTIS framework by incorporating adversarial training for improved reconstruction performance. The feasibility of this new framework, referred to as MANTIS-GAN, was evaluated for T2 mapping in simulated brain imaging datasets and real knee imaging datasets.
THEORY
This section describes the extension of MANTIS to MANTIS-GAN tailored for T2 mapping based on a single exponential decay model. This new framework could also be applied for mapping other MR parameters with corresponding MR signal models.
MANTIS: Deep Learning-based Parameter Mapping with Model-Consistency
In the setup for T2 mapping, the jth echo image can be reconstructed from a subset of k-space measurements as:
| [1] |
where the dj is the undersampled k-space data, ij is the to-be-reconstructed image with an image size of nx×ny, ε represents the complex Gaussian noise (19). E is the encoding matrix, which can be further expanded as:
| [2] |
Here, F is an encoding operator for fast Fourier Transform and M is an undersampling mask to selectively acquire k-space locations. The signal evolution for T2 mapping follows the exponential decay at the jth echo (TEj) as:
| [3] |
where I0 and T2 is the proton density and spin-spin relaxation time, respectively. A model-based reconstruction scheme, by incorporating Eq [3] into Eq. [1], can be formulated as:
| [4] |
where ‖·‖2 denotes the l2 norm and t is the number of acquired echoes.
Inspired by the model-based reconstruction, the original MANTIS framework reformulates the Eq[4] into a network training loss. As shown in Figure 1, an end-to-end mapping CNN with network parameters θ is designated to directly convert undersampled images into the parameter maps through domain transform learning. This first loss term (loss 1 in the figure) ensures the fact that the mapping CNN can output parameter maps that, by following the MR physics, can produce undersampled k-space data consistent with the acquired k-space measurements. In addition, the standard supervised learning can be treated as a strong regularizer, where the second loss term (loss 2 in the figure) provides that the mapping CNN generates similar parametric maps to the reference parameter maps in the sense of l2 norm. Overall, this optimization problem is then reformulated to minimize a training loss as:
| [5] |
Where λ1 and λ2 are weight factors to balance two loss terms, respectively, assuming that there are training image datasets including reference parameter maps (I0, T2) and the corresponding undersampled images iu which can be obtained by using zero-filling reconstruction with a pre-defined undersampling mask M on the fully-sampled images is an expectation operator given the training sample iu belongs to the data distribution P i(u) of the undersampled image datasets.
Figure 1:
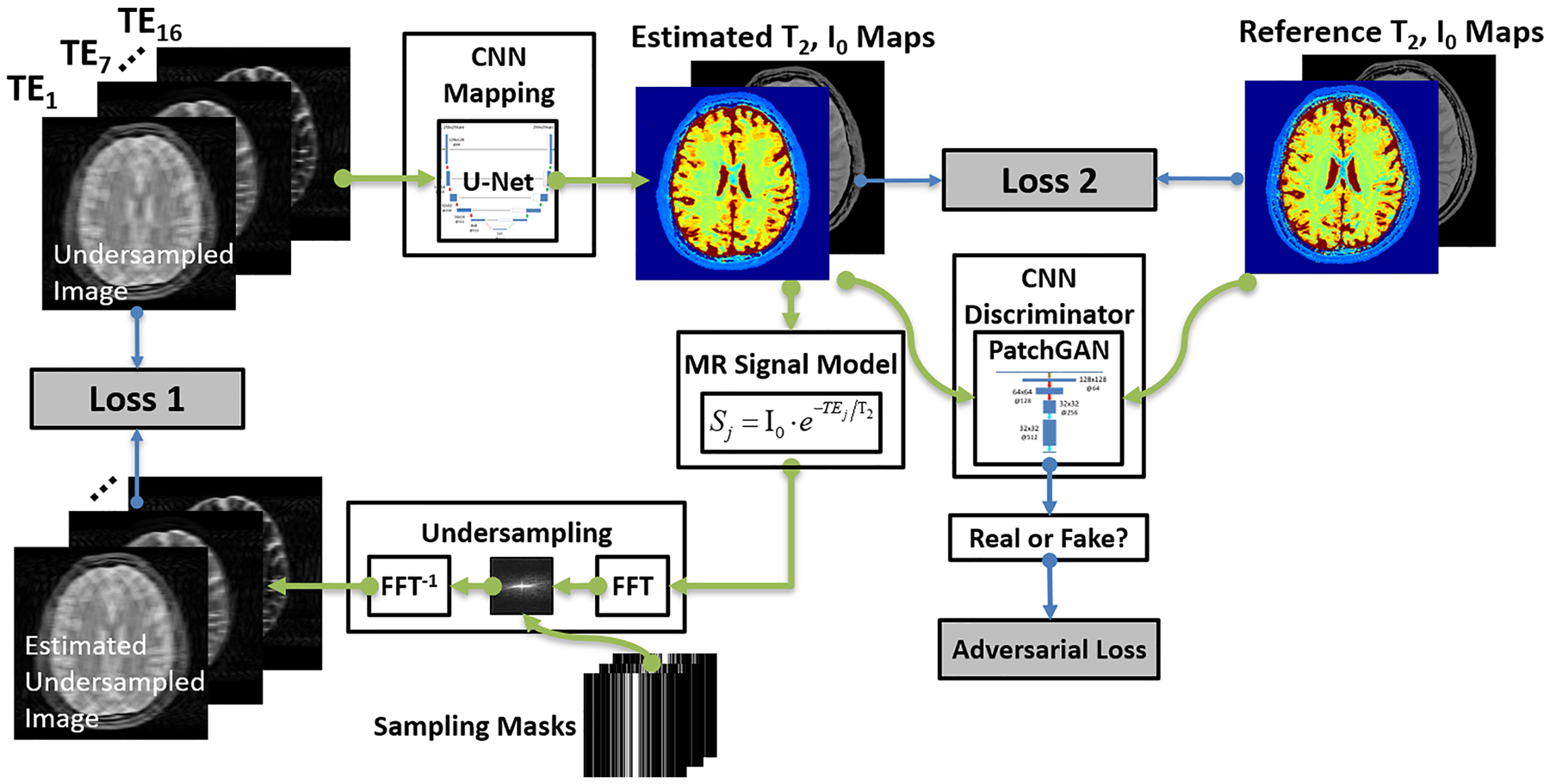
The schematic demonstration of the MANTIS-GAN framework. The MANTIS framework uses two components, including the first loss term (loss 1) to enforce data consistency between the synthetic undersampled data and the acquired k-space measurements; and the second loss term (loss 2) to ensure the similarity between the estimated parameter maps and the reference parameter maps. Building on the foundation of this framework, MANTIS-GAN introduces the third adversarial loss highlighting that estimated maps resemble the same tissue features and image sharpness as the reference maps from fully sampled data. The MANTIS-GAN framework synergizes the data-driven and MR physics-informed knowledge and introduces adversarial training for improved detail preservation.
Adversarial Loss
While these two l2 norm loss terms can ensure favorable reconstruction by removing noise and artifacts, recent studies have found that sole use of pixel-wise loss terms such as l1 or l2 norm can result in image blurring and loss of image texture (11,15–18). To alleviate this problem, GAN has been recently introduced to enforce image sharpness and texture preservation, as shown in several image restoration applications(15–18). More specifically, GAN uses a CNN discriminator to assess the similarity between the output of CNN mapping and the references. An adversarial loss can then be implemented into the training framework as a third loss term in Figure 1. The adversarial loss can capture multiple-level local and global features so it can better represent image texture and pattern than the simple loss does. Mathematically, a multiple-layer CNN discriminator D((I0,T2) |δ) : (I0,T2) →1 with network parameters δ is designed to distinguish reconstructed parameter maps versus reference parameter maps from the data distribution P(I0,T2) of the reference map datasets. This discriminator D outputs a probability value to measure how likely the estimated comes from the reference map datasets. The adversarial loss can be formatted as:
| [6] |
MANTIS-GAN: MANTIS with Adversarial Network
By combining all three loss terms, a full loss function can be written as:
| [7] |
Here λ3 is a weight factor in balancing the GAN effect on the overall reconstruction. The full loss function can then be optimized in the training step using a two-player minimax game(14) as:
| [8] |
where G aims to minimize this loss function against the adversary D that seeks to maximize it. With successful training, the GAN theory ensures that this competing scheme can result in an optimal to generate parameter maps indistinguishable from the real reference maps based on the judgment of the discriminator D. Once the training is completed and satisfied, the CNN mapping can be fixed and directly applied to convert newly undersampled images into parameter maps for the reconstruction.
METHODS
Image Datasets
Simulated Brain Data
Twenty digital brain models made from 20 healthy adults with intersubject anatomical variabilities were obtained from the BrainWeb project (https://brainweb.bic.mni.mcgill.ca/). Each brain model was acquired by registering and averaging four whole-head high-resolution isotropic (1 mm3) T1-, T2-, and I0-weighted MRI scans from each subject. A 3D tissue mask covering the whole head for eleven tissue types including gray matter, white matter, cerebrospinal fluid was created by classifying the voxel intensities from all MR images using a fuzzy minimum distance classification algorithm(20). These models provided realistic brain structural features that were ideal for generating image datasets with brain anatomical information. Different tissue relaxation parameters, including T1,T2 and I0, were assigned to each tissue type based on previous literature values (21,22). The synthetic image data were generated using our MRiLab (23) simulation system on the brain models. The MRiLab (https://leoliuf.github.io/MRiLab/) is an open-source Bloch-simulation system, which is capable of simulating MR formulation for various pulse sequences given radiofrequency (RF) pulses, gradient waveforms, and acquisition schemes. After loading the digital model, a virtual MRI scan was configured to specify the pulse sequence, which defines time-varying RF pulses and imaging gradients to obtain the desired image contrast, resolution, and acquisition trajectory. The simulation was performed through a discrete-time solution of the Bloch-equation by mean of rotation and exponential scaling matrices at each time throughout the prescribed sequence (23–25). The acquired signal from all voxels in the digital model at the prescribed acquisition windows was then collected to fill the k-space. Upon completion, a fully-sampled image was generated by performing a fast Fourier transform on the k-space data. A schematic description of the simulation workflow is shown in Figure 2. A multi-echo spin-echo T2 mapping sequence was used to simulate axial brain MR images using the following imaging parameters: 16 linear echo times/ repetition time (TEs/TR) = [10, 20, 30, …, 160]/2500 ms, flip angle = 90°, slice thickness = 3mm, pixel bandwidth = 488Hz/pixel, number of slices = 40, field of view = 22×22cm2, and acquired image matrix = 256×256. There was a total of 800 image slices for all subjects.
Figure 2:
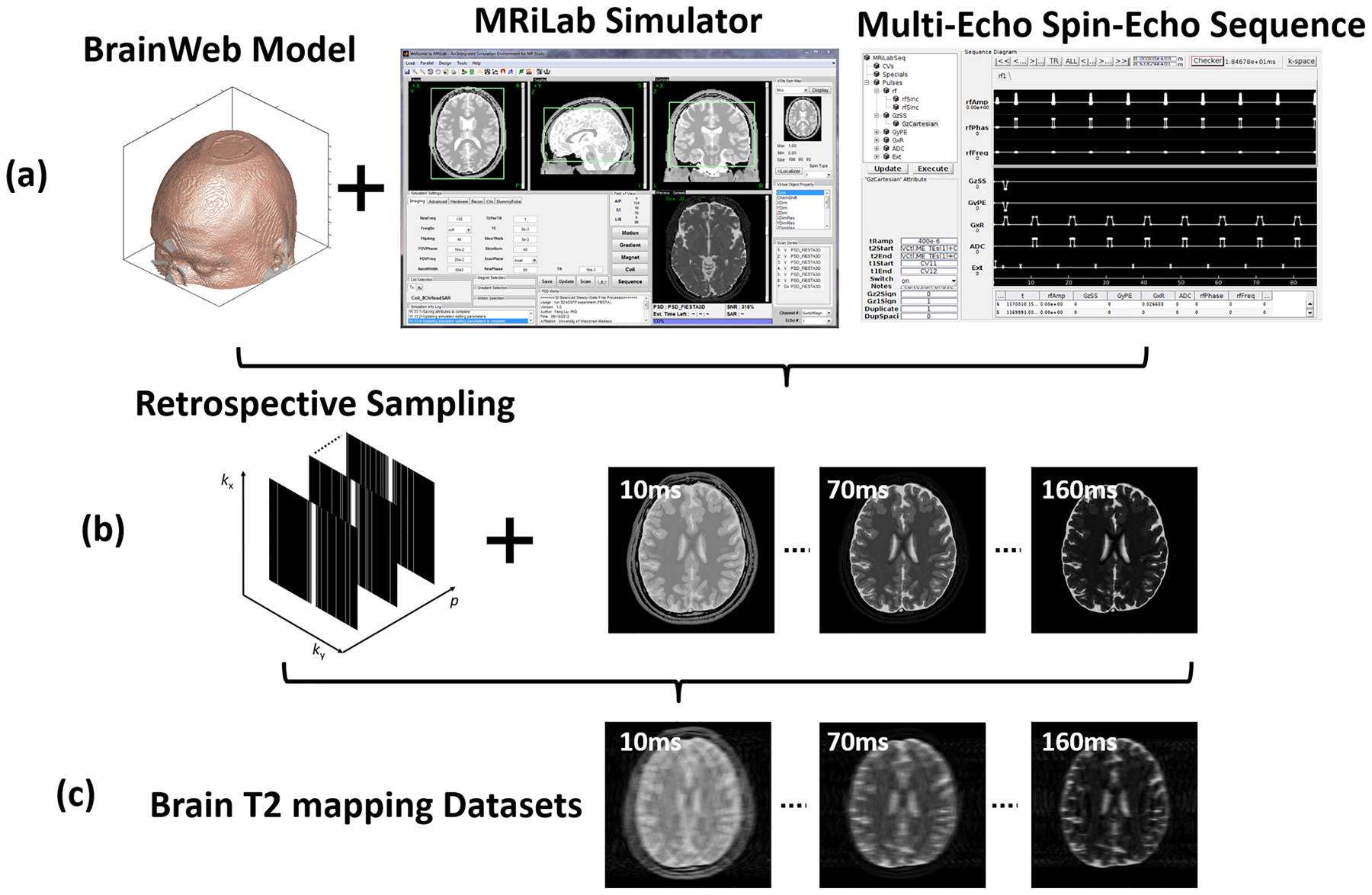
The schematic demonstration for the simulated brain image datasets. (a) One of 20 McGill BrainWeb phantoms applied to generate realistic brain MR datasets using the MRiLab simulator and a multi-echo spin-echo sequence for T2 mapping at 1.5T. (b) 1D Cartesian variable-density undersampling masks used for 16 echoes. (c) The generated undersampled T2 mapping images for evaluating deep learning-based reconstruction algorithms.
In-Vivo Knee Data
This retrospective study was performed using T2 mapping images of the knee acquired in 110 symptomatic patients using a 3T GE scanner (Signa Excite Hdx, GE Healthcare, Waukesha, Wisconsin) and an eight-channel phased-array extremity coil (InVivo, Orlando, Florida). The study was approved by the Institutional Review Board and had a waiver of written informed consent. The imaging parameter for the applied multi-echo spin-echo T2 mapping sequence includes: 8 echo times/repetition time (TEs/TR) = [7, 16, 25, 34, 43, 52, 62, 71]/1500 ms, flip angle = 90°, slice thickness = 3–3.2mm, pixel bandwidth = 122Hz/pixel, number of slices = 18–20, field of view = 16×16cm2, acquired image matrix = 320×256, and total scan time = 9min. The images were all acquired in the sagittal plane and were reconstructed on the MR scanner using the vendor-provided method (CartiGram, GE Healthcare, Waukesha, Wisconsin). The reconstructed images were saved as DICOM files after the coil combination and had a mean signal-to-noise ratio (SNR) of ~150 at the first echo image. There was a total of 2107 image slices for all subjects.
Retrospective undersampling was performed to generate the undersampled multi-echo images by multiplying the reference fully sampled k-space data with the undersampling masks using a zero-filling reconstruction. An acceleration rate (R)=8 was evaluated for both brain and knee image datasets with an undersampling mask generated using one-dimensional variable-density Cartesian random undersampling patterns (26). The mask had a fully sampled 5% central k-space, and the sampling pattern varied for each echo to create temporal incoherence following the compressed sensing strategy. The reference T2 and I0 maps were generated by fitting the fully-sampled multi-echo images into the exponential decay model in Eq. [3] using a pixel-wise standard nonlinear least-squares algorithm.
Implementation and Training of the Neural Network
For the end-to-end CNN mapping, a U-Net architecture (12) was adapted from a previous image-to-image translation study (27) into MANTIS and MANTIS-GAN. For the adversarial configuration, a PatchGAN (27) architecture was used for the discriminator network, which aims to differentiate real versus artificial maps using image patch-based assessment in the adversarial process. The choice of such combination is supported by the promising performance of our recent GAN-based architecture in image reconstruction (15). An illustration of the applied U-Net and PatchGAN is shown in Figure 3. The network was coded in Python (Python Software Foundation, Wilmington, Delaware) and used the Keras package (28) running Tensorflow computing backend (29) on a 64-bit Ubuntu Linux system.
Figure 3:

The configuration of U-Net and PatchGAN in MANTIS-GAN for end-to-end CNN mapping and adversarial training. The U-Net consists of a paired encoder and decoder network. Several shortcut connections were used to transfer image features directly between encoder and decoder to enhance the mapping performance. The configuration of the convolution layers is shown as image size @ the total number of 2D filters. Abbreviation includes BN: Batch Normalization; ReLU: Rectified Linear Unit activation; Conv: 2D convolution; Deconv: 2D deconvolution
The subjects were randomly split into 80%, 10%, and 10% for training, validation, and testing. During the training step, the undersampled images are concatenated from all the echoes together as the input of U-Net. The initialization of network parameters followed the strategy as shown in Ref (30), and an adaptive gradient descent optimization (ADAM) algorithm (31) at a fixed learning rate of 0.0002 was used to update the network parameters. A mini-batch training was performed with each batch consisting of 3 image slices for one iteration. Total iteration steps corresponding to 200 epochs were carried out to ensure convergence of the training (Figure 4), and the best model was determined as the one that had the lowest combined loss 1 + loss 2 value on the validation datasets. A grid search was performed to find the optimal weight factors in the loss function (Eq. [7]). They were λ1=0.2, λ2 =1 and λ3=0.1 for brain images and λ1=0.1, λ2 =1 and λ3=0.01 for knee images in training MANTIS-GAN. MANTIS used the same sets of λ1 and λ2 weights to make a fair comparison. All training and evaluation were conducted on a personal computer hosting an Intel Xeon W3520 CPU, 32 GB global RAM, and one NVidia GTX 1080Ti graphic card which has 3584 CUDA cores and 11GB GPU RAM.
Figure 4:
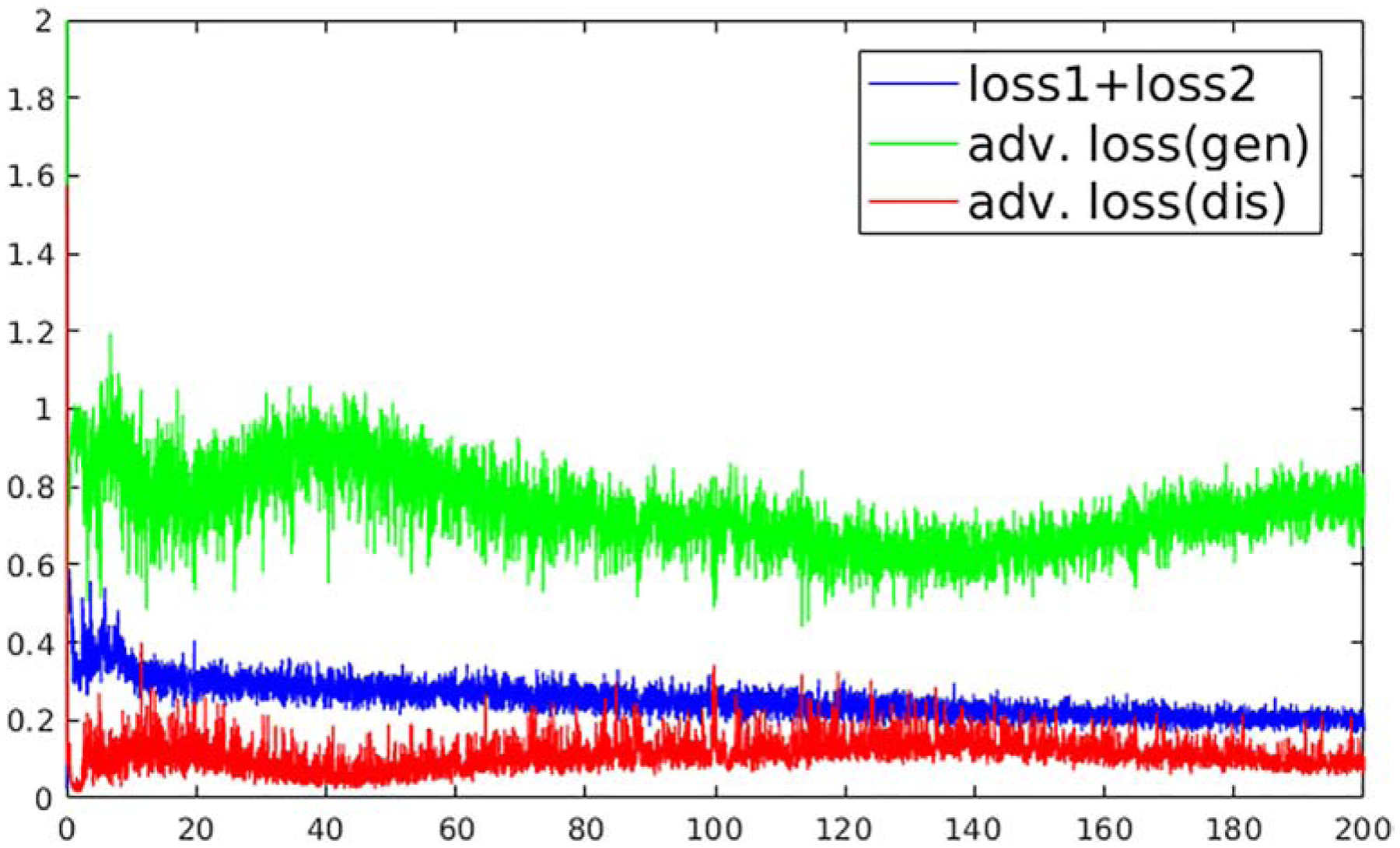
The overall losses as a function of the training process at each epoch for training MANTIS-GAN on the brain image datasets. The image loss (loss 1 + loss 2) decreases during the training and converges into stable status after 180 epochs. The adversarial training demonstrates a competing form of adversarial loss behavior for generator (U-Net) and discriminator (PatchGAN) (without the logarithm for display purposes). The adversarial training creates a mechanism to mutually improve generator and discriminator to improve the final reconstruction output.
Evaluation of Reconstruction Methods
The reconstruction result of MANTIS-GAN was compared with the state-of-the-art joint x-p (spatial-parametric) reconstruction, including one method using locally low-rank constraint (LLR (32)), and another method using a combined sparsity and low-rank constraint (k-t SLR (33)) on the multiecho image-series. The LLR reconstruction followed the original implementation in Ref (32). The k-t SLR reconstruction followed the default parameter setting using the code in https://research.engineering.uiowa.edu/cbig/content/matlab-codes-k-t-slr, provided by the authors. Because the LLR and k-t SLR provided reconstructed echo images, a T2 map was then obtained by pixel-wise fitting the reconstructed images into Eq. [3] using a standard nonlinear least-squares algorithm. The MANTIS-GAN was also compared with the original MANTIS without adversarial learning.
Three quantitative metrics focusing on different image aspects were used to assess the global difference between the reconstructed T2 maps and the reference T2 maps. The normalized Root Mean Squared Error (nRMSE) and Structural Similarity (SSIM) index were used to assess the overall reconstruction error and the similarity with respect to the reference, respectively. The relative reduction of Tenengrad measure (34,35) between the reconstructed maps and reference was used to assess the loss of image sharpness. Because this metric is sensitive to the changes of local characteristics of pronounced image edges, a higher Tenengrad value indicates sharper image appearance, thus lower reduction of Tenengrad in contrast to reference indicates better sharpness preservation of the reconstructed maps. Differences of these measures between methods were evaluated using a paired Wilcoxon signed-rank test with statistical significance defined as a p-value less than 0.05.
The regional assessment was performed in the knee images using Region-of-interest (ROI) analysis. The patellar, femoral and tibial cartilage subsections and meniscus of the knee joint were manually segmented by a senior imaging scientist under the supervision of a musculoskeletal radiologist for all testing knee images. The mean T2 values were then obtained from LLR, k-t SLR, MANTIS, and MANTIS-GAN. The agreement between the reconstructed and reference T2 values were evaluated using the Bland-Altman analysis(36), with a significance level defined as p<0.05.
RESULTS
Figure 5 shows representative T2 maps (top row) and proton density I0 maps (bottom row) estimated from different reconstruction methods, respectively, for testing brain datasets. The LLR reconstruction generated parameter maps with inferior image quality, as indicated by the noticeable artifacts and noises. The k-t SLR outperformed the LLR method as it restored some image details but remained residual artifacts. In contrast, the deep learning-based methods removed most of the artifacts, although the original MANTIS created apparent blurriness at the tissue boundaries due to the high image acceleration. The MANTIS-GAN provided the optimal reconstruction with well-preserved image sharpness, clarity, and tissue texture similar to the reference parameter maps.
Figure 5:
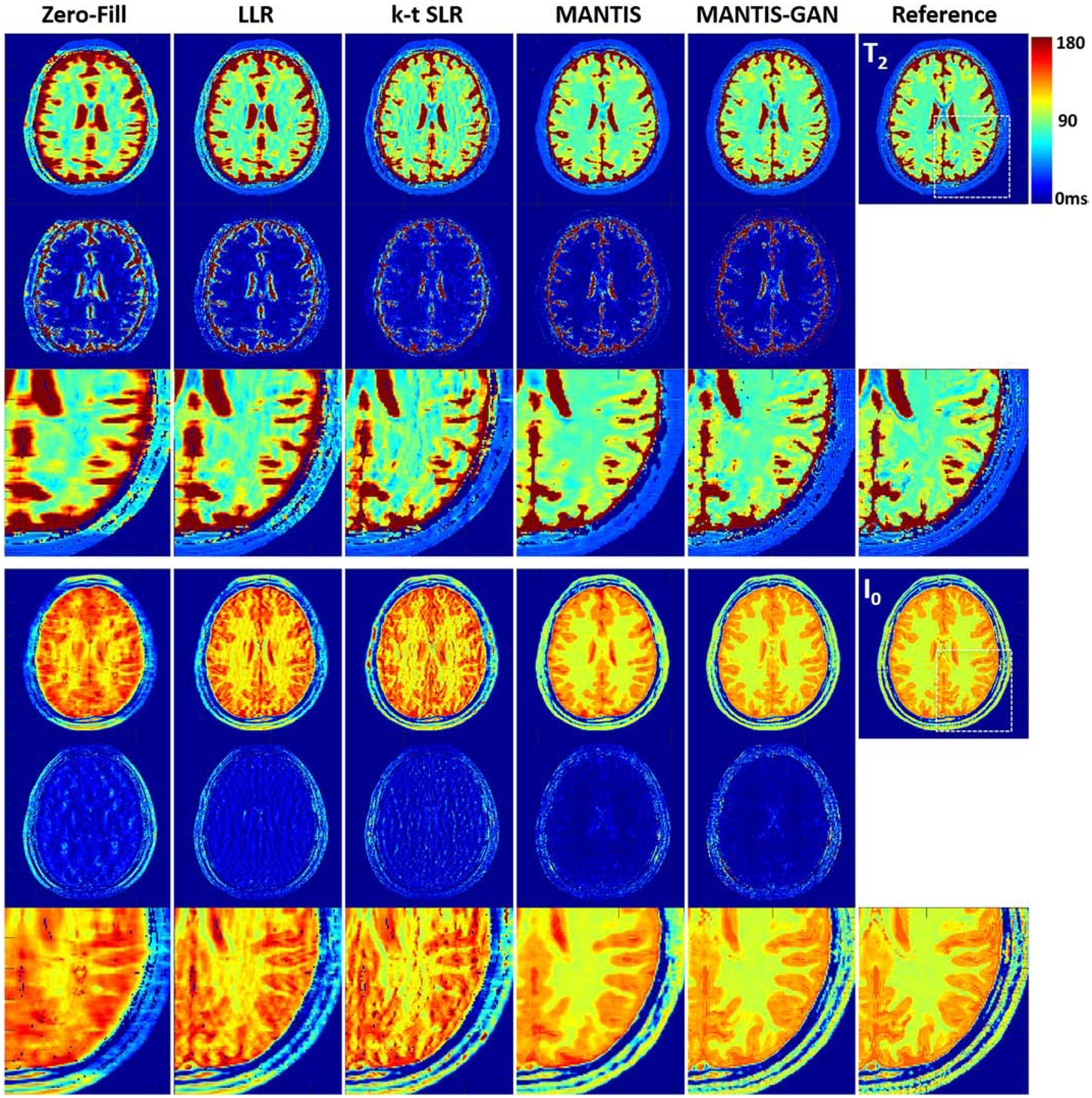
Comparison of T2 and I0 maps reconstructed from MANTIS-GAN and MANTIS with maps from joint x-p reconstruction methods at an acceleration rate R=8 in one simulated axial brain slice. The difference maps under the reconstructed T2 and I0 maps show the absolute pixel-wise error at the same color scale. MANTIS removed most of the image artifact but resulted in image blurring at the tissue boundaries. MANTIS-GAN generated nearly artifact-free T2 and I0 maps with well-preserved image sharpness, clarity, and tissue texture like the reference maps. The joint x-p reconstruction methods resulted in parameter maps at reduced image sharpness and remaining residual artifacts.
Figure 6 demonstrates the comparison of generated T2 maps from different reconstruction methods for a testing knee dataset. Similar to the example for the brain, there was an observation that MANTIS-GAN provided nearly artifact-free T2 maps while maintaining better image sharpness and more realistic tissue texture in comparison with the original MANTIS, the LLR and k-t SLR methods.
Figure 6:
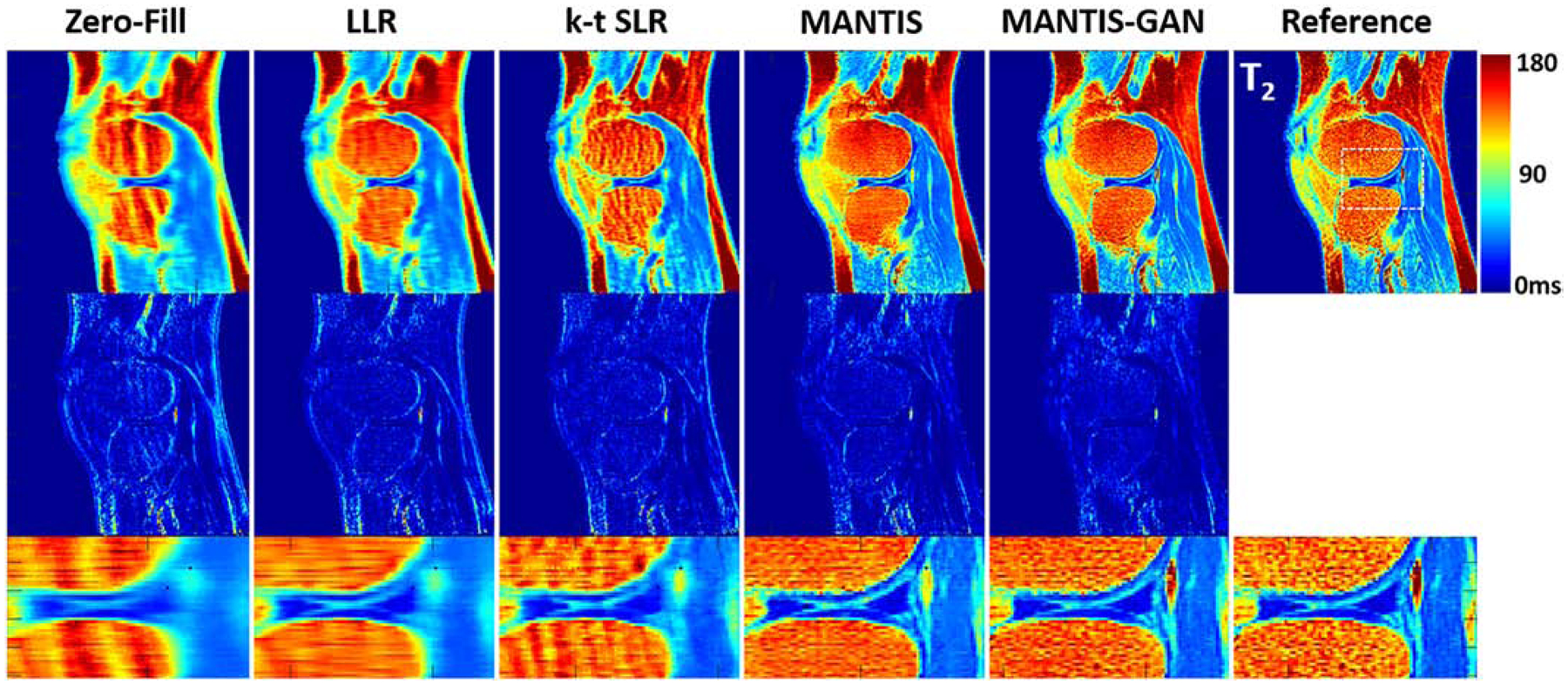
Comparison of T2 maps reconstructed from MANTIS-GAN and MANTIS with maps from joint x-p reconstruction methods at an acceleration rate R=8 in one real sagittal knee slice. The difference maps under the reconstructed T2 maps show the absolute pixel-wise error at the same color scale. MANTIS and MANTIS-GAN removed most of the image artifact, and MANTIS-GAN generated better bone texture and sharper image appearance that is comparable to the reference maps. Other methods cannot remove the residual artifacts caused by the high undersampling rate.
The qualitative observations in the exemplary figures were further confirmed by the group-wise quantitative analysis, as shown in Table 1, which summarizes the averaged nRMSE, SSIM, and Tenengrad measures between the reference and the reconstructed T2 maps in all the testing datasets for brain and knee, respectively. In general, The MANTIS and MANTIS-GAN reconstruction outperformed the sparsity and low rankness-based LLR and k-t SLR methods for all metrics with p<0.001. Compared with MANTIS, MANTIS-GAN yielded the sharper image appearance (lower Tenengrad: p<0.001 for brain, p=0.03 for knee) and the higher similarity (higher SSIM: p=0.01 for brain, p=0.01 for knee) to the reference. Noise suppression was slightly better (lower nRMSE: p=0.04 for brain, p=0.01 for knee) for MANTIS in contrast to MANTIS-GAN.
Table 1:
The mean and standard deviation (SD) of nRMSE, SSIM, and Tenengrad measures on testing datasets for brain and knee joint, respectively. MANTIS-GAN achieved the reconstruction performance with the highest image sharpness (i.e., lowest Tenengrad measures) and best texture preservation (i.e., highest SSIM measures) in contrast to the reference. MANTIS achieved the greatest noise suppression (i.e., lowest nRMSE measures).
| Methods | Mean ± SD at Brain Datasets | Mean ± SD at Knee Datasets | ||||
|---|---|---|---|---|---|---|
| nRMSE (%) | SSIM (%) | Tenengrad (%) | nRMSE (%) | SSIM (%) | Tenengrad (%) | |
| LLR | 10.9 ± 4.2 | 50.2 ± 5.3 | 35.4 ± 6.3 | 13.7 ± 3.4 | 58.2 ± 3.1 | 41.7 ± 8.3 |
| k-t SLR | 6.8 ± 2.5 | 66.5 ± 3.4 | 20.6 ± 4.3 | 11.4 ± 2.5 | 69.8 ± 3.5 | 19.1 ± 2.2 |
| MANTIS | 3.4 ± 1.8 | 83.1 ± 1.9 | 15.6 ± 3.9 | 7.1 ± 1.9 | 81.1 ± 2.1 | 11.6 ± 3.1 |
| MANTIS-GAN | 3.6 ± 2.1 | 85.1 ± 2.6 | 9.2 ± 3.2 | 7.3 ± 2.2 | 83.2 ± 2.4 | 10.1 ± 2.3 |
The Bland-Altman plots were shown in Figures 7 to compare the reference versus reconstructed T2 maps in the cartilage subsections and meniscus. In contrast to LLR and k-t SLR, which typically overestimated T2 values, both MANTIS and MANTIS-GAN had a similar unbiased estimation of T2 values (p>0.05). For both cartilage subsections and meniscus, they achieved a more considerable agreement with the reference T2 values, as indicated by the narrower limits of agreement lines (i.e., the dashed lines).
Figure 7:
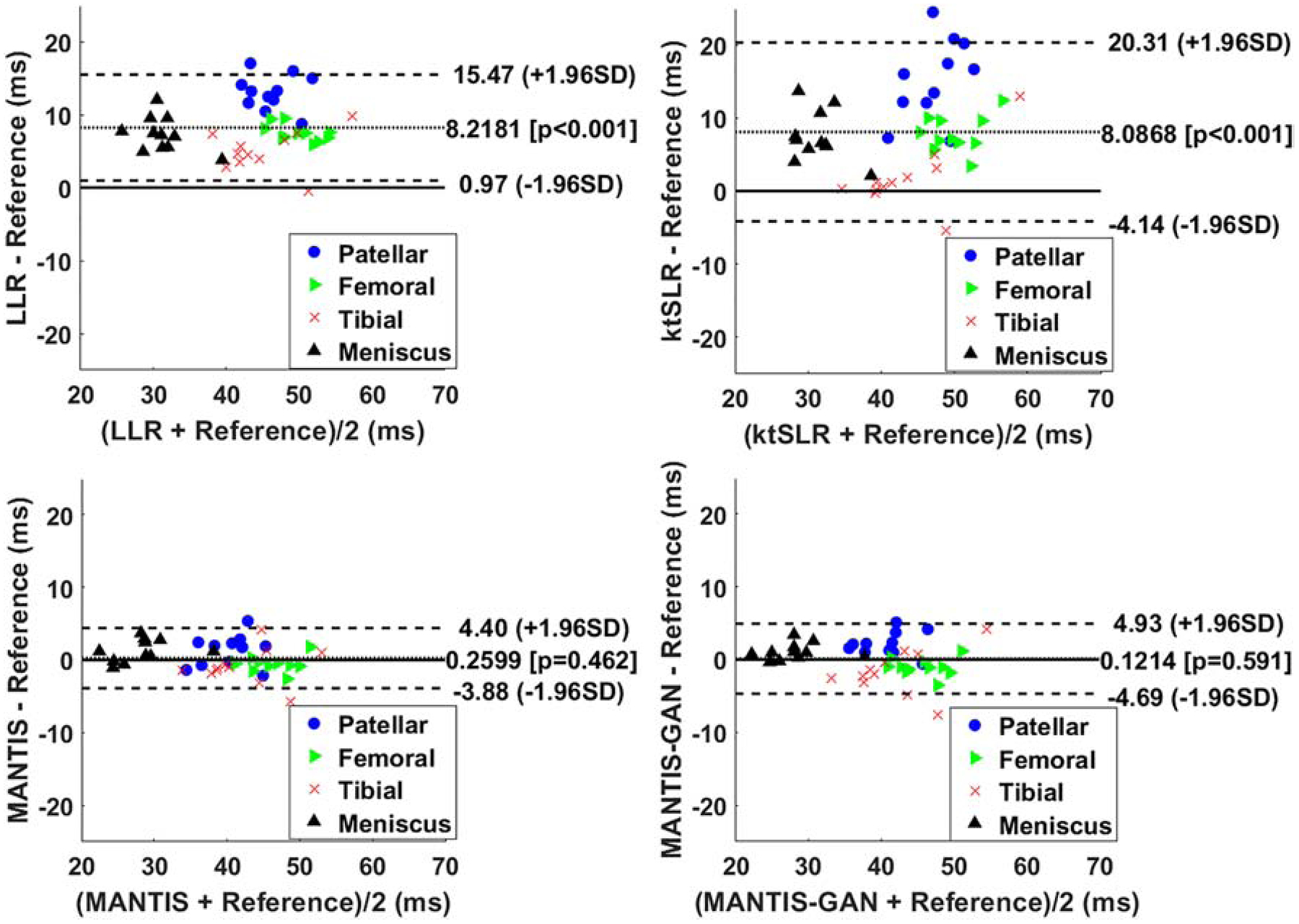
The Bland-Altman plots for the agreement of the regional cartilage and meniscus T2 values in the testing knee datasets between the reference and the T2 maps reconstructed from different methods at an acceleration rate R=8. MANTIS and MANTIS-GAN achieved unbiased estimation (p>0.05) of the T2 values for cartilage and meniscus with narrower limits of agreements (the dashed lines), which are calculated at the ±1.96*standard deviation of the mean differences.
DISCUSSION & CONCLUSIONS
In this study, a deep learning-based reconstruction framework called MANTIS-GAN was proposed for rapid and efficient MR parameter mapping and was evaluated for T2 mapping in the brain and the knee joint. Building on the foundation of MANTIS, the newly proposed MANTIS-GAN with adversarial learning not only maintained the original features of MANTIS but also enhanced the CNN mapping performance by enforcing a generation of high-quality parameter maps with image texture and sharpness preservation at a high acceleration rate.
Adversarial learning has proven to be effective in preserving perceptional image texture and sharpness in reconstructed images, as previously shown in (15,17,18) for static MR image reconstruction. While the pure pixel-wise losses such as l1/l2 norm and the hybrid of l1/l2 norm have been widely applied for many imaging studies, these simple loss functions aim to suppress the image noise and artifacts but can sometimes inevitably sacrifice image details and sharpness (13). The reconstructed images may alter the underlying image texture and the noise spectrum thus can result in the variation of image information. The reconstructed images using adversarial loss is more advantageous for maintaining image textures and patterns that present visually favorable appearance. Mathematically, successful convergence of the adversarial training can guarantee that the restored images and the training references fall into the same data distribution in a transformed high dimensional manifold (37,38). As shown in this study, adversarial learning can be directly extended and applied to the domain of parameter maps to enforce the accurate image-to-parameter domain transform, meanwhile maintaining favorable preservation to image details. In both brain and knee applications, the perseveration of tissue structure can be important in delineating and evaluating small lesions and subtle tissue abnormalities caused by early pathologies, which otherwise could be missed due to image blurring.
Adversarial learning is also known to be challenging to train as the competitive nature of the CNN mapping (G) and CNN discriminator (D) can cause the learning process to be unstable(39). The resulted generation of image hallucinations (i.e., pseudo image structure) is malignant for image diagnosis. The MANTIS-GAN alleviates this concern by implementing the data consistency enforcement so that data fidelity loss (loss 1) can prevent degradation of the adversarial process from generating hallucinated features in parameter maps. The combination of all loss components in MANTIS-GAN is important as it imposes not only the efficient and rapid image feature learning but also the information consistency to provide robust end-to-end CNN mapping. It should also be noted that the optimization of the loss weights warrants further investigation. As the weight setting differs for different image datasets in our study via the grid search, it is highly likely that the optimal weights are dependent on the aspects of the training hyperparameters, such as the network architecture and the training datasets. In contrast to the manual and brute-force method for tuning loss weights, which can be tedious, time-consuming, and less repeatable. The recent proposed deep hyperparameter learning may provide a convenient solution by treating the loss weights as extra learnable variables and dynamically adjust them during the network training(40). Moreover, the adversarial learning can be further stabilized and improved by investigating several recent GAN architectures such as Wasserstein GAN (WGAN) (39), WGAN with Gradient Penalty (WGAN-GP) (41), Least Square GAN (LS-GAN) (42), and Deep Regret Analytic GAN (DRAGAN) (43), all of which are proven to improve the adversarial process.
There are several limitations in the current proof-of-concept study. Firstly, the MANTIS-GAN used the DICOM images after coil combination despite training CNN can be better using multi-coil k-space data. Similar to our previous deep learning reconstruction work for static MR images in Ref. (15), the extension of MANTIS-GAN for multi-coil data is entirely possible given access to the adequate multi-coil datasets and advanced GPU devices with more GPU memory. In addition, there are no limits for our method to reconstruct other undersampling trajectories. The MANTIS-GAN framework can also be extended to process non-Cartesian data such as spiral and radial by incorporating gridding and regridding operations and a density compensation function in the training process, similar to that in standard iterative non-Cartesian reconstruction. Secondly, the feasibility study of T2 mapping used a mono-exponential decay model for reconstructing multi-echo spin-echo images. Although this simple model might be suboptimal for this sequence due to the effects of stimulated echoes, non-ideal slice selection (44,45), it is expected that further improvement can be realized by using optimized imaging protocols and more advanced signal models, such as using the Bloch-simulation-based model to produce more reliable T2 parameter estimations (45). Thirdly, adversarial learning in our study was applied to the full-scale image. While this implementation is preferable for anatomies such as white and gray matters in the brain with comparable size and spatial distribution, in another application such as knee joint, the sizeable structures, including bone and muscle, could dominate GAN effort. Therefore, balanced optimization might be achieved through providing more attention to cartilage and meniscus in the knee to balance GAN effect in new GAN strategies. Finally, the research is warranted to investigate how and to what extent that MANTIS-GAN can be generalized to various imaging protocols and MR scanning environments for robust and reliable parameter mapping. For example, further studies are needed to investigate the generalization and robustness of the trained models at the presence of imaging protocol discrepancy between training and testing datasets. Future studies are also needed to validate the tolerance of MANTIS-GAN on image noise at a wide range of SNR levels.
In conclusion, we have demonstrated that the proposed MANTIS-GAN framework by synergistically incorporating the end-to-end CNN mapping, model enforced data consistency, and adversarial learning represents a promising deep learning approach for realizing efficient, rapid and high-quality MR parameter mapping.
ACKNOWLAGEMENT
Research support was provided by National Institute of Health grant P41-EB022544.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declarations of interest: none
REFERENCES
- 1.Margaret Cheng HL, Stikov N, Ghugre NR, Wright GA. Practical medical applications of quantitative MR relaxometry. J. Magn. Reson. Imaging 2012;36:805–824 doi: 10.1002/jmri.23718. [DOI] [PubMed] [Google Scholar]
- 2.Hammernik K, Klatzer T, Kobler E, et al. Learning a Variational Network for Reconstruction of Accelerated MRI Data. Magn. Reson. Med 2017;79:3055–3071 doi: 10.1002/mrm.26977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wang S, Su Z, Ying L, et al. Accelerating Magnetic Resonance Imaging Via Deep Learning In: 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI). IEEE; 2016. pp. 514–517. doi: 10.1109/ISBI.2016.7493320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Schlemper J, Caballero J, Hajnal JV., Price A, Rueckert D. A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans. Med. Imaging 2017:1–1 doi: 10.1007/978-3-319-59050-9_51. [DOI] [PubMed] [Google Scholar]
- 5.Han Y, Yoo J, Kim HH, Shin HJ, Sung K, Ye JC. Deep learning with domain adaptation for accelerated projection-reconstruction MR. Magn. Reson. Med 2018;80:1189–1205 doi: 10.1002/mrm.27106. [DOI] [PubMed] [Google Scholar]
- 6.Eo T, Jun Y, Kim T, Jang J, Lee HJ, Hwang D. KIKI-net: Cross-domain convolutional neural networks for reconstructing undersampled magnetic resonance images. Magn. Reson. Med 2018;80:2188–2201 doi: 10.1002/mrm.27201. [DOI] [PubMed] [Google Scholar]
- 7.Zhu B, Liu JZ, Cauley SF, Rosen BR, Rosen MS. Image reconstruction by domain-transform manifold learning. Nature 2018;555:487–492 doi: 10.1038/nature25988. [DOI] [PubMed] [Google Scholar]
- 8.Akçakaya M, Moeller S, Weingärtner S, Uğurbil K. Scan-specific robust artificial-neural-networks for k-space interpolation (RAKI) reconstruction: Database-free deep learning for fast imaging. Magn. Reson. Med 2019;81:439–453 doi: 10.1002/mrm.27420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Biswas S, Aggarwal HK, Jacob M. Dynamic MRI using model-based deep learning and SToRM priors: MoDL-SToRM. Magn. Reson. Med 2019. doi: 10.1002/mrm.27706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Malavé MO, Baron CA, Koundinyan SP, et al. Reconstruction of undersampled 3D non-Cartesian image-based navigators for coronary MRA using an unrolled deep learning model. Magn. Reson. Med 2020;84:800–812 doi: 10.1002/mrm.28177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Liu F, Feng L, Kijowski R. MANTIS: Model-Augmented Neural neTwork with Incoherent k-space Sampling for efficient MR parameter mapping. Magn. Reson. Med 2019;82:174–188 doi: 10.1002/mrm.27707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation In: Navab N, Hornegger J, Wells WM, Frangi AF, editors. Medical Image Computing and Computer-Assisted Intervention -- MICCAI 2015: 18th International Conference, Munich, Germany, October 5–9, 2015, Proceedings, Part III. Cham: Springer International Publishing; 2015. pp. 234–241. doi: 10.1007/978-3-319-24574-4_28. [DOI] [Google Scholar]
- 13.Zhao H, Gallo O, Frosio I, Kautz J. Loss Functions for Image Restoration With Neural Networks. IEEE Trans. Comput. Imaging 2017;3:47–57 doi: 10.1109/TCI.2016.2644865. [DOI] [Google Scholar]
- 14.Goodfellow IJ, Pouget-Abadie J, Mirza M, et al. Generative Adversarial Networks. ArXiv e-prints 2014. [Google Scholar]
- 15.Liu F, Samsonov A, Chen L, Kijowski R, Feng L. SANTIS: Sampling-Augmented Neural neTwork with Incoherent Structure for MR image reconstruction. Magn. Reson. Med 2019;82:1890–1904 doi: 10.1002/mrm.27827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Liu F, Feng L. Towards High-Performance Rapid Quantitative Imaging via Model-based Deep Adversarial Learning. In: ISMRM Workshop on Data Sampling & Image Reconstruction.; 2020. [Google Scholar]
- 17.Quan TM, Nguyen-Duc T, Jeong W-K. Compressed Sensing MRI Reconstruction using a Generative Adversarial Network with a Cyclic Loss. IEEE Trans. Med. Imaging 2017;37:1488–1497 doi: 10.1109/TMI.2018.2820120. [DOI] [PubMed] [Google Scholar]
- 18.Mardani M, Gong E, Cheng JY, et al. Deep Generative Adversarial Neural Networks for Compressive Sensing (GANCS) MRI. IEEE Trans. Med. Imaging 2018:1–1 doi: 10.1109/TMI.2018.2858752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pruessmann Klaas P.,. Advances in Sensitivity Encoding With Arbitrary\nk-Space Trajectories. 2001;651:638–651. [DOI] [PubMed] [Google Scholar]
- 20.Aubert-Broche B, Griffin M, Pike GB, Evans AC, Collins DL. Twenty new digital brain phantoms for creation of validation image data bases. IEEE Trans. Med. Imaging 2006;25:1410–1416 doi: 10.1109/TMI.2006.883453. [DOI] [PubMed] [Google Scholar]
- 21.Stanisz GJ, Odrobina EE, Pun J, et al. T1, T2 relaxation and magnetization transfer in tissue at 3T. Magn Reson Med 2005;54:507–512 doi: 10.1002/mrm.20605. [DOI] [PubMed] [Google Scholar]
- 22.Brown RW, Cheng YCN, Haacke EM, Thompson MR, Venkatesan R. Magnetic Resonance Imaging: Physical Principles and Sequence Design: Second Edition. (Brown RW, Cheng Y-CN, Haacke EM, Thompson MR, Venkatesan R, editors.) Chichester, UK: Wiley Blackwell; 2014. doi: 10.1002/9781118633953. [DOI] [Google Scholar]
- 23.Liu F, Velikina JV., Block WF, Kijowski R, Samsonov AA. Fast Realistic MRI Simulations Based on Generalized Multi-Pool Exchange Tissue Model. IEEE Trans. Med. Imaging 2017;36:527–537 doi: 10.1109/TMI.2016.2620961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bittoun J, Taquin J, Sauzade M. A computer algorithm for the simulation of any nuclear magnetic resonance (NMR) imaging method. Magn Reson Imaging 1984;2:113–120. [DOI] [PubMed] [Google Scholar]
- 25.Benoit-Cattin H, Collewet G, Belaroussi B, Saint-Jalmes H, Odet C. The SIMRI project: a versatile and interactive MRI simulator. J. Magn. Reson 2005;173:97–115 doi: 10.1016/j.jmr.2004.09.027. [DOI] [PubMed] [Google Scholar]
- 26.Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med 2007;58:1182–1195 doi: 10.1002/mrm.21391. [DOI] [PubMed] [Google Scholar]
- 27.Isola P, Zhu J-Y, Zhou T, Efros AA. Image-to-Image Translation with Conditional Adversarial Networks. ArXiv e-prints 2016. [Google Scholar]
- 28.Chollet François. Keras. GitHub; Published 2015. [Google Scholar]
- 29.Abadi M, Agarwal A, Barham P, et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. ArXiv e-prints 2016. doi: 10.1109/TIP.2003.819861. [DOI] [Google Scholar]
- 30.He K, Zhang X, Ren S, Sun J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. ArXiv e-prints 2015;1502. [Google Scholar]
- 31.Kingma DP, Ba J. Adam: A Method for Stochastic Optimization. ArXiv e-prints 2014. [Google Scholar]
- 32.Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magn. Reson. Med 2015;73:655–661 doi: 10.1002/mrm.25161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lingala SG, Hu Y, DiBella E, Jacob M. Accelerated Dynamic MRI Exploiting Sparsity and Low-Rank Structure: k-t SLR. IEEE Trans. Med. Imaging 2011;30:1042–1054 doi: 10.1109/TMI.2010.2100850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Krotkov EP. Active Computer Vision by Cooperative Focus and Stereo. New York, NY: Springer New York; 1989. doi: 10.1007/978-1-4613-9663-5. [DOI] [Google Scholar]
- 35.Buerkle A, Schmoeckel F, Kiefer M, et al. Vision-based closed-loop control of mobile microrobots for microhandling tasks In: Nelson BJ, Breguet J-M, editors. Microrobotics and Microassembly III. Vol. 4568 SPIE; 2001. p. 187. doi: 10.1117/12.444125. [DOI] [Google Scholar]
- 36.Giavarina D Understanding Bland Altman analysis. Biochem. Medica 2015;25:141–151 doi: 10.11613/BM.2015.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Green B, Horel T, Papachristos AV. Modeling Contagion Through Social Networks to Explain and Predict Gunshot Violence in Chicago, 2006 to 2014. JAMA Intern. Med 2017;177:326 doi: 10.1001/jamainternmed.2016.8245. [DOI] [PubMed] [Google Scholar]
- 38.Ye JC, Han Y, Cha E. Deep Convolutional Framelets: A General Deep Learning Framework for Inverse Problems. ArXiv e-prints 2017. [Google Scholar]
- 39.Arjovsky M, Chintala S, Bottou L. Wasserstein GAN. 2017. [Google Scholar]
- 40.Cipolla R, Gal Y, Kendall A. Multi-task Learning Using Uncertainty to Weigh Losses for Scene Geometry and Semantics. Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit 2018:7482–7491 doi: 10.1109/CVPR.2018.00781. [DOI] [Google Scholar]
- 41.Gulrajani I, Ahmed F, Arjovsky M, Dumoulin V, Courville A. Improved Training of Wasserstein GANs. ArXiv e-prints 2017. [Google Scholar]
- 42.Mao X, Li Q, Xie H, Lau RYK, Wang Z, Smolley SP. Least Squares Generative Adversarial Networks. ArXiv e-prints 2016. [DOI] [PubMed] [Google Scholar]
- 43.Kodali N, Abernethy J, Hays J, Kira Z. On Convergence and Stability of GANs. ArXiv e-prints 2017. [Google Scholar]
- 44.Hennig J Multiecho imaging sequences with low refocusing flip angles. J. Magn. Reson 1988;78:397–407 doi: 10.1016/0022-2364(88)90128-X. [DOI] [Google Scholar]
- 45.Ben-Eliezer N, Sodickson DK, Block KT. Rapid and accurate T2 mapping from multi-spin-echo data using bloch-simulation-based reconstruction. Magn. Reson. Med 2015;73:809–817 doi: 10.1002/mrm.25156. [DOI] [PMC free article] [PubMed] [Google Scholar]


