History and Evolution of Modeling in Biotechnology: Modeling & Simulation, Application and Hardware Performance

Graphical abstract

Abstract

Biological systems are typically composed of highly interconnected subunits and possess an inherent complexity that make monitoring, control and optimization of a bioprocess a challenging task. Today a toolset of modeling techniques can provide guidance in understanding complexity and in meeting those challenges. Over the last four decades, computational performance increased exponentially. This increase in hardware capacity allowed ever more detailed and computationally intensive models approaching a “one-to-one” representation of the biological reality. Fueled by governmental guidelines like the PAT initiative of the FDA, novel soft sensors and techniques were developed in the past to ensure product quality and provide data in real time. The estimation of current process state and prediction of future process course eventually enabled dynamic process control. In this review, past, present and envisioned future of models in biotechnology are compared and discussed with regard to application in process monitoring, control and optimization. In addition, hardware requirements and availability to fit the needs of increasingly more complex models are summarized. The major techniques and diverse approaches of modeling in industrial biotechnology are compared, and current as well as future trends and perspectives are outlined.

1. Introduction

The inherent complexity of biological systems makes monitoring, control and optimization challenging tasks to successfully design and guide a bioprocess [1], [2], [3]. The complexity arises from various interconnected subunits in the biological system. The nonlinear nature of the interconnections including feedforward cascades and feedback loops of biochemical reactions complicates the assessment of such systems by basic observations. Hereby modeling presents a valuable toolset to capture and cope with the inherent complexity of the biological system under investigation by mathematical means [3]. Model development has evolved over decades which is visualized in a timeline covering more than one century of model concepts, computational infrastructure, monitoring-, control- and optimization concepts as well as computationally intensive models and potential future trends of modeling in biotechnology (Fig. 1). Furthermore, fields of application of process models are summarized (Fig. 2). A model is typically applied for a broad range of different tasks, which include control respectively optimization of a biotechnological process e.g. by increasing product yields and productivity of the process. This is particularly interesting for industrial applications. These applications include design and establishment of novel processes, optimization of existing processes as well as quality control purposes to maintain product quality [4]. Product quality is ensured by assessing stability of critical process attributes (CPAs) to supervise robustness and reproducibility. One prominent concept for model-assisted quality control is often referred to as Quality by Design (QbD) concept, which is part of the Process Analytical Technology (PAT) regulatory framework as outlined by the US Food and Drug Administration (FDA). Part of PAT is to obtain better process understanding by assessment of the CPAs preferably in real time [5], [6], [7]. Here a model assisted monitoring strategy e.g. in form of soft sensors can potentially make up for the inaccessibility of some process variables as well as poorly resolved data (e.g. biomass concentration). Soft sensors are a combination of software models that may use hardware sensor inputs to derive, new quantities online. Considerable time delays for data collection along with laborious measurements may therefore be avoided [1]. Prominent examples for soft sensors include the use of artificial neural networks (ANNs) respectively metabolic networks with stoichiometric description of the involved biochemical reactions [8]. Soft sensor models implemented in computer programs deliver information in a similar way to hardware sensors. Therefore, sufficient real time data is available to allow fault detection. Furthermore, an advanced process control concept (e.g. feeding strategy) is realizable that aims for an optimized process outcome in terms of improved productivity and process efficiency (see Table 1) [1]. The first reports of model assumptions and mathematical representations thereof date back to the early 1900s. Even before the basic understanding of genetic material as the source of cellular information, growth behavior of microorganisms was targeted and described by mathematical means. In 1912, the authors Penfold & Norris studied the generation time of Eberthella typhosa and developed, what is assumed to be, the first kinetic principle of microbial growth [9] before effects like temperature and other factors effecting growth have been described by mathematical means (e.g. 1946 Hinshelwood) [10]. Penfold & Norris whereas were among the first to describe growth as a hyperbolic function of substrate concentration (peptone and glucose). Their findings correspond to the commonly known growth model of Monod on which he worked on in the 1940s. Monod postulated a dependence of the specific growth rate µ of Bacillus subtilis and Escherichia coli on substrate concentration following a hyperbolic function where bacterial growth reaches a maximum value (µ_max) and does not increase anymore when substrate concentration is increased further [11]. In 1913 Michaelis & Menten already described a mechanistic approach for the dependence of enzymatic action on substrate concentration yielding essentially the same equation that Monod postulated for microbial growth around three decades later in the 1940s [12]. In the following years Monod’s model was discussed critically and extended, e.g. by a description of substrate utilization in the absence of growth. The term for cellular maintenance metabolism was introduced in 1958 by Herbert [13]. Initially proposed dynamic models were only scarcely applied due to a complex written model presentation, lack of trust and limited computer capacity [14]. Furthermore, access to computer capacity to run simulations was limited to programming specialist with expertise in programming languages e.g. the general-purpose language for numeric computation FORTRAN. The increasing model complexity with extensive mathematical expressions incorporating temporarily and, for more complex models, spatially variable elements, demanded more computational capacity as well as novel modeling platforms. The continuing development of more powerful computers, along with their ease of availability, has enabled the application of more complex modeling approaches in biotechnological research. The development of novel and readily accessible software for modeling and simulation furthermore eliminated the necessity of advanced programming skills which were so far restricted to programming specialists [15]. In this review, past, present and envisioned future of models in biotechnology are compared and discussed with regard to application in process monitoring, control and optimization. For this purpose, hardware requirements and availability are discussed, major techniques and diverse approaches of modeling in industrial biotechnology are compared, and current as well as future trends and perspectives are outlined.

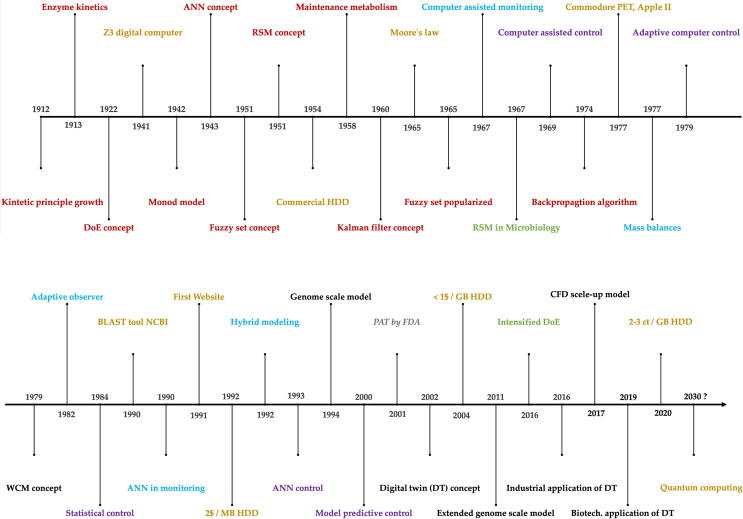
Fig. 1.

Timeline of model concepts (red), computational infrastructure (brown), monitoring- (blue), control- (purple) and optimization concepts (green) as well as computationally intensive models and potential future trends (black) in biotechnology. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

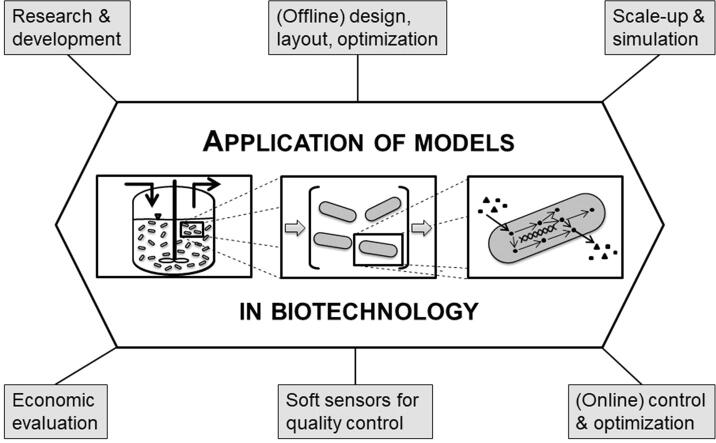
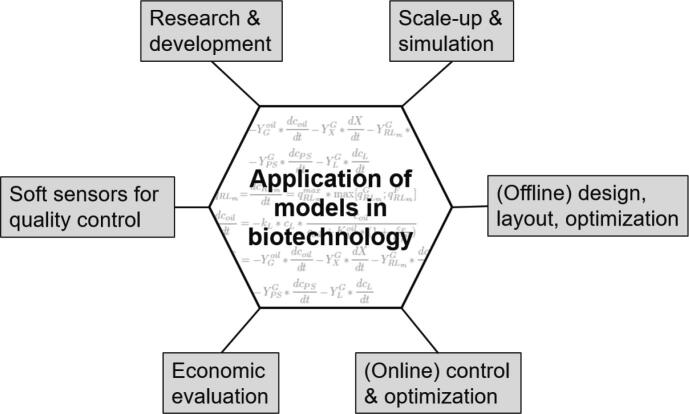
Fig. 2.

Fields of application of process models.

Table 1.

Recent development (2017–2020) of soft sensors for monitoring and control tasks in different bioprocesses.

Soft sensor	Hardware sensor	Model	Control task	Organism / Product	Source
X, qS, µ, YX/S	In-/off gas analyzer	Mass balance	Glucose feed, qS and lactose (inducer)	E. coli / GFP	[60]
X, N, product precoursor	In-/off gas analyzer	Particle filter algorithm + kinetic nonlinear model	Glucose feed, qS precursor feed, N feed	P. chrysogenum / penicillin	[61]
X	2D - fluorescence spectroscopy	Multivariate adaptive regression splines algorithm	–	E. coli / recombinant human Cu/Zn superoxide dismutase	[62]
X, S	In-/off gas analyzer	Mass balance, unstructured model	Vinasses-molasses feed, constant S concentration	C. necator / PHA	[63]
Total wet cell weight	In-/off gas analyzer; DO probe, weighing scale (for feed rate)	Recurrent neural network	Methanol feed	P. pastoris / intracellular hepatitis B surface antigen	[64]
X, Nitrate, Lutein	In silico experiment with computed data sets	Data-driven model, ANN + physics-based noise filter (simple kinetic model)	Nitrate feed	Desmodesmus sp. / lutein	[59]
OTR, OUR (no off gas needed), viable X, metabolic state	DO probe, thermometer, pressure, mass flow controller (process air and CO2), capacitance sensor	Mass balance, dynamic kLa model, two-segment linear model	–	CHO cells / IgG1 monoclonal antibody	[65]
X in continuous culture	In-/off gas analyzer	Carbon- and degree of reduction balance	Retention rate, S in feed	Haloferax mediterranei / bioremidation	[66]
X, lactose, lactic acid, pH	Base pump (ammonia addition), pH probe	Biokinetic model, mixed weak acid/base model, Monte Carlo simulations for considering uncertainties	–	Streptococcus thermophilus / lactic acid	[67]
Glucose, cumulative OTR dynamic OUR	Agitator speed, DO probe, mass flow controller (inlet gas flow), offline glucose measurement for parameter correction	Mass balance	Glucose feed	CHO cells / “therapeutic proteins”	[68]

X = Biomass concentration; q_S = Biomass specific substrate uptake rate; µ = specific growth rate; Y_X/S = Yield coefficient biomass / substrate; N = Nitrogen;

S = Substrate concentration; DO = dissolved oxygen; OTR/OUR = oxygen transfer/uptake rate.

2. History of computer and hardware development

For this section, several data sources and specifications of computer hardware development were used. These sources are provided as additional section before the references 1.

2.1. Processing power and microprocessor development

In 1941, German engineer Konrad Zuse completed building the first programmable, fully automatic digital computer, which was known as Z3. With 2200 electromechanical relays and a weight of around one metric ton, the Z3 performed calculations of floating-point numbers in a range of a few seconds [16]. With the initial development and advancement of metal–oxidesemiconductor field-effect transistors (MOSFETs) in the 1960s, higher transistor densities could be reached. It was not until a decade later that the first microprocessor integrated circuit chips were developed in 1969–1971, which opened up the potential of significantly smaller computer design, both in industry and personal computers for home use ^A.

The first home computers became available in 1977: The Radio Shack TRS-80, the Commodore PET and the Apple II, which utilized processors operation at a frequency range from 1 to 10 MHz with a transistor count of approx. 3500–8500. As part of further advancement of the integrated circuit chip technology, rapid miniaturization of MOSFETs followed which allowed for even high transistor densities on similarly sized chips, which furthermore led to increased clock rates. An increase in transistor count with a predicted doubling time of 2 years was first claimed in 1965 (revised in 1975) by Gordon Moore, the CEO of Intel, and is known as MOORE's law [17]. Development of smaller transistors and fabrication technologies is the key driving force behind MOORE's law. As fabrication technologies cannot be arbitrarily small, it is believed that MOORE's law has come close to its end nowadays [18]. Furthermore, there is no direct proportional correlation between transistor count and processing power [19]. One suitable method to measure processing power commonly required for biotechnological applications is the number of floating-point operations that a microprocessor can perform each second (FLOPS), with common units million operations (megaFLOPS, MFLOPS) and billion operations (gigaFLOPS, GFLOPS). A dramatic and exponential 1000-fold increase in microprocessor FLOPS can be observed from the mid-1980s (below 0.5 MFLOPS) to 2002–2003 (0.5 GFLOPS) (Fig. 3A) ^A.

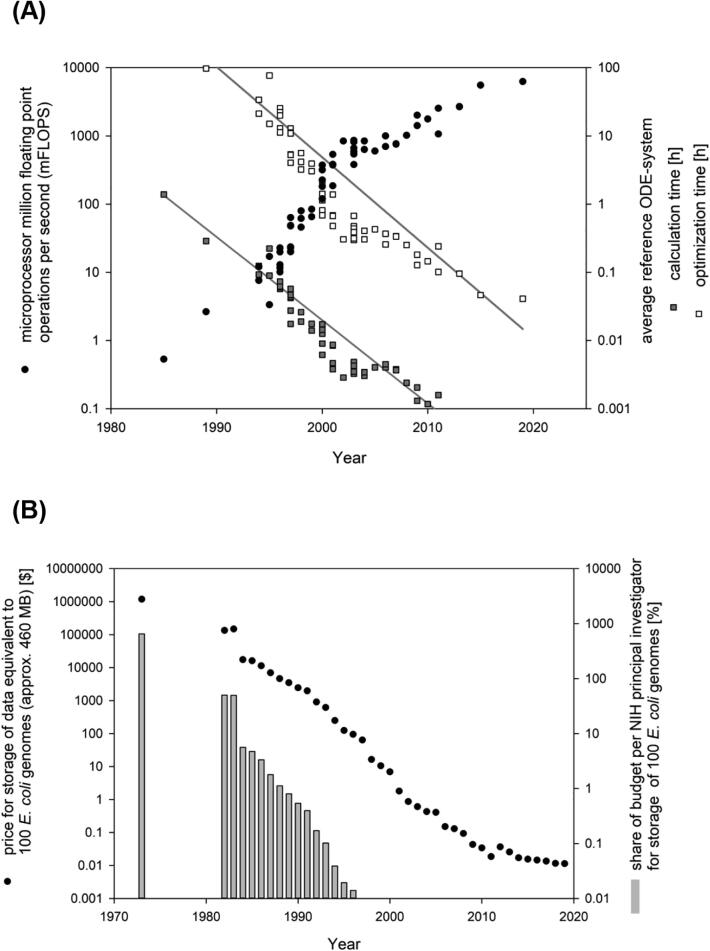
Fig. 3.

(A) Development of microprocessor power, given in million floating point operations per second (mFLOPS) (filled circles) and average time required to solve (empty squares) or optimize (filled squares) a reference ODE (ordinary differential equation) system starting from the 1980s. The reference ODE system consists of 11 equations and 36 parameters 19 solved using MATLAB ode15s package and fminsearch 5 parameter optimization with initial deviations of 20% from the final values. (B) Price development in USD for local data storage equivalent to 100 E. coli genomes (filled circles) in comparison to the average annual budget of an NIH principal investigator (grey bars). Data and specifications are listed as additional section before the references.

2.1.1. General-purpose computing on graphics processing units (GPGPU)

In the last two decades, powerful graphics processing units (GPUs) have been developed to handle the increasing amount of demand graphical tasks. They were designed to facilitate the high number of computations performed in graphics rendering, which they received from the central processing unit (CPU). Eventually, GPUs became more powerful than CPUs. Even though GPUs typically operate at lower frequencies, they have a significantly higher number of cores. It is for this reason that GPUs are very efficient in processing graphical data per second compared to CPUs.

Nowadays, current CPUs yield roughly 0.1 TFLOPS using 12 cores, while state-of-the-art graphic cards yield more than 10 TFLOPS using several hundred cores. It is for this reason that GPUs were increasingly used in calculation tasks beside graphics rendering, a technology frame that is referred to as general-purpose computing on graphics processing units (GPGPU) ^A.

Many different hardware and software developers are involved in GPGPU projects, such as NVIDIA CUDA, a software development kit (SDK) and application programming interface (API), Microsoft DirectCompute API or the MATLAB Jacket library (ArrayFire, Atlanta, Georgia USA) that enables GPGPU capabilities using the Parallel Computing Toolbox. In general, significant performance increases can be achieved by converting data into graphical format and using the GPU process it. It should be noted however, that even though in terms of maximum FLOPS graphic cards are more effective, they are by design highly optimized for specific tasks, which results in significant reductions in processing power when confronted with non-native calculations.

2.1.2. Processing requirements for modeling and simulation

To visualize and grasp a correlation for this amount of processing power, a reference system for biotechnological process modeling was used. The reference system constitutes a medium complexity bioreactor process model with 11 coupled ordinary differential equations describing standard measured variables (such as biomass, substrates, products and by-products) and 36 parameters including yield coefficients and inhibition constants [20]. Using MATLAB mathematical computing environment software (The MathWorks, Natick, MA, USA) and the ode15s numerical ODE solver package, floating point operations were counted and required time were calculated based on development of processing power for: 1. solving the ODE system with standard settings over 100 h (Fig. 3A) and 2. performing parameter optimization for 5 parameters using the fminsearch package with standard settings and initial deviations of 20% from the final values (Fig. 3A) ^A.

Assuming industry and research institutions to have state-of-the-art processing power and defined thresholds for feasibility, real-time applications using the reference system became feasible between 2001 and 2008 (solving time less than one minute, or solving time less than 10 s, respectively). While parameter optimization is not necessarily time critical in all cases, a few methods with real-time or semi-continuous parameter optimization exist [21] which, depending on the complexity of the system, have an even higher demand for processing power. For these cases, the maximum system size that can be simulated and optimized depends on available processing power, desired interval of simulation on optimization and maximum allowed deviation from given trajectories or predefined sets of parameters. It can be concluded that today’s processing power is sufficient for most applications, however, complex tasks of simulation and optimization on a larger scale (see also whole cell models) cannot yet be performed in real time.

2.1.3. Quantum computing

A quantum processor is a processor whose function is based on quantum mechanical states rather than the laws of classical physics or computer science.

At its core, the technology is based on qubits (quantum bits), which are manipulable two-state quantum systems. As such, they are correctly described by quantum mechanics and have only two states that can be reliably distinguished by measurements. The qubit plays an analogous role comparable to the bit in conventional computers. It is the smallest possible data storage unit. Since 2018, increasing interest of governments, research organizations as well as computer and technology companies worldwide in quantum computer technology has driven early development of first quantum computer proof-of-concepts. On a small laboratory scale, quantum computers with a up to 12 qubits have already been realized e.g. to model the isomerization mechanism of diazene [22], [23]. In many regards, quantum computing is considered to be one of the key technologies of the 21st century, as vast increases in computing power are anticipated. This new technology may ultimately open up new possibility for real-time simulation and manipulation of comprehensively complex biological systems, such as full reconstructions of cellular metabolism to create true digital twins of living cells.

2.2. Data storage and memory development

In 1954, Reynold Johnson and his team at IBM developed the first commercial hard Disk Drive (HDD), which was referred to as Model 350. The first units were commercially available in 1956. Model 350 weighted over one metric ton with a storage capacity around 3.75 MB of data. While the general concept of storage of digital data in magnetic material in HDDs has not changed, the technology was refined in the following years, such as by modifications of the read/write head. In the following decades, new developments yielded dramatic increases in data density per area which led to overall reductions in costs per bit. Overall, this dramatic increase in data storage density and capacity established HDDs as the preferred form of computer data storage ^A.

2.2.1. Mass storage for the mass market

The first HDDS for the mass market were available in the late 1970s to early 1980s, with prices of several hundred US dollars per MB. Up until 2010, HDDs were available in ever increasing capacities and lowered prices (Fig. 3B). In 1992, the average price per MB decreased to approximately 2 dollars, which is roughly the equivalent of storing 100 genomes of E. coli strains for 1000 US dollars (Fig. 3B), more than one hundred times cheaper than a decade ago in 1982. Considering available funds per research group, in the mid-1980s, the price for storing 100 genomes of E. coli equaled almost 10% of the yearly budget of a NIH principal investigator, which dropped below 0.1% only a decade later in the mid-1990s. Thereafter, storage and analysis of genetic data became feasible for research groups even without focus on special information technology equipment ^A.

In 2004, prices dropped below 1 US dollar per 1 GB of storage capacity, and further decreased until today in 2020, 1 GB of storage capacity is priced at 2–3 cents. Consequently, this means that the NCBI GenBank genetic sequence database [24], an annotated collection of all publicly available DNA sequences, currently featuring 216 million entries with a total size of roughly 400 GB, nowadays takes up disk base worth less than 10 US dollars. It can thus be concluded that pricing of disk storage capacity is no longer an issue, and consequently, there is an increasing demand for mass storage solutions with faster read/write speeds at similarly low prices, as visualized by the rise of the solid-state disk (SSD) technology. While SSD technology was introduced to the market in the 1990s, competitive price-per-storage ratios were not achieved until the 2010s. Nowadays, SSD technology is still roughly 10 times more expensive than the HDD equivalent ^A.

2.2.2. Random-access memory

Random-access memory (RAM) is a specific type of fast read/write memory that is typically used to store executable code or working data to facilitate fast access. One standard task for investigating biological system is the search for information in databases, such as genetic code or metabolic pathway information. For this task, typically a search is either performed locally or on a different remote computer/server, which requires the data to be sent over a network or the internet. Having sufficient RAM on the computer executing the search to load the entire information to be analyzed is crucial for time-efficient search tasks.

One example for this is the comparison of genomes and search for similarities by appropriate tools through a database, such as the basic local alignment and search tool (BLAST) of the NCBI, which is available since 1990 [25]. Starting in early 1970s, along with the development of the first home computers, both mass storage and RAM were developed simultaneously leading to constant increases in capacity up to today. A good estimate for RAM pricing over the time is that RAM was constantly between 10-times more expensive than HDDs in the early 1980s (approximately 3000 $ vs. 300 $) and 100-times more expensive than HDDs in the early 2000s (0.4 $ vs. 0.04 $). Nowadays, fast RAM is roughly 100–300 times more expensive than current HDDs. With this information on availability and pricing, it can be concluded that, since RAM is not meant to accommodate large amounts of data, RAM was not a bottleneck for development of biotechnological techniques. When the BLAST algorithm became available in 1990, the price for RAM to be able to load one entire genome of E. coli (4–8 MB) for search against a database was roughly 150–300 $ ^A.

2.3. Internet & network communication bandwidth

The first server hosting the first website (info.cern.ch) in the world wide web was put up by British scientist Tim Berners-Lee at CERN in 1991. Ever since then, rapid development in terms of hardware and software for internet access and application followed. The internet quickly found its way into daily life in many areas from professional applications to leisure.

A major part of the development includes connection speed and bandwidth. Comparing the speed of earliest forms of home internet access by dial-up via phone line and modem (0.014 Mbps–0.056 Mbps) to current technologies, a more than 1000-fold increase took place over the last three decades, as visualized by the current average worldwide household internet connection download speed of 75.41 Mbps in 2020 ^A.

With the development of the first technologies greatly exceeding modem connection speed, commonly referred to as broadband connections such as digital subscriber lines (DSL), the internet became relevant as a fast and easy alternative for data transfer. With the development of more powerful and thus more demanding mobile devices and smartphones, technologies for mobile internet connection rapidly evolved.

While in the mid 1990s, transfer of an E. coli genome took 10–30 min, with today’s average connection speed of 75.41 Mbps, this is achieved in roughly half a second. Nowadays, current fast mobile internet connections of the fourth generation (4G) lower this further in the range of millisecond. New developments of mobile internet via the fifth generation (5G) that are currently being developed will surpass fastest existing technologies by at least a factor of 10. It is however for reasons beside bandwidth such as localization and positioning as well as latency that 5G will be a key technology in the coming decade.

Currently, there are virtually no applications where internet bandwidth is limiting. Essentially, bandwidth only becomes an issue when real-time applications demand fast transfer of larger lumps of data in restricted amount of time. It is mainly future envisioned applications with demanding amounts of data transfer where bandwidth might be an issue. These envisioned applications include streaming of virtual reality and augmented reality material in higher quality and transfer of video material in real-time for digital image processing, such as for communication of autonomous vehicles.

3. Modeling techniques for online estimation of state variables

During early development of a bioprocess it is crucial to gather information on the biological basis, commonly represented by correlations and kinetics as well as knowledge of as many parameter values and time course of state variables as possible to understand and optimize the process. When reaching production phase, critical process parameters must be monitored and deviations of process drifts from an expected optimal trend detected to ensure quality, process efficiency and safety [26], [27]. The monitoring of process data, ideally in real-time, is often difficult because suitable sensors for online measurements are not always available. A result is a lack of well resolved or even missing process data of important process variables. This lack of data led to the development of indirect data assessment via the combination of hardware sensors and process models, so called soft sensors, to derive so far inaccessible data [1], [27], [28]. Conventional online bioprocess monitoring until the 1970s commonly relied on electrochemical probes for in situ measurement of pH (glass electrodes), pO₂ (Clark-electrode), pCO₂ (Severinghaus electrode) and temperature (resistance thermometer) [29], [30], [31], [32]. A development towards optodes and micro sensor arrays followed, which enabled measurements with less lag times and more convenient placement and size of sensor systems [33], [34], [35], [36], [37]. Besides from these easily accessible and online measurable parameters important state variables like biomass, substrate and product concentrations were measured offline or at-line [27]. The state variables could then only be assessed with a considerable time delay making immediate and automated corrective control actions basically impossible [38]. Furthermore, offline methods are laborious, have a low resolution and require skilled workers hence are relevant parts of the overall manufacturing costs [1], [27], [38], [39]. Murao and Yamashite were pioneers of computer assisted monitoring concepts for bioprocesses in 1967 [40]. So called soft sensors rely on computer models that are combined with hardware sensor data. Soft sensors are used to estimate real-time information, predict future process trends or display what already happened of formerly inaccessible state variables (see Table 1) either by employing unspecific data (e.g. spectra) and empirical modeling approaches (e.g. ANNs) or process measurements (e.g. in/off gas) and mechanistic or pseudo-mechanistic models (e.g. mass balances, stoichiometric growth models) [1], [38], [40]. The PAT regulatory framework of the FDA names soft sensors as central tools for real time monitoring and control of critical quality attributes [5]. Before the introduction of soft sensors important state variables have not been accessible. With the development of the PAT initiative, this has led to a breakthrough in process and quality control. Soft sensors are now commonly used today especially in the pharmaceutical industry. Different model techniques for online estimation of state variables were developed over time: (i) 1960s: filtering techniques e.g. (extended) Kalman filter [41], [42], (ii) 1970s: balancing equations [43], (iii) 1980s: adaptive estimator/observer [44], [45] (iv) 1990s: artificial neural networks (ANN) [46] and (v) 1990s: hybrid modeling [47].

3.1. Filtering techniques – the (extended) Kalman filter

In the 1960s Kalman developed the Kalman filter algorithm for improved reliability of estimated data and noise filtering. The filter was used for state estimation of linear systems. The filter was extended by Kalman & Bucy to non-linear systems using model linearization (extended Kalman filter) [41], [42]. To deploy the filter for state estimation, a model to describe the (non)-linear system and a priori knowledge of stochastic properties like mean and covariance of measurement errors and noise disturbance are required [8] The accuracy of the before stated requirements largely determine the efficiency of the Kalman filter method. The Kalman filter has been used for estimation of growth rate, biomass, respiratory quotient, yield as well as substrate and product concentration in combination with hardware like HPLC (high-performance liquid chromatography), NIR (near infrared spectroscopy) and FIA (flow injection analysis) [48], [49], [50], [51].

3.2. Mass balances

In the 1970s Cooney et al. proposed to use elemental balances for estimation of fermentation parameters by using an overall chemical reaction to describe cell mass as shown in (1) [43]

$$\alpha C_a{H}_b{O}_c+\beta O_2+\gamma N{H}_3\to C_d{H}_e{O}_f{N}_g+\delta C{O}_2+\epsilon H_{2}O$$ (1)

where the educts account for substrate, oxygen and ammonia and the products are cell mass and the metabolic end products carbon dioxide and water. Requirements are that the chemical formulae are constant and known (indices a-g) and stoichiometric coefficients $\alpha -\epsilon$ can be calculated from elemental balancing in combination with measured oxygen uptake rate (OUR) and the carbon evolution rate (CER). The use of balancing equations has been reviewed and applied in the past [1], [40], [52] and is still reported for current research (see Table 1).

3.3. Adaptive observer

An adaptive observer or adaptive estimator as proposed in the 1980s eliminates the inherent disadvantage like model linearization required for the extended Kalman filter and the need of knowledge on model uncertainty [40]. The adaptive observer updates the estimated model outputs with a corrective term proportional to the difference between measured and model predicted values. Additionally, unknown kinetic parameters may also be updated according to the prediction error [8]. In the 1980s, the group of Shioya was among the first to report an estimation of biomass concentration and specific growth rate in a fed batch cultivation of Saccharomyces cerevisiae by an extended adaptive Kalman filter algorithm. The algorithm deployed moving averages, dynamic mass balances and an adaptive noise covariance matrix of the system which was updated according to the prediction error [44], [45].

3.4. Neural networks

In the 1990s new approaches to predict process variables independent of a process model but by using artificial neural networks (ANNs) respectively pattern recognition based on historical cultivation data was proposed [46], [53]. The very beginnings of the ANNs date back to 1943 were McCulloch & Pitts proposed a computational model inspired by the brain [54]. A neural network is composed of layered interconnected nodes (~neurons). The network is fed at the input layer with scaled data, which is then propagated through the so-called “hidden layer” to the output layer. Signal strength is thereby altered by scalar weights at each connection of the nodes [46], [55]. In 1990, Thibault et al. introduced the approach of McCulloch & Pitts to dynamic bioprocess modeling. They computed biomass and substrate concentrations for a continuous stirred tank reactor and described the neural network as “accurate with a certain degree of noise immunity” with the advantage that no a priori knowledge on the interrelations of important variables is required like in other modeling approaches [46]. ANNs have been used in the recent years for monitoring bioprocesses in combination with UV/Vis or fluorescence spectroscopy [56], [57]. Furthermore, ANNs have been employed for various monitoring purposes in combination with an electronic nose as extensively reviewed by Hu et al [58].

3.5. Hybrid models

In 1992 Psichogios and Ungar proposed a hybrid of neural network and a first principle model to predict biomass and substrate concentration as well as growth rate for a fed batch bioreactor. They concluded that the combination of the partial first principles model incorporating available a priori process knowledge complemented by the neural network as estimator for unmeasurable and difficult to assess process parameters shows better properties than a stand-alone neural network with respect to accuracy of inter- and extrapolation. Furthermore, the hybrid model is easier to analyze and interpret also requiring significantly less training data than the standard “black box” neural network [47]. In 2019 Zhang et al. proposed a different hybrid model combining physics-based and data-driven modeling for online monitoring, prediction and optimization of a fed-batch micro algal lutein production process. The authors concluded that hybrid modeling is an useful potential tool for compensation of low quality and quantity of available data. Furthermore, in an industrial environment, it is an effective strategy to overcome the lack of a priori knowledge on physical mechanisms of the process, high costs caused by frequent sampling and laborious measurements as well as challenges in pre-determining set points for fed batch processes [59]. Table 1 provides an overview of the most recent trends in soft sensor development for bioprocess monitoring.

4. Modeling in process control

Adjustment of the extracellular environment is basically the only way to direct intracellular mechanisms in order to achieve a desired outcome [40]. In 1969 Grayson and Yamashita et al. were among the first to describe computer controlled biotechnological processes with Grayson mentioning the use of computer control for pilot plants as well as for large-scale bioreactors [40], [69], [70], [71]. In the early 1970s L.K. Nyiri presented a concept for data acquisition and analysis as well as computer control for bioprocess engineering suggesting online optimization and multilevel control strategies [71], [72]. In 1982 Rolf and Lim describe “an enormous impact in the area of real time computer applications” triggered by relatively inexpensive and reliable computer hardware as well as by the advent of microprocessors which made the integration of computer control to fermentation processes feasible. Advanced control concepts suggested in the 1950s and 1960s could be applied only in the 1970s with the till then unprecedented improvements and availability of computer hardware [71]. Low level control loops with simple proportional-integral-derivative (PID) controllers for temperature, pH and DO are still widely applied today in industrial biotechnological processes. Many relevant parameters such as productivity, growth rate and biomass concentration can usually not directly be measured online and are therefore mostly indirectly derived from primary data. To control growth rate or biomass concentration, static PID controllers are insufficient because they do not consider time-varying process dynamics that would cause changes of optimal PID parameters. To circumvent this drawback, PID controllers can be coupled with systems that update the parameters for proper control response of a dynamic process [73]. Different advanced model-based strategies for bioprocess control are available today that consider partly the complex dynamics and current state of a bioprocess such as (i) 1970s: adaptive control [74], (ii) 1980s: statistical process control [75], (iii) 1980s: fuzzy control [76], (iv) 1990s: ANN control [77] and (v) 2000s: model predictive control (MPC) [78].

4.1. Adaptive & nonlinear control

Due to the time varying nature of a bioprocess’s characteristics, it is beneficial to adjust the control parameters during the cultivation process to respond to process dynamics [79]. Adaptive controllers are based on non-linear algorithms. They dynamically update parameters during the operation following the non-linear bioprocess dynamics or uncertainties. In 1958 Rudolf E. Kalman, known for the invention of the Kalman filter, discussed a “machine” that automatically optimizes its control system to regulate an arbitrary dynamic process [80], [81]. In 1979, McInnis et al. were among the first to report an adaptive controller using a microcomputer to control dissolved oxygen levels in biological wastewater treatment [74]. Bastin et al. discussed an adaptive controller to regulate an anaerobic fermentation process for waste degradation in 1983 [82]. One year later, in 1984, Dochain and Bastin summarized adaptive control algorithms for nonlinear bacterial growth systems to control substrate concentration or production rate. They emphasized that their developed algorithms have the original feature that parameter estimation is performed simultaneously to the control action [83]. Adaptive control is still applied today. For example, in one of the most recent approaches in 2019, Abadli et al. used generic model control in combination with a linear Kalman filter for reconstruction of assumed unmeasurable variables to compute an adaptive control strategy. They aimed to maximize biomass production in a fed-batch cultivation of E. coli with the developed adaptive controller by optimal feeding. They aimed to maintain the substrate concentration in-between limitation and excess, the latter to prevent acetate formation. Therefore, they assembled a macroscopic model composed of nonlinear differential equations considering the respiratory and respiro-fermentative metabolic pathways. With their control strategy based on that model an operation within the boundary between those two metabolic regimes was possible [84].

4.2. Statistical control

It is often difficult to develop an accurate deterministic model for a bioprocess due the complexity of microbial reactions and changing characteristics of microbial nature over time. (Multivariate) statistical control concepts rely on time-series of historical data coupled with a statistical method e.g. for discrimination of state variables of regression analysis. Therefore, no a priori process knowledge is required making the approach empirical with the potential to detect and correct deviations of abnormal batches from an ideal process course in real time. An advantage for this data-driven technique is that comparably few resources are required, and model development times are short. On the other hand, the success of this method significantly depends on data quality and how representative the collected process information was [75], [85]. In 1984, Kishimoto et al. were among the first to develop an experimentally validated statistical control strategy for a bioprocess. They used historic data from “several” fed batch cultivations of Saccharomyces cerevisiae to develop a statistical method to discriminate state variables of regression analysis. They experimentally confirmed their statistical control concept for the control of glutamic acid production [75]. In 2019 a multivariate statistical process control model in combination with Raman spectroscopy and correlation optimized wrapping method for alignment of desynchronized historical data has been applied for early detection of abnormal operation conditions and contaminated batches for antibody production in cell cultures [86]. For this being rather a monitoring than a control procedure only few statistic control concepts are reported in the recent years. In 2016 Duran-Villalobos et al. reported a statistical control concept based on an adaptive multiway partial least squares model in combination with a quadratic cost function to optimize operating conditions of a subsequent batch. The batch to batch optimization strategy was then benchmarked with a fed-batch fermentation simulation of S. cerevisiae. The authors reported an almost 5-fold increase of biomass yield in <20 batches [87]. In 2020 the same authors applied their previously developed multivariate statistical process model to “a realistic industrial-scale fed-batch penicillin simulator” for batch to batch optimization of penicillin yield by adjusting the glucose feed rate [88].

4.3. Fuzzy control

The term “fuzzy set” has been popularized by Lotfi Zadeh in 1965. Whereas the term first appeared more than a decade earlier in a paper in French (“ensembles flous”), written by the Austrian mathematician Karl Menger [89], [90], [91]. For fuzzy sets, the membership of an element in a set can be assessed gradually. This means elements of a fuzzy set can have a certain degree of membership in contrast to the binary assessment of element membership in classical set theory. For fuzzy (sub-) sets elements of a universe set are assigned to the real unit interval [0, 1] by the so called membership function, a generalized characteristic function [92]. Fuzzy control has originally been deployed for an automatic train system in Japan in 1983 outperforming common PID controllers. For bioprocess control the fuzzy control concept is of special interest because it can compensate for uncertainties arising from the non-linear structure of such processes without the necessity of a complex process model [76], [93], [94]. In 1985 fuzzy control concepts were applied for the first time to a bioprocess to produce glutamic acid by controlling the sugar feed rate as claimed by the authors. They reported that their control system based on fuzzy theory could accurately control sugar feed rate to maintain sugar concentration in “a suitable range” for glutamic acid production. Furthermore, they reported that their control system was insensitive to changes in sugar lots and activity of the microorganism during operation [76]. Fuzzy control has been applied in industry in a bioprocess for the large-scale and long term (2 years) production of Vitamin B₂. Fuzzy control was used by the authors to adjust pH as well as feed rate for substrate. The vitamin B2 production as well as yield could be improved by 6–16% and 4–11% respectively compared to common controllers [95]. Recent articles on the application for fuzzy control seem to be limited. One of the most recent works from 2018 deployed a fuzzy control system to control dissolved oxygen levels for a heterologous protein expression process using recombinant E. coli [96].

4.4. Neural network control

The development of neural networks which model a biological neuron has its origin in the 1940s and was initially described by McCulloch & Pitts (see previous section) [54]. The back-propagation learning algorithm for neural network training was first applied in the PhD thesis of Paul Werbos in 1974 for estimation of a dynamic model that predicts nationalism and social communications [97], [98]. Rumelhart, Hinton and Williams rediscovered and popularized the in nowadays widely applied technique for neural network training in the mid 1980s [98], [99]. A neural network can be used to calculate a control output signal hence function as an automatic controller [100]. As described here previously for statistical controller, neural networks rely on historical data and development does not require detailed a priori process knowledge hence reducing model development time [101]. Linko et al. suggested a neural network for the control of a fermentation process to produce glucoamylase [102]. In 1993 Chtourou et al. were among the first to apply a neural network for non-linear control of a continuous stirred tank reactor. The neural controller regulated the dilution rate to maintain a certain substrate concentration [77]. Only few recent neural network control applications are described among them the work of Peng et al. from 2013. The authors combined a genetic algorithm with an ANN for optimization of the production of marine bacteriocin. For the control strategy fermentation parameters were optimized stagewise using the combination of ANN and genetic algorithm to create an optimal control trajectory. By that the authors increased the production of marine bacteriocin by 26% [103]. In 2019 Beiroti et al. developed a control strategy based on a recurrent neural network (RNN) for the production of hepatitis B surface antigen in a methanol fed batch with Pichia pastoris. The authors reported that the newly developed RNN was used in a PID control system for maintaining a predefined specific growth rate at a constant value by adjusting the methanol feed rate. They report that the RNN based feedback controller has a “significantly higher process efficiency” than a conventional open-loop controller with predefined feeding strategy [104].

4.5. Model predictive control

MPC accounts for computer algorithms that use process models for predicting current output and future responses of a system. MPC algorithms optimize future process behavior by predicting a sequence of variable adjustments at every control interval. The re-calculation of the optimal sequence is repeated for every control interval which length (minute wise to once an hour) varies depending on the latency of the process [38], [105]. To calculate the required control action a cost function is minimized over the whole process time allowing to follow a variables’ trajectory e.g. maximize productivity or minimize costs, respectively [79], [106], [107]. The success of MPC depends on the suitability of the applied model as well as on the availability of online measurements for modeled compounds e.g. by soft sensing. If the latter cannot be considered, e.g. due to probe failure a so-called model-plant mismatch can occur. If the controller does not recognize the deviation between model and plant, then the resulting control action will not be sufficient to minimize this deviation [38]. MPC history begins in the 1960s with the development of modern control concepts in the works of Rudolf Kalman and the closely related minimum time optimal control problem and linear programming discussed by Zadeh and Whalen in 1962 [41], [105], [108], [109], [110]. At first mostly used in the petrochemical industry, MPC became also a prominent advanced control solution in many other disciplines as reviewed by Quin et al [105]. The very core of ever MPC algorithm is the moving horizon approach also known as “open loop optimal feedback” proposed in 1963 by Propoi [109], [111], [112]. In 1978 Richalet et al. first summarized applications for as they called it model predictive heuristic control (MPHC) [113]. In 2003 Qui et al. reported >4600 applications for MPC but none explicitly assigned to bioprocesses [105]. Zhu et al. were among the first to propose MPC applications for bioprocesses in the year 2000. They transferred the concepts of model predictive control from chemical engineering (e.g. for regulation of size distribution in industrial crystallizers) to a continuous yeast bioreactor. They developed a dynamic model, which combined population balance equations (PBE) to estimate cell mass distribution with substrate mass balance. The numerical solution procedure to approximate the PBE model by an interconnected set of nonlinear ODEs included orthogonal collocation on finite elements. By linearization and temporally discretizing the ODEs of the PBE model the resulting linear state space model could be applied to the MPC concept. The control variable was the discretized cell number distribution and the manipulated variables were dilution rate as well as substrate concentration in the feed solution. With the MP controller the authors were able to stabilize steady-state conditions and periodic solutions for the continuous yeast bioreactor [78]. Also, in the year 2000 Kovárová-Kovar proposed a MPC based on an ANN which replaced a knowledge-based model for riboflavin formation. The optimization goal was to maximize total product titer as well as product yield. The manipulated variable was the feed rate and the authors were able to increase product concentration and yield by >10% [114]. MPC strategies can be distinguished by the inherent optimization problem. For example, MPCs have been used in the recent years to follow the trajectory of biomass concentration [115] or substrate concentration [116] respectively. Other than following a trajectory an MPC approach can also be used to maximize a process variable namely product (ethanol) concentration as shown in 2016 by Chang et al. The authors used a dynamic flux balance model and adjusted feed rate as well as DO to maximize ethanol concentrations which they could increase by 8.0–14.7% compared to the conventional open-loop operating policy [117]. Table 2 provides an overview of the most recent trends for applied modeling technqiues in bioprocess control.

Table 2.

Most recently (2016 – today) applied modeling techniques in bioprocess control.

Model category / applied model	(Control) task	Organism/Product	Source / Year
Adaptive control / generic model control & linear Kalman filter	Maximize biomass production & maintain substrate concentration at optimum by optimal feeding strategy	E. coli / biomass	[84] /2019
Statistical control / multivariate statistical control model, Raman spectroscopy & correlation optimized wrapping	Early detection of abnormal operation conditions and contaminated batches for antibody production in cell cultures	Chinese hamster ovary (CHO) cell line / IgG antibodies	[86] /2019
Statistical control / adaptive multiway partial least squares model & quadratic cost function	Batch to batch optimization of biomass- respectively penicillin yield by adjusting glucose feeding	S. cerevisiae / penicillin	[87], [88] / 2016–2020
Fuzzy control / fuzzy control system	Dissolved oxygen (DO) levels	E. coli / heterologous protein	[96] / 2018
Neural network control / RNN	Controlling growth rate by methanol feeding strategy	P. pastoris / hepatitis B surface antigen	[104] / 2019
Model predictive control / dynamic flux balance model	Maximizing ethanol concentration by adjusting feed rate & DO levels	S. cerevisiae / ethanol	[117] / 2016

5. Process optimization and integrative modeling concepts

Depending on the product and consumer acceptance, non-GMOs are often preferred in bioprocesses. Therefore, strain engineering cannot be performed which would optimize the process outcome. This leaves smart process control as the go to option to maximize production efficiency. Bioprocesses optimization today is in many cases still empirical and involves either laborious design of experiment (DoE) or availability of representative data along with data driven methods (e.g. ANNs). This makes process development time consuming and costly [118]. Traditional empirical process development based on expert knowledge and trial-and-error cycles is associated with long development times that increase the time-to-market hence leading to a loss in profits [27], [119]. Including mathematical models into the DoE workflow presents a powerful tool to accelerate the optimization of bioprocess that are subjected to dynamic changes in culture-, environmental and feed conditions as reviewed by Abt et al. The overall goal of DoE is to optimize process variables with respect to a desired result (e.g. product titer) respectively to validate a hypothesis. The most commonly applied method for experimental design is statistical DoE [118].

Ronald A. Fisher, a British statistician and pioneer of statistical DoE, first introduced the concept of statistical planning and evaluation for field experiments in agriculture to assess the effect of e.g. fertilizer treatments on crop growth in the 1920s as summarized by Box [120]. In his early works, Fisher grouped different lands with the same experimental conditions in blocks. When he compared the blocked experiments, he was able to increase precision and decrease the error. After the introduction of Fishers concepts for randomization, replication and blocking they fast became state-of-the-art practice. Different authors adopted Fishers techniques for experimental design as reviewed in [121] among them Box and Wilson who introduced the response surface method (RSM) in 1951 [122]. RSM may be used for the optimization of multi parameter processes and accounts for “a collection of statistical techniques used for studying the relationships between measured responses and independent input variables” [123]. In their work Box and Wilson used a polynomial model to approximate an optimized response with a sequence of experiments [122]. When applied to a bioprocess the RSM on the one hand bears the advantage that only little process knowledge is required but on the other hand a static model is used which neglects process dynamics and trajectories. The still rarely used RSM concept was applied for bioprocesses in 1967 by Auden et al. The group was among the first to perform growth medium optimization using RSM [124]. In traditional DoE, experimental space is adapted in an iterative, costly and time-consuming manner with a sequence of experiments [118], [125]. This is because process variables and boundaries of process variables in traditional DoE are defined by expert knowledge which does not consider process dynamics [118], [126], [127]. This may lead to poor decision making and is opposed to the quality by design (QbD) approach issued in the guideline Q8(R2) of the international conference of harmonization (ICH) [118], [128]. By deploying model-assisted DoE, the number of experiments for an iterative adaptation of the experimental space may be reduced and process dynamics included into the decision process [118]. Experiments can be designed to optimize the process itself along with the process model (iterative learning) [129] or to estimate model parameters (model-based design of experiments) [130]. For iterative learning mechanistic, empirical or hybrid models were used and are usually updated batch-to-batch [131], [132], [133]. Whereas in 2007 Teixeira et al. reported to update their process model sample-to-sample. While running the experiments, the metabolic model was reparametrized at each sampling point to recalculate the optimal feeding strategy of glucose and glutamine to produce a recombinant glycoprotein in BHK-21A cultures [134]. In 2012 Morales-Rodriguez et al. worked on the comparably new approach of optimizing a bioprocess by identifying sources of uncertainties. Uncertainties were identified via global sensitivity analysis. Subsequently an uncertainty analysis was conducted to quantify their effect on performance evaluation metrics and stochastic programming was used for process development considering these uncertainties [135]. In 2016 Stosch et al. introduced the concept of what they referred to as intensified DoE to upstream bioprocess optimization and development. Intensified DoE is a hybrid solution that combines the inherent process knowledge of mathematical models with statistical DoE. Stosch et al. evaluated intraexperimental variations in combination with dynamic modeling to exploit the process operation space in a manner of DoE. They concluded that the number of experiments, in limit, can be decreased by the number of intraexperimental variations per experiment [136]. In the follow-up work of Stosch et al. in 2017 they were able to reduce the amount of required experiments by 40% compared to traditional DoE. Here they combined DoE methods with a hybrid model framework to characterize an E. coli cultivation process [137].

6. Current research and future trends

When looking at current research and possible future trends (Fig. 4) one may notice that models tend to get more detailed becoming an ever more accurate representation of reality. Initially proposed in 1979, whole cell models (WCMs) represent such a trend towards a higher degree of model accuracy [138]. The construction and validation of comprehensive WCMs that mirror cellular physiology considering e.g. transcription, regulation and protein expression pathways is an extensive task. WCMs consider the incorporated use of all genes, gene products and molecules predicting how genotype determines phenotype. When built the WCMs may be used as a digital microscope to unmask potentially hidden biochemical interconnections which are difficult or impossible to asses with physical experiments. Karr et al. described the key features of their bacterial whole cell models as: “single cellularity; functional, genetic, molecular, and temporal completeness; biophysical realism including temporal dynamics and stochastic variation; species-specificity; and model integration and reproducibility”. Dror et al. report that with increasing computational power, it becomes possible to capture molecular dynamics of cells (e.g. protein folding, drug binding, and membrane transport) in atomic detail. Conceivable applications for WCMs are in (personalized) medicine, bioengineering and bioscience [139], [140], [141]. In parallel flux balance models of bacterial metabolism (in genome-scale) were constructed and updated to represent the cellular metabolic network in ever more detail. Varma and Palsson reported the first static genome-scale flux balance model in 1994 [142]. The flux balance models have been extended to account for transcription, translation and signaling [143], [144], [145]. In 2011 Orth et al. presented a reconstruction of the genome of E. coli considering 1366 genes (covers ~ 32% of 4325 E. coli ORF) and 2251 metabolic reactions with 1136 unique metabolites [146]. The scale-up of bioreactors and biotechnological processes is a critical operation in industrial biotechnology. In many cases, due to limitations in the applied methodology, a scale-up results in reduced titers, yields or productivities [147]. For the layout and design of bioreactors, mainly of the stirred tank type, there was a strong focus on the numerical simulation and analysis of local effects in the 1980's [148], [149], [150]. However, the models developed at that time could not be used for the modeling of entire reactors due to a lack of computing power [151]. The validation was usually carried out with simple substance mixtures on laboratory scale. Complex or industrial systems have only been investigated to a limited extent. Due to various interconnected dependencies such as bubble size distribution, local turbulence variable backmixing, concentration distribution and mass transfer the results of the investigated laboratory systems can hardly be transferred to industrial scale [152], [153]. In 2014 the authors Jablonski & Lukaszewicz described a method for the evaluation of microbial biomass concentration for ADM1. The calibration of the model was performed using real world data from a CSTR reactor. To calculate the initial state of microorganism communities that utilize acetate and propionate the specific anaerobic activity was used [154]. In the following year the same group published an article using an optimized ADM1 model that could simulate a continuous fermentation process using rapeseed oilcake as substrate with high accuracy [155]. In a different study, the successful application of a model to a large-scale industrial process has for example been realized with the anaerobic digestion model no.1 (ADM1). It has successfully been applied to describe the performance of a full-scale anaerobic sludge digester of a municipal waste water treatment plant. The authors performed a model calibration (dataset of 200 days) and validation (independent dataset of 360 days) to describe parameters like chemical oxygen demand, pH, alkalinity as well as methane production [156]. For the description of biological cellular systems, various approaches such as unstructured kinetic models or population models are common, which can be solved with numerical methods [20], [157], [158], [159]. To obtain detailed information about the flow conditions in bioreactors, these models are combined with CFD (computational fluid dynamics) methods. Thus, changes of mass transfer surfaces and relevant properties can be tracked in time and space. This also allows a representation of the flow conditions, heterogeneities and mixing processes in the system, which can be used for scale transfer of biotechnological processes accounting for effects on biomass resulting due to an industrial scale-up [160]. As such, by combining CFD and model for microbially catalyzed reactions, specific cell states such as stress response as well as (specific) production rates can be predicted depending on the geometry and scaling of the bioreactor [161], [162]. The application of these approaches in real-time is nowadays still restricted to comparably simple systems at lower resolutions, as merging CFD and dynamic models for microbially catalyzed reactions is accompanied by a high demand of processing power. In the future, these integrated approaches are a promising trend for a truly knowledge-based bioreactor scale-up and layout [147]. Eventually, once real-time operation is made feasible, this approach can be advanced to a framework for online control of bioprocesses. The ultimate digital representation of an entire process is the so called “digital twin”. The digital twin as fully digitized process may be used to reduce the amount of experiments required drastically and to approximate optimal working conditions. The digital twin concept was introduced by Michael Grieves originally for the formation of a product lifecycle management center in 2002. He reported that the concept of the digital twin “is based on the idea that a digital informational construct about a physical system could be created as an entity on its own. This digital information would be a “twin” of the information that was embedded within the physical system itself and be linked with that physical system through the entire lifecycle of the system” [163]. The concept remained the same over the years since its introduction in 2002. The term “digital twin” whereas evolved from originally “mirrored spaces model” (2005) to “information mirroring model” (2006) and finally “digital twin” [164], [165], [166], [167], [168]. Grieves summarized his works in 2019 and mentions John Vickers of NASA who coined the name digital twin for the model [168]. NASA has been using the name in their technology roadmaps for sustainable space exploration in 2010 [169]. The VP of Software Research at GE, Colin Harris, introduced the digital twin as a tool for industrial processes in 2016 2(Fig. 4).

Fig. 4.

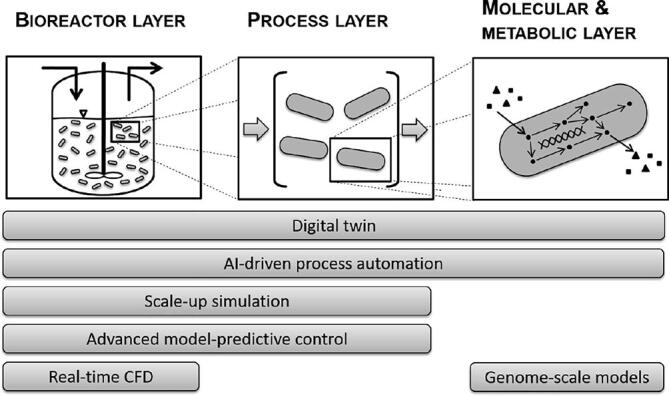
Trends of future and current model-based techniques with proposed assignment to bioreactor, process and molecular & metabolic layer of modeling.

In his presentation, he remotely mitigated damages of a wind turbine by interacting with a voice-activated software, which he called “Twin”. For digital twins in bioprocesses, Zobel-Roos et al. oppose efforts to benefits of digital twins for applications in biologics manufacturing with regard to the QbD and PAT framework [170]. The application of digital twins to develop “smart” processes for “Biopharma 4.0” has recently been reported by Nargund et al. in 2019. They state that digital twins enable real time process analysis, control, extrapolation and optimization which may be summarized as predictive manufacturing [171]. A decade in the future, industry will be heavily influenced by concepts like internet of things and machine learning. These concepts are related to the generic term industry 4.0. A higher or full degree of automation without the need for operators to interfere into the bioprocess will be achieved. If an intervention is needed after all, the process will be controllable and monitored remotely. All bioprocesses could be entirely mirrored by a digital twin which is used for simulations and predictions. Growing data clouds with increasing data density, quantity and quality along with new, prior unmeasurable state variables will become reality [172].

With an evolving industrial bioeconomy, a new demand and specific requirements for model-based methods emerged. In a bio-economy, the aim is to use substrates such as sugars or organic acids as efficiently as possible. One of the main sources of carbon, for example, are lignocellulosic hydrolyzates. However, the composition of this substrate is strongly dependent on the batch and raw material used. Especially with regard to a preferably complete conversion of the substrates within the framework of efficient processes, problems arise in process optimization, as different process sequences are always necessary (e.g. real-time adjustment of feed rates/profile). For this purpose, an optimization using real-time data is necessary, which requires specialized soft sensors and models. These can for example be realized using AI-based methods (Fig. 4). Therefore, especially in the context of complex biological problems, AI provides an interesting and versatile framework for model development with the potential for broad applications.

7. Summary and outlook

In the last decades a strong continued development and advancement of modeling techniques as well as a concomitant improvement of hardware resources has taken place. Due to increasing capacities of new hardware, performance-intensive concepts become realizable. Currently, computing capacity only reaches its limits for specific applications with very high performance requirements (e.g. CFD or WCM). Furthermore, current trends are also determined by fields of application, such as the emerging industrial bioeconomy. Future industrial processes will only be successful if they are closely interwoven in process development steps and optimized for resource and cost efficiency. This leads to a trend towards an adaptive advanced process control. The general data availability and density is increasing, also due to high-throughput omics platform technologies as well as new soft sensors concepts. Initially fueled by governmental guidelines like the PAT initiative of the FDA, novel soft sensors and techniques have since then evolved to ensure product quality and provide data in real time. The aim of future modeling approaches will be to create broadly applicable, flexible, and robust technologies for industrial biotechnology. Added value from this integrative concept will result from the interaction between the biological and technical components as a driving force for future cutting-edge technologies and their way into commercial application. Altogether, modeling will play an increasingly important role in biotechnology, which will ultimately lead to the application of models in several fields of the process development chain as well as a higher degree of automation and integrative process development and management in the near future.

8. Additional online sources for computer hardware development and comparison

• a.Historical development: https://www.computerhistory.org/timeline/computers/, accessed 05/2020
• b.HDD and RAM pricing and performance data: http://www.jcmit.net/, accessed 05/2020
• c.Linpack algorithm for CPU performance: Jack J. Dongarra, http://netlib.org/benchmark/performance.pdf, accessed 06/2020
• d.MATLAB program for counting floating point operations: Hang Qian, Counting the Floating Point Operations (FLOPS), 2020, https://www.mathworks.com/matlabcentral/fileexchange/50608-counting-the-floating-point-operations-flops, MATLAB Central File Exchange, accessed 06/2020
• e.CPU performance data: Roy Longbottom, http://www.roylongbottom.org.uk/linpack%20results.htm, http://www.netlib.org/benchmark/linpackjava/timings_list.html, https://setiathome.berkeley.edu/cpu_list.php, accessed 06/2020
• f.NIH principal investigator budget: NIH Office of Budget Homepage, https://officeofbudget.od.nih.gov/, NIH Data Book (NDB), https://report.nih.gov/nihdatabook/, accessed 05/2020
• g.NCBI database volume: https://www.ncbi.nlm.nih.gov/genbank/statistics/, accessed 02/2020
• h.Internet bandwidth comparison by country and year: Speedtest Global Index, Ookla LLC, Seattle, WA, USA, https://www.speedtest.net/global-index, accessed 02/2020

CRediT authorship contribution statement

Philipp Noll: Conceptualization, Methodology, Formal analysis, Investigation, Writing - original draft, Writing - review & editing, Visualization. Marius Henkel: Conceptualization, Methodology, Formal analysis, Investigation, Writing - original draft, Writing - review & editing, Visualization, Supervision, Project administration.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.