Typicality of functional connectivity robustly captures motion artifacts in rs‐fMRI across datasets, atlases, and preprocessing pipelines

Abstract

Functional connectivity analysis of resting‐state fMRI data has recently become one of the most common approaches to characterizing individual brain function. It has been widely suggested that the functional connectivity matrix is a useful approximate representation of the brain's connectivity, potentially providing behaviorally or clinically relevant markers. However, functional connectivity estimates are known to be detrimentally affected by various artifacts, including those due to in‐scanner head motion. Moreover, as individual functional connections generally covary only very weakly with head motion estimates, motion influence is difficult to quantify robustly, and prone to be neglected in practice. Although the use of individual estimates of head motion, or group‐level correlation of motion and functional connectivity has been suggested, a sufficiently sensitive measure of individual functional connectivity quality has not yet been established. We propose a new intuitive summary index, Typicality of Functional Connectivity, to capture deviations from standard brain functional connectivity patterns. In a resting‐state fMRI dataset of 245 healthy subjects, this measure was significantly correlated with individual head motion metrics. The results were further robustly reproduced across atlas granularity, preprocessing options, and other datasets, including 1,081 subjects from the Human Connectome Project. In principle, Typicality of Functional Connectivity should be sensitive also to other types of artifacts, processing errors, and possibly also brain pathology, allowing extensive use in data quality screening and quantification in functional connectivity studies as well as methodological investigations.

In current resting‐state fMRI studies, there is a need for a sufficiently sensitive measure of individual functional connectivity quality. In this article, we presented a new method of functional connectivity quality evaluation for rs‐fMRI data. This measure is significantly correlated with motion metrics and the results hold across atlases, preprocessing pipelines as well as different datasets including a validation set of 1,081 subjects from the Human Connectome Project.

1. INTRODUCTION

Imaging techniques play a pivotal role in medical research nowadays. Functional magnetic resonance imaging (fMRI) is one of the most common methods for research into brain function. Resting‐state fMRI (rs‐fMRI) is a very prolific and popular subcategory of fMRI measurements. In 1995, Biswal and colleagues found that the correlation of low‐frequency fluctuations (<≈ 0.1 Hz) in blood oxygen level‐dependent (BOLD) signals is a manifestation of the functional connectivity (FC) of the brain. Later studies confirmed that fMRI fluctuations are tightly coupled with the underlying neural activity (Nir, Hasson, Levy, Yeshurun, & Malach, 2006; Schölvinck, Maier, Ye, Duyn, & Leopold, 2010). These spontaneous low‐frequency fluctuations in the BOLD signal are therefore used to investigate the functional architecture of the brain (Lee, Smyser, & Shimony, 2013).

A common approach to the analysis of rs‐fMRI data is to assess FC, defined as temporal dependence of neuronal activity patterns (Friston, Frith, Liddle, & Frackowiak, 1993), and thus determine which regions are functionally connected. Regions are defined based on a reasonable brain parcellation. Although there is no consensus on optimal parcellation (Arslan et al., 2018; Eickhoff, Yeo, & Genon, 2018), it has been suggested that the matrix of FC among all brain regions may be a suitable representation of the brain connectivity, potentially providing behaviorally or clinically relevant markers (Biswal et al., 2010; Buckner, Krienen, & Yeo, 2013; Van Dijk et al., 2009).

Like any other imaging technique, fMRI is also affected by unwanted artifacts. There are many non‐neuronal sources of signal variability such as thermal noise, physiological sources (created by the cardiac and respiratory cycles), scanner and head coil heterogeneities, spiking, chemical shifts, radiofrequency interferences, or subject movement (Bianciardi et al., 2009; Chang & Glover, 2009; Murphy, Birn, & Bandettini, 2013; Poldrack, Mumford, & Nichols, 2011). Scanner head motion has long been recognized as a source of artifacts in rs‐fMRI (Friston, Williams, Howard, Frackowiak, & Turner, 1996; Hajnal et al., 1994). These artifacts originate in changes in head position that can yield many forms from small involuntary drifts to brief impulsive movements (Patel et al., 2014). They induce undesirable, artificial effects that manifest in complex temporal and spatial patterns (Biswal et al., 1995; Friston et al., 1996; Hajnal et al., 1994; Hlinka, Alexakis, Hardman, Siddiqui, & Auer, 2010; Patel et al., 2014; Spisák et al., 2014). Recent studies showed that even small head movements, in the range of 0.5–1 mm, can induce systematic biases in correlation strength and thus they can profoundly influence the final estimates of FC (Hlinka et al., 2010; Van Dijk, Sabuncu, & Buckner, 2012; Power, Barnes, Snyder, Schlaggar, & Petersen, 2012; Satterthwaite et al., 2012; Bright & Murphy, 2013; Mowinckel, Espeseth, & Westlye, 2012; Satterthwaite et al., 2013; Tyszka, Kennedy, Paul, & Adolphs, 2014; Yan, Cheung, et al.,2013). Typical motion artifact manifests as increased short‐range connectivity and reduced long‐range connectivity, although gross head motion can also increase long‐range connectivity (Power et al., 2012, 2014; Power, Schlaggar, & Petersen, 2015; Satterthwaite et al., 2012, 2019). These effects influence the correlation values as well as the derived connectivity measures characterizing the network topology (Yan, Craddock, et al., 2013; Ciric et al., 2017). Therefore, they have been both a point of concern and controversy for rs‐FC investigations (Bright & Murphy, 2013; Carbonell, Bellec, & Shmuel, 2011; Fair et al., 2013; Maclaren, Herbst, Speck, & Zaitsev, 2013; Muschelli et al., 2014; Shmueli et al., 2007).

In common practice, fMRI data preprocessing is used to reduce the noise. Preprocessing usually includes image realignment, spatial smoothing, filtering, and confound regression (Van Dijk et al., 2009). There is no consensus on the optimal preprocessing strategy that should be applied to rs‐fMRI data (Aurich et al., 2015; Caballero‐Gaudes & Reynolds, 2017). Since no preprocessing is completely successful in removing the motion influence (Ciric et al., 2017; Siegel et al., 2017), it is vital for connectivity studies to be able to quantify the amount of motion artifacts present in FC matrices. However, a reliable measure of FC quality has not yet been established. The absence of robust FC quality measure renders the estimation of the amount of motion artifact in an FC matrix impossible. We propose a new measure—Typicality of functional connectivity (TFC), that is based on a correlation of a single FC matrix with a typical FC matrix. We analyze it across different datasets, atlases, and preprocessing pipelines.

The individual deviations from a typical FC matrix might not be entirely attributable to artifacts and could be of neural origin. Nevertheless, we suggest that the most prominent deviations are likely to be dominated by non‐neuronal related signal changes and thus could identify potentially problematic subjects. Therefore, such measure can be helpful in investigations of individuals and populations whose in‐scanner movement profiles may differ subtly, for instance when comparing controls to subjects of different ages (e.g., during development or aging) or to individuals experiencing involuntary or repetitive movements (e.g., tics or tremors) (Bright & Murphy, 2013; Muschelli et al., 2014). By definition, it should be sensitive also to other types of artifacts, processing errors, and possibly also brain pathology, allowing extensive use in data quality screening and quantification in FC studies as well as methodological investigations, such as the evaluation of preprocessing pipeline performances and the decision on suitable brain parcellation.

2. MATERIALS AND METHODS

2.1. Data acquisition

2.1.1. Main dataset

For the main study, we took a dataset with 245 healthy subjects (148 right‐handed, 132 females, mean age 29.22/standard deviation 6.99). Participants were informed about the experimental procedures and provided written informed consent. The study design was approved by the local Ethics Committee of the Institute of Clinical and Experimental Medicine and the Psychiatric Center Prague. Each volunteer underwent MRI scanning that included 10 minutes of resting‐state functional magnetic resonance imaging acquisitions with eyes closed and acquisition of a T1‐weighted and T2‐weighted anatomical scan.

Scanning was performed with a 3T MRI scanner (Siemens; Magnetom Trio) located at the Institute of Clinical and Experimental Medicine in Prague, Czech Republic. Functional images were obtained using T2‐weighted echo‐planar imaging (EPI) with BOLD contrast. GE‐EPIs (TR/TE = 2,000/30 ms) comprised 35 axial slices—acquired continuously in descending order covering the entire cerebrum (48 × 64 voxels, voxel size = 3 × 3 × 3 mm³). A three‐dimensional high‐resolution T1‐weighted image (TR/TE/TI = 2,300/4.6/900 ms), (170 slices, 162 × 210 voxels, voxel = 1 × 1 × 1 mm³) covering the entire brain was used for anatomical reference. T2‐weighted images were also acquired but not used in the current study.

2.1.2. Alternative dataset

For confirmation and additional analyses, we took a different dataset of 84 healthy subjects (80 right‐handed, 48 males, mean age 30.83/standard deviation 8.48). Each volunteer underwent MRI scanning that included 10 min of resting‐state functional magnetic resonance imaging acquisitions with eyes closed and acquisition of a T1‐weighted and T2‐weighted anatomical scan. Scanning was performed with a 3T MRI scanner (Siemens; Magnetom Trio). Functional images were obtained using T2‐weighted echo‐planar imaging (EPI) with BOLD contrast. GE‐EPIs (TR/TE = 2500/30 ms) comprised 44 axial slices acquired continuously in descending order covering the entire cerebrum (64 × 64 voxels, voxel size = 2 × 2 × 2 mm³). A three‐dimensional high‐resolution T1‐weighted image (TR/TE/TI = 2,300/4.6/900 ms, 169 slices, 176 × 189 voxels, voxel = 1 × 1 × 1 mm³) covering the entire brain was used for anatomical reference (for more details see Tomeček et al., 2020).

2.1.3. Human Connectome project

To be able to repeat and generalize our results, we analyzed preprocessed rs‐fMRI of 1,081 subjects from the WU‐Minn Human Connectome Project (in this article referred to simply as “HCP”). Data were downloaded from the HCP S1200 Release Resting‐State fMRI 1 FIX‐Denoised (Extended) package. We used the first 15 min of resting‐state scans with left–right phase‐encoding directions.

Structural dataset acquisitions included high resolution T1‐weighted and T2‐weighted images (TR/TE/TI = 2400/2.14/1,000 ms, voxel = 0.7 × 0.7 × 0.7 mm³, 256 sagittal slices). Resting‐state fMRI was acquired at 2 mm isotropic resolution, TR = 720 ms, TE = 33.1 ms, slice thickness of 2.0 mm, 72 slices. (for more details see Uğurbil et al. (2013)).

Data were already preprocessed (including spatial distortion correction, motion correction, spatial registration, normalization to MNI coordinates) and denoised using the FIX ICA‐based automated method. Artifacts, such as head motion or cardiac pulsation, are regressed out from high‐pass filtered data, along with 12 head‐motion‐related confound regressors (more details in Van Essen et al., 2013; Burgess et al., 2016).

2.2. Preprocessing

2.2.1. Stringent

Initial data preprocessing was performed using a combination of the SPM12 software package (Wellcome Department of Cognitive Neurology, London, UK) and CONN toolbox (McGovern Institute for Brain Research, MIT, USA) running under MATLAB (The Mathworks). CONNs default preprocessing pipeline (defaultMNI) comprises of the following steps: (1) functional realignment and unwarping, (2) slice‐timing correction, (3) structural segmentation into white matter and cerebrospinal fluid & structural normalization to the MNI space, (4) functional normalization to the MNI space, (5) outlier detection, and (6) smoothing with 8 mm kernel size.

The default denoising steps in the CONN toolbox included a component‐based noise correction method (CompCor) performing regression of six head‐motion parameters (acquired during the correction of head‐motion) with their first order temporal derivatives and five principal components of white‐matter and cerebrospinal fluid (Behzadi et al., 2007). This default preprocessing might be suboptimal due to not suppressing the motion artifacts sufficiently (potential remedy could be including 24 instead of 12 motion parameters, although adding quadratic expansions showed similar preprocessing efficacy, see Parkes, Fulcher, Yücel, & Fornito, 2018), or due to removing some part of the neural‐induced signals (for discussion on the use of components in preprocessing see Barton et al., 2019). Time series from defined regions of interest were additionally linearly detrended to remove possible signal drift and finally filtered by a band‐pass filter with cutoff frequencies 0.009–0.08 Hz. This preprocessing pipeline is labeled as stringent further in the manuscript.

To form FC matrices, we cross‐correlated the ROI‐based average BOLD time series. In line with the most common practice, we use the Pearson correlation coefficient to quantify FC and form FC matrices. Note that although other nonlinear approaches for FC assessment have been proposed, the linear Pearson correlation coefficient was shown to be sufficient under standard conditions (Hartman, Hlinka, Palus, Mantini, & Corbetta, 2011; Hlinka, Palus, Vejmelka, Mantini, & Corbetta, 2011). Fisher's r‐to‐z transformation (Zar, 1999) was applied to each correlation coefficient to increase the normality of the distribution of correlation values.

2.2.2. Moderate

We additionally used two more lenient processing setups in our analyses. In comparison with the stringent pipeline, the moderate denoising steps only included regression of six head‐motion parameters and one principal component of white‐matter and cerebrospinal fluid. A band‐pass filter with broader cutoff frequencies of 0.004–0.1 Hz was applied.

2.2.3. Mild

The mild preprocessing consists of only CONNs default preprocessing pipeline—defaultMNI. No further filtering or regression was done.

2.3. Atlas choice

We chose a parcellation based on Craddock atlas because it offers an option to select the number of ROIs that represent spatially coherent regions with homogeneous connectivity. For each subject, we calculated 23 FC matrices that differ in the number of ROIs: ranging from 10 to 840 ROIs. With the increasing number of ROIs, the size of each ROI decreases (Figure S1). If not stated otherwise, the default parcellation is into 200 regions (on average comprising 91.9 ± 18.8 voxels). The regions in Craddock atlas are created using a spectral clustering algorithm with various similarity metrics and group‐level clustering schemes (for details see Craddock, James, Holtzheimer, Hu, & Mayberg, 2012).

Moreover, to assess generalization to other types of atlases, we also used AAL atlas (90 ROIs) ‐the most common anatomical atlas (Tzourio‐Mazoyer et al., 2002).

2.4. Quantifying motion

Reporting motion statistics should be fundamental for any fMRI study, but Waheed et al. (2016) analyzed 100 most recent fMRI studies, and only 10% provided a table of motion metrics. Two of the most used motion metrics are framewise displacement (FD) and the derivative of root mean square variance over voxels (DVARS). We used mean FD and mean DVARS to quantify the amount of motion during a given scanning session. Distribution of each metric is available in Figure S2.

2.4.1. Framewise displacement

FD represents a summarizing parameter of six head motion parameters (translational displacements along X, Y, and Z axes and rotational displacements of the pitch, yaw, and roll) from one volume to the next. It is an average of the rotation and translation parameters differences (Equation 1). (Power et al., 2012).

$$F{D}_i=\left|∆d_{\mathit{ix}}\right|+\left|∆d_{\mathit{iy}}\right|+\left|∆d_{\mathit{iz}}\right|+\left|∆{\alpha }_i\right|+\left|∆{\beta }_i\right|+\left|∆{\gamma }_i\right|$$ (1)

where the displacement of i ‐th brain volume in x‐direction is ∆d_ix = d_{(i − 1)x} − d_ix and similarly for the other rigid body parameters. Rotational displacements were converted from degrees to millimeters by calculating displacement on the surface of a sphere of radius 50 mm.

2.4.2. Derivative of root mean square variance over voxels

The DVARS quantifies changes of intensities between two images and it is calculated as the root mean square value of the differentiated BOLD time series within a spatial mask at every time‐point (Eq. 2)(Smyser et al., 2010). DVARS is not derived from realignment parameters, and thus it could reflect any kind of bias. Nevertheless, the head motion has been proven to be a significant contributor to fluctuations in DVARS (Fair et al., 2013). The quantity is calculated after FC processing and it is defined as:

$$\mathit{\text{DVARS}}{\left(∆I\right)}_i=\sqrt{〈{\left[∆I_i\left(\overrightarrow{x}\right)\right]}^2〉}=\sqrt{〈{\left[I_i\left(\overrightarrow{x}\right)-I_{i-1}\left(\overrightarrow{x}\right)\right]}^2〉}$$ (2)

where $I_i\left(\overrightarrow{x}\right)$ is image intensity at locus $\overrightarrow{x}$ on frame i and angle brackets denote the spatial average over the whole brain.

2.5. Measuring FC quality

Estimating connectivity quality and assessing its relationship with motion is vital for all connectivity studies. Currently, there is no measure used in literature that allows quantifying it per subject. Here we present our new metric along metrics proposed by other groups.

2.5.1. Typicality of functional connectivity

We propose the TFC as a new measure for how to estimate FC quality. It is based on a correlation between an individual subjects FC matrix and a typical FC matrix of a given cohort (Equation 3). To exclude the influence of diagonal values, we vectorized the upper triangular form of all FC matrices (ignoring the diagonal elements).

$$\mathit{TF}{C}_i=\frac{(1+r_P\left(F{C}_i,\overline{\mathit{FC}}\right)}{2}$$ (3)

where i is a subject's index, r_P is a Pearson correlation coefficient and $\overline{\mathit{FC}}$ is the typical FC matrix. Throughout the manuscript, Spearman correlation is denoted as r_S and Pearson correlation as r_P. TFC ranges between 0 and 1, where 0 is a complete anti‐correlation, .5 is a correlation of 0, and 1 is a maximal correlation with the typical FC matrix.

As the template, we use the mean FC matrix of 10% subjects with the lowest motion (lowest mean FD). Taking mean FC across the whole dataset instead of 10% of subjects gives similar results (Figure S3). Subjects are taken from the Alternative dataset (see Section 2). Thus no subjects need to be eliminated from further analyses. If an alternative dataset with similar preprocessing is not at disposal, low‐movement subjects from the same dataset can be used. We assume that by averaging FC matrices of low‐movement subjects, we obtain a useful estimate of awake human brain FC. While minor or moderate deviations may represent effects of interest corresponding to inter‐individual variation in brain function, larger anomalies are likely to arise due to artifactual sources of signal variation and should be subject to screening.

2.5.2. Euclidean L² distance

Instead of using correlation as a similarity measure with the typical matrix, we also used distance (Ponsoda et al., 2017). More specifically, the Euclidean L ² distance defined as the mean distance between FC values from an upper triangular form of a single FC matrix (without diagonal) and corresponding typical FC values, resulting in a nonnegative value characterizing matrix typicality (Equation 4).

$$d_i=\frac{1}{N}\sum _{j=1}^N{\left(F{C}_i^j-\overline{F{C}^j}\right)}^2$$ (4)

where i is a subject's index, j is an FC value index, $\overline{\mathit{FC}}$ is the typical FC matrix, and N is the number of FC values.

2.5.3. Geodesic distance

Introduced by Venkatesh, Jaja, and Pessoa (2020), the reasoning behind this distance metric is that the correlation matrices lie on a nonlinear space. Geodesic distance between two points on the positive semidefinite cone (e.g., two FC matrices) is the shortest path between them along the manifold. Since it is not guaranteed that the typical FC matrix would lie on the manifold, we define this quality measure as the mean geodesic distance between a full FC matrix and all other FC matrices (Equation 5).

$$d_i=\frac{1}{N}\sum _{j=1}^N\sqrt{\mathit{\text{trace}}({\log }^2\left(F{C}_i^{\frac{1}{2}}F{C}_{j}F{C}_i^{\frac{1}{2}}\right)})$$ (5)

where i, j are subject's indices.

2.5.4. Quality control‐functional connectivity

In literature, the most used way to evaluate the presence of a motion artifact are quality control‐functional connectivity (QC‐FC) values (Ciric et al., 2017; Parkes et al., 2018; Power et al., 2014; Satterthwaite et al., 2012). This group measure examines how motion affects FC values for each pair of regions across subjects. Each FC value is directly correlated with a summary motion statistic (either mean FD or mean DVARS) across subjects. The median of these values shows if motion tends to increase or decrease connectivity and a correlation of QC‐FC with distance reveals the presence of spurious distance dependence.

2.6. tSNR

The temporal signal to noise ratio is a useful measure of data quality (Bodurka, Ye, Petridou, Murphy, & Bandettini, 2007). Van Dijk et al. (2012) have found that low values of tSNR identify subjects with high head motion or other causes of data instability. For each ROI, the mean signal is divided by the standard deviation over the BOLD run, and tSNR is calculated as the mean tSNR value across all ROIs in the brain (Equation 6). An alternative is using a voxel‐based tSNR, where the signal from each gray matter voxel with signal values >150 is used instead of ROIs.

$$\mathit{tSN}{R}_r=\frac{\frac{\sum _{t=1}^{T}S\left(r,t\right)}{T}}{\sqrt{\frac{\sum _{t=1}^T({\left(S\left(r,t\right)-\overline{S\left(r\right)}\right)}^2}{T}}}$$

$$\mathit{tSN}\mathrm{R}=\frac{1}{R}\sum _{r=1}^R\mathit{tSN}{R}_r$$ (6)

where S(r,t) is the signal magnitude at the ROI r in the time t. $\overline{\mathit{S}\left(\mathit{r}\right)}$ is a temporal mean. T is the number of all brain volumes and R is the number of all ROIs.

3. RESULTS

We used TFC to estimate per subject quality and we analyzed it with respect to motion, atlas size, and preprocessing. We used FC matrices with stringent preprocessing parcellated into 200 ROIs using Craddock atlas as a default setup. The TFC metric was based on a comparison with the mean FC matrix of 10% subjects with the lowest mean FD from the Alternative dataset. Using the Spearman correlation, we found that it is significantly correlated with motion metrics ($r_{\mathit{S}}^{\mathit{\text{DVARS}}}=-.37,p<{10}^{-8},r_S^{\mathit{FD}}=-.20,p=.002$; Table 1), meaning that an FC matrix of a subject with high mean head movement is less similar to the typical FC matrix compared to low‐movement subjects (Figure 1a, Figure S4). A correlation coefficient between a motion metric and TFC demonstrates a dependence between FC quality and gross head motion. The effect is more prominent in a high‐moving subgroup of subjects (Figure S5). Both FD and DVARS are significantly related to FC quality but mean DVARS shows a generally higher absolute correlation than mean FD.

TABLE 1.

Correlation of different measures of FC quality with motion metrics

	DVARS		FD
	Spearman	Pearson	Spearman	Pearson
TFC	−0.37 (2 × 10−9)	−0.38 (7.3 × 10−10)	−0.20 (0.002)	−0.23 (2.8 × 10−4)
L 2 distance	0.01 (0.87)	−0.09 (0.18)	−0.02 (0.81)	0.13 (0.05)
Geodesic distance	−0.10 (0.11)	0.39 (2 × 10−10)	−0.13 (0.04)	−0.08 (0.20)

Note: Only TFC shows significant correlations for both motion metrics and both Pearson and Spearman correlations. The corresponding p‐values are in brackets. Statistically significant (p < .05) correlation values are set in bold.

FIGURE 1.

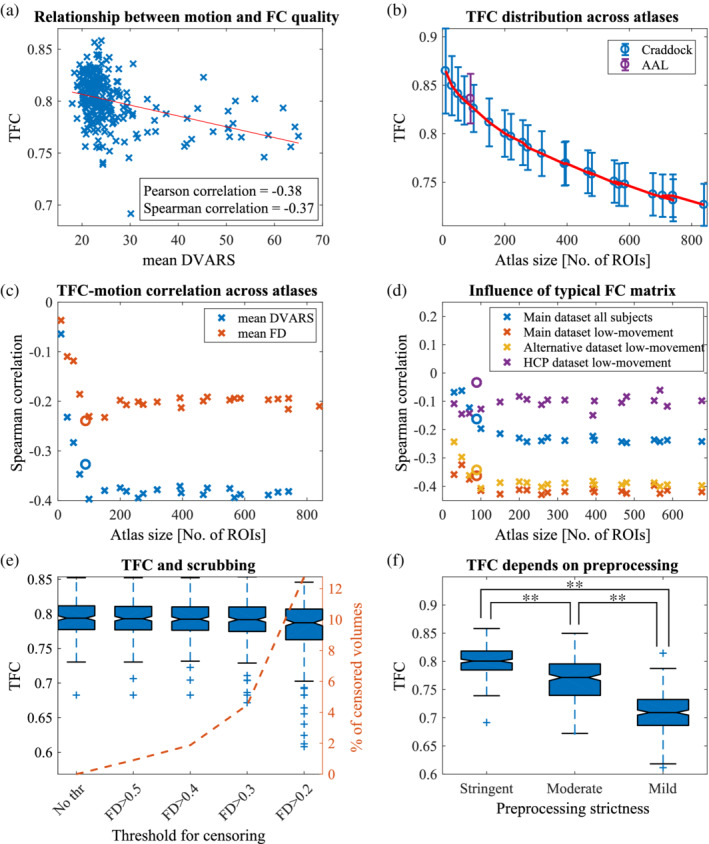
Analysis of new FC quality metric—TFC. a) The significant relationship between mean DVARS and TFC (for FD see Figure S4) proves that subjects with worse FC quality (lower correlation coefficient between a single FC matrix and the typical FC matrix) exhibit higher levels of motion. Calculated for Craddock atlas with 200 ROIs. (b) The quality of functional connectivity is decreasing as the number of ROIs increases. Mean ± standard deviation of TFC across atlases is plotted. Purple mark indicates AAL atlas. (c) Spearman correlations between TFC and two summarizing motion metrics for atlases with different number of ROIs. Except for the very small atlases, the relationship between FC quality and motion is constant. A circle mark indicates AAL atlas. (d) The highest absolute correlation of the TFC‐DVARS dependence is obtained if low‐movement subjects of the same dataset are used for the calculation of the typical FC matrix. Although, it is comparable to using low‐motion subjects of a different dataset. Because the typical matrix of the Main dataset is comparable to a typical matrix of the Alternative dataset (r_P = .86, p < 10⁻¹⁶) and similar to the typical matrix of HCP dataset (r_P = .68, p < 10⁻¹⁶). Using all subjects from the same dataset yields lower correlations. (e) High movement volumes were censored based on an increasingly strict threshold. No substantial changes in TFC distributions are observable. (f) Comparison of quality of FC matrices of all subjects for three different preprocessing pipelines with different levels of strictness; stringent being the strictest and mild the most lenient. FC matrices with more strict preprocessing are significantly more similar to the typical FC matrix (paired t‐tests)

Instead of TFC, we also tried a method based on Euclidean L ² distance from the typical FC matrix and mean geodesic distance from the cohort. Unlike TFC measure, which shows significant both Spearman and Pearson quality‐motion correlations, the correlations of L ² distance with motion were significant only using Pearson correlation and FD ($r_{\mathit{P}}^{\mathit{FD}}=.13,p=.05$) because this relationship was driven mainly by outliers. Correlations with geodesic distance also did not show consistent significances and yielded only two significant results ($r_{\mathit{P}}^{\mathit{\text{DVARS}}}=.39,p<{10}^{-9},r_{\mathit{S}}^{\mathit{FD}}=-.13,p=.04$; Table 1).

Since motion parameters may contain outliers and Spearman correlation is less sensitive to outliers compared to Pearson correlation (see de Winter, de Samuel, Gosling, & Potter, 2016), we prefer to use it throughout the manuscript when assessing the relationship with motion.

We further analyzed only TFC as a quality measure. We evaluated it for every subject across Craddock atlases with varying number and size of ROIs, from 10 to 840 regions, and for AAL atlas with 90 ROIs. From Figure 1b, it is evident that FC quality decreases as the atlas size increases. Therefore, more detailed FC matrices are of worse quality. We investigated whether this gradual decrease is driven by the increased effect of motion on signals in small regions. We calculated correlations between motion and TFC across variously detailed atlases and found that, except for atlases with less than 100 regions, the relationship is stable ($r_{\mathit{S}}^{\mathit{\text{DVARS}}}\approx -0.38,p<{10}^{-9},r_{\mathit{S}}^{\mathit{FD}}\approx -0.23,p\approx .001$; Figure 1c). AAL atlas shows similar results to Craddock atlas of corresponding size ($r_{\mathit{S}}^{\mathit{\text{DVARS}}}=-.33,p<{10}^{-7},r_{\mathit{S}}^{\mathit{FD}}=-.24,p<{10}^{-4}$).

By default, the typical FC matrix is based on connectivity estimates of subjects from a different dataset (identical preprocessing pipeline). The correlation with motion would be only slightly stronger if based on low‐movement subjects from the same dataset (for the price of losing 10% subjects). If we use all subjects from the current dataset for the calculation of the typical FC matrix, the observed relationships are weaker (Figure 1d), possibly due to the presence of various types of noises. Even using a different dataset with different preprocessing, such as HCP, still gives significant results (only for DVARS).

Censoring volumes acquired during periods of high‐motion is a widespread preprocessing step in rs‐FC studies. We varied the threshold for volume exclusion from FD > 0.2 to FD > 0.5 in order to analyze the effect of volume censoring on TFC (Figure 1e). Censoring was performed only after preprocessing was complete and only for the motion corrupted volume (although we obtained similar results if two volumes before and one after were discarded as well). Only a few FC matrices seemed to degrade in quality. We did not observe a substantial change of TFC even under the strictest conditions, where more than 15% of volumes were excluded on average.

Besides the influence of ROI size and censoring on FC quality, we also analyzed the influence of data preprocessing on FC quality. We compared FC quality for three different preprocessing pipelines based on their strictness—stringent, moderate, and mild. In Figure 1f we see that with the increasing strictness the individual FC matrices more resemble the typical FC matrix: mean (TFC_stringent) = 0.80, mean (TFC_moderate) = 0.77, mean (TFC_mild) = 0.71. These TFC distributions are statistically different based on paired t‐test between every pair of preprocessing pipelines (all p‐values <10⁻¹⁶). For all these cases, we used the typical FC matrix of a dataset with stringent preprocessing, but results were similar if each preprocessing stream used its own FC matrix as a golden standard (Figure S6).

To compare TFC with other quality measures, we calculated QC‐FC values. We obtained a positive median of QC‐FC and significant negative correlation between QC‐FC and distance for both quality control metrics ($r_{\mathit{S}}^{\mathit{FD}}=-.13,p<{10}^{-9},r_{\mathit{S}}^{\mathit{\text{DVARS}}}=-.02,p=.02$ (Figure 2a,b). Nevertheless, only 21% of DVARS‐FC values (resp. 13% for FD) were significant (Figure 2c). The relationship between QC‐FC and distance is constant across atlases of various sizes (Figure 2d).

FIGURE 2.

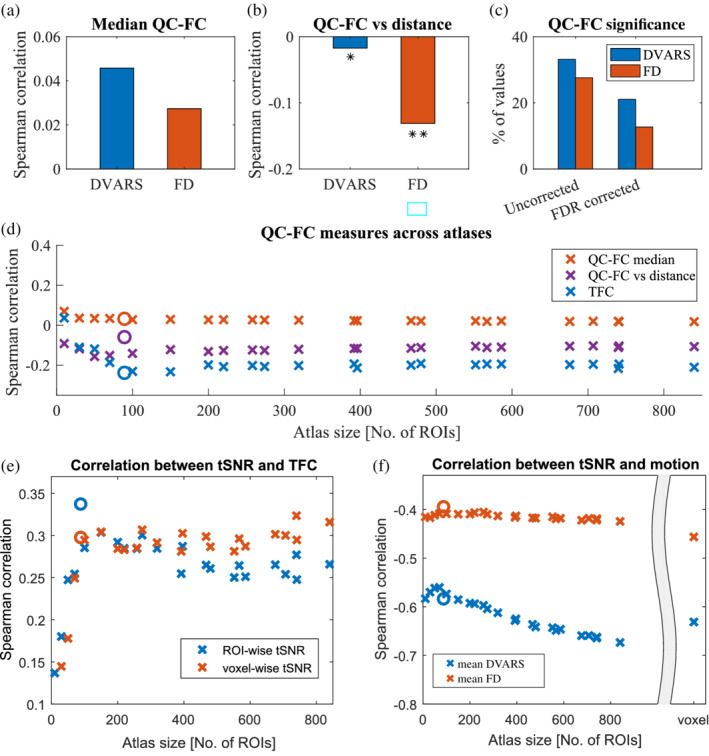
Comparison of TFC with other measures of FC and data quality. (a) The QC‐FC correlations quantify the association between inter‐individual variance in functional connectivity and gross head motion. A positive median of QC‐FC values signifies that head motion increases connectivity (for both FD and DVARS). (b) This effect is more prominent for short‐links and it is more specifically related to motion as correlations are stronger when FD models quality controls. *signifies p < .05, ** p < .001 (c) On the other hand, the amount of edges that are significantly affected by movements is more easily detectable with DVARS. (d) Above mentioned effects are stable across atlases with different number of ROIs. Magnitudes of TFC correlations are higher than the median of DVARS‐FC, proving its viability as an estimator. Plotted only for mean DVARS but results with FD are similar. A circle mark indicates AAL atlas. (e) tSNR measures different data aspects than TFC as the correlation is weak. Nevertheless, it is significant and positive. (f) With decreasing size of ROIs, the relationship between tSNR and mean DVARS gets stronger. This trend is not present for FD, suggesting that the phenomenon is potentially caused by other types of noise than a head movement

So far, we focused only on the quality of connectivity matrices, but the noisiness of the underlying BOLD time series can also be estimated in the form of tSNR. It is apparent that tSNR measures different data aspects compared to TFC as they correlate only weakly (mean r_S = .26, all p‐values <10⁻⁶) (Figure 2e). We obtained similar results for both voxel‐wise and ROI‐wise tSNR. To test whether there is a change in tSNR‐motion relationship across parcellations, we correlated it with FD and DVARS across differently sized atlases (Figure 2f). DVARS displays a progressive increase of absolute correlation with tSNR, unlike FD (changes of correlations between smallest and highest atlas: $∆r_{\mathit{S}}^{\mathit{\text{DVARS}}}=0.13,∆r_{\mathit{S}}^{\mathit{FD}}=0$, all p‐values <10⁻¹¹).

To demonstrate the robustness of our methods, we applied the same analysis to the HCP dataset. Even though it is a dataset with a different preprocessing pipeline, we observed only slightly higher magnitudes of TFC compared to the main dataset (Figure 3a). Similarly, TFC magnitudes were decreasing with increasing atlas size. Again, TFC significantly correlated with both motion metrics ($r_{\mathit{S}}^{\mathit{\text{DVARS}}}=-.13,p<{10}^{-5},r_{\mathit{S}}^{\mathit{FD}}=-.23,p<{10}^{-12}$). Using AAL parcellation yielded FC matrices of higher quality with a lower amount of motion (weaker TFC‐motion correlation, especially for FD, $r_{\mathit{S}}^{\mathit{FD}}=-.11,p<{10}^{-4}$). We confirm that the TFC‐motion relationship is stable across various atlases (except for the smallest ones). In general, mean FD showed stronger absolute correlations with TFC (Figure 3b). When analyzing QC‐FC values, only the median FD‐FC values showed a spurious increase in connectivity (Figure 3c). Moreover, we did not obtain a significant correlation between QC‐FC values and distance (p > .05 for both FD and DVARS), proving successful mitigation of distance dependence and other motion‐related impurities for the HCP preprocessing pipeline. On the contrary, a relatively high amount of FC values was correlated with head movements (>50% for FD). Based both on QC‐FC and TFC, the head motion effect on connectivity seems to be constant and independent of ROI size (Figure 3d).

FIGURE 3.

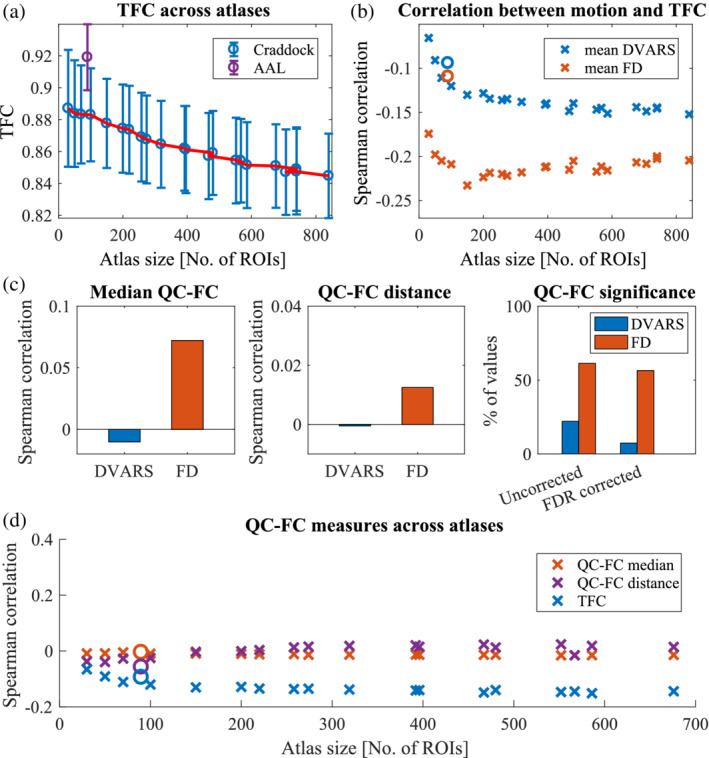
HCP dataset quality assessment. (a) The HCP dataset shows higher magnitudes of TFC compared to the Main dataset. Similarly, TFC is decreasing with decreasing atlas size. A purple mark indicates AAL atlas. (b) Again, the TFC‐motion relationship is stable across various atlases (except for the smallest ones). Mean FD shows a stronger absolute correlation with TFC. A circle mark indicates AAL atlas. (c) In the analysis of QC‐FC values, only the median FD‐FC values shows a spurious increase in connectivity. Moreover, the correlation between QC‐FC values and distance was not significant, proving successful mitigation of distance dependence for the HCP preprocessing pipeline. Nevertheless, a relatively high amount of FC values is correlated with head movements (>50% for FD). (d) Even in the HCP dataset, TFC significantly correlated with the motion (mean FD). Based both on FD‐FC and TFC, the head motion effect on connectivity seems to be constant and independent of ROI size

Several times, when comparing results across differently sized atlases, we observed an effect of atlas size when up to 100 ROIs were used. This effect might be driven by two factors: by the number of regions or by the size of regions. To test the first hypothesis, we randomly selected 50, 100, 150, … , 700 ROIs out of an atlas with 950 ROIs. We calculated both TFC and ROI‐based tSNR and analyzed their relationship with head movement 1,000 times. In this scenario, the number of voxels in a region is fixed (21.9 ± 0.3) and only the number of regions varies. Neither based tSNR nor TFC depends on the number of regions. We only observed a small gradual increase in the TFC‐motion relationship when only a few regions were selected (Figure 4a).

FIGURE 4.

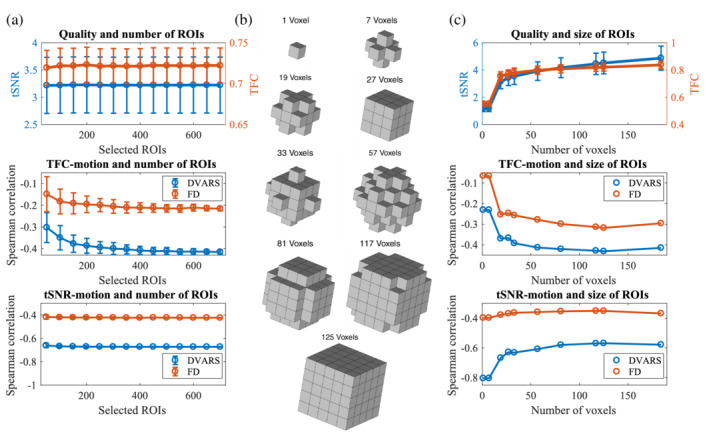
Are atlas size effects driven by the number of regions or by the number of voxels? (a) In an atlas with 950 ROIs, we randomly selected 50, 100, 150, … , 700 ROIs to get quality estimates depending only on the number of regions but independent of the number of voxels. Neither ROI‐based tSNR nor TFC changes with the number of regions. Only the relationship between TFC and motion is slightly weaker for smaller numbers of regions. (b) To create a brain parcellation with a fixed number of regions but a varying number of voxels, we built different geometrical shapes around a central voxel of a region. (c) Within an atlas of 100 ROIs, we varied the number of voxels that formed a region. Both voxel‐based tSNR and TFC depend on the number of voxels. Moreover, while the tSNR‐DVARS relationship is stronger for the smaller number of voxels, the opposite is present for the TFC‐motion relationships

To test the second hypothesis, we took an atlas with 100 ROIs (183.8 ± 35.8 voxels per region) and we created different geometrical shapes around the central voxel that varied in the number of voxels (Figure 4b). Un‐smoothed data were analyzed to avoid the effect of smoothing kernel size. We used FSL routines (FMRIB Software Library v5.0, Analysis Group, FMRIB, Oxford, UK) to create our parcellation schemes. Both tSNR and TFC increase with the increasing number of voxels. On the contrary, TFC‐motion dependence is weaker for the low number of voxels (Figure 4c). These results suggest that regions with few voxels produced noisier data and FC matrices. Additionally, when choosing only a few regions (<100), it is more difficult to estimate a significant relationship between quality and movement.

4. DISCUSSION

4.1. Estimation of FC quality

The lack of a gold standard for FC quality estimation has hampered direct comparison among different groups (neurodevelopmental, aging, and neuropsychiatric), preprocessing pipelines, and brain parcellations. We introduced a new measure (TFC) to describe the quality of a FC per subject. This measure is based on a correlation of a single FC matrix with the low‐motion group‐average connectivity matrix. As we showed, it provides a reliable estimate of FC quality with respect to motion and possibly other types of noise. Low‐movement subject's FC matrices are strongly correlated with the typical FC matrix compared to high‐movement subjects, despite the fact that even our high‐movement subjects were healthy controls and would meet inclusion criteria for analyses in most MRI laboratories (Figure S2). Moreover, by visual inspection, it is apparent that subjects with low TFC either lost the modular structure present at the typical FC matrix or show a general artifactual increase in connectivity (Figure S7).

An alternative measure to TFC could be Euclidean L ² distance from the typical FC matrix or mean geodesic distance from the cohort, but our results suggest that these measures are less specifically related to motion. One of the reasons could be that they are more sensitive to other global artifacts.

Currently, many studies propose QC‐FC values as a measure of motion impact (Ciric et al., 2017; Power et al., 2015; Power, Plitt, Kundu, Bandettini, & Martin, 2017). QC‐FC values are correlations between vectors of summary quality (motion) control values (e.g., mean FD, mean DVARS) with vectors of outcome measures (FC values) across subjects. A limitation of this measure is that it is used only on a group level and it does not allow single subject descriptions. We confirmed that head movements generally increase connectivity (median QC‐FC similar to the one reported in Ciric et al. (2017) and Parkes et al. (2018) for corresponding preprocessing pipeline) and that it affects distance dependency ‐ increased short‐range connectivity and decreased long‐range connectivity (Power et al., 2012, 2015; Satterthwaite et al., 2019). This spatial pattern is specifically related to motion as we found stronger dependence for FD. As reported in Ciric et al. (2017), the number of links related to motion varies significantly (in our results less than 25% QC‐FC values significant). Power et al. (2015) warned about the possible difficulty of establishing reliable QC‐FC correlation if there is little variability in the QC measure. Moreover, QC‐FC values are sensitive to outlying values and a few scans with marked abnormalities can obscure relationships present across most other datasets (Power et al., 2017). Finally, they were criticized that they lie on a flawed assumption that “artifact‐free” rs‐FC is unrelated to motion QC measures (Williams & Snellenberg, 2019). That is why QC‐FC should be complemented with other assessments.

Several other metrics have also been adopted in prior studies, including FD‐DVARS correlations (Muschelli et al., 2014). DVARS was used as a predictor of data quality rather than an estimate of the amount of motion. Before the preprocessing, DVARS strongly correlates with FD, and this similarity diminishes with processing (Power et al., 2014). That is why DVARS could serve as a marker of nuisances in an FC matrix (Hallquist, Hwang, & Luna, 2013; Power et al., 2012, 2014). Nevertheless, DVARS changes during processing steps, even when the motion artifact is not filtered out (Spisák et al., 2014). Therefore, it is not recommended to use the FD‐DVARS relationship as an FC quality estimate, but rather it is advised to use DVARS as a motion metric. Another metric sometimes used to assess the presence of motion and the success of denoising strategies are FD‐BOLD signal correlations. It has been suggested that the positive FD‐BOLD correlations (especially in primary and supplementary motor areas) may reflect motion‐related neural activity (Yan, Cheung, et al.,2013, Yan, Craddock, et al., 2013). However, according to Power et al. (2015), these correlations are probably not related to neural activity. Finally, Saad et al. (2013) proposed a global correlation (i.e., mean across all FC values) as a quality estimator, but the reported correlation with motion was not statistically significant.

Other methods entail identification and exclusion of time points for which head movement exceeds a certain threshold (Patel et al., 2014; Power et al., 2014). Such threshold becomes increasingly stringent as the effects of motion have received greater recognition (Engelhardt et al., 2017). Recently, overly aggressive censoring of volumes was reported due to motion estimates that were artifactually inflated by respiratory artifacts (Gratton et al., 2020). We did not investigate such measures (e.g., ∆r reported in several articles (Power et al., 2012, 2014; Power, Barnes, Snyder, Schlaggar, & Petersen, 2013; Power, Lynch, et al., 2019; Power, Silver, et al., 2019) or MAC‐RSFC (Williams & Snellenberg, 2019)) because they require data scrubbing and our goal was to avoid discarding any frames/time points. Nevertheless, we investigated the influence of censoring on TFC. We did not observe substantial changes in the results of the analysis, even under the strict threshold (censoring volumes where FD >0.2). Moreover, according to Muschelli et al. (2014), censoring seems to be unnecessary or even be detrimental when CompCor approaches are used for denoising resting‐state data.

Corrections of group‐level statistics are commonly implemented by regressing a summary motion metric for each subject (Satterthwaite et al., 2012; Van Dijk et al., 2012; Yan, Cheung, et al., 2013; Power et al., 2014). However, we propose that adding TFC measure could bring further advantages, especially in investigations of potentially problematic individuals, populations in which head‐movement profiles differ subtly (e.g., children or elderly cohorts) or individuals experiencing involuntary or repetitive movements (e.g., tics or tremors). TFC offers extensive use in data quality screening and quantification in FC studies as well as methodological investigations.

4.2. Effect of ROI size

After introducing the TFC measure, our secondary goal was to analyze it under different conditions such as different preprocessing pipelines, varying atlas sizes, or across censoring thresholds. While the censoring did not have a substantial effect, as already discussed, the increasing strictness of the preprocessing pipeline did generally increase TFC values.

For the first time, we now discuss the interesting but unexplored topic of the influence atlas size on FC quality. The impossibility of optimal brain MRI parcellation makes the definition of regions of interest arbitrary. The number of ROIs ranges from 10 to 10⁴ in voxel‐based studies (for review, see Zalesky et al., 2010; Shen, Tokoglu, Papademetris, & Constable, 2013). However, how ROI size affects FC is unclear. Therefore, we examined the quality of FC matrices of varying sizes with respect to motion; the size of FC matrices varied from 10 to 840 ROIs, according to Craddock atlas.

We found an effect of ROI size on the FC quality, meaning a finer parcellation yielded noisier FC matrices. According to QC‐FC values, this effect is not related to head movements as medians QC‐FC and QC‐FC correlations with distance were constant across atlases. Using TFC confirmed that the decrease in quality is specifically related to other types of noise, only large ROIs (atlas with <100 ROIs) showed increasing absolute correlation between TFC and DVARS/FD with decreasing ROI size. However, large ROIs carry the risk that the mean time course may not represent any of the constituent time courses if different functional areas are included (Shen et al., 2013). Moreover, if analyzing too few regions, it is more difficult to establish a reliable relationship with gross head motion.

Using tSNR, we analyzed if the ROI size also affects BOLD signal quality. tSNR is a well‐established estimator of data quality, considering all types of noise. Unfortunately, the tSNR value is highly dependent on recording parameters, and thus it is difficult to compare it across studies. Nevertheless, similarly to Van Dijk et al. (2012), who reported strong Pearson correlation between voxel‐based tSNR and RMS ($r_{\mathit{P}}^{\mathrm{RMS}}=-.57,\mathit{p}<.001$), we also report significant Spearman correlation between voxel‐based tSNR and both mean FD ($r_{\mathit{S}}^{\mathit{FD}}=-.46,p<{10}^{-16}$) and mean DVARS ($r_{\mathit{S}}^{\mathit{\text{DVARS}}}=-0.63,p<{10}^{-16}$). According to Figure 2f, there is a gradual decrease in correlation between tSNR and DVARS with increasing atlas granularity. Such results suggest that there is an increasing effect of noise on the BOLD signal. Nevertheless, it might be more specifically related to other types of noise than a head movement. We conjecture that this observation could be potentially linked to the fact that DVARS is by definition sensitive to temporal signal variations beyond those reflected in (apparent) head motion, and might thus reflect more strongly other sources of artifactual signal variation such as cardiac pulsation (Murphy et al., 2013) or respiratory rate variability (Fair et al., 2020). Although the motion is believed to have a dominant effect on frame‐to‐frame signal intensity changes (Fair et al., 2013; Hlinka et al., 2010; Smyser et al., 2010).

In conclusion, both time‐series and FC matrices based on smaller ROIs are noisier. It is the size of regions (number of voxels) and not the number of regions that plays a critical role here. Moreover, we argue that motion is not the main driving effect behind this quality decrease. In all fMRI studies, it is advised that applied atlas parcellation should be chosen carefully with respect to the application and expected outcomes. Our finding that the less detailed FC matrices are of better quality is useful for all FC studies when a detailed FC matrix is not necessary, so finer brain parcellation can be sacrificed for more robust estimates of connectivity. Our recommendation here is in line with the one of Zalesky et al. (2010) that if possible, less detailed atlases will produce more robust results because they are less susceptible to noise. Nevertheless, large ROIs must be created carefully, and we do not recommend using Craddock atlas with less than 100 ROIs.

4.3. Limitations and future directions

To ensure the robustness of our findings, we have replicated the analysis on the HCP dataset. We replicated all our obtained results and proved TFC to be a reliable FC quality estimator. The HCP dataset was preprocessed using a severe preprocessing pipeline (including censoring time points). Therefore, it is generally of better FC quality (higher TFC) compared to our dataset. That is why the obtained correlations with head movements were generally lower, that is, the head motion is less present in the dataset. That could also be the reason why the QC‐FC correlation diminished, as reported in Ciric et al. (2017), where ICA‐AROMA was the only method to show virtually no QC‐FC distance‐dependence. Again, we did not find a significant change in the TFC‐motion relationship except for the very small atlases.

The question arises as to which motion metric is optimal. Currently, the most used motion parameters across studies are DVARS and FD (Waheed et al., 2016). As Power et al. (2012) pointed out, it is difficult to quantify the effect of motion with only one parameter. Nevertheless, according to our dataset mean DVARS showed the strongest correlation with FC quality (r_S up to −.4). Contrarily, the HCP dataset exhibited the strongest correlations between FD and TFC (r_S up to −.25). Other summarizing parameters, such as maximum DVARS or DVARS variance, could be used as well because they capture other features of motion (big spike‐like movements, constant small drift). However, Van Dijk et al. (2012) showed that they are all highly correlated (the mean motion was strongly correlated with both max motion and a number of movements). Therefore, we reported only mean FD and mean DVARS.

Every quality metric employing FD or DVARS is limited by the precision of the measure itself (Power et al., 2015). Since motion takes the form of regionally heterogeneous effects on FC estimates, better measurements of motion can yield better predictions of FC quality. For example, using slice‐derived motion metrics rather than volume‐derived estimates could be beneficial because they are only a simplification of movement over the acquisition of all slices (Beall & Lowe, 2014). Nevertheless, Satterthwaite et al. (2013) and Yan, Cheung, et al. (2013) found that motion correction with voxel‐wise motion metrics offered insufficient advantages over the more easily computed general models.

Another possible improvement is using a shorter TR. The rapid subTR displacements were thought to play a significant role in regional motion artifact interactions (Spisák et al., 2014). Nevertheless, previous studies found that sub‐TR FD traces are noisier and less useful in identifying outlying time points (Power et al., 2014). While it is true that the large movements are divided into several smaller movements, they get lost amidst the constant respiratory‐related motion.

Recently, Power, Lynch, et al. (2019); Power, Silver, et al. (2019) found out that there are multiple respiration‐related effects present in realignment parameters, some of them manifesting as high‐frequency fluctuations. Therefore, realignment parameters, typically considered as a direct indicator of head motion, may as well reflect other modulations such as respiratory motion effects on the magnetic field that have no association with actual head motion (Fair et al., 2020). Although these effects are routinely filtered out from the gray matter signal, hence do not affect resulting FC values, they can negatively affect methods for motion correction (scrubbing, spike regression) or degrade the FC‐motion relationship (Williams & Snellenberg, 2019). Indeed, we observed lower correlations of TFC with motion metrics in the HCP dataset with a sub‐second sampling rate. Future studies could use dips in DVARS that still seem to reflect the true head movements or FD values that are notch filtered and a 4‐TR differential is calculated as recommended in Gratton et al. (2020) and Power, Lynch, et al. (2019); Power, Silver, et al. (2019).

Moreover, the respiration‐related high‐frequency fluctuations in motion in fast‐TR fMRI datasets are also reported (in an aliased form) in standard single band TR datasets. Suggested low‐pass filtering of motion metrics can increase their link with fMRI signal quality, especially in studies of older subjects or cohorts with increased body mass index (Gratton et al., 2020). Thanks to the shorter TRs of multiband data, it is now possible to identify respiration‐related content and so the future studies could focus on its relationship with FC quality.

Unfortunately, we are not able to provide a single value that would separate bad and good FC matrices due to the complexity of all contributing factors, such as the lack of ground truth of FC. Therefore, the decision on which scanning session should be discarded is still based only on a summary motion statistic reaching some threshold (for example RMS movement over half a voxels width (Power et al., 2013) or more than 20 volumes with RMS greater than 0.25 mm (Ciric et al., 2017)). We only propose adding the TFC measure for group‐level corrections. Other directions for mitigating the motion artifact include using multi‐echo imaging (Power et al., 2018) or using head molds (Power, Lynch, et al., 2019; Power, Silver, et al., 2019).

A possible objection is that the typical connectivity matrix is not an appropriate golden standard. While a perfect estimate of clean FC without any effect of artifacts is not achievable, we assume that by averaging FC matrices of low‐movement subjects, we obtain a useful estimate of typical awake human brain FC. Obtained results prove that the observed individual differences significantly reflect artifacts, in particular those resulting from head motion. Thus, using TFC is a useful measure identifying potentially problematic subjects. Moreover, we found that the group‐average FC matrices from different groups were very similar (correlation of the typical matrix from the Main dataset with similarly preprocessed typical FC of the Alternative dataset is r_P = .86, p < 10⁻¹⁶, resp. r_P = .68, p < 10⁻¹⁶ between Main and HCP dataset). Therefore, we obtained similar results regardless of the applied typical FC matrix. Moreover, using the typical FC matrix from a different dataset has the advantage that no degrees of freedom are lost, that is, subjects used for the computation of the typical FC matrix do not have to be discarded from subsequent analyses.

While deviation of individual FC from the typical FC might happen not only due to artifacts but also due to meaningful interindividual variability in “true neuronal” FC, in practice, the FC deviations from the typical FC arise due to a mix of artifacts/noise and the presence of specific individual FC patterns. Our rationale here is thus not that any deviation from typical FC is only and fully due to artifacts, but instead that the most significant deviations from the typical FC are likely to be substantially affected by artifacts.

5. CONCLUSION

In current resting‐state fMRI studies, there is a need for a sufficiently sensitive measure of individual FC quality. In this article, we presented a new method of FC quality evaluation for rs‐fMRI data. The TFC captures deviation from the standard brain connectivity patterns. We found that this metric is significantly correlated with motion metrics across different datasets, parcellations, and preprocessing pipelines. Furthermore, we used it to demonstrate that there is a gradual decrease in the connectivity quality and the data quality in more detailed brain parcellations with ROIs composed of fewer voxels. This quality decrease is not related to head motion, but to other types of noise as the motion‐quality relationship remained constant across parcellations. In conclusion, TFC allows extensive use in screening data quality, comparing high‐movement groups or denoising strategies, and choosing optimal brain parcellation. Our findings should be considered when a robust estimate of connectivity is more important than fine brain parcellation.

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are openly available in Mendeley repository at https://doi.org/10.17632/crx7d22pym.1

Supporting information

Figure S1 ROI sizes for 23 atlases based on Craddock spectral clustering method and for anatomical AAL atlas (in purple). The ROI size decreases with the increasing number of ROIs. The mean size (number of voxels) with ± standard deviation is plotted.

Figure S2: Mean of DVARS and FD are metrics commonly used to describe the gross head movement of a given subject. Based on the motion metrics, all subjects would meet the inclusion criteria for analysis in most MRI laboratories. The distributions of tSNR and motion metrics (represented by mean FD and mean DVARS) for the 245 subjects used in this study are plotted.

Figure S3: Using a different number of subjects for the typical FC matrix calculation. As the template of FC, we used the mean FC matrix of 10% of subjects with the lowest motion (lowest mean FD) from the Alternative dataset. Using 10% of subjects yields the highest correlation between mean DVARS and TFC. If subjects from the same dataset are used (and further excluded), the strongest correlations are obtained when selecting only low‐movement subjects. Rows indicate what dataset was used for the typical matrix (Main, Alternative, HCP). Columns represent the correlation of TFC for the given setup with either mean DVARS or FD.

Figure S4: Relationship between mean FD and TFC. Although the correlation is lower compared to mean DVARS, it is still significant, meaning subjects with worse FC quality show a higher amount of motion during the scanning session.

Figure S5: To further investigate the effects of head movements, we split the dataset into two parts based on varying thresholds of mean FD. We further analyze the high‐movement group. Subsets containing only a small percentage of subjects (10, 15, 20%) with the highest mean FD show a stronger correlation between TFC and both (a) mean DVARS and (b) mean FD. Therefore, the effect of head movement is more pronounced in subjects with higher motion. We obtained similar results if the subsets were created based on thresholding DVARS.

Figure S6: Comparison of TFC based on preprocessing. Differences between TFC distributions are significant even if each preprocessing stream used its own typical FC matrix as the golden standard, that is, matrices with moderate preprocessing were compared to a typical matrix also with moderate preprocessing.

Figure S7: Examples of FC matrices with moderate preprocessing for different subjects based on their TFC. (a) Typical FC matrix for Craddock atlas with 100 ROIs. (b) Examples of subjects with the highest TFC. Their FC matrix accurately preserved the modular structure similar to the typical matrix. (c) Examples of subjects with the lowest TFC. Based on visual inspection, their FC matrices do not correspond to the typical matrix, even though their head movement might not be prominent.

Kopal J, Pidnebesna A, Tomeček D, Tintěra J, Hlinka J. Typicality of functional connectivity robustly captures motion artifacts in rs‐fMRI across datasets, atlases, and preprocessing pipelines. Hum Brain Mapp. 2020;41:5325–5340. 10.1002/hbm.25195