Abstract
With increased awareness on the importance of gloves arising from the COVID-19 pandemic, people are expected to continue using them even after the pandemic recedes. This scenario in a way increased the rubber solid waste disposal problem; therefore, the production of biodegradable gloves may be an option to overcome this problem. However, the need to study the shelf life of biodegradable gloves is crucial before commercialization. There are well-established models to address the failure properties of gloves as stated in the American Society for Testing and Material (ASTM) D7160. In this study, polysaccharide-based material-filled natural rubber latex (PFNRL) gloves, which are biodegradable gloves, were subjected to an accelerated aging process at different temperatures of 50–80 °C for 1–120 days. Prediction models based on Arrhenius and shift factors were used to estimate the shelf life of the PFNRL gloves. Based on the results obtained, the estimated time for the PFNRL gloves to retain 75% of their tensile strength at shelf temperature (30 °C) based on Arrhenius and shift factor models was 2.8 years. Verification on the activation energy based on the shift factor model indicated that the shelf life of PFNRL gloves is 2.9 years, which is only a 3.6% difference. The value obtained is aligned with the requirement in accordance with ASTM D7160, which states that only up to a maximum of 3 years’ shelf life is allowed for the gloves under accelerated aging conditions.
Introduction
Malaysia is the world’s largest manufacturer of rubber gloves; over 200 billion gloves are manufactured annually, with a market share of about 65%.1 In 2019, Malaysia exported about 182 billion gloves, while for 2020, because of the on-going COVID-19 global pandemic, the Malaysian Rubber Glove Manufacturers Association (MARGMA) estimates it to be as high as 240 billion pieces. Given the acute surge in demand and single-use personal protective equipment, it will directly contribute to the gloves’ waste disposal problems. In Malaysia, the clinical waste including rubber gloves has risen 27% for almost 2 months since the movement control order has been implemented.2
Biodegradation is one of the green alternatives to overcome the gloves’ waste disposal problem. Attempts to replace common calcium carbonate with biofillers such as polysaccharides, eggshell, and chitosan in natural rubber (NR) latex gloves are frequently discussed.3,4 It was reported that the microbes as well as fungi are able to degrade the NR even though the process is time-consuming.5,6 Therefore, the incorporation of polysaccharides into the NR latex system is targeted to accelerate the activities of the microorganisms, thus enabling the gloves to degrade effectively.7 The polysaccharides are very beneficial for the biodegradation process where it may serve as nutrients to the microbes, which enhanced the biodegradability of the gloves.5 In nature, microorganisms will form the catalytic enzymes for the biodegradation process.8 In the case of biodegradable gloves, the degradation process is accomplished by microorganism activities via enzymatic cleavage in polysaccharides as well as the oxidation process in the rubber backbone chain.7
Significant changes in glove formulation such as addition of polysaccharides to the NR latex system require comprehensive studies including product shelf life. Besides, the need to study the shelf life of biodegradable gloves is crucial before commercialization. Shelf life is commonly estimated using two types of stability testing which are real-time and accelerated stability tests.9,10 For the real-time stability test, a product is stored under predetermined storage conditions, while for accelerated stability tests, a product is stored at elevated stress conditions such as temperature, pH, and humidity and the changes are monitored until it fails based on a specification requirement such as the time taken to reach the threshold value.11 The shelf life determined on real-time aging is generally preferred for an estimated value based on accelerated data as it can provide the best data to ensure that the product meets the specifications without degrading over the time frame of the requirements. However, real-time data collection is known to undergo a very slow degradation rate at near ambient temperature. In addition, for biodegradable gloves, real-time aging is impractical as it is time-consuming for the industry to market the product, especially to fulfil the shelf-life requirement.12,13 For more immediate results, the short-term accelerated method offers an advantage to estimate a more liable and conservative shelf life that supports a practical shelf life.
Mainly, there are two models present in the literature on the life estimation of an elastomer, namely, Arrhenius and Williams–Landel–Ferry (WLF) models.14 However, a widely used method to predict the shelf life is through kinetic modeling based on the Arrhenius equation.15−17 In order to simulate the situation, the products are normally stored at a higher temperature than room temperature under clearly defined controlled conditions. Upon completion of the aging test, the physical property of the products is measured, usually at room temperature. The shelf life is then estimated by extrapolating the property’s value from the accelerated aging at the expected storage temperature.18 The activation energy of the materials can be determined from the slope of the linear Arrhenius behavior.
The prediction of butyl rubber-based composite (BRC) service lifetime was conducted by Nguyen-Tri and co-researchers19 based on extrapolation of the Arrhenius plot at different temperatures. They obtained an activation energy of 157 kJ·mol–1 from the Arrhenius curve where the mechanical properties of BRC remained at acceptable values until 344 days at 80 °C. The decrease in mechanical values was observed after 2 days at 120 °C. Meanwhile, Das and Schroeder18 used different methods of extrapolation for shelf-life estimation of NR latex examination gloves, which were based on the Q-factor and Arrhenius activation energy methods. They predicted the shelf life of nonchlorinated NR latex gloves as being up to 3.25 years at room temperature. However, it needs to be highlighted that their work is based on the creep test using a 50 kPa load on the fingertip of the gloves only. On the other hand, Le Huy and Evrard20 determined the shelf life and service life estimation of a few types of rubbers (butadiene–styrene rubber/NR; hydrogenated acrylonitrile–butadiene copolymer; nitrile rubber/polyvinyl chloride; ethylene–propylene–diene terpolymer) using Arrhenius and WLF models. They concluded that the WLF model is appropriate for lifetime predictions when the polymer is subjected to an aging condition that is controlled by a viscoelastic process (e.g., relaxation, creep) similar to the service life. In contrast, when physicochemical mechanisms are dominant, the Arrhenius model is the most widely used model for estimating an accelerated test result concerning the effect of temperature.
Numerous studies have been published mainly focused on the different types of biodegradable fillers with diverse methods of improving its compatibility, mechanical strength, and biodegradability of NR latex films.21−23 However, little work has been carried out on the shelf life of the biodegradable product. In this work, the shelf life of polysaccharide-based material-filled NR latex (PFNRL) gloves, biodegradable gloves, was predicted via two models which are based on the Arrhenius and shift factor as recommended by the standard requirement of examination gloves (ASTM D7160). The activation energy was then verified by another approach suggested by ASTM D7160; hence, the predicted shelf life of PFNRL gloves via this approach can be compared with those of the earlier models used. This work aims to identify the shelf life of PFNRL gloves and to compare the variation of the values predicted by the aforementioned models. The results obtained were referred with the ASTM D7160 requirement for the acceptance limit of the shelf life.
Results and Discussion
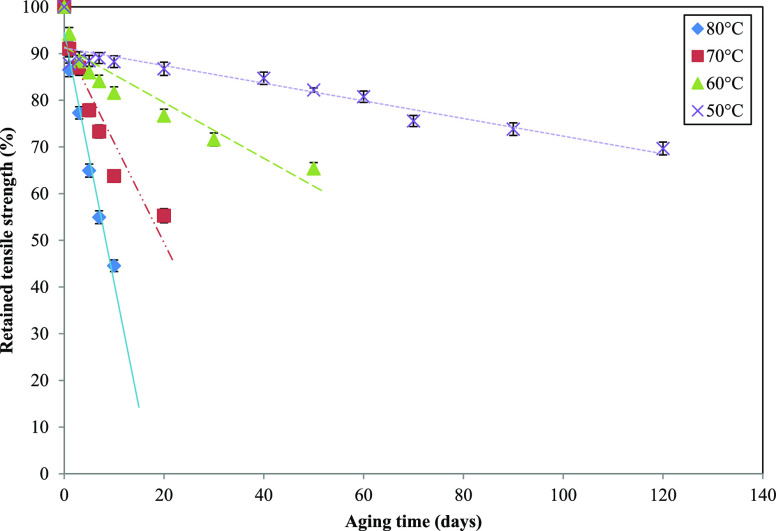
Based on our research work, the tensile strength is chosen as the property to determine the shelf life as stated in the ASTM D3578. The PFNRL gloves’ tensile strength used in this work is consistent with our previous research work.3Figure 1 shows the percentage retention of tensile strength at four different temperatures within 120 days for PFNRL gloves. The percentage of tensile strength retention was calculated based on eq 1. A threshold value of 75% retention was chosen for this study as recommended according to ASTM D7160.24 The threshold is chosen based on the point where the degree of degradation approaches the minimum acceptable value for the property being tested per product design specification. Based on the graph, the percentage retention of tensile strength gradually decreased with time at a degradation temperature of 50 °C before it decreased rapidly when the temperature increased to 80 °C. From Figure 1, the time required for each temperature to reach a threshold of 75% retained tensile strength was tabulated in Table 1.
Figure 1.
Variation of the tensile strength retention of PFNRL gloves with aging time at various aging temperatures.
Table 1. Time Required to Reach the Threshold of 75% Tensile Strength Retention at Different Accelerated Aging Temperatures.
| temperature (°C) | 1000/T (1000/K) | time (days) of 75% retention |
|---|---|---|
| 50 | 3.10 | 86 |
| 60 | 3.00 | 28 |
| 70 | 2.92 | 8 |
| 80 | 2.83 | 4 |
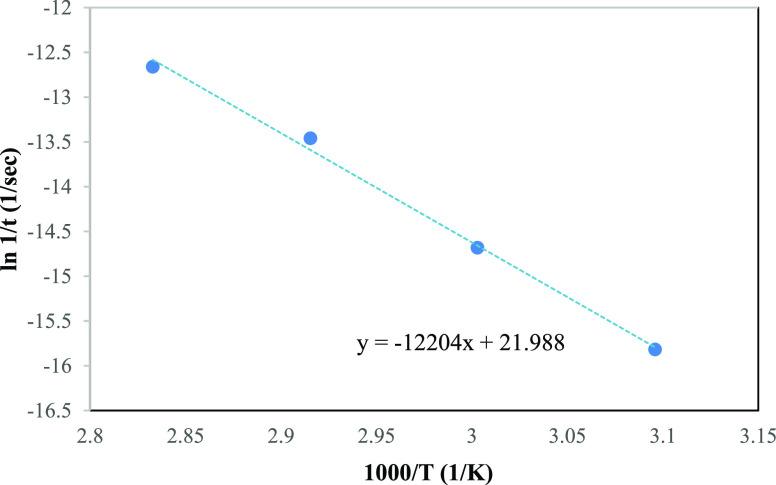
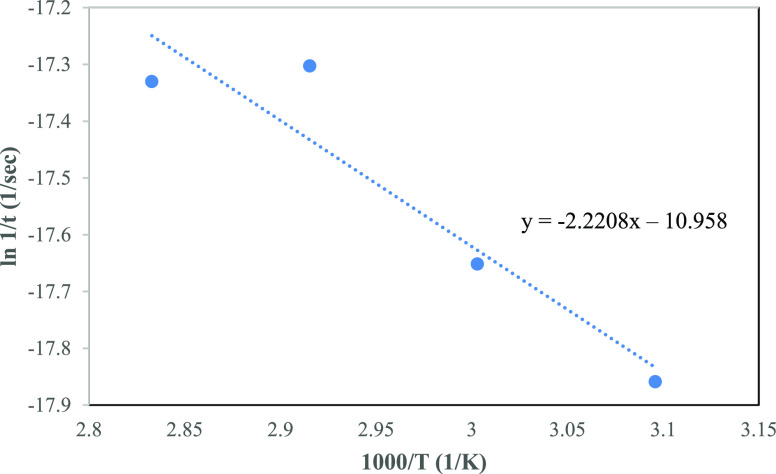
Based on Table 1, the time taken for the tensile strength retention to reduce to 75% is further used to plot graphs of ln(1/t) versus 10,000/T as shown in Figures 2 and 3 in which the slopes of the lines connecting the data points were used in both models to extrapolate and predict the shelf life.
Figure 2.
Arrhenius plot using the Arrhenius model for different accelerated aging temperatures of PFNRL gloves.
Figure 3.
Arrhenius plot using the shift factor model for different accelerated aging temperatures of PFNRL gloves.
Arrhenius Model
For data analysis and extrapolation, BS EN 455-4 recommends applying the method of least squares to the experimental data.25 The Arrhenius model is also required to find the best straight line fit through the experimental data point as in Figure 2. A linear extrapolation of the straight line generated allows the prediction of shelf life at a lower temperature. To plot the graph, the term ln(k) from eq 3 was taken as ln(1/t in s) and the t (time) was obtained from Table 1 for the respective accelerated aging temperature. The data obtained reasonably fit the relationship of eq 3, which gives the best straight line that fits through the experimental data points. By comparing the regression equation in Figure 2 with eq 3, the activation energy and the shelf life of PFNRL gloves at 30 °C with 75% retention of tensile strength can be calculated. The activation energy can be obtained from the slope of the line, while the shelf life of PFNRL gloves can be obtained by solving the regression equation with T = 30 °C. The results are tabulated in Table 4.
Table 4. Shelf Life and Activation Energy Prediction According to Various Approaches.
| Arrhenius model | shift factor model | verification of activation energy | |
|---|---|---|---|
| shelf life (year) | 2.8 | 2.8 | 2.9 |
| activation energy (kJ/mol) | 101.46 | (activation energy was based on 83 kJ/mol) | 101.52 |
Shift Factor Model
The shift factor model requires the data to be shifted to a selected reference temperature and activation energy. In this model, the time at each respective temperature (from Table 1) was shifted to equivalent times at a common reference temperature by multiplying them with the Arrhenius shift factor, aT, according to ISO 407426 (refer to Table 2). The shift factors were based on the activation energy of 83 kJ/mol at a reference temperature of 30 °C. As in the previous model, a single straight line was generated to give the best straight line, which fit through the experimental data points (refer to Figure 3). Based on the regression equation in Figure 3, the predicted lifetime at 30 °C with 75% retention of tensile strength can also be calculated and the results are tabulated in Table 4.
Table 2. Time Required to Reach the Threshold of 75% Tensile Strength Retention.
| temperature (°C) | shift factor for a reference temperature at 30 °C | shifted time (days) to reach 75% retention |
|---|---|---|
| 50 | 7.69 | 660 |
| 60 | 19.46 | 537 |
| 70 | 46.63 | 378 |
| 80 | 106.34 | 389 |
Verification of the Activation Energy
Because of the differences in the activation energy from the shift factor model, verification of activation energy was carried out to find the actual activation energy. By using the data from ISO 4074, the shift factor can also be calculated based on eq 5. Based on that equation, the times taken for the tensile strength of PFNRL gloves to fall to 75% at the respective temperatures (from Table 1) were used to obtain the shift factor. Table 3 shows the shift factor as well as its respective activation energy, Ea, for each temperature pair. The actual activation energy was calculated using eq 4.
Table 3. Actual Activation Energy for Every Shift Factor.
| shift factora | actual Ea (kJ/mol) |
|---|---|
| aT1 = 3.11 | 101.52 |
| aT2 = 3.40 | 116.13 |
| aT3 = 2.22 | 80.24 |
aT1 = t50°C/t60°C, aT2 = t60°C/t70°C, aT3 = t70°C/t80°C.
Based on ASTM D7160, the shift factor needs to be recalculated if the actual activation energy is not comparable to the estimated value (83 ± 2 kJ/mol) at all temperature ranges. As presented in Table 3, none of the actual activation energy met that requirement. Thus, the shift factor at shelf temperature was recalculated using eq 4 where T1 is T30°C, T2 is the lowest accelerated aging temperature, and Ea is the actual activation energy for the lowest temperature pair. In this case, the lowest temperature pair would be aT1. Based on the shift factor at shelf temperature, the predicted shelf life can be calculated using eq 5 where t1 is t30°C and t2 is the time at the lowest accelerated aging temperature. The results are tabulated in Table 4.
Verification of Prediction Time
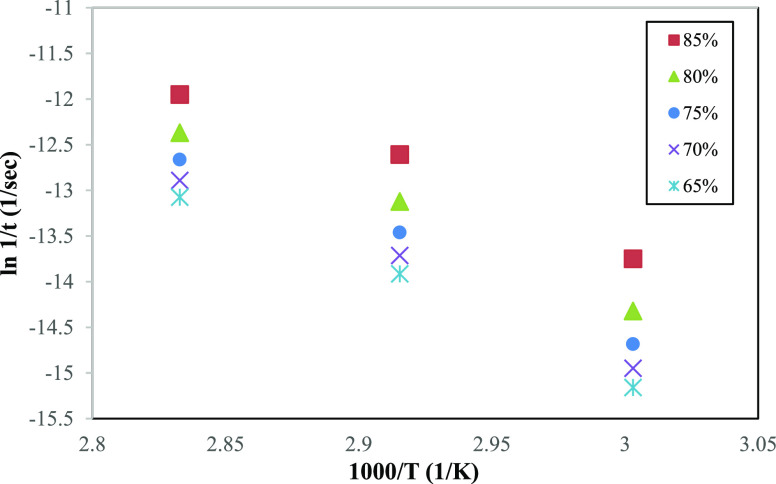
A preliminary test was conducted to verify the time predicted based on the Arrhenius model with real time based on accelerated aging. Choosing 85, 80, 75, 70, and 65% of the retained tensile strength of PFNRL gloves as the failure criteria, the corresponding time to reach these limits are presented in Table 5. Based on the Arrhenius model, the linear and parallel plots of reciprocal time for tensile strength properties to fall to 85, 80, 75, 70, and 65% with various aging temperatures (60, 70, and 80 °C) of PFNRL gloves are shown in Figure 4. The plot is based on two postulations; (1) constant effective activation energy throughout the experimental temperature range and (2) the change in tensile strength during accelerated aging in accordance with Arrhenius behavior.
Table 5. Time Required to Reach the Threshold of 85, 80, 75, 70, and 65% Retained Tensile Strength.
| time (days) |
||||||
|---|---|---|---|---|---|---|
| temperature (°C) | 10,000/T (1/K) | 85% retention | 80% retention | 75% retention | 70% retention | 65% retention |
| 60 | 3.00 | 11 | 19 | 28 | 36 | 44 |
| 70 | 2.92 | 3 | 6 | 8 | 10 | 13 |
| 80 | 2.83 | 2 | 3 | 4 | 5 | 6 |
Figure 4.
Arrhenius plot of retained tensile strength at 85, 80, 75, 70, and 65% for PFNRL gloves.
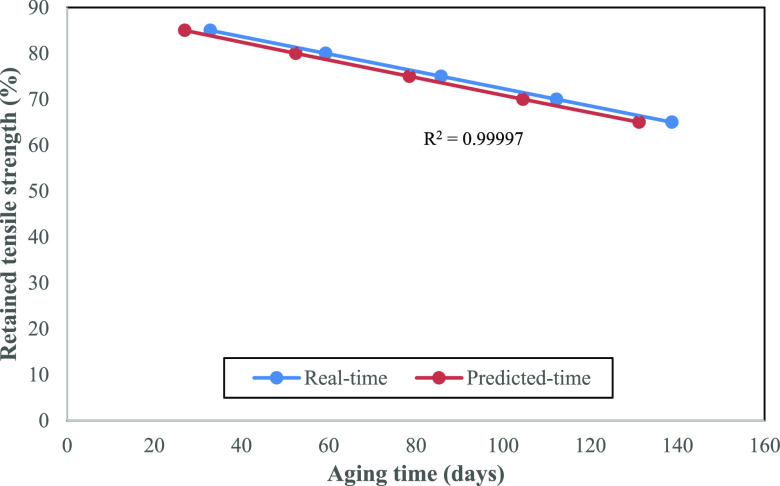
Based on Figure 4, the predicted times at 50 °C with 85, 80, 75, 70, and 65% retention of tensile strength were obtained from the regression equation of each retained tensile strength. In comparison with real-time accelerated aging, the times required to reach thresholds of 85, 80, 75, 70, and 65% retained tensile strength at 50 °C were obtained from Figure 1. Both data (real and predicted time) are presented in Figure 5.
Figure 5.
Tensile strength retention of PFNRL gloves at 50 °C aging temperature.
Discussion
For all temperatures tested in this study, the tensile strength retention demonstrates a trend that decreased with prolonged aging time (refer to Figure 1). The test carried out at 80 °C showed a more dramatic decrease in tensile strength compared to other temperatures. On the other hand, lower aging temperatures need a longer time for a significant reduction of tensile strength. The reduction of tensile strength is governed by the degradation of the rubber backbone chain together with the changes in the sulfur cross-link system because of heat aging and oxidation.27 All unsaturated rubbers are subject to degradation due to the attack by thermal degradation and oxo-degradation. It is well established that the aging of rubbers at elevated temperatures causes chain scission and/or cross-linking.28
During the earlier stages of thermal aging, there is cross-links rearrangement from a polysulfidic to a monosulfidic chain.29 Fluctuations at some points are probably caused by the balancing between the cross-link scission and the cross-link formation in the polymer. Both cross-link scission and cross-link formation occur simultaneously, and these reactions occur all the time in the aging process. The mechanism of cross-links rearrangement leads to an increment of rubber stiffness and embrittlement, while chain scission lowers the cross-link density, resulting in rubber softening and loss of elastic properties. In other words, the hardness of a rubber increases if the cross-link density increases and decreases upon breakage of the chains.30
On further heating, oxygen-free radicals attack the unsaturated backbone chain, leading to main chain degradation, which caused a drastic reduction of tensile strength at the final stage of the aging process.31 In a work by Choudhury et al.,32 on further heating for a prolonged period at 70 °C, the tensile strength and elongation at break properties were drastically decreased. Besides, thermal energy also provides the activation energy required for the initiation of oxidation, thus accelerating the overall process of degradation.33 After different durations of exposure to heat and oxygen, the mechanical properties of NR films such as the deterioration of tensile strength is observed, leading to polymer failure. If minor changes in tensile strength have been detected, a longer shelf life may be expected, while if appreciable changes occurred, the shelf life may be short.28
It has been suggested that the accelerated temperature aging should be conducted within the range of 50–80 °C.24 When the sample is subjected to a higher temperature, significant changes in the rate of degradation will be observed. As the temperature increases, it becomes more feasible to estimate the degradation behavior in a short period. However, in the case of lower temperatures, the process requires more time for the sample to degrade. Furthermore, ASTM D7160 has stated that the lowest test temperature chosen needs to consider the time taken to reach the threshold value of at least 8–10 weeks. Similarly, the lowest temperature shall be chosen to ensure that the necessary threshold value is reached. Therefore, a maximum period of 120 days at a minimum accelerated aging temperature of 50 °C and the retention of tensile strength below 75% carried out in this work is an appropriate selection of aging durations.
Figures 2 and 3 show the Arrhenius plot with two different models of prediction. It is found that the data fit better on the Arrhenius model compared to the shift factor model. This might be due to the difference in the activation energy used. Based on the Arrhenius model, the activation energy was calculated as 101.46 kJ/mol, while for the shift factor model, the activation energy was 83 kJ/mol, which was taken from literature.24,26 Hence, further verification of the activation energy was conducted to find the actual activation energy.
A comparison of the shelf life and activation energies derived from various models as discussed earlier is summarized in Table 4. Based on the results, there are rather similar values of the shelf life and activation energies calculated in all approaches. Both models estimated 2.8 years for the PFNRL gloves to fall to 75% of tensile strength retention at 30 °C. Furthermore, after the activation energy was verified, the shelf life of PFNRL gloves did not differ much, calculated at 2.9 years, which is only a 3.6% difference. The value obtained is according to the requirement of ASTM D3578, which states that only up to a maximum of 3 years’ shelf life is allowed for the gloves under accelerated aging conditions.24 The verified activation energy also has a value similar to the activation energy from the Arrhenius model, proving that the model is valid to estimate the shelf life of PFNRL gloves. Even though the average activation energy for many chemical reactions is 83 kJ/mol, the actual values found in practice vary widely.26 Grimm34 and Mandel et al.35 determined the activation energies for the oxidation of NR to be in the range of 84–117 kJ/mol. Meanwhile, Mott and Roland36 found that the activation energies of aging of NR in air and seawater were 90 ± 4 and 63 ± 3 kJ/mol, respectively.
Based on Table 4, a similar shelf life could be expected for other PFNRL gloves, perhaps from a different lot, of the same manufacturer, with a similar source of raw materials, formulation, and manufacturing processes. The aforementioned results are also based on the temperature at 30 °C. It is prudent to expect that there might be storage conditions above 30 °C, depending on the countries. Under such conditions, the current set of samples would probably not survive more than 3 years according to all approaches discussed earlier. Based on the accelerated study, a maximum of 3 years’ shelf life is tolerable for examination gloves according to ASTM D7160. Thus, a close monitoring of room temperature storage in some hospitals, laboratories, and private homes in countries that have tropical or subtropical climates needs to be done as the temperature may vary in the range of 30–40 °C.11
As shown in Figure 5, even the decrease of tensile strength upon real-time accelerated aging was time-consuming compared to the predicted time, but the trend obtained was similar. Besides, the decrement of tensile strength retention is also aligned with prolonged aging time. This indicates that the real-time accelerated aging at 50 °C concurs with the value determined via prediction analysis. It was supported by the calculation of Pearson’s coefficient of correlation (eq 6), where the R2 value obtained was 0.99997. It indicates an almost perfect positive relationship between the two data sets.
Conclusions
In conclusion, the shelf life of PFNRL gloves was estimated at 2.8 years when its tensile strength reduced to 75% retention at 30 °C according to both Arrhenius and shift factor models without the verification of activation energy. This gives an overview that PFNRL gloves can survive up to 2.8 years, provided they are stored at a similar shelf temperature with a comparable source of raw materials, formulation, and manufacturing process.
Materials and Methodology
Materials
NR latex with the initial properties of dry rubber content of 60.08 wt %, total solid content of 61.00 wt %, mechanical stability time of 1140 s, and volatile fatty acid number not exceeding 0.2 was purchased from Zarm Scientific and Supplies Sdn. Bhd. (Penang, Malaysia). Meanwhile, the dispersion of polysaccharide material was produced in-house and other compounding ingredients such as diethyldithiocarbamate, zinc oxide (ZnO), 2,2′-methylene-bis(4-methyl-6-tert-butylphenol), and sulfur were obtained from Farben (Malaysia) Sdn. Bhd., whereas calcium nitrate [Ca(NO3)2], nitric acid 65%, chloroform, and potassium hydroxide (KOH) were purchased from Merck Sdn. Bhd.
Latex Compound Preparation and Gloves Production
The preparation of the NR latex compound was carried out following a previous study.5 All ingredients were mixed and stirred for 2 h at a stirring speed of 270 rpm under room temperature. The compound was subjected to prevulcanization at 70 °C in a water bath until chloroform number 2 (desired degree of cross-link formation inside NR latex particles) was achieved. The prevulcanized latex compound was left for a maturation process for 24 h under room temperature.
The preheated formers were dipped into the coagulant tank followed by the latex tank with the desired dwell time to obtain a thin film of PFNRL gloves. The gloves were dried in an oven at 110 °C until the gloves were cured. They were then taken out from the oven and stripped off with the assistance of calcium carbonate powder.
Accelerated Aging Test
The PFNRL gloves were exposed to different temperatures (50, 60, 70, and 80 °C) continuously in a hot air oven (Memmert, Germany) for 1–120 days. The PFNRL gloves were taken out after specific durations and conditioned under room temperature for at least 16 h before being subjected to tensile strength testing. This must be completed in 96 h from the time of removal from the oven following ASTM D573.37
Tensile Strength Test
The tensile strength test was carried out according to ASTM D41238 using an Instron Machine (Model 3366 USA) with a crosshead speed of 500 mm/min. The PFNRL gloves were cut into dumbbell shapes and the thickness of the samples was measured before testing. The mean readings of tensile strength based on the average of five samples were calculated and reported.
Retention of Tensile Strength
The percentage of tensile strength retention with time was used to determine the degradation rate of PFNRL gloves by following eq 1
| 1 |
where σi is the initial tensile strength and σa is the aged tensile strength of the PFNRL gloves.
Shelf-Life Determination
Tensile strength test was carried out according to ASTM D7160.24 The product shelf life can be determined using the Arrhenius equation as stated in eq 2
| 2 |
where k is the reaction rate constant, A is a constant related to the property of interest, Ea is the activation energy, R is the universal gas constant (8.314 J/K mol), and T is the temperature of interest (in kelvin).
The first order of the Arrhenius equation was derived from eq 2, yielding
| 3 |
Meanwhile, the shift factor, aT, can be expressed as eq 4
| 4 |
where k1 is the rate constant at T1 and k2 is the rate constant at T2 (T1 < T2).
Alternatively, aT can also be determined experimentally using eq 5
| 5 |
where t1 is the time at T1 until a threshold is reached and t2 is the time at T2 until a threshold is reached (T1 < T2).
Pearson Coefficient of Correlation, R-Value
The Pearson correlation coefficient (R2) for two data sets was calculated using eq 6. The calculated value was used to determine the characteristics and strength of the relationship between two data sets.
| 6 |
where X̅ and Y̅ are the mean values for data x and y, respectively, σx and σy are the standard deviations for data x and y, xi and yi are the data for respective datasets, and n is the number of data in the dataset.
Acknowledgments
The authors gratefully acknowledge the facilities and support provided by the School of Materials & Mineral Resources Engineering, Universiti Sains Malaysia. They are also grateful for the financial support from a research grant (grant no: 203/PBAHAN/6071353).
Author Contributions
The manuscript was produced through equal contributions from all authors. All authors have approved the final version of the manuscript.
The authors declare no competing financial interest.
References
- https://www.bloombergquint.com/businessweek/the-pandemic-is-a-bonanza-for-malaysia-s-medical-glove-industry (accessed on August 06, 2020).
- https://cilisos.my/heres-how-malaysia-deals-with-clinical-waste-thats-increased-since-the-pandemic/ (accessed on August 06, 2020).
- Misman M. A.; Azura A. R. Overview on the potential of biodegradable natural rubber latex gloves for commercialization. Adv. Mater. Res. 2014, 844, 486–489. 10.4028/www.scientific.net/amr.844.486. [DOI] [Google Scholar]
- Ghani H.; Abd Karim S. F.; Ramli R.; Musa M.; Jaapar J. Effect of bio fillers on mechanical properties of natural rubber latex films. Key Eng. Mater. 2019, 797, 249–254. 10.4028/www.scientific.net/kem.797.249. [DOI] [Google Scholar]
- Misman M. A.; Azura A. R. Utilization of starch to accelerate the growth of degrading microorganisms on the surface of natural rubber latex films. J. Chem. Chem. Eng. 2013, 7, 137. [Google Scholar]
- Bode H. B.; Kerkhoff K.; Jendrossek D. Bacterial degradation of natural and synthetic rubber. Biomacromolecules 2001, 2, 295–303. 10.1021/bm005638h. [DOI] [PubMed] [Google Scholar]
- Afiq M. M.; Azura A. R. Effect of sago starch loadings on soil decomposition of natural rubber latex (NRL) composite films mechanical properties. Int. Biodeterior. Biodegrad. 2013, 85, 139–149. 10.1016/j.ibiod.2013.06.016. [DOI] [Google Scholar]
- Hadad D.; Geresh S.; Sivan A. Biodegradation of polyethylene by the thermophilic bacterium Brevibacillus borstelensis. J. Appl. Microbiol. 2005, 98, 1093–1100. 10.1111/j.1365-2672.2005.02553.x. [DOI] [PubMed] [Google Scholar]
- Magari R. T. Assessing shelf life using real-time and accelerated stability tests. BioPharm Int. 2003, 16, 36–48. [Google Scholar]
- Haouet M. N.; Tommasino M.; Mercuri M. L.; Benedetti F.; Di Bella S.; Framboas M.; Pelli S.; Altissimi M. S. Experimental accelerated shelf life determination of a ready-to-eat processed food. Ital. J. Food Saf. 2018, 7, 6919. 10.4081/ijfs.2018.6919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawar N.; Arora M.; Naved T.; Tyagi V. K. Stabilities studies of formulations containing Eucalyptus oil. Indo Global J. Pharm. Sci. 2013, 3, 174–180. [Google Scholar]
- Magari R. T.; Munoz-Antoni I.; Baker J.; Flagler D. J. Determining shelf life by comparing degradations at elevated temperatures. J. Clin. Lab. Anal. 2004, 18, 159–164. 10.1002/jcla.20016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- https://www.safetyandhealthmagazine.com/articles/determining-the-shelf-life-of-gloves-shouldn-t-be-a-stretch-2 (accessed on August 06, 2020).
- Das S.; Chaudhuri A. Estimation of life of an elastomeric component: A stochastic model. Def. Sci. J. 2011, 61, 257–263. 10.14429/dsj.61.295. [DOI] [Google Scholar]
- Stadler R.; Maurer A. Methods for durability testing and lifetime estimation of thermal interface materials in batteries. Batteries 2019, 5, 34. 10.3390/batteries5010034. [DOI] [Google Scholar]
- Magari R. T. Estimating degradation in real time and accelerated stability tests with random lot-to-lot variation: A simulation study. J. Pharm. Sci. 2002, 91, 893–899. 10.1002/jps.10092. [DOI] [PubMed] [Google Scholar]
- Dixon D.; Boyd A. Degradation and accelerated ageing of poly(ether block amide) thermoplastic elastomers. Polym. Eng. Sci. 2011, 51, 2203–2209. 10.1002/pen.21992. [DOI] [Google Scholar]
- Das S. S.; Schroeder L. W. Estimation of shelf life of natural rubber latex exam-gloves based on creep behavior. J. Biomed. Mater. Res., Part B 2008, 85, 398–408. 10.1002/jbm.b.30958. [DOI] [PubMed] [Google Scholar]
- Nguyen-Tri P.; Triki E.; Nguyen T. A. Butyl rubber-based composite: Thermal degradation and prediction of service lifetime. J. Compos. Sci. 2019, 3, 48. 10.3390/jcs3020048. [DOI] [Google Scholar]
- Le Huy M.; Evrard G. Methodologies for lifetime predictions of rubber using Arrhenius and WLF models. Die Angewandte Makromolekulare Chemie 1998, 261–262, 135–142. . [DOI] [Google Scholar]
- Anand K.; Varghese S.; Kurian T.; Bose S. Effect of starch nanocrystals on natural rubber latex vulcanizate properties. Prog. Rubber, Plast. Recycl. Technol. 2018, 34, 75–87. 10.1177/147776061803400201. [DOI] [Google Scholar]
- Daud S.; Ismail H.; Bakar A. A. Soil burial study of palm kernel shell-filled natural rubber composites: The effect of filler loading and presence of silane coupling agent. BioResources 2016, 11, 8686–8702. 10.15376/biores.11.4.8686-8702. [DOI] [Google Scholar]
- Lay M.; Samat S. N. A.; Hwa K. T.; Rashid A. A. Ecofriendly latex films from cassava starch-filled radiation pre-vulcanized natural rubber latex. Radiat. Eff. Defects Solids 2019, 174, 741–751. 10.1080/10420150.2019.1649261. [DOI] [Google Scholar]
- ASTM . D7160-16, Standard Practice for Determination of Expiration Dating for Medical Gloves; ASTM International: West Conshohocken, PA, USA, 2016. [Google Scholar]
- BS EN . 455-4, Medical gloves for single use requirements and testing for shelf life determination, Brussels, Belgium, 2009. [Google Scholar]
- ISO . 4074:2015, Natural rubber latex male condoms—Requirements and test methods; ISO Central Secretariat: Geneva, Switzerland, 2015. [Google Scholar]
- Manaila E.; Stelescu M.; Craciun G. Degradation studies realized on natural rubber and plasticized potato starch based eco-composites obtained by peroxide cross-linking. Int. J. Mol. Sci. 2018, 19, 2862. 10.3390/ijms19102862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Natural Rubber Materials: Composites and Nanocomposites; Thomas S., Chan C. H., Pothen L. A., Joy J. P., Maria H. J., Eds.; RSC Publisher: Cambridge, UK, 2014; Vol. 2. [Google Scholar]
- Gopisathi S.; Park C.; Huh Y. I.; Jeon J.; Yun C. H.; Won J.; Jeong K.-U.; Nah C. Enhancing the Reversion Resistance, Crosslinking Density and Thermo-mechanical Properties of Accelerated Sulfur Cured Chlorobutyl Rubber Using 4,4′-Bis (Maleimido) Diphenyl Methane. Rubber Chem. Technol. 2019, 92, 110–128. 10.5254/rct.18.82605. [DOI] [Google Scholar]
- Zaghdoudi M.; Kömmling A.; Jaunich M.; Wolff D. Scission, cross-linking, and physical relaxation during thermal degradation of elastomers. Polymers 2019, 11, 1280. 10.3390/polym11081280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anh T. H.; Vu-Khanh T. Effects of thermal aging on fracture performance of polychloroprene. J. Mater. Sci. 2005, 40, 5243–5248. 10.1007/s10853-005-4418-x. [DOI] [Google Scholar]
- Choudhury A.; Bhowmick A. K.; Soddemann M. Effect of organo-modified clay on accelerated aging resistance of hydrogenated nitrile rubber nanocomposites and their life time prediction. Polym. Degrad. Stab. 2010, 95, 2555–2562. 10.1016/j.polymdegradstab.2010.07.032. [DOI] [Google Scholar]
- Tiganis B. E.; Burn L. S. The effects of heat aging on acrylonitrile-butadiene-styrene (ABS) blends. Durability Build. Mater. Compon. 1999, 8, 912–922. [Google Scholar]
- Grimm W. Storage conditions for stability testing in the EC, Japan and USA; the most important market for drug products. Drug Dev. Ind. Pharm. 1993, 19, 2795–2830. 10.3109/03639049309050178. [DOI] [Google Scholar]
- Mandel J.; Roth F. L.; Steel M. N.; Stiehler R. D. Measurement of the aging of rubber vulcanizates. J. Res. Natl. Bur. Stand., Sect. C 1959, 63, 141–145. 10.6028/jres.063c.019. [DOI] [Google Scholar]
- Mott P. H.; Roland C. M. Aging of natural rubber in air and seawater. Rubber Chem. Technol. 2001, 74, 79–88. 10.5254/1.3547641. [DOI] [Google Scholar]
- ASTM . D573-04, Standard Test Method for Rubber—Deterioration in an Air Oven; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- ASTM . D412-16, Standard Test Methods for Vulcanized Rubber and Thermoplastic Elastomers—Tension; ASTM International: West Conshohocken, PA, USA, 2016. [Google Scholar]