Atrial Fibrillation Detection During Sepsis: Study on MIMIC III ICU Data

Abstract

Sepsis is defined by life-threatening organ dysfunction during infection and is one of the leading causes of critical illness. During sepsis, there is high risk that new-onset of atrial fibrillation (AF) can occur, which is associated with significant morbidity and mortality. As a result, computer aided automated and reliable detection of new-onset AF during sepsis is crucial, especially for the critically ill patients in the intensive care unit (ICU). In this paper, a novel automated and robust two-step algorithm to detect AF from ICU patients using electrocardiogram (ECG) signals is presented. First, several statistical parameters including root mean square of successive differences, Shannon entropy, and sample entropy were calculated from the heart rate for the screening of possible AF segments. Next, Poincaré plot-based features along with P-wave characteristics were used to reduce false positive detection of AF, caused by the premature atrial and ventricular beats. A subset of the Medical Information Mart for Intensive Care (MIMIC) III database containing 198 subjects was used in this study. During the training and validation phases, both the simple thresholding as well as machine learning classifiers achieved very high segment-wise AF classification performance. Finally, we tested the performance of our proposed algorithm using two independent test data sets and compared the performance with two state-of-the-art methods. The algorithm achieved an overall 100% sensitivity, 98% specificity, 98.99% accuracy, 98% positive predictive value, and 100% negative predictive value on the subject-wise AF detection, thus showing the efficacy of our proposed algorithm in critically ill sepsis patients. The annotations of the data have been made publicly available for other investigators.

I. Introduction

SEPSIS is a life-threatening, dysregulated response to infection and is one of the major causes of critical illness, affecting more than 1.5 million Americans yearly at an annual cost of over $20 billion [1]. Atrial fibrillation (AF) is a common and deadly complication of sepsis, associated with poor outcomes during hospitalization and conferring risk for significant adverse events long thereafter [2]. New-onset AF during sepsis is a common and deadly dysrhythmia during sepsis, affecting nearly 1 in 5 septic patients [3], [4] and is associated with significant morbidity and mortality [5]. Patients with sepsis have 6-fold higher risk of new-onset AF as compared with hospitalized patients with other diagnoses and similar cardiovascular risk factors. In [6], 44% of septic shock patients were found to have new-onset AF in a medical intensive care unit (ICU), thus, showing the need for automated AF detection during sepsis. However, risk factors and, possibly, mechanisms of new-AF during sepsis differ from traditional AF. Currently, research in new-onset AF during sepsis is limited by the inability to detect AF onset at scale. Reliable automated AF detection within stored electrocardiogram (ECG) waveform data is a necessary first step to predict, investigate mechanisms and evaluate treatment strategies for new-onset AF during sepsis.

To the best of our knowledge, automated AF detection for critically ill sepsis patients has not been studied to date. Most AF detectors are developed and validated using the widely used MIT-BIH atrial fibrillation database, in which the patients were ambulatory and mostly paroxysmal AF was recorded. AF detection in critically ill sepsis patients presents unique challenges. Critically ill patients suffer from frequent non-AF dysrhythmias and ectopic beats that are a common source of false positive AF detection. Additionally, the longitudinal ECG waveform data recorded from critically ill ICU patients can potentially suffer from unique types of noise artifacts [7]. In order to address these, in this study, we propose a novel automated AF detection solution designed for the challenging ICU environment that is based on combining features from three approaches to discriminate AF from non-AF ECG tracings collected from critically ill sepsis patients.

There are three major contributions of this work. First, we present an automated AF detection algorithm from ICU sepsis patients that extracts features from R-wave interval variability, Poincaré plots and P-wave based characteristics. By combining these, we not only detect the distinct repeated patterns of premature atrial/ventricular contractions (PAC/PVCs), but we also detect the absence of regular P-waves in AF subjects more accurately. Moreover, we introduce a new feature called short segment-wise PR ratio. With a set of intelligent rules developed with these features, we demonstrate a reduction in false positive AF detections due to PAC/PVC beats, which are commonly found in critically ill sepsis patients. The second contribution is that we train, validate and test our algorithm using a large amount of data. Two independent blind test datasets containing ~1,657 and ~2,552 hours of ECG recordings were used, and we compare the performance of the proposed method with two state-of-the-art algorithms. The third major contribution is that we provide annotations of arrhythmia including atrial fibrillation which required time-intensive manual review by clinicians; this will allow other investigators to work on this database.

II. Related Works

AF detection algorithms from electrocardiogram signals are primarily based on two factors: analysis of atrial activities or ventricular responses [8].

Atrial activity analysis methods incorporate the absence of P-waves or the presence of fibrillatory waves (f-waves). Wavelet analysis-based QRS (defined as the complex wave formed by Q wave, R wave and S waves which occur in rapid succession) detection and hidden Markov model-based P-wave isolation methods along with time and spectral parameters were used to detect AF-prone patients in [9]. The average number of f-waves in a TQ interval (defined as the distance between T-wave offset and Q-wave onset) was used as a characteristic parameter to detect AF in [10]. In [11], a surface ECG-based AF detection method is presented in which a remainder ECG is created by cancelling the ventricular activity followed by estimating its power spectrum. In [12], the expectation-maximization algorithm is used to create a Gaussian mixture model of the P-wave feature space; this model is then used to identify P-wave absence and finally, detecting AF.

Ventricular response-based methods rely on analyzing different properties of RR interval (defined as the distance between two successive R-peaks) irregularities. Discrete wavelet transform of RR intervals was used to identify periods of high heart rate variability coefficient in [13] which was followed by fractal analysis to classify these high variability periods into AF or sinus rhythms. In [14], standard density histograms of RR intervals and difference between successive RR intervals were first calculated. Next, the Kolmogorov-Smirnov test was used to compare the similarity between the standard and test density histograms to determine the AF status. Several time domain statistics and Shannon entropy, calculated from RR interval series after ectopic beat filtering, were used for AF detection in [15]. In [16], symbolic dynamics was obtained from the preprocessed RR interval series which was followed by calculating Shannon entropy from the symbolic sequence to determine the presence of AF. In order to detect AF from short ECG recordings and optimize entropy estimates, the coefficient of sample entropy (COSEn) was developed in [17]. In [18], the density histogram of delta RR intervals (defined as the difference between two successive RR intervals) was used to detect an AF event and later determine the boundary of AF. The Lorentz plot obtained from the RR time series was implemented in [19] to detect AF as well as atrial tachycardia. RR interval irregularity-based statistical parameters and COSEn along with random forest classifier model were presented in [20]. In [21], an end-to-end model combining the convolutional and recurrent neural networks is presented to extract high level features from RR intervals in order to detect AF.

Few detectors have been described that explore both the RR variability and atrial activity. PR interval (defined as the distance between P-wave offset and R-wave onset) variability, along with RR Markov score, were used to classify AF in [22], while P-wave absence, heart rate irregularity and atrial activity were explored in [23]. In [24], RR interval irregularity, f-wave presence, absence of P-waves and noise level are combined with a fuzzy logic classifier to detect occult paroxysmal AF.

Apart from analyzing atrial and ventricular activities, some other approaches have been described that do not require determination of QRS or P-wave peak positions. In [25], an automated method based on stationary wavelet transform-based features along with a support vector machine is described. In [26], the ECG signal was first de-noised with discrete wavelet transform, followed by independent component analysis to reduce dimensionality. Finally, AF classification was performed using naïve Bayes and a Gaussian mixture model. Average framing percentage energy obtained from wavelet packet transform of ECG signals and probabilistic neural network classifiers were used to detect AF in [27]. In [28], variational mode decomposition to extract features along with using a deep belief network as the classifier is described. The short-term Fourier transform and stationary wavelet transform were used to convert ECG segments into a two-dimensional matrix, which was used to train a deep convolutional neural network in [29]. In [30], the stationary wavelet transform was used to decompose the TQ interval into four levels; the relative wavelet energy was then calculated to detect AF.

The AF detection algorithms that rely on the absence of P-waves perform poorly in the presence of noise. They are also vulnerable to noise and drifting of the ECG signal baseline, which can make P-wave detection challenging [29], [31]. The majority of AF detection algorithms depend on the analysis of RR interval variability, complexity, and randomness, where atrial activity is not usually explored [32]. As a result, in the presence of premature atrial contraction (PAC) and premature ventricular contraction (PVC) beats, rhythm-based detectors are prone to produce false alarms [24].

In order to solve these issues, we aim to develop, validate, and evaluate a novel AF detection algorithm that incorporates the critical elements of long-term ECG analysis, premature atrial and ventricular beat detection, and AF identification in a large-scale electronic health database from the critically ill. It is to be noted that a preliminary study using this MIMIC III subset is reported by the authors in [33], although only RR interval-based variability was used since subjects with ectopic beats were excluded and fewer subjects were analyzed.

III. Description of The Database

In this study, a subset of the Medical Information Mart for Intensive Care (MIMIC) III dataset containing 198 subjects was used. MIMIC III is a large open source medical record database publicly available in PhysioNet [34]. MIMIC III contains de-identified health-related data from approximately sixty thousand patients who stayed in critical care units of the Beth Israel Deaconess Medical Center between 2001 and 2012 [35]. It includes a variety of information such as patient demographics, laboratory test results, vital sign measurements, medications, nurse and physician notes, imaging reports, and out-of-hospital mortality, which are some of the notable parameters among many others. In many patients, MIMIC III links continuous ECG waveforms to a wealth of time-varying clinical and hemodynamic data. The sampling frequency of the ECG recordings was 125 Hz and the measuring unit was millivolt (mV).

Among 58,976 ICU admissions within MIMIC III, 14,831 admissions for adults were identified with sepsis according to international classification of diseases, ninth revision (ICD-9) codes. Among these patients, 2,975 patients had ECG waveforms linked to clinical data. Since the ECG recordings were very long (average 38 hours), creating annotations was a manually intensive task. As a result, four batches of 50 ECG waveforms from patients hospitalized with sepsis were randomly selected. ECG signals were annotated by board certified physicians specializing in AF management (DDM).

For this study, among those four batches, one batch was used for training, one for validation, and two for testing the algorithm. The training batch contained 50 subjects, among which 25 were AF and the remaining were normal sinus rhythm (NSR). These subjects were randomly chosen by the physicians, who also provided the annotations of the data. Similarly, the validation batch consisted of 49 subjects, 11 with AF. For the validation batch, approximately half of the subjects were randomly selected by the physicians based on the nurse-charted AF status [36]. However, when annotated by visual inspection (DDM), the nurse-charted AF status was found to have several false positives due to noise, PAC/PVCs, or other reasons. As a result, the validation batch had 11 AF subjects while the rest had NSR with PAC/PVCs. The two test batches included 50 and 49 subjects. These batches were randomly selected by the physicians to contain equal numbers of AF and non-AF subjects. The first test batch contained only AF and NSR, whereas the second test batch included subjects with PAC/PVCs, subjects with AF, and subjects with NSR, as several PAC/PVC subjects were found in the randomly chosen MIMIC III sepsis subset. Two subjects were excluded as their signals contained a majority of noisy data or there was a lack of any signal in the recording. AF algorithm testing was blinded to the AF episodes identified by the gold standard manual ascertainment. The AF annotations were made publicly available, to facilitate further research, at https://doi.org/10.6084/m9.figshare.12149091.v1 and http://biosignal.uconn.edu/resources/.

IV. Methods

Our proposed automated AF detection algorithm consists of several major steps. First, preprocessing is performed to discard noisy ECG segments, followed by R peak detection. Next, from ECGs that are devoid of noise, several RR interval, Poincaré plot, and P-wave based features are extracted. Finally, from the extracted features, a set of empirical rules are derived to discriminate AF from non-AF.

A. Preprocessing of the ECG Signal

Each ECG recording is divided into two-minute non-overlapping segments [19]. These segments are then checked automatically whether they have analyzable ECG signal or not by using both time and frequency domain characteristics [7]. A two-minute ECG segment is classified as analyzable if it contains identifiable QRS complexes; details of this criterion can be found in [7]. Next, the clean detected two-minute segments are then subjected to standard normalization consisting of mean subtraction and converting to unit variance. Then the R-peaks of the ECG signals are determined by a newly developed R-peak detection algorithm, VERB. VERB stands for variable frequency complex demodulation (VFCDM) based ECG reconstruction and beat detection [37]. VERB can reconstruct the ECG using VFCDM-based sub-band decomposition, which enhances the QRS complex detection [37].

B. Feature Extraction from ECG

AF is a cardiac arrhythmia with uncoordinated and irregular atrial activation [38]. In other words, AF refers to irregularly irregular heart beat intervals with increased beat-to-beat variability and complexity [15]. The RR intervals during an AF episode vary randomly compared to those in an NSR segment. Fig. 1 shows representative 30-second ECG segments and their corresponding heart rates (HR) obtained from both the NSR and AF subjects. The HR for the NSR segment shown in Fig. 1 (b) varies around the 70 beats-per-minute (BPM) range, whereas the AF HR shown in Fig. 1 (d) is randomly varying in a large range of 50–150 BPM.

Fig. 1.

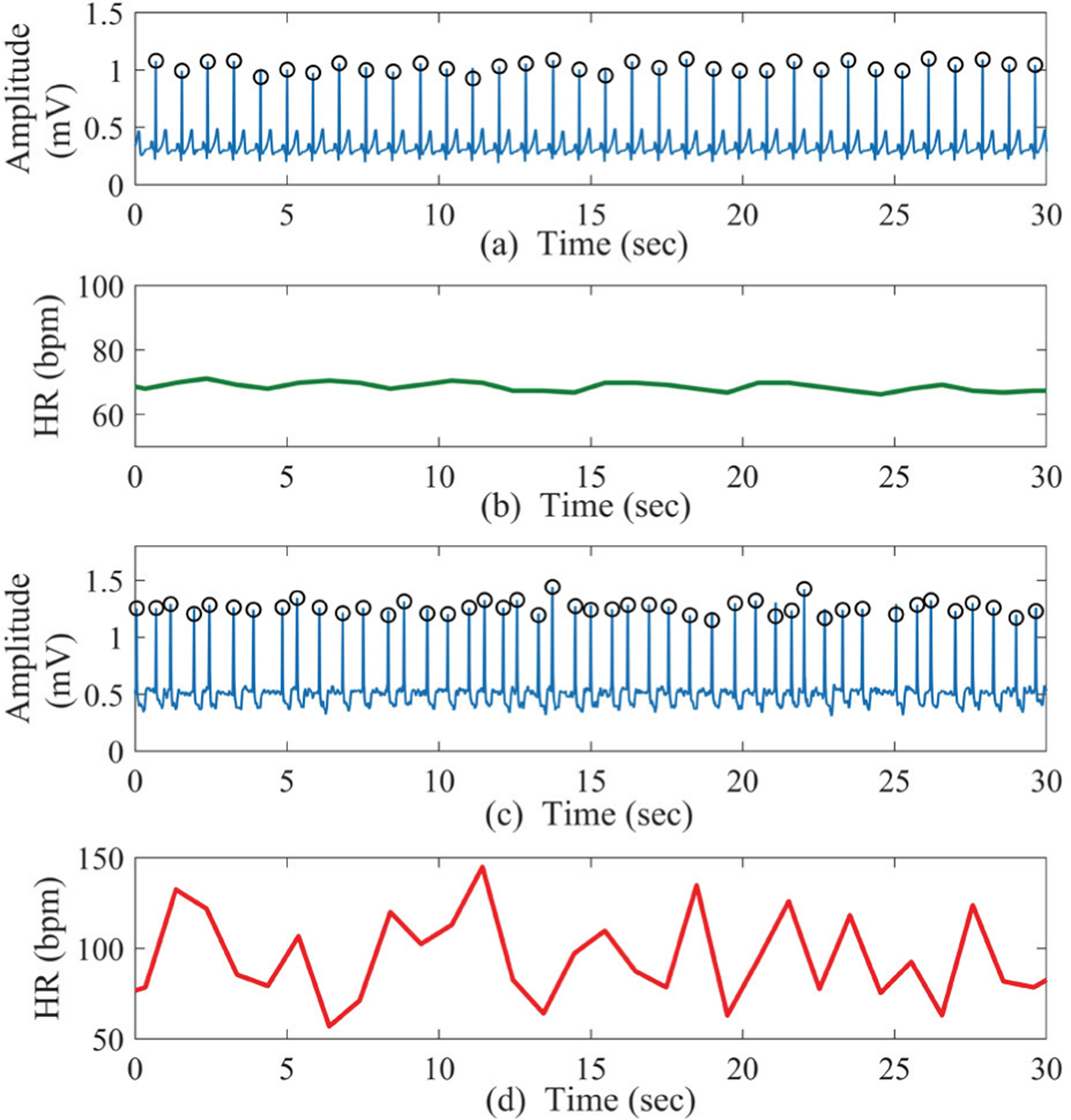
(a) Sample 30-second NSR ECG recording and (b) the corresponding HR; (c) sample 30-second AF ECG segment and (d) the corresponding HR. The QRS peaks are denoted by black circles.

In order to use this randomness and variability of the HR as AF-discriminating characteristics, several commonly implemented statistical parameters have been used in this paper. These include the root mean square of successive differences (RMSSD), Shannon entropy (ShaEn) and sample entropy (SampEn). These features were calculated because they are reported to capture the randomness and variation of the HR during AF rhythm, thus, discriminating AF from NSR [15], [33]. Moreover, these features are computationally simple unlike the recent machine learning methods which are computationally taxing [29], [39].

RMSSD is a statistical parameter which can estimate the beat-to-beat variability of HR. The RMSSD value is expected to be higher in AF subjects than in NSR subjects, as AF exhibits higher variability than regular rhythms. If x(i) is a sequence of length l then the RMSSD is calculated as:

$$\mathit{\text{RMSSD}}=\sqrt{\frac{1}{l-1}\sum _{i=1}^{l-1}{\left(x\left(i+1\right)-x\left(i\right)\right)}^2}$$ (1)

However, for each ECG segment, RMSSD has been divided by the mean of the HR to counter the variability among different subjects and segments.

Shannon entropy is a statistical measurement which calculates the uncertainty of a random variable and is expected to be higher in AF subjects as they have highly irregular RR intervals compared to NSR subjects [40].

Sample entropy is a measure of randomness. For a time series, SampEn is the negative logarithm of the conditional probability that two sequences similar for m points remain similar at the next point, where self-matches are excluded [41]. SampEn has two main parameters: template length ‘m’ and tolerance ‘r’. In this study, to estimate SampEn, m =1 and r =60 ms were selected [17]. The value of SampEn is also expected to be higher for the AF subjects.

Figure 2 shows the scatter plots obtained using the AF and NSR segments of the training data. Fig. 2 (a) shows the scatter plot from RMSSD and sample entropy while Fig. 2 (b) shows the scatter plot generated using Shannon and sample entropy. From the plots, it is evident that sample entropy is the best approach as it separates AF and NSR segments quite well. However, both RMSSD and Shannon entropy have lots of overlap between AF and NSR. As a result, only sample entropy is used here as the initial computational feature to discriminate possible AF from NSR.

Fig. 2.

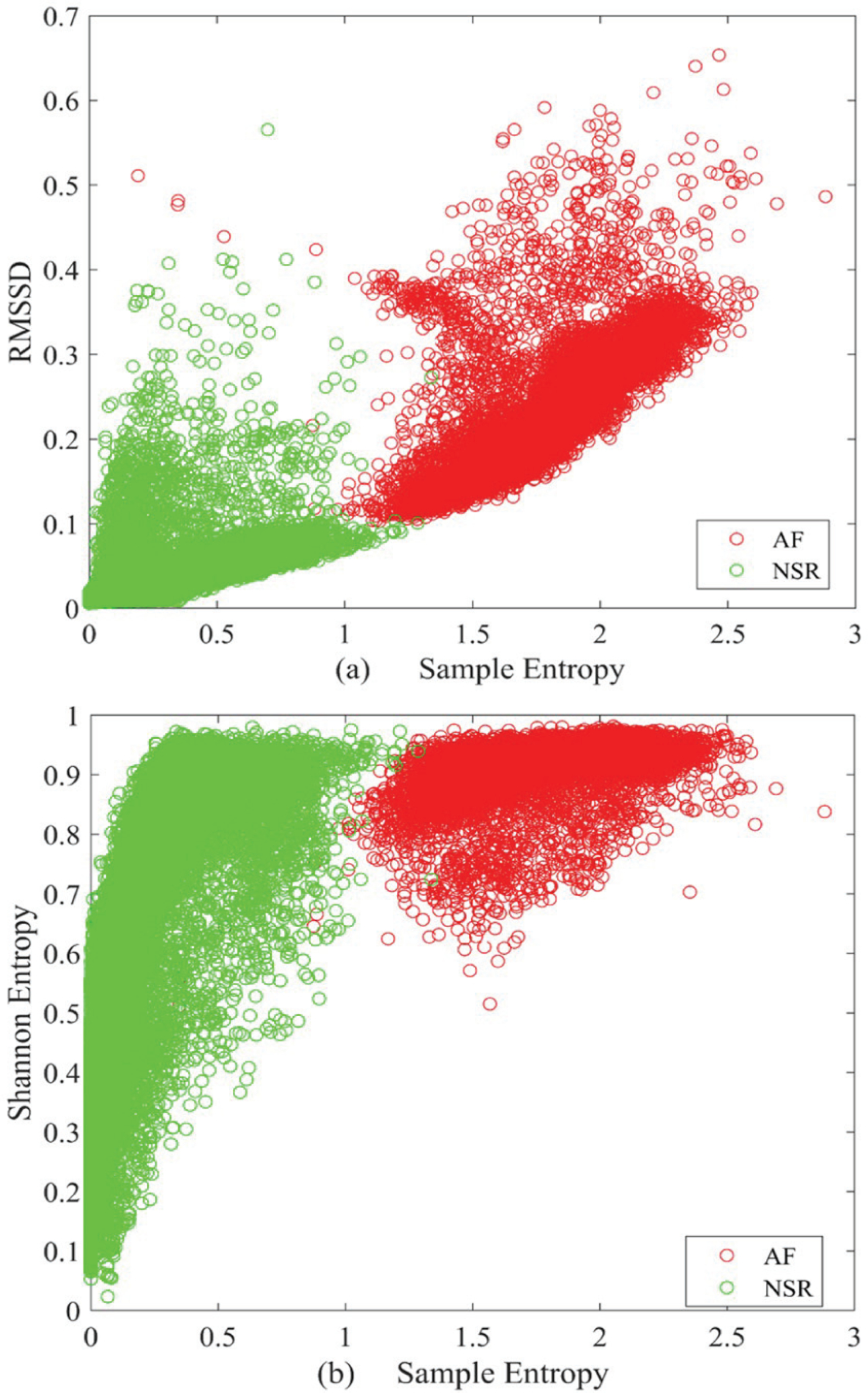
Scatter plots generated from the AF and NSR segments of the training data: (a) RMSSD vs. sample entropy and (b) Shannon vs. sample entropy.

C. PAC/PVC Detection

PAC occurs when an ectopic focus originating in the atrium leads to premature activation of the atria prior to regular sinoa-trial node activation whereas a PVC occurs when a similar process occurs in the ventricle [42]. PACs and PVCs can cause symptoms similar to AF, e.g., the sensation of an irregular pulse or having skipped beats. Previously described RMSSD, sample entrpy and Shannon entropy features are suitable to detect the variation and randomness of the HRV. However, the problem with the PAC/PVCs is that these arrhythmias also introduce randomness and variation into the HR signal. In other words, PAC/PVCs can mimic the irregular beat patterns of typical AF. As a result, when compared to the AF segments, the previously calculated statistical features from PAC/PVC segments exhibit similar characteristics of AF. This results in false positive AF detection.

Fig. 3 (a) shows a sample PAC ECG segment and the corresponding HR is presented in Fig. 3 (b). From Fig. 3 (b) it is clear that the HR has much variation (compared to the NSR HR shown in Fig. 1 (b)), especially in the PAC beats. As a result, this kind of ECG segment cannot be correctly determined as non-AF with the previously extracted SampEn feature; we need to obtain different types of features tailored to the unique characteristics of PAC/PVC.

Fig. 3.

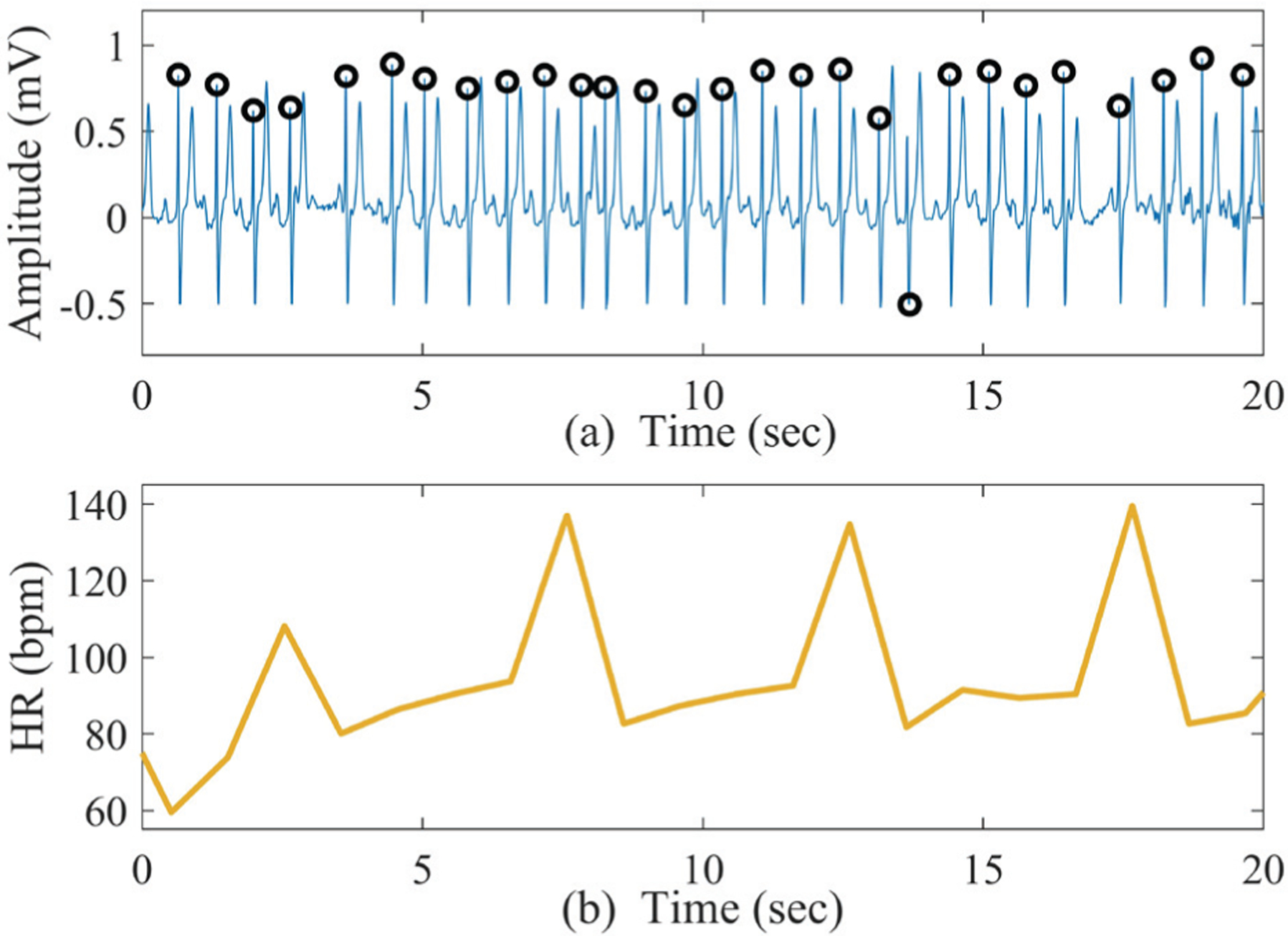
Sample ECG segment with PAC rhythms; (b) corresponding HR generated from Fig. 3 (a).

1). PAC/PVC Features From Poincaré Plots:

One of the main characteristics of ideal PAC/PVC is that the premature beats are repeated in some pattern. This leads to high variability in the corresponding HR; however, this variation occurs in a repeated fashion. To detect the repeated patterns in the PAC/PVC segments, we used Poincaré plots. A Poincaré plot is based on the differences of the heart rate: one axis has the difference in heart rates of the current beat to the next beat while another axis has the difference in the heart rates of the current beat to the previous beat [42].

For the PAC/PVC rhythms, a distinct repeated kite-shaped pattern emerges in the Poincaré plot, while for AF there is no such pattern because the HR differences are random. Fig. 4 shows sample Poincaré plots derived from PAC, AF, and NSR segments. From the figure, it is evident that distinct kite-shaped patterns are present in the Poincaré plots for PAC subjects (Fig. 4 (b)), while for AF, the pattern is random (Fig. 4 (c)).

Fig. 4.

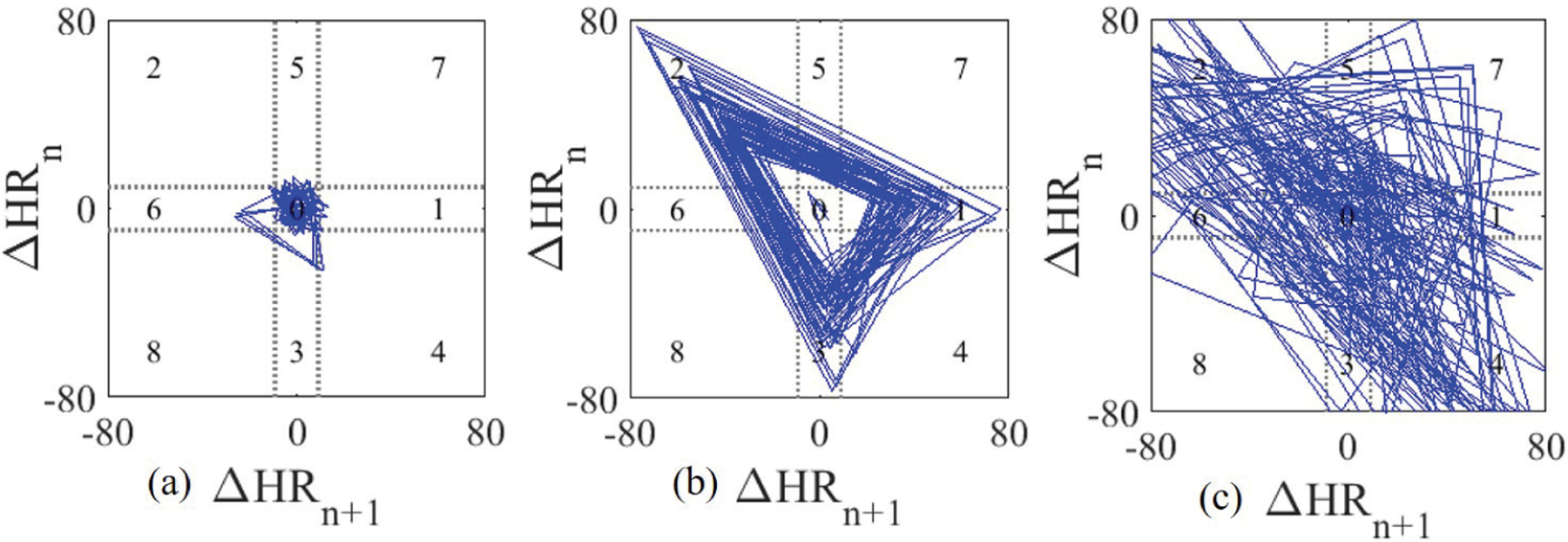
Sample Poincaré plots generated from 2-minute (a) NSR, (b) PAC and (c) AF segments.

To capture the distinct patterns for PAC/PVC, the Poincaré plot is subdivided into nine quadrants. These quadrants’ boundaries were set optimally based on the experimental data and details about the Poincaré plot formation can be found in [42]. From the Poincaré plot, two features are extracted to discriminate the PAC/PVC patterns from AF.

First, we calculate how many times the kite-shaped pattern is repeated, which is essentially the repetition number of ‘1-2-3’ or ‘4-5-6’ sequences [42] and this number is denoted by “Count”. The value of “Count” is expected to be higher for PAC/PVC segments due to the repeated triangular pattern.

Next, we calculate the ratio of the number of points that fall inside the zero quadrant to the total number of data points in the Poincaré plot, and refer to this as the zero ratio (denoted by “ZR”). This ratio is expected to be very low for AF segments, as shown in Fig. 4 (c). Based on these two features, the following rules are imposed:

$$\begin{gathered} \mathit{\text{if\hspace{0.17em}}}ZR>T{H}_{ZR,}\mathit{\text{\hspace{0.17em}\hspace{0.17em}decision}}=\mathit{\text{non-}}AF. \\ \mathit{\text{else\hspace{0.17em}if\hspace{0.17em}Count}}>T{H}_{\mathit{\text{count}},}\mathit{\text{\hspace{0.17em}\hspace{0.17em}decision}}=\mathit{\text{non-}}AF \end{gathered}$$ (2)

Until this point, we have used SampEn and Poincaré based features, which are based on QRS information only. However, this may not be sufficient for other PAC/PVC subjects as there are many variations among the PAC/PVC patterns and not all patterns are repetitive, thus making the Poincaré features inconsistent. To address this, we seek the assistance of other characteristics of the ECG signal in order to identify PACs from AF.

2). PP Rhythm Based PAC Detection Features:

Ideally, in the AF segments there should be no P-waves, whereas for the PAC/PVC subjects, P-waves will be followed by the QRS complexes. As a result, we detect the P-waves in the input ECG segments and use this ideal case to enhance the QRS variation-based detect AF detection. This approach was selected to improve accuracy and eliminate false positive AF detection from PAC/PVCs.

Towards this approach, from the input 2-minute ECG segments, the location of the P-waves are determined using a modified P-wave detection algorithm [43]. First, possible P-wave locations are calculated from both the positive and negative sides of the ECG segment. Once the initial P-wave locations are obtained, several adaptive heuristic thresholds are imposed to obtain the corrected P-wave locations. Details about the algorithm can be found in [43].

Next, from the P-wave locations, several features are obtained. Generally, for the PAC case, a P-wave will be associated with each QRS complex. Moreover, for the same reason, the P-wave locations will also be regular in the PAC subjects compared to the AF subjects. As a result, we calculate the following two features to separate PACs from AF:

PR_ratio = number of P-waves in each segment/number of R peaks in that segment.

P_samp= Similar to QRS locations, the P-P interval series is calculated from the P-wave locations. Next, SampEn is calculated from the P-P intervals for measuring the P-wave irregularity, and this feature is denoted as P_samp here.

PR_ratio is expected to be close to 1 for PAC/PVC (i.e., non-AF subjects) whereas for the AF subjects, PR_ratio is expected to be quite low. Conversely, P_samp is expected to be higher for AF subjects (due to irregular P-waves) and much lower for PAC/PVC, due to less variation in the P-wave locations.

Fig. 5 (a) shows the P-wave detection for a sample non-AF ECG segment where it is clear that for every QRS, a P-wave is present and detected correctly. Fig. 5 (b) shows the scatter plot of PR_ratio and P_samp values obtained from AF and non-AF subjects. From the plot, it is clear that the two features have good discriminating properties to classify AF and non-AFs. The non-AF segments have mostly high PR_ratio values while P_samp has high values for the AF segments.

Fig. 5.

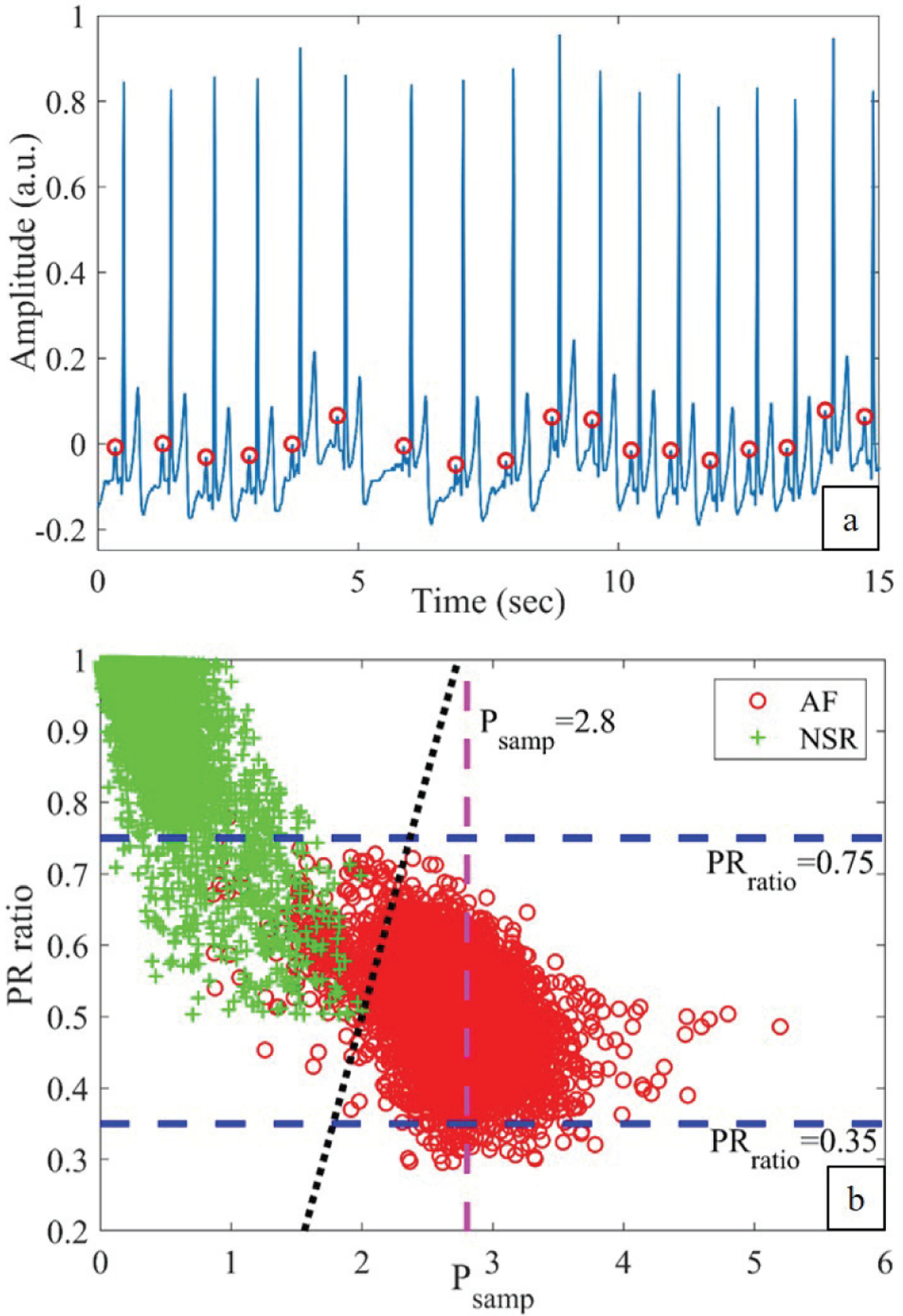
(a) P-waves detected from a sample PAC (non-AF) ECG segment. (b) Scatter plot of P_samp and PR_ratio obtained from AF and NSR segments.

Based on these characteristics, we set the following strict rules for these two parameters:

$$\begin{gathered} \mathit{\text{if\hspace{0.17em}}}P{R}_{\mathit{\text{ratio}}}>0.75,\mathit{\text{\hspace{0.17em}\hspace{0.17em}decision}}=\mathit{\text{non-}}AF \\ \mathit{\text{else\hspace{0.17em}if\hspace{0.17em}}}{P}_{\mathit{\text{samp}}}>2.8,\mathit{\text{\hspace{0.17em}\hspace{0.17em}decision}}=AF \\ \mathit{\text{else\hspace{0.17em}if\hspace{0.17em}}}P{R}_{\mathit{\text{ratio}}}<0.35,\mathit{\text{\hspace{0.17em}\hspace{0.17em}decision}}=AF \end{gathered}$$ (3)

Fig. 5 (b) shows the three linear regions in dashed lines which correspond to (3). Ideally, for every QRS complex, a P-wave should be present for the NSR segments. As a result, the PR_ratio should be close to 1 for NSR while for AF segments it should be low. To incorporate this observation, the upper and lower limits for the PR_ratio were empirically chosen to be 0.75 and 0.35, respectively, and these limits are shown as two horizontal dashed lines in Fig. 5 (b). Similarly, P_samp has high values for the AF segments compared to the NSR segments and as a result, the threshold was empirically chosen to be 2.8 based on the training data. In Fig. 5 (b), the vertical dashed line corresponds to P_samp=2.8.

However, the above-mentioned conditions are strict rules only, meaning these are only “one-way” rules. To make a decision for the segments which do not satisfy these conditions, we have used the following condition, which is essentially a linear plane separating both categories.

$$\begin{gathered} \mathit{\text{if\hspace{0.17em}}}\left(0.79\times P_{\mathit{\text{samp}}}-1.16\times P{R}_{\mathit{\text{ratio}}}\right)\ge 1,\mathit{\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}decision}}=AF \\ \mathit{\text{else\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}decision}}=\mathit{\text{non-}}AF \end{gathered}$$ (4)

This is found by drawing a separating line for the two categories. The line corresponding to (4) is shown as a black dotted line in Fig. 5 (b). Many possible lines can be drawn; however, this is chosen to reduce the number of false positive AF detections.

3). Proposed Short Segment-wise PR Ratio (PR_seg):

By calculating the PR ratio as the PAC/PVC discriminating feature, we can reclassify some of the falsely detected AF as non-AF. However, this sole criterion can fail in many cases, especially where there are many PAC beats in a 2-minute segment. The underlying reason is that when there are many PAC beats, P-waves are absent in some particular PAC beats; thus over the entire 2-minute, PR_ratio becomes low although we detect P-waves in other portions of that 2-minute segment. Note that PAC beats may be repetitive but not all the beats in a 2-minute segment will have PACs. This will result in a low PR_ratio. However, for the AF segments, the PR_ratio is consistently low as during AF, P-waves are not theoretically present in the ECG waveforms.

To solve the issue of some PAC/PVC segments having a low PR_ratio, we sub-divide the 2-minute ECG segment into several non-overlapping smaller segments or windows (this number is denoted by N_seg) and calculate the PR ratio for each smaller segment/window. As a result, we have N_seg number of PR ratios, each corresponding to a smaller segment and this ratio is denoted by PR_seg. The advantage of this newly-proposed short segment-wise PR ratio is that, although in a small segment consisting of many PAC beats (resulting in decreased presence of P-waves), the short segment-wise PR ratio is low, in other windows where there are fewer PAC beats, the PR_seg is still close to 1.

Fig. 6 shows two 10-second windows of a sample 2-minute ECG segment along with the detected P-waves (marked in red circles). From Fig. 6 (a), it is clear that we do not have consistent P-waves in that short segment; thus PR_seg is low. However, in Fig. 6 (b), we show another 10-second window of the same 2-minute ECG segment which has consistent P-waves and thus, the PR_seg for this window becomes 1.

Fig. 6.

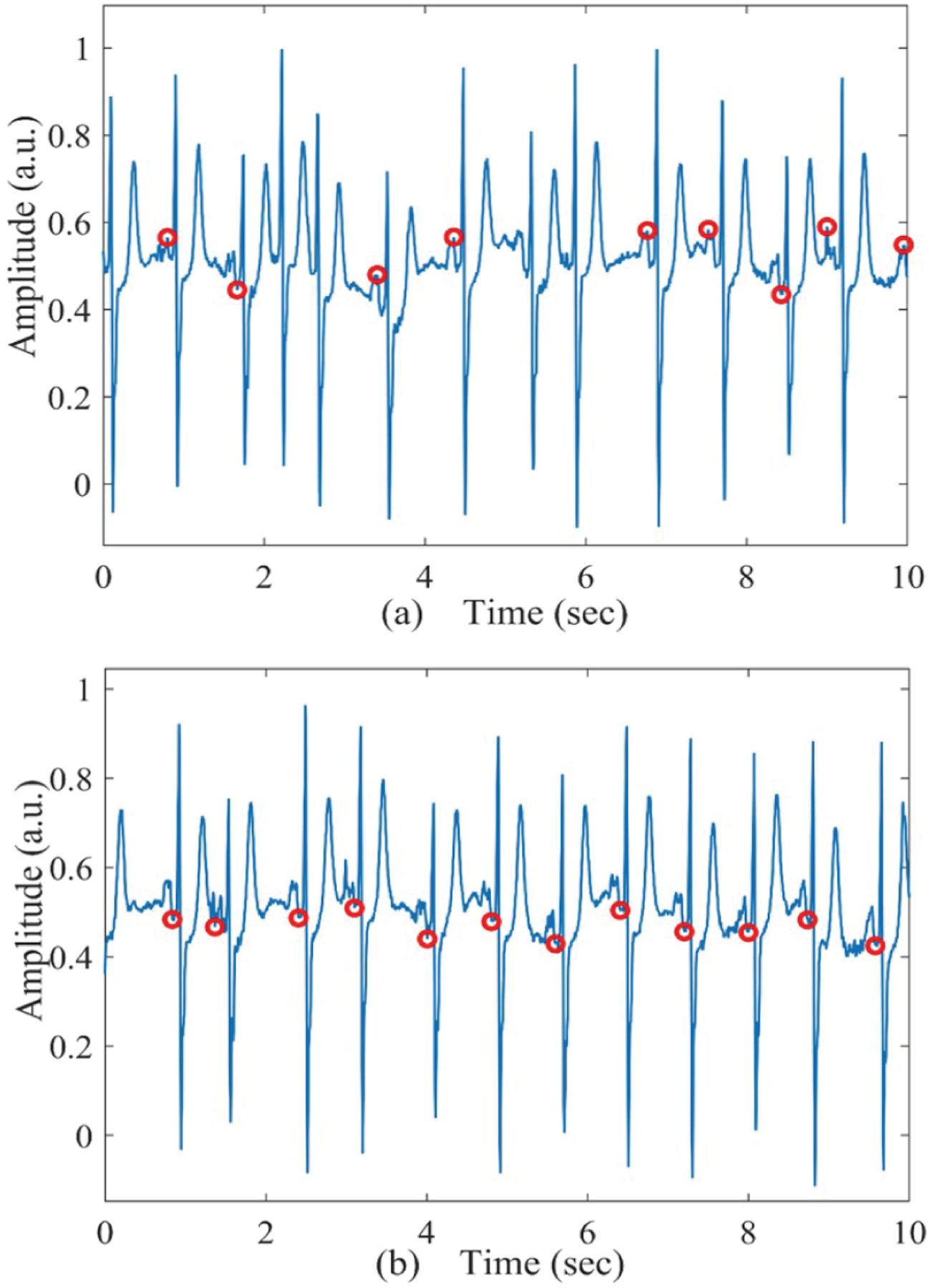
(a) Sample 10-second PAC (non-AF) ECG segment with low PR_ratio. (b) Sample 10-second PAC (non-AF) ECG segment with high PR_ratio.

In order to obtain a single parameter from all the N_seg number of small ECG windows, we calculate the mean of the top three PR_seg from N_seg available ratios and denote this mean as MPR_seg. This MPR_seg is used to discriminate AF from non-AF:

$$\mathit{\text{if\hspace{0.17em}}}MP{R}_{\mathit{\text{seg}}}>T{H}_{\mathit{\text{seg}},}\mathit{\text{\hspace{0.17em}\hspace{0.17em}decision}}=\mathit{\text{non-}}AF$$ (5)

The above condition is used as another strict rule.

D. AF vs. Non-AF Classification Scheme

Finally, all the above-mentioned conditions are put together in order to discriminate AF from non-AF ECG segments. First, based on the RR intervals, SampEn is calculated and a threshold TH_samp is used to identify the possible AF segments. This detection by SampEn is essentially an initial screening; the “possible AF” decision may include PAC/PVC segments as false positive detections of AF.

Next, on the “possible AF” detected segments, we run the PAC/PVC detection criteria to reduce false positive AF detection. Towards this approach, we first impose all the previously mentioned “strict rules” obtained from both the Poincaré plot and P-wave based features. In other words, first we check the two strict conditions obtained from the Poincaré plots (i.e., (2)). Next, strict rules for PR_ratio and P_samp are checked (i.e., (3)), followed by imposing the last strict rule on our proposed PR_seg feature (i.e., (5)). The order of these strict rules is based on the fact that R peaks of ECG signals can be detected more accurately and easily than can P-wave peaks, as P-wave detection is often prone to noise. Finally, only for those segments which do not satisfy any of the strict rules, the AF status is determined based on the linear rule as described in (4). Fig. 7 shows the flow chart of the proposed AF vs. non-AF detection algorithm; PAC/PVC and NSR are considered as non-AF.

Fig. 7.

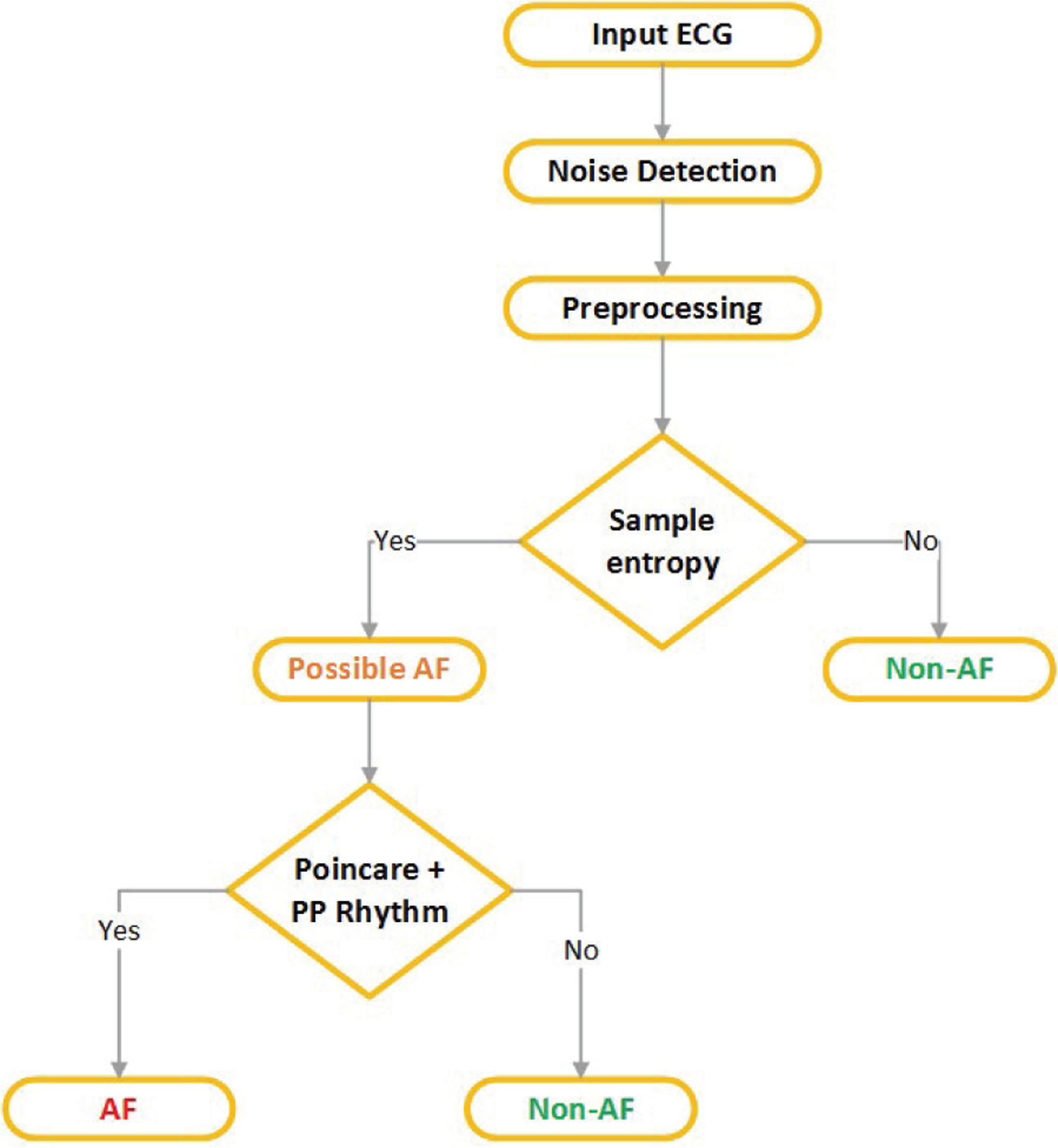
Flow chart of the proposed AF vs non-AF discrimination algorithm.

E. Machine Learning Classifiers

Although a flowchart of our complete automated AF detection algorithm is shown in Fig. 7, we further explore if the extracted three RR interval-based features along with different machine learning classifier algorithms yield better performance than SampEn for the initial AF screening. To analyze this, several machine learning classifiers, including support vector machine (SVM), discriminant analysis (DA) and k-nearest neighbor (k-NN), were implemented in this study.

Linear discriminant analysis is one of the simplest methods for classification, in which a discriminant projection is learnt to enlarge the between-class distance and reduce the within-class distance in order to improve the classification accuracy [44]. For the DA, both linear and quadratic boundaries along with Mahalanobis distance were analyzed in this study. SVM is another very popular classifier for binary problems, in which a maximum margin between the training and test data is constructed [45]; the samples which are closest to the decision boundary are called the support vectors. Both the linear and radial basis function (RBF) kernels were used. Finally, k-NN classifier is also a supervised learning method with desirable computational speed along with acceptable classification accuracy [46]. Based on majority voting and the distance from the “k” closest samples, a new test sample is classified. In k-NN, the Euclidean distance is used with the variation of “k” values, which denotes the number of the nearest neighbors to be used.

For all these classifiers, the three previously extracted RR interval variability-based features— RMSSD, SampEn and ShaEn— were fed to the model.

V. Results

The MIMIC III database subset used in this study consisted of 4 independent batches: training, validation and two test batches. First, we performed segment-wise analysis on the training data. Next, subject-wise performance was measured on the validation and test data sets, as it is most important clinically to determine whether a patient has AF or not. To make subject-wise decisions, we analyzed three consecutive 2-minute segments and the data was determined to have AF only if three consecutive 2-minute segments were found to be AF. This choice was driven by the current clinical literature showing that AF events lasting longer than 6 minutes confer thromboembolic risk and are thus of greater clinical relevance [47], [48].

A. Results on Training Data

In the first stage, we performed the parameter training using the training batch, which consisted of 50 subjects; 25 of them had AF while the rest had NSR. From those 50 subjects, a total of ~1,301 hours of ECG recordings were analyzed. After performing the noise detection and preprocessing procedures, we had a total of 9,920 2-minute AF segments and 18,834 2-minute NSR segments and all of these 28,754 2-minute ECG segments were used for the training.

From these training segments, we calculated RMSSD, sample, and Shannon entropy and then set thresholds to classify AF segments from NSR. Table I shows the sensitivity (SEN), specificity (SPE), accuracy (ACC), positive predictive value, (PPV) and negative predictive value (NPV) obtained from the training segments using those three features and empirical threshold (TH). From the table, it is clear that sample entropy obtained the highest performance among these three features and the overall accuracy was 99.10% using the training data.

Table I.

Performance of the Extracted Features on the Training Data

Feature Name	TH	SEN (%)	SPE (%)	ACC (%)	PPV (%)	NPV (%)
RMSSD	0.12	97.95	95.97	96.65	92.76	98.89
ShaEn	0.85	87.54	80.60	82.99	70.39	92.47
SampEn	1.0	98.50	99.42	99.10	98.90	99.21

Next, we analyzed the performance of these three features with SVM, DA, and k-NN classifiers. To this end, the well-established K-fold cross validation method was used. The training data was split into K disjoint partitions (K=10) and each time (K-1) folds were used for training while the last fold was treated as test; the whole process was repeated “K” times [49]. Table II compares the classification performance of different classifiers with varying hyper-parameters. From the table, it is clear that all the reported models have high classification accuracy and among them, the k-NN with Euclidean distance achieved the best performance, resulting in sensitivity, specificity, and accuracy of 98.40%, 99.80%, and 99.32%, respectively. These metrics are almost similar to the results obtained from using only the sample entropy with simple thresholding (TH=1); which resulted in 98.50% sensitivity, 99.42% specificity, and 99.10% accuracy. As a result, to keep the algorithm simple, we only used SampEn hereafter.

Table II.

Performance Comparison of Different Classifiers

Classifier Name	Type/Hyper parameter	Sensitivity (%)	Specificity (%)	Accuracy (%)
DA	Linear	98.34	99.30	98.99
	Quadratic	98.83	97.83	98.18
	Mahalanobis	98.83	98.03	98.31
SVM	Linear	98.56	99.16	98.95
	RBF	98.57	99.56	99.22
k-NN	k=9 Euclidean	98.40	99.80	99.32

B. Results on Validation Data

Next, the algorithm was tested on the validation dataset where subject-wise classification accuracy was analyzed. As previously mentioned, if three consecutive 2-minute segments were detected as AF, then the subject-wise decision is AF.

The validation set contained 49 subjects, of which 11 were AF. From these 49 subjects, a total of ~1,800 hours of ECG recordings were analyzed; subsequently 39,241 segments were found to be clean by the noise detection method. With only the SampEn feature, the algorithm correctly detected AF in all AF subjects. However, SampEn also detected 10 false positives (FP) subjects, resulting in a low PPV of 52.38% and specificity of 73.68%. Seven of the false positive AF cases had PAC/PVC patterns, which led to more variation in the RR-based parameters, and thus, made the PAC/PVC subjects look more like AF than NSR when using SampEn alone to determine AF status. For the rest of the false positive subjects, SampEn detected AF only in very short portions of the data.

The next step of our procedure involves P-wave detection and Poincaré features to detect PAC/PVCs so that the number of false positives is reduced. After extracting the PAC discriminating features (as explained in the Methods section), and using the decision conditions, the number of false positive AF detections was reduced from 10 to 2, (correctly detecting 8 FP AF subjects as non-AF). Table III shows the confusion matrix using the validation data for both approaches: with and without PAC detection steps. With the PAC detection step, we have only 2 subjects with NSR detected as AF. As a result, the sensitivity, specificity, accuracy, PPV, and NPV became 100%, 94.74%, 95.92%, 84.62%, and 100%, respectively.

Table III.

Confusion Matrix on Validation Data

With only SampEn				With Proposed Method
True Label		Predicted label		True Label		Predicted label
		AF	non-AF			AF	non-AF
	AF	11	0		AF	11	0
	non-AF	10	28		non-AF	2	36

To compare our results to other algorithms as reference, we further implemented two state-of-the-art AF detection algorithms: the statistical parameter-based method (Das et al. [15]) and COSEn-based approach (Lake et al. [17]). Several previously published studies [20], [24] used this COSEn-based method to compare their proposed algorithms in custom datasets. Table IV shows the performance of these two algorithms (i.e., [15] and [17]) on the validation data. From Table IV, it can be seen that the statistical parameter (Das et al. [15]) and COSEn (Lake et al. [17]) based methods result in 8 and 9 FP AF subjects, respectively, which is significantly higher than the 2 FP with our proposed method.

Table IV.

Comparison on the Validation Data

Statistical Method [15]				COSEn Method [17]
True Label		Predicted label		True Label		Predicted label
		AF	non-AF			AF	non-AF
	AF	11	0		AF	11	0
	non-AF	8	30		non-AF	9	29

C. Results on Test Data

After we incorporated the PAC/PVC detection steps and finalized the conditions and parameters, we ran the complete algorithm to test the untrained data. We tested the performance of the proposed algorithm on two sets of independent test data. Both test data sets were annotated by the cardiologists and the ground truth was kept hidden from the algorithm for blind verification.

1). Results on First Test Set:

Test set one contained 24 AF and 25 NSR subjects. Similar to the training and validation sets, this test set also contains very long-term recording. A total of ~1,657 hours of ECG data were analyzed and after preprocessing, 35,038 segments were found to be free of noise artifacts by the algorithm. Since this test set does not include any PAC/PVC subjects, this is less challenging. As expected, the algorithm detected all 24 AF subjects correctly, resulting in 100% accuracy. Table V gives the confusion matrix of test set one; this shows that we have correctly classified all 49 subjects. Next, the performance of the statistical parameter-based method (Das et al. [15]) and COSEn-based approach (Lake et al. [17]) are presented in Table VI. From the table it is clear that the Das et al. method gave 1 FP whereas the COSEn-based method resulted in 8 FP. This shows the superiority of our proposed algorithm.

Table V.

Confusion Matrix on Test Set 1

True Label	Predicted Label
	AF	non-AF
AF	24	0
non-AF	0	25

Table VI.

Comparison on Test Set 1

Statistical Method [15]				COSEn Method [17]
True Label		Predicted label		True Label		Predicted label
		AF	non-AF			AF	non-AF
	AF	24	0		AF	24	0
	non-AF	1	24		non-AF	8	17

2). Results on Second Test Set:

Test set two contained 50 subjects, including 25 AF subjects; the rest of the subjects had NSR with PAC/PVCs, hence this data set is more challenging. From these 50 subjects, ~2,552 hours of ECG data were analyzed and after preprocessing, 57,787 2-minute segments were used for the next step. Without the PAC detection criteria (i.e., with only SampEn), the algorithm detected 29 subjects as AF, thus giving 4 FP subjects. However, after using the combined AF detection algorithm, the number of false positives was reduced from 4 to 1. As a result, on the second test set, the algorithm achieved 100% sensitivity, 96% specificity, and 98% accuracy. Table VII shows the confusion matrices on test set two and it shows that with the inclusion of the PAC detection step, we have only 1 misclassified subject. As we did with the validation and first test sets, we also compared the two state-of-the-art methods on test set two and the outcome is reported in Table VIII. It can be seen from Table VIII that 5 and 12 FP AF subjects were detected by the statistical parameter (Das et al. [15]) and COSEn (Lake et al. [17]) based methods, respectively, which is much higher than by our proposed method (only 1 FP).

Table VII.

Confusion Matrix on Test Set 2

With only SampEn				With Proposed Method
True Label		Predicted label		True Label		Predicted label
		AF	non-AF			AF	non-AF
	AF	25	0		AF	25	0
	non-AF	4	21		non-AF	1	24

Table VIII.

Comparison on Test Set 2

Statistical Method [15]				COSEn Method [17]
True Label		Predicted label		True Label		Predicted label
		AF	non-AF			AF	non-AF
	AF	25	0		AF	25	0
	non-AF	5	20		non-AF	12	13

Overall, combining the two test data sets, we have 99 subjects including 49 AF subjects. Table IX shows the overall confusion matrix by combining the two test sets. From the table, the overall sensitivity, specificity, accuracy, PPV, and NPV of our proposed method are found to be 100%, 98%, 98.99%, 98%, and 100%.

Table IX.

Confusion Matrix on Overall Test Set

True Label	Predicted Label
	AF	non-AF
AF	49	0
non-AF	1	49

VI. Discussion

We described a novel approach to detect AF during sepsis from ICU patients using RR interval variability, Poincaré plots and P-wave information. RR interval-based SampEn captured the dynamics and randomness of AF rhythms. However, false positives (FP) were detected when PAC/PVCs were present, as PAC/PVCs can mimic the irregular patterns of AF by introducing high RR interval variability. To solve this, we extracted Poincaré plot-based features derived from the differences of HR; these features detected the repeated triangular patterns of PAC/PVCs and reclassified some FP segments as non-AF by separating them from AF. However, Poincaré plot-based features were not sufficient, as many PAC/PVCs did not show the ideal triangular pattern in the Poincaré plot. As a result, P-wave based properties were explored to discriminate AF from PAC/PVCs. As P-waves are ideally not present (or are irregular if present) in AF, we analyzed the absence and irregularity of P-waves. To do so, we extracted PR_ratio, P_samp and PR_seg; P_samp determined the irregularity of PP intervals whereas PR_ratio was directly related with the one-to-one ratio between R and P-waves. Moreover, the newly proposed short segment-wise PR ratio (PR_seg) contributed significantly in reducing the FP, in particular. The underlying reason was that when the presence of P-waves was not consistent throughout the entire 2-minute PAC/PVC segment due to very high ectopic beats, PR_ratio failed; however, PR_seg could identify those types of PAC/PVC segments. As a result, when we incorporated P-wave based features, Poincaré plots and SampEn into our approach, the number of FP subjects was reduced from 10 to 2 in the validation set and from 4 to 1 in the second test set.

To be useful clinically, AF detection algorithms must be accurate and avoid FP detections to reduce alert fatigue. One major challenge facing our desired AF detection algorithm was to reduce the FP decisions among the critically ill patients. Since these patients are often on telemetry for a long period, there is a high probability of false AF decisions. For example, even if only 6 minutes of consecutive ECG signal are incorrectly determined as AF from a total recording of 50 hours, the subject-wise decision is still AF; thus resulting in FP for AF detection. Critically ill sepsis patients have a higher risk for ECG abnormalities, PACs/PVCs, and arrhythmias other than new-onset, thus making accurate AF detection very difficult. Traditional AF detection algorithms based on only RR interval-based variability can have poor performance, as shown here. In order to have reliable and accurate AF detection from critically ill sepsis patients, P-wave characteristics (i.e., atrial activity) and potential PAC/PVC repetition patterns along with RR interval variability were needed. Thus, considering the significance and amount of analyzed data, the performance of our algorithm is noteworthy and suggests potential clinical utility.

For the initial AF screening step, although we have used only SampEn, other features along with the machine learning classifiers can be used. However, there is no significant difference between the performance of the classifiers and the SampEn alone, as shown in Tables I and II. The possible explanation is that AF caused significant random variation in the RR intervals when compared to the NSR segments. SampEn was able to capture this randomness quite well, as shown in Fig. 2; the two categories (AF and NSR) are almost linearly separable by using SampEn. As a result, SampEn based thresholding achieved 99.10% accuracy for the initial AF screening. RMSSD also showed good distinguishing properties with 96.65% accuracy, which is only a few percent lower than SampEn. When SampEn is combined with RMSSD and Shannon entropy, the classifiers improved the performance very little — from 99.10% to 99.32%. This establishes that if very good features showing linearly separable characteristics can be extracted, then simple thresholding can achieve similar performance to machine learning classifiers. As a result, for the initial “possible AF” screening step, we used only SampEn. Moreover, SampEn-based simple thresholding is computationally less demanding when compared to the machine learning classifiers.

The majority of the previously described methods rely on solely RR interval-based features. Some methods worked by using the P-wave characteristics, although only the P-wave itself is not suitable. Only in a few studies, both RR variability and P-wave based features were used [22]–[24]. Poincaré [42] and Lorentz [19] plot-based methods can provide discriminative patterns for AF and PAC, however, the impact of P-wave based properties along with Poincaré/Lorentz plots was not studied. We believe they can play a vital role in false alarm reduction for critically ill ICU patients. We are one of the first ones to combine features from all three domains—RR interval variability, Poincaré plot and P-wave characteristics—to perform AF detection.

Next, we wanted to find out why our proposed method is performing better than the statistical and COSEn-based methods. One possible reason is that our study population has frequent ectopic beats and other abnormal rhythms. It was analyzed in [17] that COSEn can detect the AF rhythms, but its performance degrades in the presence of PAC/PVCs as these rhythms have variations similar to AF, thus making it difficult to separate from AF. Similar results were also reported in [20], [24], where it was shown that COSEn detected AF, however, with the presence of premature beats, its performance decreased. For the Das et al. [15] method, although the ectopic beat filtering was performed, when excessive beats were present, the reported features resulted in many false positive AF identifications. Another reason could be that for very long-term ICU recordings, to determine whether a subject has AF or not, the algorithm needs to be very accurate. Most of the published methods report the segment-wise accuracy. However, as we discuss in this paper, for the “subject-wise scenario” if only 6 minutes of consecutive AF is found, the individual subject’s decision will still be a false positive. Since our proposed method not only accounts for the RR interval variability, but also considers PP rhythm-based features (P_samp and PR_seg), high subject-wise accuracy is obtained. Although our data sets do not reflect the actual prevalence of AF in the relevant population, we expect the above noted features to be relevant for AF detection. In order to develop the algorithm, we needed potentially equal numbers of subjects from both groups, hence, the true prevalence was disturbed. However, since our algorithm was developed using a large database and further tested using two separate blind data sets, we hope the mismatch in AF prevalence will not affect the classification performance.

There have been many reports of detecting AF based on short data segments (as short as 10 seconds in CinC 2017 challenge, 12 beats for the COSEn method [17], and others). However, our criterion was to detect subject-wise AF status from 6 minutes of data; this was driven by the current clinical literature showing that AF events lasting longer than 6 minutes confer thromboembolic risk [47], [48]. In order to study how the duration of consecutive segments affected the subject-wise AF decision for different methods, we have varied the duration of AF decisions from 4 to 10 minutes and counted the FP decisions from test set 2. Fig. 8 shows how the number of FPs varies with the different durations of consecutive segments. From the figure, it is evident that for all durations, our proposed method gives fewer FPs than the other two methods. With increased duration for subject-wise AF decision, the number of FPs is expected to decrease, and Fig. 8 illustrates this point. As shown in Fig. 8, if 10 consecutive minutes of AF are used to decide subject-wise AF, then the statistical method [15] detected 4 FP subjects while the COSEn [17] detected 6 FP subjects; our proposed method detected only 1 FP. This difference of FPs is more prominent for short durations as evident from Fig. 8. Ultimately, the clinical evidence noted above necessitated our choice of 6 minutes of data for AF detection.

Fig. 8.

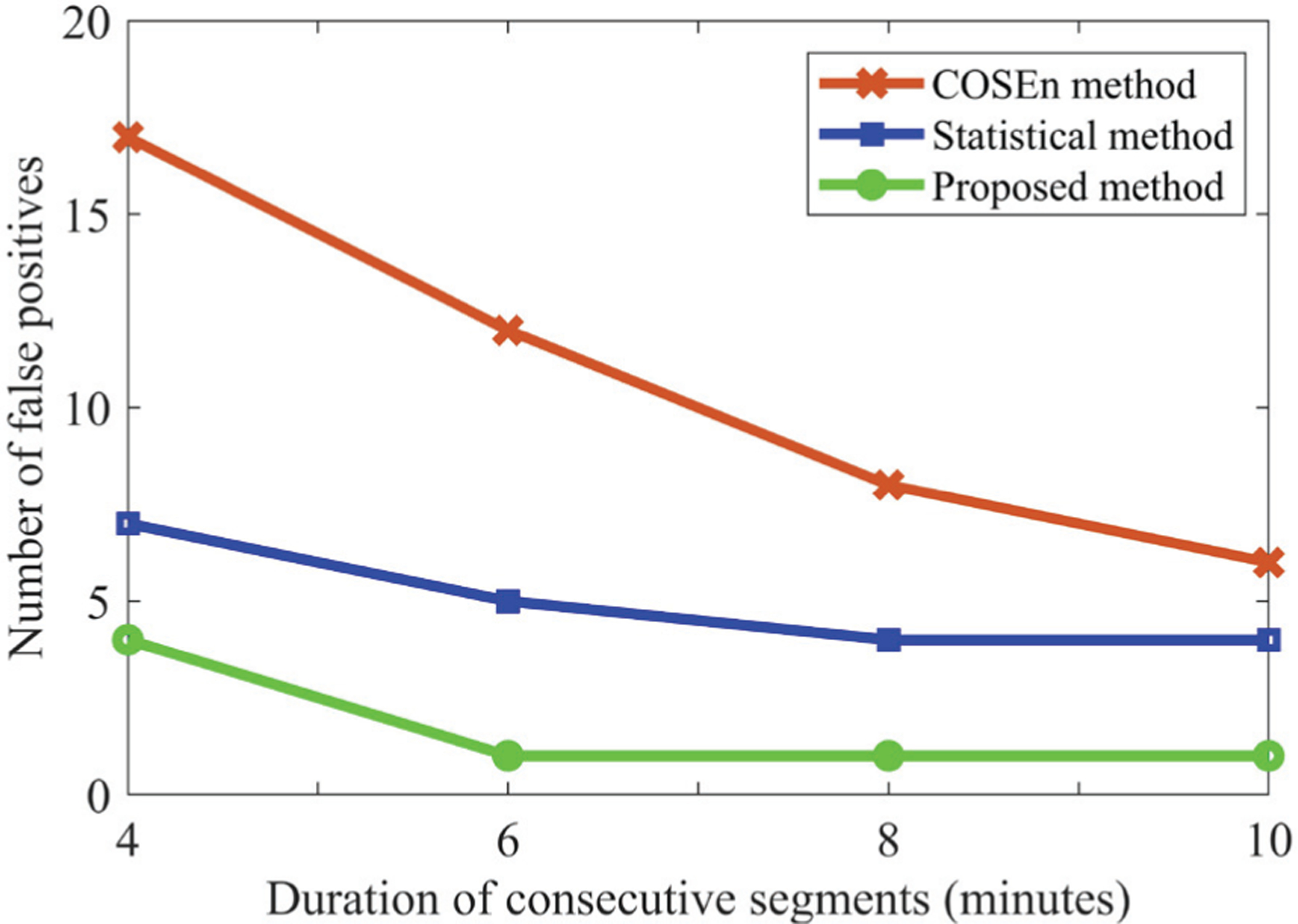
Number of false positive AF detections with different durations of consecutive segments, for three methods.

The main contributions of this study are three-fold: first, we have developed and validated an automated AF detection algorithm for critically ill sepsis patients, which is found to be highly accurate in the presence of ectopic beats and can reduce false positive AF alarms. Secondly, we have used a large number of ECG recordings to train, validate, and test the algorithm. The training, validation, and two test sets contain different subjects which prevented overfitting. Finally, we provide new annotations for MIMIC III waveform subset. Other researchers can easily use these annotations as a tool to carry out further development, which will certainly help in AF management for critically ill patients.

Finally, there are several limitations of our study. Although we have used a large number of ECG recordings obtained from 200 subjects (~4,209 hours of ECG data for testing alone), this is still a single-center study; data may differ at other centers. Further validation of the proposed automated AF detection algorithm in other settings is certainly warranted. We have largely concentrated on ectopic beat detection; other kinds of abnormalities can also be explored in the future if more annotations are provided. The 6 minute rule for subject-wise AF decision is derived based on the clinical studies which focused on the relation of AF and risk of stroke [47], [48]; further insights can also be explored to find out what may be the best criteria for subject-wise AF decision.

VII. Conclusion

In this study, we have presented a novel approach to detect AF from ICU patients during sepsis using the MIMIC III ECG waveform database subset. Not only have we extracted several statistical parameters from the RR interval series along with the Poincaré plots, but we have also used P-wave properties to discriminate AF from non-AF. With the combination of empirical rules and thresholds, the proposed algorithm achieved high performance on both the training and validation data. Moreover, when the algorithm was applied to two independent test data sets, it also achieved high AF detection accuracy and superior performance than two state-of-the-art methods, thus showing the effectiveness of the presented method for real life scenarios. This is one of the first works to detect new-onset AF in critically ill sepsis patients using the MIMIC III waveform database. We are providing our annotations to facilitate further research with this database for other researchers. Since new-onset AF during sepsis can significantly increase complications and risk of poor outcomes, this study can be helpful to expand research into AF during sepsis by allowing rapid scaling up of AF detection in banked ECG waveform data and improve clinical detection of AF among the critically ill. Future studies can explore whether enhanced AF detection may improve patient outcomes by informing more rapid and better informed treatment.