An interpretable low-complexity machine learning framework for robust exome-based in-silico diagnosis of Crohn’s disease patients

Abstract

Whole exome sequencing (WES) data are allowing researchers to pinpoint the causes of many Mendelian disorders. In time, sequencing data will be crucial to solve the genome interpretation puzzle, which aims at uncovering the genotype-to-phenotype relationship, but for the moment many conceptual and technical problems need to be addressed. In particular, very few attempts at the in-silico diagnosis of oligo-to-polygenic disorders have been made so far, due to the complexity of the challenge, the relative scarcity of the data and issues such as batch effects and data heterogeneity, which are confounder factors for machine learning (ML) methods. Here, we propose a method for the exome-based in-silico diagnosis of Crohn’s disease (CD) patients which addresses many of the current methodological issues. First, we devise a rational ML-friendly feature representation for WES data based on the gene mutational burden concept, which is suitable for small sample sizes datasets. Second, we propose a Neural Network (NN) with parameter tying and heavy regularization, in order to limit its complexity and thus the risk of over-fitting. We trained and tested our NN on 3 CD case-controls datasets, comparing the performance with the participants of previous CAGI challenges. We show that, notwithstanding the limited NN complexity, it outperforms the previous approaches. Moreover, we interpret the NN predictions by analyzing the learned patterns at the variant and gene level and investigating the decision process leading to each prediction.

INTRODUCTION

Sequencing technologies are producing large amounts of data (1), allowing detailed analysis of the human genetic variability and its relation with phenotypic traits such as the susceptibility to genetic disorders (2). Whole exome sequencing (WES) focuses only on the 1–2% of our genome that is responsible for encoding genes and is thus more affordable than WGS. Nonetheless, it is able to sample the genetic variation with highest chance to have a functional impact, such as missense single nucleotide variants (SNVs) (3). So far WES has indeed been extremely valuable for the discovery of the molecular mechanisms underlying many genetic diseases (2,4).

Large genetic studies are nowadays very common, meaning that increasing amount of data is becoming available to bioinformaticians, sometimes even in the form of case-controls datasets targeting particular genetic disorders with uncertain aetiology (5–7). These kinds of studies are thus allowing researchers to start investigating the diagnostic potential of machine learning (ML) methods (5,8), paving the way for future clinical applications and potentially improving our comprehension of the basis of poorly understood genetic disorders (5,9).

Notwithstanding the clear scientific opportunity of applying cutting-edge ML methods directly to the exome-based in-silico diagnosis of oligo-to-polygenic genetic traits, many issues need to be solved in order to reach this goal: standardized, homogeneous and high-quality case-controls sequencing data for training and testing of ML methods are indeed still relatively difficult to obtain, due to the following three common issues. First, in many studies some level of batch effect bias is present between cases and controls, due for example to the different technologies or experimental settings in which the positive and negative samples have been sequenced. Second, the selection of the individuals in the cohorts is crucial: in the case of polygenic disorders, for example, disease-unrelated factors such as the different ethnicity between cases and controls may indeed easily provide a stronger discrimination signal than the feeble contributions due to variants differentially accumulated on sensible genes. Third, on the phenotypic annotation side is equally difficult to ensure that all the cases have the same disease severity and that all the symptoms have been annotated following the same criteria and with the same level of detail. To the best of our knowledge, only a limited number of exome-based in-silico diagnostic tools targeting non-trivial genetic traits with state-of-the-art ML methods have been published so far, such as (8,10–11) for Crohn’s disease (CD) and (12) for Bipolar Disorder. Other approaches relied on more classical statistical methods such as empirical disease risk scores (6,7).

The application of cutting-edge ML methods to the diagnosis of non trivial genetic disorders presents indeed various technical challenges, due to (i) the intrinsic complexity of the problem, which would require sophisticate non-linear models to be solved, the (ii) generally high level of noise in the data and (iii) the widespread presence of confounding effects (e.g. batch effects and heterogeneous phenotypic annotations). Moreover, (iv) due to experimental and clinical difficulties, a small amount of samples are generally available in each dataset. Limited sample size coupled with the large amount of information encoded in each exome (WES identifies around 10–20k variants per individual) pose indeed a clear problem for the successful application of ML methods (8), specifically in relation to the risk of learning dataset-related characteristics (over-fitting) or unwanted signal due to confounding effects (e.g. batch effects or ethnicity) instead of disease-mechanisms-related patterns.

In this study we tackle these difficult problems and we address them by devising a novel Neural Networks (NN) approach, called CDkoma, for the exome-based in-silico diagnosis of oligo-to-polygenic genetic disorders. We apply it to the prediction of CD patients from healthy controls on the case-controls datasets used in the 2011, 2013 and 2016 editions of the Critical Assessment of Genome Interpretation (CAGI) (8). We show that our NN improves over the performances obtained by state of the art methods in the past CAGI challenges, but at the same time we put a lot of effort into limiting the detrimental effects of the data-related issues mentioned above. In particular, (i) we designed our model to allow non-linear inference while minimizing the number of trainable parameters by heavily using weight sharing and regularization and (ii) we propose an exome sequencing feature encoding scheme based on the biological concept of gene mutational burden that allows us to meaningfully condense the information contained in WES data into a small tensorial representation suitable for ML applications on small sample sized data.

At last, we show that our NN allows also the interpretation of its predictions providing insights on the variants and gene-level learned patterns, ultimately permitting the investigating the decision process leading to each case/control prediction.

MATERIALS AND METHODS

Datasets

The datasets used in this study are taken from the CAGI2 (2011), CAGI3 (2013) and CAGI4 (2016) CD prediction challenge, which had the goal of distinguish between exomes of CD patients and healthy individuals by analysing their exomes. We obtained them with the permission of Dr Andre Franke (CAGI3 and 4), while the CAGI2 dataset is publicly available.

The CAGI2 dataset contains 56 exomes, consisting of 42 cases and 14 controls. This dataset is known to suffer from batch effect bias due to the fact that the cases and the controls have been sequenced in different settings (5,8), resulting in trivially identifiable differences between the positive and negative samples (e.g. with a PCA).

The CAGI3 dataset contains 66 sequenced exomes, divided into 51 cases and 15 controls. The samples are organized into 28 different pedigrees and two discordant twin pairs (8) and a certain degree of batch effect is noticeable with a clustering procedure (5), although the effect is less severe than in the CAGI2 dataset.

The CAGI4 dataset is the largest and highest quality dataset available. It contains 111 sequenced exomes, divided into 64 cases and 47 controls. The cases are unrelated and only two pairs of controls are related, with also no relationship with the datasets from past CAGI editions (8). Further details about how this data has been collected can be found in (5,8). All the datasets are provided as VCF files listing the observed variants, further details about them are available in Supplementary Material Section S1.

Encoding the exome sequencing data into ML-understandable features

We used Annovar (13) to annotate the VCF files in the CAGI CD datasets, obtaining a tab-separated files with functional annotations for all the variants observed (see Supplementary Material Section S5 for more details).

One of the most crucial aspects of the application of ML methods to any specific domain of interest is related to finding the most suitable way to encode real-world information into ML-understandable feature vectors, which correspond to the multi-dimensional data points on which the ML algorithm perform inference for classification or regression. Such vectors should contain ideally all the information available from the data, and at the same time their encoding should be as efficient as possible in order to minimize their size (the number of features used), which is generally proportional to the complexity of the model and thus closely linked to the risk of over-fitting. Moreover, a limited number of dimensions allows computationally faster training procedure of the ML model.

To the best of our knowledge, a well-defined method to encode exome sequencing information into feature vectors for the purpose of in-silico diagnosis of oligo-to-polygenic genetic disorders has not been proposed yet. The approaches used so far encode the observed variants by listing them and annotating their deleteriousness with variant-effect predictors (10) or by one-hot encoding the genotype information within each chromosome (12), but the main drawback of both of these approaches is that the size of the resulting feature vectors is proportional to the number of variants observed on the input exomes, which is likely around ten or twenty thousands. Notwithstanding the widespread use of WES technologies, most case-control datasets available nowadays still have a limited sample size (few hundreds samples), which requires some prudence when using feature vectors with too many dimensions.

A feature encoding based on gene-level aggregation of variants

In this study, we devised a general strategy to encode WES data into ML-ready feature vectors which is particularly suitable for small sample size datasets, because it encodes the genetic information in a compact form by aggregating the variants at the gene level. Instead of encoding sequentially all the variants annotated in the VCFs, which would result in large and unstructured feature vectors (10,12), we define the genes to be the smallest conceptual entity in our model, and we thus aggregate all the observed variants on the genes on which they are mapped, by counting how many times each type of variant occur in each gene. Biologically, this concept can be viewed as analogous to quantify and encode the genes mutational burden observed in the data (14), which corresponds to the amount of (possibly damaging) mutations carried by the genes covered by the WES. This is nevertheless conceptually different from existing mutation burden testing approaches such as (15–17), since the goal of our study is mainly predictive and not just explanatory (18).

While there are many possible ways to encode this burden, such as quantifying the functional impact of each variant with variant-effect predictors such as CADD (19), M-CAP (20) or DEOGEN2 (21), encoding the distributions of these scores by binning them into a fixed-size feature vector, in our study we did not use this approach because, due to the limited amount of data available for training and testing, we preferred to adopt an even simpler approach. In this context, we believe that proposing a (i) simple encoding which (ii) drastically reduces the feature vectors size required to represent sequencing data and which (iii) does not require third-party functional prediction tools enhances greatly its generality and thus its wide applicability, for example across data types (WGS, WES) and organisms, since most of the functional predictions are available only for humans.

For each gene we thus counted the number of variants mapped by Annovar on it, organizing them in the following 9 classes: ‘exonic’, ‘UTR3’, ‘UTR5’, ‘ncRNA exonic’, ‘ncRNA intronic’, ‘upstream’, ‘downstream’, ‘intronic’ and ‘splicing’. Each exome is thus summarized into a matrix (called tensor in NN jargon) with size 9 × N_g, where N_g is the number of the genes considered among the entire Human exome.

Since in this study we focus on the in-silico diagnosis of CD patients, we extracted from PhenoPedia (22) the list of genes involved in CD, obtaining two possible values for N_g = {222, 691}, which correspond to the genes referenced in at least 2 or 1 publication. The full list is available in Supplementary Material.

As a last step, we added two extra dimensions to each of the gene feature vectors, representing the (i) RVIS (23) gene-burden score and (ii) the publication weight score extracted from PhenoPedia, which is proportional to the number of publications in which each gene has been associated with CD. These two additional features are suppose to provide general information about the relevance of the gene for human health (RVIS) and its degree of involvement in CD. The total number of gene features is thus F_g = 11.

The final shape of our feature encoding scheme for each exome is thus F_g × N_g. The feature representation of a dataset with M samples is thus a 3D tensor with shape M × (N_g × F_g).

The Neural Network model

The tensorial exome feature representation described so far cannot be used as input for every ML method, because most of them (e.g. RandomForest, Support Vector Machines) assume that each sample is represented by a 1-dimensional vector. A solution to this issue would be to concatenate the N_g gene feature vectors within each exome, but this would lead to a vector with shape 1 × (N_g · F_g) and, in conventional ML methods, to a number of parameters proportional to N_g · F_g ≫ M, which would be excessive due to the small number of samples M in the CAGI datasets. On the other hand, Neural Networks (NN) can natively deal with more structured tensorial feature vectors as input, and the number of trainable parameters can be reduced by using weight sharing (also called parameter tying).

We thus devised a NN model specific for the exome-based in-silico diagnosis of CD patients, and we kept its complexity in terms of trainable parameters as low as possible in order to limit the risk of over-fitting. Our NN, called CDkoma, is shown in Figure 1 and has two neurons, called G (yellow) and P (dark green). The G neuron has W_g = F_g = 11 weights and each application of G takes as input one 11-dimensional vector describing one of the N_g genes selected. The first layer of the network thus consists of N_g applications of the same neuron G, similarly to a 1-dimensional convolutional layer, followed by LeakyReLU activations (24). Then, we filter these values with a Dropout layer (25) with a probability P = 0.1 of discarding each input value. The final layer of the network consists of the neuron P, which implements a Logistic Regression over the values computed by the G neurons and outputs probability-like scores, where predictions close to 1 indicate higher likelihood of CD.

Figure 1.

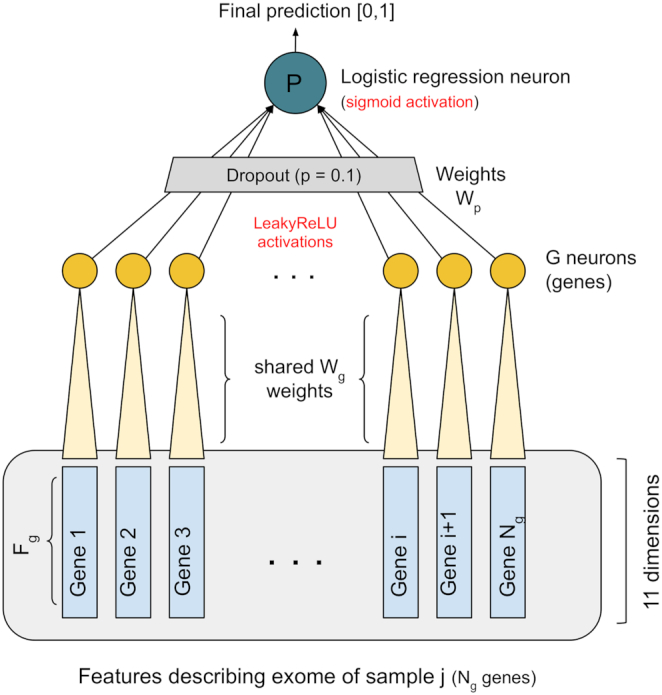
Figure showing the structure of the CDkoma NN. The feature vector describing each exome is a tensor with shape (F_g × N_g), encoding the N_g most relevant CD genes. The G neuron is applied iteratively to each 11-dimensional feature vectors encoding the CD genes, each time using the same weights W_g. The N_g LeakyReLU activations from the applications of the G neuron are filtered by a Dropout layer and the final neuron P aggregates all the resulting activations into a logistic regression that yields the final, probability-like, diagnostic score.

Further details about the NN are available in Supplementary Material Section S2. The implementation is available at: https://bitbucket.org/eddiewrc/cdkoma.

Evaluation of the predictions

We evaluated the performance of CDkoma in four different prediction settings. First, we trained it on the CAGI4 dataset, which is the highest quality one (8) and we tested it on the CAGI3 and CAGI2 datasets. We then trained CDkoma on the CAGI3 dataset, which is the second most reliable dataset (8), and tested it on the CAGI4 data. In the last assessment, we concatenated the CAGI2, 3 and 4 datasets and we performed a leave-one-out (LOO) cross validation on the 233 resulting samples.

As evaluation metrics we used the Sensitivity (SEN), Specificity (SPE), Balanced Accuracy (BAC), Precision (PRE), Matthews Correlation Coefficient (MCC), Area Under the ROC curve (AUC) and the Area Under the Precision-Recall curve (AUPRC).

RESULTS

Performance of the CAGI dataset

We evaluated the performance of our NN method, called CDkoma, by training and testing it on CD datasets from past editions of the CAGI challenge. To test CDkoma on the CAGI4 dataset, we trained it on the CAGI3 data. To test our method on the CAGI2 and 3 datasets, we trained it on the CAGI4 data, which appears to be the highest quality dataset among the three (8). To corroborate this observation, Supplementary Figures S1 and 2 show that, when using our gene-burden-based feature encoding described in Methods, CAGI3 and 4 datasets do not present any obvious bias able to trivially distinguish cases from controls in terms of type of variants observed (see Supplementary Figure S1) or mean number of variants mapped on the N_g selected genes (see Supplementary Figures S2 and 8). On the other side, this effect is visible on the CAGI2 dataset, in which controls have a significantly higher number of variants mapped on each gene and thus we decided not to use this dataset for training.

Table 1 shows the prediction performance of CDkoma over the three CAGI datasets, both while using the larger (691) or the smaller (222) sets of CD genes. In general, the performance of CDkoma is higher when using the larger set of genes, probably due to the fact that more information about the genetic variability in each sample is available to the predictor, but the two settings are comparable. CDkoma has a good precision, meaning that nearly 90% of the samples diagnosed with CD in CAGI3 and 2 datasets are actually affected by it, and 77% of them in the CAGI4 dataset, which is appears to be the hardest CD prediction challenge proposed so far (8).

Table 1.

Performance of CDkoma using the small and large set of genes on the 3 CAGI datasets

Target	Genes	Sen	Spe	Bac	Pre	MCC	AUC	AUPRC
CAGI4	691	72.2	70.2	71.3	77.0	42.1	74.4	80.5
	222	52.3	74.5	63.4	73.9	26.9	64.2	68.9
CAGI3	691	96.2	60.0	78.1	89.3	63.2	82.5	93.1
	222	94.2	60.0	77.1	89.1	59.0	79.3	91.8
CAGI2	691	93.0	64.3	78.7	88.9	60.5	74.3	86.6
	222	97.7	57.1	77.4	87.5	64.7	71.4	84.4

The abbreviations of the evaluation metrics used are explained in ‘Materials and Methods’ section.

Supplementary Table S1 shows the prediction performances obtained by conventional ML methods such as Logistic Regression, Support Vector Machine, Random Forest and a fully connected feed forward NN (DenseNN) on the same data. Notwithstanding the larger number of parameters used by these models, these approaches fail to obtain results that are significantly better than random on the CAGI4 dataset and they perform at least 13% lower than CDkoma on the CAGI3 dataset.

Supplementary Figure S3 shows that, notwithstanding the small sample size, the performances of our NN are always significantly higher than the random baseline.

Comparison with past CAGI CD challenges

We compared the predictions obtained by CDkoma (using the full set of 691 CD-related genes) with the results obtained by CAGI participants on the three datasets. Table 2 shows this comparison, with most results reported from (8). We also reported the performance of (11), which was the winner of the 2016 CD challenge, and from the recently published AVA,Dx (26). To reach this result, they used ML methods such as Naive Bayes or Random Forest along with inputed marker SNPs information from third-party GWAS studies to distinguish between CD cases and controls.

Table 2.

Comparison our NN (CDkoma) performance (in terms of AUC) with the best scores obtained in previous CAGI assessments

Target set	# Method	AUC
CAGI4	CDkoma	74
	GWAS marked SNPs + ML a	72
	Ensemble	66
	Manual prediction	63
	Transductive SVM	60
	Key variants weighting	59
CAGI3	Biclustering	87
	Mixed pedigree 1	84
	CDkoma	83
	Mixed pedigree 3	80
	Count of SNVs in CD genes	74
	AVA,Dxb	69
CAGI2	CDkoma	74
	Manual prediction	68
	SNV co-occurrence	68
	Biclustering	67
	Count SNVs in CD genes	66

^a result reported from (11), ^b result reported from (26).

CAGI results have been reported from (8).

The details of the other methods mentioned in Table 2 are described in (8), but we will briefly recap them here for sake of clarity. Key variants weighting consists in ranking the samples in function of the number of known CD-causing SNVs present in the exomes. Biclustering is the procedure of performing a K-means clustering on the samples with k = 2, based on the observed variants. Ensemble method performs its prediction by combining the scores obtained by the other approaches described here. Manual prediction is the diagnostic assessment performed by a human expert. Methods based on counting the number of SNVs in CD genes produces a diagnostic score from the total number of variants observed. Transductive SVM involves the application of transductive learning (27) on a set of variants statistically significantly associated with CD.

Table 2 shows the sorted comparison between the performances obtained from our NN model (CDkoma) with respect to the methods presented in the past CAGI challenges, reported from (8). We show the comparison of the AUC scores because it is the metric used in CAGI evaluations (5). We can see that on the three datasets, our NN is ranked first two out of three times. In particular, in the CAGI4 and 2 datasets, our NN is ranked first, respectively 3% and 9% better than the best methods presented in the respective challenges. For what concerns the CAGI3 dataset, our NN is ranked third, 5% lower than the best performing biclustering approach. As observed in (8), the success of this relatively simple method (an unsupervised k-means clustering with k = 2) could be due to the fact that there is a batch effect bias that helps discriminating cases from controls at the level of the variants distribution.

The comparison shown in Table 2 is meant to show how the prediction performance of CDkoma relates to the previously developed tools, but, although very similar, the prediction settings are not completely identical since the scores reported from (8) have been obtained in true blind test settings. Moreover, the CAGI4 dataset was not available as training set to test methods on the CAGI2 and 3 datasets. CDkoma performances on the CAGI4 data, on the other hand, are directly comparable because both CAGI2 and 3 datasets were available to researchers as training sets to solve the CAGI4 challenge.

Leave-one out cross-validation

As additional validation, we merged the CAGI2, 3 and CAGI4 datasets and we performed an LOO cross-validation on the resulting set, which contains 233 samples, 158 of which are CD patients. Supplementary Table S2 shows the results obtained by CDkoma when using the set of 222 or 691 CD-related genes. From this additional assessment we can see that our method obtains consistent performance across different evaluation settings. The AUCs are comparable with the ones shown in Table 1 and the AUPRC curve and the high precision (81.6) indicates that most of the time our model predicts a sample to be associated with CD, the prediction is correct.

The NN predictions correlate with the disease’s age of onset

The CAGI4 dataset is also annotated with the age of onset of CD on the cases. After obtaining the probability like predictions from CDkoma, we thus investigated whether the NN scores were somehow reflecting the severity of the disease, measured by the age of onset. Supplementary Figure S5 shows the correlation between CDkoma predictions and the age of onset on the CAGI4 dataset. It is important to notice that onset-related information is not passed to the NN at any time, and thus CDkoma is not specifically trained to reflect this property. CDkoma predictions have a negative correlation with the age of onset, meaning that higher scores are assigned to individuals which show symptoms of CD earlier in their life, possibly indicating a stronger phenotype. The Spearman correlation is r_s = −0.27, with significant P-values (P = 0.03), notwithstanding the limited number of samples. The CAGI4 cases have generally a very young age (<15 years). In particular, the youngest cases (1–2 years) might have a monogenic cause of disease, for which our model is not particularly suited, since it is based on the gene burden concept instead of single driving variants. CDkoma has been trained on the CAGI3 dataset to perform this analysis, but onset ages are not available for that dataset.

DISCUSSION

The ghost in the machine: opening the NN black-box to allow a biological interpretation

Besides the prediction of the likelihood of each sample to be associated with CD, we believe that the application of ML methods in Bioinformatics should also focus on the interpretation of the model’s decision, in order to extract information about the biological aspects of the phenomena under study. NN are known to be one of the most difficult ML to interpret when it comes to understanding how the trained model actually makes its predictions. Notwithstanding these difficulties, we worked on the analysis of the meaning of the weights used to process each gene feature vector and of the patterns of activations of the G neurons when predicting each sample, investigating their contributions towards the final prediction.

In a NN, each neuron’s activation a(x, w) is computed as a function f of the input values x multiplied by the learned weights w, in the following way: a(x, w) = f(∑_∀ix_iw_i). This means that, in order to give a contribution to the activation of the neuron, a feature x_i needs to be multiplied by a non-zero weight w_i, otherwise its contribution becomes null. This means that considering the absolute value of the weights W_g learned by the NN can thus be used as a first way to investigate how much importance the network assigns to each input variant type, provided that the features have comparable values.

Moreover, the pattern of activations 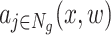produced by the first layer of the NN, which is composed by N_g applications of the G neuron (see Figure 1), can be used to investigate, for each predicted sample, which genes were active in that exome and whether they voted towards a ‘disease’ (class 1) or a ‘control’ (class 0) prediction outcome in the final layer/neuron P. In the following, we restricted these interpretation attempts to the set of 222 genes which are referenced as CD-related in at least two publications in order to get the most biologically consistent interpretation possible, reducing the risk of factoring in spurious associations between genes and CD and thus providing more robust results.

Exonic and UTR variants are the most relevant features

We extracted the W_g = 11 weights of the G neuron learned when training CDkoma over the CAGI3 (orange) and 4 (blue) datasets, which contain the most reliable data available, using the set of 222 genes, which are referenced as CD-related in at least two publications. By analyzing the absolute value of these weights, it is possible to understand how much relevance the NN assigned to each of them, since all the features assume comparable values, as shown in Supplementary Figures S1, 2 and 4. .

Figure 2 shows the relevance, normalized over the x axis, of each of the features describing each gene in each exome. Interestingly, the pattern of feature relevance are very similar regardless of the dataset used to train CDkoma, indicating a good consistency between independent training procedures on different data. The features representing the amount of UTR5 and exonic variants accumulated on each gene are generally the most important features, followed by the number of UTR3 variants. This suggest that, besides the exonic variants, UTR5 variants carry a important signal for the CD prediction in the NN’s view. Other kinds of variation, such as intronic variants, appear to be marginal, while splicing, upstream and exonic ncRNA variants have effectively near zero contribution. This is justified by the fact that these types of variants are quite rare in the CAGI datasets (see Supplementary Figures S1 and 4). Intronic non-coding variants and the RVIS score are assigned a noticeable contribution only when training on the CAGI3 dataset.

Figure 2.

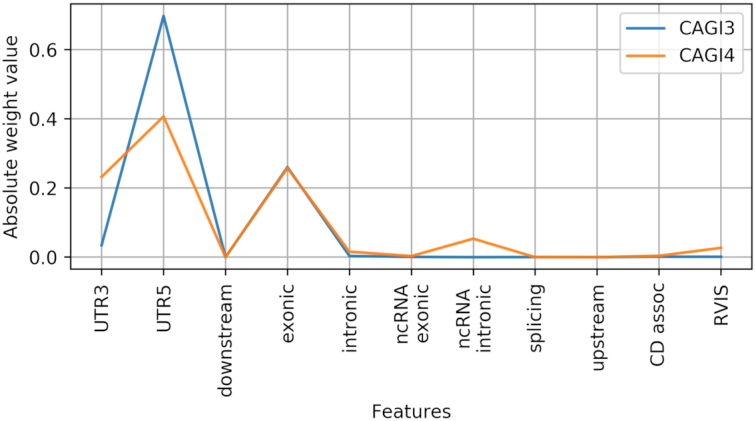
Plot showing the normalized absolute value of the weights learned by the G neuron on the CAGI3 (blue) and 4 (orange) datasets.

Analysis of the most relevant genes across the CAGI datasets

The G neuron is used to transform the input features vectors into gene-level activations using the same 11 weights W_g for all the genes in all the exomes, similarly to a simple 1-dimensional convolutional layer. When predicting each sample/exome, the G neuron slides on the list of selected N_g genes, producing an ‘activation’ value which influences the final prediction computed by the last layer P of the NN (see Figure 1).

Similarly to what we did for the gene-level features in Section 4.2, if we isolate the weights W_p learned by the final neuron P and we compute their absolute value, we can extract the relevance that the NN has assigned to each gene and compare them among the datasets.

In Figure 3 we show the absolute relevance assigned to each gene by CDkoma while training on the CAGI3 and 4 datasets. For each dataset we show only the 25 most relevant genes selected by the NN among the 222 genes in the initial pool, ranked by increasing weight. To rapidly identify genes that are ranked high on both datasets, we highlighted them with an asterisk.

Figure 3.

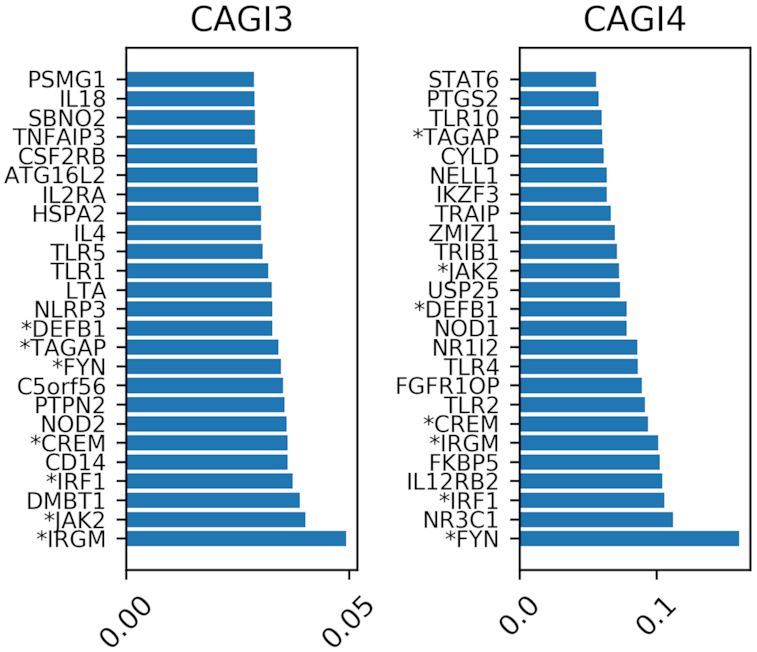
Figure showing the 25 most relevant genes in the models trained on the CAGI3 and 4 datasets. The asterisk before the gene name indicates that the gene has been selected as highly relevant while training on both datasets.

We can see that IRGM, JAK2, IRF1, TAGAP, DEFB1 and CREM are deemed highly relevant during both trainings. In other cases, closely related genes are picked up, such as NOD1 in CAGI4 versus NOD2 in CAGI3; or TLR1 and TLR5 in CAGI3 versus TLR2, TLR4 and TLR10 in CAGI4.

GWAS studies have identified over 200 loci to be associated with CD (28,29), the most strongly being NOD2, which was among the top 25 most relevant genes for the CAGI3 dataset (Figure 3). It should be noted that although NOD2 did not rank among the top 25 most relevant genes for the CAGI4 dataset, the CYLD gene, which is located immediately adjacent to the NOD2 gene on chromosome 16, was ranked high in the CAGI4 dataset. Identification of NOD2, an intracellular pattern recognition receptor that recognizes bacterial molecules and stimulates an immune reaction, has highlighted the importance of innate immunity in CD. This was further underscored by associations of other genes involved in innate mucosal defense, such as some genes of the TLR pattern recognition gene family or beta-defensins. Besides innate immunity, GWAS findings also highlighted various aspects of the adaptive immune response: T-cell activation (IL2, IL2RA), T-helper-17 cell differentiation (JAK2, IL2, IRF4), and T-cell and B-cell regulation (TAGAP, IRF5). Another important causal gene for CD is ATG16L1. Association of ATG16L1 with CD implicated the autophagy pathway in disease pathogenesis, with subsequent associations (IRGM, LRRK2) reinforcing this view. Other disease-associated pathways are the NF-κB (TNFAIP3, PTPN2, NFKB1) and IL23R (IL23R, STAT3, STAT4) pathways. Many of the genes identified in this study as among the most relevant genes, function in these major disease associated pathways.

Diving into how the single predictions are computed

So far, the analysis of our NN has been focused at the level of the datasets, since we compared the relevance of the features assigned by CDkoma during the training process. Ideally, the ultimate goal of ML interpretation would be to directly ask the algorithm which decision process it followed in order to reach the specific prediction associated with each sample. This is for example possible with Random Forests (21,30), but it is usually not trivial to achieve with NN.

Here we attempted this kind of analysis in the CD prediction context. To do so, we took the gene-level activations of each sample and we multiplied them by the weights W_p of the last layer’s neuron P. This is the exact same operation performed by CDkoma during each forward pass, but in this case we stopped before summing them up to compute the final prediction from the neuron P (see Figure 1). Since the activation of the P neuron, which is a Logistic Regression over the G neuron activations, is Sigmoidal and thus monotinically increasing, we can interpret these values by saying that all the positive values obtained are voting for the ‘CD case’ class (1) while all the negative values are voting for the ‘control’ class since they are effectively lowering the final probability.

This allows us to investigate the meaning of the gene-level activations patterns specific to the exome of each sample in the target dataset, providing insight in the (i) CDkoma decision strategy and (ii) on the disease mechanisms itself, as perceived by a non-linear ML method trained to differentiate between cases and controls. Supplementary Figure S6 shows a global view of the genes activation profiles across the datasets.

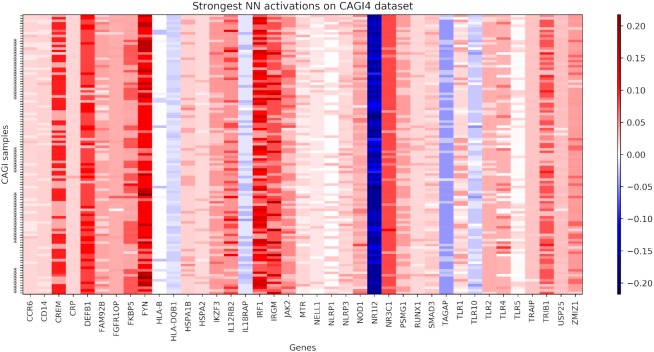
In Figure 4 we represented as heatmap the activation profiles of the 111 samples in CAGI4 (y-axis). Rows marked with an asterisk correspond to the CD cases. For visualization purposes, we selected only the genes with strongest activation signals among the 222 genes in the list. The red and blue colors indicate respectively positive and negative activations. We can see that the genes that were previously selected as most relevant (see Figure 3) present indeed generally strong positive (FYN, IRF1, IRGM, CREM, DEFB1) or negative (NR1I2, TAGAP) activations. Other genes have more variable activation pattern, such as FKBP5, IL12RB2, TLR4, TLR10 and ZMIZ1.

Figure 4.

NN gene activation patterns when predicting the CAGI4 dataset. Samples are listed on the y-axis and the asterisks indicates positive samples. The genes with the highest activations are shown on the x-axis. Red colors indicate that the activation is pushing towards the positive class (CD case), while blue colors indicate genes voting for the negative (controls) class.

With respect to Figure 3, here we can distinguish between genes with consistent positive (red) or negative (blue) values. While it is straightforward to assume that the accumulation of variants on the genes with positive scores might indeed have a direct effect on the development of CD, it is unclear whether genes with strong negative values can be considered protective for CD, since, due to the small sample size, controls may be enriched for variants on NR1I2 and TAGAP by chance. In CAGI3 and CAGI4 datasets, NR1I2 controls do not have a significantly larger amounts of variants with respect to the cases (P-values of 0.42 and 0.49, respectively), while the controls on CAGI3 present more variants than cases on TAGAP (P-value = 0.009), but not on CAGI4 (P-value = 0.59) (see Supplementary Figure S9). We thus cannot clearly identify those two genes as protective because the behavior likely driving our model towards this conclusion is not consistent across our two main datasets.

The activations of each gene, shown as the columns of Figure 4, present different levels of correlation with the actual cases/controls labels (shown as asterisks on the y-axis). Genes with a correlated pattern of activation throughout the entire dataset are correctly steering the final prediction towards the disease/healthy class. In Supplementary Figure S7 we ranked the genes in function of the Pearson correlation of their activations with respect to the class labels, and we shows the 25 most correlated genes. Indeed, FKBP5, HLA-B, HSPA2 and IRGM (whose activations are shown in Figure 4) are also present in such a selection. The correlations are generally low, ranging from 0.3 to 0.11, meaning that there is no a single or few genes able to well discriminate the case/control classes, but many small and noisy contributions need to be properly aggregated by the NN in order to compute the final prediction, as it should be expected from a highly non-Mendelian disease such as CD.

CONCLUSION

In this paper we proposed a genome interpretation framework for the exome-based in-silico diagnosis of oligo-to-polygenic disorders and we applied it to the prediction of CD patients from controls. We addressed the conceptual and technical problems hindering this task by suggesting a feature encoding scheme based on the gene mutational burden reasoning which is suitable for small sample size datasets. We coupled this feature representation with a specifically designed low-complexity Neural Network (NN), called CDkoma, with parameter tying and heavy regularization that can perform inference with reduced risk of over-fitting. We trained and tested our model on the CAGI2, 3 and 4 CD datasets, showing that our NN outperforms many of the methods developed so far for exome-based CD diagnosis.

CDkoma shows good performances while using only a number of trainable parameters that is proportional to the number of samples in the datasets. The NN contains indeed only 11 + N_g trainable weights, where N_g is the number of the CD-related genes selected as input, ensuring that the number of parameters is proportional. we to the number of samples in the datasets even when working with small sample sizes. This, along with a strong regularization, allows the model to perform meaningful inference from limited data in the most robust way even in noisy and data-scarce conditions. In situations involving noisy and small sample size data, we show that a model with reduced complexity can avoid the pitfalls of over-fitting (see comparison with more complex models in Supplementary Table S1) and at the same time can offer nice opportunities for interpretation, by highlighting the most relevant aspects in the model’s decision process.

As a last step in this study, we indeed exploited the simplicity of CDkoma to take a detailed look at the patterns learned by the NN, analyzing the genes to which the NN assigned the highest relevance and attempting an interpretation of the per-sample predictions produced by the model, following its decision process through its layers.

SUPPLEMENTARY DATA

Supplementary Data are available at NARGAB Online.

FUNDING

Fonds Wetenschappelijk Onderzoek (FWO) Post-doctoral Fellowship (to D.R.).

Conflict of interest statement. None declared.