Bayesian correlation is a robust gene similarity measure for single-cell RNA-seq data

Abstract

Assessing similarity is highly important for bioinformatics algorithms to determine correlations between biological information. A common problem is that similarity can appear by chance, particularly for low expressed entities. This is especially relevant in single-cell RNA-seq (scRNA-seq) data because read counts are much lower compared to bulk RNA-seq. Recently, a Bayesian correlation scheme that assigns low similarity to genes that have low confidence expression estimates has been proposed to assess similarity for bulk RNA-seq. Our goal is to extend the properties of the Bayesian correlation in scRNA-seq data by considering three ways to compute similarity. First, we compute the similarity of pairs of genes over all cells. Second, we identify specific cell populations and compute the correlation in those populations. Third, we compute the similarity of pairs of genes over all clusters, by considering the total mRNA expression. We demonstrate that Bayesian correlations are more reproducible than Pearson correlations. Compared to Pearson correlations, Bayesian correlations have a smaller dependence on the number of input cells. We show that the Bayesian correlation algorithm assigns high similarity values to genes with a biological relevance in a specific population. We conclude that Bayesian correlation is a robust similarity measure in scRNA-seq data.

INTRODUCTION

Single-cell RNA-seq (scRNA-seq) is one of the most recent advances in single-cell technologies and it has been widely used to study multiple biological processes (1–9). Standard bulk RNA sequencing retrieves the average of RNA expression from all cells in a specific sample, thus providing an overall picture of the transcriptional activity at a given time point from a mixed population of cells. However, within the study of heterogeneous populations it is not possible to understand the contribution of individual cell types, which is needed to dissect precise mechanisms. scRNA-seq overcomes the limitations of bulk RNA-seq by sequencing mRNA in each cell individually, making it possible to study cells at a genome-wide transcriptional level within heterogeneous samples. However, due to the small amount of mRNA sequenced within a cell, typically 80–85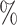 of all genes remain undetected, a phenomenon known as dropout. This results in an incomplete picture of the mRNA expression pattern within a cell.

A similarity measure in mathematics is a function, with real values, that quantifies how similar two objects are. Several techniques use different notions of similarity to visualize data such as PCA or t-SNE. Some techniques use similarity to cluster cells in scRNA-seq, such as Seurat (10), SCENIC (11) or Cell Ranger (12).

The similarity measure is important because it determines the clustering. Kim et al. (13) benchmarked the Pearson distance and Euclidean distance methods to cluster cells and found that correlation metrics perform better than the Euclidean distance metrics. Recently, Skinnider et al. (14) evaluated the multiple existing methods to assess gene-to-gene similarity and cell-to-cell similarity and their performance to cluster cells, reconstruct cell networks or link gene expression to diseases in different conditions. A review of the clustering methods has been done by Qi et al. (15).

Assessing similarity between genes is challenging since measurements of small populations with large uncertainties may lead to false correlations. If a gene’s expression is so low that it only registers zero or a few reads per cell, then its expression pattern across cells cannot be meaningfully related to that of other genes; there is simply too much uncertainty about the real expression levels of that gene. In a typical scRNA-seq dataset, the majority of genes may be in this situation, so that gene–gene correlation analysis is swamped with meaningless or spurious correlations.

In the context of this project, we aim to determine similarity of genes in two distinct conditions. Assessing similarity between genes has previously been used in biology for biomarker discovery in cancer (16,17), to find patterns in gene expression (18) or to build gene expression networks (19,20). There are methods that use the notion of similarity to infer the gene regulatory dynamics. Some examples are SCENIC (11) or NetworkInference (21). These techniques rely on data transformations and corrections of the dropout, but do not incorporate a notion of uncertainties in the measurements.

Noise in gene expression measurements has been modeled and studied to identify differentially expressed genes (22–24). Recently, uncertainties have been incorporated in methods to study differential expression in RNA-seq experiments (25). Noise is especially important in scRNA-seq because of the low number of read counts. Therefore, methods to assess similarity in bulk RNA-seq may not be appropriate for scRNA-seq. Thus, methods need to be modified properly in order to maintain reproducibility. A simple solution is the removal of cells with a low number of read counts and low expressed genes, which is the currently used method of single-cell analysis (26). However, there is not a systematic method to select a threshold and it highly depends on the population being studied.

In order to address limitations dependent on the noise, Bayesian statistics have been used to study biological processes (27,28). Bayesian statistics have been used for high-throughput sequencing (HTS) experiments, Hardcastle and Kelly (29) developed methods to assess differential expression in paired samples and proved that their Bayesian method outperforms generalized linear models. For scRNA-seq data, Sekula et al. (30) proposed a Bayesian scheme to identify differentially expressed genes. Recently, we have proposed a Bayesian correlation scheme to asses similarity between two entities in HTS experiments (31,32). Such Bayesian correlation considers uncertainties in the measurements, and therefore, assign low values to correlations coming from low expressed genes using a prior belief and compute posterior belief based on data observation. In our previous work, we have shown the properties of the different possible priors and we have proved that the Bayesian correlation computation is a kernel. However, there are several considerations that need to be addressed to adapt the method for scRNA-seq data. Thus, we set out to develop new Bayesian methods to create better clustering algorithms than the ones currently available.

One of the main considerations that needs to be addressed to deal with similarity between genes in scRNA-seq comes from the bias in the observations because of false zero counts, which occur in most genes because of the low amount of mRNA sequenced in each cell. Our methodology could be applied directly to the unique molecular identifier (UMI) matrix. However, there are several methods to correct for the dropout by imputing gene expression based on the gene expression of other cells. For example, MAGIC corrects gene expression with the gene expression of other cells modeled as a diffusion map (33). scImpute corrects the dropout using similar cells and genes not affected by dropout (34). SAVER uses a negative binomial to model gene expression in each cell and corrects dropout using the expression of other genes as predictors in a LASSO regression (35,36). All these methods follow the same principle by sacrificing part of the single-cell structure of the data in order to obtain a better resolution of the different populations. It is unclear how these corrections affect the similarity between genes and it needs to be addressed.

An additional consideration that needs to be addressed in scRNA-seq experiments is the number of sequenced cells. Simulation methods for scRNA-seq data are not a mature field and could not reproduce all the biological mechanisms present in an experiment. To study the effect of the number of cells on the reproducibility of the results, we sequenced parenchymal and non-parenchymal cells from a mouse liver. To test the sensitivity of the methods, four samples with an increasing number of input cells were explored (1000, 2000, 5000 and 10 000 cells). To avoid biological noise, samples sequenced were from the same animal. Thereafter, in order to study the effect of biological noise, we compare the hepatocytes from our samples with hepatocytes from the mouse cell atlas (MCA) (37).

In this manuscript, we show that Bayesian correlation is a robust similarity measure for pairs of genes in single-cell RNA-seq. We show that the reproducibility of Bayesian correlation is higher than the reproducibility of Pearson correlation. We show that the results obtained with Bayesian correlation have a small dependence on the number of cells, making the method suitable to study rare populations. Finally, we show that biologically relevant genes tend to appear more often in the top correlated pairs using Bayesian correlations.

MATERIALS AND METHODS

Mathematical formulation of the Bayesian correlation method

After counting the aligned reads to exons and debarcoding the reads from cells, the output of an scRNA-seq experiment is the n × m UMI matrix, R, where n is the number of genes and m is the number of cells. Ideally, we would correlate the true fraction of UMIs, p_ie, of gene i in cell e. A trivial approximation is to normalize the data dividing every UMI by the total number of UMIs in that cell, that is 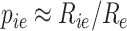. Bayesian schemes try to approximate p_ie using a prior belief and compute posterior belief based on data observation.

Assume we have R_ie UMIs of gene i in cell e and the total UMIs in that cell are R_e. The empirical estimate is 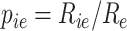. Then, Pearson correlation can be computed as

(1)

while the Bayesian scheme would give us

(2)

where is the prior that is updated with the experimentally observed UMIs leading to the posterior. In that scenario, the covariance and variance are computed as

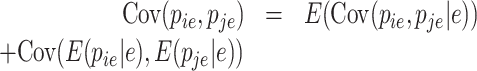(3)

and

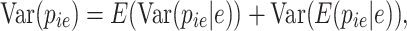(4)

with

(5)

Then, the Bayesian correlation is defined as

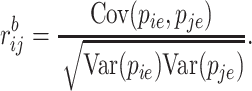(6)

We computed the Pearson coefficients with the R function cor, and the Bayesian correlations were computed with a custom R script. See the ‘Data Availability’ section.

Cell isolation

Hepatocytes were isolated by a two-step collagenase perfusion. Animals were anesthetized (fentanyl 50 μg/kg, midazolam 5 mg/kg, medetomidine 500 μg/kg, i.p.), immobilized in a supine position and the liver and portal vein exposed. The portal vein was cannulated with a 22G catheter and perfusion at 4 ml/min with the buffers allowed to run to waste through an incision in the inferior vena cava. The liver was perfused with 10 ml of HBSS (Mg²⁺, Ca²⁺ free,10 mM HEPES, pH 7) followed by 25 ml of HBSS containing EDTA (10 mM HEPES, pH 7, 5 mM EDTA). The EDTA was removed from the liver by perfusion with 10 ml of HBSS followed by digestion with 25 ml of HBSS containing collagenase [10 mM HEPES, 1 mM CaCl₂, 0.5 mg/ml collagenase IV, 0.01 mg/ml collagenase 1A (Sigma)]. The liver was then removed and the cells released by cutting the capsule and gentle agitation of the digested liver in stop buffer (HBSS, 10 mM HEPES, pH 7, 5 mM EDTA, 10 mM citrate, 1 FBS) and passed through a 70 μm filter. The cell suspension was spun at 30 × g for 5 min to pellet most of the hepatocyte fraction, the supernatant collected and remnant cells pelleted at 250 × g for 5 min. The cell pellet was washed once in stop buffer and resuspended in 20 isotonic Percoll and overlaid on a layer of 80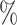 isotonic Percoll and spun at 500 × g for 10 min. The cells at the interface of the two Percoll layers were collected and washed in PBS, resuspended in PBS and counted using a cell counter (BioRad TC 20). This resulted in a cell suspension with a diminished number of hepatocytes but contained enough to allow the sequencing of a representative number of cells.

Library preparation

scRNA-seq libraries were prepared from 1000, 2000, 5000 and 10 000 cells using the Chromium Single Cell 3′ Library & Gel Bead Kit v3 (10x Genomics). Libraries were prepared according to the manufacturer’s protocol.

Sequencing

Sequencing was performed on a NovaSeq 6000 S2 flow cell. Read 1 consisted of 26 cycles (10x Genomics barcode plus UMI) followed by a single Illumina i7 index read of 8 cycles and read 2 of 91 cycles to determine transcript-specific sequence information.

Read alignment

The function cellranger count from Cell Ranger was used to transform the fastq files with the parameter expect-cells set to 1000, 2000, 5000 or 10 000. The reference genome was the mm10 available at Illumina Cell Ranger web page. Next, we used cellranger mat2csv to generate the UMI matrix.

Data preprocessing

First, we created an SCE object with the function SingleCellExperiment from the R package SingleCellExperiment.

The UMI matrix was filtered as follows: first, genes with 0 reads were excluded; second, cells with >15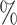 of UMIs in mitochondrial genes were removed (mitochondrial gene list is included in the Supplementary Material). Cells with >25 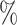UMIs in globin genes were removed. Finally, only genes expressing >1 UMI in at least two cells were considered. Additionally, for the 5000-sample, a cell containing 110 270 UMIs was considered an outlier and it was removed because the second cell with most UMIs had 26 038 UMIs.

MCA data acquisition

We downloaded the Liver1_rm.batch_dge.txt file containing the gene expression from the MCA and the MCA_CellAssignments.csv containing cell information. Batch=Liver_1 was included for analysis. Only genes expressing >1 UMI in at least two cells were considered. Cells with Annotation containing the word hepatocyte were considered hepatocytes. In total, 166 hepatocytes were considered for analysis.

Dimensionality reduction and clustering

In order to cluster the data and find the different cell populations and their markers, we followed the procedure of Seurat 2 (10). The filtered UMI matrix was transformed into a Seurat object with CreateSeuratObject with parameters min.cells = 1 and min.genes = 2. We normalized the data with the R function NormalizeData from Seurat with parameters normalization.method = ‘LogNormalize’ and scale.factor = 10 000. Then, the data were scaled with the Seurat function ScaleData with parameter vars.to.regress = c(‘nUMI’). The different clusters were identified using the Seurat function FindClusters with parameters reduction.type = ‘pca’, dims.use = 1:8, resolution = 1.0, print.output = 0 and save.SNN = TRUE. t-SNE dimensionality reduction was done with the Seurat function RunTSNE with parameters dims.use = 1:8 and do.fast = TRUE. The different markers of each cluster were identified with the function FindAllMarkers with parameters only.pos = TRUE, min.pct = 0.25 and thresh.use = 0.25.

Dropout correction

We corrected the dropout from the UMI matrix with the magic function from the R package Rmagic with the parameters genes set equal to ‘allgenes’ and default parameters. Any resulting negative expression was replaced with 0.

Notions of similarity

In this manuscript, we consider three notions of similarity between genes: (i) All-cell correlation: The correlation of gene i and gene j is the correlation coefficient using all cells. (ii) Cluster correlation: The correlation of gene i and gene j is the correlation coefficient using each cluster as condition, where the gene expression is the sum of the gene expression in all cells. That is, let K be the number of clusters, and let be the UMIs of gene i of cell n in cluster j. We transformed our K matrices in the reduced n × k dimensional matrix (B_ij) as follows:

(7)

where K_j is the number of cells in cluster K. The Bayesian correlation algorithm is applied to the bulk-like RNA-seq matrix (B_ij). (iii) In-cluster correlation: The correlation of gene i and gene j is the correlation coefficient using all cells in a specific cluster.

Evaluation criteria

In order to evaluate the robustness of the method, we compare the results of the method on two datasets, and we look at the intersection of the identified pairs above a certain threshold. Mathematically, let X_A be a UMI matrix, A = {A₁, A₂, …} be the set of the pairs sorted by correlation and A^N ≔ {A₁, …, A_N} be the first N elements of A. We define the agreement between two datasets, X_A and X_B, as , where 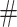denotes the number of elements in a set. If the two datasets are coming from different samples, the agreement is called reproducibility. The intersection is computed with the R function intersect applied to the gene names of the UMI matrices.

RESULTS

Bayesian correlation and Pearson correlation agreement increases with the number of cells

We studied the first notion of similarity: all-cell correlation. To study the effect of the number of cells on the reproducibility of the results, the Bayesian correlation was computed and was compared with the Pearson correlation.

After the data processing, we ended up with four samples of 705, 1213, 2939 and 5520 cells. We refer to these samples as 1000-sample, 2000-sample, 5000-sample and 10k-sample.

Our first step was to compare our Bayesian similarity measure, using as a prior 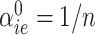and 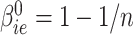with Pearson correlation. In doing so, we split the samples into two groups, randomly assigning half of the cells to group A and the other half to group B. All pairwise correlations were independently computed for each group. In Figure 1A, we observed that the agreement between the two groups is higher using the Bayesian method. As the number of input cells increases, the agreement between the two groups increases. In Figure 1B, scatter plot of Bayesian correlation and Pearson correlation for all pairs of genes is shown. The Bayesian correlation was systematically lower. In Figure 1C, the distributions of gene expression of the top 3000 correlated pairs for Bayesian and Pearson correlations are shown. This result shows that the Bayesian correlation algorithm tends to identify correlations in genes that are highly expressed, compared with the correlations identified by Pearson correlation that identifies correlations in low expressed genes. We observed some low expressed genes among the Bayesian correlations, showing that Bayesian correlation is not equivalent to a higher threshold.

Figure 1.

All-cell correlation. (A) Percentage of pairs of correlated genes found in the two random groups as a function of the number of links sorted by correlation include repetitions (A correlated with B and B correlated with A are both included). (B) Scatter plot of the Pearson correlation (x-axis) and Bayesian correlation (y-axis) for all genes, colored by the logarithm of the density. (C) Histogram of the total expression of the genes found in the top 3000 links.

Bayesian correlation is more robust than Pearson correlation to study similarity within small populations

We have shown a pronounced discrepancy between Pearson and Bayesian correlations when the number of input cells is small. This result motivated us to study correlations within the different populations found in our data. The identification of the different cell populations in our samples can be found in Appendix A.

First, we restricted our analysis to the hepatocyte fraction. There are 33, 58, 111 and 200 hepatocytes in the 1000-sample, 2000-sample, 5000-sample and 10k-sample, respectively. Each dataset was split into two random groups. In Figure 2A (solid line), we observe that the agreement between the two groups using both methods, Pearson and Bayesian, is poor (below 5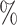). For Pearson correlations, this is due to the fact that the small number of cells results in thousands of Pearson coefficients equal to 1. The Bayesian methods gave us a slight improvement in the reproducibility, but there are not enough data to get a marked improvement from the posterior. However, when the dropout is corrected (dashed lines) the reproducibility increases drastically. As before, we observe that the agreement using Bayesian correlations is higher than that using Pearson correlations. We do not discern change for different levels of MAGIC correction.

Figure 2.

In-cluster correlation: example of hepatocytes. (A) Percentage of pairs of correlated genes found in the two random samples as a function of the number of links sorted by correction for different values of MAGIC correction. (B) Percentage of pairs of correlated genes found in the two random samples as a function of the number of links sorted by correlation. (C) Scatter plot of the Pearson correlation (x-axis) and Bayesian correlation (y-axis) for all genes, colored by the logarithm of the density. (D) Histogram of the total expression of the genes found in the top 3000 links.

Next, we restricted our analysis to the MAGIC corrected data. In Figure 2B, we observed that the reproducibility for correlations within small clusters is much higher with the Bayesian correlation algorithm than with Pearson correlation. This difference was more pronounced for a small sample size, with around 90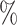 of irreproducible results for Pearson in the 1000-sample and 2000-sample scenarios. The Bayesian correlation was systematically lower compared with the Pearson correlation (Figure 2C). This effect decreased with the increase in the number of input cells. The distribution of the expression of the genes in the top 3000 correlated pairs for Bayesian and Pearson correlations is shown in Figure 2D. The Pearson method identified correlations in low expressed genes that are not considered by the Bayesian method.

In Supplementary Figure S1, we include all the other cell clusters and show that the agreement with Bayesian correlations is higher than the agreement with Pearson correlations in all our populations.

Taken together, our results suggest that Bayesian correlations are more robust than Pearson correlations for small populations by lowering the similarity between pairs of low expressed genes.

Bayesian correlation is more robust than Pearson correlation to study cluster similarity

Single-cell sequencing allows the study of cells individually. However, combined with clustering techniques, it is possible to obtain bulk-like RNA-seq samples from pure populations. In this section, the single cells are grouped to study Bayesian cluster correlation.

To test the reproducibility, the UMI matrix was split into two datasets and then the transformation of Equation (7) was applied.

We showed that the reproducibility of our method is higher when the Bayesian method is applied. The agreement between Pearson correlations and Bayesian correlations increased with the number of cells (Figure 3A). In Figure 3B, scatter plots of the Bayesian correlation (y-axis) versus the Pearson correlation (x-axis) are shown. The Bayesian correlation was systematically lowered. In Figure 3C, the distributions of the gene expression of the genes in the top 3000 correlated pairs for Bayesian and Pearson correlations are shown. As in the previous sections, the genes identified only by Pearson correlations were low expressed.

Figure 3.

Cluster correlation. (A) Percentage of pairs of correlated genes found in the two random samples as a function of the number of links sorted by correlation. (B) Scatter plot of the Pearson correlation (x-axis) and Bayesian correlation (y-axis) for all genes, colored by the logarithm of the density. (C) Histogram of the total expression of the genes found in the top 3000 links.

Taken together, this suggests that Bayesian correlations are more robust than Pearson correlations for pseudo-bulk RNA-seq samples.

Robustness of Bayesian method for a varying number of cells

Thus far, to study the reproducibility of our method, we have compared it with the Pearson correlation by splitting each of our datasets into two groups. To determine the importance of the number of cells in an experiment, we next studied the agreement between our different samples.

In the previous sections, a strong disagreement between Bayesian and Pearson methods was observed in the cluster correlations and in-cluster correlations. For this reason, we restricted our analysis to those two scenarios.

We first restricted our analysis to the cluster identified as the hepatocyte population with the MAGIC corrected data. Figure 4A shows an agreement between the different samples of around 50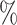 for the top 20 000 links with the Bayesian method. On the contrary, Pearson correlation showed a low agreement between samples, which was close to 0.

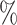Figure 4.

Percentage of correlated pairs found in the different samples using the Bayesian (red line) and the Pearson (blue line) method as a function of the number of links considered sorted by correlation. (A) Correlation in hepatocytes. (B) Correlation in all clusters. (C) Reproducibility between the hepatocytes from our samples and the hepatocytes from the MCA.

Second, we transformed our samples in bulk-like samples by means of Equation (7). In Figure 4B, we observed that the agreement between samples is around 60 with the Bayesian method when 1000 links are considered. For the Pearson correlation, the agreement between the samples is smaller and it reaches 30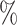 when 10 000 links are considered.

Bayesian correlations are more robust than Pearson correlations to biological noise

So far, we have shown that Bayesian correlations are more resilient to noise than Pearson correlations in our samples. A next step is to study the effect of the biological noise. In doing so, we compare our data with publicly available data from the MCA.

In Supplementary Figure S2A, we show that, after splitting the MCA hepatocytes into two groups, the agreement between the groups is higher with the Bayesian correlation algorithm than with the Pearson correlation. Therefore, the MCA hepatocytes present similar properties to ours.

In Figure 4C, we show the agreement between our hepatocytes and the MCA hepatocytes. In doing so, we compare directly their UMI matrix with ours; differences regarding the sample preparation, their microwell sequencing or small differences due the reference genome are not studied in detail. We observe that using Bayesian correlation, the samples show a higher reproducibility than using Pearson correlations.

Taken together, these results suggest that Bayesian correlations are more resistant to biological noise than Pearson correlations.

Bayesian in-cluster correlation assigns high values to cell population markers

We have shown that Bayesian correlation increases the reproducibility by assigning low correlations to low expressed genes. In this section, we demonstrate that the genes present among the most highly correlated pairs of genes are biologically meaningful.

In order to investigate the biological meaning of the correlated pairs found with our Bayesian method, a set of hepatocyte markers from PanglaoDB (38) was downloaded on 17 April 2019. Figure 5 shows the percentage of genes in the top correlations that are in this public database as a function of the number of links considered for the different clusters with in-cluster correlation. For the four samples, one cluster contained more genes of the database among the top correlated links than the others. In the four cases, that cluster was the one identified as the hepatocyte cluster.

Figure 5.

(A) 1000-sample, (B) 2000-sample, (C) 5000-sample and (D) 10k-sample. Percentage of genes in the top correlated pairs that are in the hepatocyte marker list from PanglaoDB as a function of the number of links considered sorted by Bayesian correlation. The correlation is computed as in a cluster correlation for each cluster independently identified with Seurat.

We have shown that the Bayesian correlation can be used to identify cell populations by looking at the genes present in the top correlated pairs. To investigate further the performance of this identification method, we compared it with two analogous methods. The first method is the same method using Pearson correlation. The second method is to intersect the markers obtained with Seurat with the hepatocyte marker list.

In order to make a fair comparison, when N genes are considered with the latter identification method, we choose the number of links that result in N unique genes. Figure 6A shows that for a small number of genes the Bayesian correlation algorithm selected more hepatocyte markers than Seurat or Pearson correlation. For a larger number of cells (Figure 6B–D), the Bayesian correlation and Seurat showed a similar performance and both are higher than Pearson correlation. When a large number of genes (e.g. 100 genes) are considered, the three methods show a similar performance.

Figure 6.

(A) 1000-sample, (B) 2000-sample, (C) 5000-sample and (D) 10k-sample. Percentage of genes in the top correlated pairs in the hepatocyte marker list from PanglaoDB as a function of the number of genes considered in the top pairs sorted by correlation (red and green) and by P-value in the markers identified by Seurat (blue).

These results suggest that Bayesian correlation assigns higher similarity values to pairs of genes that are biologically relevant.

DISCUSSION

We have presented a similarity measure of genes in scRNA-seq data, which suppresses correlations from low expressed genes, by extending the notion of Bayesian similarity (31) from RNA-seq to scRNA-seq data. Our new Bayesian method allows scientists to study similarity between pairs of genes without discarding low expressed entities and avoiding biases. Thus, this new methodology is more resilient to noise and gives more reproducible results compared to the Pearson method. Moreover, the Bayesian scheme assigns high correlation to biologically relevant genes.

After splitting our samples into two groups, we observed that the Bayesian correlation is more reproducible than the Pearson correlation because it is not biased by low expressed genes. There was a more pronounced effect when the number of input cells was small. This result suggests that the Bayesian method can be useful to study very heterogeneous and rare populations.

We have observed that the dropout correction increases the reproducibility. Restricting the same methodology to our different clusters, after correcting the dropout we observed that the agreement of the Bayesian correlations was higher than Pearson correlation. As before, we have seen that this difference in the methods decreases as the number of input cells increases.

Since the all-cell correlation is biased by the number of cells in a cluster, we decided to study the cluster correlation by summing the gene expression of all cells for each gene. Clusters with low cell numbers have low total reads and therefore are less resilient to noise. Note that the Bayesian correlation accounts for the total number of reads when computing the correlation. Applying the same methodology to the clusters, we observed that Bayesian correlations were more reproducible and are not biased by low expressed genes compared to Pearson correlations.

After studying the three notions of correlation in our different samples, we have compared the results of the different samples, by comparing 1000 to 2000, 2000 to 5000 and 5000 to 10k. We studied the correlation in hepatocytes and found that the agreement between samples was around 50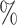 for the Bayesian method and close to 0 for the Pearson correlations. Then, we studied the cluster correlation and showed that the samples agree more with the Bayesian correlation than with the Pearson correlation.

Low expressed genes were detected in the top correlated genes using Bayesian correlations; therefore, the method is not equivalent to a threshold.

In order to understand the biological noise, we have downloaded hepatocyte data from the MCA. Comparing their data with ours, we have observed that the reproducibility is higher when Bayesian correlations are considered.

In all the considered scenarios, we have observed that the agreement between the groups and samples was larger when using Bayesian correlations. Moreover, we observed that this effect appears by systematically lowering the correlations coming from low expressed genes. Therefore, we conclude that Bayesian correlations are more robust than Pearson correlations.

To study the biological relevance of the correlated pairs identified by Bayesian correlation, we compared them with genes specific for hepatocytes from PanglaoDB. We have shown that the genes among the top correlated pairs tend to include more markers than Pearson correlation. Interestingly, when the number of cells is small, the performance of the method to identify markers is higher than the performance of Seurat (10). There are two things that explain this fact. First, Bayesian correlation assigns higher values to high expressed genes; since markers are highly expressed, they appear more. Second, genes with a specific functionality tend to be correlated with other genes important for that function since the pathways that activate them act on the entire population. Moreover, there are different types of hepatocytes (e.g. periportal and pericentral) and in those the expression of the markers is correlated.

The ability of the method to identify markers and the increased reproducibility between the different experiments suggested that the method could be adapted for cell type identification. The optimal way to modify the Bayesian correlation algorithm for cell population identification, as well as a performance comparison with other identification methods such as SingleR (39), is left for future work.

We will further extend the Bayesian notion of similarity to mass cytometry (40) and CITE-seq (41). By combining transcriptomic and proteomic analytical tools, we will build clustering methods to merge and validate results from single-cell omic datasets. Development of a pipeline that integrates transcriptomic and proteomic data will clearly allow synergistic effects that cannot be identified by studying data independently.

Although our work mainly addresses bioinformatics questions, the dataset we have generated can be very useful for experiment design for liver researchers. First, we provide a dataset of healthy mouse liver sequenced with high coverage. Second, our results show which cell populations can be identified within an scRNA-seq experiment and how many input cells need to be used.

CONCLUSION

Taken together, our results show that results from Bayesian correlations are more reproducible than results from Pearson correlations and have a higher biological relevance for analysis of scRNA-seq. Moreover, the number of sequenced cells has a small influence in Bayesian correlation results compared with Pearson correlation. Therefore, Bayesian correlation is a more robust measure of similarity for pairs of genes in scRNA-seq.

DATA AVAILABILITY

All data are available on Genome Expression Omnibus repository with the GEO accession number GSE134134. The R function BaCo to compute the Bayesian correlation is available at https://github.com/dsancheztaltavull/Bayesian-Correlations/.

APPENDIX A: CELL TYPE IDENTIFICATION

During the preparation of this bioinformatics manuscript, we created a dataset that can be useful for liver researchers. Our main goal is far from unraveling liver dynamics; however, we consider helpful for liver researchers to have an analysis of the biological samples. In this appendix, we describe the populations identified by Seurat clustering as well as the markers, and their statistical significance, we use to classify them.

scRNA-seq samples allow the identification of multiple parenchymal and non-parenchymal cell populations

We have identified 10, 10, 14 and 18 different cell populations in our 1000-sample, 2000-sample, 5000-sample and 10k-sample, respectively. The multiple populations are shown in Figure A1.

Figure A1.

t-SNE visualization of our data; cells are colored by the cluster they belong to. (A) 1000-sample; (B) 2000-sample; (C) 5000-sample; (D) 10k-sample.

Cell types identified and markers

1000-sample

Unsupervised clustering of the 1000-cell sample identified 10 transcriptionally distinct populations. The different cell populations were identified using previously published markers from the literature.

• Cluster 0: Endothelial cells

  Markers: Pecam1, Ushbp1, Oit3, F8, Bmp2, C1qtnf1, Mmrn2, Pcdh12, Dpp4, Tek, S100a1, Tie1, Egfl7, Scarf1, Stab2, Lyve1, Icam2, Sox18, Flt4 and Nr2f2 (42–54).

• Cluster 1: Macrophages

  Markers: Adgre1, Csf1r, Cd163, Cd68, Marco, Vsig4, Irf7 and Clec4f (43,55–59).

• Cluster 2: Stellate cells

  Markers: Reln, Sparc, Col1a2, Rbp1, Des, Bmp5 and Lrat (48,59–65).

• Cluster 3: Cholangiocytes

  Markers: Krt7 , Krt19, Epcam, Sox9 and St14 (59,66).

• Cluster 4: NK/T cells

  T-cell markers: Cd3g, Cd247, Gata3, CD28, Lat, Cst7, Cd3e and Cd4. NK cell markers: Nkg7, XcL1, CCl5, Cd7 and Gzmb (59,67,68).

• Cluster 5: Endothelial cells

  Markers: Egfl7. Bmp2 and Clec4g (43,47,69).

• Cluster 6: Dendritic cells

  Markers: Itgax Xcr1, Flt3, Cd24a, Ccr2 and Clec9a (56,67,70–72).

• Cluster 7: Endothelial cells

  Markers: Pecam1, Ushbp1, Mmrn2, Tek, Flt4 and Nr2f2 (43–46,48,53,54).

• Cluster 8: Hepatocytes

  Markers: Alb, Ass1, Cyp2f2, Asgr1, Apoa1, Mup3, Pck1 and G6pc (43,59).

• Cluster 9: Immune cells of lymphoid branch

  Markers: Siglech, Ly6d and Runx2 (73–76).

2000-sample

Unsupervised clustering of the 2000-cell sample identified 10 transcriptionally distinct populations. The different cell populations were identified using previously published markers from the literature.

• Cluster 0: Endothelial cells

  Markers: Pecam1, Ushbp1, Oit3, F8, Bmp2, Mmrn2, Pcdh12, Dpp4, Tek, S100a1, Scarf1, Stab2, Lyve1, Icam2, Sox18, Egfl7, Flt4, Nr2f2 and Tie1 (42–54).

• Cluster 1: Macrophages

  Markers: Adgre1, Csf1r, Cd163, Vsig4, Marco, Cd68, Cd5l, Irf7 and Clec4f (43,55–59).

• Cluster 2: Endothelial cells

  Markers: Clec4g, Egfl7, Bmp2, Oit3 and Mmrn2 (43,47,69).

• Cluster 3: NK/T cells

  T-cell markers: Cd3g, Cd247, CD28, Lat, Cst7 and Cd3e. NK cell markers: Nkg7, Xcl1, CCl5, Cd7 and Gzmb (59,67,68).

• Cluster 4: Stellate cells

  Markers: Hhip, Reln, Sparc, Col1a2, Rbp1, Des and Lrat (48,59–64,77).

• Cluster 5: Cholangiocytes

  Markers: Krt7, Krt19, Sox9, Epcam and Muc1 (59,66,78).

• Cluster 6: Dendritic cells

  Markers: Xcr1, Flt3, Cd24a, Ccr2, Clec9a and Itgax (56,67,70–72).

• Cluster 7: Hepatocytes

  Markers: Alb, Hnf4a, Ass1, Cyp2f2, Cyp2e1, Asgr1, Apoa1, Mup3, Pck1 and G6pc (43,59).

• Cluster 8: Endothelial cells

  Markers: Pcdh12, Sox18 and Nr2f2 (43,52,54).

• Cluster 9: Immune cells of the lymphoid branch

  Markers: Ly6d, Sell, Cd19, Ms4a1, Ltb and Cd37 (59,67,76,79).

5000-sample

Unsupervised clustering of the 5000-cell sample identified 14 transcriptionally distinct populations. The different cell populations were identified using previously published markers from the literature.

• Cluster 0: Endothelial cells

  Markers: Pecam1, Ushbp1, Oit3, F8, Bmp2, Pcdh12, Dpp4, Tek, S100a1, Scarf1, Stab2, Lyve1, Icam2, Sox18, Egfl7, Flt4, Nr2f2 and Tie1 (42–54).

• Cluster 1: Endothelial cells

  Markers: Pecam1, Ushbp1, Oit3, F8, Bmp2, Mmrn2, Pcdh12, Dpp4, Tek, S100a1, Stab2, Lyve1, Icam2, Sox18, Egfl7, Flt4, Nr2f2 and Tie1 (42–54).

• Cluster 2: Macrophages

  Markers: Adgre1, Csf1r, Cd163, Vsig4, Marco, Cd68, Cd5l, Irf7 and Clec4f (43,55–59).

• Cluster 3: Endothelial cells

  Markers: Pecam1, Oit3, F8, Bmp2, Mmrn2, S100a1, Icam2, Egfl7 and Clec4g (42–45,47,48,50–54,69).

• Cluster 4: T and NK cells

  T-cell markers: Cd3g, Cd247, Trac, CD28, Lat, Cst7 and Cd3e. NK cell markers: Nkg7, Xcl1, CCl5, Cd7 and Gzmb (59,67,68).

• Cluster 5: Macrophages

  Markers: Clec4f, Csf1r, Cd163, Vsig4, Marco, Cd68 and Cd5l (43,56–59).

• Cluster 6: Stellate cells

  Markers: Hhip, Reln, Sparc, Col1a2, Rbp1, Des and Lrat (48,59–63,65,77).

• Cluster 7: Cholangiocytes

  Markers: Krt7, Krt19, Sox9, Epcam, Muc1 and St14 (59,66,78).

• Cluster 8: Dendritic cells

  Markers: Xcr1, Flt3, Cd24a, Ccr2 and Clec9a (56,67,71,72).

• Cluster 9: Hepatocytes

  Markers: Alb, Ass1, Cyp2f2, Cyp2e1, Asgr1, Apoa1, Mup3, Pck1 and G6pc (43,59).

• Cluster 10: Endothelial cells

  Markers: Pecam1, Oit3, F8, Bmp2, Mmrn2, Dpp4, Tek, S100a1, Stab2, Sox18, Egfl7, Flt4, Nr2f2 and Tie1 (42–48,50,52–54).

• Cluster 11: B cells

  Markers: Cd19, Ms4a1, Ltb, Cd37, Cd22, Cd79a, Cd79b and Cd69 (59,67,79,80).

• Cluster 12: Immune cells of the lymphoid branch

  Markers: Siglech, Ly6d, Runx2 and Klra17 (73–76).

• Cluster 13: Unknown

10k-sample

Unsupervised clustering of the 10k-cell sample identified 17 transcriptionally distinct populations. The different cell populations were identified using previously published markers from the literature.

• Cluster 0: Endothelial cells

  Markers: Clec4g, Pecam1 and Tek (42,44,69).

• Cluster 1: Endothelial cells

  Markers: Clec4g, Pecam1, Dpp4 and Lyve1 (42,43,49,69).

• Cluster 2: Macrophages

  Markers: Csf1r, Adgre1, Cd163, Vsig4, Marco, Cd68, Cd5l, Irf7 and Clec4f (55–59).

• Cluster 3: Macrophages

  Markers: Adgre1, Csf1r, Cd163, Vsig4, Marco, Cd68, Cd5l, Irf7 and Clec4f (55–59).

• Cluster 4: Endothelial cells

  Markers: Oit3, Bmp2, Mmrn2, Icam2, Sox18, Flt4, Clec4g and Egfl7 (43,45–48,50–54,69).

• Cluster 5: NK cells/T cells

  T-cell markers: Trac, Cd3g and Cd2. NK cell markers: Nkg7, Xcl1 and CCl5 (59,67,68).

• Cluster 6: Endothelial cells

  Markers: Pecam1, Ushbp1, Bmp2, Stab2, Egfl7 and Clec4g (42,43,45–48,50–54,69).

• Cluster 7: Stellate cells

  Markers: Hhip, Reln, Sparc, Rbp1, Des, BMp5, Pdgfrb, Lrat and Hand2 (48,59–65,77,81–83).

• Cluster 8: Cholangiocytes

  Markers: Krt7, Krt19, Sox9, Epcam, Muc1 and St14 (59,66,78).

• Cluster 9: Hepatocytes

  Markers: Alb, Apoa1, Mup3, Ass1, Cyp2f2, Cyp2e1, Asgr1, Pck1 and G6pc (43,59).

• Cluster 10: Dendritic cells

  Markers: Xcr1, Ccr2, Itgax, Flt3, Cd24a and Ccr2 (56,67,70–72).

• Cluster 11: Immune cells: B cells

  Markers: Cd19, Ms4a1 and Ltb (59,67,79).

• Cluster 12: Stellate cells

  Markers: Hand2, Hhip, Sparc1, Des, Reln and Rbp1 (48,59–63,77).

• Cluster 13: Unknown

• Cluster 14: Immune cells from the lymphoid branch

  Markers: Siglech, Runx2 and Klra17 (73–76).

• Cluster 15: Stellate cells

  Markers: Pdgfrb, Lrat, Hand2, Hhip, Reln, Sparc, Des and Rbp1 (48,59–63,77,81).

• Cluster 16: Unknown

• Cluster 17: Endothelial cells

  Markers: Ptprb and Pecam1 (42,84).

SUPPLEMENTARY DATA

Supplementary Data are available at NARGAB Online.

FUNDING

Swiss National Science Foundation [166594, 173157]; University of Bern Initiator Grant [39027].

Conflict of interest statement. None declared.