A random forest-based framework for genotyping and accuracy assessment of copy number variations

Abstract

Detection of copy number variations (CNVs) is essential for uncovering genetic factors underlying human diseases. However, CNV detection by current methods is prone to error, and precisely identifying CNVs from paired-end whole genome sequencing (WGS) data is still challenging. Here, we present a framework, CNV-JACG, for Judging the Accuracy of CNVs and Genotyping using paired-end WGS data. CNV-JACG is based on a random forest model trained on 21 distinctive features characterizing the CNV region and its breakpoints. Using the data from the 1000 Genomes Project, Genome in a Bottle Consortium, the Human Genome Structural Variation Consortium and in-house technical replicates, we show that CNV-JACG has superior sensitivity over the latest genotyping method, SV², particularly for the small CNVs (≤1 kb). We also demonstrate that CNV-JACG outperforms SV² in terms of Mendelian inconsistency in trios and concordance between technical replicates. Our study suggests that CNV-JACG would be a useful tool in assessing the accuracy of CNVs to meet the ever-growing needs for uncovering the missing heritability linked to CNVs.

INTRODUCTION

Copy number variations (CNVs) are imbalanced structural variants characterized by alterations in the number of copies of DNA segments >50 bp (1). CNVs can alter gene dosage, disrupt coding sequences and affect gene regulation. They are also known to underlie Mendelian diseases and, without a doubt, represent an essential portion of missing heritability in human complex diseases, such as neurodevelopmental disorders and congenital anomalies (2–7). It is therefore crucial to uncover the disease-associated CNVs and affected genes; however, CNV detection by current methods is prone to error and evaluating the accuracy of CNV calls remains challenging.

Whole genome sequencing (WGS) is by far the most effective technology for detecting the full spectrum of CNVs with single-nucleotide resolution at the breakpoints, especially those mostly uncharacterized CNVs in non-coding regions (8–10). For paired-end short read WGS data, read-depth (RD), read pairs (RP), split reads (SR) and assembly (AS) are the commonly used CNV detection approaches, yet each of these approaches has its caveats and limitations in detecting CNVs of different sizes and types (11,12). RD approach searches for regions with abnormal read depth by assuming that the sequencing reads are uniformly distributed across the normal diploid genome, yet such assumption is not necessarily valid in practice. Genomic regions that are repeat-rich or with GC-bias tend to be highly variable in read depth (12–16). Consequently, the RD approach lacks specificity in detecting CNVs in these problematic regions (11). RP approach identifies CNVs based on RP with mapped insert size significantly different from expected, thereby making it insensitive to small deletions due to the difficulty in detecting small differences in insert size from normal background variability (17). SR approach uses soft-clip reads spanning the breakpoints to detect CNVs. It has the potential for precisely identifying the breakpoints but is insensitive to large CNVs (11,12). Moreover, both RP and SR approaches show obvious disadvantages in detecting non-allelic homologous recombination-induced CNVs as the abnormal read-pairs and soft-clip reads can merely be found due to the identical ‘low copy repeats’-induced junction reads (18,19). Based on the above detection approaches, many CNV calling tools are now available but the results vary significantly even among tools using the same underlying approach. No single tool can detect all sizes or types of CNVs with high sensitivity and precision (10–11,20).

One straightforward strategy to improve precision is to filter out all CNVs located in the repeat-rich or segmental duplication regions because these CNVs tend to be false positive calls. Though simple, this strategy may lead to the loss of clinically relevant CNVs as these problematic regions comprise ∼55% of the human genome and some disease-associated CNVs indeed fall on these regions (21–26). Another commonly used strategy is to integrate CNVs detected by multiple tools and select highly confident and credible ones consistently called by several tools. This strategy can improve precision, at the cost of a higher false negative rate, since the overlap between CNVs called by different tools is low (20,27–30). Recently developed tools such as SVmine and FusorSV, using data mining approach to combine CNVs detected by various tools in a more optimized way, were reported to offer superior sensitivity, specificity and breakpoint accuracy over the individual tools (31,32). More robust ways to assess the accuracy of CNVs are experimental methods, such as quantitative and long polymerase chain reaction (PCR), or manual curation using Integrative Genomics Viewer (IGV) plot (33); however, both assessment measures are labor and cost-intensive, especially when a huge number of CNVs are to be assessed. A recently published CNV genotyping tool named SV² attempts to evaluate the CNV accuracy in silico by considering four features informative for the presence of CNVs: depth of coverage, discordant paired-ends, split-reads and heterozygous allele ratio (34). In fact, through our experience of manual curation and PCR validation of CNVs from short read WGS data (35,36), we noticed that other sequence features in addition to those already included in the individual RD/RP/SR detection tools, particularly those around the potential breakpoints, can effectively distinguish true CNVs from the noise. Here, we present an CNV genotyping framework, named CNV-JACG, which takes into account 21 features for each putative CNV and uses supervised random forest (RF) to perform accuracy assessment and genotyping.

MATERIALS AND METHODS

The framework of CNV-JACG

CNV-JACG starts with extraction of 21 features (see the section of ‘Feature extraction’ below) for each of the user-input CNVs. After feature extraction, it applies the RF classifier, i.e. a pre-determined threshold for each of the 21 features, trained on the true and false deletions and duplications respectively in training dataset to predict whether a putative CNV is likely to be a true CNV.

Input of CNV-JACG

CNV-JACG requires two types of input: the genomic coordinates of CNVs and BAM file(s) of the same or target sample(s). The coordinate file is a BED file containing chromosome, start position (1-based), end position and type (‘DEL’ or ‘DUP’) of the CNV(s) of interest. The BAM file is the compressed binary version of a Sequence Alignment/Map (SAM) file storing biological sequences aligned to a reference genome (37). We recommend a basic quality control on the fastq file (e.g. by FastQC) before sequence alignment. The BAM file should contain the ‘SA’ tag, which could be generated by BWA ‘mem’ (38). For multiple BAM files input, the target BAM files can be inputted as a list separated by comma for the –bam parameter.

Selection of fixed genomic regions for scaling read depth-related features

In order to accommodate WGS data of various coverage, normalization is needed for features related to read depth, i.e. number of reads. To normalize efficiently, we searched for invariant genomic regions that are depleted of CNVs and meanwhile closely resemble the mean diploid coverage of all chromosomes. We first divided the whole human reference genome (hg19) into non-overlapping windows with size of 1Mb. We then used 100 in-house WGS data of healthy controls (paired-end 150 bp, ∼40×) to calculate the mean and standard deviation (SD) of the sequencing depth for each window. For each autosome, we chose one window (i) with a mean depth resembling the average (∼40×), (ii) having the lowest SD and (iii) not overlapping any CNV reported in Database of Genomic Variants (DGV) and GnomAD-SV (>50% reciprocal overlap) (39,40), which resulted in a selection of 22 fixed regions (Supplementary Table S1). For each input BAM file, CNV-JACG calculates the mean depth across these 22 selected regions and uses the computed mean depth as the denominator to scale the depth-related features (see below). This scaling process would allow CNV-JACG to be robust for both high and low coverage WGS data.

Feature extraction

A total of 21 distinctive features are computed from the BAM file for the CNVs specified in the user input BED file, including 13 characterizing the breakpoints of CNVs, 6 featuring the region overlapped and 2 related to called variants within the CNV (Table 1):

Table 1.

Twenty-one features selected for RF classification of CNVs

1. Features around the breakpoints

   Features around the left and right breakpoints (150 bp up- and downstream) are considered separately as the feature signals for both breakpoints are not always identical.

   1. Repeats at the breakpoints (n = 2): ‘Left.Repeat’ and ‘Right.Repeat’— correspond to whether the left/right breakpoint located within a repeat region (simple repeat, repeat masker or segmental duplication; binary value: yes = 1; no = 0).

   2. Orientation of RP at the breakpoints (n = 4): two features — ‘Left.RL’ and ‘Right.RL’ — denote the scaled number of RP at the left/right breakpoint supporting right-left (RL) RP orientation while normal Illumina RP orientation is left-right, which indicates the occurrence of tandem direct duplication or translocation on the same chromosome (33,41–43). Similarly, two features — ‘Left.LL.RR’ and ‘Right.LL.RR’ — represent the scaled number of RP mapped at the left/right breakpoint, supporting left-left (LL) or right-right (RR) RP orientation, which indicates the occurrence of tandem/inserted inverted duplication or inversion (33,41–43).

   3. Support of soft clip reads (SCRs) (n = 7): three features — ‘Left.SCR’, ‘Right.SCR’ and ‘Left.Right.SCR’ — record the scaled number of SCRs, excluding the secondary and PCR-induced duplication reads, with sequence at the left/right/both breakpoint(s) supporting the CNV respectively. Two features — ‘Left.SCR.cluster’ and ‘Right.SCR.cluster’ — denote if there exists a cluster of at least two SCRs on the left breakpoint that can be aligned to the right breakpoint or to a third position (for inserted duplication) (value: yes = 1, no = 0) and likewise for the right breakpoint. Two other features — ‘DI’ and ‘IN’— represent the scaled number of SCRs with the direct/inversed mapping orientation for clipped sequence and the non-clipped sequence at both breakpoints.

2. Features for the region encompassed by the CNV

   1. Mean depth of coverage: ‘Mean.depth’ —represents the scaled mean read depth of the CNV.

   2. Length: ‘Length’ of the CNV (value > 50).

   3. Microhomology: One feature— ‘Microhomo’ —represents the scaled number of reads with the same micro-homologous sequences around the breakpoints (19). The discrepancy between the complementary alignment cigar of the original and supplementary aligned SCRs, e.g. CIGAR strings of 90M60S for the original alignment and 88S62M for the supplementary alignment may indicate that this is a read supporting a 2-bp micro-homologous sequence.

   4. GC content: GC content (‘GC’) within the CNV region (value: 0–100).

   5. Repeat Percentage: ‘Repeat.Pct’—denotes the proportion of a given CNV region that overlap with RepeatMakser or/and segmental duplications (44,45).

   6. Number of common SNP: ‘Common_SNP’—denotes the number of common single nucleotide polymorphisms (SNPs) with MAF > 0.1 in the 1000 Genomes Project (1KGP) Phase 3 data that are located within the CNV region (if any) (46).

3. The called variants within the CNV

Two features related to the variants called within the CNV region, including the number of heterozygous SNPs (‘Het_SNP’ among the common SNPs mentioned in (ii) f)), and the probability of heterozygosity of this CNV region (‘Het_Prob’; calculated by Bayesian model P(Observed Genotype| MAF in 1KGP)). For each 1KGP common SNP position within the CNV region, we extracted the covered reads from the bam file and defined the genotype as heterozygous if it has >3 reference allele support reads, >3 alternative allele support reads and the proportion of alternative allele support reads > 0.2; meanwhile the probability of heterozygosity was calculated by a Bayesian model mentioned above. The mean of the probability of heterozygosity of all 1KGP common SNP positions was taken as the ‘Het_Prob’ of the CNV region.

Rationale for defining true and false training CNVs using trios

Among all public WGS data, the individual—NA12878—from 1KGP has been most extensively studied and has several versions of benchmark CNVs available. Nevertheless, machine learning on a limited number of CNVs, particularly for duplications, of one individual cannot learn as broad the representation of each feature as possible and poor generalization to new data (47,48). We reasoned that high quality training data with a good diversity-to-noise ratio can be obtained from parent-offspring trios by considering the consistency between calling tools and Mendelian inheritance, which can be used to complement the more accurate but less diverse small dataset. To illustrate this, sequencing data of the NA12878 trio (including the parents: NA12891 and NA12892) and the benchmark CNVs of NA12878 was used. Consistently across three versions of benchmark CNVs of NA12878 as well as the CNVs of NA12878 recorded in DGV, we observed that the CNVs set obtained under both the two criteria: (i) inherited from either one of the parents and (ii) detected by at least three tools achieved the highest F1-score (Supplementary Figure S1). Whereas the CNVs meet all these three criteria of (i) not inherited, (ii) detected by only one tool and (iii) not recorded in DGV database characterized mostly false CNV calls. These criteria were thus used to define the true and false CNVs in the training data.

Training data construction and random forest model training

We applied the above criteria to our nine in-house trios to generate training CNVs and built two classifiers, one for deletions and another for duplications (35). We extracted the aforementioned 21 features for each of these training CNVs and evaluated the feature distribution among different groups (Supplementary Figures S2 and 3). We then used this dataset to train the RF model. We applied the R package ‘randomForest’ in the training process (49). After parameter tuning, we used the optimal parameter ‘ntree = 200, mtry = 10’ for deletion classifier and ‘ntree = 450, mtry = 10’ for duplication classifier of which the out of bag (OOB) error rate was the lowest after our iteration trial. The importance of the 21 features was assessed using the standard output of RF as well as Boruta algorithm, which recruits three random features as comparison, thereby the importance of each feature could be more clearly decided (50). We also evaluated the relationship between OOB error rate and the size of training dataset by down-sampling the training deletions to subsets with 11 different size (five replicates for each size).

Sequencing data

Six paired-end WGS datasets were used in this study for training and performance evaluation. We used nine parents-offspring trios (healthy parents + one child with Hirschsprung disease (HSCR), East and Southeast Asian ancestry) previously published (35), totaling 27 samples sequenced by Illumina HiSeqX Ten (2 × 150 bp, ∼35×), as the training data. Evaluation of the performance of CNV-JACG was performed on HuRef/Venter genome (NS12911), three trios from the Human Genome Structural Variation Consortium (HGSV), two trios from 1KGP, one trio from Genome in a Bottle (GIAB) consortium (read length truncated from 2 × 250 bp to 2 × 150 bp) and on 11 pairs of technical replicates (11 DNA samples being sequenced twice, totaling 22 WGS data; 2 × 150 bp, ∼30×) (36). More detail information of the publically obtained sequencing data were list in Supplementary Table S2. The details of sample preparation and sequencing pipeline for the 11 pairs of replicates were described in our previous studies (35,36).

CNV calling

We used four complementary tools: CNVnator (based on RD) (51), Delly (based on SR and RP) (52), Lumpy (based on SR, RP and RD) (53) and Seeksv (based on SR, RP and RD) (54) to call CNVs. These tools were selected as a result of our survey on the currently available CNV detection tools in terms of their underlying detection method, popularity, running time, resources consumption, persistence in software update, ease-of-use, and most importantly, their complementarity and accuracy (10–12,20,55). The parameter for ‘bin-size’ in CNVnator was set as 50 bp and the parameters in the other three tools were set as default. As Seeksv incorporates duplications into insertions, we extracted insertions with depth higher than 100× as the putative duplications detected by Seeksv. The putative CNVs <50 bp or not on ‘regular’ chromosomes were removed. Then, for each individual, we generated a file combining CNVs detected by any of these four tools termed ‘pre-detection’ in this study. CNVs detected by multiple tools and with >50% reciprocal overlap were merged using BEDtools (56), and the breakpoint retained with the priority of Lumpy, Delly, Seeksv and lastly CNVnator. This program for merging CNVs from different tools is also included in CNV-JACG framework.

It is noteworthy that the tools used to produce the input CNV pre-detection set are not limited to the four tools mentioned above. To demonstrate this, we applied two more tools: GRIDSS (based on SR, RP and AS) (57) and SvABA (based on SR, RP and AS) (58) with default parameters to the six trios listed in Supplementary Table S2.

Performance evaluation of CNV-JACG and comparison with SV²

We compared the performance of CNV-JACG with that of SV² (34) using the same dataset. SV² assesses the accuracy of CNVs using support vector machine (SVM) model trained on both high and low coverage WGS data, including NA12878 and other 1KGP samples. The default parameter was used when running SV² and the CNVs passing all the filters with the ‘PASS’ mark were extracted for comparison. All the input BAM file used for evaluation were generated by Illumina short read technology as mentioned above. Two CNVs with >50% reciprocal overlap were considered as the same CNVs. All the P-values were calculated by two-sided t-test.

Comparing the sensitivity using benchmark CNVs in 1KGP and GIAB

For NA12878 from 1KGP, we used deletions present in all the following three versions as the final benchmark deletions: the deletions produced by the tools of (i) SVclassify, (ii) MetaSV and (iii) those generated based on long-reads sequencing platform of PacBio (27,59–60) (see ‘DATA AVAILABILITY AND MATERIALS’).

For the Ashkenazim trio HG002-HG003-HG004 from GIAB, we downloaded the consortium defined ‘high confident and sequence resolved’ tier 1 SV result (61) (see ‘DATA AVAILABILITY AND MATERIALS’) and extracted the deletions satisfying all of the following criteria as the benchmark: (i) ‘PASS’, (ii) Illexactcalls ≥3, i.e. called by at least three tools based on Illumina short read sequencing data, (iii) NumTechsExac ≥ 2, i.e. discovered by at least two technologies, (iv) ‘MendelianError = FALSE’ and (v) the genotypes for both parents are not missing. The benchmark deletions of NS12911 were also downloaded from GIAB (see ‘DATA AVAILABILITY AND MATERIALS’).

We did not consider duplications in this evaluation because duplications were not included as part of the benchmark sets. We used CNV-JACG and SV² to assess the accuracy of the above benchmark deletions and calculated the sensitivity by the number of deletions predicted to be true positive, against the number of true/reference deletions.

Comparing the false positive rate using NA12878 and Ashkenazim trio

To compare the false positive rate of CNV-JACG and SV², we first defined the negative deletions as those detected by only one tool (out of the four tools: CNVnator, Delly, Lumpy and Seeksv) and not present in the benchmark deletion sets (>50% reciprocal overlap). In order to acquire highly confident negative deletions, for NA12878, we used the union set of the three benchmark versions mentioned above as the benchmark deletion set. For the Ashkenazim trio (HG002, HG003 and HG004), the unfiltered ‘high confident and sequence resolved’ tier 1 deletions defined by GIAB were used as the benchmark deletion set. Next, we assessed the accuracy of these negative deletions by CNV-JACG and SV² and calculated the false positive rate by the proportion of negative deletions that was predicted to be true.

Comparing Mendelian inconsistent rate using six trios

We applied CNV-JACG and SV² to the pre-detected CNVs of six trios (Trio 1–6, Supplementary Table S2). We then calculated the Mendelian inconsistent rate (MIR) of CNVs (the number of non-inherited CNVs present only in the offspring divided by the total number of CNVs in the offspring) per offspring. With a sensitive pre-detection CNV set, violation of Mendelian inheritance most likely reflects false positives in the offspring, together with smaller number of false negatives in the parents as well as rare occurrence of true de novo CNVs as a result of germline or postzygotic mutation. Thus, we considered MIR as an alternative indicator of the level of overall false positive rate (62).

Comparing concordance rate using 11 pairs of technical replicates

To evaluate the robustness of our method, we also applied CNV-JACG and SV² to the pre-detected CNVs of 11 pairs of technical replicates to evaluate their performances. We generated these technical replicates through sequencing the DNA samples of 11 individuals twice using the same machine, under the same library preparation and sequencing protocols. In theory, we expected to detect nearly identical CNVs in each pair of replicates; however, false CNVs induced by sequencing artifacts, false positive/negative CNVs detected by CNV calling tools, and other unpredictable factors can lead to genotype discordance between the replicates (63). We defined the concordance rate by the number of CNVs present in both replicates over the number of CNVs detected in each individual and thereby resulting in two concordance rates for each pair of replicates. Here, we considered the CNVs concordance rate as an alternative indicator for the performance of different methods, for which, the higher the better.

RESULTS

Overview of CNV-JACG

CNV-JACG is an open-source framework based on RF for Judging the Accuracy of CNVs and Genotyping CNVs (https://github.com/sunnyzxh/CNV-JACG). Our framework considered a comprehensive set of 21 features in training and in assessing CNVs accuracy. All the 21 features are selected for their superior abilities in differentiating true and false CNVs (Supplementary Figures S2–4) based on our prior experience of experimental validation and manual curation (35–36,64), which include (i) 13 features characterizing the breakpoints of CNVs, (ii) six features of the region overlapped and (iii) two related to called variants within the CNV (Table 1, Figure 1 and ‘MATERIALS AND METHODS’ section). CNV-JACG can execute in two modes: (i) the individual-based accuracy-judgement mode that predicts true from putative CNVs of a given sample and (ii) the population-based genotyping mode that predicts the presence/absence of CNVs of interest for all target samples.

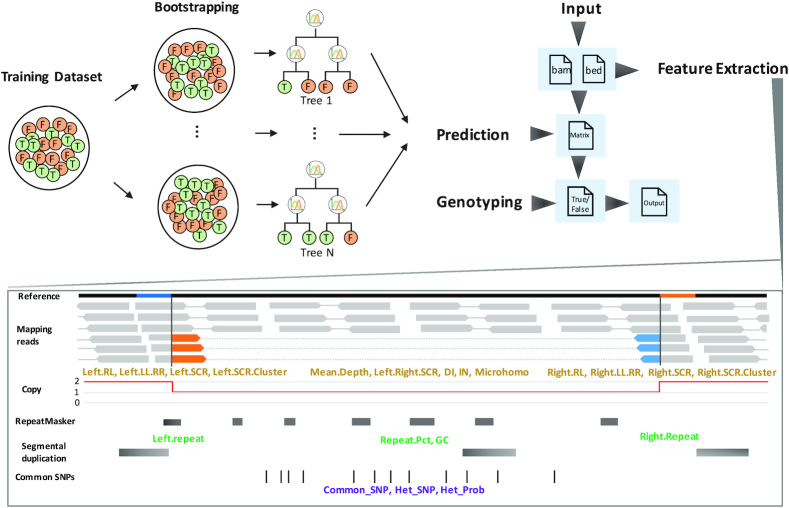
Figure 1.

The workflow of CNV-JACG. The top right panel shows the general workflow of CNV-JACG, which takes bam file(s) and bed file (containing the coordinates of CNVs to-be assessed) as input and goes through the feature extraction, prediction, genotyping processes and finally output the result containing the predicted category (‘true’ or ‘false’), genotype (number of copy) as well as the value of each feature. The top left panel is a schematic diagram of the process of RF model training. Through a bootstrapping sampling process, the model learns from the true and false CNVs about the pattern of 21 features and generate N trees readily for predicting the true and false category for a test CNV. The bottom panel is a schematic diagram of feature extraction, the mapping reads in orange/blue indicates soft-clip reads, and they are mapped to the region with their same color in the reference. The features in yellowish brown are extracted from mapping reads, and those in green are extracted from reference genome as well as the external repetitive region (including RepeatMasker and segmental duplication), the features in purple are extracted from mapping reads and external common SNPs of 1000 Genomes Project.

Training of random forest classifiers

We assembled a training dataset of 19,525 true and 25,268 false deletions, and 570 true and 1,506 false duplications defined by inheritance and consensus between CNV callers using nine in-house trios (27 samples, see ‘MATERIAL AND METHODS’ section). Down-sampling of the training deletions shown a negative relationship between OOB error rate and the number of training deletions (Supplementary Figure S5), indicating that an adequate number of training data is needed in order to achieve a low OOB error rate. Two RF classifiers were built for deletions and duplications, respectively, based on the selected 21 discriminating features. For each of these features, a marked difference in the distribution between the true and false groups for both deletions (Supplementary Figure S2) and duplications (Supplementary Figure S3) was observed in the training set. The standard RF output ‘Mean Decrease Accuracy’ and ‘Mean Decrease Gini’ showed the ranked importance of each feature (Supplementary Figure S4B and D). In addition, all features were proven to be important by Boruta algorithm, with ‘Mean.depth’, ‘Length’ and ‘DI’ showing the greatest discriminatory power for deletions, and ‘Length’, ‘Left.RL’ and ‘Repeat.Pct’ for duplications (Supplementary Figure S4A and C) (50). The OOB error rate for deletion and duplication training is 1.29 and 2.94%, respectively.

Performance evaluation using benchmark CNVs

The performance of CNV-JACG was first assessed using three sets of short-read WGS data of (i) a 1KGP sample (NA12878) and (ii) the Ashkenazim trio HG002-HG003-HG004 in GIAB and (iii) the HuRef/Venter genome (NS12911), based on the available benchmark deletions. The results were compared with those of SV² with respect to sensitivity, i.e. the proportion of benchmark deletions that were successfully predicted to be true. Duplications were not considered in this evaluation as they were not included as part of the benchmark sets.

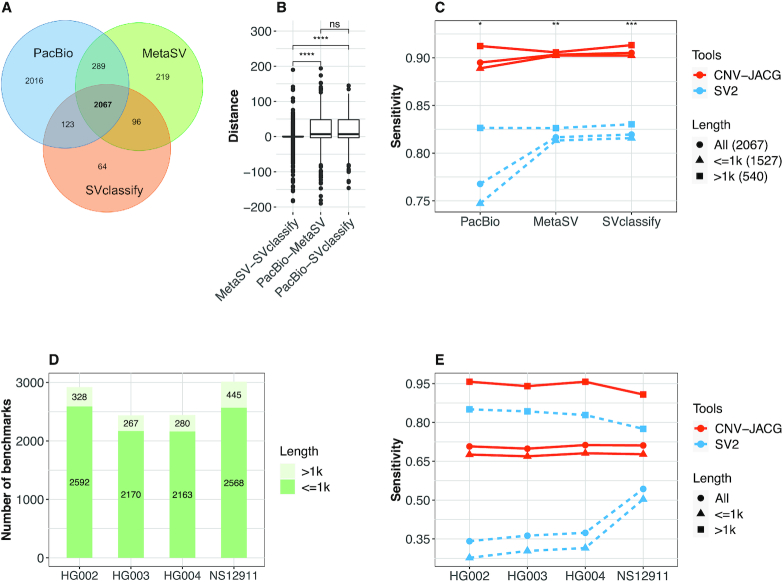
For the well-studied sample NA12878, there are three versions—SVclassify, MetaSV and PacBio—of benchmark deletions available (the numbers are 2350, 2671 and 4495, respectively), which showed varying levels of overlap (Figure 2A). Of note, for PacBio data, 45% of the deletions are uniquely called. This is because PacBio long-read sequencing approach is more powerful in detecting small deletions. Around 82% (3674 out of 4495) of the deletions detected by PacBio are small (≤1 kb), among which only 42% (1527 out of 3674) could be detected using the Illumina short-read approach (65). As CNV-JACG targets on short-read sequencing data, we therefore retained only the 2067 deletions shared by all the three versions as the final benchmark deletions of NA12878. In addition, for each of the final benchmark deletions, the breakpoints of the three versions are not always identical. Larger deviation in the positions of the breakpoints was found between sequencing approaches (long-read sequencing of PacBio versus short-read sequencing of MetaSV and SVclassify) than between different detection tools on data sequenced by the same platform (Figure 2B). For fair comparison, we kept the original breakpoint positions of each version, and evaluated the sensitivity separately.

Figure 2.

Sensitivity comparison of CNV-JACG and SV² using benchmark deletions in sample NA12878, NS12911 and trio HG002-HG003-HG004. (A) The Venn diagram of the overlap deletions of PacBio, MetaSV and SVclassify for sample NA12878. (B) The breakpoint distances for each of the 2067 shared deletions between each pair of three deletion versions. (C) The sensitivity of SV² and CNV-JACG for the benchmark deletions of different length under three versions of breakpoint positions: PacBio, SVclassify and MetaSV. (D) The number of benchmark deletions (>1 and ≤1 kb) of each member of the trio HG002-HG003-HG004 and NS12911. (E) The sensitivity of SV² and CNV-JACG on the benchmark deletions of HG002, HG003, HG004 and NS12911. P values were calculated by two-sided t-test, * <0.05; ** <0.01; *** <0.001; **** <0.0001.

As shown in Figure 2C, CNV-JACG significantly outperformed SV² overall irrespective of the benchmark deletion versions (sensitivity: 0.90 versus 0.77 for PacBio, 0.90 versus 0.81 for MetaSV and 0.91 versus 0.82 for SVclassify, respectively). Of note, the improvement in sensitivity was more profound for the small deletions ≤1 kb. Interestingly, while the sensitivity of SV² was similar and higher for MetaSV and SVclassify (0.81 and 0.82, respectively), a much lower sensitivity of 0.75 was observed when using PacBio benchmark deletion version. In contrast, CNV-JACG performed consistently well for small deletions among all three breakpoint versions (0.89, 0.90, 0.90, for PacBio, MetaSV and SVcalssify, respectively), which suggested that CNV-JACG is more insensitive for breakpoint deviation than SV².

For the Ashkenazim trio, we obtained 2920, 2437 and 2443 benchmark deletions from the samples HG002, HG003 and HG004, respectively (‘MATERIAL AND METHODS’ section, Figure 2D). As the deletions were derived from at least 30 callers from five different read datasets, inevitably a large portion of the given breakpoints represent the approximate positions refined from all different callers rather than the precise breakpoints (61). Similar to the scenario of NA12878 above, under the influence of breakpoint deviation, the sensitivity of SV² was low for all of the three samples (on average: 0.36), which was mainly driven by the low sensitivity of detecting small deletions (averaging 0.30). In contrast, CNV-JACG performed much better irrespective of the size (on average 0.71 for all deletions, and 0.68 for small size deletions). Of note, for large deletions >1 kb, CNV-JACG achieved a much higher sensitivity of 0.95 than SV² (0.84), even though theoretically SV² should had its best performance given the relatively stronger signals of features used (depth of coverage, discordant paired-ends and split-reads) in the case of large deletions (Figure 2E). For NS12911, we obtained 3013 benchmark deletions, which were detected based on genome-wide long Sanger reads and WGS data (2 × 100 bp, 40× and 100×) (29,66). Similarly, CNV-JACG had higher sensitivity than SV² (0.71 versus 0.54) for smaller deletions, and for deletions >1 kb, CNV-JACG achieved a much higher sensitivity of 0.91 (Figure 2D and E).

To evaluate the minimal coverage that CNV-JACG could work sensitively, we down-sampled the bam file of NA12878 (48.8×) to coverages of 1×, 5×, 10×, 15×, 20×, 25×, 30×, 35× and 40× and performed the sensitivity comparison with SV² separately. For simplicity, we used only the MetaSV breakpoints, since both CNV-JACG and SV² have intermediate sensitivities under MetaSV breakpoints (Figure 2C). As shown in the Supplementary Figure S6, CNV-JACG worked well with coverage of at least 10×. The sensitivity reaches 0.85 at 10× coverage and starts to converge at 15× (close to 0.9). In view of this, we recommended a minimum of 10× genomic coverage for assessing the accuracy of CNVs using CNV-JACG.

To further evaluate the false positive rate, we obtained 6,564, 6,275, 5,066, 6,169 negative deletions for NA12878, HG002, HG003 and HG004 respectively (see ‘MATERIAL AND METHODS’ section). After accuracy assessment of these negative deletions by CNV-JACG and SV², the false positive rate was calculated by the proportion of negative deletions that was predicted to be true. As shown in Table 2, in general, CNV-JACG achieved a lower false positive rate than SV² for all the four samples, indicating that CNV-JACG was not only more sensitive, but also had a lower false positive rate than SV².

Table 2.

False positive rate of CNV-JACG and SV² using benchmark deletions

Sample	Tool	False deletion	Predicted as true	False positive rate
NA12878	SV2	6564	245	0.0373
	CNV-JACG	6564	237	0.0361
HG002	SV2	6275	206	0.0329
	CNV-JACG	6275	188	0.0299
HG003	SV2	5066	169	0.0333
	CNV-JACG	5066	167	0.0329
HG004	SV2	6169	203	0.0329
	CNV-JACG	6169	199	0.0322

Evaluation of Mendelian inconsistency using trios

We next evaluated the Mendelian inconsistency using WGS data of six trios comprising two trios from the 1KGP, three trios from HGSV and one trio from GIAB. The Mendelian inconsistency is particularly relevant to studies of rare diseases in which truly de novo CNVs are believed to be more deleterious and may have larger phenotypic effects. In fact, observed Mendelian inconsistency reflects the combined phenomenon of false negatives in the biological parents, false positives in the offspring, as well as true de novo CNVs. As the number of de novo CNVs was estimated to be 0.05–0.16 per genome (67–70) and the pre-detection using four complementary tools is expected to capture most of the true CNVs in our study, the majority of the Mendelian inconsistent CNVs is believed to be false positives in the offspring. Hence, we consider MIR as a good proxy for evaluating the overall level of false positive rate of different methods (62).

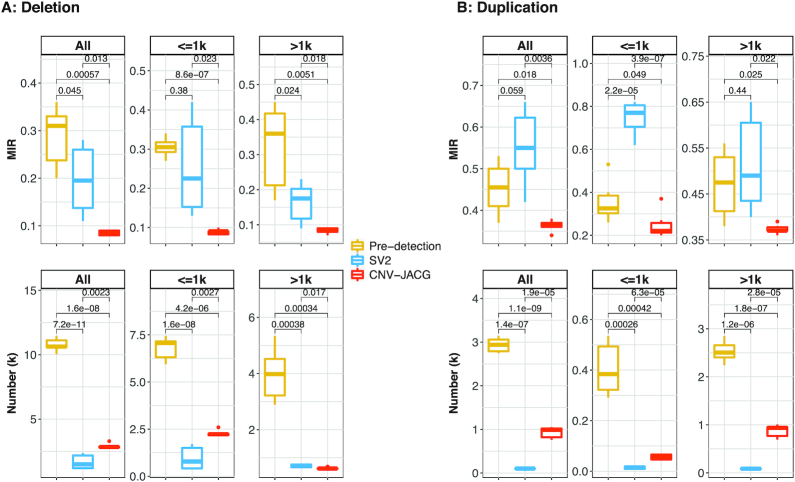
For all deletions, the mean MIR was the highest for the unfiltered pre-detection CNVs (0.288). Assessment of accuracy by SV² decreased the mean MIR to 0.197 and the reduction was more striking by CNV-JACG (to 0.085, P-value = 1.3 × 10⁻²). In addition to having the lowest Mendelian error rate, CNV-JACG retained more deletions (mean n = 2901) when compared to SV² (mean n = 1658) (Figure 3A). For all duplications, CNV-JACG also achieved the lowest mean MIR of 0.363 (P-value = 3.6 × 10⁻³ compared to SV²) with more duplications retained (mean n = 930) in contrast to a higher mean MIR of 0.552 for duplications in SV² (mean n = 100) (Figure 3B). The superior outperformance of CNV-JACG compared to SV² was observed for both small ≤1 kb and large >1 kb CNVs, interestingly, for deletions, the improvement was more significant for small deletions, while for duplications, the advancement was more obvious for large ones (Figure 3). These results showed that CNV-JACG substantially improves the overall accuracy of CNVs and outperforms SV² in terms of MIR for both deletions and duplications.

Figure 3.

The Mendelian inconsistency rate and number of CNVs in six trios. The box plots of the Mendelian inconsistent rate (MIR) and number of detected deletions (A) and duplications (B) for all, ≤1 kb, and >1 kb obtained by pre-detection, SV² and CNV-JACG (denoted by different color) for six trios are shown. MIR is the proportion of CNVs that present only in the child but in neither of his/her biological parents. Pre-detection indicates the combined CNV calls detected by CNVnator, Delly, Lumpy and Seeksv. SV² and CNV-JACG indicate the CNV calls (subset of Pre-detection) assessed to be true by each of them. Boxes denote the interquartile range (IQR). Ranges of whiskers are at most 1.5-fold of the IQR from the box and points outside the whiskers are outliers. P-values were calculated by two-sided t-test.

To demonstrate that CNV-JACG is generalizable to callers other than the four we used in training dataset, in addition to the above comparison wherein the training and testing data were generated from the same set of four callers (LUMPY, DELLY, CNVnator and Seeksv), we also generated the testing data by applying another set of three callers (CNVnator, GRIDSS and SVaba) while keeping the training data unchanged. For this new testing data, we observed a very similar result as the original testing data such that CNV-JACG had lower MIR than SV² while retaining more CNVs (Supplementary Figure S7), suggesting that the performance of CNV-JACG is robust against the choice of callers in the testing dataset.

Evaluation of concordance using 11 pairs of technical replicates

As another independent evaluation of our method, we applied CNV-JACG and SV² to WGS data of 11 pairs of technical replicates from our laboratory. The performance was evaluated based on the CNVs concordance rate between each pair of technical replicates, which was defined as the proportion of CNVs present in both individuals within each replicate (‘MATERIAL AND METHODS’ section).

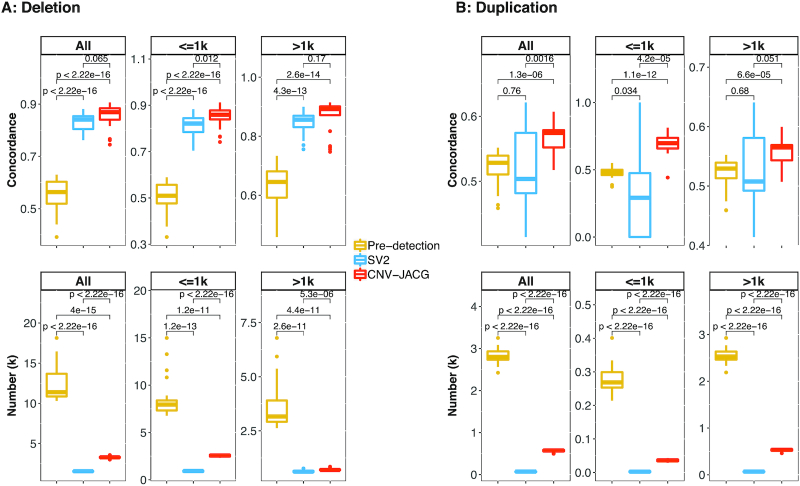
As shown in Figure 4A, for all deletions, the pre-detection had the lowest mean concordance rate of 0.55, SV² achieved a higher mean concordance rate of 0.83 while CNV-JACG had the highest value of 0.85 (P-value = 0.065, compared to SV²). In addition to having the best concordance rate, CNV-JACG also kept a reasonable mean number of 3280 deletions (pre-detection: n = 12309, SV²: n = 1548). For all duplications, CNV-JACG had a mean concordance rate (0.57) significantly higher than that of pre-detection and SV² (0.52, P-value = 1.3 × 10⁻⁶ and 0.51, P-value = 1.6 × 10⁻³), respectively) while retaining more duplications than SV² (on average: 564 versus 67, Figure 4B). The outperformance of CNV-JACG was more significant for the small CNVs than for the large ones, in particular, CNV-JACG achieved a substantially higher mean concordance rate of 0.69 for smaller duplications (≤1 kb; mean n = 36) compared to 0.48 (P-value = 1.1 × 10⁻¹²) for pre-detection (mean n = 279) and 0.30 (P-value = 4.2 × 10⁻⁵) for SV² (mean n = 3) (Figure 4). These results suggested that CNV-JACG outperformed SV² in terms of CNVs concordance for both deletions and duplications.

Figure 4.

Concordance of CNVs called between 11 pairs of technical replicates. Box plot of concordance and number for deletions (A) and duplications (B) for all, ≤1k and >1k size range, under pre-detection, SV² and CNV-JACG (denoted by different box color). Pre-detection indicates the combined CNV calls detected by CNVnator, Delly, Lumpy and Seeksv. SV² and CNV-JACG indicate the CNV calls (subset of pre-detection) assessed to be true by each of them. Each box consists of 22 values, e.g., we calculated two concordance rates for both cases of each replicate pair. Boxes denote the IQR, and the ranges of whiskers are at most 1.5-fold of the IQR from the box, the points outside whiskers are outliers. P-values were calculated by two-sided t-test.

Computational consideration

The computation time depends on the coverage of WGS data and the number of CNVs to be assessed. For a conventional setting, processing a single genome of ∼30× WGS data, with ∼3000 to be assessed CNVs in a single thread took about 4GB of RAM and 30 min on an Intel Xeon E5–2683 v4 2.1GHz processor.

DISCUSSION

In this study, we describe CNV-JACG, a simple RF-based framework that efficiently assesses and improves accuracy of CNVs called from WGS data. CNV-JACG is distinctive from the existing state-of-the-art CNV assessment methods in its utilization of machine learning coupled with the completeness of considering 21 discriminating features, especially those ignored by current detection tools. Such approach allows us to sensitively and accurately assess both deletions and duplications over a wide range of sizes, particularly for small CNVs ≤ 1 kb that are undetectable by earlier CNV detection technologies such as SNP array. Although the detection of the small CNVs improves substantially using WGS data, they are still largely missed due to weak read depth signals and indistinguishable abnormity in insert size from the background for tools based on RD and/or RP methods. Even SR based tools can detect these small CNVs with higher sensitivity, the results are usually prone to false discovery for those located on GC-rich and repeat regions due to the high mapping error of junction reads in these regions. Given the limitations of these three commonly used detection methods, it is necessary to conduct post-detection accuracy assessment by considering more comprehensively the features that can characterize the genuineness of CNVs.

The substantial improvement of CNV-JACG over the latest assessment method SV² lies not only in our usage of a unique, comprehensive set of discriminating features but also in its insensitivity to breakpoint deviation. This is particularly important as many CNV detection tools are now available, choosing multiple tools and merging the call sets become favorable in many CNV studies. Moreover, the merging strategies varies considerably, though >50% reciprocal overlap is most widely used. The coordinates of the final merged CNVs can be the maximum-range of all CNV calls, the positions shared by most of the detection tools, or the positions given by the tool the researcher trusts most, or more often the approximate boundaries of copy number variable region than the precise breakpoints. As the degree of breakpoint deviation is theoretically negative correlated with the signal of split-reads, the breakpoint deviation could be a potential reason for the false negative result of the assessment tool. For SV², when assessing small CNVs ≤ 1 kb, the signals of the two features: depth of coverage and discordant paired-ends, are generally weak. In this situation, SV² relies heavily on the number of split-reads spanning the given coordinates, which makes SV² very sensitive to breakpoint deviation. In contrast, CNV-JACG considers features around 150-bp up- and downstream of the given coordinates rather than focusing on the exact given positions, and combines many other features rather than just the number of split-reads when assessing ≤1 kb CNVs. This strategy allows CNV-JACG to be less sensitive to the breakpoint deviation and results in a much higher sensitivity against the benchmark dataset compare to SV².

A critical strategy of our method is the utilization of trio WGS as training data. We showed that it is in fact feasible to use credible high coverage WGS data together with criteria of inheritance and concordance between CNV calling tools to generate a more extensive training dataset of true and false CNVs while minimizing noise. This can overcome the limitations of using the single or small set of benchmark CNVs; for example, in the case of NA12878 where there is no duplication in the benchmark versions generated based on short-read WGS data and with small number of benchmark deletions available. In this study, we did not use the 27 high coverage WGS data of 1KGP Phase 3 as training data as SV² and FusorSV did (32,34,71). One of the major concerns is the unmatched read type with our in-house data (read length: 250bp vs 150bp), which might induce bias when doing prediction. The other concern is the absence of false CNV set required by RF in the public data, which, in contrast, could be easily generated using trio data. Of note, our nine in-house WGS trios could be easily extended with similar performance to other trios for generating training datasets, e.g. the Trio 1–5 listed in Supplementary Table S2 (Supplementary Figure S8); however, it is noteworthy that optimal performance may not be achieved if the training dataset is heterogeneous in terms of read length (Supplementary Figure S9).

By applying the RF trained on the trio WGS data, we demonstrated that CNV-JACG outperformed SV², achieving higher sensitivity across all sizes and versions of benchmark deletions. The lower Mendelian inconsistency and higher CNV concordance would advance the discovery of CNVs implicated in complex and rare diseases; however, the performance of CNV-JACG in assessing the accuracy of duplications shows room for improvement. Although the use of nine in-house WGS trios could produce training duplication data, we cannot directly evaluate the prediction accuracy due to the lack of useful benchmark duplications. For instances, all the three benchmark sets of NA12878 do not include benchmark duplications and only five confident duplications can be obtained from DGV Gold Standard and Stringent Variants (>80% reciprocal overlap with the duplications detected by at least two tools we used here). Although CNV-JACG performed better than SV² in detecting these five benchmark duplications (Supplementary Table S3), this comparison lacked credibility due to the small sample size. On the other hand, the indirect indicators of Mendelian inconsistency rate and concordance for pre-detected duplications showed much limited improvement by CNV-JACG than for pre-detected deletions, which could be attributed to both the higher complexity of duplications and the smaller number of duplications for training. To overcome this challenge, a larger training data for duplications is needed.

In summary, CNV-JACG is a simple, easy-to-use framework for accuracy assessment and genotyping of CNVs. By supervised learning of a comprehensive set of 21 discriminating CNV features, CNV-JACG has superior performance in both sensitivity and accuracy and can be applied to any pair-end WGS data. Our study suggests that CNV-JACG will be a useful tool in assessing CNV accuracy for uncovering the genetic risk of CNVs for both population and family-based studies.

DECLARATIONS

Ethics approval and consent to participate

The study was approved by the institutional review board of The University of Hong Kong together with the Hospital Authority (IRB: UW 06-349T/1374).

Consent for publication

Publication of the de-identified results from all consenting participants was approved.

DATA AVAILABILITY AND MATERIALS

All the training datasets generated and analyzed in this article, as well as the source code of framework CNV-JACG (v1.1) is readily available from GitHub at - https://github.com/sunnyzxh/CNV-JACG under GNU General Public License.

• Web resource of NA12878 benchmark CNVs:

• SVclassify, ftp://ftp-trace.ncbi.nlm.nih.gov/giab/ftp/technical/svclassify_Manuscript/Supplementary_Information/Personalis_1000_Genomes_deduplicated_deletions.bed (60)

• MetaSV, ftp://ftp-trace.ncbi.nlm.nih.gov/giab/ftp/technical/svclassify_Manuscript/Supplementary_Information/metasv_trio_validation/NA12878_svs.vcf.gz (27)

• PacBio data at Genome in a Bottle Consortium (∼44×; contributed by Mt. Sinai School of Medicine), ftp://ftp-trace.ncbi.nlm.nih.gov/giab/ftp/data/NA12878/NA12878_PacBio_MtSinai/NA12878.sorted.vcf.gz (59).

• Web resource of Ashkenazim trio benchmark CNVs:

• ftp://ftp-trace.ncbi.nlm.nih.gov/giab/ftp/data/AshkenazimTrio/analysis/NIST_SVs_Integration_v0.6/HG002_SVs_Tier1_v0.6.vcf.gz.

• Web resource of NS12911 benchmark CNVs:

• https://ftp-trace.ncbi.nlm.nih.gov/giab/ftp/technical/HuRef_Bina_GoldSet/venter_gold_hiqual_DEL.vcf

• Coordinates of Repeat regions:

• RepeatMasker, http://www.repeatmasker.org/genomes/hg19/RepeatMasker-rm405-db20140131/hg19.fa.out.gz

• Segmental Duplications, http://humanparalogy.gs.washington.edu/build37/data/GRCh37GenomicSuperDup.tab

• 1000 Genomes Project Phase III SNPs

• ftp://ftp-trace.ncbi.nih.gov/1000genomes/ftp/release//20130502//ALL.wgs.phase3_shapeit2_mvncall_integrated_v5b.20130502.sites.vcf.gz

• All the open source software used in this study are cited in the text.

SUPPLEMENTARY DATA

Supplementary Data are available at NARGAB Online.

FUNDING

Theme-based Research Scheme [T12C-714/14-R to P.K.T.]; Health Medical Research Fund [06171636 to C.S.T.]; General Research Fund [17128515 to P.C.S., 17109918 to P.K.T., 17113420 to C.S.T.].

Conflict of interest statement. None declared.