An empirical bayesian approach for testing gene expression fold change and its application in detecting global dosage effects

Abstract

We are motivated by biological studies intended to understand global gene expression fold change. Biologists have generally adopted a fixed cutoff to determine the significance of fold changes in gene expression studies (e.g. by using an observed fold change equal to two as a fixed threshold). Scientists can also use a t-test or a modified differential expression test to assess the significance of fold changes. However, these methods either fail to take advantage of the high dimensionality of gene expression data or fail to test fold change directly. Our research develops a new empirical Bayesian approach to substantially improve the power and accuracy of fold-change detection. Specifically, we more accurately estimate gene-wise error variation in the log of fold change. We then adopt a t-test with adjusted degrees of freedom for significance assessment. We apply our method to a dosage study in Arabidopsis and a Down syndrome study in humans to illustrate the utility of our approach. We also present a simulation study based on real datasets to demonstrate the accuracy of our method relative to error variance estimation and power in fold-change detection. Our developed R package with a detailed user manual is publicly available on GitHub at https://github.com/cuiyingbeicheng/Foldseq.

INTRODUCTION

Detecting genes that express differently between case and control conditions is a fundamental problem in functional genomic studies. There are two different ways to quantify differential expressions, either by mean gene expression difference or by fold change. These two criteria lead to two different ranked lists of significant genes. Top ranked genes selected by the expression difference method often have higher mean expression levels but relatively smaller fold change, and the opposite is true when using the fold change criterion. The vast majority of available statistical methods and software packages test significant gene expression difference between treatment groups. However, there are scenarios where testing expression fold change is a more natural question to inquire. This calls for development of sophisticated data analysis methods to satisfy the need.

Aneuploidy, or the presence of an abnormal number of individual chromosomes in the genome, is a well-known phenomenon found in many different organisms. Aneuploidy originates during cell division when sister chromosomes do not separate properly between two cells. An extra or missing copy of a chromosome is a common cause of genetic disorders, including human birth defects such as Down syndrome (DS) and Edwards syndrome. DS, otherwise known as trisomy 21, arises from an extra copy of chromosome 21. English physician John Langdon Down (1) first documented the condition in 1866, hence its name ‘Down syndrome.’ The additional genetic materials from chromosome 21 is thought to alter the course of normal development and thus lead to characteristics associated with DS. Similarly, Edwards syndrome (also known as trisomy 18) features an extra copy of chromosome 18 due to errors in cell division, known as meiotic nondisjunction. Different from DS, the developmental problems resulting from trisomy 18 pose greater threats to health in the early months and years of life; among babies with the condition who are carried to term, approximately only half will be born alive.

Aneuploidy has long been known to produce severe phenotypic consequences. Similar phenomena have been observed and documented in eukaryotes, including yeast, protozoa, vertebrates and especially the plant kingdom (2–7); more specifically, the addition or subtraction of a single chromosome in the entire set is more detrimental than altering the dosage of the complete complement. To better understand global gene expression differences in aneuploidy, a comprehensive analysis of such differences for all five trisomies and in diploids, triploids and tetraploids of Arabidopsis thaliana was conducted (8). Results indicated that, in general, gene expression on the varied chromosome ranged from compensation to a dosage effect, whereas genes from the remainder of the genome exhibited anywhere from no effect to reduced expression approaching the inverse level of chromosomal imbalance. In addition, gene functional analysis indicated that ribosomal, proteasomal and gene body methylated genes were less modulated compared with all gene classes, whereas transcription factors, signal transduction components and organelle-targeted protein genes were more tightly inversely affected (8). These findings suggest that the addition or subtraction of a single chromosome will invoke global gene expression changes, including in the varied chromosome and the remainder of the genome. Such altered regulatory stoichiometry is a major contributor to genetic imbalance.

An important task when analyzing aneuploid data compared to normal diploid data is to identify gene groups (both cis- and trans-genes) that exhibit a dosage effect, compensation effect, or inverse dosage effect. Statistically, this task requires testing the fold change of gene expression in comparison between aneuploidy and diploid data. At present, no sophisticated data analysis methods or ready-to-use software package is available for detecting genome-wide fold changes; researchers typically use computational tools designed to detect differentially expressed (DE) genes. For example, in a recent trisomy study on Arabidopsis (8) and transcriptomic analysis of DS (9), edgeR and DESeq (10–12) were used to identify genes with an expression level greater or less than normal; however, this strategy is suboptimal because edgeR and DESeq are intended to test gene expression differences rather than to test fold-change statistics directly. In this paper, we demonstrate that testing fold change directly can identify more fold change-relevant genes than testing expression differences in search of fold change.

Specifically, we propose a hierarchical model on the log of fold change between two comparison groups. In an aneuploid experiment or observational study, the comparison groups include an aneuploid group (disease group) and diploid group (control/healthy group). For the constructed hierarchical model, we put an inverse gamma prior on the error variance for each gene. An empirical Bayesian approach is adopted to produce gene-specific error variance estimation, which generates more accurate estimates than currently available approaches as information is borrowed across observations from all genes. We then use the improved error variance estimates to test null hypotheses of fold change. We also construct a t-type test on the log of fold change statistics using our improved error variance estimate and its corresponding adjusted degrees of freedom. To evaluate performance, we adopt public RNA-seq datasets along with simulation studies based on real datasets. We demonstrate that, compared to the usual t-test, edgeR and DESeq methods, error variance estimation is substantially improved by our new approach. The power of detecting true fold change while controlling the false discovery rate (FDR) is also greatly enhanced. We call our new method the Foldseq approach, and our developed R package is publicly available on GitHub at https://github.com/cuiyingbeicheng/Foldseq.

MATERIALS AND METHODS

Data model

To ground our method, we will first introduce relevant notations. Let denote the normalized gene expression of gene g of replicate j in treatment group i, where i = 1 for the control group and i = 2 for the treatment group, j = 1, …, n_i and g = 1, …, G. Our proposed method can be easily extended to a multiple-group comparison scenario. To illustrate our approach, we use a two-group comparison as an example here.

Suppose the control group and the treatment group have the population mean expression 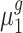and 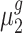, respectively. The objective of our study is to detect whether the ratio of 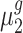and (i.e. fold change) is within or outside a region of interest, such as

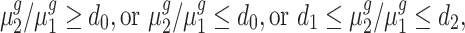(1)

among others, with strong statistical evidence.

As the mean gene expression ratio is of interest for our purposes, we define variable , where and g = 1, …, G. This logarithmic transformation permits the fold-change variable to be modeled on the entire real space. Typically, the log of fold change uses base 2. We retain this conventional approach and thus use base 2 in our method. The 0.5’s in the numerator and denominator are intended to avoid extreme observations when taking the log transformation.

We model that 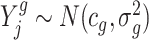, where c_g and denote the gene-specific mean and variance of the log fold change, respectively. Often there are only a few replicates (i.e. two or three) in gene expression studies due to the expenses associated with biological replicate acquisition and sequencing experiments. A usual t-test that is only based on 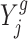, c_g, and is unreliable because gene-wise estimation of the variance parameter is not accurate when using only a few replicates. To improve the estimation of 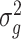, we adopt a Bayesian approach to borrow information across genes. Specifically, we assume 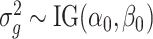, which is a commonly used conjugate prior for variance parameters.

Let 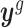denote all observations from gene g; that is, 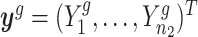. We derive that the posterior distribution of given is

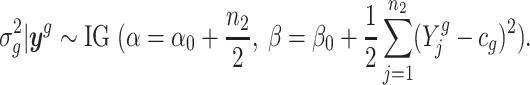(2)

We propose using the posterior mean of 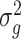, , 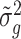as the estimate of 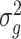, where

(3)

To test our hypotheses of interest, such as the null hypotheses in (1), we construct the following t-statistic

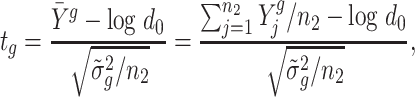(4)

where d₀ can be replaced by d₁ and d₂ to test regions with two-sided boundaries. At last, we use Storey’s method (13) to control the FDR at a desired level.

Hyperparameter estimation

To implement our method, we still need to estimate hyperparameters α₀ and β₀. A number of methods have been proposed to infer the gene-wise hyperparameters using Empirical Bayes (EB) methods. For microarray data, Newton et al. proposed to use Gamma and log-normal distributions to model microarray expression data and applied EB models to estimate hyperparameters (14). Smyth popularized the hierarchical model proposed by Lönnstedt and Speed (15) and applied EB method to estimate hyperparameters. More EB methods have been developed for analyzing sequencing-based transcriptomic data. In particular, Hardcastle and Kelly developed baySeq, in which the authors used EB method to determine the prior distributions (16). Robinson et al. developed edgeR, where an EB method was to moderate the degree of overdispersion across transcripts (10). Wu et al. presented an improved EB shrinkage estimate of dispersion parameters and demonstrated improved DE detection (17). Love et al. developed DESeq2 (18), where an EB method was used for dispersion estimation.

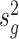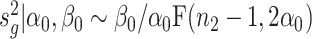Inspired by the method in limma (19), we propose the following estimation approach. Specifically, we compute the sample estimate of gene-wise variance, denoted by , where . We can show that , which is a scaled F-distribution. Let 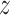_g denote with a natural base, such that 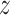_g is distributed as a constant plus Fisher’s 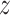distribution as demonstrated in (19). The distribution of 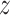_g is roughly normal with

(5)

(6)

where ψ( · ) and ψ′( · ) denote the digamma and trigamma functions, respectively.

Let e_g = _g − ψ((n₂ − 1)/2) + log((n₂ − 1)/2), in which case we have E(e_g) = log(β₀/α₀) − ψ((n₂ − 1)/2) + log((n₂ − 1)/2), and where . We therefore estimate α₀ by solving 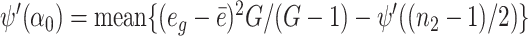. To solve this equation, we use Newton’s iteration. Specifically, let a denote 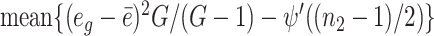. In the initial iteration, we set . In the kth iteration, we let α^{(k + 1)} = α^(k) + ψ′(α^(k)){1 − ψ′(α^(k))/a}/ψ′(α^(k)). The iteration stops once |α^{(k + 1)} − α^(k)|/α^(k) < ε, where ε is a small positive number. After convergence, the estimate of α₀ is denoted by . We estimate .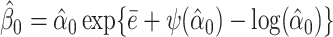

RESULTS

Simulation study

Simulation setting

To ensure that our simulation results are reproducible in real data analysis, we simulated data based on real datasets in (8); we simulated 18 000 genes in total. Each gene has n₁ replicates in the control group and n₂ replicates in the treatment group. We let n₁ = 3 based on the number of replicates in (8) for the dosage effect analysis in Arabidopsis. To assess the parameter estimation and detection power of our proposed method, we let n₂ be 3, 5, 7 and 9, respectively. To simulate observations for the control group, we randomly selected 18,000 genes from the control group of trisomy 1 in the Arabidopsis analysis and directly used their observations as X₁₁, X₁₂ and X₁₃. We first simulated the log fold change (with base 2); that is, 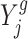’s, and then simulate observations for the treatment group. Specifically, we follow the procedure as described below:

1. Set α₀ and β₀ based on Arabidopsis trisomy 1 dataset. Then simulate .

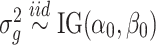2. Randomly select certain proportion (e.g. 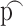= 30%) genes to have significant fold change (i.e. DE genes) of c₀ with c_g = log₂(c₀). For the other (1-p) genes, we set them to have no change, i.e. c_g = log₂(1) = 0. Simulate .

3. Calculate the observations in the treatment group with .

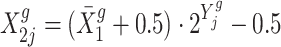We consider three different parameter settings for α and β, respectively, with α = 3, 4, 5 and β = 0.15, 0.18, 0.20 and three choices for the magnitude of fold change c₀: 1.3,1.5 and 2.0. For each of these 27 settings, we repeated 100 times.

Simulation results

We compared our proposed Foldseq method with five competing methods: (i) the usual t-test without a Bayesian shrinkage prior; (ii) the edgeR method; (iii) the DESeq2 method; (iv) the voom method (20); and (v) a two-group EB t-test method, which modifies the one group EB t-test in our proposed Foldseq method. By comparing our method to the naive t-test, we examined the power gain of using a Bayesian prior. We chose the edgeR, DESeq2 and voom algorithms for comparison because they are the most commonly used methods for testing DE genes.

Figure 1 shows the absolute biases of α₀ estimates (left panel) and absolute biases of β₀ (right panel); specifically, 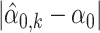and , where k = 1, …, K and K = 100 index the 100-round simulation. Figure 1 suggests that with n₁ = n₂ = 3, the absolute biases of α₀ and β₀ estimates are small. When n₁ = 3 and n₂ increases to 5, 7 and 9, respectively, the absolute biases of the estimates of α₀ and β₀ decline as the sample size increases. Table 1 summarizes the averaged bias (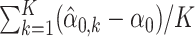) and mean squared error (MSE) () across 100 simulations. The results in Table 1 suggest satisfactory and stable estimation results across repeated simulations.

Figure 1.

Absolute biases of estimates with 3, 5, 7 and 9 treatment replicates, respectively. Left panel shows absolute biases of estimates of α₀; right panel shows absolute biases of estimates of β₀.

Table 1.

Average bias and MSE across 100 simulations

		rep =3		rep = 5		rep = 7		rep = 9
	True	Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE
α	1.221	0.020	0.001	0.013	0.000	0.012	0.000	0.012	0.000
β	0.189	0.005	0.000	0.003	0.000	0.003	0.000	0.003	0.000

We next compared the performance of error variance estimate , 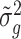’s, of Foldseq, with the usual sample estimates that are used in t-tests, 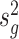’s. We set n₁ = n₂ = 3; Figure 2 plots the MSEs, variances and biases of 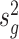’s and 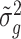’s with respect to the true ’s, which shows that our variance estimates 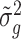’s are closer to the truth on average than sample estimates obtained without Bayesian shrinkage.

Figure 2.

MSE, variance and bias for naive variance estimator and Bayesian estimator. In each plot, the left box plot shows the result for the naive estimator, and the right box plot shows the result for the Bayesian estimator.

Additionally, we compared the power of fold-change detection between Foldseq and the five competing methods. To be precise, the null hypothesis considered by edgeR, DESeq2 and voom methods is ; whereas for t-test, the two group test and Foldseq, the hypothesis is 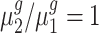. The two null hypotheses are equivalent, but the former focuses on the mean difference whereas the later focuses on the mean ratio (i.e. fold change). Thus, we expect the tests using different statistics (either difference or ratio) to exhibit different power, and the one using the observed fold-change statistics to detect fold change will have higher power than methods using mean-difference statistics. Figure 3 summarizes mean AUCs (n₁ = n₂ = 3) of all these methods in comparison across 100-round simulation for each simulation setting. As expected, Foldseq demonstrated a larger AUC compared to other methods, suggesting improvement in the power of fold-change detection as well as better gene ranking.

Figure 3.

Mean AUC across 100 simulations for our proposed Foldseq method, the two group test, the usual t-test, voom, DESeq2 and edgeR for each simulation setting.

Furthermore, we examined the top 5000 most significant genes declared by each method. Averaging across 100-round simulation, 82.6% of these genes selected by Foldseq were true positives. The proportion of true positives were 58.1, 78.0, 63.7 and 76.1%, respectively, for DESeq2, usual t-test, voom and the two group test. Figure 4 shows a Venn diagram illustrating the overlapping pattern among the top 5000 significant genes selected by each method in four-round simulation when α = 3, β = 0.18 and true positives have fold change 1.3. The Venn diagram suggests that our proposed Foldseq method has the most number of overlapping genes than any other method in comparison.

Figure 4.

Venn diagram showing 4 times of simulation results of top 5000 most significant genes selected selected by Foldseq, DESeq2, t-test, limma/voom and the two group test where α = 3, β = 0.18 and fold change of 1.3.

Finally, we examined the true FDRs produced by these methods when controlling empirical FDRs at 0.2, 0.1, 0.05 and 0.01, respectively. The results for simulation setting with α = 3, β = 0.18 and fold change of 1.3 are presented in Table 2. Table 2 indicates that only Foldseq, the usual t-test and DESeq2 control empirical FDRs under true FDRs. In addition, the usual t-test is more conservative than both Foldseq and DESeq2. The edgeR, voom and two group methods are liberal under most FDR thresholds.

Table 2.

True FDRs when controlling empirical FDRs at 0.2, 0.1, 0.05 and 0.01 for the simulation setting with α = 3, β = 0.18 and fold change as 1.3 for true positive genes

FDR	Foldseq	2Group	t-test	voom	DESeq2	edgeR
0.2	0.020	0.228	0.000	0.532	0.030	0.065
0.1	0.010	0.176	0.000	0.431	0.010	0.050
0.05	0.010	0.150	0.000	0.345	0.010	0.030
0.01	0.000	0.126	0.000	0.000	0.010	0.020

Analysis of dosage effects and dosage compensation in Arabidopsis thaliana

Changes in the dosage of part of the genome have long been known to produce much more severe phenotypic consequences than changes in the number of whole genomes (2–4). Therefore, a simple assumption emerged that this phenotypic effect resulted from varied genes showing a dosage effect; in other words, the gene expression fold change matches the gene copy number change for genes on the varied chromosome. However, other evidence in maize and Drosophila has revealed the presence of global genome-wide cascading modulations (21–25), presumably because transcription factors and signal transduction components are dosage-sensitive (26–30) and their targets would be modulated regardless of the chromosomal locations of the latter.

To more comprehensively understand the molecular basis of genetic imbalance characterized by aneuploidies, researchers (8) gathered a complete set of primary trisomies of Arabidopsis and compared their gene expression fold changes with the normal diploid. Specifically, mature leaf tissues from all five trisomies and the normal diploid of A. thaliana were collected. There were two biological replicates for each trisomy and three biological replicates for the normal diploid. RNA-seq experiments were conducted for each replicate to measure gene expressions. Raw gene expression data were then normalized using an External RNA Controls Consortium (ERCC) spike-in followed by polyA RNA isolation to detect any transacting effects of aneuploidy on global gene expression (31).

We retrieved normalized gene expression data published in (8) and reanalyzed them using our new statistical method. Figure 5 plots the sample averages of fold changes, indicated by 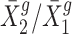’s across biological replicates, respectively, for cis- and trans-genes for each trisomy. Figure 5 presents a wide spread in gene expression ratio distributions comparing trisomies with the normal diploid. We further examined the ratio distributions for two gene categories: genes present on the varied chromosome (cis) and genes in the remainder of the genome (trans). For each trisomy, the ratio distribution of the cis-genes suggests a mode between 1.0 (dosage compensation) and 1.5 (dosage effect) with a wide spread that extends above and below these levels. For each trisomy, the ratio distribution of the trans-genes suggests a mode between 2/3 (inverse dosage effect) and 1.0 (no modulation), also with a wide spread. The fact that the cis and trans effects are modulated coordinately to some extent suggests a common influence of the aneuploid state on gene expression on the varied and unvaried chromosomes.

Figure 5.

Observed sample average fold-change distributions of gene expression in each trisomy compared with diploid. A ratio of 1.50 represents a gene-dosage effect in cis, whereas 1.00 represents dosage compensation. A ratio of 0.67 represents the inverse ratio of gene expression in trans. Ratio values are demarcated with labeled vertical lines at 0.67, 1.00 and 1.50.

To statistically test the above conclusions, we applied our method to these trisomies. We estimated hyperparameters using the method illustrated in the ‘Materials and Methods’ section. For instance, to compare trisomy 1 and the diploid, our estimate of α₀ is 1.22 and of β₀ is 0.19. Then, for each cis-gene, we tested 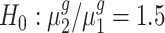. We controlled the FDR at the 0.05 level. By rejecting the null hypothesis, we further clustered genes with 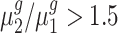and genes with 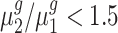. For each trans-gene, we tested 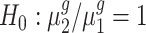. By rejecting the null hypothesis, depending on the fold-change direction, we also clustered genes with and genes with 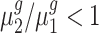. We summarized the number of genes in each category using our inference procedure for all five trisomies compared to the diploid; findings appear in Table 3.

Table 3.

Fold-change detection results for Arabidopsis trisomies

	cis-genes			trans-genes
Trisomy
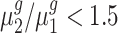
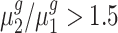
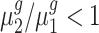
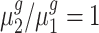
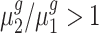
1	2736	3455	50	2984	14 217	409
2	2302	1379	206	4315	13 448	2595
3	3892	744	338	8506	8474	2741
4	1496	2159	26	3008	16 733	530
5	2122	3389	127	1872	15 331	1439

Our test results substantiate the observations in (8) and provide detailed numerical evidence of the global gene expression effects of the additional chromosome in each trisomy. For instance, for cis-genes in trisomy 1, we found 2736 genes with a fold change <1.5 and only 50 genes with a fold change >1.5 with strong statistical support. This pattern reinforces the observations that the cis-genes’ distribution has a median between a dosage effect (1.5 fold change) and dosage compensation (no fold change). Our finding also suggests that numerically, ∼45% of the cis-genes ((2736 + 50)/(2736 + 3455 + 50)) and approximately one-fifth of the trans-genes are being modulated in trisomy 1. Similar conclusions can be drawn for all these five trisomies. Specifically, higher percentages of cis-genes in trisomies 2 and 3 are modulated than for cis-genes in trisomies 1, 4 and 5; and higher percentages of trans-genes in trisomies 2 and 3 are modulated compared to those in trisomies 1, 4 and 5.

Analysis of trisomy 21 Down syndrome gene expression data

Trisomy 21, most often caused by the non-disjunction of chromosome 21 in oocytes, leads to DS and is the most common autosomal aneuploidy among live births. Due to its high frequency, DS has become an important model for exploring the consequences of trisomy in humans. Several studies have focused on elucidating the molecular consequences attributable to the presence of an extra copy of the chromosome 21 (9,32–34). Among them, a study in 2018 by Gonzales et al. (9) analyzed gene expression levels via RNA-seq data analysis from trisomic- and disomic-induced pluripotent stem cells (iPSCs) and differentiated cortical neurons derived from the same individual with DS. In the original study, researchers (9) applied DESeq to identify differentially expressed genes. To evaluate Foldseq, here we reanalyze their data from iPSC cultures using our proposed Foldseq algorithm. To ensure a fair comparison, we only considered genes that appeared in both analyses: 217 genes from chromosome 21 and 25 621 genes in the rest of the genome. Between DESeq and Foldseq, when using the same FDR level of 0.1, Foldseq identified eight upregulated genes compared to 13 identified by DESeq, five of which were identified by both methods. We found that the actual expression levels of the three genes identified solely by Foldseq (S100B, EVA1C and OLIG2) were low and their variance was relatively high, which may explain why DESeq did not identify them as differentially expressed. By contrast, the variance between the log fold change was stable and relatively moderate, which enabled these genes to be identified by our method. Interestingly, S100B is a gene known to have increased expression levels in DS and is associated with Alzheimer’s disease, a pathology that manifests early in adults with DS (35–38). Also, OLIG2, a gene known to have altered expression in DS, is associated with key consequences during brain development (39,40). At last, EVA1C, a slit receptor located in the DS critical region, has been shown to be expressed in axons and to serve a key function in neural circuit formation in the developing nervous system of mice (41).

The differences between methods are even more striking upon examining downregulated genes on chromosome 21: our method identified the four genes deemed downregulated by Gonzales et al. (CBR3, COL6A1, DSCAM and TRPM2) along with six new genes not previously considered downregulated by DESeq. Among them, we found BACE2, a gene identified in previous investigations for its influence in Alzheimer’s disease and DS. Although the exact role of BACE2 has not been clearly identified (42–44), (38) pointed out that this gene may have a protective role in the development of Alzheimer’s disease in adults with DS. The downregulation of this chromosome 21 gene identified by our method may provide insight into the gene’s association with DS-related Alzheimer’s disease, further highlighting the importance of Foldseq.

Analysis of genome-wide expression values for 25 621 genes indicated that Foldseq detected no significant fold changes in expression levels between trisomic and disomic cells in 23 567 genes (91.98%), whereas DESeq found 24 700 genes (96.4%) with no significant change. Strikingly, Foldseq found 1528 genes (5.96%) that were statistically upregulated in trisomic cells compared to only 429 genes (1.67%) found by DESeq, a difference of 1099 genes. At last, the number of downregulated genes identified by both methods was similar: 526 genes (2.05%) and 492 genes(1.92%) for Foldseq and DESeq, respectively. We believe that these differences, particularly in the high number of upregulated genes solely identified by Foldseq, could influence enrichment analysis. To test this supposition, we used DAVID (45), a Gene Ontology (GO) term (46) enrichment analysis method, to identify enriched pathways, similar to (9).

Our results show a similar pattern to that described by (9), wherein iPS trisomic cells exhibit increased transcript levels of genes involved in neurogenesis and neuronal function. The main difference is that certain genes, which Foldseq identified as significantly upregulated in trisomic cells and which have known functions in the neuronal pathway, were undetected by DESeq. For example, CNTN2, a known gene with an important function in axon elongation or axonal guidance (47), was considered upregulated by Foldseq but found to have no statistical significance by DESeq. This gene was in turn detected by GO analysis in different pathways related to axon guidance (GO:0007411) or central nervous system development (GO:0007417). Among other genes considered differentially expressed by Foldseq and not DESeq, we found additional key genes involved in axonal growth and guidance; examples include RET (48), neuroligin Y (NLGN4Y) and neuroligin X (NLGN4X ), which are synaptic cell-adhesion molecules that connect postsynaptic neurons at synapses. Along with neurexins, these proteins are key components of the molecular machinery that controls synaptic transmission (49) and SPTBN4, a spectrin protein known as βIV with key functions at the axon initial segments and nodes of Ranvier (50,51).

We believe that these results demonstrate the benefit of using Foldseq to analyze gene expression data from aneuploid genomes. As we discovered, Foldseq can detect statistically significant gene expression fold changes (that went unnoticed by DESeq) with known and proven functions in the pathology of DS, the organization and development of the nervous system, and axonal growth. These findings show that Foldseq could provide a more accurate picture of genome-wide variations in genomic expression occurring in aneuploidies.

DISCUSSION

Tests of differential expression and fold change involve two related hypotheses. Many gene expression experiments concern the former hypothesis while others concern the latter. Several sophisticated statistical methods have been developed to address differential expression. The vast biological community tends to directly apply methods of differential expression to test fold change, although others have applied the naive t-test. We used two real datasets to demonstrate that, if data analysis concerns fold change, then a test based on fold-change statistics provides more accurate and powerful results. In addition, a Bayesian prior that shares information across genes can substantially improve inferential results compared to a naive method without priors.

Computational time is an important factor for algorithms analyzing high throughput genomic data. For Foldseq, we conducted a comprehensive survey on the computational time cost for various combinations of gene numbers and sample sizes on a commodity compute server. The results are presented in Table 4. The survey results show that Foldseq’s computational time is <1 s for all of these settings.

Table 4.

Computational time (in seconds) of FoldSeq for different number of genes and sample size in each treatment group

No. of genes	3 replicates	5 replicates	7 replicates	9 replicates
10 000	0.58	0.57	0.52	0.59
12 000	0.56	0.68	0.52	0.68
15 000	0.32	0.57	0.54	0.75
18 000	0.41	0.53	0.58	0.84
20 000	0.42	0.53	0.60	0.74

CONCLUSION

In this paper, we have proposed a new approach to detect gene expression fold change between two comparison groups. Our method could be generalized to any high-throughput microarray and sequencing experiment. Specifically, we constructed a model on the log of fold change for each gene, where the error variance of each gene was modeled as a random sample from an inverse gamma distribution. Hyperparameters in the inverse gamma prior were estimated by observations from all genes. Due to the large number of genes in a typical gene expression experiment, our hyperparameter estimation was accurate. A t-type test with adjusted degrees of freedom was developed for hypothesis testing. Real data analysis and simulation data analysis that mimicked actual datasets revealed our new approach, the Foldseq method, to be superior to existing methods for detecting gene expression fold change; specifically, our approach demonstrated improved power while controlling the FDR at a desired level. Our R package is freely available on GitHub at https://github.com/cuiyingbeicheng/Foldseq.

DATA AVAILABILITY

Sequencing gene expression data for the A. thaliana study described in this paper have been deposited in the Gene Expression Omnibus (GEO) database with accession no. GSE79676. Sequencing gene expression data for the DS study described in this paper have been deposited in GEO with accession no. GSE101942. The Foldseq R package is available on GitHub at https://github.com/cuiyingbeicheng/Foldseq.

FUNDING

National Science Foundation [1615789, 1853556 to T.J.].

Conflict of interest statement. None declared.