Abstract
Genomes are spatiotemporally organized within the cell nucleus. Genome-wide chromosome conformation capture (Hi-C) technologies have uncovered the 3D genome organization. Furthermore, live-cell imaging experiments have revealed that genomes are functional in 4D. Although computational modeling methods can convert 2D Hi-C data into population-averaged static 3D genome models, exploring 4D genome nature based on 2D Hi-C data remains lacking. Here, we describe a 4D simulation method, PHi-C (polymer dynamics deciphered from Hi-C data), that depicts 4D genome features from 2D Hi-C data by polymer modeling. PHi-C allows users to interpret 2D Hi-C data as physical interaction parameters within single chromosomes. The physical interaction parameters can then be used in the simulations and analyses to demonstrate dynamic characteristics of genomic loci and chromosomes as observed in live-cell imaging experiments. PHi-C is available at https://github.com/soyashinkai/PHi-C.
INTRODUCTION
Genomes consist of 1D DNA sequences and are spatiotemporally organized within the cell nucleus. Contact frequencies in the form of matrix data, measured using genome-wide chromosome conformation capture (Hi-C) technologies, have uncovered 3D features of average genome organization in a cell population (1,2). Moreover, live-cell imaging experiments can reveal dynamic chromatin organization in response to biological perturbations within single cells (3–5). Proper expression of genes should require orchestration of their regulatory elements within the dynamic 3D genome organization. Bridging the gap between these different sets of data derived from population and single cells is a challenge for modeling dynamic genome organization (6,7).
Every Hi-C experiment provides 2D contact matrix data for a population of cells. Several computational modeling methods have been developed to reconstruct population-averaged static 3D genome structures from 2D contact matrix data and predict Hi-C data (8–10). In addition, there has been the development of not only bioinformatic normalization techniques in Hi-C matrix data processing to reduce experimental biases by matrix balancing (11–13) but also probabilistic modeling to eliminate systematic biases (14,15). However, the meaning of a contact matrix as quantitative probability data has not been discussed; moreover, both a concept and a computational method to explore dynamic 3D genome organization remain lacking.
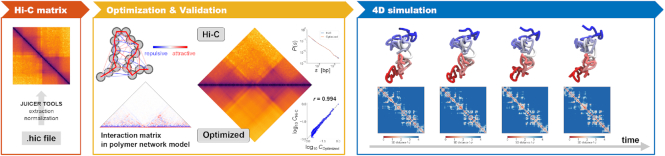
Here, we propose PHi-C (polymer dynamics deciphered from Hi-C data), a simulation tool that can overcome these challenges by polymer modeling from a mathematical perspective and at low computational cost. PHi-C is a method that deciphers Hi-C data into polymer dynamics simulations (Figure 1). PHi-C uses Hi-C contact matrix data generated from a hic file through JUICER (16) as input (Supplementary Figure S1A). PHi-C assumes that a genomic region of interest at an appropriate resolution can be modeled using a polymer network model, in which one monomer corresponds to the genomic bin size of the contact matrix data with attractive and repulsive interaction parameters between all pairs of monomers described as matrix data (see the ‘Materials and Methods’ section). Instead of finding optimized 3D conformations, we can utilize the optimization procedure (Supplementary Figure S1B and S1C) to obtain optimal interaction parameters of the polymer network model by using an analytical relationship between the parameters and the contact matrix. We can then reconstruct an optimized contact matrix validated by input Hi-C matrix data using Pearson’s correlation r. Finally, we can perform polymer dynamics simulations of the polymer network model equipped with the optimal interaction parameters.
Figure 1.
Overview of PHi-C pipeline. Hi-C contact matrix data generated from a hic file through JUICER are deciphered by the PHi-C optimization algorithm based on the polymer network model. Then, 4D polymer dynamics simulations of the polymer network model with the optimized interaction parameters are carried out.
MATERIALS AND METHODS
Defining contacts in polymer modeling
The bead–spring model in polymer physics consists of N beads (or monomers) connected by N − 1 harmonic springs along the polymer backbone (Figure 2), where a polymer conformation is represented by 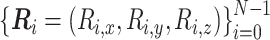 and the characteristic length between adjacent monomers is expressed by b (17). The linearity of the harmonic springs enables us to analytically calculate the probability of the conformation
and the characteristic length between adjacent monomers is expressed by b (17). The linearity of the harmonic springs enables us to analytically calculate the probability of the conformation 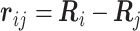 between the ith and jth monomers as follows:
between the ith and jth monomers as follows: 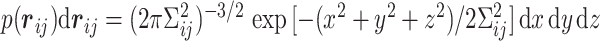 , where
, where 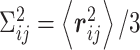 is the variance for space coordinate (i.e. x, y,
is the variance for space coordinate (i.e. x, y, 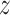 ). Then, the probability density function for the distance
). Then, the probability density function for the distance 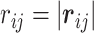 becomes
becomes  . So far, a mathematical expression to define contacts within the contact distance σ has been written by
. So far, a mathematical expression to define contacts within the contact distance σ has been written by 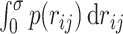 (7,18). However, the expression makes it difficult to improve further analytical calculations. Therefore, we introduced the contact Gaussian kernel with σ (Figure 2). Then, the contact probability between the ith and jth monomers is represented by
(7,18). However, the expression makes it difficult to improve further analytical calculations. Therefore, we introduced the contact Gaussian kernel with σ (Figure 2). Then, the contact probability between the ith and jth monomers is represented by 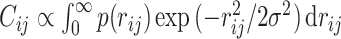 . Finally, under the normalization Cii = 1, the contact probability can be expressed as
. Finally, under the normalization Cii = 1, the contact probability can be expressed as
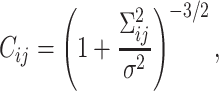 |
(1) |
which means that the ratio of the conformational fluctuation Σij to the contact distance σ is a physically important parameter to define the contacts. Note that Equation (1) was also recently derived with a similar consideration (19).
Figure 2.
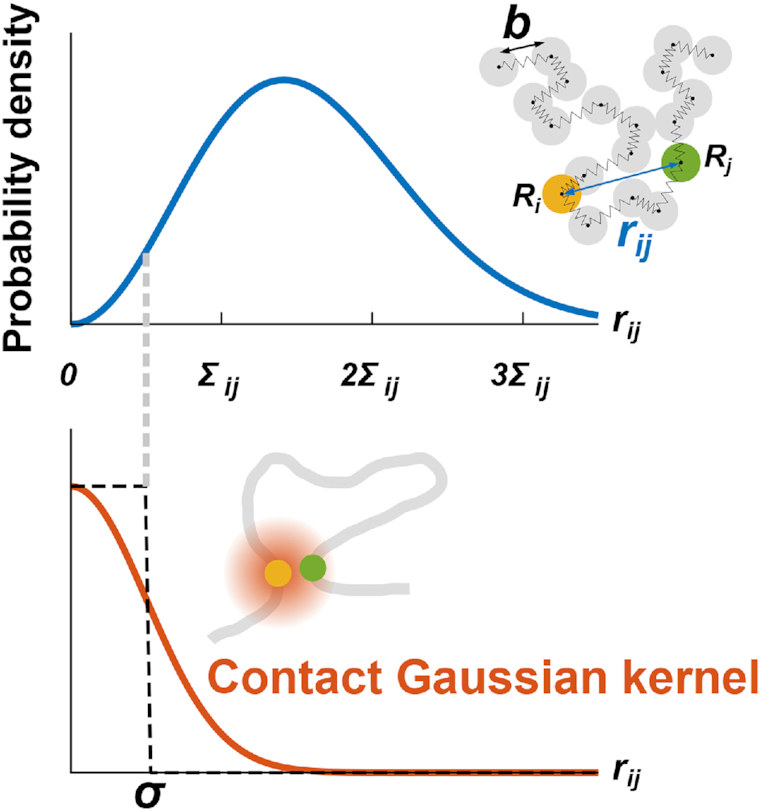
(Upper) In the bead–spring model, the probability density of the distance rij between the ith and jth beads (or monomers) is characterized by only the standard deviation Σij. (Lower) The contact Gaussian kernel function can capture contacts with the contact distance σ.
Matrix transformations between polymer network model and contact matrix
The polymer network model is a generalized model of the bead–spring model and the Gaussian network model (20–22), and is characterized by the interaction matrix 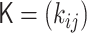 , which is an N × N matrix for an N-monomer polymer system. The element kij generally represents the intensity of attractive or repulsive interaction between the ith and jth monomers. Therefore, the matrix satisfies kii = 0 and
, which is an N × N matrix for an N-monomer polymer system. The element kij generally represents the intensity of attractive or repulsive interaction between the ith and jth monomers. Therefore, the matrix satisfies kii = 0 and 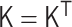 . Basically, the elastic force between two monomers results from an attractive interaction with a positive value. Furthermore, here, we take into account negative values, which represent repulsive interactions between monomers.
. Basically, the elastic force between two monomers results from an attractive interaction with a positive value. Furthermore, here, we take into account negative values, which represent repulsive interactions between monomers.
Through analytical calculations in the theoretical framework of the polymer network model (see Supplementary Data), we found matrix transformations between the interaction matrix of the polymer network model 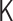 and the contact matrix
and the contact matrix 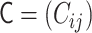 (Figure 3):
(Figure 3): 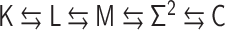 , where the matrices
, where the matrices  ,
, 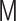 and
and 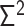 represent the Laplacian, covariance and variance matrices, respectively. The analytical matrix transformations are straightforwardly implemented in our Python codes using the NumPy package.
represent the Laplacian, covariance and variance matrices, respectively. The analytical matrix transformations are straightforwardly implemented in our Python codes using the NumPy package.
Figure 3.
The polymer network model is characterized by connectivity between all pairs of monomers, expressed by the interaction matrix kij. The matrix kij is reversibly converted into the contact matrix Cij through matrix transformations 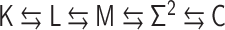 . Each matrix has dimensionless values with a normalization factor.
. Each matrix has dimensionless values with a normalization factor.
Overview of PHi-C
PHi-C enables us to decipher Hi-C data into polymer dynamics simulation. PHi-C is based on the theory of the polymer network model and defining contacts between two monomers on the polymer (Supplementary Data). The theoretical framework provides the following matrix transformations (Figure 3), where the matrix size is N × N: (i) the normalized interaction matrix 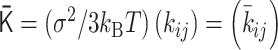 into the normalized Laplacian matrix
into the normalized Laplacian matrix 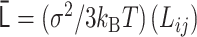 by
by 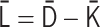 , where the normalized degree matrix
, where the normalized degree matrix 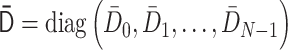 , where
, where 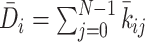 . (ii) As
. (ii) As 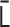 is real symmetric,
is real symmetric, 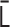 is diagonalizable. Furthermore, as long as
is diagonalizable. Furthermore, as long as 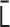 is positive semidefinite, the N eigenvalues satisfy
is positive semidefinite, the N eigenvalues satisfy 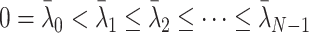 . Therefore,
. Therefore, 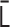 can be transformed into the normalized covariance matrix relative to the center of mass
can be transformed into the normalized covariance matrix relative to the center of mass 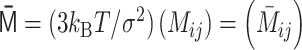 by
by 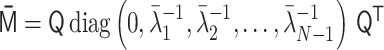 , where
, where 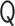 is the orthogonal matrix satisfying
is the orthogonal matrix satisfying 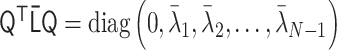 . (iii)
. (iii) 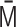 into the normalized variance matrix
into the normalized variance matrix 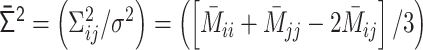 . (iv)
. (iv) 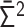 into the contact matrix
into the contact matrix 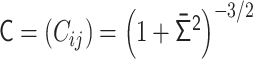 . Note that the normalized Laplacian matrix
. Note that the normalized Laplacian matrix 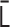 should be positive semidefinite. In terms of physics, the positive semidefiniteness is a necessary and sufficient condition for the stability of the polymer network model (Supplementary Data). Therefore, the normalized interaction matrix
should be positive semidefinite. In terms of physics, the positive semidefiniteness is a necessary and sufficient condition for the stability of the polymer network model (Supplementary Data). Therefore, the normalized interaction matrix 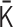 is restricted by the positive-semidefinite condition of
is restricted by the positive-semidefinite condition of 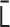 . Theoretically, the matrix transformations between
. Theoretically, the matrix transformations between 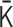 and
and 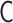 are invertible, and we had found the inverse matrix transformations from
are invertible, and we had found the inverse matrix transformations from 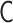 to
to 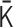 . However, when we apply the inverse transformations to experimental Hi-C data, it does not work. The reason is that the inverse-transformed Laplacian matrix does not satisfy the positive-semidefinite condition. That is, we could not use the inverse matrix transformations straightforwardly. Thus, we developed an optimization procedure, described below, to obtain an optimal interaction matrix
. However, when we apply the inverse transformations to experimental Hi-C data, it does not work. The reason is that the inverse-transformed Laplacian matrix does not satisfy the positive-semidefinite condition. That is, we could not use the inverse matrix transformations straightforwardly. Thus, we developed an optimization procedure, described below, to obtain an optimal interaction matrix 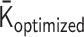 from an experimental contact matrix
from an experimental contact matrix  .
.
The matrix 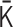 describing attractive and repulsive interactions of the polymer network model is optimized so that the difference between an input Hi-C contact matrix
describing attractive and repulsive interactions of the polymer network model is optimized so that the difference between an input Hi-C contact matrix  and the reconstructed contact matrix
and the reconstructed contact matrix  , through the above transformations, is minimized. Finally, a 4D simulation of the polymer network model with the optimized matrix
, through the above transformations, is minimized. Finally, a 4D simulation of the polymer network model with the optimized matrix 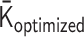 is performed. Below, we describe each step in Figure 1 in detail.
is performed. Below, we describe each step in Figure 1 in detail.
Input data
PHi-C requires N × N contact matrix data for a genomic region of interest as an input, which are generated through the JUICER and JUICER TOOLS (16) from public Hi-C data with a normalization option (VC/VC_SQRT/KR). Here, we used the KR normalization (23). In our theoretical framework, the diagonal elements of the contact matrix should satisfy Cii = 1, so we additionally normalized the contact matrix such that the shape of the contact probability as a function of genomic distance P(s) is unaltered, with an interpolation if needed (Supplementary Figure S1A). Note that the interpolation may result in artifacts for sparse contact matrix data. Besides, our physical assumption for the polymer network model in the equilibrium state requires that an input contact matrix should be dense so that each element value of the contact matrix has a meaning as a probability. Therefore, according to the depth of sequence reads, the matrix size N and the binning resolution should be tuned so that a contact matrix becomes as dense as possible with fewer interpolations. Finally, we obtained a normalized Hi-C contact matrix  .
.
Optimization and validation
The optimization algorithm is designed to minimize the Frobenius norm  as a cost function, where the contact matrix
as a cost function, where the contact matrix  is generated from the normalized interaction matrix
is generated from the normalized interaction matrix 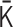 . At every optimization step, an integer pair (i, j) is randomly selected, and the values of
. At every optimization step, an integer pair (i, j) is randomly selected, and the values of 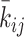 and
and 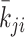 are slightly altered. If the alteration decreases the cost function, the matrix
are slightly altered. If the alteration decreases the cost function, the matrix 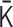 is updated, and the positive semidefiniteness of the Laplacian matrix generated from the updated
is updated, and the positive semidefiniteness of the Laplacian matrix generated from the updated 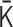 is checked. A flowchart of the algorithm is presented in Supplementary Figure S1B.
is checked. A flowchart of the algorithm is presented in Supplementary Figure S1B.
As our optimization method is based on the random sampling of integer pairs, the amount of calculation in the procedure is proportional to O(N2). In our demo codes, the hyperparameters for the optimization are tuned, and it takes ∼13 min to obtain an optimized solution for N = 97, even on our laptop PC (Intel® Core™ i7-6600U, dual-core 2.60 GHz). Detail benchmarks in the optimization procedure with changing matrix size are summarized at https://github.com/soyashinkai/PHi-C#benchmark-of-the-optimization-procedure.
After optimization, an optimized contact matrix 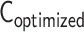 is converted from an optimized matrix
is converted from an optimized matrix  . To assess the compatibility between contact matrices
. To assess the compatibility between contact matrices 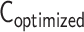 and
and  in a logarithmic scale, we used Pearson’s correlation coefficient r.
in a logarithmic scale, we used Pearson’s correlation coefficient r.
Polymer dynamics simulation
We performed 4D simulations of the polymer network model by using the normalized interaction matrix 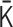 . First,
. First, 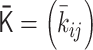 is converted into the normalized Laplacian matrix
is converted into the normalized Laplacian matrix 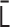 . Using the eigendecomposition of the matrix
. Using the eigendecomposition of the matrix 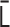 , the normalized eigenvalues
, the normalized eigenvalues 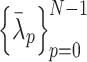 and the orthogonal matrix
and the orthogonal matrix 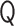 are obtained. For a normalized polymer conformation vector
are obtained. For a normalized polymer conformation vector 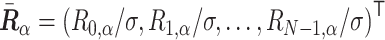 , where Ri,α stands for the α (= x, y,
, where Ri,α stands for the α (= x, y, 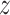 ) coordinate of the ith monomer, the converted vector
) coordinate of the ith monomer, the converted vector 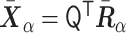 satisfies the variance relationship
satisfies the variance relationship 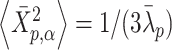 for
for 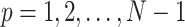 . Therefore, an initial conformation of the converted vector in thermal equilibrium is given:
. Therefore, an initial conformation of the converted vector in thermal equilibrium is given: 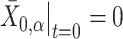 , so that the center of mass is the origin and
, so that the center of mass is the origin and 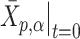 is a random variable obeying the normal distribution with mean 0 and variance
is a random variable obeying the normal distribution with mean 0 and variance 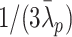 for
for 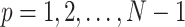 . Then, the initial normalized conformation in thermal equilibrium is calculated as
. Then, the initial normalized conformation in thermal equilibrium is calculated as 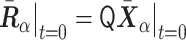 . Finally, to calculate the polymer dynamics, we numerically integrated the stochastic differential equation (SDE) by using Heun’s method (24): the integral algorithm assures the second-order convergence in ε (25) and is defined by first predicting
. Finally, to calculate the polymer dynamics, we numerically integrated the stochastic differential equation (SDE) by using Heun’s method (24): the integral algorithm assures the second-order convergence in ε (25) and is defined by first predicting
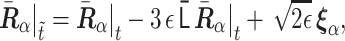 |
(2) |
and then correcting
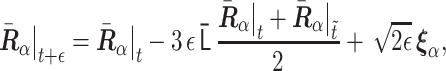 |
(3) |
where the vector 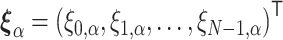 consists of random variables
consists of random variables 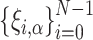 obeying the normal distribution with mean 0 and variance 1. The parameter
obeying the normal distribution with mean 0 and variance 1. The parameter 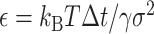 is nondimensional and represents a normalized step time, and it determines the accuracy of the SDE integration. Δt stands for the step time of the integration in actual time. Here, we set ε = 0.0001.
is nondimensional and represents a normalized step time, and it determines the accuracy of the SDE integration. Δt stands for the step time of the integration in actual time. Here, we set ε = 0.0001.
Visualization of polymer conformation
The code for polymer dynamics simulation outputs XYZ and PSF files to visualize the simulated polymer dynamics. Polymer conformations were visualized using VMD (26) by reading these files.
Contact probability of fractal polymers
When a polymer globule composed of N monomers is organized with the average diameter R, the average polymer conformation can be characterized by the scaling law 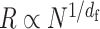 , where df represent the fractal dimension. Here, the fractal polymer with df is a generalized model of the bead–spring model with the scaling
, where df represent the fractal dimension. Here, the fractal polymer with df is a generalized model of the bead–spring model with the scaling 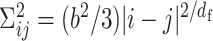 , and the fractal dimension can characterize polymer condensation states (27,28) (Supplementary Figure S2A). Substituting the scaling into Equation (1), we obtained a mathematical relation for the contact probability as a function of genomic distance s,
, and the fractal dimension can characterize polymer condensation states (27,28) (Supplementary Figure S2A). Substituting the scaling into Equation (1), we obtained a mathematical relation for the contact probability as a function of genomic distance s,
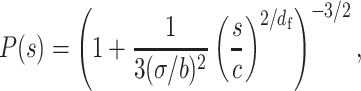 |
(4) |
where c is the genomic size corresponding to a modeled monomer. Theoretical curves for the decay show two features (Figure 4A): (i) the ratio σ/b results in a rounded shape at a small genomic distance and (ii) the fractal dimension determines the scaling at a large genomic distance,
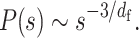 |
(5) |
Equations (4) and (5) allow us to extract physical information, σ/b and df, from experimental P(s) data by fitting the parameters.
Figure 4.
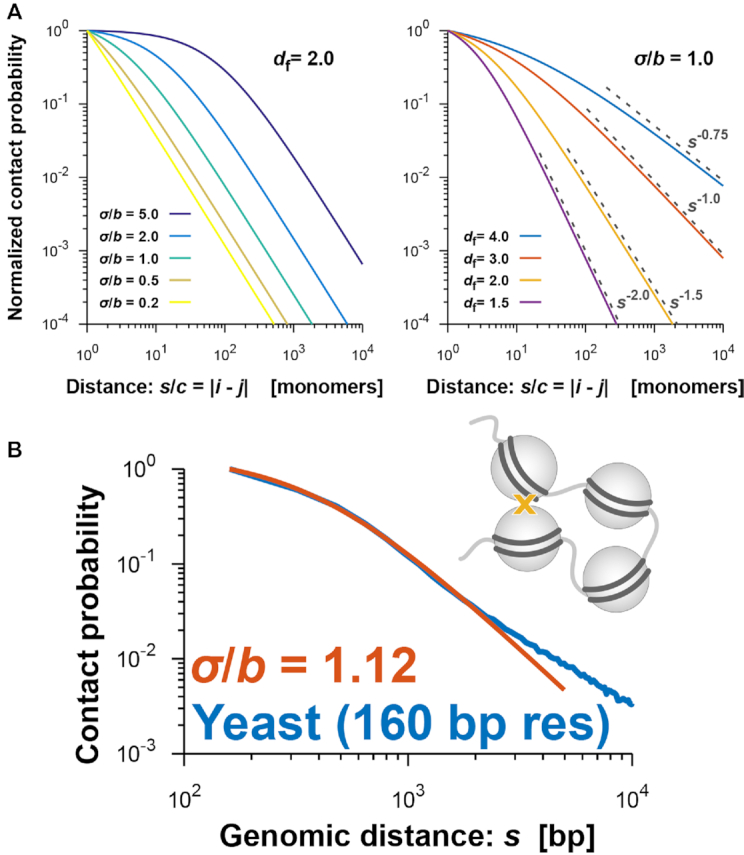
(A) Theoretical curves of the contact probability P(s) in Equation (4). P(s) is normalized by the value at s/c = |i − j| = 1, where i and j are monomer indices of the fractal polymer and c represents the genomic size corresponding to every monomer. (Left) P(s) for fixed df = 2.0 and σ/b = 0.2, 0.5, 1.0, 2.0 and 5.0. (Right) P(s) for fixed σ/b = 1.0 and df = 1.5, 2.0, 3.0 and 4.0. Theoretical scaling relations, as in Equation (5), are shown. (B) Contact probability (blue) for yeast cells with 160-bp nucleosome resolution (31) as a function of genomic distance averaged across the genome, and the theoretically fitted curve (orange) at a small genomic distance.
Fitting contact probability
In terms of the fractal polymer, the contact probability, P(s), from high-resolution Hi-C data was fitted by Equations (4) and (5) for small and large genomic regions, respectively. The ratio σ/b and the fractal dimension df are the fitted parameters, and c stands for the genomic size corresponding to the bin size of the Hi-C matrix. We used the nonlinear least-squares Marquardt–Levenberg algorithm on GNUPLOT.
Calculating mean-squared displacement of genome loci
We re-analyzed movements of Nanog and Oct4 loci in mouse embryonic stem cells (mESCs) measured by Ochiai et al. (29). In each session of live imaging, 3D time series of a genome locus (Nanog or Oct4) and the nucleus center of mass, 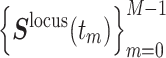 and
and 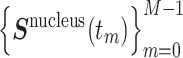 , were simultaneously acquired, where the maximum frame number was M = 50, the time interval was Δt = 10 s and tm = m Δt (
, were simultaneously acquired, where the maximum frame number was M = 50, the time interval was Δt = 10 s and tm = m Δt (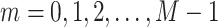 ). To eliminate the effect of the nucleus movement, we dealt with the locus movement relative to the nucleus center described by the time series
). To eliminate the effect of the nucleus movement, we dealt with the locus movement relative to the nucleus center described by the time series 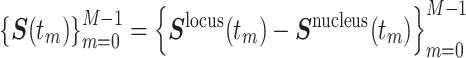 . Then, the time-averaged mean-squared displacement (TAMSD) for a time series
. Then, the time-averaged mean-squared displacement (TAMSD) for a time series 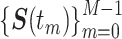 was calculated as follows:
was calculated as follows:
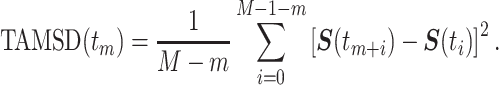 |
(6) |
Calculating theoretical MSD curve
The optimized matrix 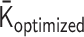 derives a theoretical MSD curve for the ith monomer in the polymer network model as follows [Equation (S23) in Supplementary Data]:
derives a theoretical MSD curve for the ith monomer in the polymer network model as follows [Equation (S23) in Supplementary Data]:
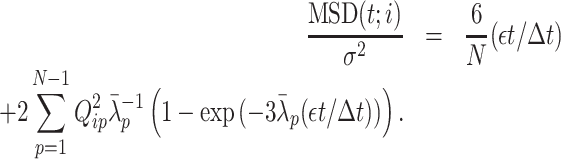 |
(7) |
Here, not only is the MSD normalized by σ2 in the length scale, but the time step is also normalized in time; that is, MSD/σ2 and εt/Δt are dimensionless.
Calculating radius of gyration
As we described in the ‘Polymer Dynamics Simulation’ section, a normalized polymer conformation 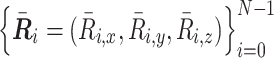 in thermal equilibrium can be sampled on the basis of the optimized matrix
in thermal equilibrium can be sampled on the basis of the optimized matrix 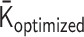 . Therefore, we can estimate the physical conformations of the 50.5-Mb genomic regions around Nanog and Oct4 loci in mESCs by calculating the radius of gyration. By using two integers nstart and nend corresponding to the 50.5-Mb region, the radius of gyration is calculated as
. Therefore, we can estimate the physical conformations of the 50.5-Mb genomic regions around Nanog and Oct4 loci in mESCs by calculating the radius of gyration. By using two integers nstart and nend corresponding to the 50.5-Mb region, the radius of gyration is calculated as
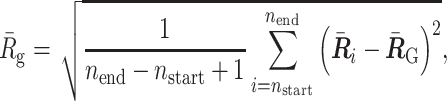 |
(8) |
where 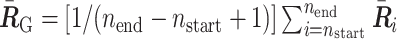 represents the center of mass of the polymer conformation of the 50.5-Mb genomic region.
represents the center of mass of the polymer conformation of the 50.5-Mb genomic region.
Simulating polymer dynamics during chromosome condensation
We applied PHi-C to Hi-C data during mitotic chromosome formation in chicken DT-40 cells (30). We used the second dataset of chromosome 7 (binned at 100 kb) for the wild type at G2 (0 min), 5, 15, 30 and 60 min. We eliminated the centromere region due to the lack of associated read counts. Through the optimization of PHi-C, we obtained the optimized matrices 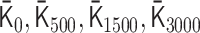 and
and 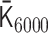 , respectively (Supplementary Figure S5). Here, the suffix n of the matrix
, respectively (Supplementary Figure S5). Here, the suffix n of the matrix 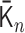 represents the time
represents the time 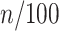 min for the Hi-C data. To simulate the polymer dynamics during chromosome condensation, we linearly interpolated the matrices
min for the Hi-C data. To simulate the polymer dynamics during chromosome condensation, we linearly interpolated the matrices 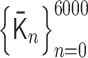 as follows:
as follows: 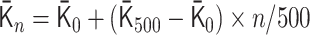 for 0 ≤ n < 500,
for 0 ≤ n < 500, 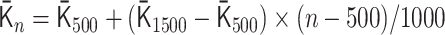 for 500 ≤ n < 1500,
for 500 ≤ n < 1500, 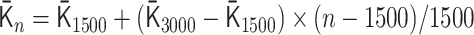 for 1500 ≤ n < 3000 and
for 1500 ≤ n < 3000 and 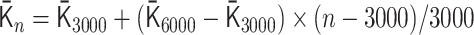 for 3000 ≤ n ≤ 6000. By using
for 3000 ≤ n ≤ 6000. By using 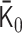 , an initial polymer conformation was sampled. Then, the polymer dynamics between
, an initial polymer conformation was sampled. Then, the polymer dynamics between 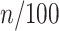 and
and 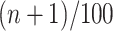 min was calculated by 1000 steps of numerical integration with
min was calculated by 1000 steps of numerical integration with 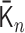 based on the integral algorithm [Equations (2) and (3)).
based on the integral algorithm [Equations (2) and (3)).
In the visualization, we fixed the center of mass of polymer conformations to the origin (Figure 7B, Supplementary Videos S4 and S5).
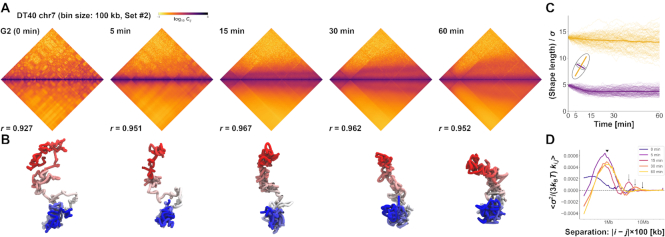
Figure 7.
Demonstrations of PHi-C for Hi-C data of DT-40 cells. (A) PHi-C analysis for chromosome 7 of DT-40 cells at G2 (0 min), 5, 15, 30 and 60 min. Contact matrices of the Hi-C experiment with 100-kb bins (upper) and optimized contact matrices with the correlation value (lower). (B) Snapshots of polymer conformations in a 4D polymer dynamics simulation. (C) Time series of the shape lengths of the major (yellow) and minor (purple) axes for polymer conformations in 100 polymer dynamics simulations starting from the same initial conformation. Thick curves represent the averages. (D) Curves of optimized interaction parameters, 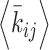 , averaged at each genomic distance (separation, |i − j| × 100 kb). A triangle indicates a position of a local peak inducing compaction within 2 Mb. Arrows indicate positions of a local peak generating periodicity of attractive interactions around 4, 6 and 10 Mb at 15, 30 and 60 min, respectively.
, averaged at each genomic distance (separation, |i − j| × 100 kb). A triangle indicates a position of a local peak inducing compaction within 2 Mb. Arrows indicate positions of a local peak generating periodicity of attractive interactions around 4, 6 and 10 Mb at 15, 30 and 60 min, respectively.
Calculating shape length of polymer conformation
To quantify the characteristic shape of a polymer conformation 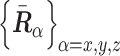 during chromosome condensation, we evaluated the characteristic shape lengths as an ellipsoidal conformation based on the gyration tensor
during chromosome condensation, we evaluated the characteristic shape lengths as an ellipsoidal conformation based on the gyration tensor 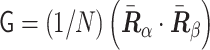 . We calculated the three eigenvalues
. We calculated the three eigenvalues 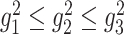 of the tensor
of the tensor 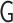 . Then, we adopted g3 and
. Then, we adopted g3 and 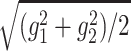 as the characteristic shape lengths of the major and minor axes, respectively (Figure 7C).
as the characteristic shape lengths of the major and minor axes, respectively (Figure 7C).
Code availability
Python codes of PHi-C are available at https://github.com/soyashinkai/PHi-C.
Data availability
Published publicly available Hi-C data were used in this study: Ohno et al. (31) (BioProject: PRJNA427106), Rao et al. (12) (GEO: GSE63525), Bonev et al. (32) (GEO: GSE96107) and Gibcus et al. (30) (GEO: GSE102740). Input Hi-C matrix data of PHi-C were generated through the JUICER and JUICER TOOLS (16).
RESULTS
Validation of PHi-C’s theoretical assumption regarding chromosome contact
First, we evaluated PHi-C’s theoretical assumption about chromosome contact. Here, we started with a simple polymer model called the bead–spring model, in which the characteristic length b between adjacent beads (or monomers) represents the physical size corresponding to one genomic bin of the contact matrix data (see the ‘Materials and Methods’ section). To mathematically define the contact between a pair of monomers, we introduced the contact Gaussian kernel with the contact distance σ (Figure 2). Almost computational 3D genome modeling techniques have relied on a conventionally assumed mathematical relationship: Hi-C contact matrix data, Cij, should be a function of the spatial distance, rij, between the ith and jth monomers in a polymer model. Although this relationship is reasonable to elucidate the population-averaged static 3D genome structures, the assumption cannot be extended beyond a static perspective of the 3D genome. As shown in Equation (1), we elucidated the following relationship: the contact matrix data, Cij, is a function of not the spatial distance, rij, but the dynamic range, Σij, between the ith and jth monomers in a polymer model. The dynamic property of chromatin fibers should contribute to the chromosome contacts in Hi-C experiments.
The above mathematical assumption can be used to derive the theoretical scaling relationship of the contact probability, 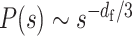 [Equation (5)], as a function of genomic distance s in terms of the fractal dimension of polymer organization df (27) (Supplementary Figure S2A). In addition, interestingly, the ratio of the contact distance to the length between adjacent monomers, σ/b, makes the shape of the contact probability rounder at a small genomic distance (Figure 4A). This phenomenon implies that the rounded shape conveys information about the ratio σ/b. As we predicted, such a rounded shape was observed in yeast Hi-C data at nucleosome resolution (binned at 160 bp) (31). The fitted value was σ/b = 1.12, supporting our theoretical framework about contact and suggesting that contacts mainly occur within a distance corresponding to the size of a nucleosome in this super-resolution Hi-C experiment (Figure 4B, Supplementary Figure S2B). Other high-resolution Hi-C data for human GM12878 (12) revealed σ/b = 1.38, suggesting that cross-linking of Hi-C experiments almost exactly captures chromosome contacts with the binned resolution (Supplementary Figure S2C).
[Equation (5)], as a function of genomic distance s in terms of the fractal dimension of polymer organization df (27) (Supplementary Figure S2A). In addition, interestingly, the ratio of the contact distance to the length between adjacent monomers, σ/b, makes the shape of the contact probability rounder at a small genomic distance (Figure 4A). This phenomenon implies that the rounded shape conveys information about the ratio σ/b. As we predicted, such a rounded shape was observed in yeast Hi-C data at nucleosome resolution (binned at 160 bp) (31). The fitted value was σ/b = 1.12, supporting our theoretical framework about contact and suggesting that contacts mainly occur within a distance corresponding to the size of a nucleosome in this super-resolution Hi-C experiment (Figure 4B, Supplementary Figure S2B). Other high-resolution Hi-C data for human GM12878 (12) revealed σ/b = 1.38, suggesting that cross-linking of Hi-C experiments almost exactly captures chromosome contacts with the binned resolution (Supplementary Figure S2C).
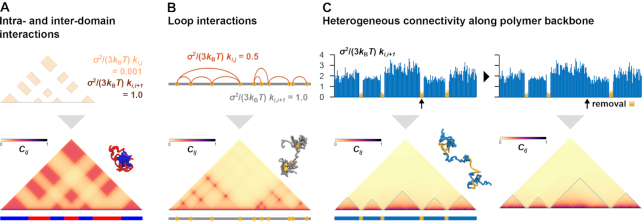
Matrix transformations in PHi-C’s polymer modeling allow for fast optimization, painting any contact pattern and 4D simulations
To decipher Hi-C contact matrix data computationally, the optimization procedure of PHi-C is essential and based on analytical matrix transformations between the polymer network model and the contact matrix (Figure 3, ‘Materials and Methods’ section). The matrix transformations provided us with a low computational cost optimization strategy that can be applied to find optimal interaction parameters of the polymer network model without sampling optimal static 3D polymer conformations (Supplementary Figure S1B and S1C). Moreover, we can depict any contact pattern in a moment by using the matrix transformations and perform polymer dynamics simulations by designing interactions in the polymer network model (Figure 5, Supplementary Videos S1–S3). Intra- and interdomain interactions generate a checkerboard pattern reminiscent of A/B compartments (1,2), and the attractive interaction domains form a combined domain (Figure 5A). Loop interactions show a clear punctate pattern (Figure 5B). Furthermore, we can depict a topologically associating domain (TAD)-like pattern (1,2) by only tuning heterogeneous connectivity along the polymer backbone, where less connected regions behave as domain boundaries (Figure 5C, left). The 3D conformation suggests that the boundary regions are physically elongated with insulating inter-TAD-like-domain interactions. In addition, the removal of a boundary part causes the adjacent domain fusion (Figure 5C, right) that reminds us of fusions of TADs (10,33).
Figure 5.
Painting contact patterns for intra- and interdomain interactions (A), loop interactions (B) and heterogeneous connectivity along the polymer backbone (C). (Upper) Designed interactions in the polymer network model. (Lower) Converted contact matrix, with a snapshot of polymer conformations in the polymer dynamics simulation (Supplementary Videos S1–S3). (C) TAD-like domains are highlighted by dashed lines. (Right) Removal of a domain-boundary part (yellow) results in domain fusion.
PHi-C analysis provides physical insights into dynamic genome organization of mouse embryonic stem cells
So far, computational approaches to reconstruct static 3D genome structures from Hi-C data are not able to explain the dynamic movement of chromatin in living cells. However, our PHi-C method can provide not only 4D simulations but also the theoretical MSD curves as the dynamic features of chromatin. Therefore, we can compare and predict the differences in the dynamic movement of genomic loci based on Hi-C data.
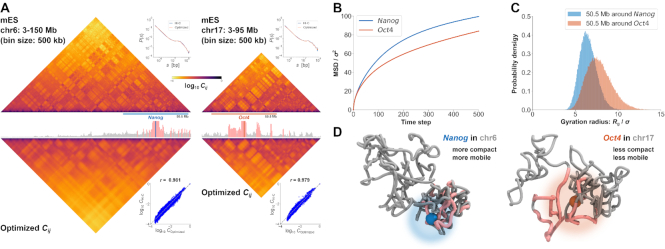
To investigate how PHi-C explains 4D features of chromosomes within living cells, we applied this approach to Hi-C data for mESCs (32). A live-cell imaging experiment showed a marked difference in the movements of Nanog and Oct4 loci in mESCs (29): statistically significant enhancement of Nanog diffusive movement compared with Oct4 diffusive movement was revealed (Supplementary Figure S3). The optimization step of the PHi-C analysis for chromosomes 6 and 17 provided optimized contact matrices with correlations of >97% between the Hi-C and optimized contact matrices (Figure 6A). The MSD curves that were theoretically derived from the optimized data for the Nanog locus on chromosome 6 and the Oct4 locus on chromosome 17 are consistent with the experimental dynamics (Figure 6B). We also compared the physical sizes of 50.5-Mb genomic regions around the Nanog and Oct4 loci, with the inclusion of several areas that highly interact with each locus, and observed more compact organization of the Nanog region (Figure 6C). Taking together, these findings indicate that PHi-C analysis can provide new insights into genome organization and dynamics: for example, a region of 50.5 Mb around Nanog adopts a more compact organization than an equivalent region around Oct4, and the Nanog locus on chromosome 6 is more mobile than the Oct4 locus on chromosome 17 (Figure 6D).
Figure 6.
Demonstrations of PHi-C for Hi-C data of mESCs. (A) PHi-C analysis for chromosomes 6 (left) and 17 (right) of mESCs. (Upper) Contact matrices of the Hi-C experiment (binned at 500 kb), and contact probabilities as a function of genomic distance. (Middle) 4C-like profiles of Nanog (left) and Oct4 (right) loci. High-interaction regions are highlighted (pink). (Lower) Optimized contact matrices by PHi-C, and correlation plots between 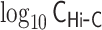 and
and 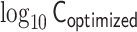 . (B) Theoretical MSD curves of Nanog and Oct4 loci. (C) Probability densities of the gyration radius of 105 conformations for the 50.5-Mb genomic regions around Nanog and Oct4 loci in mESCs. (D) Polymer models derived from PHi-C analysis for Nanog and Oct4 loci on chromosomes 6 and 17, respectively. Pink highlighted regions on the polymer models correspond to the regions in the 4C-like profile of (A).
. (B) Theoretical MSD curves of Nanog and Oct4 loci. (C) Probability densities of the gyration radius of 105 conformations for the 50.5-Mb genomic regions around Nanog and Oct4 loci in mESCs. (D) Polymer models derived from PHi-C analysis for Nanog and Oct4 loci on chromosomes 6 and 17, respectively. Pink highlighted regions on the polymer models correspond to the regions in the 4C-like profile of (A).
4D simulations of PHi-C enable to demonstrate the dynamic chromosome condensation process of chicken cells
Finally, we used PHi-C to demonstrate the dynamic chromosome condensation process for the highly synchronous entry of DT-40 cells, which revealed a pathway for mitotic chromosome formation (30). The optimized contact matrices at five different time points were reconstructed with high correlations (Figure 7A, Supplementary Figure S4). Using the optimized interaction parameters in the polymer network model (Supplementary Figure S5), we conducted 4D simulations starting from a comparatively elongated conformation at 0 min. The polymer conformation dynamically changed into a rod-shaped structure, revealing the condensation state of chromosomes at prometaphase (Figure 7B, Supplementary Videos S4 and S5). We evaluated dynamic changes in polymer conformations in simulations by calculating the characteristic shape lengths of the major and minor axes. As observed by microscopy, rapid and gradual decreases in the minor and major axes within 15 and 60 min indicated thin and thick rod-shaped formations, respectively (Figure 7C). In addition, the optimized interaction parameters averaged at each genomic separation represent not only strong compaction within 2 Mb during mitosis but also increase of periodicity of long-range attractive interactions from 3 to 12 Mb in prometaphase (Figure 7D). These physical findings are consistent with a helical organization in rod-shaped chromosomes during prometaphase (30).
DISCUSSION
PHi-C provides dynamic 3D genome features by deciphering Hi-C data into polymer dynamics. In the development of the PHi-C method, the derivation of Equation (1) is critical to bridging the gap between the contact matrix data and the dynamics property of the polymer model. As shown in Figure 2, the Gaussian contact kernel with the contact distance σ is mathematically able to take into account variations of the chromosome contact distance in Hi-C experiments. In addition, our prediction that the finite contact distance affects the rounded shape of the contact probability P(s) was verified to super-resolution Hi-C data for yeast and human GM12878 cells (Figure 3, Supplementary Figure S2). At least, our mathematical consideration must be correct as a first approximation to understand the meaning of the contact frequency, but there would be a mathematical improvement to express the more detailed quantitative probability data.
The PHi-C optimization procedure relies on the matrix transformations between the interaction matrix 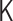 of the polymer network model and the contact matrix
of the polymer network model and the contact matrix 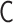 (Figure 3). Within the range of the theoretical framework, the relation
(Figure 3). Within the range of the theoretical framework, the relation 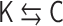 means a one-to-one correspondence. There exists the analytical inverse transformation from
means a one-to-one correspondence. There exists the analytical inverse transformation from 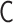 to
to 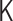 . However, applying the inverse transformation to experimental Hi-C data caused numerical divergence. Experimental noise of Hi-C data and the effect of the matrix normalization would be the reason. In the optimization algorithm, the Frobenius norm
. However, applying the inverse transformation to experimental Hi-C data caused numerical divergence. Experimental noise of Hi-C data and the effect of the matrix normalization would be the reason. In the optimization algorithm, the Frobenius norm  as a cost function allows for obtaining an optimized solution
as a cost function allows for obtaining an optimized solution 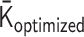 so that the logarithmic values of the reconstructed contact matrix data are close to the experimental Hi-C data. So far, the cost function is practically better in PHi-C, but there would be other cost functions. Further mathematical development regarding the optimization is needed.
so that the logarithmic values of the reconstructed contact matrix data are close to the experimental Hi-C data. So far, the cost function is practically better in PHi-C, but there would be other cost functions. Further mathematical development regarding the optimization is needed.
In principle, as shown in Figure 5, the matrix transformations enable us to depict any contact patterns. In other words, the interaction matrix 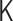 physically implies a mean field of the population-averaged chromosome folding. Therefore, our polymer modeling cannot take into account some active processes on chromosomes known as the loop extrusion model to explain the mechanisms of TAD formation (34). Recent experiments have shown that enrichment of specific proteins on TAD boundaries promotes such active processes to form TADs (35–37). However, as long as a reconstructed contact matrix by our PHi-C method shows a good agreement with an experimental contact matrix, the stochastic and dynamic nature in our polymer model might be a mechanism to maintain the TAD formation.
physically implies a mean field of the population-averaged chromosome folding. Therefore, our polymer modeling cannot take into account some active processes on chromosomes known as the loop extrusion model to explain the mechanisms of TAD formation (34). Recent experiments have shown that enrichment of specific proteins on TAD boundaries promotes such active processes to form TADs (35–37). However, as long as a reconstructed contact matrix by our PHi-C method shows a good agreement with an experimental contact matrix, the stochastic and dynamic nature in our polymer model might be a mechanism to maintain the TAD formation.
Both GC content and mappability play non-negligible roles in predicting the contact probability between two regions (14). Besides, restriction enzyme sequence specificity means that the chimeric reads generated will have different lengths and occur at different densities. Although we presumed a fixed binning of the Hi-C data, variable-sized binning would be a better pre-process to normalize Hi-C data. In the polymer network model in our PHi-C method, the physical distance between adjacent beads [i.e. the ith and (i + 1)th beads] in 3D space relates to the matrix element ki,i+1. Therefore, it is not essential how long each bead includes the genomic region. As long as an N × N variable-sized binning contact matrix is mathematically normalized in the sense of probability, we can apply our PHi-C method to the variable-sized binning contact matrix.
Our PHi-C method is not always applicable to all the input contact matrices. Our theoretical assumption of the polymer network model in the equilibrium state requires that a contact matrix should be dense, where each element value of the contact matrix has a meaning as a probability: given an interaction matrix 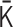 , all elements of the converted contact matrix
, all elements of the converted contact matrix 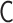 are nonzero. However, there would be a lot of sparse Hi-C matrices due to the depth of sequence reads and binning resolutions. Based on our benchmarking to carry out Hi-C procedures, the upper value of the matrix size would be N = 500 practically. We should develop a physical theory and computational methods for sparse and large-sized contact matrices.
are nonzero. However, there would be a lot of sparse Hi-C matrices due to the depth of sequence reads and binning resolutions. Based on our benchmarking to carry out Hi-C procedures, the upper value of the matrix size would be N = 500 practically. We should develop a physical theory and computational methods for sparse and large-sized contact matrices.
Unlike other computational modeling methods to reconstruct 3D genome structures, PHi-C requires only the contact matrix data for single chromosomes to convert into the interaction matrix of the polymer network model. Since the theory of the model assumes thermal equilibrium within a chromosome, the contact matrix data must be dense and deep so that the data can be characterized as a probability measure. Therefore, the bin size of the contact matrix data in the PHi-C analysis is limited according to the amount of the sequencing reads. Moreover, introducing additional physical parameters is not needed except for the nondimensional parameter ε to carry out the 4D simulations. The spatial and time scales are normalized by the physical parameters σ (m) and 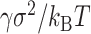 (s), respectively (Supplementary Data). Fitting the MSD data, in live-cell imaging experiments, with the theoretical function [Equation (S23) in Supplementary Data] could determine the parameters.
(s), respectively (Supplementary Data). Fitting the MSD data, in live-cell imaging experiments, with the theoretical function [Equation (S23) in Supplementary Data] could determine the parameters.
We have shown that PHi-C can decipher Hi-C data into polymer dynamics, based on a mathematical theory of chromosome contacts in the polymer network model. As shown for mESC Hi-C data, PHi-C analysis can bridge the gap between Hi-C data and imaging data with respect to chromatin dynamics in living cells. In addition, PHi-C’s theoretical basis allows for the depiction of any Hi-C pattern by designing the appropriate interaction parameters, which supports a model for TAD formation: physical chromatin stiffness based on certain molecular interactions creates insulation at TAD boundaries (38). Polymer modeling studies have revealed that chromatin modifications alter the physical properties of chromatin fibers and affect chromosome organization (13,39). Because PHi-C analysis can extract physical interaction parameters from Hi-C data, it should be elucidated which molecular interactions on chromatin are related to physical parameters. Further comprehensive PHi-C analysis could provide physical insights into molecular interactions on chromosomes.
Supplementary Material
ACKNOWLEDGEMENTS
We thank K. Shiroguchi and K. Kinoshita for helpful comments. We thank M. Marti-Renom and M. Di Stefano for stimulative discussions. We thank I. Hiratani for critical reading of this manuscript.
SUPPLEMENTARY DATA
Supplementary Data are available at NARGAB Online.
FUNDING
JSPS KAKENHI [JP16H01408 and JP18H04720 to S.S., JP18H05412 to S.O.]; JST CREST [JPMJCR1511 to S.O.].
Conflict of interest statement. None declared.
REFERENCES
- 1. Dekker J., Marti-Renom M.A., Mirny L.A.. Exploring the three-dimensional organization of genomes: interpreting chromatin interaction data. Nat. Rev. Genet. 2013; 14:390–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Bonev B., Cavalli G.. Organization and function of the 3D genome. Nat. Rev. Genet. 2016; 17:661–678. [DOI] [PubMed] [Google Scholar]
- 3. Nozaki T., Imai R., Tanbo M., Nagashima R., Tamura S., Tani T., Joti Y., Tomita M., Hibino K., Kanemaki M.T. et al.. Dynamic organization of chromatin domains revealed by super-resolution live-cell imaging. Mol. Cell. 2017; 67:282–293. [DOI] [PubMed] [Google Scholar]
- 4. Hauer M.H., Seeber A., Singh V., Thierry R., Sack R., Amitai A., Kryzhanovska M., Eglinger J., Holcman D., Owen-Hughes T. et al.. Histone degradation in response to DNA damage enhances chromatin dynamics and recombination rates. Nat. Struct. Mol. Biol. 2017; 24:99–107. [DOI] [PubMed] [Google Scholar]
- 5. Nagashima R., Hibino K., Ashwin S.S., Babokhov M., Fujishiro S., Imai R., Nozaki T., Tamura S., Tani T., Kimura H. et al.. Single nucleosome imaging reveals loose genome chromatin networks via active RNA polymerase II. J. Cell Biol. 2019; 218:1511–1530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Marti-Renom M.A., Mirny L.A.. Bridging the resolution gap in structural modeling of 3D genome organization. PLoS Comput. Biol. 2011; 7:e1002125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Fudenberg G., Imakaev M.. FISH-ing for captured contacts: towards reconciling FISH and 3C. Nat. Methods. 2017; 14:673–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Serra F., Di Stefano M., Spill Y.G., Cuartero Y., Goodstadt M., Baù D., Marti-Renom M.A.. Restraint-based three-dimensional modeling of genomes and genomic domains. FEBS Lett. 2015; 589:2987–2995. [DOI] [PubMed] [Google Scholar]
- 9. Paulsen J., Sekelja M., Oldenburg A.R., Barateau A., Briand N., Delbarre E., Shah A., Sørensen A.L., Vigouroux C., Buendia B. et al.. Chrom3D: three-dimensional genome modeling from Hi-C and nuclear lamin–genome contacts. Genome Biol. 2017; 18:21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Bianco S., Lupiáñez D.G., Chiariello A.M., Annunziatella C., Kraft K., Schøpflin R., Wittler L., Andrey G., Vingron M., Pombo A. et al.. Polymer physics predicts the effects of structural variants on chromatin architecture. Nat. Genet. 2018; 50:662–667. [DOI] [PubMed] [Google Scholar]
- 11. Imakaev M., Fudenberg G., McCord R.P., Naumova N., Goloborodko A., Lajoie B.R., Dekker J., Mirny L.A.. Iterative correction of Hi-C data reveals hallmarks of chromosome organization. Nat. Methods. 2012; 9:999–1003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Rao S.P., Huntley M., Durand N., Stamenova E., Bochkov I., Robinson J., Sanborn A., Machol I., Omer A., Lander E. et al.. A 3D map of the human genome at kilobase resolution reveals principles of chromatin looping. Cell. 2014; 159:1665–1680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Serra F., Baù D., Goodstadt M., Castillo D., Filion G.J., Marti-Renom M.A.. Automatic analysis and 3D-modelling of Hi-C data using TADbit reveals structural features of the fly chromatin colors. PLoS Comput. Biol. 2017; 13:e1005665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Yaffe E., Tanay A.. Probabilistic modeling of Hi-C contact maps eliminates systematic biases to characterize global chromosomal architecture. Nat. Genet. 2011; 43:1059–1065. [DOI] [PubMed] [Google Scholar]
- 15. Hu M., Deng K., Selvaraj S., Qin Z., Ren B., Liu J.S.. HiCNorm: removing biases in Hi-C data via Poisson regression. Bioinformatics. 2012; 28:3131–3133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Durand N.C., Shamim M.S., Machol I., Rao S.S., Huntley M.H., Lander E.S., Aiden E.L.. Juicer provides a one-click system for analyzing loop-resolution Hi-C experiments. Cell Syst. 2016; 3:95–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Doi M., Edwards S.F.. The Theory of Polymer Dynamics. 1988; Oxford: Oxford University Press. [Google Scholar]
- 18. Giorgetti L., Heard E.. Closing the loop: 3C versus DNA FISH. Genome Biol. 2016; 17:215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Le Treut G., Képès F., Orland H.. A polymer model for the quantitative reconstruction of chromosome architecture from HiC and GAM data. Biophys. J. 2018; 115:2286–2294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Bahar I., Atilgan A.R., Erman B.. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold. Des. 1997; 2:173–181. [DOI] [PubMed] [Google Scholar]
- 21. Sauerwald N., Zhang S., Kingsford C., Bahar I.. Chromosomal dynamics predicted by an elastic network model explains genome-wide accessibility and long-range couplings. Nucleic Acids Res. 2017; 45:3663–3673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Grimm J., Dolgushev M.. Dynamics of networks in a viscoelastic and active environment. Soft Matter. 2018; 14:1171–1180. [DOI] [PubMed] [Google Scholar]
- 23. Knight P.A., Ruiz D.. A fast algorithm for matrix balancing. IMA J. Numer. Anal. 2012; 33:1029–1047. [Google Scholar]
- 24. Sekimoto K. Stochastic Energetics. 2010; Berlin: Springer. [Google Scholar]
- 25. Gardiner C. Stochastic Methods: A Handbook for the Natural and Social Sciences. 2009; Berlin: Springer. [Google Scholar]
- 26. Humphrey W., Dalke A., Schulten K.. VMD: visual molecular dynamics. J. Mol. Graph. 1996; 14:33–38. [DOI] [PubMed] [Google Scholar]
- 27. Shinkai S., Nozaki T., Maeshima K., Togashi Y.. Dynamic nucleosome movement provides structural information of topological chromatin domains in living human cells. PLoS Comput. Biol. 2016; 12:e1005136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Shinkai S., Nozaki T., Maeshima K., Togashi Y.. Bridging the dynamics and organization of chromatin domains by mathematical modeling. Nucleus. 2017; 8:353–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Ochiai H., Sugawara T., Yamamoto T.. Simultaneous live imaging of the transcription and nuclear position of specific genes. Nucleic Acids Res. 2015; 43:e127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Gibcus J.H., Samejima K., Goloborodko A., Samejima I., Naumova N., Nuebler J., Kanemaki M.T., Xie L., Paulson J.R., Earnshaw W.C. et al.. A pathway for mitotic chromosome formation. Science. 2018; 359:eaao6135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Ohno M., Ando T., Priest D.G., Kumar V., Yoshida Y., Taniguchi Y.. Sub-nucleosomal genome structure reveals distinct nucleosome folding motifs. Cell. 2019; 176:520–534. [DOI] [PubMed] [Google Scholar]
- 32. Bonev B., Mendelson Cohen N., Szabo Q., Fritsch L., Papadopoulos G.L., Lubling Y., Xu X., Lv X., Hugnot J.-P., Tanay A. et al.. Multiscale 3D genome rewiring during mouse neural development. Cell. 2017; 171:557–572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Lupiáñez D., Kraft K., Heinrich V., Krawitz P., Brancati F., Klopocki E., Horn D., Kayserili H., Opitz J., Laxova R. et al.. Disruptions of topological chromatin domains cause pathogenic rewiring of gene–enhancer interactions. Cell. 2015; 161:1012–1025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Fudenberg G., Imakaev M., Lu C., Goloborodko A., Abdennur N., Mirny L.A.. Formation of chromosomal domains by loop extrusion. Cell Rep. 2016; 15:2038–2049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Sanborn A.L., Rao S.S.P., Huang S.-C., Durand N.C., Huntley M.H., Jewett A.I., Bochkov I.D., Chinnappan D., Cutkosky A., Li J. et al.. Chromatin extrusion explains key features of loop and domain formation in wild-type and engineered genomes. Proc. Natl. Acad. Sci. U.S.A. 2015; 112:E6456–E6465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Haarhuis J.H., van der Weide R.H., Blomen V.A., Yáñez-Cuna J.O., Amendola M., van Ruiten M.S., Krijger P.H., Teunissen H., Medema R.H., van Steensel B. et al.. The cohesin release factor WAPL restricts chromatin loop extension. Cell. 2017; 169:693–707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Wutz G., Várnai C., Nagasaka K., Cisneros D.A., Stocsits R.R., Tang W., Schoenfelder S., Jessberger G., Muhar M., Hossain M.J. et al.. Topologically associating domains and chromatin loops depend on cohesin and are regulated by CTCF, WAPL, and PDS5 proteins. EMBO J. 2017; 36:3573–3599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Dixon J., Gorkin D., Ren B.. Chromatin domains: the unit of chromosome organization. Mol. Cell. 2016; 62:668–680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Di Pierro M., Cheng R.R., Lieberman Aiden E., Wolynes P.G., Onuchic J.N.. De novo prediction of human chromosome structures: epigenetic marking patterns encode genome architecture. Proc. Natl. Acad. Sci. U.S.A. 2017; 114:12126–12131. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Published publicly available Hi-C data were used in this study: Ohno et al. (31) (BioProject: PRJNA427106), Rao et al. (12) (GEO: GSE63525), Bonev et al. (32) (GEO: GSE96107) and Gibcus et al. (30) (GEO: GSE102740). Input Hi-C matrix data of PHi-C were generated through the JUICER and JUICER TOOLS (16).