Deep Learning Based Spectral Unmixing for Optoacoustic Imaging of Tissue Oxygen Saturation

Abstract

Label free imaging of oxygenation distribution in tissues is highly desired in numerous biomedical applications, but is still elusive, in particular in sub-epidermal measurements. Eigenspectra multispectral optoacoustic tomography (eMSOT) and its Bayesian-based implementation have been introduced to offer accurate label-free blood oxygen saturation (sO₂) maps in tissues. The method uses the eigenspectra model of light fluence in tissue to account for the spectral changes due to the wavelength dependent attenuation of light with tissue depth. eMSOT relies on the solution of an inverse problem bounded by a number of ad hoc hand-engineered constraints. Despite the quantitative advantage offered by eMSOT, both the non-convex nature of the optimization problem and the possible suboptimality of the constraints may lead to reduced accuracy. We present herein a neural network architecture that is able to learn how to solve the inverse problem of eMSOT by directly regressing from a set of input spectra to the desired fluence values. The architecture is composed of a combination of recurrent and convolutional layers and uses both spectral and spatial features for inference. We train an ensemble of such networks using solely simulated data and demonstrate how this approach can improve the accuracy of sO₂ computation over the original eMSOT, not only in simulations but also in experimental datasets obtained from blood phantoms and small animals (mice) in vivo. The use of a deep-learning approach in optoacoustic sO₂ imaging is confirmed herein for the first time on ground truth sO₂ values experimentally obtained in vivo and ex vivo.

I. Introduction

Hemoglobin oxygen saturation is an important indicator of tissue function and disease. Quantification and spatial mapping of oxygen saturation (sO₂) in tissue provides valuable information for studies of tumor hypoxia [1], muscle activity [2], brain activation [3], metabolism [4] and other processes [5]. Modern imaging techniques that can provide quantitative spatial maps of sO₂ are limited ether by penetration depth [6], or by resolution [7]. Multispectral Optoacoustic Tomography (MSOT) can uniquely produce high resolution label-free spatial maps of sO₂ in deep tissue by unmixing the recorded optoacoustic (OA) spectra using the reference spectral signatures of oxygenated and deoxygenated hemoglobin [8–10]. The method opens a new way to study tissue oxygenation breaking though the barriers of other imaging techniques. However, the accuracy of sO₂ quantification in MSOT is limited by the fact that optical fluence varies with the location in the sample and wavelength of light, which affects the recorded OA spectra in a non-linear way [11–14]. This phenomenon, known as spectral coloring or spectral corruption, typically worsens with tissue depth and is challenging to model or predict due to the dependence of light fluence on the typically unknown optical properties in the whole illuminated region. Spectral coloring needs to be accounted for in order to achieve acceptable sO₂ quantification accuracy.

Several methods that reverse the effect of spectral coloring have been proposed [15–25]. One family of methods use a light propagation model that is described by the Radiative Transfer Equation (RTE) [15, 20, 21, 23, 24] or its approximations [15–17, 19, 21, 25] and attempt to invert a model predicting optical fluence. However, the application of these methods to sO₂ quantification in experimental data is challenging due to long computational times, reliance on perfect image reconstruction, and the need for accurate knowledge of various setup specific factors, e.g. illumination. Recently, eigenspectra MSOT (eMSOT) methodology was proposed [26]. The approach makes use of a simple linear spectral model for the wavelength dependence of optical fluence, termed the eigenspectra model, that describes fluence spectra based on only three parameters, termed the eigenfluence parameters. The spectral unmixing problem in eMSOT is formulated as the eigenspectra model inversion that relies on optimization to find the eigenfluence parameters that accurately predict the spectrum of the optical fluence. The eigenspectra model is inverted using a set of several sparsely distributed locations in the region-of-interest (ROI) simultaneously, allowing to analyze well-reconstructed parts of the data. However, eMSOT inversion is based on a number of constraints. Such constraints in eMSOT are hand engineered, with the specific values of certain parameters selected in an ad hoc manner. These constraints aim to enforce spatial smoothness or depth-dependence of the eigenfluence parameters, and may not be entirely accurate or sufficient, and therefore may lead to inaccuracies with certain samples.

A Bayesian variant of eMSOT was developed that models the constraints as prior distributions and takes into account the noise in the recorded spectra [27]. This algorithm assumes that noise is spatially non-uniform, which can improve sO₂ estimation, especially in deep-seated, highly absorbing structures. Nevertheless, Bayesian eMSOT also suffers from the major restrictions of eMSOT such as the ad hoc constraints and the non-convex nature of the optimization problem. Additionally, it requires longer computational times for convergence as compared to the original eMSOT.

Herein we examine deep-learning (DL) for improving eMSOT. DL was selected due to its advantages over other types of machine learning (ML) methods, in particular its performance when learning highly non-linear mappings. ML, and DL in particular, has been previously proposed for optoacoustic sO₂ quantification. Ref. [28, 29] use convolutional neural networks (CNN) that are trained with simulated images. Since training occurs in the spatial domain (whole images), certain spatial features may be learned that do not always capture the appearance of the experimental data, which may affect the performance of the method. A fully connected architecture has been recently proposed to analyze OA spectra [30], independently of spatial dependencies. The method considers an OA spectrum without any knowledge of its location in tissue or neighboring spectra, and maps it to the corresponding sO₂ value. This allows for straightforward training and application since no spatial structure needs to be learned. However, such an approach is limited in accuracy since the problem of decoupling fluence and absorption is generally ill-posed [26], i.e. various combinations of fluence and absorption spectra may result in the same measured OA spectrum. In this respect, spectral information alone is not adequate for inferring blood oxygenation while a combination of spectral and spatial features is required. In [31], a random forest approach has been considered. To account for the spatial context, the method relies on so called Fluence Contribution Maps that are computed for a given system using the Monte Carlo simulations, which may be a potential drawback if the optical properties of the imaged objects significantly deviate from the ones assumed in simulations. Consequently, none of these methods has been demonstrated with experimental data against ground truth sO₂ values.

In this work, we consider the eMSOT framework, which operates on spatially distributed spectra and takes into account spectral and spatial information. We hypothesized that the eMSOT inversion could be replaced by a neural network which learns how to map a set of spatially distributed input spectra to the corresponding eigenfluence parameters. The neural network works without specifying any ad hoc inversion parameters or constraints but instead learns such constraints from a large simulated set of training data. Due to the prominent dependence of fluence on tissue depth, we use an architecture for the neural network that is based on a bi-directional recurrent neural network (RNN). The input spectra are split in a sequence depth-wise, where spectra measured at a similar depth constitute one point in the sequence. Using training, validation and test data derived from simulations, we show that the proposed architecture is well-suited to learn how to solve the inverse problem in eMSOT for data that covers a wide range of tissue appearances, physiologically relevant optical parameters and sO₂ levels. We demonstrate that DL-based eMSOT gives more accurate sO₂ estimates than conventional eMSOT on the simulated test data. Using the proposed architecture, we train an ensemble of networks that outperforms conventional eMSOT in the majority of cases for experimental datasets of blood phantoms and small animals, although no experimental data were used in training.

II. Methods

A. Forward Model

In optoacoustics, illumination of tissue by a short laser pulse leads to the generation of ultrasound waves through thermoelastic expansion of the tissue due to light absorption. The ultrasound waves propagate towards the detectors and pressure signals are recorded. An image reconstruction algorithm is then applied to reconstruct the location- and wavelength-dependent initial pressure rise p₀ that relates to the optical fluence Φ and tissue absorption μ_a as follows [32]:

$$p_0\left(\mathbf{\text{r}},\lambda \right)=\Gamma \left(\mathbf{\text{r}}\right)\Phi \left(\mathbf{\text{r}},\lambda \right){\mu }_a\left(\mathbf{\text{r}},\lambda \right),$$ (1)

where r denotes the spatial coordinates, λ is the illumination wavelength and Γ is the spatially varying Grüneisen parameter.

In eigenspectra MSOT, correcting for the effects of fluence is achieved by using a linear spectral model for the normalized fluence ${\Phi }^{\prime }\left(\mathbf{\text{r}},\lambda \right)=\mathbf{\text{Φ}}\left(\mathbf{\text{r}},\lambda \right)/{\Vert \mathbf{\text{Φ}}\left(\mathbf{\text{r}}\right)\Vert }_2$, Φ(r) being a vector corresponding to the fluence spectrum at position r; and ${\Vert \mathbf{\text{Φ}}\left(\mathbf{\text{r}}\right)\Vert }_2$ being the l₂-norm of the optical fluence spectrum [26]. It has been hypothesized that the fluence spectra in tissue cannot be arbitrary but instead can be approximated by a low-dimensional spectral model. Such a model is derived by performing principal component analysis (PCA) on a training set of normalized fluence spectra. The spectra in the dataset are simulated to capture the variability of fluence due to tissue depth and varying sO₂. It has been confirmed in simulations and experiments that only 3 principal components ${\Phi }_{\text{i}}\left(\lambda \right),i=1\dots 3$ derived by PCA along with the mean spectrum of the training dataset Φ_M (λ) are enough to approximate normalized fluence spectra in tissue as follows [26]:

$${\Phi }^{\prime }\left(\mathbf{\text{r}},\lambda \right)={\Phi }_{\text{M}}\left(\lambda \right)+\sum _{i=1}^3{m}_{\text{i}}\left(\mathbf{\text{r}}\right){\Phi }_{\text{i}}\left(\lambda \right),$$ (2)

where Φ_M (λ), ${\Phi }_{\text{i}}\left(\lambda \right),i=1\dots 3$ are termed the eigenspectra, and m_i are scalars referred to as the eigenfluence parameters. For a known spectrum Φ′(r,λ), the eigenparameters can be computed by projecting), Φ′(r,λ) onto the eigenspectra: $m_i=\langle {\Phi }^{\prime }\left(\mathbf{\text{r}}\right)-{\text{Φ}}_{\text{M}},{\text{Φ}}_{\text{i}}\rangle$, where $\langle ,\rangle$, denotes inner product.

In the near-infrared spectral region, the model for tissue absorption is [33]:

$${\mu }_a\left(\mathbf{\text{r}},\lambda \right)=c_{\text{HHb}}\left(\mathbf{\text{r}}\right){\epsilon }_{\text{HHb}}\left(\lambda \right)+c_{\text{HbO}2}\left(\mathbf{\text{r}}\right){\epsilon }_{\text{HbO}2}\left(\lambda \right),$$ (3)

where c_HHb and c_HbO2 are the concentrations of deoxy- and oxyhemoglobin, respectively; and ε_HHb and ε_HbO2 are the corresponding absorption spectra. To exclude the spatially varying Grüneisen parameter from consideration, eMSOT considers normalized initial pressure spectra (or simply normalized OA spectra), i.e. ${\mathbf{\text{p}}}^{\prime }\left(\mathbf{\text{r}}\right)={\mathbf{\text{p}}}_0\left(\mathbf{\text{r}}\right)/{\Vert {\mathbf{\text{p}}}_0\left(\mathbf{\text{r}}\right)\Vert }_2$. The eigenspectra model for a normalized OA spectrum therefore is [26]:

$$\begin{gathered} \widehat{p}\left(\mathbf{\text{r}},\lambda ,\mathbf{\text{θ}}\right)=\left({\Phi }_{\text{M}}\left(\lambda \right)+\sum _{i=1}^3{m}_{\text{i}}\left(\mathbf{\text{r}}\right){\varphi }_{\text{i}}\left(\lambda \right)\right) \\ .\left({c^{\prime }}_{\text{HHb}}\left(\mathbf{\text{r}}\right){\epsilon }_{\text{HHb}}\left(\lambda \right)+{c^{\prime }}_{\text{HbO}2}\left(\mathbf{\text{r}}\right){\epsilon }_{\text{HbO}2}\left(\lambda \right)\right). \end{gathered}$$ (4)

where ${c^{\prime }}_{\text{HHb}}$ and ${c^{\prime }}_{\text{HbO}2}$ are relative concentrations of deoxygenated and oxygenated hemoglobin, respectively, and $\mathbf{\theta }=\left(m_1,m_2,m_3,{c^{\prime }}_{\text{HHb}},{c^{\prime }}_{\text{HbO}2}\right)$ is a vector of model parameters. In this study, a set of illumination wavelength from 700 nm to 900 nm with a step size of 10 nm (21 in total) is utilized.

B. eMSOT Algorithm Overview

Fig. 1 schematically describes the steps of eMSOT algorithm (top row) as well as the steps of the proposed modification based on the use of a neural network (bottom row). eMSOT can be summarized in the following steps:

1. Grid Setup. A sparse grid $\text{G}=\left\{{\mathbf{\text{r}}}^{\left(k,l\right)}|k=1\dots n_{\text{ln}},l=1\dots n_{\text{pt}}\right\}$ of points is placed in the ROI by intersecting n_ln radial lines and n_pt circles with decreasing radii. Fig. 1A shows an example of a grid G consisting of n_ln = 8 and n_pt = 8, i.e. 64 grid points in total (red dots) overlaid with a simulated OA image (grayscale). The spectra p(r) at spatial locations determined by the grid points $\mathbf{\text{r}}\in \text{G}$ are selected for inversion and normalized.

2. Priors. Linear unmixing and Finite Element Method (FEM) simulation of light propagation governed by the Diffusion Equation [33] are used to obtain an estimate of optical fluence for the imaged object. This results in prior estimates ${\widehat{m}}_1\left(\mathbf{\text{r}}\right)$, ${\widehat{m}}_2\left(\mathbf{\text{r}}\right)$ and ${\widehat{m}}_3\left(\mathbf{\text{r}}\right)$ of the eigenfluence parameters m₁(r), m₂(r) and m₃(r), respectively. Fig. 1B demonstrates maps of ${\widehat{m}}_1\left(\mathbf{\text{r}}\right)$, ${\widehat{m}}_2\left(\mathbf{\text{r}}\right)$ and ${\widehat{m}}_3\left(\mathbf{\text{r}}\right)$ for the dataset shown in Fig. 1A.

3. Inversion. In this key step, model inversion is performed by using a constrained minimization procedure as described in the Supplementary Material Sec. I. In the Bayesian version of the eMSOT algorithm, the inverse problem is derived in a probabilistic framework, with constraints replaced by prior distributions of the sought parameters and the level of noise in the measured signal taken into account [27]. At the core, however, still lies an optimization procedure. Fig. 1C schematically shows this step, with Fig. 1D demonstrating the output of the inversion, which is an estimate of the eigenfluence parameters for each grid point.

4. Interpolation. With the values of the eigenfluence parameters $m_i^{\left(k,l\right)}:i=1\dots 3,k=1\dots n_{\text{ln}},l=1\dots n_{\text{pt}}$ for the grid points $\mathbf{\text{r}}\in \text{G}$ available, interpolation is used to estimate the values of the eigenfluence parameters for every pixel within the convex hull of G [27]. Fig. 1E shows the resulting maps of the eigenfluence parameters overlaid in color with the simulated dataset shown in Fig. 1A (shown in grayscale).

5. sO₂ Estimation. For every pixel within the convex hull of G, the corresponding values of the eigenfluence parameters are used to reconstruct the estimated fluence. The effect of spectral coloring is then reverted and the resulting spectra, i.e. scaled true absorption spectra, are unmixed linearly for the relative concentrations ${c^{\prime }}_{\text{HbO}2}$ and ${c^{\prime }}_{\text{HHb}}$ of oxy- and deoxyhemoglobin, respectively that are used to compute sO₂ [27]. Fig. 1F demonstrates the sO₂ computed by eMSOT in color overlaid with the p₀ map shown in grayscale.

Fig. 1: Original eMSOT and DL-eMSOT.

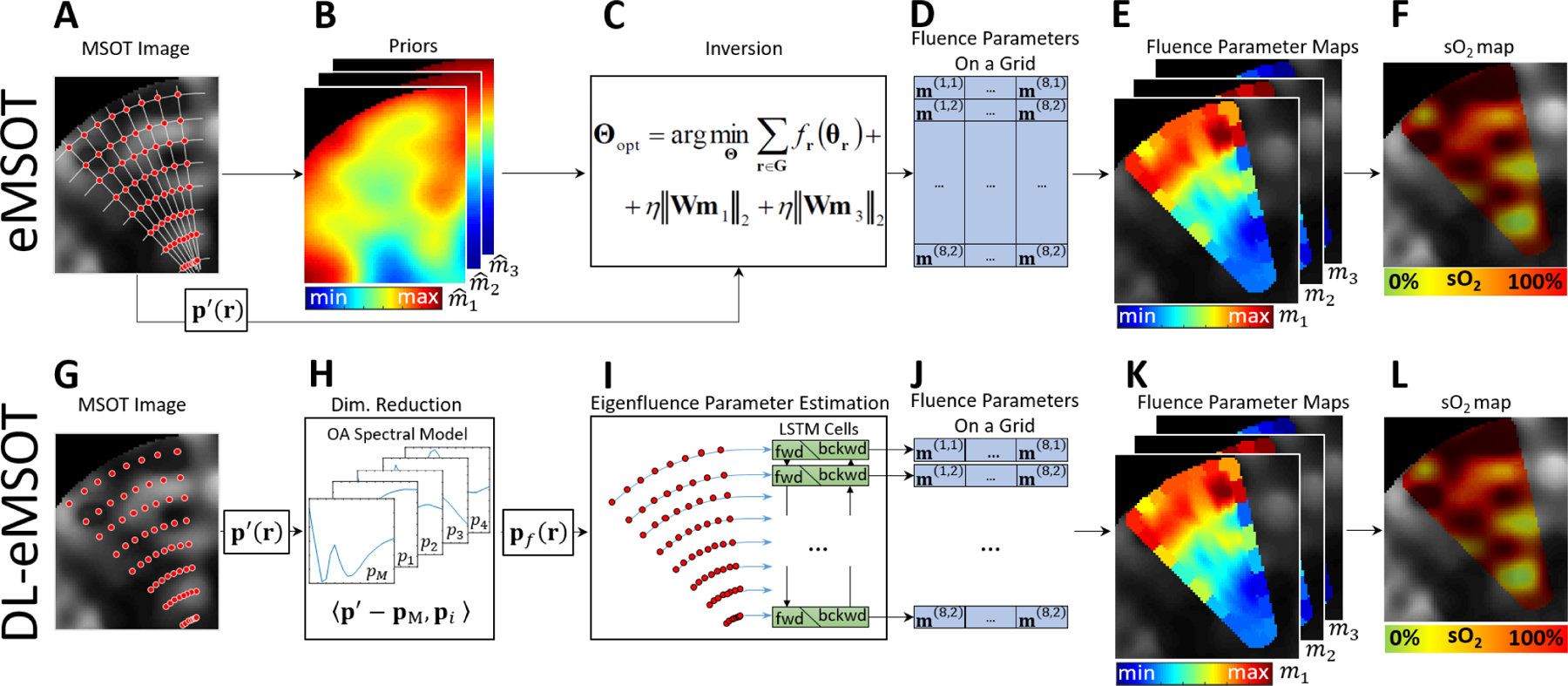
(A-F) Steps of eMSOT. (A) A grid of points (red dots) is applied to the dataset in the region of interest. (B) A simulation of light propagation is used to produce crude prior estimates of the eigenfluence parameters. (C) The priors obtained in (B) are used with the spectra sampled at the locations specified by the grid in (A) in the inversion step (optimization procedure). (D) The output of (C) is the eigenfluence parameters for the grid points. The values of the eigenfluence parameters are then interpolated between the grid points (E) and are used to estimate and correct for fluence. (F) The corrected spectra are linearly unmixed, resulting in an sO₂ estimation map. (G-L) Steps of DL-eMSOT. (G) A grid of points (red dots) is applied to the dataset in the region of interest. (H) The spectra sampled at the locations specified by the grid in (G) are projected on a OA spectral model to reduce data dimensionality. (I) The resulting data p_f are fed into a neural network based on a combination of RNN and CNN. (J) The output of the neural network is the eigenfluence parameters for the grid points. (K) The values of the eigenfluence parameters are interpolated between the grid points and are used to estimate and correct for fluence. (L) The corrected spectra are linearly unmixed, resulting in an sO₂ estimation map.

A more detailed description of eMSOT can be found in the Supplementary Material (Sec. I).

C. Deep Learning Based eMSOT

While eMSOT has been shown to provide a much more accurate estimation of sO₂ in tissue as compared to the commonly used linear unmixing method, its accuracy is not absolute. Among other reasons, this is due to the inversion relying on ad hoc, hand-engineered constraints (Suppl. Eqs. S2–4) and regularization terms. The Bayesian version of eMSOT implements the mentioned constraints as prior distributions in an attempt to optimize the parameters of the distributions to improve the estimation accuracy while simultaneously weighing the measurements according to the amount of noise present. While certain progress has been made, the method is still prone to errors.

In this study, we aim to replace the optimization procedure in the inversion step with a neural network, resulting in a Deep Learning based eMSOT (DL-eMSOT). A function that maps the set of original spectra to the set of eigenfluence parameters is learned by means of an appropriately trained neural network. In this way, inversion constraints, such as the spatial dependencies of the eigenfluence parameters, are learned from data rather than being hard-coded, which may improve the accuracy of the method.

C.1. DL-eMSOT Overview

The proposed method is summarized in Fig. 1G–L and consists of the following steps:

1. Grid Setup. The first step involves grid placement and spectra extraction and normalization, which are identical to step 1 of eMSOT described above. Here we fix n_ln = 8 and n_pt = 8. Fig. 1G shows an example of a grid G consisting of n_ln = 8 and n_pt = 8 grid points (red dots) overlaid with a simulated OA image (grayscale).

2. Dimensionality Reduction. Unlike eMSOT, after the normalization of the measured spectra, the resulting set of the normalized spectra ${\mathbf{\text{p}}}^{\prime }\left(\mathbf{\text{r}}\right),\mathbf{\text{r}}\in \mathbf{\text{G}}$ (dimensions 8×8×21) are projected on a 4-dimensional OA spectral model, previously described in [27], to obtain input features ${\text{p}}_f\left(\mathbf{\text{r}}\right),\mathbf{\text{r}}\in \text{G}$ (dimensions 8×8×4) as follows:

   $${\mathbf{\text{p}}}_f\left(\mathbf{\text{r}}\right)=\left\{{\langle {\mathbf{\text{p}}}^{\prime }-{\mathbf{\text{p}}}_{\text{M}},{\mathbf{\text{p}}}_i\rangle }_{\lambda }|i=1,\dots ,4\right\}$$ (5)

   where p_M is the mean spectrum of the OA spectral model and p_i are the four spectral components of the model that are created by performing PCA on a training set of normalized OA spectra [27]. The OA spectral model describes all possible normalized OA spectra found in tissue under the assumption of hemoglobin being the main absorber. ${\mathbf{\text{p}}}_f\left(\mathbf{\text{r}}\right),\mathbf{\text{r}}\in \text{G}$ are used as input data for the neural network. Fig. 1H illustrates this step which is similar to the traditional dimensionality reduction through PCA frequently used in ML, the difference being that PCA in the case of DL-eMSOT is not computed on the data used for training of the algorithm, but rather on a pre-computed dataset described in [27].

3. Eigenfluence parameter estimation. The estimation of the eigenfluence parameters is performed by feeding the input features ${\mathbf{\text{p}}}_f\left(\mathbf{\text{r}}\right),\mathbf{\text{r}}\in \mathbf{\text{G}}$ to the neural network that is based on a bi-directional Recurrent Neural Network. Fig. 1I schematically demonstrates the process. RNNs work with sequential data, therefore the input features need to be split into a sequence. Since the depth dependence of fluence is prominent, the input features are split depth-wise, i.e. the input features stemming from the spectra recorded at the same depth constitute one point in the input sequence. The network itself consists of two LSTM cells. One accepts inputs from the superficial layers of pixels first, the other one is starting at the deepest pixels. The output of the cells is then resized using a fully connected layer and reshaped into the 8×8×3 shape followed by two convolutional layers to incorporate further spatial, non depth-related dependencies. The output (shape 8×8×3) represents the eigenfluence parameters for the spectra in the grid. Fig. 1J shows the output of step 3 as a tensor of the eigenfluence parameters for the spectra in the grid. More details on the architecture of the network are provided in the following subsection.

4. Interpolation. This step is identical to step 4 of eMSOT. Fig. 1K shows the resulting maps of the eigenfluence parameters overlaid with the simulated dataset shown in Fig. 1G (grayscale).

5. sO₂quantification. This step is identical to step 5 of eMSOT. Fig. 1L shows the resulting sO₂ map overlaid with the dataset shown in Fig. 1G.

To summarize, the proposed DL-eMSOT algorithm differs from eMSOT in (1) the data preprocessing step and (2) the eigenfluence parameter inference step. In the data preprocessing, DL-eMSOT works with data of reduced dimensionality and uses a OA spectral model previously introduced in [27] to achieve this dimensionality reduction. In the eigenfluence parameter estimation step, DL-eMSOT maps directly the input features to the corresponding eigenfluence parameters by employing a neural network rather than performing inversion using an optimization algorithm. Moreover, DL-eMSOT does not require prior estimates of eigenfluence parameters (step 2 of eMSOT). We train an ensemble of 50 neural networks and their median-filtered output for improved results.

C.2. Architecture

The core of the DL-eMSOT architecture was selected to be a bi-directional RNN. The intuition behind this design selection is the following. The shape of the light fluence spectrum and thus the art of spectral corruption at a specific point depends on the absorption spectra of the surrounding tissue. The spectral corruption manifests itself stronger as the imaging depth increases, while the shallow tissue spectra strongly affect the appearance of the deep tissue spectra. Both of these observations have been hard-coded as spatial constraints in eMSOT (Suppl. Eqs. S2–4) which were crucial for achieving good performance. Since RNNs are ideal in capturing dependencies along sequences, we selected an RNN that operates across the tissue depth to capture the prominent depth dependency of spectral corruption. The grid that samples the spectra for eMSOT can be viewed as containing several layers of points coming from similar depth making it suitable as an input to an RNN. To capture neighbor dependencies between spectra with similar depth we allowed a relatively large number of hidden units in the RNN cells (1024) to allow for more expressive power, as well as applied several convolutional layers to the output of the RNN. Fig. 2 demonstrates the used architecture schematically and a detailed description of the parameters used is provided below.

Fig. 2:

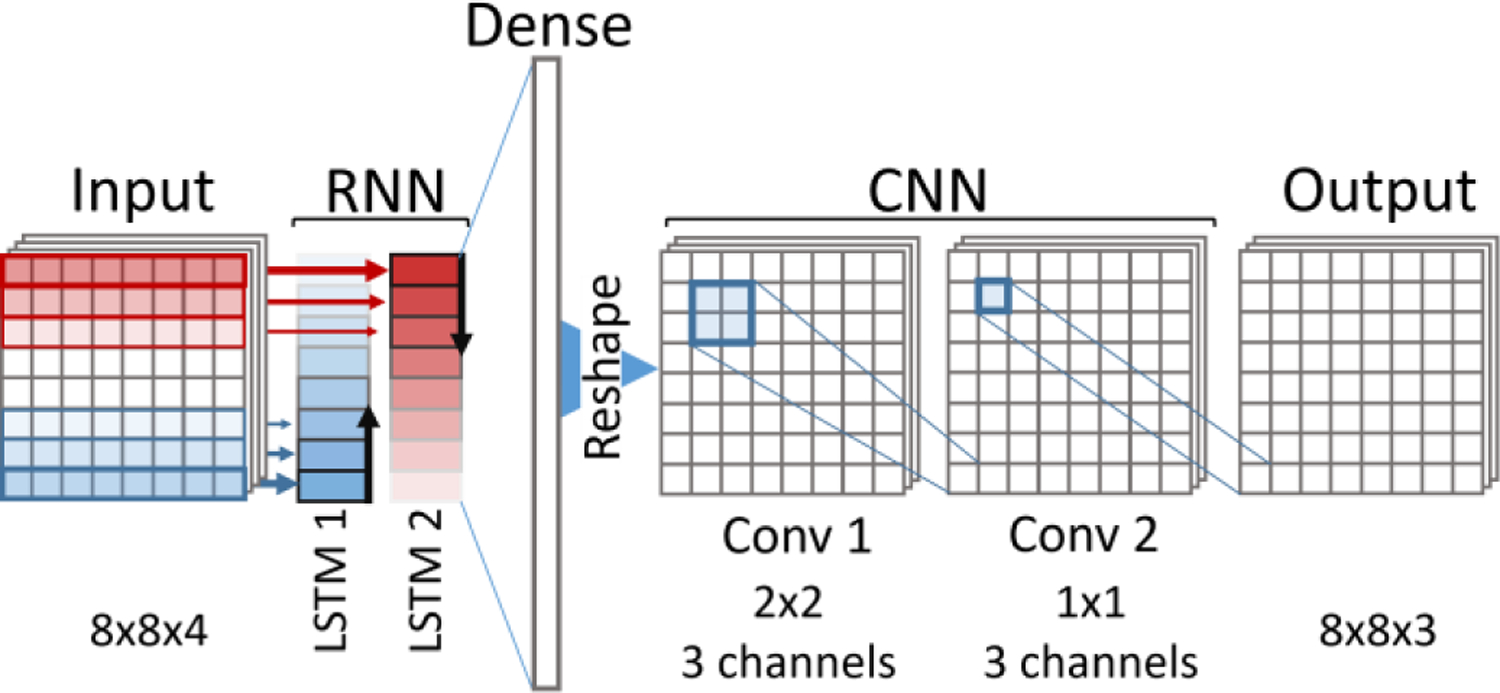
DL-eMSOT Architecture.

Input is the tensor of input features. Its size is 8×8×4, 8×8 corresponds to grid dimensions and 4 being the number of features corresponding to each spectrum after dimensionality reduction. The features corresponding to each of the grid layers are concatenated into a single vector thus resulting in a 8×32 tensor, which can be viewed as a sequence of 8 feature vectors that will be used as an input to the bi-directional RNN.

The bi-directional RNN is the core element of the architecture and consists of two LSTM cells of identical structure (1×32 input vector, 1×1024 output vector, depth 8). In our experiments we found that using a bi-directional RNN was crucial for achieving optimal performance, while network depth or the number of output neurons per layer were of reduced importance (see Sec. II-D Competing Architectures) The outputs of the two LSTMs are concatenated into an 8×2048 tensor, and reshaped into a 1×16,384 vector to be passed through a dense layer.

Dense layer with 192 output units serves as a means of resizing the output of the bi-directional RNN to the desired output size. The output of the dense layer is reshaped into a 8×8×3 tensor which has the shape of the network output (3 eigenparameters per spectrum on an 8×8 grid).

Two convolutional layers of the CNN block (Conv. 1 with 3 2×2 filters and Conv. 2 with 3 1×1 filters) are meant to add expressive power to the network and allow to better account for any local spatial dependencies, specifically within a layer of spectra coming from the same depth.

Tanh are used as activation functions in all layers.

Further notes on the selection of certain hyperparameters (i.e. grid size and ensemble size) are available in the Supplementary Material (Sec. IV).

D. Competing Architectures

For reference, we train two more models based on a simple architecture consisting of six fully connected layers and evaluate their performance on simulated data as described above. Similarly to the network proposed in [30], the model termed DENSE (sO₂) maps a single input spectrum directly to the corresponding sO₂ value, therefore not taking into account any spatial information. The second model termed DENSE (fluence) attempts to solve the inverse problem of eMSOT, but with a less sophisticated architecture than the one proposed for DL-eMSOT. The structure of input and output of this network is therefore identical to that of the proposed RNN based architecture, but the network is based solely on fully connected layers. Details on the reference models are provided in the Supplementary Material (Sec. II).

E. Training

Both all the DL-eMSOT models as well as all the models from the competing architectures were trained with the same parameters (batch size: 128; Loss: L2; Optimizer: ADAM; epochs: 200).

During training, every OA spectrum was augmented with white Gaussian noise $ϵ~N\left(\mu ,\sigma \right)$ with zero mean μ and standard deviation σ randomly sampled from the uniform distribution σ ~ U (.005– .015) before performing the dimensionality reduction.

The best model was selected by evaluating the absolute error in sO₂ estimation on a validation dataset (see Sec. III-C) every 10 training iterations. If the obtained result was better than that of the previously selected best model, the current model was saved as the new best model. Otherwise, the current model was discarded.

DENSE (fluence) was trained using the same data as the DL-eMSOT. DENSE (sO₂) used the same training dataset, but every spectrum was considered as a separate example unlike DL-eMSOT and DENSE (fluence), where a grid of sampled spectra constituted a training example.

F. Performance Assessment

We quantify the performance of the algorithm in terms of absolute error in sO₂ estimation:$\left|sO{2}_{a\text{lg}}-sO{2}_{GS}\right|$, where sO2_alg is the sO₂ value obtained by a certain algorithm and sO2_GS is the ground truth value. For simulated data, gold standard values are naturally available for every location in the image. For experimental data, gold standard values are available for certain locations (see Fig. 3). We note that we use this absolute error metric throughout the entire manuscript and it should not be confused with relative sO₂ estimation error. The errors presented herein in per cent are still absolute, since sO₂ is a ratiometric quantity measured in %.

Fig. 3: Training, validation and test data.

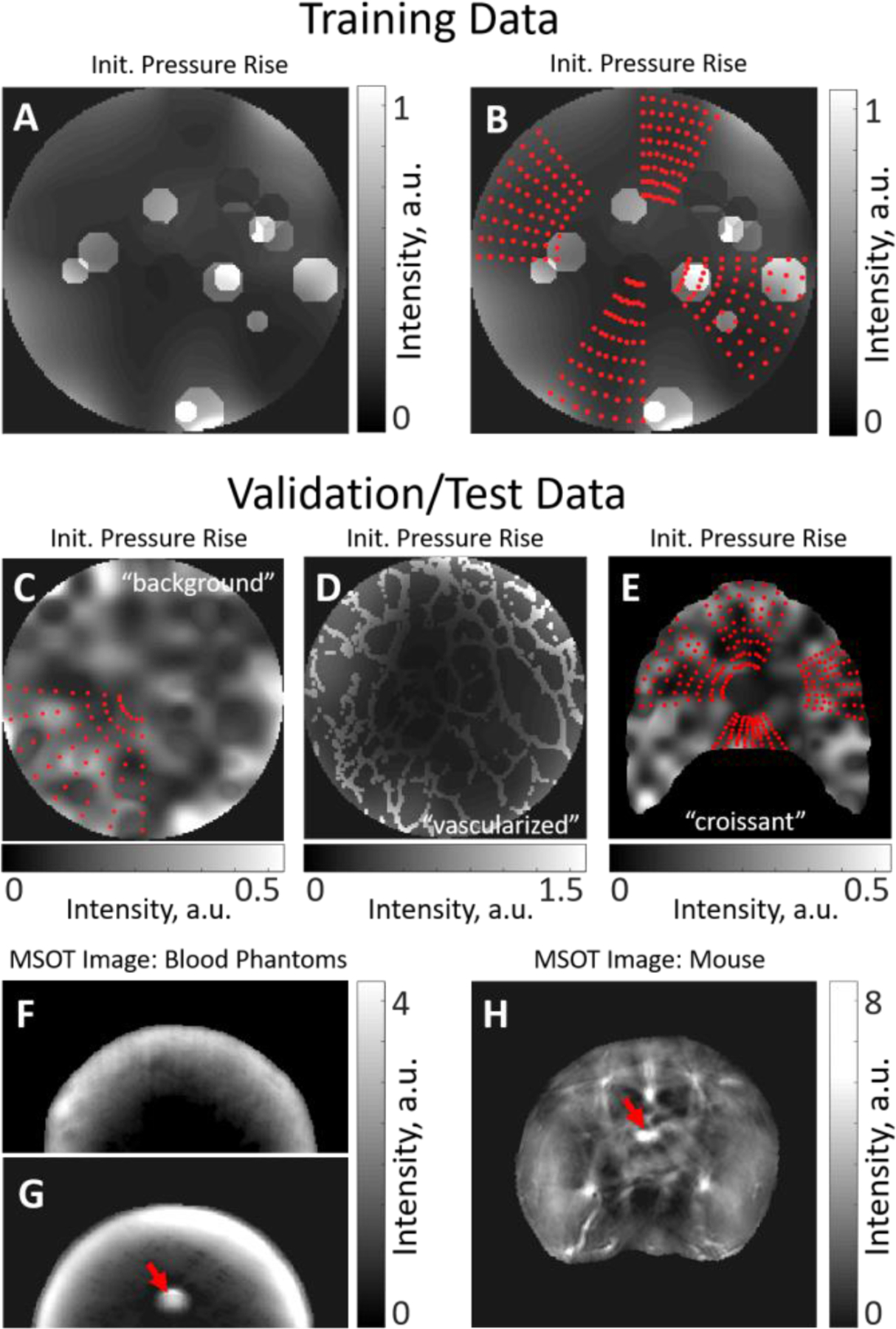
(A) Simulated OA image (one wavelength presented) used for sampling grids for training. The background is smoothly varying, with numerous randomly placed circular insertions of varying intensity. (B) Examples of four grids (red dots) determining the locations of the OA spectra sampled form the dataset presented in (A). The grids have varying width, depth and position. (C) Simulated OA image (“background” dataset, one wavelength presented) used for sampling spectra for validation and test of the trained models together with an example of a grid defining the locations of the OA spectra to be sampled. Validation and test datasets have no circular insertions but may have a more inhomogeneous background. Grids used for validation and test may be wider than the grids used for training. (D) Simulated OA image (“vascularized” dataset, one wavelength presented) used for sampling test data that shows structures simulating a network of vessels. (E) Simulated OA image (“croissant” dataset, one wavelength presented) used for sampling test data from irregularly shaped tissue. The used grids are shown with red dots. (F) A uniform blood phantom of known oxygenation and (G) a blood phantom with an inserted blood-filled capillary tube (target, red arrow) of known oxygenation. (H) An abdominal cross-section of a mouse with an inserted blood-filled capillary tube (target, red arrow) of known oxygenation.

Due to the large size of the evaluation datasets and in order to reduce computational effort, the interpolation step for the simulated data in eMSOT and DL-eMSOT was skipped and the sO₂ error is computed and reported only for the grid pixels. In the Supplementary Material we present the effect of the interpolation in the overall error in a smaller dataset. The interpolation step was retained in the case of experimental data. For the 50 trained DL-eMSOT models, test results on simulated test data are reported per model and as an ensemble, where the outputs of 50 models are median-filtered. Test results on experimental data are reported from an ensemble.

III. DATA

The generation of an appropriate training, validation and test dataset is particularly crucial for obtaining a well-trained neural network that would not only work in specific simulations, but also generalize well to cases not covered by the training dataset. Since the generation of a large and versatile experimental optoacoustic dataset of living tissue with known sO₂ values is impractical, in this work we had to resort to using simulations for the purpose of creating training, validation and test data. Nevertheless, in order for the model to have practical value, it needs to be applicable in experimental data as well. Therefore, we also test the model using a limited set of experimental MSOT images of blood phantoms and mice with available ground truth sO₂ values. We note that no experimental images are used for training the model. In the following subsections, we describe the used data in detail. Fig. 3 shows representative examples of the data used.

A. Simulations of Multispectral p₀ maps

In order to generate training, validation and test data-sets of multispectral optoacoustic images with available ground truth of fluence and sO₂ values, simulations of initial pressure rise p₀ were used. A circular slice of tissue with 1 cm radius with varying optical properties was assumed. A detailed description of the algorithm for simulating p₀ maps is provided in [27], below we provide a brief summary of the steps.

1. Optical properties of the background tissue: Randomly varying spatial maps of background tissue absorption μ_a(r) at 800 nm (isosbestic point of hemoglobin), reduced scattering μ’_s(r) (assumed constant with wavelengths) and sO₂ are generated.

2. (OPTIONAL) Optical Properties of structures: μ_a(r), μ’_s(r) and sO₂ maps of the background are augmented to represent structures.

3. Extension to multispectral range: Using the output of step 1 or 2 and the absorption spectra of hemoglobin, the optical absorption map μ_a(r, λ) is created for all the illumination wavelengths.

4. Light propagation: Light propagation through the sample is simulated by solving the Diffusion Equation using FEM [33] to obtain fluence map Φ(r, λ).

5. Multispectral p₀ map: The product of μ_a(r,λ) and Φ(r, λ) results in a simulated map of the initial pressure rise p₀(r,λ) assuming Γ(r) = 1. Such an assumption does not affect the performance of the considered algorithms since the eMSOT type of algorithms use normalized OA spectra.

Various randomly generated maps of optical properties were used to simulate a range of biological tissues [34]. Values for both μ_a(r) and μ’_s(r) were drawn from normal distributions with means and standard deviations that were different for training, validation and test data to obtain a wide range of biologically plausible scenarios. The mean values of the optical parameters as well as standard deviations for every type of dataset are presented in Supplementary Table 1.

Notably, generation of p₀ maps relies on 2D simulations of light propagation (i.e. assuming infinite sample thickness in z dimension), mainly for computational reasons. Since any fluence pattern simulated in 3D may be obtained by constructing a corresponding 2D simulation with modified optical properties, using 2D simulations in this study is justified by using an extensive set of randomly distributed optical properties.

B. Training Data

For obtaining the training data for the neural network, the following steps were performed:

1. p₀ Simulations: Simulated multispectral p₀ maps of tissue were created as described above (1,368 distinct simulations in total). The optical properties were sampled from the normal distributions with the parameters summarized in Supplementary Table 1. The random optical absorption maps were created with low spatial heterogeneity to simulate soft tissue. To include also areas of higher spatial heterogeneity due to vasculature, the simulations were augmented with 0, 4, 8 or 16 randomly located circles of optical absorption that is up to five times (exact number set randomly) higher than the background. The radius of every circle varied also randomly. The sO₂ of the circles was randomly set to be 20%–60% higher or lower than the mean sO₂ of the background. Fig. 3A shows an example of a generated p₀ map used for training.

2. Grid Placement: The grids (8 per dataset) of varying depth, angular width and location were placed on the datasets generated in step 1. Fig 3B demonstrates 4 grids (red dots) placed on the dataset shown in Fig. 3A. The grids always contained 8×8 location points.

3. Spectra Sampling: For every grid, the simulated spectra at the locations of the grid points were sampled, normalized and saved, resulting in 10,944 training examples, with one grid of spectra representing one example.

4. Labels Sampling: For every recorded spectrum, the corresponding fluence spectrum was sampled from the simulated light fluence map. Each fluence spectrum was normalized and projected on the eigenspectra, yielding a set of three real-valued parameters (m₁, m₂, m₃) corresponding to the labels. The corresponding sO₂ values are also sampled, resulting in the sO₂ labels dataset.

C. Simulated Validation and Test Data

When producing the validation and test data, the aim was to create data that is sufficiently different in structure to the training data to test the generalization ability of the trained models. Validation and test data consisted of three distinct datasets.

The “background” dataset was created as follows:

1. p₀ Simulations: Simulated multispectral p₀ maps of the background were created as described above (Section III-A), resulting in 228 distinct simulations in total. The optical properties were sampled from the distributions with the parameters summarized in Supplementary Table 1. The random absorption maps were created with spatial heterogeneity varying from low to high between datasets. No augmentations of μ_a(r), μ’_s(r) and sO₂ maps were performed.

2. Grid Placement: The grids (8 per dataset) of varying depth, angular width and location were placed on the datasets generated in step 1. The maximum width of the sampled grids exceeded that of the grids in the training data.

3. Spectra Sampling: Identical to the training data. The result is 1,824 examples.

4. Labels Sampling: Identical to the training data.

Fig. 3C shows an example of a generated p₀ map form “background” dataset with a grid (red dots). Note the width of the grid as compared to the grids shown in Fig. 3B.

The “vascularized” dataset was created as follows:

• p₀ Simulations: Simulated multispectral p₀ maps of the background were created as described above (570 distinct simulations in total). The optical properties were sampled from the distributions with the parameters summarized in Supplementary Table 1. The random absorption maps were created with low spatial heterogeneity and augmented with a structure that represents a network of large vessels.

• Grid Placement: Identical to “background” dataset.

• Spectra Sampling: Identical to the training data. The result is 4,560 examples.

• Labels Sampling: Identical to the training data.

Fig. 3D shows an example of a generated p₀ map form “vascularized” dataset.

The “croissant” dataset was created similarly to the “background” dataset, with a notable difference being the irregular shape of the simulated tissue (after which the dataset is named) as compared to other datasets. The purpose of this dataset is to examine the applicability of the considered quantification methods to a dataset with the geometry that is substantially different from that of the training data. The dataset consists of 304 simulations and 4 grids sampled per simulation (1,216 examples in total). Fig. 3E shows a generated p₀ map form “croissant” dataset with the sampled grids denoted by the red dots. We note that the field of view in Fig. 3E is 2.5×2.5 cm², while in Fig. 3A–D the field of view is 2×2 cm². More details on simulations are available in the Supplementary Material (Sec. III).

For every model, “background” dataset was shuffled and split, with 10% of the set used for model validation and 90% used for test. “Vascularized” and “croissant” datasets were used as test entirely.

D. Experimental Test Data

For the neural network to have practical value, and since it is trained purely on simulated data, it is crucial to generalize well to experimental data in terms of accuracy in sO₂ estimation. For this reason, 3 types of experimental data with the available ground truth were used that will be referred to as Uniform Phantoms, Insertion Phantoms and Mouse Data.

Phantoms.

The 2-cm-diameter cylindrical tissue mimicking phantoms were created by mixing agarose, intralipid and porcine blood. The details can be found in [26]. Each phantom contained blood of known oxygenation (0% or 100%). Two types of phantoms were used. Uniform Phantoms are homogeneous with the ground truth sO₂ values known for the whole phantom. Fig. 3F demonstrates an MSOT image (one wavelength shown) of a uniform phantom. Insertion phantoms contain a capillary tube filled with blood of known oxygenation. Fig. 3G shows an MSOT image (one wavelength shown) of an insertion phantom. The location of the capillary tube is marked with a red arrow.

Mouse Data.

All procedures involving animal experiments were approved by the Government of Upper Bavaria. Nude-Foxn1 mice were imaged under anesthesia while breathing medical air, followed by 100% O₂. A capillary tube filled with porcine blood of known oxygenation (0% or 100%) was rectally inserted in each imaged animal. More details can be found in [26]. In the final imaging stage, animals were sacrificed with an overdose of CO₂. Fig. 3H shows an MSOT image of a mouse. The location of the capillary tube is marked with a red arrow.

All experimental data has been obtained with the commercially available inVision256 system [35] and was used for test in its entirety.

IV. Results

A. Simulated Data

First we trained the neural networks (DL-eMSOT, DENSE (fluence)) using 10944 grid examples coming from 1368 simulations of p₀ maps with varying optical properties, spatial structures and sO₂ levels. DENSE (sO₂) is trained on all the available simulated OA spectra with the corresponding sO₂ values used as labels. Then we compared the performance of the resulting algorithms with conventional eMSOT for estimating sO₂ in an independent set of ~7500 test grid examples coming from simulated datasets of “background”, “vascularized” and “croissant”. The test grids included examples having larger angular width than any of the training samples. “background” and “vascularized” simulations also differed from the training simulations in terms of spatial variability of the optical properties (“background”) and type of structures present in the image (“vascularized”). The “croissant” dataset differed in simulation geometry. Table 1 provides average test results for the 50 trained DL-eMSOT models as well as for an ensemble and reference networks on datasets of “background”, “vascularized” and “croissant”. Since data from the “background” dataset was partly used for validation of the models (see Sec. III-C), it was not used for testing the performance of the ensemble. The results of eMSOT obtained on the same datasets are also shown for reference. As evident, DL-eMSOT achieves the best performance in terms of sO₂ quantification accuracy out of all the considered methods and seems to generalize well to the simulated data that is dissimilar to the training examples. Notably, DENSE (sO₂) which does not consider spatial information demonstrates performance that is worse than that of deep learning methods that take the information from the spatially distributed grid as input. DENSE (fluence) performs consistently better than the original eMSOT, but fails to outperform DL-eMSOT, which is the overall best performing algorithm in our tests.

Table 1.

Performance of eMSOT and DL-eMSOT in Simulations

	Mean Error	Median Error	Standard Deviation	[25%, 75%] Percentiles
“background” test data
eMSOT	4.9%	3.5%	4.8%	[1.5%, 6.8%]
DL-eMSOT	1.4%	0.9%	1.5%	[0.3%, 1.9%]
DL-eMSOT (ensemble)	-	-	-	-
DENSE (sO2)	7.0%	4.1%	8.4%	[1.4%, 9.7%]
DENSE (fluence)	2.8%	2.0%	2.8%	[0.8%, 3.8]
“vascularized” test data
eMSOT	11.5%	6.87%	14.25%	[2.93%, 13.78%]
DL-eMSOT	3.2%	1.8%	4.5%	[0.6%, 4.0%]
DL-eMSOT (ensemble)	3.0%	1.6%	4.2%	[0.6%, 3.7%]
DENSE (sO2)	9.9%	5.5%	12.7%	[1.9%, 12.9%]
DENSE (fluence)	5.4%	3.4%	6.1%	[1.4%, 7.1%]
“croissant’’ test data
eMSOT	4.8%	5.0%	3.4%	[1.4%, 6.5%]
DL-eMSOT	2.3%	2.5%	1.8%	[0.5%. 3.5%]
DL-eMSOT (ensemble	2.0%	2.0%	1.5%	[0.5%, 2.8%]
DENSE (sO2)	7.1%	7.1%	5.1%	[2.2%, 9.6%]
DENSE (fluence)	2.4	2.4	1.7	[0.7%, 3.3%]

Fig. 4 shows a representative example comparing the performance of eMSOT and DL-eMSOT in a multispectral p₀ simulation coming from the “background” dataset that was not used for validation of any network in the ensemble. Fig. 4A shows a simulated multispectral p₀ map (one wavelength presented) in grayscale together with a grid (red dots) defining the locations of the spectra selected for the application of the quantification methods. The red square defines the ROI shown in Fig. 4B, C. Fig. 4B, C show the sO₂ quantification results produced by eMSOT (Fig. 4B) and DL-eMSOT (Fig. 4C) with mean error of both methods indicated in the corresponding panels. Fig. 4D shows the errors produced by both methods as a function of tissue depth. It can be observed that DL-eMSOT manages to better account for spectral coloring as tissue depth increases.

Fig. 4. Performance of eMSOT and DL-eMSOT in Simulated Data.

(A) Simulated multispectral p₀ map (grayscale, one wavelength presented) with a grid shown with red dots. Red square marks the ROI shown in (B) and(C). (B, C) sO₂ for the grid shown in (A) produced by eMSOT (B) and DL-eMSOT (C) shown in color overlaid on the p₀ map. Mean sO₂ estimation error presented for both methods. (D) sO₂ estimation errors produced by eMSOT (red, mean shown in green) and DL-eMSOT (blue, mean shown in cyan) presented per tissue depth.

B. Experimental Data

To test the ability of the DL-based eMSOT to generalize to experimental data, we applied an ensemble of 50 neural networks to experimental data.

B.1. Phantoms

Fig. 5 demonstrates the performance of DL-eMSOT ensemble on experimental datasets of the following types: Uniform Phantom (Fig.5A–B), and Insertion Phantom (Fig.5C–F). Fig. 5A shows an MSOT image of a uniform deoxygenated phantom with the color-coded map of sO₂ estimated by DL-eMSOT. Fig. 5B demonstrates the absolute sO₂ estimation errors obtained by eMSOT (red, green) and DL-eMSOT (blue, cyan) within the same ROI shown in Fig. 5A. The presented errors are sorted per pixel depth. It can be readily seen that DL-eMSOT estimates sO₂ with better accuracy. Fig. 5C shows an MSOT image of an insertion phantom with the color-coded map of sO₂ estimated by DL-eMSOT. The location of the tube filled with deoxygenated blood is marked with a red arrow. The white arrows (I and II) denote the positions at which the spectra analyzed in Fig. 5E, F, respectively, were measured. Fig. 5D shows errors in sO₂ estimation obtained by eMSOT and DL-eMSOT at the location of the inserted tube. Fig 5E, F demonstrate the spectra measured at locations I and II, respectively, shown in Fig. 5C (black) together with the corresponding fits obtained by eMSOT (red) and DL-eMSOT (blue). Notably, the spectra produced using the eigenfluence parameters found by DL-eMSOT are meaningful.

Fig. 5: Comparison of DL-eMSOT and eMSOT for sO₂ estimation in phantom data.

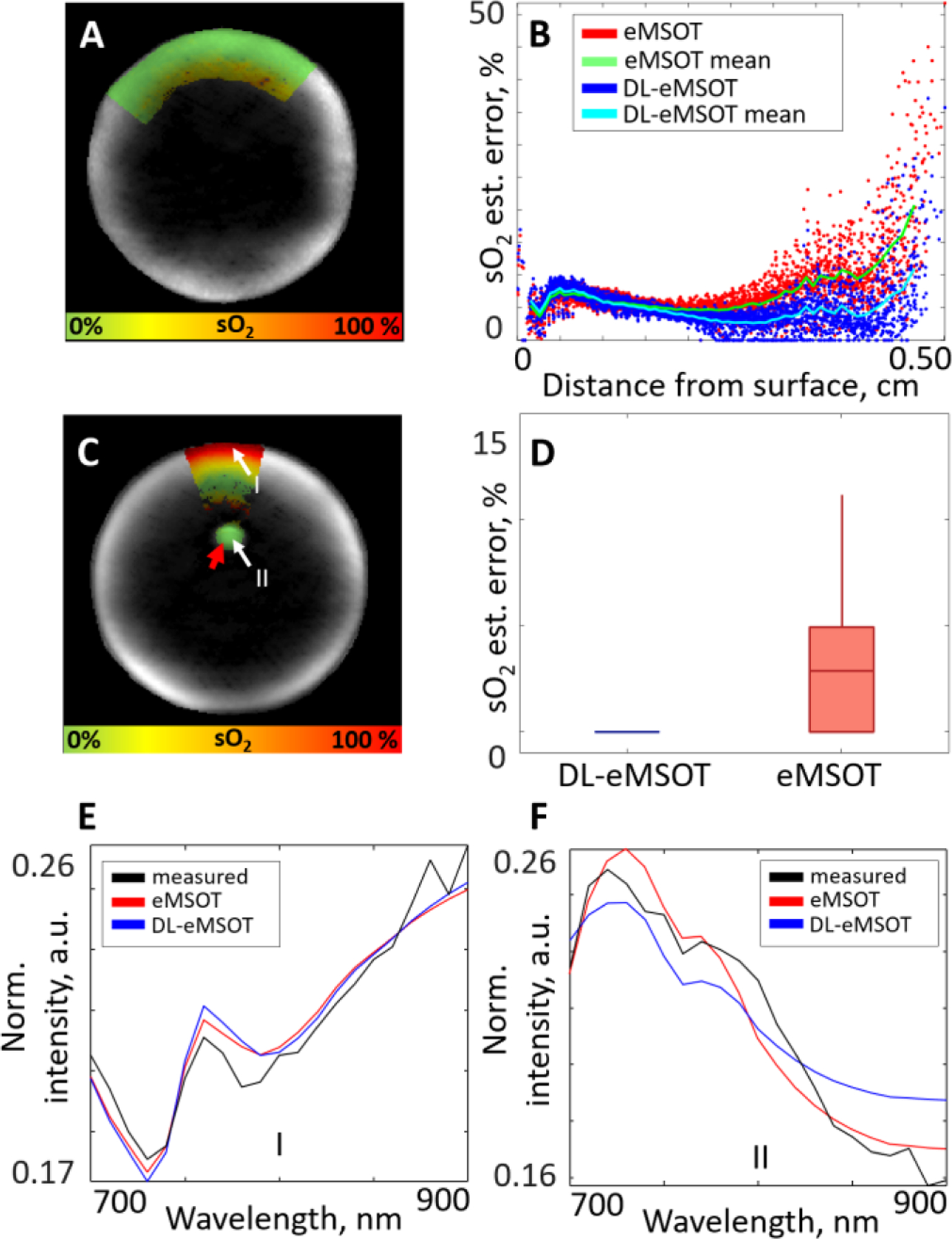
(A) An MSOT image (one wavelength presented) of a deoxygenated uniform blood phantom with the overlaid color-coded result of DL-eMSOT application. (B) Errors in sO₂ estimation for eMSOT (red/green) and DL-eMSOT (blue/cyan) for the phantom shown in (A) on the same grid, presented per pixel depth. (C) An MSOT image (one wavelength presented) of a blood phantom with a capillary tube (target) filled with deoxygenated blood (red arrow) with the overlaid color-coded result of DL-eMSOT application. The labels I and II mark the locations of the spectra presented in (E) and (F), respectively. (D) Errors in sO₂ estimation for eMSOT and DL-eMSOT at the location of the target shown in (C). (E, F) Spectra at locations shown in (C) (black), together with the corresponding fits obtained with eMSOT (red) or DL-eMSOT (blue) algorithms.

B.2. Mouse Data

Fig. 6A, C show MSOT images of abdominal cross-sections of two mice with the color-coded maps of sO₂ estimated by DL-eMSOT. The locations of the tubes filled with blood of known oxygenation (0% in Fig. 6A and 100% in Fig. 6C) are marked with red arrows in respective panels. Fig. 6B shows errors in sO₂ estimation obtained by eMSOT and DL-eMSOT at the location of the inserted tube. Fig. 6C shows errors in sO₂ estimation obtained by eMSOT and DL-eMSOT (ensemble, best performing model and worst performing model) at the location of the inserted tube. It can be observed that the dataset presented in Fig. 6C, D constitutes a challenging case for the single RNN-based models as there is high discrepancy between the best and the worst performing models. This case highlights the importance of using an ensemble of models for reducing the upper bound of error.

Fig. 6: Comparison of DL-eMSOT and eMSOT for sO₂ estimation in experimental animal data.

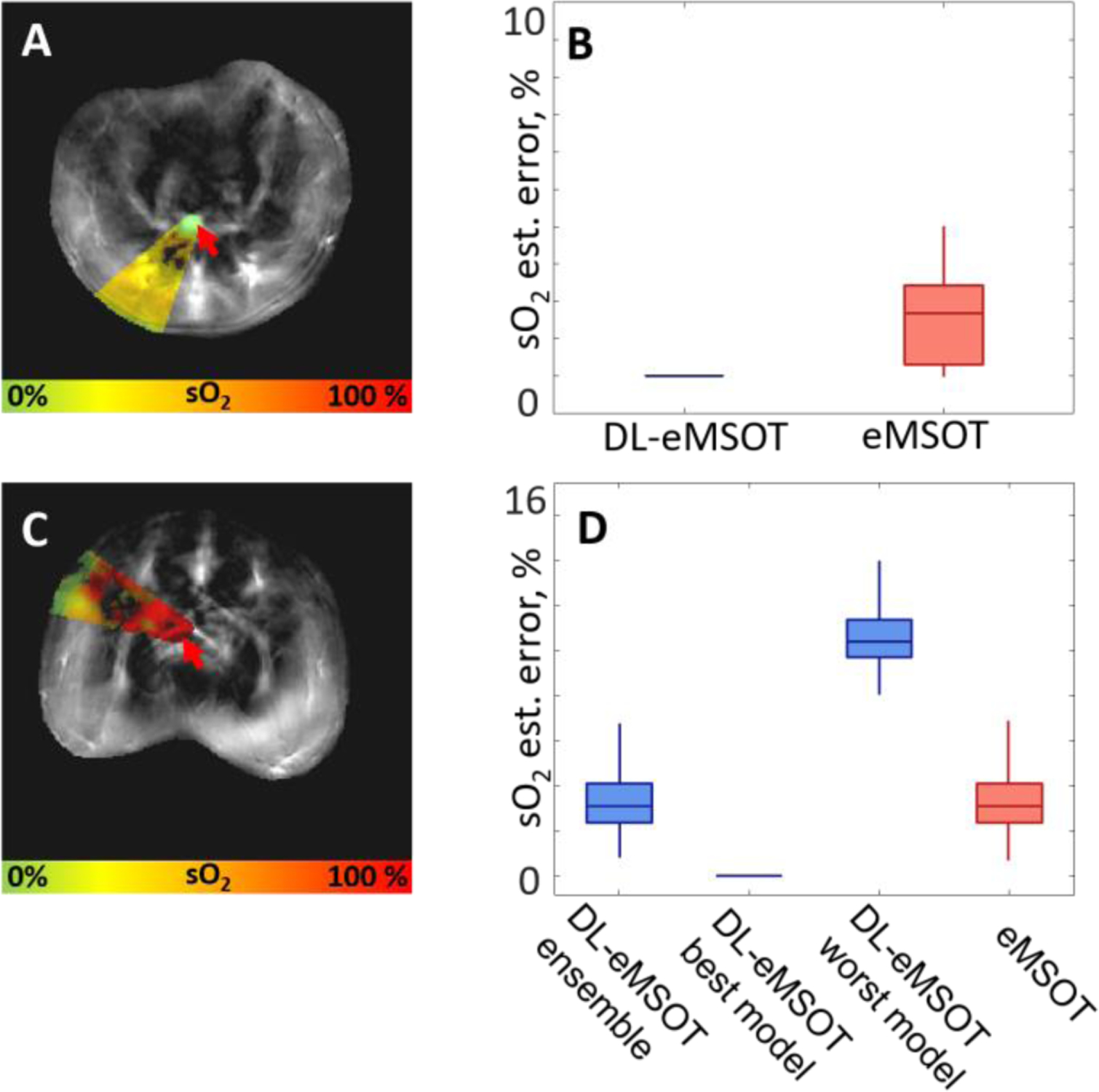
(A, C) MSOT images (one wavelength presented) of abdominal cross-sections of two mice with capillary tubes (targets) filled with blood of known oxygenation (0% (A) and 100% (C), red arrows) with the overlaid color-coded results of DL-eMSOT application. (B) sO₂ estimation errors of eMSOT and DL-eMSOT obtained at the location of the target shown in (A). (D) sO₂ estimation errors of eMSOT and DL-eMSOT (ensemble, best performing model and worst performing model) obtained at the location of the target shown in (C).

Fig. 7 summarizes and compares the performance of DL-eMSOT and eMSOT in all available experimental datasets (25 in total) with the corresponding ground truth: uniform phantoms (Fig. 7A), insertion phantoms (Fig. 7B) and mouse data (Fig. 7C). The results are grouped per ground truth sO₂ level: 0% (left panels) and 100% (right panels). Black dashed lines separate results obtained for separate datasets. As evident, DL-eMSOT outperforms eMSOT in 21 cases out of 25 and achieves comparable sO₂ estimation accuracy in 3 of the remaining 4 cases.

Fig. 7: Evaluation of DL-eMSOT performance with experimental data.

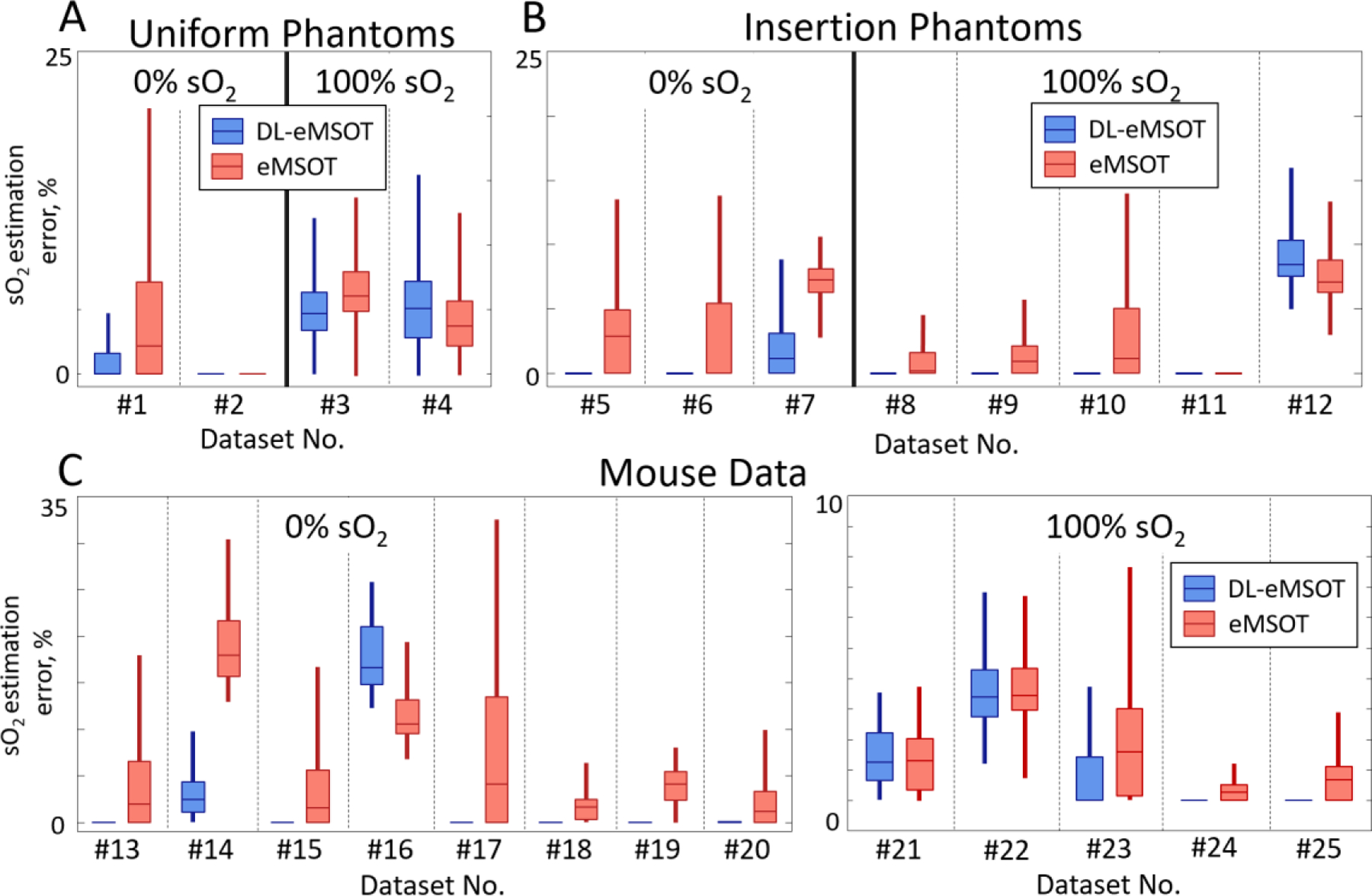
(A-C) Errors in sO₂ estimation for eMSOT (red) and DL-eMSOT (blue) algorithms in (A) uniform phantoms, (B) phantoms with insertions and (C) mouse data. Boxplots represent data mean and 25^th and 75^th percentiles of data; whiskers cover ~96% of data. Dashed black lines separate results for distinct datasets (25 in total).

The performance of DENSE (fluence) and DENSE (sO₂) on the available experimental data is presented in the Supplementary Material (Sec. V). In summary, DENSE (sO₂) produces very high errors (up to ~90%) in some of the considered cases while DENSE (fluence) is much more robust and is often comparable in its performance to eMSOT and DL-EMSOT, highlighting the importance of the spatial context in the problem of fluence correction.

V. Discussion and Conclusion

An increasingly popular technology, DL has been proposed for solving a variety of problems in imaging [36, 37]. In optoacoustic imaging in particular, DL has been considered for image reconstruction [38], artifact removal [39, 40] and sO₂ quantification [28, 30]. In this study, we design an architecture to solve the inverse problem of eMSOT, i.e. correcting a set of input optoacoustic spectra for light fluence and computing sO₂. We observe that the proposed methodology improves the sO₂ quantification accuracy as compared to eMSOT.

The combination of spectral and spatial information is essential for achieving sO₂ quantification accuracy in MSOT. A straightforward way to incorporate the spatial information into the analysis is to use CNN-based architectures [28, 29]. However, due to the need to use simulated data for training, the resulting networks would be biased by the structure of the training data impeding their generalization. Sparse sampling of the analyzed spectra used in DL-eMSOT alleviates this problem while still providing spatial context, ensuring both adequate performance and generalization to experimental data.

Due to the strong dependence of optical fluence on tissue depth, we split the input spectra into a sequence along the tissue depth, i.e. spectra at the same tissue depth constitute one element of the input sequence. Accordingly, we base the architecture of the neural network on a bi-directional RNN that has been designed to handle sequential data well. We find that the proposed architecture is better suited for learning to solve the inverse problem of eMSOT than a less sophisticated architecture that is designed without the specific problem characteristics in mind. Importantly, in this study we have not performed an exhaustive search for the optimal architecture. Our results rather highlight the importance of tailoring the used architecture to the problem at hand as well as the significance of spatial context in quantitative MSOT imaging.

Because of the lack of OA data with the available ground truth for fluence, we use simulations to obtain data for training the neural network. It is important to note that our simulations do not take into account many physical phenomena that occur in the scanner during imaging. We do not simulate wave propagation, spatial and electric impulse responses of the detectors or effects and artifacts introduced by reconstruction. Despite these simplifications, we find that the ensemble of 50 networks trained on our simulated data performs better than the original eMSOT in both simulated and experimental test data.

In addition to better performance in sO₂ estimation accuracy, the proposed method provides potential advantages in terms of processing speed, especially if multiple grids are analyzed simultaneously. Since eMSOT requires ~5 sec per inversion, total inversion time for the test dataset “vascularized” would be approximately 6.3 hours, compared to only 6 minutes for the ensemble of 50 networks. On the other hand, DL-eMSOT still displays errors of ~20% when estimating sO₂ from experimental data. Moreover, in certain cases models in the ensemble show considerable discrepancy in the estimated sO₂ values. Unfortunately, neural networks do not allow for detailed analysis of suboptimal performance. We assume that including more physical phenomena (acoustic wave propagation, image reconstruction, etc.) in the simulations that produce the training data will improve the performance of the algorithm, potentially allowing to use a single model instead of an ensemble.

The major limitation in developing accurate sO₂ quantification methods for MSOT, including DL-eMSOT, is the lack of experimental data with available ground truth sO₂ values. With our experimental setup, we were able to produce only two extreme sO₂ values (0% and 100%) in a stable manner and the performance on such a limited dataset is not necessarily indicative of method’s true capabilities. Ideally, data with the whole range of possible sO₂ values available as ground truth is needed to properly validate the performance of the quantification algorithms.

We have presented a novel sO₂ quantification method for MSOT that is based on eMSOT with a neural network employed for model inversion. With more realistic training data available, it should be possible to further improve quantification accuracy of the algorithm, and possibly use the approach for inverting more complex models that take into account various absorbers (e.g. fat, exogenous contrast agents), bringing MSOT closer to disease screening and diagnosis as well as clinical studies.