Statistical mechanics of chromosomes: in vivo and in silico approaches reveal high-level organization and structure arise exclusively through mechanical feedback between loop extruders and chromatin substrate properties

Abstract

The revolution in understanding higher order chromosome dynamics and organization derives from treating the chromosome as a chain polymer and adapting appropriate polymer-based physical principles. Using basic principles, such as entropic fluctuations and timescales of relaxation of Rouse polymer chains, one can recapitulate the dominant features of chromatin motion observed in vivo. An emerging challenge is to relate the mechanical properties of chromatin to more nuanced organizational principles such as ubiquitous DNA loops. Toward this goal, we introduce a real-time numerical simulation model of a long chain polymer in the presence of histones and condensin, encoding physical principles of chromosome dynamics with coupled histone and condensin sources of transient loop generation. An exact experimental correlate of the model was obtained through analysis of a model-matching fluorescently labeled circular chromosome in live yeast cells. We show that experimentally observed chromosome compaction and variance in compaction are reproduced only with tandem interactions between histone and condensin, not from either individually. The hierarchical loop structures that emerge upon incorporation of histone and condensin activities significantly impact the dynamic and structural properties of chromatin. Moreover, simulations reveal that tandem condensin–histone activity is responsible for higher order chromosomal structures, including recently observed Z-loops.

INTRODUCTION

Discovery of the nucleosome has had a profound influence on our understanding of chromatin compaction and how DNA packaging (epigenetics) amplifies the information content of the genome. The most significant advance beyond nucleosome composition and structure (see below) can be attributed to lessons from polymer physics applied to long chain polymers such as DNA. Using simple representations of bead–spring polymer chains, organizational concepts and metrics such as chromosome territories, contact probabilities and mean squared displacement (MSD) can be accounted for. The next level of description entails modifications of fluctuating bead–spring chains with histone dynamics, loop extrusion motors (via condensin and cohesin) and consequences thereof.

An octamer of histone proteins acts as a spool around which DNA winds ∼1.6×. This leads to an ∼7-fold compaction of the DNA chain. The histone octamer is a highly stable unit, composed of two nearly symmetrical halves (1). The histones are known to be dynamic during transcription in a manner dependent on RNA polymerase II (2–10). Individual histones display different dynamic properties within actively transcribed or silent regions. Histone H2B is dynamic at both active and inactive loci, whereas histone H3 is dynamic predominantly at active loci (11,12). Histone H3 displays rapid exchange at highly transcribed regions, such as rRNA gene loci, associated with the incorporation of an H3 variant (8,9,13). Histones are stable during metaphase in HeLa cells when transcription is silenced, and when transcription resumes at the onset of anaphase, histones are more dynamic (2). Similarly, histones are dynamic during a single cell cycle in yeast (14,15).

Condensins are large multi-subunit protein complexes that are largely responsible for chromosome condensation. Each condensin complex is composed of five subunits, among them three non-SMC regulatory subunits (one kleisin subunit, Brn1, and two HEAT-repeat subunits, Ycs4 and Ycg1) and a pair of core SMC subunits, known as Smc2 and Smc4. Condensin contributes to the formation of chromosome territories (16), provides the foundation for the chromosome axis, upon which chromosome loops emanate, and plays a fundamental role in the organization of the centromere into a bottle brush that can resist tension from spindle microtubules in mitosis (17,18).

How condensin functions has been the subject of several recent studies. Terakawa et al. (19) have shown that condensin behaves as a mechanochemical motor moving along its DNA substrate (19), and there is biological evidence for loop extrusion behavior (20). By applying a constant flow to extend DNA, DNA loops formed via condensin activity are readily apparent, and moreover the loop size grows gradually at a varying rate based on the tension present on the DNA to which condensin is bound. This behavior is called loop extrusion.

Through simulations that recapitulate in vitro findings, one can query the consequences of motor stepping on a thermodynamically mobile substrate. Unlike the behavior of motor proteins on DNA sheets under flow, or kinesin-like microtubule-based motor proteins walking on a rigid microtubule, the behavior of the chromatin substrate has a disproportionate contribution to the behavior of a generic DNA-based translocase. Translocation along a floppy substrate is more akin to the random walk of a segment of a fluctuating polymer chain [e.g. a subdiffusive Rouse chain (21)]. As the translocase steps, the underlying substrate undergoes fluctuations that randomize the direction of the next step (22).

The statistical mechanics of polymer behavior and protein translocation provide a powerful tool to build intuition for understanding experimental observations and making physically accurate hypotheses. Using simple assumptions of proximity-based substrate binding and tension-dependent throttling of loop extrusion, we can establish the rules for loop persistence and extrusion. The simulation (RotoStep) highlights potential new functions for tethers along the chromosome and how the distribution of tethers will be intimately involved in loop formation at a distance. Previous in silico models of condensin (22,23) did not throttle condensin loop extrusion in a tension-dependent manner, did not simulate histones and did not consider how changes in the persistence length of chromatin may alter condensin behavior. In this study, we describe how histone-induced physical properties of the chromatin substrate interact with condensin-generated loop extrusion using both simulation and experimental systems. As our in vitro understanding evolves regarding how condensin extrudes loops, simulations of condensin interactions with the dynamic and varied nuclear environment will provide key insights into the spatiotemporal organization of chromatin in vivo. Simulations run at the scaled rate of the experimental system enable direct comparison to biological observations.

Through detailed comparisons of experimental observations and numerical simulations of the dynamics of small, circular chromosomes, we found that condensin loop extrusion activity on chromatin (histone-compacted DNA) more closely recapitulated experimental observations than condensin on free DNA with respect to both dynamics and morphological behavior of the DNA. The small folding structures formed by histones create strong feedback with large loops caused by loop extrusion activities of condensin, giving rise to hierarchical loops, significantly impacting the dynamics of the circular chromosome. Furthermore, the simulations support the hypothesis that tandem condensin–histone activity is responsible for higher order chromosomal structures. Finally, our model simulations yield an emergent structure, recently observed Z-loop structures (24), demonstrating that the condensin stepping model on a histone-regulated tensile substrate is sufficient to recapitulate in vitro observations.

MATERIALS AND METHODS

Experimental methods

To generate strain JLY1056 with ycg1–2 mutation, first the DNA strain T3000 (25) was cured of the original pT431 strain by growth on YPG and plating on 5-FOA plates. The resultant yeast was transformed with SPC42-mCherry to replace the original Venus tag to generate JLY1038. The JLY1056 strain was generated by transforming JLY1038 with the plasmid p290, kindly provided by Damien D’Amours (University of Ottawa), after digestion with XhoI and XbaI to introduce the ycg1–2 allele. JLY1056 colonies were screened for temperature sensitivity to 42°C.

Mutant spt10Δ was obtained based on the same carrier dicentric plasmid chromosome pT431. The strain LVY1003 was generated by generating a null allele of SPT10 by removal of the open reading frame using the primers

GTGTACCGATCAAGAACAACTCTAGACTTCCGCCAAAGTGATTATCAACAAAcggatccccgggttaattaa and

GTACAAACTTTATAGTTTCTAGGGTTGGTGATGTGACCGTCTCTGGCAGAGgaattcgagctcgtttaaac. The lowercase letters have homology to pFA6a-KAN, which was used to generate the knockout fragment. The dicentric plasmid, pT431 isolate 2, was transformed into the SPT10::KAN and screened using the GFP signal. All strains were grown in liquid media at 24°C.

All biological experiments were performed using at least three different liquid yeast cultures grown on separate days. All strains were grown to mid-logarithmic phase before imaging. JLY1056 was grown at 37°C for 3 h before imaging for restrictive temperature imaging; all other strains were grown at 24°C for 4 h before imaging. Strains were grown in YCAT-galactose media with 0.5 mg/ml additional adenine and methionine. Four hours before imaging, cells with the dicentric plasmid pT431 were washed and incubated in SG (synthetic-containing galactose) media lacking methionine with 0.5 mg/ml additional adenine to induce the recombinase to excise the ARS sequence of the plasmid. Cells were then resuspended in YPD for 20 min to repress transcription from the GAL1 promoter and activate the second, conditional centromere (25). Cells were then washed and resuspended in YC-complete media with 2% filter sterile glucose.

Strains were imaged on untreated glass coverslips. Time lapses were performed at room temperature (25°C) using an Eclipse Ti wide-field inverted microscope (Nikon) with a 100× Apo TIRF 1.49 NA objective (Nikon) and Clara charge-coupled device camera (Andor) using Nikon NIS Elements imaging software (Nikon). At each 30 s interval, a seven-step Z-stack of 300 nm step size was acquired in the GFP and RFP channels for a duration of 20 min. A single trans-image was acquired at each interval (Supplementary Figure S1).

Time lapse images of strains containing dicentric plasmids were analyzed using a custom MATLAB GUI, population_GUI_v1_2.m. The GUI allows users to select plasmid signals in the GFP channel, select a background region in the GFP channel for background subtraction, generate and alter a binary mask based on background subtraction of plasmid signal and select spindle pole bodies (SPBs) in the RFP channel. Only cells containing a single plasmid signal were analyzed. Signals that drifted out of focus were not recorded for that time point. Signals that collapsed the spindle were not recorded during the collapse. Signals that were too dim for proper binary mask segmentation were not recorded. The data for each plasmid signal were saved in a .MAT file for summary analysis of plasmid signal length.

Chromosome simulator

The simulator was developed in C++, using DataTank (2002) as user interface, which allows users to input model parameters and visualize in pellucid graphical interface. The C++ program parses 3D coordinates of the chromosome into a time series as the output. The output file can be directly read and DataTank provides built-in tools for visualization and analyses. A copy of the simulator is provided. For the workflow of the simulation pipeline, one can refer to (26).

Polymer chain model

The simulator adopts a bead–spring polymer model (26) of the plasmid chromosome as the baseline upon which to add the action of histones and condensins. A plasmid chromosome is discretized into 386 beads connected by springs, with each bead representing roughly 30 bp of DNA. It attains a circular structure with two sites pinned in space, corresponding to centromeres tethered to SPBs. The dynamics of the tethered chromosome is driven by a combination of forces described below, giving a stochastic differential equation model for the 3D dynamics of a circular chromosome in a live cell environment.

The dynamics of each bead on the chromatin chain is governed by the following forces: the spring force between itself and nearest neighbor beads or tether site, so that all beads have two springs attached; the drag force on the bead in the nucleoplasm; the restoring force that penalizes bending of the chain from Euler–Bernoulli beam theory; and a random white noise force due to thermal fluctuations consistent with Brownian motion. See (17) for details.

Histones and SMC proteins

Histones

Histones are modeled according to published results (1). Histone units are not modeled as masses. Instead, each histone is modeled as a seven-bead subloop along the chain (each unit represents 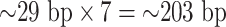). The subloops are formed by applying virtual springs at two attachment sites. Each spring pulls two attachment sites close, and thus the chromosomal region in between forms a loop structure. The histone spring is five times stronger than the springs connecting polymer beads. Any form of sliding of histones along the chain is not allowed during the entire simulation. For example, histone 1 forms a loop from bead 1 to bead 7. Histone 2 is forbidden to intrude this region until histone 1 releases from the chromosome. The polymer is fully loaded by histones by default, which means that seven-bead substructures cover nearly the entire polymer without overlapping, due to a high degree of enrichment of nucleosomes in observations. Each histone unit periodically attaches to and detaches from the chromatin chain to simulate the turnover of histones observed in vivo. The turnover mechanism is achieved by setting an intrinsic timer to each unit. One histone unit switches status between forming a loop and releasing a loop once the timer exceeds the predefined deadline. In simulation, in order to stochastically vary the average number of active histones, one can tune either the total number of histones in the simulation or the on/off period of the histones. Moreover, winding DNA under high tension is capable of unwinding histones, which is consistent with observations of force-dependent unwinding and rewinding mechanism.

In the simulation, neither the mass of histones nor the higher order structural interactions between nucleosomes are considered upon this point. We focus instead on the consequences of the loop structures. Supplementary Figure S2D shows an example of the geometry of the chromosome while interacting with a histone. The ring-like substructure remains until the histone detaches from the DNA.

Condensins

The simulation model of condensin complexes we construct is based on the loop extrusion observation published recently (20). The hypothetical model of such a complex is a ring structure that anchors on a segment of DNA. The rest portion of DNA is grabbed and pulled by the complex through its ring structure and completes the extrusion activity. In our model, each complex is modeled as a spring attaching to the DNA strand, with one end anchored at a fixed site, which is called ‘the strong site’. The strong end does not release upon high local tension. The other attachment site of the complex, ‘the weak site’, moves along the chain, attaches to a farther segment of the DNA and then the spring pulls the two ends close again to complete the extrusion activity. Moreover, after a predefined period of extrusion, the spring releases and restarts to extrude another loop. Instead of a multistep relaxation process, the loop releases and disappears instantly. This mechanism is in accord with the sudden disruption of the condensin complex after actively extruding the loop for a certain period of time in our model. Supplementary Figure S2A–C shows how a condensin evolves in a short period in an illustrative condition. The extrusion rate was amplified compared with real simulations, for clear observation of the loop extrusion behavior.

In this study, we have implemented a decay function in the translocase motor, such that after a set time period, the spring releases and rebinds to another bead in the vicinity. Ganji et al. (20) observed that the extrusion rate decreases as the tension increases along the DNA. We have embedded a variable extrusion rate into the condensin model, by assigning a customized function to govern the time lapse between which a condensin takes a move. A condensin is able to sense the local tension at its attachment sites. The predefined function then computes the time lapse based on the tension, lengthening the time period after which the condensin takes another move if strong local tension is reported, thereby slowing down the extrusion rate (Supplementary Figure S3B and C). By default, the function scales the time lapse proportional to the tension. The local tension is represented by the spring length, and hence the function computing the time gap τ is

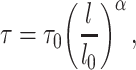(1)

where 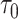is a predefined intrinsic time lapse for all condensins, and the parameters 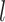and 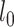are the actual spring length at a given time point and the rest length of the DNA spring (10 nm) at the attachment sites, respectively. The α parameter controls the steepness of the function. The extrusion rate, r, is inversely proportional to the time lapse r ∼ 1/τ, so that the extrusion rate decays inversely proportional to 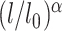. α is set to 1 as the default in simulations.

Another property of condensin states that after a certain period of extrusion, which is called the ‘lifetime’, the spring releases and rebinds to extrude another loop (Supplementary Figure S3E). Instead of a multistep relaxation process, the loop releases and disappears instantly. The predefined lifetime is significantly larger than the time gap for the condensin to take a move, in order to guarantee its ability to form a large loop. This mechanism is in accordance with the sudden disruption of the condensin loop in experiments. It is worth noting that the extrusion behavior in our model is not a strictly sequential extrusion process. There are cases where a condensin takes a step but the size of the extruded loop shrinks (Supplementary Figure S3D). In simulation, this phenomenon is not rare, due to the complex 3D structure of the chromosome under external influences including thermal fluctuations. We favor this implementation because sudden shrinkage of condensin loops is a potential explanation of the instant releases observed in experiments.

The histones and condensins we introduce into the simulation do not conflict with each other. That is, a bead is capable of being wound around a histone while also part of a condensin-extruded loop. The proteins are able to attach to every bead, except the two end beads of the circular chromosome that are used to model sister centromeres.

RESULTS

Structural proteins condense DNA

Our in silico simulations of condensin interacting with the chromatin substrate are based upon a small, dicentric, circular chromosome, whose behavior we can visualize in vivo in the budding yeast Saccharomyces cerevisiae. The circular chromosome pT431 (25) contains a tandem tet-operator (tetO) array (5.5 kb labeled on the ∼11 kb plasmid), between one constitutive and one conditionally functional centromere (25). Yeast cells were grown to log phase in SD-methionine media for 3 h to induce excision of the origin of replication (ARS). The conditional centromere was activated by growth in the presence of glucose. Thus, upon imaging, the circular chromosome is a single DNA molecule with two active centromeres. TetO/TetR-GFP signals that were between and displaced from SPBs (Spc42-mCherry) are indicative of bioriented attachment (25). Mitotic cells are identified based on the distance between SPBs and the presence of a bud. Fluorescent images are acquired every 30 s for 20 min resulting in 41 time point measurements, and the length of the GFP signals is measured using a customized MATLAB GUI (23). Signals that were too dim due to photobleaching or z-drift were not measured for that time point (see the ‘Materials and Methods’ section), resulting in time lapse measurements of GFP signal lengths. This method estimates the signal with a minimum-sized oval and acts as the metric for compactness of the signal. The TetO/TetR-GFP signal fluctuates over almost a decade in length, as observed in the distribution of molecules ranging from a diffraction-limited focus (∼250 nm) to decondensed molecules spanning the distance between sister kinetochore microtubule plus ends (1600 nm). In this way, we have adequate dynamic range to assess the contribution of chromatin proteins. The tetO/TetR-GFP signals captured during microscopy are processed through image processing pipelines to obtain a length measurement for quantitative analysis.

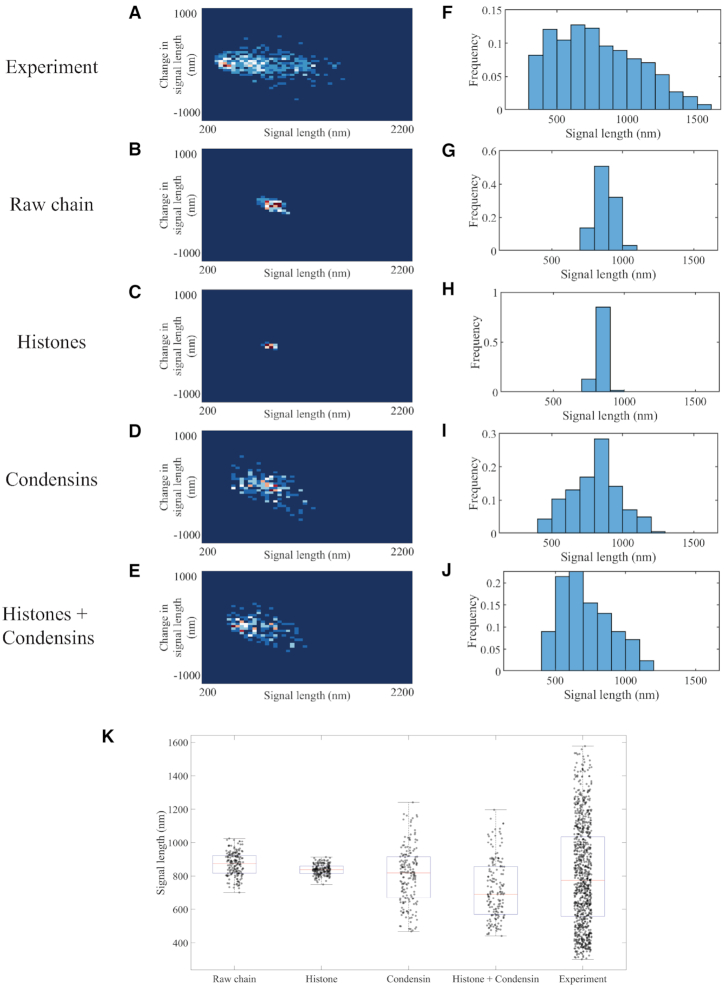
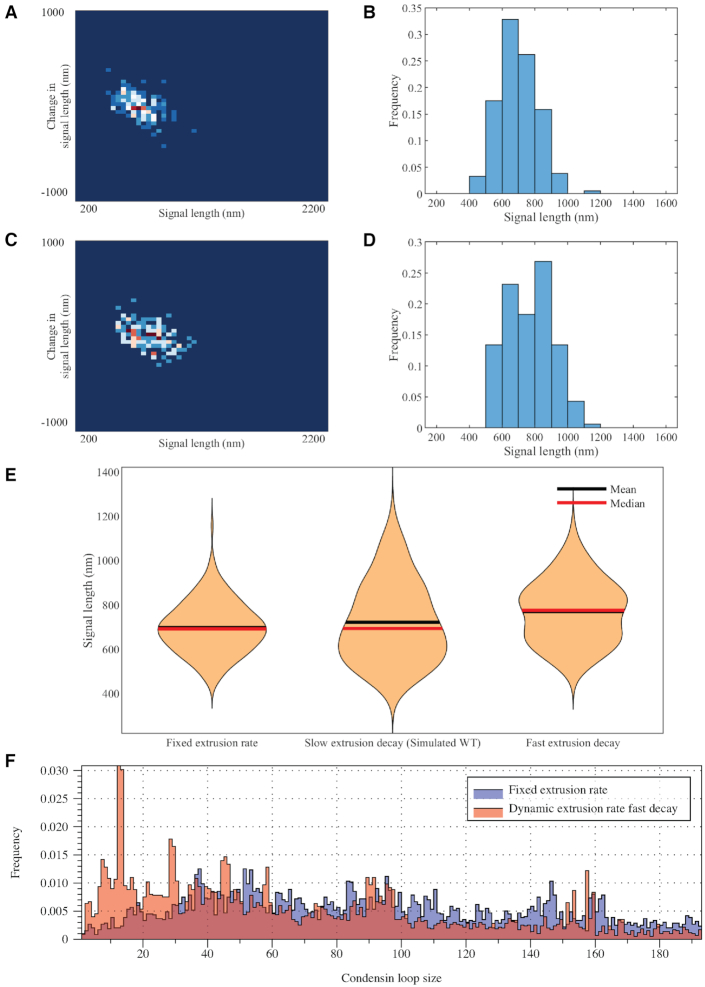
To quantitate signal variations, we used a density map to display change in signal length as a function of current signal length. The change in signal length is measured by the difference between the current signal length and the signal length observed one timestep previously. The frequency is displayed by color code. The signal length histogram for experimental images (Figure 1A) reveals a distribution skewed toward the compact state (∼250 nm) with mean and median between 600 and 700 nm. The most frequently observed signal length is between 500 and 600 nm, showing a compact structure of the signal. The density heatmap in addition shows frequent signal fluctuations by several observations located off the center of the y-axis. These are indicative of large signal extensions within the 30 s interval. The fit for the distribution supports the skewness of the distribution: instead of a symmetric Gaussian distribution, a bimodal two-term Gaussian fits the data better. The plasmid signals reveal the characteristics of the dynamics of chromosomes in vivo, condensed while dynamic. This compactness is essential in chromosomal organization through the division process. Chromatin is in a highly dynamic state, commensurate with the various enzymatic machineries that require access depending on demands for replication, transcription or DNA repair.

Figure 1.

Signal length analyses of experimental and simulated plasmid signals. Density heatmaps (A–E) of plasmid signal lengths versus change in plasmid signal length per time interval (30 s) and histograms (F–J) of plasmid signal length for experimental data; simulated data with only polymeric DNA; simulated data with DNA and histones; simulated data with DNA and six condensin complexes; and simulated data with DNA, histones and six condensin complexes, respectively. Data for each simulation figure are for a total of 183 time lapses selected from three independent simulations. Time lapses are chosen only after the equilibrium state has been reached. Data for experimental samples are from a total of 925 observations. (K) Signal length box plot versus distinct classes of proteins in the simulation. The red lines represent median, the blue boxes show 25 and 75 percent quantiles, and the whiskers extend to the most extreme data points not considered as outliers. Each dot represents one data point.

In simulations, we constrain the model with comparable scale and geometrical restrictions to match the in vivo circular chromosome. During each simulation, we extract signals from a ‘labeled’ region of the chromosome at the exact same position with a proper numerical transformation. The statistics generated through experiments and simulations are directly compared. In this way, we provide insights into the contribution of substrate stiffness in loop formation, and a potential tension feedback between the substrate and motor protein. The fluorescent region of DNA is highlighted in simulated data for a direct comparison of simulated and experimental microscopy signals. All simulations are based on a bead–spring polymer model of DNA in a fluid drag environment (see the ‘Materials and Methods’ section). The total 11 kb plasmid chromosome is discretized into 386 beads, with each bead representing roughly 10 nm (29 bp) of DNA. Bead 1 and bead 139 are pinned at stationary positions to simulate tethered, static centromeres in the nucleus. Beads are connected by springs governed by a linear force law and a bending rigidity law. The persistence length of DNA is 50 nm, set by an additional hinge force in the simulation that controls the rigidity. Thermodynamic fluctuations influence the dynamics of all beads, and the range the substrate explores can be tested as a metric for the mobility and stiffness of the polymer chain. The fluid environment is assigned a viscosity of 0.01 P. Given the estimation of nuclear viscosity to be 141 P (27), the simulation is a 14 100-fold speedup of the in vivo process, so that 0.15 s simulation time is equivalent to ∼35 min real time.

We compare simulation results of signal length for the raw polymer chain; polymer chain with histones; polymer chain with condensins; and finally, polymer chain with both histones and condensins. To directly compare the simulation to experimental images, we convolve the beads representing the tetO arrays with a point spread function from a fluorescence microscope used to image the tetO arrays through the program Microscope Simulator 2 (28). We extract the simulated signal length through the experimental pipeline, thereby providing direct comparison between simulated and experimental results. Our goal is to identify potential mechanisms acting on the chain that reproduce the experimental behavior: condensed signals with significant length fluctuations.

The raw polymer chain model shows large signal lengths (∼900 nm), with minimal fluctuations (Figure 1C and H). The simulated signal lengths are symmetrically distributed, predominantly between 800 and 900 nm, with ±150 nm variation. While thermal motion acts as the only external source for energy, the elongated chain gently fluctuates (Figure 2A), not inducing drastic signal length change. The system lacks the ability to exhibit variations at a comparable length scale to authentic chromosomes in vivo. Moreover, the large average signal length suggests that additional activity is acting to compact the structure and drive its fluctuations.

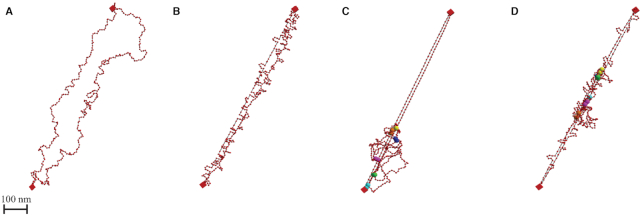
Figure 2.

Geometry of simulated plasmid chromosome. 3D geometry of simulated polymer model after reaching equilibrium. Red beads are the discretized units connected through springs (black segments). Two red boxes represent centromeres that are fixed in space. (A) Geometry of the raw polymer chain model. (B) Geometry of the polymer model with histones. Loops along the strand show locations of histones. (C) Geometry of the polymer model with condensins. Large spheres with the same color are the attachment sites of a condensin complex. (D) Geometry of the polymer model with both histones and condensins.

To introduce virtual histones in the simulation system, we embed static cross-linkers that bind to the chromosome chain (see the ‘Materials and Methods’ section). The polymer chain plus histones adopts a stable structure with a lower level of fluctuations (Figure 1C and H). The compact geometry created by histones suppresses fluctuations (Figure 2B). The reduction of the circular chromosome’s contour length via histone compaction, while the two centromeres remain separated by 800 nm due to spindle attachment, leads to a taut chromatin substrate. In other words, histones stiffen the polymer chain by creating rigid substructures yet fail to reduce the signal size. Observations with 800–900 ± 50 nm signal lengths account for over 90% of the total observations. Frequent compact signals, such as the small round signals observed in vivo, never appear in simulations, even with histones fully loaded. The signal length in this system is dictated by the two centromeres of the dicentric chromosome ‘pinned’ to kinetochore microtubules. We conclude there must be additional mechanisms that lead to the extreme fluctuations of these polymers in vivo relative to the condensed structure of a histone-bound polymer.

Condensin is a DNA-based motor protein with the ability to translocate along double-stranded DNA at relatively high velocities (60 bp/s) (19). A simple representation in which one of the condensin subunits is modeled as a spring attaching to the DNA strand, with another subunit anchored at a fixed site and second more mobile subunit, reveals how such a spring can lead to loop extrusion activity. Loops are extruded as a consequence of the mobile subunit stepping to the closest bead in space, rather than the next bead in the sequence of the chain (22). A customized function governs the rate at which the weak site takes one action in order to simulate the decaying extrusion rate found in experiments (see the ‘Materials and Methods’ section).

We include six condensins in the polymer model. The number of condensins is informed by the finding that condensin is enriched ∼3-fold in pericentric regions relative to chromosome arms (∼1/10 kb chromosome arms, 3/10 kb in pericentromere) (29). Considering the centromeres are the site of cohesin recruitment (30), and the circular chromosome contains two centromeres, we included six condensin molecules. When condensin is introduced to the polymer model, the signals exhibit intense signal length fluctuations, observed through both the geometry and the plots (Figures 1D and I, and 2C). In simulations, condensins continue to extrude loops, creating large-scale substructures. These DNA translocase motors inject energy into the system, leading to more observations with extreme structures. The histogram reveals an extreme distribution of signal lengths ranging between 400 and 1200 nm, in agreement with experimental data. However, the most frequent signal lengths remain in the 800–900 nm range, without skewness toward 250 nm as in experiments.

The most faithful recapitulation of experimental results by the model arises with the tandem coupling of histones and condensins, producing a compact structure with intense fluctuations. The most frequent signal lengths are around 500 nm, and the distribution is right-skewed (Figure 1J). The heatmap shifts its center from 800 to 500 nm while maintaining both the vertical spread (Figure 1E) and extreme signal lengths up to 1200 nm. The box plot shows a direct comparison of averaged signal lengths (Figure 1K). The synergistic interplay between histones, condensins and the DNA plasmid successfully shortens the signal length while preserving large excursions. Thus, the model supports loop extrusion activity of condensins in tandem with histone activity as a viable mechanism for the experimental behavior.

Supplementary Figure S4A shows the signal length distributions of individual time lapses of 35 independent cells as a combined box plot. The plasmids are highly dynamic over the 20-min time period. Although statistical discrepancy occurs between experimental data and simulated data due to additional biological variables (e.g. microtubule dynamics that influence the position of the tethered beads, crowding in the cell), the similarity in variability and skewness of the signal length distribution is indicative of qualitative agreement with the numerical model. The high P-value of the normalized two-sample Kolmogorov–Smirnov test between the experimental wild-type (WT) data and the full model simulation data also suggests that the model generates condensed yet dynamic signals, consistent with experimental observations (Supplementary Table S1).

The geometry conveys intuition as to how condensins and histones succeed in compacting the chromosome structure (Figure 2). Condensins create large loop structures, which should be floppy and highly mobile, but histones form substructures that stiffen the loops: the tandem effect is efficient compaction. The large loops become dense bulbs (Figure 2D). The mobility drops significantly for beads on these loops when histones are embedded, indicating that, in cases where the fluorescently tagged region is interacting with condensin, the signal will be dense. Meanwhile, the extrusion behavior is able to stretch the chromosome spine. When the fluorescent region is not interacting with condensin, the region will be stretched along the chromosomal spine, posing strong candidates for the large observed signals. As a result, we observe highly variable signal lengths without defined periods, and the chromosome signal can be either remarkably small or extremely large. The overall compactness of the chromosome is achieved by the feedback between large tension-dependent loop extrusion of condensins and the generation of tension and dense substructures by histones. When histones and condensins are both activated and large loops have been formed, high-tension regions are created along the main spine. These high-tension domains restrict the extrusion activity of condensin, forcing them to be relatively stable. Therefore, the system is biased toward compact configurations, consistent with frequent experimental compact signals.

The volatile compact structure is created by the synergy between compaction and tension generation of histones and the tension-modulated loop generation of condensin. Condensins drive fluctuations by actively extruding loops along the chromosome in segments of low tension. Histones, on the other hand, compact the large loops formed by condensin while generating the tension that modulates loop generation. These two DNA-binding proteins, which are considered as two primary classes of proteins that compact and package DNA, lead to a compact highly fluctuating chromosomal structure, reconstructing conclusions from experimental observations.

In a condensin-concentrated environment, histone enrichment leads to stable DNA structure

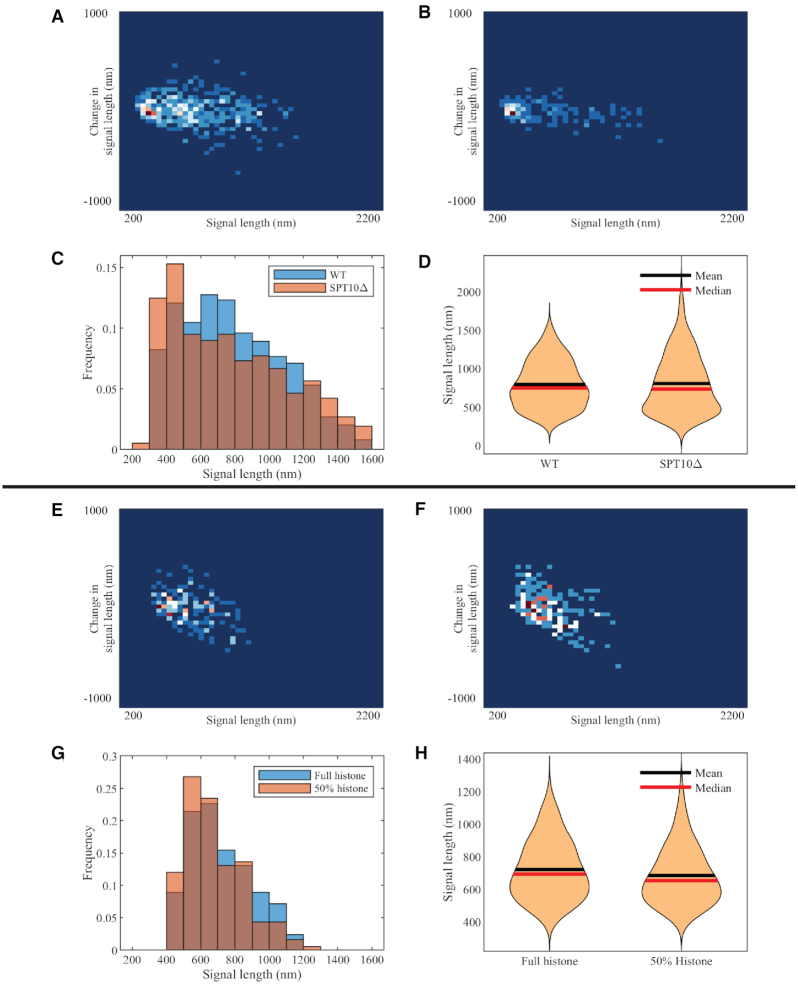
The simulations provide an opportunity to query the relationship between substrate stiffness (the polymer chain), compaction (histones) and extrusion (condensins). The complexity of these interactions is such that the model may provide critical insights that lie beyond one’s intuition. In order to explore the predictive powers of the model, we implemented mutants that reduce the concentration of histones. The yeast SPT10 gene is a histone H3 acetylase with a role in transcriptional regulation and sequence-specific activator of histone gene expression (31). The mutation spt10Δ results in depletion of histone synthesis, leading to a significant drop in histone concentration (32). The spt10Δ mutant has an equivalent impact on histone depletion from chromosomes and minichromosomes as used herein (32–35). Unexpectedly, the depletion of histones does not lead to significant increase in the averaged size of the chromosome, rather it causes more extreme dynamic variation in the length distribution (Figure 3C). The dicentric plasmid chromosomes are observed to be either extraordinarily large or small. Provided that histones affect the packaging and organization of DNA, this observation implies that under certain geometrical constraints, histones are not simply compaction factors.

Figure 3.

Experimental and simulated plasmid signal lengths upon histone depletion. (A) Density heatmap of WT plasmid signals. (B) Density heatmap of histone-depleted (spt10Δ) mutant plasmid signals. Combined signal length histograms (C) and signal length violin plot (D) of WT and histone-depleted (spt10Δ) mutant plasmid signals. (E) Density heatmap of simulated WT plasmid signals. (F) Density heatmap of simulated histone-depleted plasmid signals. Combined signal length histogram (G) and signal length violin plot (H) of simulated WT and simulated histone-depleted plasmids.

We are able to reconstruct similar conditions in spt10Δ phenotypes in silico by tuning parameters to decrease histone concentration. Histones are modeled as static regional loops along the polymer chain. There are periodic cycles of attachment and detachment from chromatin, causing local structural compaction. While controlling other conditions, the impact incurred by the depletion of histones can be simulated and the cause for unexpected extreme observations can be closely analyzed.

In experiments, the histone-mutated environment leads to an increase in variance, rather than the average structure (in this case, length). This is contrary to the intuitive expectation that a lack of histones will result in a decondensed state. Alternatively, histone mutation causes more extremely condensed cases of <500 nm and more extremely stretched cases of >1200 nm. Qualitative features in support of this conclusion can also be found in violin plots and a density heatmap (Figure 3).

To explore in detail what leads to these findings, we employ our simulation tools to reproduce the experiment. We apply the simulation tool with parameters that fit the WT experimental data as the comparison group. For the controlled group, to simulate the spt10Δ environment, we modify the histone activity parameters to partially suppress their activity. The most straightforward modification is to reduce the number of histones in the environment. In simulations, this can be achieved by lengthening the duration for histones to detach from the chromosome chain. When we reduce active histones by 50% in this way, we observe similar features in plasmid signal length distribution as in experiments (Supplementary Table S2).

In order to understand this finding, we explored the mechanics of condensin behavior. In a simulated histone-enriched environment, condensin turns out to be less active due to the reduction in DNA length and therefore increased tension between the tethered centromeres (Figure 2D). Condensin tends to stay in the same position for a longer duration, leading to loops that tend to maintain their size distribution over time. In a histone-depleted environment, condensin more actively extrudes loops. Recall previous studies that show the structure without histones (Figure 1). The signals are widely spread as the consequence of dynamic extrusion, leading to large variances in signal size. This reveals that in a condensin-enriched environment, concentrating histones does not monotonically condense the structure. Loops can interact with one another in a hierarchical fashion, resulting in complex consequences on chromosome organization. In conclusion, histones effectively condense large loop structures formed by other proteins (including condensin). Meanwhile, histones build local tension while attaching to the DNA, which in turn limits the mobility of condensin. These conflicting mechanisms balance, leading to an optimal organization that possesses both compactness and mobility.

Reduction of simulated condensin-mediated loops results in decompaction of simulated circular, dicentric chromosome mimicking condensin TS allele ycg1–2

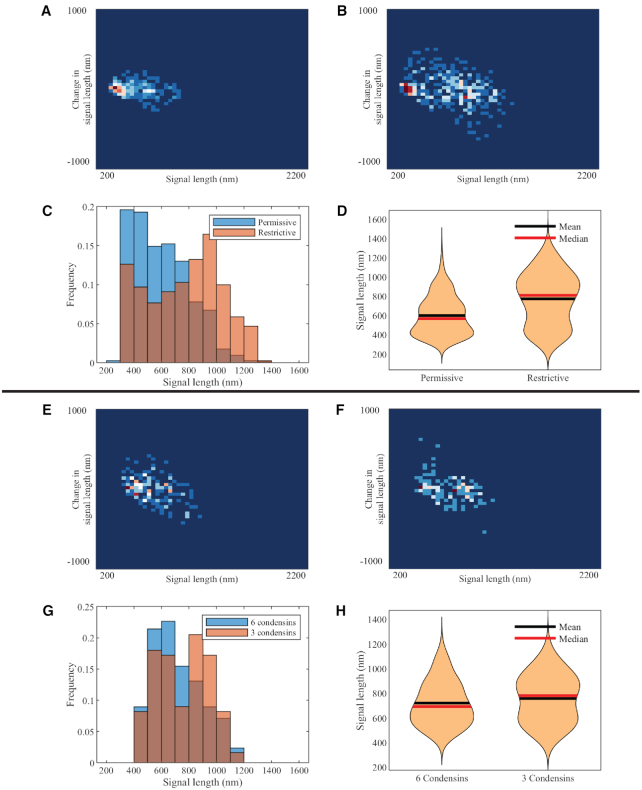
Ycg1 is a component of the condensin complex that possesses a DNA-binding domain. The mutant ycg1–2 is temperature sensitive. When they are released from G1 at the restrictive growth temperature of 37°C, the chromatin binding effect is weakened and eventually leads to depletion in attached condensins on the chromosome (36). At permissive temperature (24°C), the signal length distribution is similar to WT simulation. At restrictive temperature (37°C), the signal lengths exhibit a bimodal distribution (Figure 4C). Restrictive temperature experiments had frequent signals in excess of 800 nm in length, which was not often observed in WT experiments. A more detailed statistical analysis showed a clear bimodal distribution of signal length. The lower peak is distributed around 400 nm, similar to WT signal length. The larger peak is close to 900 nm, which is similar to raw chain cases without condensins. The bimodal distribution deviates from the control group with a right-skewed distribution.

Figure 4.

Experimental and simulated plasmid signal lengths versus condensin perturbations. Density heatmap of condensin TS mutant, ycg1–2, at permissive (A) and restrictive (B) temperatures. Combined signal length histograms (C) and signal length violin plots (D) of condensin TS mutant, ycg1–2, at permissive and restrictive signals. Density heatmap of simulated plasmids with six condensins (E) and three condensins (F). Combined signal length histograms (G) and signal length violin plots (H) of simulated plasmids with six condensins and three condensins, respectively.

To simulate the ycg1–2 mutant environment, we reduce the total number of condensins in the simulation from 6 to 3. Condensin actively extrudes loops, but occasionally releases the loop and restarts extrusion activity. Initializations corresponding to histones and the DNA chain remain unchanged. The simulation result shows a similar bimodal property as observed in experimental data (Figure 4G). The two peaks are located near 400–500 and 800–900 nm. The violin plot also displays an additional mode with increased average signal length, leading to a pear-shaped plot. Mean and median are between two peaks, and the fact that mean and median shift order implies a change of skewness. Remarkably, if we analyze the heatmap of both experimental ycg1–2 data and simulated ycg1–2 data, there are two clusters of points, suggesting the possibility that the system switches between two quasi-stable phases. One phase with denser structure corresponds to WT cases, obtaining a compact structure of 400 nm. The other phase tends toward cases without condensin, with an averaged 900 nm signal. Statistics using the condensin-depleted model to simulate ycg1–2 mutants in restrictive conditions are displayed in the Supplementary Data (Supplementary Figure S5 and Supplementary Table S3). Reducing the number of condensins causes a clear bimodal distribution, resulting in statistical agreement with the experimental data where the activity of condensin in ycg1–2 mutants is depressed by the restrictive temperature.

A hypothetical interpretation would be that the number of observations where no condensin interacts with the labeled region rises to a significant level, because of the lack of condensin. This leads to two primary phases: when condensin forms loops involving the labeled region, the signal is under WT regulation; when condensin does not interact with the labeled region, the signals retain condensin-excluded properties, showing large length and variation. Moreover, the reduction of condensin causes lower tension along the chain, which in turn enhances motility. This is supported by the wider density heatmap in the vertical direction (Figure 4F). Hence, the overall behavior of the chromosome should frequently switch between the two modes.

The analysis showed that the large loops extruded by condensin, in the presence of histones, compact the chromosome structure in the model. In addition, recall that in the histone-free simulations, condensin fails to compact the chromosome (Figures 1 and 2). This leads to the conclusion that condensin–histone cooperativity condenses and compacts the chromosome.

Tension-dependent extrusion by condensin modulates loop size in simulations

An alternative modification we employed to simulate the depletion of condensin activity is varying the tension-dependent extrusion decay rate (Figure 5). As reported by Ganji et al. (20), a condensin extrudes loops in an extension-dependent manner in a flow-stretched environment. This observation is mechanistically interpreted as tension-dependent extrusion behavior. Similar to other DNA-binding proteins, condensins are able to detect regional tension along the DNA chain at the attachment site and alter their behavior accordingly. We simulate this mechanism by introducing a loop extrusion rate that decays with tension.

Figure 5.

Comparison plots in simulations varying the tension-dependent loop extrusion behavior of condensins. Density heatmap (A) and signal length histogram (B) for simulated data where condensins extrude loops at a constant rate. Density heatmap (C) and signal length histogram (D) for simulated data where condensin loop extrusion decreases with increasing substrate tension. (E) Violin plot of signal lengths as a function of the rate of decay of loop extrusion against tension. (F) Condensin loop size (histogram sampled from single simulations) as a function of the decay rate of loop extrusion against tension.

When the extrusion rate remains fixed and independent of tension, condensin keeps extruding loops, leading to a more uniform distribution in loop size (Figure 5F). However, the uniformly distributed condensin loop distribution does not lead to effective chromosomal compactness. The signals have a Gaussian-like distribution centered at 600–700 nm. Extreme cases are less frequently observed compared to tension-dependent situations.

On the other hand, if we attenuate the tension-dependent decay mechanism and make the condensin highly sensitive to tension, the ability to extrude large loops degenerates. The concentration in small-length loops displayed in Figure 5F shows the inability of condensin in extruding large loops. As a result, a bimodal distribution is observed with two peaks at 600 and 900 nm.

The tension-dependent extrusion rate is a key mechanism for condensin when regulating chromosomal structures, enabling condensin to form and maintain large loops, which act as the primary factor leading to the compact structure of chromosomes.

DNA substrate stiffness tunes the hierarchical loop structure and chromatin motion in simulations with histones and condensins, revealing a non-monotone substrate control

In studies of polymer physics, the polymer stiffness is strongly correlated with the mobility of the polymer due to thermal fluctuations. The mobility metric of a polymer is its MSD, which is a measure of the space the polymer explores in a given time interval. From polymer physics, polymer MSD is an increasing function of persistence length, 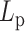. From the perspective of the spring-like characteristics of chromatin, the spring constant 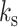is proportional to temperature T and inversely proportional to 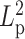(37):

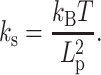(2)

This reflects the fewer entropic states that chains can adopt with greater persistence lengths, and clearly a weaker spring is floppier and will exhibit broader fluctuations and therefore exhibit higher mobility and MSD statistics.

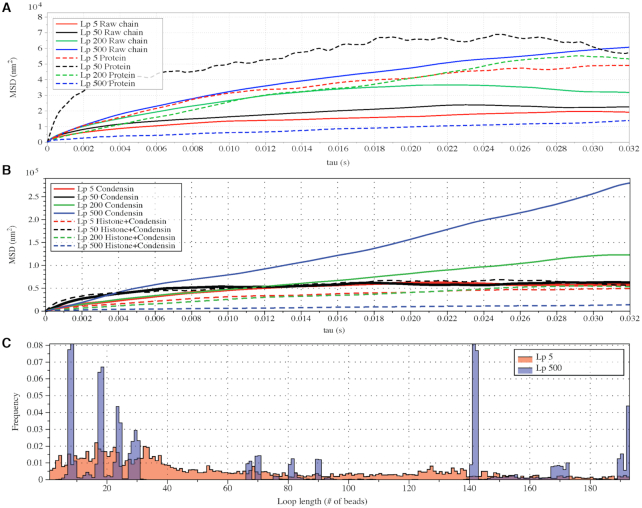
This aligns with our chromosome dynamics simulation results in the absence of histone compaction and condensin (Figure 6A, solid lines). The solid lines represent the MSD plot of raw polymers without any structural proteins as a function of lag time τ. Notice the monotonicity of MSD with increasing 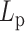, consistent with polymer physics.

Figure 6.

Varying DNA stiffness leads to non-monotone performance of hierarchical loop structures caused by histones and condensins. (A) Simulated MSD plot as a function of τ. 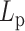varies from 5 to 500 nm. Solid lines correspond to simulations without both histones and condensins. Dashed lines demonstrate statistics of simulation results with both histones and condensins. (B) Simulated MSD plot as a function of τ. 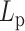varies from 5 to 500 nm. Solid lines correspond to simulations without histones. Dashed lines demonstrate statistics of simulation results with both histones and condensins. (C) Cumulative distribution in the sizes of loops for condensin loops, compared between highly flexible chains in red (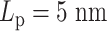) and stiffer chains in blue ().

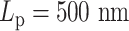Strikingly, however, non-monotonicity is observed in MSD as a function of persistence length when histones and condensins are included (Figure 6A, dashed lines). As 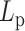increases, the MSD increases at first for flexible chains, but decreases for stiff systems with 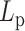in the 200–500 nm range. This implies that the loop structures affect the mobility of a polymer and modify its fundamental structural properties. While chromatin changes that increase or decrease 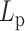will clearly manifest as changes in MSD, the relationship between these parameters cannot be simply deduced from experimental observations in the complex cellular milieu.

We explore these effects by examining the behavior of condensin. Figure 6C shows the condensin loop size histogram during one simulation. Besides the loop size, the motility of condensin can also be inferred from this figure. For highly flexible chains 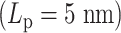, the loops are highly dynamic and exhibit a broad distribution. For stiffer chains 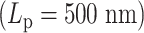, the loops cluster into discrete size classes (number of beads/loop).

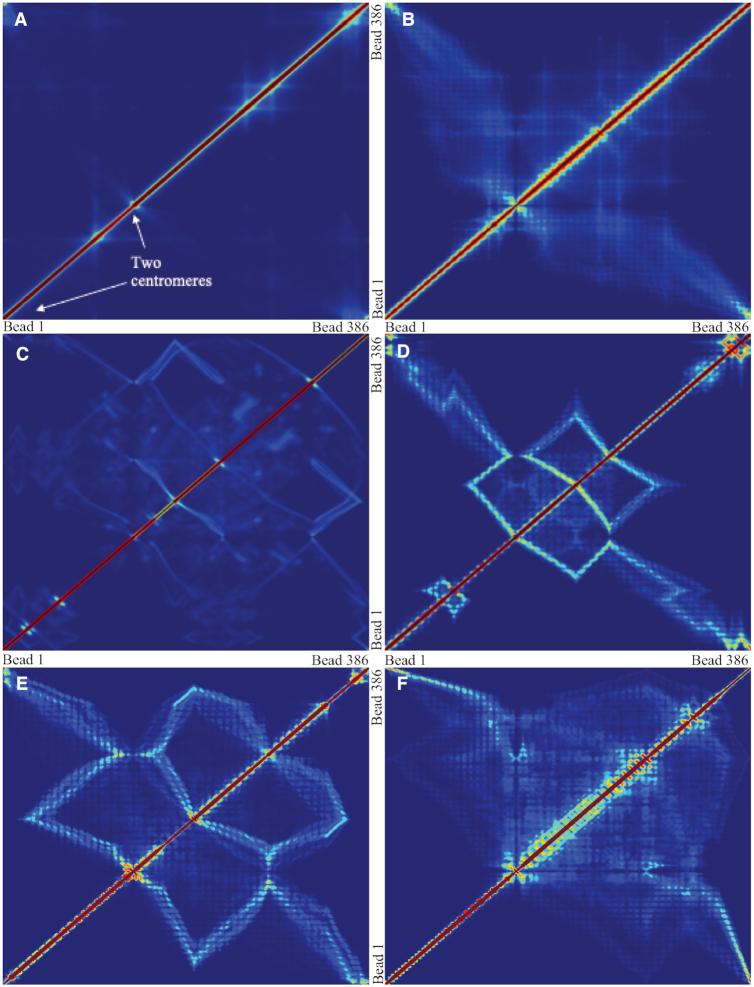
Similar conclusions can also be observed in the contact frequency map (Figure 7A–F). Condensin promotes contacts between separated segments of DNA by forming cross-links between them. Histones, on the other hand, lead to local contacts, which is represented by increased contacts in regions near the diagonal. In flexible chains, the average contacts were evenly increased, with few strong spots. However, in stiff chains, condensin leads to more persistent loops (Figure 6C). Contacts within the loops are apparent as squares off the diagonal (Figure 7D and E). This supports the statement that while histones are enriched, condensin is more static in stiffer chains. They prefer to form large, stationary loops. Meanwhile, condensins in a flexible chain are more dynamic, revealed by the vague signals in the contact maps. This property is not only due to the tension dependence of condensin, but also affected by the geometrical restriction prescribed in the plasmid system.

Figure 7.

Contact frequency maps of simulated plasmids with varying DNA stiffness. Contacts are measured by counting frequencies where two beads are within 30 nm. (A) Condensins, 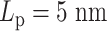. (B) Condensins and histones, 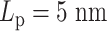. (C) Condensins, 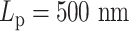. (D–F) Condensins and histones, 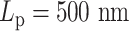, three realizations. Red region represents high pairwise contact frequency in a contact map. Zero values in diagonal due to exclusion of self-contacts. Beads corresponding to two centromeres are indicated in panel (A).

The structural impact caused by histones can be further investigated through additional data analyses. As previously mentioned, histones interact with large condensin loops to create hierarchical loop structures, which consequently reduce the mobility of the chromosome. Statistical evidence is provided in Figure 6B. In general, involving histones would lower the MSD plateau, which implies a drop in mobility of the chromatin, compared to systems without histones. We hypothesize that this drop is caused not only by the collapse of large condensin loops, but also by the tension generated via histones that creates a feedback loop with tension-dependent extrusion behavior of condensins. If histones only function as compactors of large loops, the MSD changes should be at similar levels across systems with different stiffness. However, while drastic decay in MSD can be found in stiff systems (Figure 6B, blue lines), in slack (low tension) systems we observe negligible difference (Figure 6B, black lines). In our hypothesis, histones pull loops closer while also reducing available free polymer to make larger loops. But furthermore, histones generate tension along the chromosome chain, leading to modified behavior across domains with varying stiffness. In stiff systems, histones generate extreme tension, which inhibits the stepping motion of condensins along the taut chain. Eventually, the overall mobility as revealed by MSD is extraordinarily low in high-stiffness systems. In slack systems, on the other hand, histones fail to generate sufficient tension to restrict the motion of condensins. This observation in our simulation suggests a strong feedback between the functions of histones and condensins that regulates both the structure and dynamics of the plasmid.

Presumably, this extreme difference in loop structure and dynamics in systems with heterogeneous stiffness is responsible for observed WT chromatin mobility. In stiff strains, large, static loops are further compacted by histones. As a result, the chromosome chain is highly condensed with very limited fluctuations in space. The synergetic mechanism of hierarchical loops formed by histone and condensin leads to the sharp decrease in MSD for stiffer chains.

Numerical experiments were designed to introduce heterogeneity in persistence length 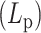on one chromosome chain. To model potential differences in 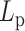along the chain, we adjusted the bending rigidity for 193 beads to one persistence length 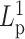and assign the other 193 beads with another persistence length 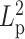. In addition, the simulation includes histones and condensins as described above. MSD was analyzed over the fluorescent region. The fluorescent region is also evenly divided into the two heterogeneous segments, minimizing any bias of comparison in regional MSD.

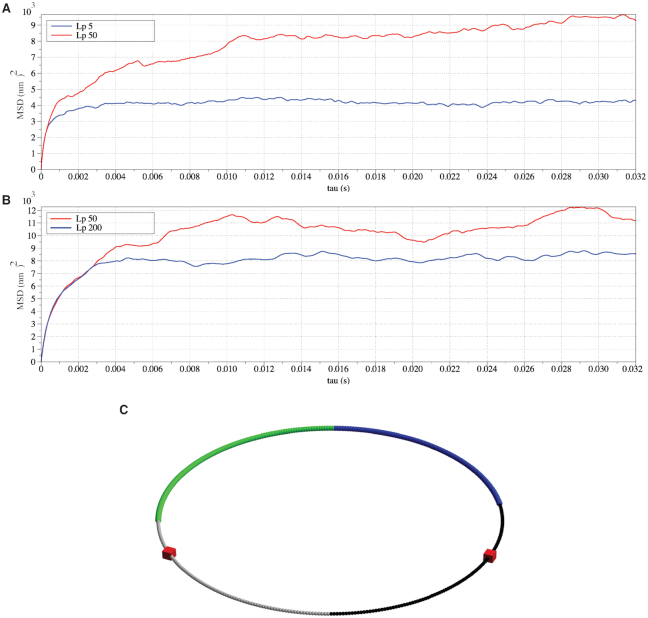
Similar to the experiments conducted on independent chains (Figure 6), monotonicity also vanishes on the heterogeneous chains (Figure 8). The MSD plateau of regions with 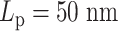dominates both plateaus of alternative regions 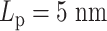and .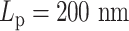

Figure 8.

Regional MSD plots for simulated heterogeneous plasmid chromosomes. Regional MSD plots over the fluorescent region of simulated heterogeneous plasmid chromosomes. The plasmid is evenly split into two halves of unique stiffness. (A) Half 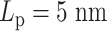versus half 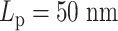. (B) Half 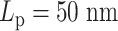versus half 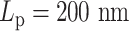. (C) The diagram of the heterogeneous plasmid in the simulation at 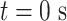. Two symmetric regions, region I and region II, attain different stiffness. The data used to generate MSD curves in panels (A) and (B) are extracted from the labeled regions, which are symmetrically distributed in either region I (green) or region II (blue). Histones and condensins are present in the simulations but not shown here for clarity. Red boxes represent the centromeres.

This supports the conclusion that hierarchical loops modify the mobility of the chromosome, and suggests that such modifications in the mobility of the chromosome may be as significant as the polymer stiffness, or even more dominant. A hypothetical explanation to the non-monotonic observation in the simulation is that, for stiff regions with 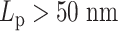, the dynamics of condensins are significantly restricted. For heterogeneous chromosomes, this will cause a gradual concentration of condensins in the stiff region. With the compaction effect of concentrated hierarchical loops, the constraints in diffusion dominate the enhanced mobility caused by greater polymer stiffness. As a result, the MSD of a stiffer region with 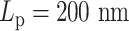drops compared to the flexible region with 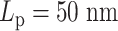. In the other experiment with less overall stiffness (half 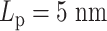, half 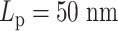), the effect of hierarchical loops is not significant enough to overcome the effect of amplified stiffness, and thus the MSD still increases with increasing .

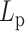Simulations with multiple condensins exhibit Z-loops

Figure 7D and E shows the pairwise contact frequency for stiff polymers with 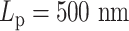, which is 10 times stiffer than common DNA. However, the simulation is still valuable because qualitative conclusions are more visible and are easy to interpret in this system. One major feature the contact map shows is the line segments. A bright polyline connects two centromeres (bead 0 and bead 138). Through careful observation, we explain the formation of such a bright polyline by the tightly tethered backbone of the plasmid chromosome. Figure 9A and B provides an illustration of the relationship between circular loops and higher order chromosome organizational structure (Z-loops) and the associated contact map features (box lines). The loop structures create local substructures, occupying a large portion of the chromosome. The remaining segments are tightly tethered by the centromeres, forming two parallel lines between the poles (Figure 9A). Beads near the centromere axis (the dashed line) stay close and confined, which are often detected as contacts (bead 1 with bead 15, bead 2 with bead 14, etc.). Additionally, looped beads may get close to the axis due to diffusion, making extra contacts (e.g. bead 4 with bead 14). Consequently, a bright path connecting two centromeres is observed in the contact map. This explains that there are persistent contacts between beads that are far apart, and the pairs form a path that linearly connects two centromeres on the contact maps (Figure 7D–F).

Figure 9.

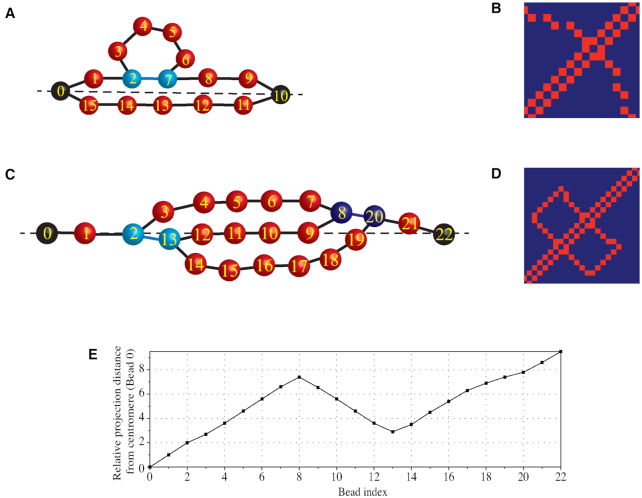
Illustrative diagrams of the contact map and the Z-loop structure. (A) A simplified diagram of the circular plasmid of high stiffness, tightly tethered by the centromeres. (B) The contact map of panel (A). Beads near the centromere axis (the dashed line) stay close and make contacts (bead 1 with bead 15, bead 2 with bead 14, etc.). Additionally, looped beads may get close to the axis, making extra contacts (e.g. bead 4 with bead 14). Consequently, a bright path connecting two centromeres is observed in the contact map. (C) A simplified diagram of the Z-loop formed by two interacting condensin loops. In both panels (A) and (C), black beads are centromeres. Beads not colored in red are attachment sites of condensins. All beads are indexed sequentially. Beads are located closer to the centromere axis than they appear in the diagrams. (D) The contact map of panel (C). A box-shaped line pattern is observed, which can be used as an indicator for such a Z-loop structure. (E) The relative projection distance, plotted from panel (C). Each bead is projected onto the centromere axis (the dashed line) and then the distance to the centromere (bead 0) is measured. A reverse trend is observed from bead 8 to bead 13, which can be used as another indicator for a Z-loop structure.

In addition, there are minor box line structures near the diagonal. These are evidence for Z-loops. One large loop formed by a condensin lands one of its attachment sites on another loop structure, leading to a double-connection structure (Figure 10A). Under external tethering and protein compaction, the thermal fluctuations of this structure are constrained. Consequently, the existence of Z-loops remarkably reduces the volume of the chromosome. Recently published work reports that the Z-loop structure caused by condensins has been visualized in in vitro experiments (24). The experimental approach was similar to the method adopted by the Ganji group: utilizing real-time imaging techniques to observe a tethered, separated, flow-stretched DNA interacting with condensins. They discovered that loops extruded by two condensins interact with each other, even when far apart. In close proximity, they observed that condensin complexes are able to traverse each other and form Z-loop structures.

Figure 10.

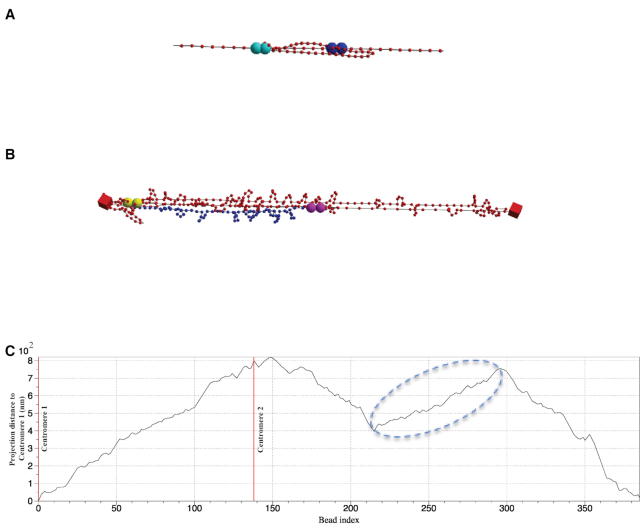
Graphical demonstration of Z-loop structures. (A) Graphical demonstration of Z-loop structure on a linear polymer chain formed by two interacting condensin loops. Large spheres with the same color code represent two attachment sites for a single condensin complex. (B) Snapshot of Z-loop structure in WT plasmid simulations. Blue labeled segment represents the backward segment caused by a Z-loop. (C) Projection distance from centromere 1 (bead 0) as a function of bead index at the instance of panel (B). Two centromeres’ positions are labeled as red vertical lines (bead 0 and bead 138). Circled region corresponds to inverse chromosome segment labeled in panel (B).

Another quantitative method to demonstrate the existence of Z-loops is to plot the projection distance from centromere 1 as a function of bead index. We project each bead on the axis formed between two centromeres (the centromere axis). Then, the distance between the projection and the centromere is measured and plotted. Figure 9C–E uses a hypothetical Z-loop configuration and distance metrics to illustrate how both the contact map and the projection distance plot reveal signatures of a Z-loop structure. Provided the chromosome is taut, when a Z-loop forms, the 3-fold structure is tightly tethered along the centromere axial direction (Figure 9C, dashed line). Thus, the structure is highly confined near the centromere axis. This particular structure creates a closed box line pattern in the contact map (Figure 9D), and also creates a reverse trend (successive beads reversing from farther to closer) in the projected distance plot (Figure 9E). The reverse trend reflects the inner segment of the Z-loop structure (Figure 9C, bead 8 to bead 13).

In addition to observations in stiff chromosomes, this structure is commonly observed in other simulated chromosomes as multiple dynamic loops intertwine and interact (Figure 10B). As shown in Figure 10C, the curve obtains an increasing trend from the starting centromere (bead 0) to another centromere (bead 138) and tends to decrease while circling back. Local zigzags are usually caused by small-scale loops formed by histones. Flat regions or variable regions may correspond to large, floppy loops caused by condensins. A reverse trend, such as the emphasized region in Figure 10C, is mostly likely the signature of Z-loops as illustrated in Figures 9 and 10. We emphasize that Z-loops are extremely hard to identify experimentally and numerically, due to much higher structural complexity of chromosomes, both geometric and topological. Both the stretched chromosomal geometry and exactly two interacting condensin loops are necessary for clear observation of Z-loops. Interactions involving more than two condensins lead to less visible contact statistics (cf. Figure 7F).

The Z-loop structure can be regarded as a higher order loop structure. In terms of function in the nucleus, it efficiently enhances chromosomal compaction. Moreover, the appearance of Z-loops, the 3-fold loop structure consisting of two condensin complexes, indicates the existence of various higher order looping structures involving multiple DNA-binding proteins. Thus, condensins may achieve chromosomal condensation via various higher order looping structures.

DISCUSSION

The balance between condensins and histones affects compaction of simulated, circular chromosome

Surprisingly, a slight variation in binding–unbinding kinetics of histones and condensins will cause unanticipated effects on chromosomal organization. Nucleosome occupancy is broadly affected by DNA transcription, replication, recombination and repair (38–40). In budding yeast, nucleosome occupancy is regulated by the DNA sequence (41,42). These studies suggest less nucleosome occupancy with AT-rich sequences. Modeling of nucleosome positioning suggests it is regulated by an interplay of DNA sequence and chromatin (35,43). Aging in both yeast (44) and mammalian cells (45) is associated with lower numbers of nucleosome occupancy. Mammalian cells that lack high mobility group box protein 1 (HMGB1), a non-histone binding nuclear protein, have reduced nucleosome occupancy (46). Thus, there are many mechanisms that can be employed by the cell to alter nucleosome occupancy and thus chromosome structure and dynamics. We proceed to fix histone kinetics and explore the consequences of modifications in the average extrusion rate of condensins. More specifically, the default extrusion rate for the tension-free system is increased, while the extrusion decay function remains unchanged. In all cases, whether the average condensin extrusion rate is increased or decreased, we observe increases in the average signal length. This observation does not occur if histones are excluded in the simulation.

This result suggests there is a delicate balance between histone and condensin kinetics within the hierarchical structures whose tandem effect induces a compact chromosome structure. We seek explanations through model simulations, and the following insight is revealed upon careful examination of the dynamics of condensins. Condensins with low extrusion rate barely function as their name implies when histones are also active. The loops generated are small, resulting in a similar structure and dynamics without condensins. Likewise, condensins with high extrusion rate keep extruding loops along the chain, inducing hyperactive dynamics not seen experimentally. As an example, the signal length histogram is spread out compared with experimental data with reasonable averaged condensin extrusion rate. Similar results are observed if the extrusion decay function against tension is modified. In both cases where condensin extrusion rate decays more drastically or mildly versus tension along the chain, the chromosomes obtain a looser structure.

Experiments with post-translational modifications (PTMs) of condensin have exhibited altered chromosome organization and condensin distribution. Deletion of Smt4, an isopeptidase that removes the PTM small ubiquitin-like modifier (SUMO) from proteins, causes a decrease in pericentric condensin clustering (47) and decreased localization of condensin to rDNA sites in budding yeast (47). In budding yeast, condensin subunits are phosphorylated by the Polo kinase Cdc5 (48) and the Aurora B kinase Ipl1 (49) in late mitosis. Condensin is also phosphorylated by Cdk1 (50) and regulates early condensation in mitosis (51). Thus, it is possible that condensin loop extrusion can be altered via a PTM.

Clearly the geometric restriction of the plasmid chromosome is a microcosm of larger chromosomes, and the tandem feedback between condensins and histones may require different relative rates of their kinetics to optimize chromosome compaction. Presumably, condensins are able to extrude larger loops on larger chromosomes, which would interact differently with histones depending on their density. Hence, further exploration of the loop structures in other chromosome systems will be meaningful.

Tension-dependent extrusion rate affects the compactness and mobility of simulated, circular chromosomes

The observation of loop extrusion of reconstituted condensins on DNA (20) revealed the following important mechanisms to condensin-based loop extrusion. First, condensin activity induces loop extrusion rather than formation of random cross-links between two DNA loci. Second, the extrusion activity is strictly ATP hydrolysis dependent. Lastly, the extrusion rate decays proportional to the degree of extension of DNA. However, the underlying cause of the decay of the extrusion rate remains poorly understood.

In these experiments, the DNA is subject to a specific geometrical configuration. A linear piece of λ-DNA is tethered at two ends with an end-to-end distance smaller than its contour length. Hence, as the condensin complex builds up the loop, the DNA gradually gets stretched. A reasonable hypothesis by Ganji et al. (20) is that condensin extrusion rates decay as tension builds in the tethered DNA. This hypothesis is also adopted and embedded in the simulations presented herein. Indeed, our model studies reveal that the tension-induced decay of the loop extrusion rate strongly affects chromosome structure and compaction, and these studies reveal (due to non-monotonicity in the compaction metrics) the parameter specifications for optimal compaction.

When condensins either maintain a constant extrusion rate or decay weakly, we observe large loop length fluctuations due to condensin activity. The loops created by condensin complexes continuously vary in length, with a low average loop size due to the restricted, circular structure of the plasmid chromosome. On the other hand, with a loop extrusion rate inversely proportional to tension [putatively the setting for WT condensin activity consistent with Ganji et al. (20)], condensin loops develop rapidly and are biased toward large loops in the histogram, which in turn leads to overall plasmid compression in the presence of histones. In simulations with a sharper decay function for the tension-dependent extrusion rate, large loops never form. For example, if condensin extrudes at a rate inversely proportional to the square of tension, condensins only generate small loops that do not significantly reduce chromosome volume.

The numerical experiments varying 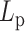(chromosome persistence length) also offer a glimpse into the essence of extrusion decay. The ability of condensins to detect local tension and respond accordingly, coupled with the presence of a heterogeneous tensile landscape due to histones, gives condensins an auto-selection mechanism for optimal loop size distributions that generates a high degree of compactness while preserving motility.

It will be very informative to conduct biological experiments that modify the stiffness of chromatin, similar to what we have done in simulation. PTMs of histones may change the stiffness of chromatin in a regional manner (52). Future experiments that alter the chromatin stiffness in a regional manner will potentially validate our model predictions.

DATA AVAILABILITY

The simulation is coded in C++, using DataTank as the user interface. All simulation scripts and some useful data analysis scripts have been made available at https://github.com/heyunyan19930924/Chromosome-Simulation as .tank files, specifically for DataTank. The simulation C++ code is attached in the .tank files.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Simons Foundation; National Science Foundation [DMS-1462992 and DMS-1816630 to M.G.F., 1929114 to K.B.]; National Institutes of Health [R37 GM32238 to K.B., Y.H., D.C., E.E.V.G. and S.C.L.D.]. Funding for open access charge: National Institutes of Health [R37 GM32238].

Conflict of interest statement. None declared.