Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Nov 3;59(22):16467–16473. doi: 10.1021/acs.inorgchem.0c02294

Na3FeH7 and Na3CoH6: Hydrogen-Rich First-Row Transition Metal Hydrides from High Pressure Synthesis

Kristina Spektor †,*, Wilson A Crichton †, Stanislav Filippov ‡,§, Sergei I Simak ‡, Andreas Fischer ∥, Ulrich Häussermann §,*
PMCID: PMC7672699  PMID: 33141575

Abstract

graphic file with name ic0c02294_0006.jpg

The formation of ternary hydrogen-rich hydrides involving the first-row transition metals TM = Fe and Co in high oxidation states is demonstrated from in situ synchrotron diffraction studies of reaction mixtures NaH–TM–H2 at p ≈ 10 GPa. Na3FeH7 and Na3CoH6 feature pentagonal bipyramidal FeH73– and octahedral CoH63– 18-electron complexes, respectively. At high pressure, high temperature (300 < T ≤ 470 °C) conditions, metal atoms are arranged as in the face-centered cubic Heusler structure, and ab initio molecular dynamics simulations suggest that the complexes undergo reorientational dynamics. Upon cooling, subtle changes in the diffraction patterns evidence reversible and rapid phase transitions associated with ordering of the complexes. During decompression, Na3FeH7 and Na3CoH6 transform to tetragonal and orthorhombic low pressure forms, respectively, which can be retained at ambient pressure. The discovery of Na3FeH7 and Na3CoH6 establishes a consecutive series of homoleptic hydrogen-rich complexes for first-row transition metals from Cr to Ni.

Short abstract

In situ synchrotron diffraction studies of reaction mixtures NaH−TM−H2 (TM = Fe, Co) at p ≈ 10 GPa revealed the formation of ternary hydrides Na3FeH7 and Na3CoH6 featuring pentagonal bipyramidal Fe(IV)H73− and octahedral Co(III)H63− complexes, respectively. The discovery of Na3FeH7 and Na3CoH6 establishes a consecutive series of homoleptic hydrogen-rich complexes for first-row transition metals from Cr to Ni.

1. Introduction

Expectations for high temperature superconductivity have stimulated intensive research efforts into binary metal–H systems at high pressures, which have resulted in the discovery of unprecedented hydrogen-rich hydrides.1−4 These hydrides, also called super- or polyhydrides, exhibit stunning compositions and hydrogen structures, which include clathrate-like cages (as in LaH10, CaH6),5−7 oligomeric chain fragments (as in NaHn),8 and two-dimensional layers (as in FeH5).9 High temperature superconductivity approaching room temperature has been predicted for alkaline earth, La, and Y hydrides with clathrate-like structures and was recently experimentally confirmed for LaH10.10

An important issue is that binary superhydrides and their interesting properties can only be observed at extreme pressures in the Mbar range (i.e., around 100 GPa). Upon pressure release, they decompose into ordinary metal hydrides and hydrogen. The situation may be different with ternary hydrides because decomposition pathways are expected to be more complex, which increases the likelihood of trapping metastable superhydride phases. Also, ternary hydrogen-rich hydrides may form at much lower pressure conditions. Indeed, it has been recently shown that the application of modest pressures of around 5 GPa can already afford new hydrogen-rich complex transition metal hydrides, CTMHs, in which group 4–6 metals attain unusually high H coordination numbers. These new CTMHs comprise homoleptic complex ions like CrH75–, NbH94–, and Ti2H146– and are semiconductors.11−14 Yet, they are recoverable to ambient pressure, and doping with hole carriers has been suggested to achieve superconductivity.14 Here, we demonstrate the accessibility of hydrogen-rich CTMHs in the Na–Fe–H and Na–Co–H systems by using pressures around 10 GPa and slightly elevated temperatures up to 470 °C. We argue that the obtained compounds establish a consecutive series of homoleptic hydrogen-rich complexes for first-row transition metals from Cr to Ni.

There are hitherto no ternary Na–Fe–H and Na–Co–H compounds reported, which is in contrast with the heavier group 8 and 9 congeners. Na3RhH6/Na3IrH6 and Na3RuH7/Na3OsH7 can be prepared when heating mixtures of NaH and transition metal in a (pressurized) hydrogen atmosphere using stainless steel autoclaves.15,16 Attainable pressures in such devices are typically restricted to a few kbar (∼0.3 GPa).17 Large volume presses (LVPs) allow for pressures much in excess of 10 GPa and can provide well-controlled p,T environments for high pressure hydrogenation reactions. LVP hydrogenations utilize an internal hydrogen source and are performed in NaCl capsules, which offer tight seals and withstand H diffusion.18 Ammonia borane, BH3NH3, which decomposes neatly into inert BN and H2 at comparatively low temperatures (200–300 °C), has been proven an ideal internal H source.19 In situ studies of hydrogenations at pressures up to 12 GPa have been recently facilitated at the beamline ID06-LVP, ESRF.20,21

2. Experimental Section

The samples for the high pressure hydrogenation experiments were prepared in an Ar filled glovebox. NaH (Sigma-Aldrich, 90%) and powdered transition metals TM (TM = Fe, Co (ABCR, 99.999%)) were thoroughly mixed at a molar ratio of 2:1 (NaH:TM) and then pressed into pellets with 1.4 mm OD and ∼0.75 mm height. NaH/TM sample pellets were surrounded by a pelletized hydrogen source BH3NH3 (Sigma-Aldrich, 97%) and sealed inside NaCl capsules with 2.4 mm OD and 2.8 mm height. The amount of BH3NH3 corresponded to an approximately 2.5 times the molar excess of H2 with respect to the transition metal.

High pressure experiments were performed at beamline ID06-LVP, ESRF (Grenoble) using 10/5 multianvil assemblies.22 The setup is sketched in Figure S1. The sample capsules, protected by 2.85 mm OD BN sleeves, were inserted into 10 mm OEL Cr-doped MgO octahedra, along with two 2.85 mm OD ZrO2 plugs and a nickel foil furnace (2.9 mm OD). Two millimeter OD circular windows were cut in the metal furnace along the beam direction to exclude additional diffraction peaks. The assemblies were then positioned between eight truncated tungsten carbide cubes (25 mm, Hawedia, ha7 grade) with 5 mm TEL fitted with pyrophyllite gaskets. Two millimeter OD amorphous SiBCN rods and 5 mm wide MgO rectangles were used as X-ray windows along the beam direction in the octahedra and the gaskets, respectively. Initially, the assemblies were compressed at rates of 0.5 bar/min (2.6–2.9 GPa/h) and, after reaching 20 bar oil pressure, the compression proceeded at a rate of 1 bar/min (3.3–3.5 GPa/h). At target pressure, the samples were heated. The heating rates varied between 9–12 °C/min at T < 300 °C and 4–5 °C/min at T > 400 °C. Pressure was estimated in situ from PXRD diffraction patterns using the NaCl equation of state.23 In the Na–Fe–H experiment, the assembly was equipped with a type C W–Re thermocouple (see Figure S1). The extracted power–temperature data were utilized to evaluate the temperatures in the Na–Co–H run.

Angle-dispersive powder X-ray diffraction patterns were collected continuously over a 2.05–10.57° 2θ range at a constant wavelength (0.2296 Å). A Detection Technology X-Scan series1 linear pixilated detector was used for data acquisition. A diffraction data set was typically saved every 32 s during compression and decompression and every 3.2 s during heating. Calibration was performed using a mixture of LaB6 (NIST SRM 660a) and Si (NIST SRM 640e) powders. The in situ data were integrated, manipulated, and visualized using the Fit2D software.24

Products of the high pressure experiments were recovered at ambient conditions in the glovebox and sealed inside glass capillaries for ex situ PXRD characterization. PXRD patterns of recovered samples were collected at the ID15B beamline at the ESRF. The measurements were performed at a monochromatic wavelength of 0.41112 Å with the beam focused to 30 × 30 μm size on the sample and diffraction data was acquired on a Mar555 flat-panel detector. The integration of 2D data was performed using the Fit2D software.25

Le Bail analysis26 and Rietveld refinement procedures27 using both in situ and ex situ PXRD data were performed with the Jana2006 software.28 In situ diffraction data were optimized by averaging 20–50 patterns collected during the temperature dwells to improve signal-to-noise ratio and minimize any possible texture contribution. All patterns were corrected for background prior to the analysis by subtracting the minimal value of observed intensity from the Iobs column. For peak shape fitting a pseudo-Voigt function was used.

DFT enthalpy calculations were performed using the Vienna Ab Initio Simulation Package (VASP)29,30 in the framework of the projector augmented wave method (PAW)31,32 within generalized gradient approximation (GGA), and employing the Perdew–Burke–Ernzerhof (PBE) parametrization of the exchange-correlation functional.33,34 The cutoff energy for the plane wave basis set was 500 eV for all simulations. Structural relaxations employed a 4 × 8 × 4 Monkhorst–Pack (MP)35 k-point grid for Pnma LP Na3CoH6 (Z = 4) and a 4 × 4 × 8 grid for P42/mnm LP Na3FeH7 (Z = 4). For the Z = 32 super cell modeling of HT-HP phases only the Γ-point (1 × 1 × 1) was considered. For the relaxations, total energies were converged to better than 10–4 eV. Total energy calculations were carried out using the tetrahedron method with Blöchl correction36 on the same k-point grids. Electronic density of states (DOS) calculations used the VASP parameters RWIGS: Na = 1.4, Fe/Co = 0.8, and H = 1.1 Å. The phonon dispersions and the phonon partial DOS were calculated on 2 × 2 × 2 MP k-point grids using the small displacement method37,38 as implemented in PhonoPy.39 Total energies were converged better than 10–8 eV. The ionic positions were relaxed before the phonon calculations.

Ab initio MD (AIMD) simulations of cubic HT-HP Na3(TM)Hn in the NVT ensemble (i.e., maintaining the number of atoms N, volume of the system V, and temperature T) were performed using the Nosé–Hoover thermostat at 300 and 1000 K. V corresponded to the experimental volumes observed at ∼10 GPa (a = 7.09 Å (360 °C, Na–Fe–H) and 7.04 Å (420 °C, Na–Co–H)) for the 1000 K simulations and was slightly compressed for the 300 K simulations. The simulation cell was a 2 × 2 × 2 supercell (Z = 32) of the experimental structure. The Brillouin zone integration was done at the Γ-point.

3. Results and Discussion

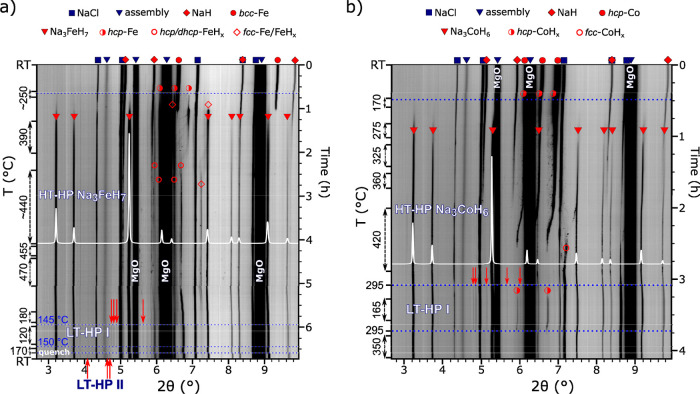
During this study, reaction mixtures NaH:TM:BH3NH3 2:1:∼0.8 (TM = Fe, Co) were employed, i.e. the TM:H2 ratio was 1:∼2.5. In the following, we describe in situ LVP hydrogenation experiments, compiled in Figure 1, during which hydride formation and phase transitions at high pressure, high temperature conditions were examined in great detail.

Figure 1.

Figure 1

Open in a new tab

Compilation of in situ PXRD patterns (λ = 0.2296 Å) showing the formation and polymorphic behavior of Na3FeH7 (a) and Na3CoH6 (b) at ∼10 GPa.

The samples were heated at a starting pressure of ∼10 GPa. Weak reflection lines indicating the formation of ternary hydride phases became visible at temperatures around 200 °C. As later described, these ternary hydride phases possess a metal composition 3Na:TM (despite the 2:1 NaH:TM ratio of the reaction mixtures) and are denoted in the following as HT-HP Na3(TM)Hn. The diffraction lines from HT-HP Na3(TM)Hn became more pronounced during a subsequent alternation of heating and temperature dwells performed to aid the completion of ternary phase formation. The highest temperatures applied were 470 and 420 °C for TM = Fe and Co, respectively. The diffraction peaks from HT-HP Na3(TM)Hn were indexed to an fcc lattice, with a varying between 7.08–7.12 Å and 7.00–7.05 Å for TM = Fe and Co, respectively, during the course of the heating and temperature dwells.

Afterward, the samples were slowly cooled, and during cooling, sets of additional, very weak reflections appeared in the PXRD patterns, indicating transformations to low temperature forms (LT-HP Na3(TM)Hn). LT-HP Na3CoH6 was seen below 300 °C. For Na3FeH7, two LT-HP phases formed upon cooling, evidenced by two distinct sets of additional weak reflections: the first below 150 °C and the second at ∼90 °C. These sets were observed to replace one another during heating–cooling cycles. In both systems, the HT-to-LT transitions appeared reversible. The weak reflections instantaneously disappeared after reheating the samples. At the same time, the HT-HP forms could not be preserved by temperature quenching. The detailed descriptions of the in situ experiments and corresponding temperature/pressure manipulations are provided in the Supporting Information (text and Figures S2–S5).

To conclude the experiments, the samples were decompressed at room temperature and subsequently recovered. The residual pressure at the end of the decompression was ∼1.9 GPa and ∼0.7 GPa for the Na–Fe–H and Na–Co–H samples, respectively. During decompression, the diffraction patterns remained unchanged, apart from obvious lattice expansion. However, the patterns of the recovered samples at ambient pressure were radically different compared to the in situ data. Accordingly, LT-HP Na3(TM)Hn underwent either decomposition or transformation to an ambient pressure form, LP Na3(TM)Hn. The inspection of peak positions and intensities of integrated 2-dimensional synchrotron PXRD data pointed strongly to isostructural relations with Na3Ru/OsH7 (space group P42/mnm (136))16 and Na3Rh/IrH6 (space group (Pnma (62))15 for the Na–Fe–H and Na–Co–H products, respectively. Patterns were then examined via Le Bail analysis,22 and structure solution using the Superflip algorithm40 yielded metal arrangements with composition 3Na:1TM, for which Wyckoff positions of the atoms coincided with those of the Na3OsH7- and Na3IrH6-type structures.

To confirm the isostructural relation between LP Na3(TM)Hn and the Na3OsH7 and Na3IrH6 types, DFT optimization of the LP structures was performed using the H atom arrangement in Na3OsH7 and Na3IrH6. The lattice parameters of the computed equilibrium structures agreed closely with those extracted from the Le Bail fits of the PXRD data. The DFT-optimized LP Na3FeH7 and Na3CoH6 structures (which are presented in Tables S1 and S2) were then used as an input for a final Rietveld refinement against experimental PXRD data, which resulted in remarkably close fits (Robs = 2.61 and 2.30%, respectively). Fractional coordinates and atomic displacement parameters of H atoms were constrained during the refinement. Rietveld plots and crystallographic data are provided in the Supporting Information (Figure S7, Tables S3 and S4), along with a description of refinement strategies.

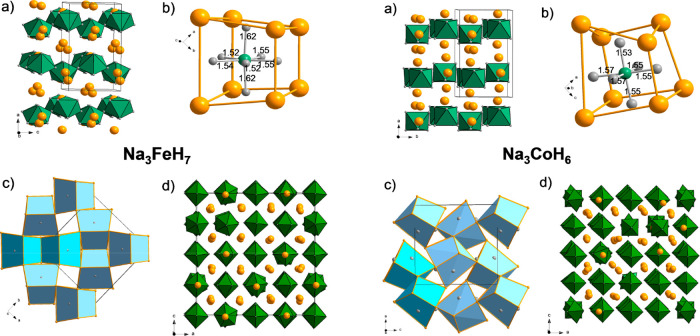
The structures of tetragonal LP Na3FeH7 and orthorhombic LP Na3CoH6 are shown in Figures 2a–c-left and a–c-right, respectively. They are built from homoleptic pentagonal bipyramidal FeH73– and octahedral CoH63– complexes. Fe–H distances to equatorial ligands are between 1.52 and 1.55 Å, whereas distances to apical ligands are elongated at 1.62 Å. The Co–H distances are in a narrow range of 1.53–1.57 Å and similar to the equatorial Fe–H distances. The structures share a common building principle in that complexes are surrounded by distorted cubes of Na ions (Figures 2b-left and b-right). The distorted Na8 cubes are then arranged as pairs by sharing a common edge, and pairs of edge-condensed cubes are connected via shared corners to yield the 3D crystal structure (Figures 2c-left and c-right).

Figure 2.

Figure 2

Open in a new tab

The structures of tetragonal LP Na3FeH7 (left) and orthorhombic LP Na3CoH6 (right) are shown. (a) P42/mnm structure of LP Na3FeH7 and Pnma structure of LP Na3CoH6 according to DFT optimization. Na ions are depicted as golden circles, and complexes of (TM)Hn3– are depicted as green polyhedra. (b) Local coordination of (TM)Hn3– complexes by 8 Na cations (distorted cube) and structure of (TM)Hn3– complexes. Na, Ni, and H atoms are depicted as golden, green, and gray circles, respectively. Interatomic TM–H distances are indicated (in Å). (c) Arrangement of distorted Na8 cubes (blue polyhedra) in the LP structures. The central building unit is a pair of edge-condensed distorted cubes (highlighted with a darker color). (d) Z = 32 MD snapshot of HT-HP Na3FeH7 and Na3CoH6 at 1000 K after equilibration. (TM)Hn3– complexes are drawn as green polyhedra.

The HT-HP forms were assumed to possess the stoichiometry of the LP phases and also to be built from FeH73– and octahedral CoH63– complexes. The in situ PXRD patterns were analyzed using Le Bail fits with the space group Fm3̅m (225). Space group and reflection intensities in combination with the 3:1 Na:TM composition of the LP phases invariably pointed to an fcc Heusler-type arrangement for the metal atoms with TM and Na occupying 4a, and 4b and 8c Wyckoff sites, respectively. This arrangement is known for K3ReH641 and A3−δRuH7−δ and A3−δOsH7−δ (A = K – Cs)16 and has been recently also established for Na3NiH5 at high p,T conditions.42 For obtaining more information about the HT-HP phases, 2 × 2 × 2 supercells (Z = 32) of the Heusler arrangement of Na and TM atoms were assembled as a starting point for ab initio MD simulations. H atoms were placed around the TM atoms according to the complex stoichiometries FeH73– and CoH63–.

The MD simulations of the HT-HP phases used the experimental volumes observed during the ∼10 GPa experiments (a = 7.09 Å (360 °C, Na–Fe–H) and 7.04 Å (420 °C, Na–Co–H)). The simulation temperature was 1000 K. After 1 ps, the hydrostatic stress was essentially zero, which indicated that the systems equilibrated (see Supporting Information, Figure S10). (TM)Hn3– complexes undergo reorientational dynamics (Figure S11), which in the case of FeH73– correspond to pseudorotations (Figures S12–S15).43 Accordingly, the fcc HT-HP Na3(TM)Hn structures represent time averaged Heusler arrangements of Na ions and dynamically disordered (TM)Hn3– complexes. Figures 2d-left and d-right display MD snapshots of HT-HP Na3FeH7 and HT-HP Na3CoH6, respectively. Rietveld refinements of HT-HP patterns employing models with H atoms partially occupying higher multiplicity Wyckoff sites to account for reorientational dynamics are provided in the Supporting Information (Figure S8, Tables S5 and S6). We conjecture that upon cooling, the reorientational dynamics of the (TM)Hn3– complexes is arrested and the subsequent ordering is exhibited as the transitions to the LT-HP forms for which structural details presently remain unknown. Dynamical disorder is frequently observed for CTMHs with high hydrogen coordinations.43

Figure 3 shows ΔH–p relations for the HT-HP and LP structures of the Na3(TM)Hn systems as extracted from DFT total energy calculations (referring to absolute zero). Formation enthalpies ΔH were calculated with respect to NaH, TM, and H2. The HT-HP model corresponded to MD snapshots which were relaxed in the considered volume range. The equilibrium volumes of the HT-HP phases are by about 10% smaller than the LP counterparts (cf. Figure S9). The ΔH–p relations suggest that below 4 GPa, the LP phases are more stable than the disordered cubic HT-HP ones. It is important to point out that formation enthalpies of both LP phases are largely negative. This implies that these phases actually do not require high pressures for thermodynamic stabilization. However, the synthesis of Na3FeH7 and Na3CoH6 requires high pressures because with pressure the decomposition temperature will increase, thus enabling the application of elevated temperatures for initiating the formation reactions. Additionally, high pressures will improve the kinetics of the heterogenous reaction between NaH and TM particles.

Figure 3.

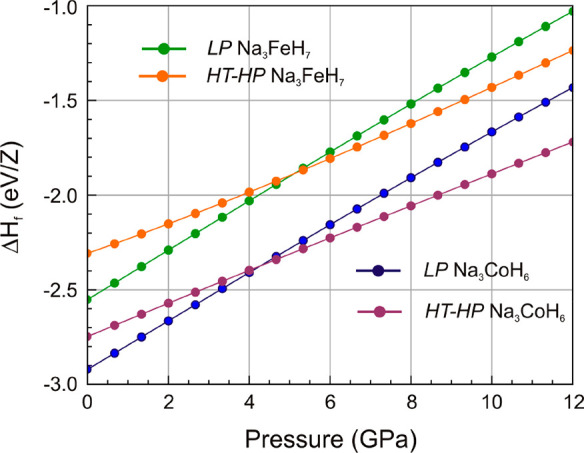
Figure 3

Open in a new tab

Enthalpy vs pressure relations of LP and HT-HP Na3(TM)Hn. Formation enthalpies refer to NaH + TM + H2.

The electronic structures of Na3FeH7 and Na3CoH6 conform to the picture of stable 18-electron complexes. The occupied states in the electronic density of states (DOS) mirror the MOs (and crystal field splitting) of isolated, idealized, pentagonal bipyramidal D5h and octahedral Oh complexes (Figure S16). The calculated band gaps are 1.5 and 2 eV for LP Na3FeH7 and Na3CoH6, respectively. The phonon DOS for LP Na3FeH7 and Na3CoH6, as shown in Figure S17, predict the stretching modes of FeH73– in a range 1400–2000 cm–1, which is at slightly higher wavenumbers compared to CrH75– present in Mg3CrH8 (1450–1650 cm–1).11 This indicates stronger Fe–H bonds as also reflected in the interatomic distances (d(Cr–H) = 1.67 Å vs d(Fe–H) = 1.56 Å). The stretching modes of CoH63– are in the range 1500–1880 cm–1, which is similar to FeH64– in e.g. Mg2FeH6.44

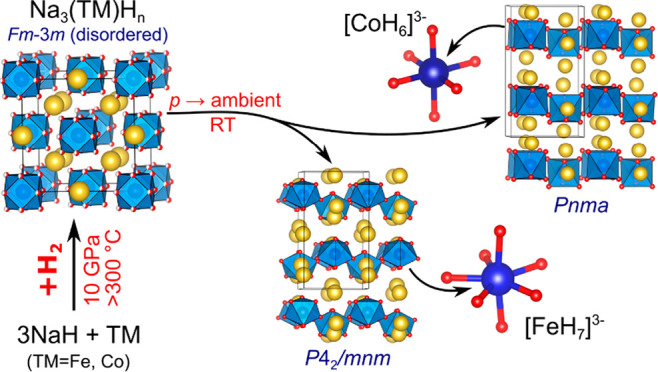
The discovery of Na3FeH7 and Na3CoH6 establishes a consistent picture of hydrogen-rich complexes for first-row transition metals from Cr to Ni, which can be based largely on ternary Mg and Na compounds. This is illustrated in Figure 4. Conventional autoclave-based synthesis, using pressurized H2 gas up to 150 kbar, affords—primarily as Mg compounds—tetrahedral d5 Mn(II)H42–, octahedral d6 Fe(II)H64–, two forms of Co complexes (saddle-shaped d10 Co(-I)H45– and square pyramidal d9 Co(I)H54–), as well as tetrahedral d10 Ni(0)H44–.45 Unsuccessful attempts to produce CTMHs with TMs to the left from Mn by conventional techniques gave rise to the perception that such complexes cannot exist with more electron-poor TMs. The recent discovery of Mg3CrH8 showed that this boundary can be crossed with the application of gigapascal pressures and established at the same time Cr(II)H75– as the first hydrogen-rich complex for first-row transition metals.11 Through use of Na as the counterion, hydrogen-rich complexes of the later first-row transition metals based on increased oxidation states can be achieved, i.e. Fe(IV)H73– and Co(III)H63–, and, as recently shown, also Ni(II)H53–.42 Note that the oxidation state for Fe in FeH73– is remarkably high in conjunction with a H ligand environment. An earlier theoretical work predicted that also Li3FeH7 may be accessible, but this compound has not yet been synthesized.46 Finally, Mn represents a special case. Earliest application of gigapascal pressures, ∼2 GPa, afforded Mg3MnH7 with octahedral d6 Mn(I)H65– complexes.47 However, we infer that when using Na as the counterion (and higher pressures), it should be possible to also synthesize Na3MnH6, possibly with the K3ReH6 structure.41 Octahedral d4 Mn(III)H63– complexes would represent the “true” member in a consecutive series of hydrogen-rich complexes in which the first-row TM carries the possibly highest attainable oxidation state.

Figure 4.

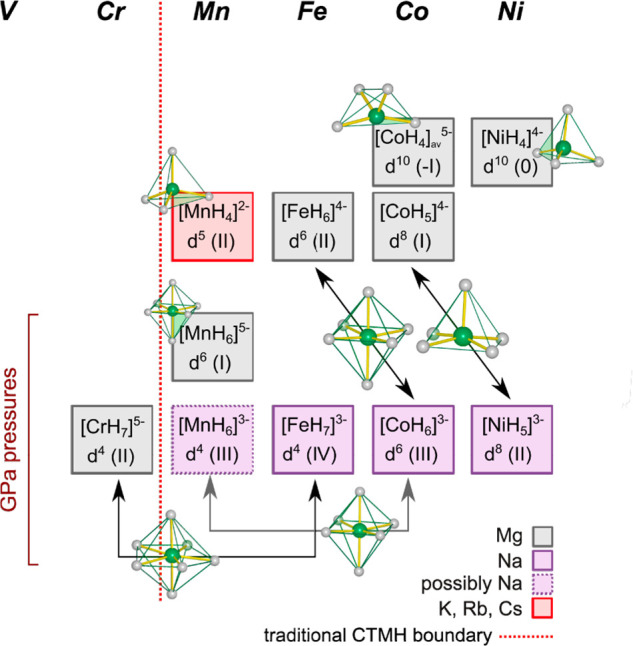
Figure 4

Open in a new tab

Compilation of conventional and hydrogen-rich CTMHs from high pressure synthesis for first-row transition metals.

4. Conclusions

It has been shown that the application of pressures in the gigapascal range systematically extends CTMHs for first-row transition metals by affording higher oxidation states for TMs, i.e. Fe(IV), Co(III), and Ni(II). Highly remarkable is also the recently reported binuclear complex Ti2H146– in quaternary BaCa2Ti2H14, which was obtained from high pressure synthesis at 4 GPa.14 Ti2H146– is composed of two face-sharing monocapped square antiprisms and features Ti in the oxidation state IV. More surprising discoveries of multinary hydrogen-rich hydrides can be expected, eventually also yielding ambient pressure recoverable superconductors. In this respect, LVP hydrogenations provide excellent opportunities for controlled synthesis of sizable quantities using pressures up to 15 GPa.

Acknowledgments

The ESRF is thanked for allocating the beamtime CH-5597 at beamline ID06-LVP. K.S. would like to thank Michael Hanfland for the help with measurements at beamline ID15B and Harald Müller for assistance with the Chemistry Laboratory facilities at ESRF. S.I.S. acknowledges support from the Swedish Government Strategic Research Area Grant in Materials Science on Functional Materials at Linköping University (Faculty Grant SFO-Mat-LiU No. 2009 00971). S.F. acknowledges the financial support from Carl Tryggers Stiftelse (CTS) för Vetenskaplig Forskning through grants 16:198 and 17:206. The computations were performed using resources provided by the Swedish National Infrastructure for Computing (SNIC) at the High Performance Computing Center North (HPC2N).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.inorgchem.0c02294.

  • Descriptions of in situ PXRD experiments, structural investigations, refinement strategies, and results from theoretical calculations; sketch of the 10/5 multianvil assembly; plots of temperature variations as a function of time; PXRD patterns showing temperature-induced phase transitions; Rietveld plots and refinements; total energy vs volume relations; diagonal and nondiagonal components of the stress tensor as a function of simulation time; 2D histograms of angular positions of H atoms in the HT-HP phases from AIMD simulations; time-dependent variation of bond angles in the HT-HP phases; electronic DOS for the LP phases; pDOS for the LP phases; crystallographic data (PDF)

Accession Codes

CCDC 2022756–2022759 contain the supplementary crystallographic data for this paper. These data can be obtained free of charge via www.ccdc.cam.ac.uk/data_request/cif, or by emailing data_request@ccdc.cam.ac.uk, or by contacting The Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK; fax: +44 1223 336033.

The authors declare no competing financial interest.

Supplementary Material

ic0c02294_si_001.pdf (4.9MB, pdf)

References

  1. Duan D.; Liu Y.; Ma Y.; Shao Z.; Liu B.; Cui T. Structures and superconductivity of hydrides at high pressures. Nat. Sci. Rev. 2017, 4, 121–135. 10.1093/nsr/nww029. [DOI] [Google Scholar]
  2. Wang H.; Li X.; Gao G.; Li Y.; Ma Y. Hydrogen-rich superconductors at high pressures. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8, e1330 10.1002/wcms.1330. [DOI] [Google Scholar]
  3. Boeri L.; Bachelet G. B. Viewpoint: the road to room-temperature conventional superconductivity. J. Phys.: Condens. Matter 2019, 31, 234002. 10.1088/1361-648X/ab0db2. [DOI] [PubMed] [Google Scholar]
  4. Zurek E.; Bi T. High-temperature superconductivity in alkaline and rare earth polyhydrides at high pressure: a theoretical perspective. J. Chem. Phys. 2019, 150, 050901. 10.1063/1.5079225. [DOI] [PubMed] [Google Scholar]
  5. Wang H.; Tse J. S.; Tanaka K.; Iitaka T.; Ma Y. Superconductive sodalite-like clathrate calcium hydride at high pressures. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, 6463–6466. 10.1073/pnas.1118168109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Liu H.; Naumov I. I.; Hoffmann R.; Ashcroft N. W.; Hemley R. J. Potential high-Tc superconducting lanthanum and yttrium hydrides at high pressure. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 6990–6995. 10.1073/pnas.1704505114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Geballe Z. M.; Liu H.; Mishra A. K.; Ahart M.; Somayazulu M.; Meng Y.; Baldini M.; Hemley R. J. Synthesis and Stability of Lanthanum Superhydrides. Angew. Chem., Int. Ed. 2018, 57, 688–692. 10.1002/anie.201709970. [DOI] [PubMed] [Google Scholar]
  8. Struzhkin V. V.; Kim D. Y.; Stavrou E.; et al. Synthesis of sodium polyhydrides at high pressures. Nat. Commun. 2016, 7, 12267. 10.1038/ncomms12267. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Pepin C. M.; Geneste G.; Dewaele A.; Mezouar M.; Loubeyre P. Synthesis of FeH5: A layered structure with atomic hydrogen slabs. Science 2017, 357, 382–385. 10.1126/science.aan0961. [DOI] [PubMed] [Google Scholar]
  10. Drozdov A. P.; et al. Superconductivity at 250 K in lanthanum hydride under high pressures. Nature 2019, 569, 528–531. 10.1038/s41586-019-1201-8. [DOI] [PubMed] [Google Scholar]
  11. Takagi S.; Iijima Y.; Sato T.; Saitoh H.; Ikeda K.; Otomo T.; Miwa K.; Ikeshoji T.; Aoki K.; Orimo S. True Boundary for the Formation of Homoleptic Transition-Metal Hydride Complexes. Angew. Chem., Int. Ed. 2015, 54, 5650–5653. 10.1002/anie.201500792. [DOI] [PubMed] [Google Scholar]
  12. Takagi S.; Orimo S. Recent Progress in Hydrogen-Rich Materials from the Perspective of Bonding Flexibility of Hydrogen. Scr. Mater. 2015, 109, 1–5. 10.1016/j.scriptamat.2015.07.024. [DOI] [Google Scholar]
  13. Takagi S.; Iijima Y.; Sato T.; Saitoh H.; Ikeda K.; Otomo T.; Miwa K.; Ikeshoji T.; Orimo S. Formation of Novel Transition Metal Hydride Complexes with Ninefold Hydrogen Coordination. Sci. Rep. 2017, 7, 44253. 10.1038/srep44253. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Yajima T.; Nakajima H.; Honda T.; Ikeda K.; Otomo T.; Takeda H.; Hiroi Z. Titanium Hydride Complex BaCa2Ti2H14 with 9-Fold Coordination. Inorg. Chem. 2020, 59, 4228–4233. 10.1021/acs.inorgchem.9b02810. [DOI] [PubMed] [Google Scholar]
  15. Bronger W.; Gehlen M.; Auffermann G. Na3RhH6, Na3IrH6 und Li3IrH6, neue komplexe Hydride mit isolierten [RhH6]3- und [IrH6]3- Oktaedern. J. Alloys Compd. 1991, 176, 255–262. 10.1016/0925-8388(91)90033-R. [DOI] [Google Scholar]
  16. Bronger W.; Sommer T.; Auffermann G.; Müller P. New alkali metal osmium- and ruthenium hydrides. J. Alloys Compd. 2002, 330–332, 536–542. 10.1016/S0925-8388(01)01536-5. [DOI] [Google Scholar]
  17. Bronger W.; Auffermann G. New Ternary Alkali-Metal-Transition-Metal Hydrides Synthesized at High Pressures: Characterization and Properties. Chem. Mater. 1998, 10, 2723–2732. 10.1021/cm980344c. [DOI] [Google Scholar]
  18. Saitoh H.; Machida A.; Aoki K. Synchrotron X-Ray Diffraction Techniques for in Situ Measurement of Hydride Formation under Several Gigapascals of Hydrogen Pressure. Chin. Sci. Bull. 2014, 59, 5290–5301. 10.1007/s11434-014-0543-8. [DOI] [Google Scholar]
  19. Nylén J.; Sato T.; Soignard E.; Yarger J. L.; Stoyanov E.; Häussermann U. Thermal Decomposition of Ammonia Borane at High Pressures. J. Chem. Phys. 2009, 131, 104506. 10.1063/1.3230973. [DOI] [Google Scholar]
  20. Spektor K.; Crichton W. A.; Konar S.; Filippov S.; Klarbring J.; Simak S. I.; Häussermann U. Unraveling Hidden Mg-Mn-H Phase Relations at High Pressures and Temperatures by in Situ Synchrotron Diffraction. Inorg. Chem. 2018, 57, 1614–1622. 10.1021/acs.inorgchem.7b02968. [DOI] [PubMed] [Google Scholar]
  21. Spektor K.; Crichton W. A.; Filippov S.; Simak S. I.; Häussermann U. Exploring the Mg-Cr-H System at High Pressure and Temperature via in Situ Synchrotron Diffraction. Inorg. Chem. 2019, 58, 11043–11050. 10.1021/acs.inorgchem.9b01569. [DOI] [PubMed] [Google Scholar]
  22. Guignard J.; Crichton W. A. The Large Volume Press Facility at ID06 Beamline of the European Synchrotron Radiation Facility as a High Pressure-High Temperature Deformation Apparatus. Rev. Sci. Instrum. 2015, 86, 085112. 10.1063/1.4928151. [DOI] [PubMed] [Google Scholar]
  23. Birch F. Equation of State and Thermodynamic Parameters of NaCl to 300 Kbar in the High-Temperature Domain. J. Geophys. Res. 1986, 91, 4949–4954. 10.1029/JB091iB05p04949. [DOI] [Google Scholar]
  24. Hammersley A. P. FIT2D: A Multi-Purpose Data Reduction, Analysis and Visualization Program. J. Appl. Crystallogr. 2016, 49, 646–652. 10.1107/S1600576716000455. [DOI] [Google Scholar]
  25. Hammersley A. P.; Svensson S. O.; Hanfland M.; Fitch A. N.; Hausermann D. Two-Dimensional Detector Software: From Real Detector to Idealised Image or Two-Theta Scan. High Pressure Res. 1996, 14, 235–248. 10.1080/08957959608201408. [DOI] [Google Scholar]
  26. Le Bail A.; Duroy H.; Fourquet J. L. Ab-Initio Structure Determination of LiSbWO6 by X-Ray Powder Diffraction. Mater. Res. Bull. 1988, 23, 447–452. 10.1016/0025-5408(88)90019-0. [DOI] [Google Scholar]
  27. Rietveld H. M. A Profile Refinement Method for Nuclear and Magnetic Structures. J. Appl. Crystallogr. 1969, 2, 65–71. 10.1107/S0021889869006558. [DOI] [Google Scholar]
  28. Petříček V.; Dušek M.; Palatinus L. Crystallographic Computing System JANA2006: General Features. Z. Kristallogr. - Cryst. Mater. 2014, 229, 345–352. 10.1515/zkri-2014-1737. [DOI] [Google Scholar]
  29. Kresse G.; Hafner J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 47, 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  30. Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  31. Blöchl P. E. Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  32. Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  33. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  34. Perdew J. P.; Burke K.; Ernzerhof M. Errata: Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1997, 78, 1396. 10.1103/PhysRevLett.78.1396. [DOI] [PubMed] [Google Scholar]
  35. Monkhorst H. J.; Pack J. D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
  36. Blöchl P. E.; Jepsen O.; Andersen O. K. Improved Tetrahedron Method for Brillouin-Zone Integrations. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 49, 16223–16233. 10.1103/PhysRevB.49.16223. [DOI] [PubMed] [Google Scholar]
  37. Kresse G.; Furthmüller J.; Hafner J. Ab initio Force Constant Approach to Phonon Dispersion Relations of Diamond and Graphite. EPL 1995, 32, 729–734. 10.1209/0295-5075/32/9/005. [DOI] [Google Scholar]
  38. Parlinski K.; Li Z. Q.; Kawazoe Y. First-Principles Determination of the Soft Mode in Cubic ZrO2. Phys. Rev. Lett. 1997, 78, 4063–4066. 10.1103/PhysRevLett.78.4063. [DOI] [Google Scholar]
  39. Togo A.; Tanaka I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. 10.1016/j.scriptamat.2015.07.021. [DOI] [Google Scholar]
  40. Palatinus L.; Chapuis G. SUPERFLIP - a Computer Program for the Solution of Crystal Structures by Charge Flipping in Arbitrary Dimensions. J. Appl. Crystallogr. 2007, 40, 786–790. 10.1107/S0021889807029238. [DOI] [Google Scholar]
  41. Bronger W.; Auffermann G.; Schilder H. K3ReH6 - Synthese, Struktur und magnetische Eigenschaften. Z. Anorg. Allg. Chem. 1998, 624, 497–500. . [DOI] [Google Scholar]
  42. Spektor K.; Crichton W. A.; Filippov S.; Klarbring J.; Simak S. I.; Fischer A.; Häussermann U. Na-Ni-H Phase Formation at High Pressures and High Temperatures: Hydrido Complexes [NiH5]3- Versus the Perovskite NaNiH3. ACS Omega 2020, 5, 8730–8743. 10.1021/acsomega.0c00239. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Takagi S.; Ikeshoji T.; Sato T.; Orimo S.-i. Pseudorotating hydride complexes with high hydrogen coordination: a class of rotatable polyanions in solid matter. Appl. Phys. Lett. 2020, 116, 173901. 10.1063/5.0002992. [DOI] [Google Scholar]
  44. Parker S. F. Spectroscopy and bonding in ternary metal hydride complexes—potential hydrogen storage media. Coord. Chem. Rev. 2010, 254, 215–234. 10.1016/j.ccr.2009.06.016. [DOI] [Google Scholar]
  45. Yvon K.; Renaudin G. Hydrides: Solid State Transition Metal Complexes. Encyclopedia of Inorganic Chemistry 2006, 1. 10.1002/0470862106.ia087. [DOI] [Google Scholar]
  46. Takagi S.; Ikeshoji T.; Matsuo M.; Sato T.; Saitoh H.; Aoki K.; Orimo S.-i. Unusual sevenfold coordination of Ru in complex hydride Na3RuH7: Prospect for formation of [FeH7]3- anion. Appl. Phys. Lett. 2013, 103, 113903. 10.1063/1.4821260. [DOI] [Google Scholar]
  47. Bortz M.; Bertheville B.; Yvon K.; Movlaev E. A.; Verbetsky V. N.; Fauth F. Mg3MnH7, Containing the First Known Hexahydridomanganese (I) Complex. J. Alloys Compd. 1998, 279, L8–L10. 10.1016/S0925-8388(98)00662-8. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ic0c02294_si_001.pdf (4.9MB, pdf)

Articles from Inorganic Chemistry are provided here courtesy of American Chemical Society

RESOURCES