Abstract
A theoretical overview of the core-to-core (3d-4f) resonant inelastic X-ray scattering (RIXS) spectra of actinide dioxides AnO2 (An = Th, U, Np, Pu, Am, Cu, Bk, Cf) is provided. The 3d-4f RIXS maps were calculated using crystal-field multiplet theory and turned out to be significantly different at the An M5 vs M4 edges, because of selection rules and final state effects. The results of the calculations allowed for a general analysis of so-called high-energy-resolution fluorescence-detected X-ray absorption (HERFD-XAS) spectra. The cuts of the calculated RIXS maps along the incident energy axis at the constant emitted energy, corresponding to the maximum of the RIXS intensity, represented the HERFD spectra and provided their comparison with calculated conventional X-ray absorption (XAS) spectra with a reduced core-hole lifetime broadening at the An M5 and M4 edges. Although the An M5 HERFD profiles were found to depart from the X-ray absorption cross-section, in terms of appearing additional transitions, the results of calculations for the An M4 edges demonstrate overall better agreement between the HERFD and XAS spectra for most dioxides, keeping in mind a restricted HERFD resolution, because of the core–hole lifetime broadening in the final state. The results confirm the utility of HERFD for the An chemical state determination and indicate the importance of calculating the entire RIXS process in order to interpret the HERFD data correctly.
Short abstract
A theoretical overview of the core-to-core resonant inelastic X-ray scattering of actinide dioxides is provided using crystal-field multiplet theory. The calculations allowed for a general analysis of high-energy-resolution fluorescence-detected X-ray absorption (HERFD-XAS) spectra and their comparison with conventional XAS.
Introduction
The application of the high-energy-resolution fluorescence detected X-ray absorption (HERFD-XAS) technique to actinide (An) compounds has led to a striking improvement in the resolution of the spectra at the An M4,5 edges (4–8 times higher, according to various estimates), because of a reduced core–hole lifetime broadening in the final state of the spectroscopic process.1−3 This can be viewed as a real breakthrough in actinide research, since the enhanced sensitivity of the method allows for probing the An oxidation state, 5f occupancy, local symmetry, (non)stoichiometry, oxygen/metal (O/M) ratio, etc. with much greater capability and efficiency. For example, the long-standing questions, such as about the oxidation path from U(IV) to U(VI) in the U–O system1,4 and possible oxidation of PuO2 to Pu(V) (see ref (5)) were successfully addressed after the employment of the HERFD-XAS technique.
However, in the light of an increasing usage of this technique by scientists involved in the actinide research, the question about how well the profiles of the HERFD-XAS spectra at the An M4,5 edges follow the X-ray absorption cross-section becomes important. This is crucial for the interpretation of recorded data with help of spectra of reference systems and/or model calculations. For example, if the HERFD-XAS spectra follow the X-ray absorption cross-section, the calculations of these spectra can be greatly simplified by just calculating the An M4,5 XAS with a significantly reduced broadening, instead of calculating the full-path core-to-core (3d-to-4f) RIXS process with transitions from the ground state to the intermediate states with a 3d hole and then to final states with a 4f hole.3,6,7
This question is especially important for the case when states with a significant degree of localization in the valence and conduction bands are involved in the spectroscopic process (in our case, 5f states), i.e., when the multiplet approach is appropriate. For example, Tanaka et al.8 found some differences between the calculated Dy(III) L3 XAS spectrum with a reduced core-hole lifetime broadening and the calculated HERFD-XAS spectrum for the region of quadrupole 2p–4f transitions. Moreover, the X-ray fluorescence yield spectra at the L2,3 edges of 3d transition metal systems were shown to depart from the X-ray absorption cross-section.9
The paper presents the results of the calculations using the crystal-field multiplet theory, which address the questions about the relationship between HERFD and conventional XAS spectra. The choice to apply these calculations to systems such as An dioxides is understandable, because An dioxides are the most commonly used materials in the nuclear industry. Mixed An dioxides are considered to be good candidates for innovative fuels in Generation IV reactors to recycle major actinides, such as U and Pu, and reduce the radioactive waste by partitioning and transmutating the minor ones, such as Np, Am, and Cm. For the optimized fuel performance, handling, and storage, it is important to gain insight on the An chemical state and cation charge distribution and on the oxygen/metal (O/M) ratio as key parameters to assess thermodynamic, chemical, and physical properties of the fuels. Furthermore, mixed-oxide systems cannot be fully understood without a thorough understanding of each binary oxides in the mix. Advanced X-ray spectroscopic tools, such as HERFD-XAS, with enhanced sensitivity help to link the changes in the electronic structure to specific macroscopic properties of the materials in question.
Computational Details
The crystal (ligand)-field multiplet approach was used in the calculations, which included the 5f and core 3d and 4f states on a single An ion in cubic symmetry.
The total Hamiltonian of a system can be written as
| 1 |
where HFI represents the Coulomb, exchange, and spin–orbit interactions for a free actinide ion and HCF describes the crystal-field splittings.
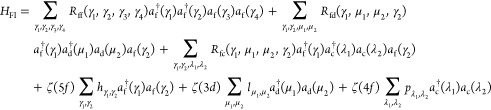 |
2 |
where the interaction between 5f electrons (Rff) and between a 5f electron and a core 3d hole (Rfd) or a core 4f hole (Rfc) is described in terms of Slater integrals, while the spin–orbit interaction for the 5f and core 3d or 4f states is described with coupling constants ζ(5f), ζ(3d) and ζ(4f), respectively, and matrix elements h, l, and p of the spin–orbit coupling operator. a† is an electron creation operator and γ, μ, and λ are combined indices to specify the spin and orbital degeneracies of 5f, 3d, and 4f states, respectively.
| 3 |
where QCF is the potential provided by the crystal environment around the actinide ion, which can be expanded, in terms of tensor operators Cqk, as
| 4 |
where Bqk are Wybourne’s crystal-field parameters. The Cq are related to the spherical harmonics as
| 5 |
For f electrons, the terms in the expansion with k ≤ 6 are nonzero. For cubic site symmetry as in actinide dioxides, only two crystal field parameters (one of rank 4 and one of rank 6) are independent. The crystal field potential can be rewritten as
| 6 |
To calculate the An HERFD spectra at the M4 (3d3/2 → 5f5/2,7p) transitions) and M5 (3d5/2 → 5f7/2,5/2 transitions) edges, the core-to-core (3d-to-4f) RIXS maps around the An Mβ (4f5/2 → 3d3/2 transitions) and An Mα (4f7/2,5/2 → 3d5/2 transitions) X-ray emission lines were calculated. In terms of electronic configurations, the 5fn → 3d95fn+1 → 4f135fn+1 excitation–de-excitation path was used. The transitions to np continuum states were neglected.
The multiplets of the ground state 5fn, intermediate state 3d95fn+1, and final state 4f135fn+1 configurations are defined by spin–orbit, electrostatic (Fk), and exchange Gk) interactions and by applied crystal field. The ab initio values of Slater integrals F2,4,6(5f,5f), F2,4(3d,5f), F2,4,6(4f,5f), G1,3,5(3d,5f), G0,2,4,6(4f,5f) and spin–orbit coupling constants ζ(5f), ζ(3d), ζ(4f) are summarized in Tables 1–3, which are related to the ground, intermediate, and final state configurations, respectively.
Table 1. Ab Initio Hartree–Fock Values of Slater Integrals and Spin-Orbit Coupling Constants in the Ground-State Configurationsa.
| Hartree–Fock Values
(eV) |
|||||
|---|---|---|---|---|---|
| n | F2(5f,5f) | F4(5f,5f) | F6(5f,5f) | ζ(5f) | |
| Th(IV) | 0 | 0 | 0 | 0 | 0 |
| U(IV) | 2 | 9.514 | 6.224 | 4.569 | 0.261 |
| Np(IV) | 3 | 9.907 | 6.489 | 4.767 | 0.297 |
| Pu(IV) | 4 | 10.282 | 6.741 | 4.955 | 0.334 |
| Am(IV) | 5 | 10.642 | 6.982 | 5.136 | 0.373 |
| Cm(IV) | 6 | 10.990 | 7.216 | 5.310 | 0.414 |
| Bk(IV) | 7 | 11.328 | 7.442 | 5.479 | 0.457 |
| Cf(IV) | 8 | 11.657 | 7.662 | 5.642 | 0.502 |
In the RIXS calculation, the Slater integrals were reduced to 80% of these values.
Table 3. Ab Initio Hartree–Fock Values of Slater Integrals and Spin-Orbit Coupling Constants in the Final-State Configurationsa.
| Hartree–Fock
Values (eV) |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F2(5f,5f) | F4(5f,5f) | F6(5f,5f) | ζ(5f) | F2(4f,5f) | F4(4f,5f) | F6(4f,5f) | G0(4f,5f) | G2(4f,5f) | G4(4f,5f) | G6(4f,5f) | ζ(4f) | |
| Th(IV) | 0 | 0 | 0 | 0.227 | 4.577 | 1.950 | 1.200 | 1.211 | 1.494 | 1.161 | 0.905 | 2.662 |
| U(IV) | 9.963 | 6.534 | 4.804 | 0.294 | 5.209 | 2.255 | 1.394 | 1.380 | 1.721 | 1.343 | 1.050 | 3.078 |
| Np(IV) | 10.332 | 6.782 | 4.989 | 0.330 | 5.503 | 2.398 | 1.485 | 1.457 | 1.826 | 1.428 | 1.117 | 3.302 |
| Pu(IV) | 10.687 | 7.020 | 5.167 | 0.368 | 5.787 | 2.536 | 1.573 | 1.531 | 1.927 | 1.509 | 1.182 | 3.538 |
| Am(IV) | 11.031 | 7.250 | 5.339 | 0.409 | 6.062 | 2.670 | 1.658 | 1.601 | 2.024 | 1.588 | 1.245 | 3.785 |
| Cm(IV) | 11.365 | 7.474 | 5.505 | 0.451 | 6.328 | 2.799 | 1.740 | 1.670 | 2.119 | 1.665 | 1.306 | 4.044 |
| Bk(IV) | 11.690 | 7.691 | 5.667 | 0.495 | 6.588 | 2.926 | 1.821 | 1.736 | 2.210 | 1.739 | 1.365 | 4.315 |
| Cf(IV) | 12.008 | 7.903 | 5.826 | 0.542 | 6.843 | 3.050 | 1.900 | 1.801 | 2.300 | 1.813 | 1.423 | 4.600 |
In the RIXS calculation, the Slater integrals were reduced to 80% of these values.
Table 2. Ab Initio Hartree-Fock Values of Slater Integrals and Spin-Orbit Coupling Constants in the Intermediate-State Configurationsa.
| Hartree–Fock Values (eV) |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| F2(5f,5f) | F4(5f,5f) | F6(5f,5f) | ζ(5f) | F2(3d,5f) | F4(3d,5f) | G1(3d,5f) | G3(3d,5f) | G5(3d,5f) | ζ(3d) | |
| Th(IV) | 0 | 0 | 0 | 0.233 | 2.192 | 1.008 | 1.694 | 1.022 | 0.714 | 66.004 |
| U(IV) | 10.025 | 6.572 | 4.831 | 0.301 | 2.564 | 1.190 | 2.003 | 1.211 | 0.847 | 73.384 |
| Np(IV) | 10.394 | 6.820 | 5.016 | 0.338 | 2.741 | 1.277 | 2.151 | 1.301 | 0.910 | 77.308 |
| Pu(IV) | 10.750 | 7.059 | 5.194 | 0.377 | 2.915 | 1.362 | 2.296 | 1.390 | 0.973 | 81.395 |
| Am(IV) | 11.093 | 7.289 | 5.366 | 0.418 | 3.085 | 1.447 | 2.439 | 1.478 | 1.035 | 85.649 |
| Cm(IV) | 11.427 | 7.512 | 5.532 | 0.461 | 3.251 | 1.529 | 2.578 | 1.563 | 1.095 | 90.076 |
| Bk(IV) | 11.754 | 7.731 | 5.695 | 0.506 | 3.410 | 1.607 | 2.710 | 1.645 | 1.152 | 94.681 |
| Cf(IV) | 12.072 | 7.943 | 5.854 | 0.553 | 3.568 | 1.685 | 2.844 | 1.727 | 1.210 | 99.468 |
In the RIXS calculation, the Slater integrals were reduced to 80% of these values.
In the actual multiplet calculations,
the Slater integrals were
reduced to 80% of their ab initio atomic values to account for intra-atomic
relaxation effects, as well as hybridization effects in solids. There
is a certain consensus to apply such a level of the Slater integral
reduction for compounds.10 The values of
Wybourne’s crystal-field parameters for cubic symmetry B04 and B0 (values for Stevens parameters can be obtained by multiplying
with 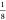 and
and 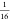 , respectively), which were used in the
calculations, are given in Table 4, along with references from where they were adopted.
In addition, the direct interatomic exchange and superexchange, treated
as a magnetic field along the z-axis and acting on
the spin S, was set to 0.001 eV.
, respectively), which were used in the
calculations, are given in Table 4, along with references from where they were adopted.
In addition, the direct interatomic exchange and superexchange, treated
as a magnetic field along the z-axis and acting on
the spin S, was set to 0.001 eV.
Table 4. Values of Wybourne’s Crystal-Field Parameters Used in the RIXS Calculation.
The 3d-to-4f RIXS maps were calculated using the Kramers–Heisenberg formula:
| 7 |
where |g⟩, |m⟩ and |f⟩ are the ground, intermediate, and final states of the spectroscopic process with energies Eg, Em, and Ef, respectively. ω and ω′ are the energies of the incident and scattered/emitted photons with polarizations q1 and q2, respectively, and Γm and Γf are the lifetime broadenings of the intermediate and final states, in terms of half width at half-maximum (HWHM) of the Lorentzian function. Operators for optical dipole transitions D are expressed in terms of spherical tensor operators Cq(1). For a transition to the intermediate state:
| 8 |
where e = (ex,ey,ez) is the polarization vector of a photon and r is the position operator. For a transition to the final state, D2 is a Hermite conjugate of D1 (D2 = D1†), which results in a complex conjugate for e. In present RIXS calculations, the 90°-scattering geometry was used, which is usually applied in HERFD experiments. The incident photons were chosen to propagate along the z-axis with linear polarization along the x-axis and parallel to the propagation direction of scattered photons (π-polarized incident photon beam with the polarization vector in the scattering plane). For these settings, the dipole transition operators become
| 9 |
and
| 10 |
The HERFD-XAS spectrum is represented by a linear cut of such a RIXS map (see, for example, ref (1)) along the diagonal of the plane defined by the incident energy axis and energy transfer axis or parallel to the incident energy axis at a constant emitted energy (the energy of the RIXS intensity maximum in this case) in the plane of the emitted versus incident energies.
The conventional XAS spectra which represent the 5fn → 3d95fn+1 transitions were calculated using the following equation:
| 11 |
.
The required Slater integrals Fk, Gk, spin–orbit coupling constants ζ, and transition-matrix elements were obtained with the TT-MULTIPLETS package including Cowan’s atomic multiplet program17 (based on the Hartree–Fock method with relativistic corrections) and Butler’s point-group program,18 which were modified by Thole.19 In the RIXS calculations, Γm and Γf were set to values of 1.6 and 0.25 eV, respectively.20 To simulate the experimental response function, the calculated spectra were additionally broadened with Gaussian with HWHM of 0.25 eV. The conventional XAS spectra are represented by calculated isotropic spectra with the reduced core–hole lifetime broadening (Γm = 0.25 eV) and 0.25 eV HWHM Gaussian convolution.
All spectra were calculated for the lowest state of the ground-state configuration. The population of states due to finite temperature was not considered.
Results and Discussion
Figures 1–8 show the results of the calculations at the An M5 edges and Figures 9–16 show the results of the calculations at the An M4 edges. These figures display the 3d-to-4f RIXS maps by using for the x-axis the incident energy scale and, for the y-axis, the energy transfer (panel (a)) and emitted energy (panel (b)) scales. Panel (c) makes a comparison between the calculated conventional XAS spectrum at the An M5 or M4 edge with a reduced core-hole lifetime broadening (0.25 eV HWHM) and a HERFD cut through the 3d-to-4f RIXS map along the incidence energy axis at an emitted energy corresponding to the RIXS maximum. These cuts are indicated by dashed lines in panel (b) of each figure. In addition, Tables 5 and 6 show the calculated ground state and the energies of lowest 50 states of the ground-state configuration, respectively, for each actinide dioxide.
Figure 1.
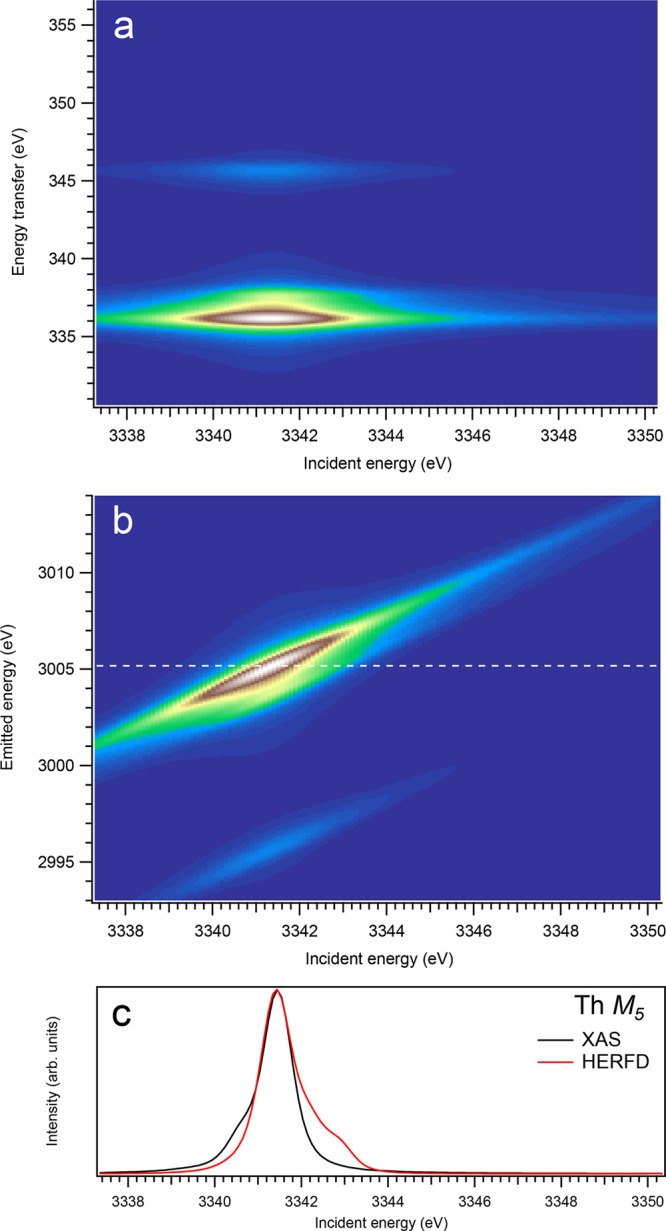
3d-to-4f RIXS map of ThO2 with the incident energy on the x-axis and the (a) energy transfer or (b) emitted energy on the y-axis. The incident energy varies across the Th M5 edge. (c) Comparison between the calculated conventional XAS spectrum (black curve) at the Th M5 edge with a reduced core–hole lifetime broadening and a HERFD cut (red curve) of the 3d-to-4f RIXS map along the incidence energy axis at an emitted energy corresponding to the RIXS maximum. This cut is indicated by a dashed line in panel (b). The spectra in panel (c) are normalized to a main maximum.
Figure 8.
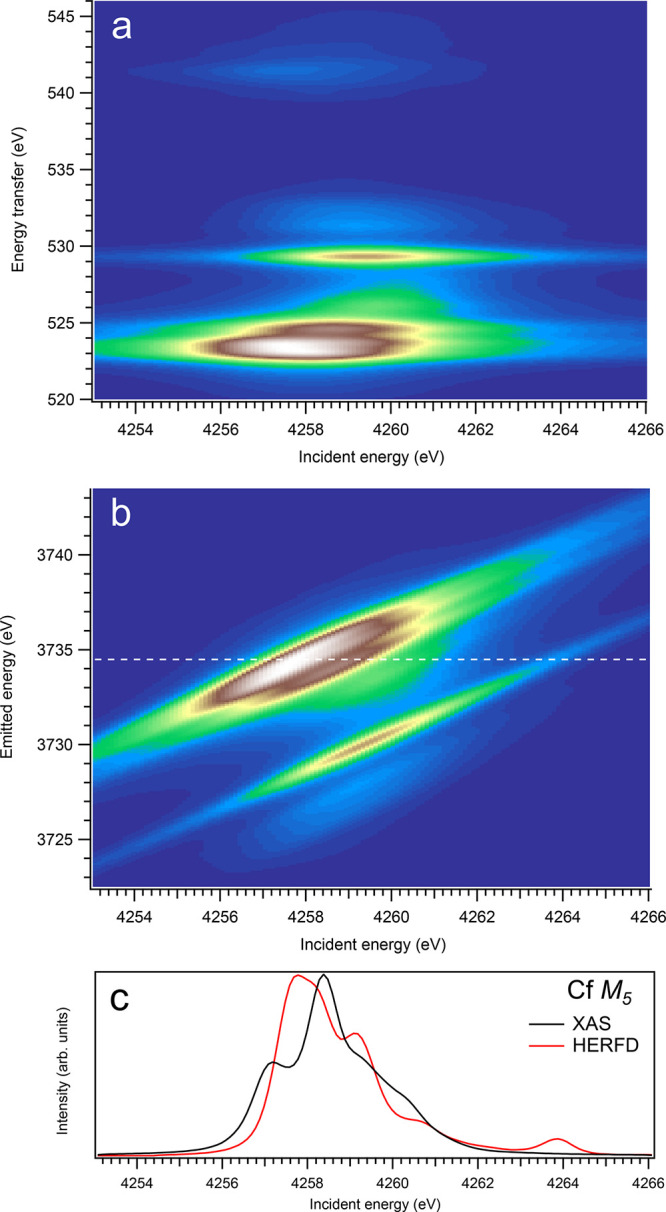
3d-to-4f RIXS map of CfO2 with the incident energy on the x-axis and the (a) energy transfer or (b) emitted energy on the y-axis. The incident energy varies across the Cf M5 edge. (c) Comparison between the calculated conventional XAS spectrum (black curve) at the Cf M5 edge with a reduced core–hole lifetime broadening and a HERFD cut (red curve) of the 3d-to-4f RIXS map along the incidence energy axis at an emitted energy corresponding to the RIXS maximum. This cut is indicated by a dashed line in panel (b). The spectra in panel (c) are normalized to a main maximum.
Figure 9.
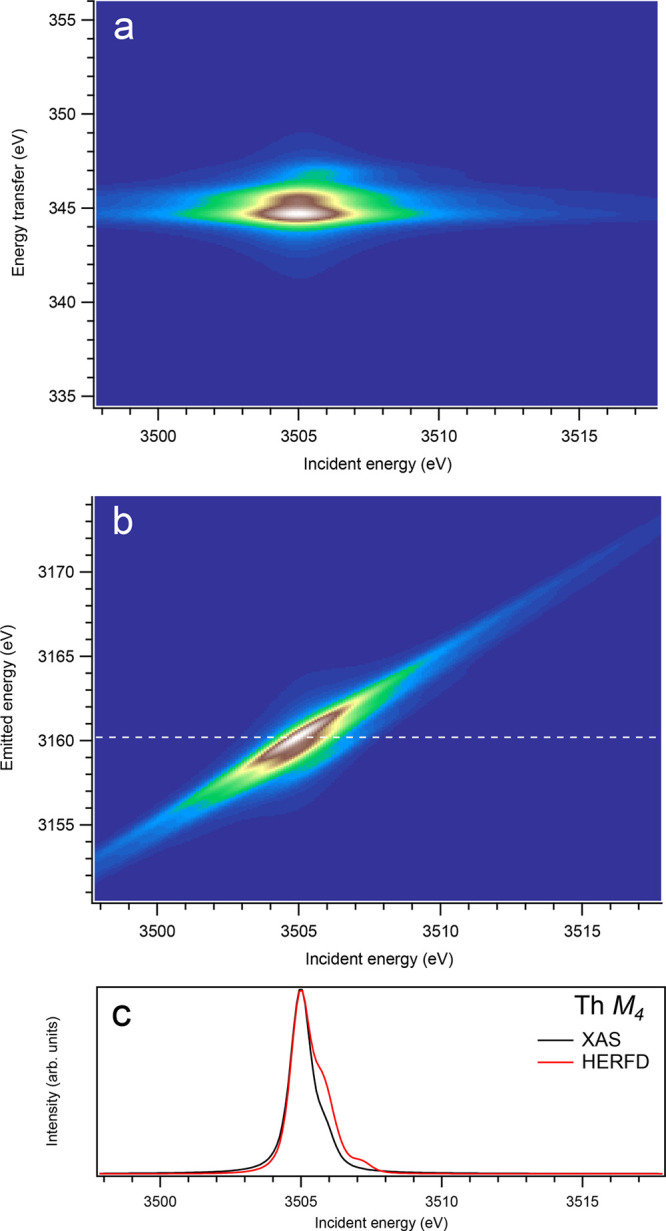
3d-to-4f RIXS map of ThO2 with the incident energy on the x-axis and the (a) energy transfer or (b) emitted energy on the y-axis. The incident energy varies across the Th M4 edge. (c) Comparison between the calculated conventional XAS spectrum (black curve) at the Th M4 edge with a reduced core–hole lifetime broadening and a HERFD cut (red curve) of the 3d-to-4f RIXS map along the incidence energy axis at an emitted energy corresponding to the RIXS maximum. This cut is indicated by a dashed line in panel (b). The spectra in panel (c) are normalized to a main maximum.
Figure 16.
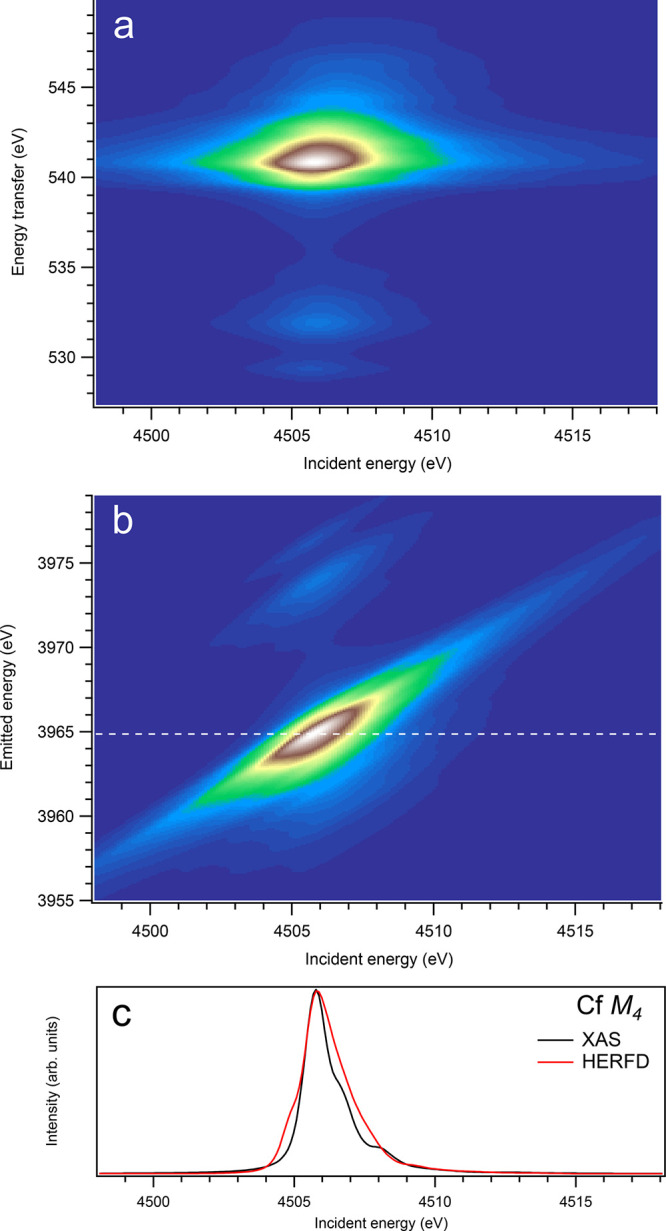
3d-to-4f RIXS map of CfO2 with the incident energy on the x-axis and the (a) energy transfer or (b) emitted energy on the y-axis. The incident energy varies across the Cf M4 edge. (c) Comparison between the calculated conventional XAS spectrum (black curve) at the Cf M4 edge with a reduced core–hole lifetime broadening and a HERFD cut (red curve) of the 3d-to-4f RIXS map along the incidence energy axis at an emitted energy corresponding to the RIXS maximum. This cut is indicated by a dashed line in panel (b). The spectra in panel (c) are normalized to a main maximum.
Table 5. Calculated Ground State of Each An Dioxidea.
| ground state | |
|---|---|
| Th(IV) | Γ1 |
| U(IV) | Γ4 |
| Np(IV) | Γ5 |
| Pu(IV) | Γ1 |
| Am(IV) | Γ7 |
| Cm(IV) | Γ1 |
| Bk(IV) | Γ5 |
| Cf(IV) | Γ2 |
Since the finite exchange field is applied along the z-axis, the notation is for C4h symmetry.
Table 6. Energies of Calculated Lowest 50 States of the Ground-State Configuration.
| Energy of Calculated Lowest
50 States (eV) |
|||||||
|---|---|---|---|---|---|---|---|
| U(IV) | Np(IV) | Pu(IV) | Am(IV) | Cm(IV) | Bk(IV) | Cf(IV) | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0.000437 | 0.000116 | 0.140209 | 0.000005 | 0.540210 | 0.002403 | 0.000690 |
| 3 | 0.000874 | 0.000869 | 0.140427 | 0.043055 | 0.540711 | 0.003639 | 0.006637 |
| 4 | 0.162052 | 0.000976 | 0.140628 | 0.043840 | 0.541201 | 0.003895 | 0.007403 |
| 5 | 0.162059 | 0.050629 | 0.281582 | 0.044352 | 0.941752 | 0.004333 | 0.007659 |
| 6 | 0.186396 | 0.050801 | 0.282453 | 0.045177 | 0.942714 | 0.006920 | 0.029101 |
| 7 | 0.186404 | 0.051268 | 0.283337 | 0.573034 | 0.943685 | 0.009664 | 0.068869 |
| 8 | 0.186433 | 0.051448 | 0.337378 | 0.573518 | 1.110897 | 0.012176 | 0.069718 |
| 9 | 0.201998 | 0.216236 | 0.337380 | 0.585869 | 1.110900 | 2.143442 | 0.070097 |
| 10 | 0.712436 | 0.217063 | 0.817785 | 0.586352 | 1.377968 | 2.144058 | 0.079095 |
| 11 | 0.712689 | 0.785632 | 0.817819 | 0.657296 | 1.378088 | 2.165868 | 0.079509 |
| 12 | 0.712947 | 0.785647 | 0.817851 | 0.657737 | 1.378172 | 2.166272 | 0.079816 |
| 13 | 0.764943 | 0.785703 | 0.894213 | 0.657968 | 1.414808 | 2.166475 | 0.086039 |
| 14 | 0.764946 | 0.785717 | 0.894234 | 0.658410 | 1.415237 | 2.166903 | 0.563345 |
| 15 | 0.866262 | 0.793086 | 0.909607 | 1.022706 | 1.415767 | 2.359622 | 0.564439 |
| 16 | 0.866292 | 0.793286 | 0.909755 | 1.022806 | 1.465954 | 2.360696 | 0.565559 |
| 17 | 0.866323 | 0.805680 | 0.909862 | 1.029538 | 1.539842 | 2.778381 | 0.610518 |
| 18 | 0.932381 | 0.806050 | 0.959631 | 1.030273 | 1.685109 | 2.779099 | 0.610559 |
| 19 | 0.932381 | 0.937444 | 0.960114 | 1.030450 | 1.685745 | 2.779881 | 0.676096 |
| 20 | 0.981504 | 0.937488 | 0.960596 | 1.031202 | 1.686419 | 2.780584 | 0.676307 |
| 21 | 0.981528 | 0.937515 | 1.319922 | 1.090889 | 1.757103 | 2.836505 | 0.676468 |
| 22 | 0.981551 | 0.937559 | 1.355774 | 1.091158 | 1.757141 | 2.837790 | 0.791793 |
| 23 | 1.088487 | 1.367596 | 1.355909 | 1.091520 | 1.800204 | 2.918306 | 0.813146 |
| 24 | 1.088545 | 1.367696 | 1.356042 | 1.091792 | 1.801407 | 2.918612 | 0.813789 |
| 25 | 1.088604 | 1.367889 | 1.387479 | 1.161742 | 1.802600 | 2.935070 | 0.815038 |
| 26 | 1.282620 | 1.367991 | 1.387608 | 1.161861 | 1.862377 | 2.935195 | 0.823320 |
| 27 | 1.282766 | 1.411611 | 1.387725 | 1.188532 | 1.863499 | 2.935286 | 0.823629 |
| 28 | 1.282919 | 1.411710 | 1.402413 | 1.188922 | 1.864563 | 2.935415 | 0.913698 |
| 29 | 1.333085 | 1.421815 | 1.402422 | 1.189253 | 1.907768 | 3.021161 | 0.914963 |
| 30 | 1.373473 | 1.422187 | 1.402462 | 1.189654 | 1.909179 | 3.021440 | 0.915984 |
| 31 | 1.373662 | 1.459308 | 1.422079 | 1.219939 | 1.910628 | 3.049033 | 0.925494 |
| 32 | 1.373854 | 1.459380 | 1.497653 | 1.220114 | 1.975964 | 3.049202 | 0.926425 |
| 33 | 1.377929 | 1.459639 | 1.497654 | 1.221170 | 2.017553 | 3.077609 | 0.927584 |
| 34 | 1.378031 | 1.459709 | 1.702734 | 1.221357 | 2.018235 | 3.077715 | 1.190593 |
| 35 | 1.378148 | 1.573486 | 1.702737 | 1.342689 | 2.022628 | 3.077739 | 1.191101 |
| 36 | 1.389335 | 1.573876 | 1.702741 | 1.343907 | 2.023032 | 3.077851 | 1.192890 |
| 37 | 1.389337 | 1.602028 | 1.730997 | 1.495170 | 2.023501 | 3.146640 | 1.194162 |
| 38 | 1.442094 | 1.602353 | 1.730999 | 1.495303 | 2.059061 | 3.147621 | 1.194576 |
| 39 | 1.563278 | 1.602451 | 1.733273 | 1.498921 | 2.086984 | 3.147907 | 1.209760 |
| 40 | 1.563475 | 1.602786 | 1.765206 | 1.499036 | 2.088230 | 3.148882 | 1.276036 |
| 41 | 1.563672 | 1.696178 | 1.765749 | 1.499445 | 2.089167 | 3.221727 | 1.276489 |
| 42 | 1.618824 | 1.696210 | 1.766284 | 1.499537 | 2.089634 | 3.221791 | 1.276865 |
| 43 | 1.619216 | 1.696340 | 1.808581 | 1.526819 | 2.090567 | 3.222110 | 1.430133 |
| 44 | 1.619610 | 1.696374 | 1.808999 | 1.527237 | 2.090696 | 3.222187 | 1.431244 |
| 45 | 1.654628 | 1.701717 | 1.809266 | 1.527761 | 2.091425 | 3.324495 | 1.432351 |
| 46 | 1.695464 | 1.701739 | 1.810614 | 1.528133 | 2.108428 | 3.325577 | 1.619385 |
| 47 | 1.695482 | 1.726803 | 1.810623 | 1.548001 | 2.108584 | 3.337795 | 1.628049 |
| 48 | 1.695498 | 1.726868 | 1.810764 | 1.548928 | 2.121231 | 3.337800 | 1.628741 |
| 49 | 1.764655 | 1.726951 | 1.816994 | 1.622409 | 2.122550 | 3.338883 | 1.628862 |
| 50 | 1.764659 | 1.727015 | 1.816997 | 1.622917 | 2.123524 | 3.339027 | 1.977611 |
Figure 3.
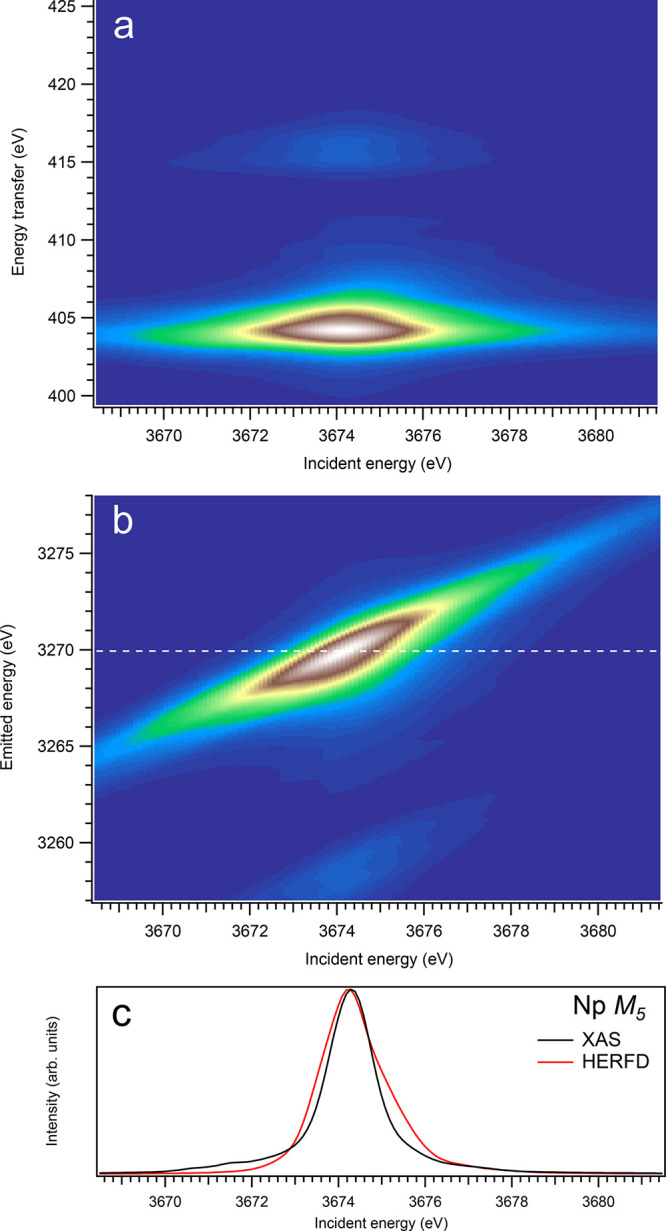
3d-to-4f RIXS map of NpO2 with the incident energy on the x-axis and the (a) energy transfer or (b) emitted energy on the y-axis. The incident energy varies across the Np M5 edge. (c) Comparison between the calculated conventional XAS spectrum (black curve) at the Np M5 edge with a reduced core–hole lifetime broadening and a HERFD cut (red curve) of the 3d-to-4f RIXS map along the incidence energy axis at an emitted energy corresponding to the RIXS maximum. This cut is indicated by a dashed line in panel (b). The spectra in panel (c) are normalized to a main maximum.
Figure 4.
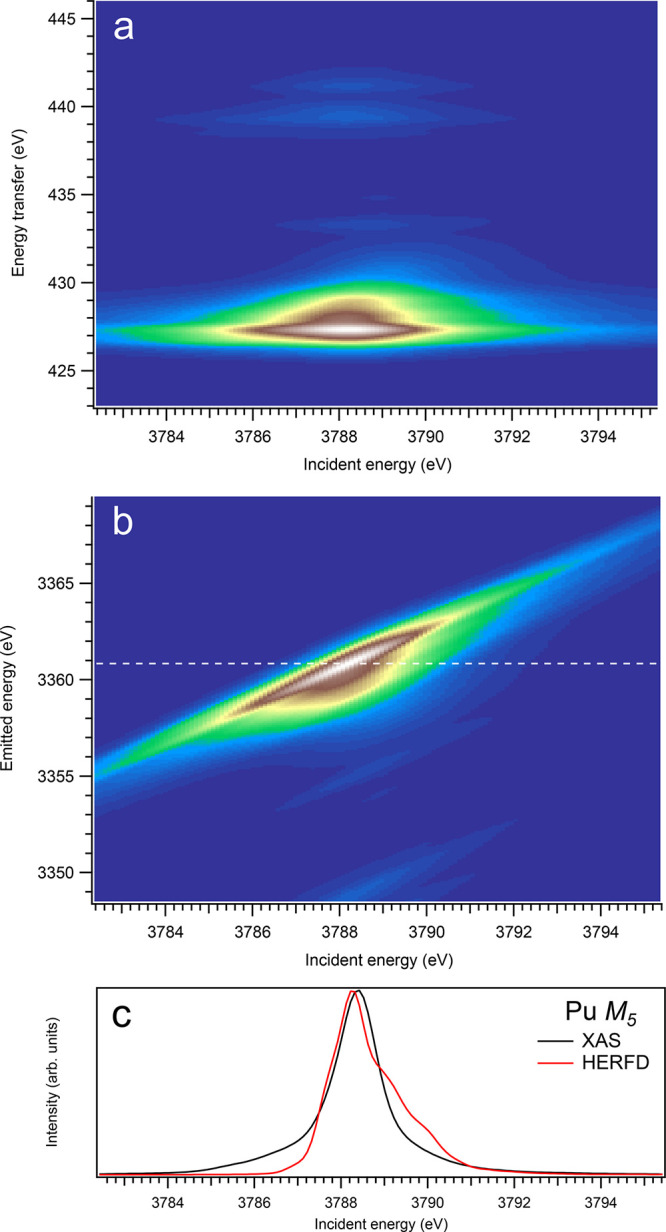
3d-to-4f RIXS map of PuO2 with the incident energy on the x-axis and the (a) energy transfer or (b) emitted energy on the y-axis. The incident energy varies across the Pu M5 edge. (c) Comparison between the calculated conventional XAS spectrum (black curve) at the Pu M5 edge with a reduced core–hole lifetime broadening and a HERFD cut (red curve) of the 3d-to-4f RIXS map along the incidence energy axis at an emitted energy corresponding to the RIXS maximum. This cut is indicated by a dashed line in panel (b). The spectra in panel (c) are normalized to a main maximum.
Figure 5.
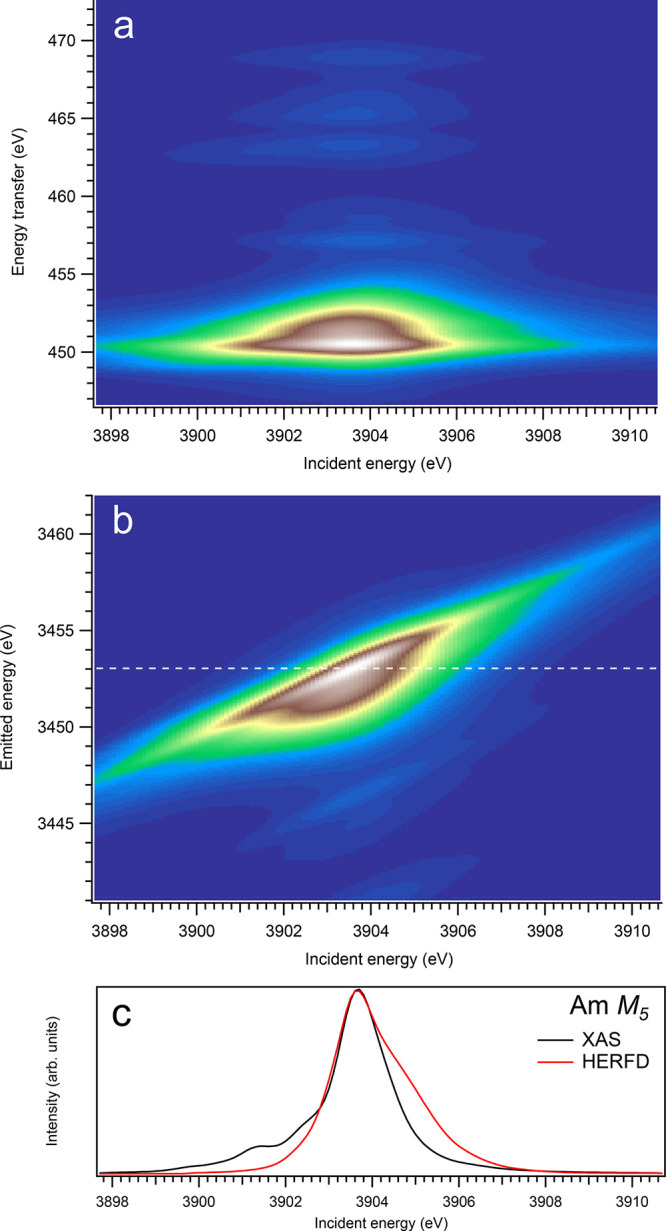
3d-to-4f RIXS map of AmO2 with the incident energy on the x-axis and the (a) energy transfer or (b) emitted energy on the y-axis. The incident energy varies across the Am M5 edge. (c) Comparison between the calculated conventional XAS spectrum (black curve) at the Am M5 edge with a reduced core–hole lifetime broadening and a HERFD cut (red curve) of the 3d-to-4f RIXS map along the incidence energy axis at an emitted energy corresponding to the RIXS maximum. This cut is indicated by a dashed line in panel (b). The spectra in panel (c) are normalized to a main maximum.
Figure 7.
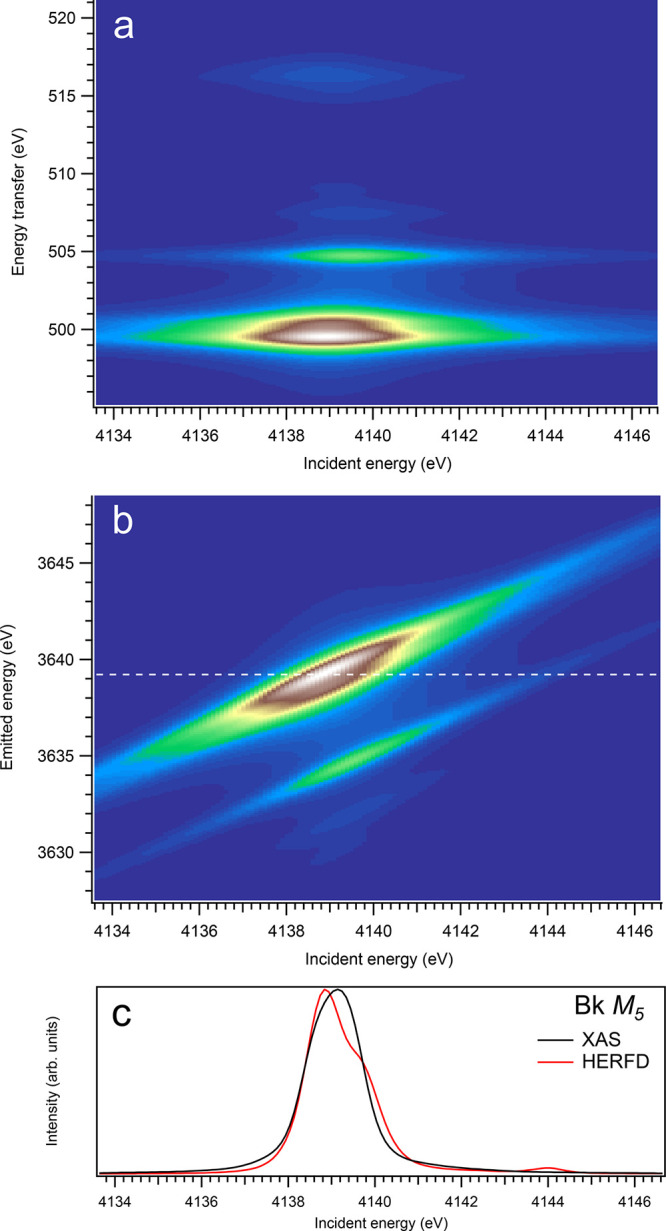
3d-to-4f RIXS map of BkO2 with the incident energy on the x-axis and the (a) energy transfer or (b) emitted energy on the y-axis. The incident energy varies across the Bk M5 edge. (c) Comparison between the calculated conventional XAS spectrum (black curve) at the Bk M5 edge with a reduced core–hole lifetime broadening and a HERFD cut (red curve) of the 3d-to-4f RIXS map along the incidence energy axis at an emitted energy corresponding to the RIXS maximum. This cut is indicated by a dashed line in panel (b). The spectra in panel (c) are normalized to a main maximum.
Figure 11.
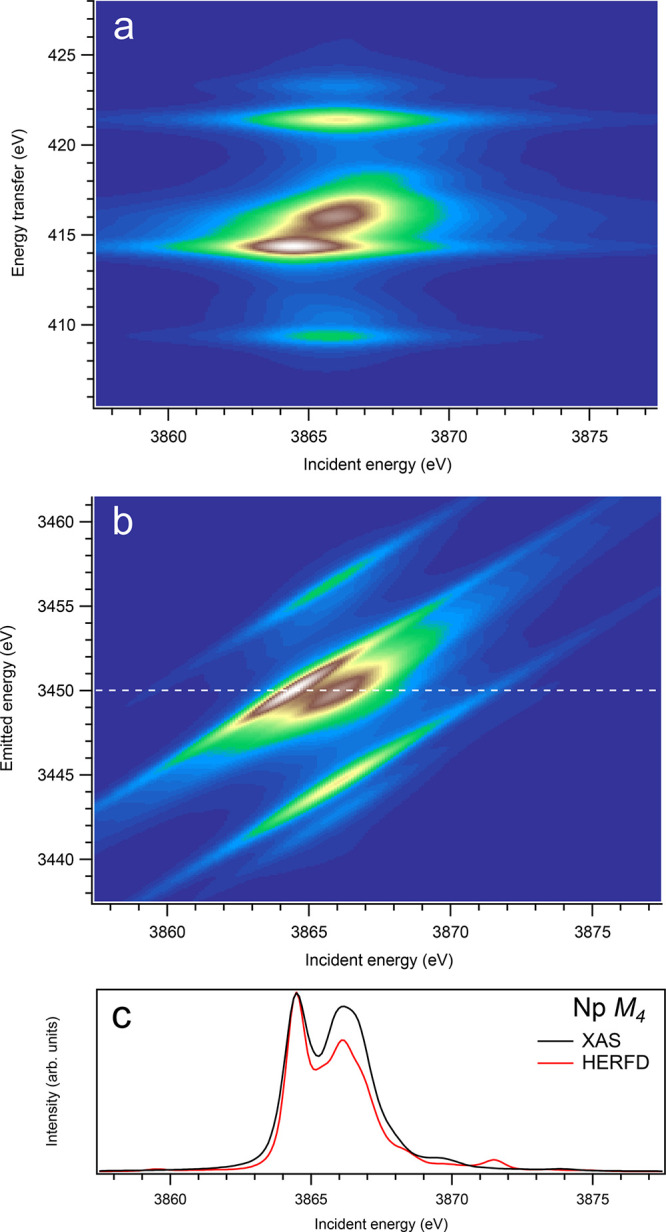
3d-to-4f RIXS map of NpO2 with the incident energy on the x-axis and the (a) energy transfer or (b) emitted energy on the y-axis. The incident energy varies across the Np M4 edge. (c) Comparison between the calculated conventional XAS spectrum (black curve) at the Np M4 edge with a reduced core–hole lifetime broadening and a HERFD cut (red curve) of the 3d-to-4f RIXS map along the incidence energy axis at an emitted energy corresponding to the RIXS maximum. This cut is indicated by a dashed line in panel (b). The spectra in panel (c) are normalized to a main maximum.
Figure 12.
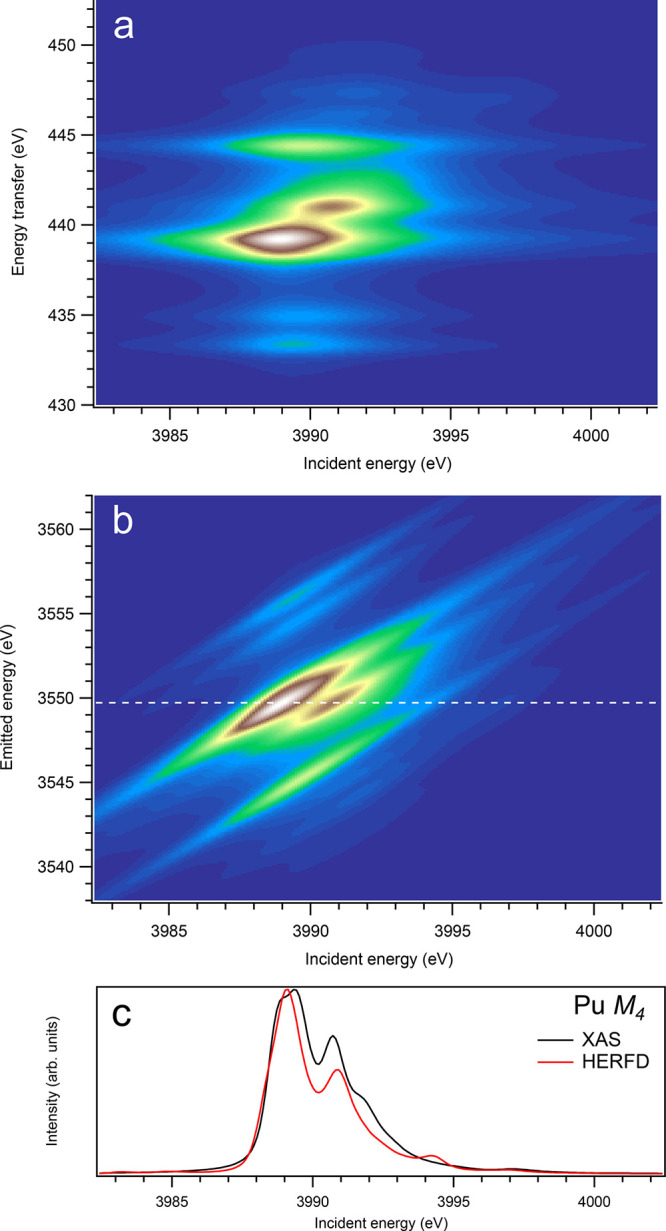
3d-to-4f RIXS map of PuO2 with the incident energy on the x-axis and the (a) energy transfer or (b) emitted energy on the y-axis. The incident energy varies across the Pu M4 edge. (c) Comparison between the calculated conventional XAS spectrum (black curve) at the Pu M4 edge with a reduced core–hole lifetime broadening and a HERFD cut (red curve) of the 3d-to-4f RIXS map along the incidence energy axis at an emitted energy corresponding to the RIXS maximum. This cut is indicated by a dashed line in panel (b). The spectra in panel (c) are normalized to a main maximum.
Figure 13.
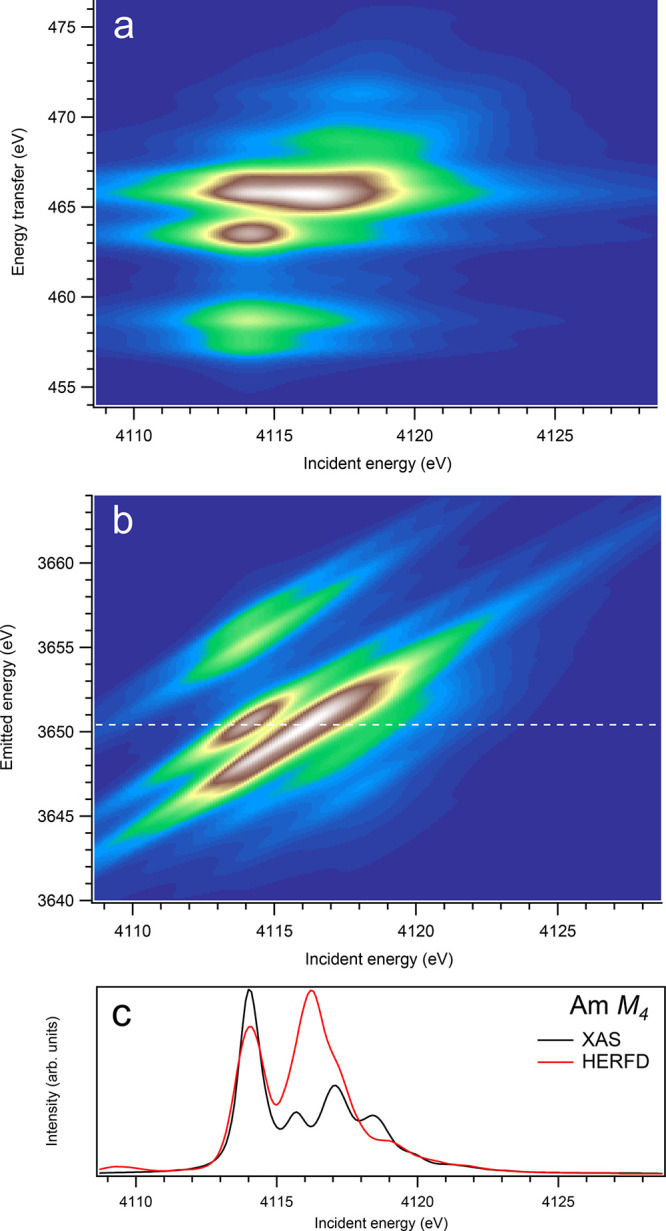
3d-to-4f RIXS map of AmO2 with the incident energy on the x-axis and the (a) energy transfer or (b) emitted energy on the y-axis. The incident energy varies across the Am M4 edge. (c) Comparison between the calculated conventional XAS spectrum (black curve) at the Am M4 edge with a reduced core–hole lifetime broadening and a HERFD cut (red curve) of the 3d-to-4f RIXS map along the incidence energy axis at an emitted energy corresponding to the RIXS maximum. This cut is indicated by a dashed line in panel (b). The spectra in panel (c) are normalized to a main maximum.
Figure 14.
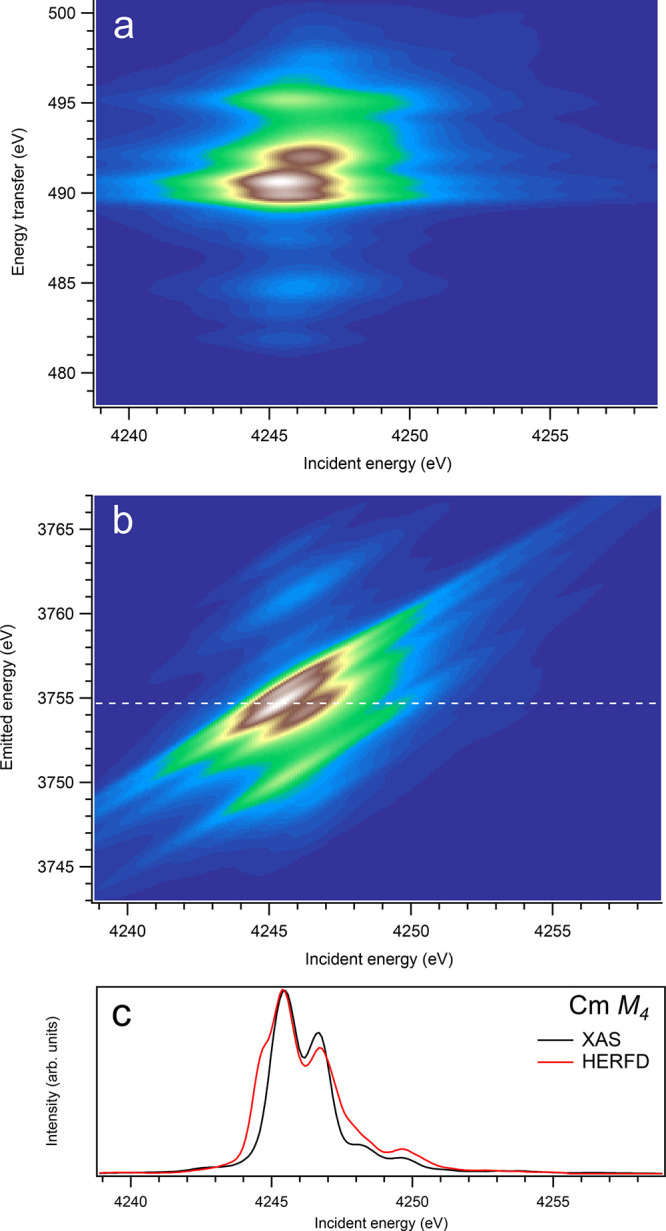
3d-to-4f RIXS map of CmO2 with the incident energy on the x-axis and the (a) energy transfer or (b) emitted energy on the y-axis. The incident energy varies across the Cm M4 edge. (c) Comparison between the calculated conventional XAS spectrum (black curve) at the Cm M4 edge with a reduced core–hole lifetime broadening and a HERFD cut (red curve) of the 3d-to-4f RIXS map along the incidence energy axis at an emitted energy corresponding to the RIXS maximum. This cut is indicated by a dashed line in panel (b). The spectra in panel (c) are normalized to a main maximum.
Figure 15.
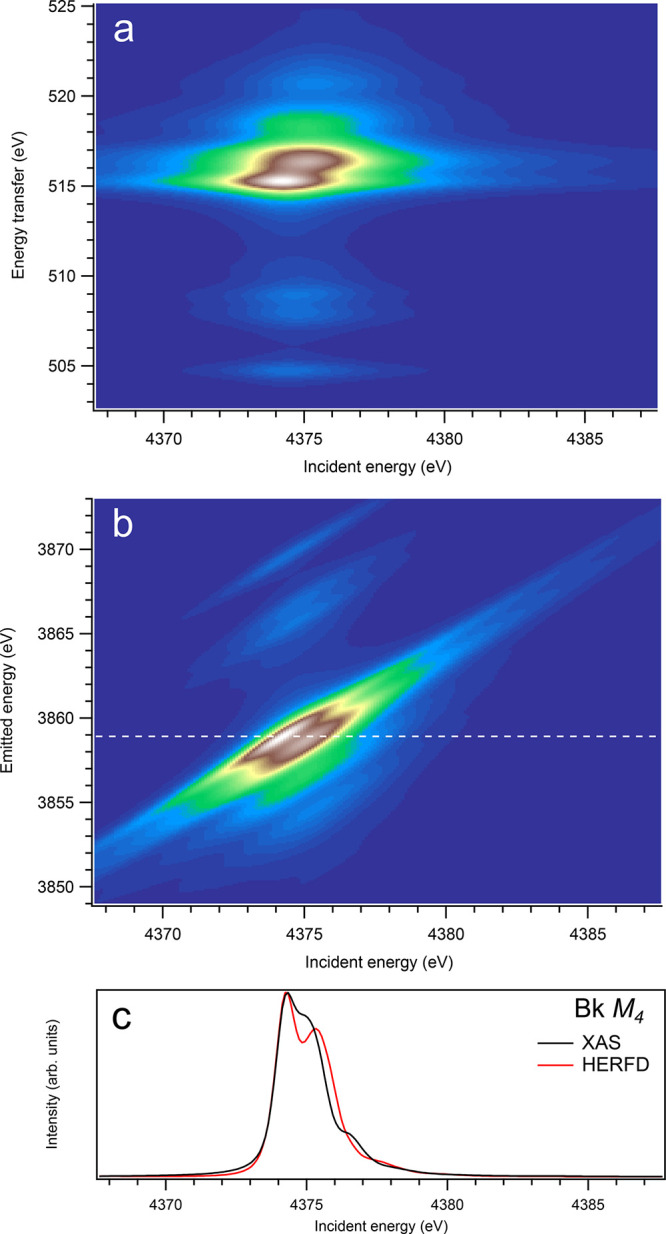
3d-to-4f RIXS map of BkO2 with the incident energy on the x-axis and the (a) energy transfer or (b) emitted energy on the y-axis. The incident energy varies across the Bk M4 edge. (c) Comparison between the calculated conventional XAS spectrum (black curve) at the Bk M4 edge with a reduced core–hole lifetime broadening and a HERFD cut (red curve) of the 3d-to-4f RIXS map along the incidence energy axis at an emitted energy corresponding to the RIXS maximum. This cut is indicated by a dashed line in panel (b). The spectra in panel (c) are normalized to a main maximum.
In contrast to earlier systematic XAS calculations at the d-edges of actinides,21 where only an atomic multiplet approach was used, it is clear that, for the spectra with a significantly improved resolution, the crystal-field interaction must be included in the calculations. This interaction affects the shape of the spectra, as has been already shown3 for ThO2, as an example. However, the crystal field influence becomes less pronounced for dioxides of late actinides, because the crystal-field strength is reduced.13 Other effects may also play a role, such as the increasing relativistic correction and degeneracy lifting of the energy levels with increasing Z.
While there are several publications where the crystal field strength in UO2, NpO2, and PuO2 is determined theoretically or from the analysis of various experimental data, much fewer publications related to the crystal field strength in AmO2 and CmO2 can be found. To set the values of crystal-field parameters B04 and B0 in our calculations for AmO2 and CmO2, a combination of the data for Am(III) and Cm(III), respectively, incorporated into the ThO2 lattice15,16 and of the B04 and B0 estimations within the unified approach for An dioxides, presented in ref (13) was used. We could not find the experimental data related to the crystal-field strength in BkO2 and CfO2; therefore, it was decided to use, in the spectral calculations for these dioxides, the same B04 and B0 values as those for CmO2.
In panel (a) in Figures 1–8, the spectral structures, representing X-ray scattering on the 4f135fn+1 multiplet states via virtual 3d95fn+1 excitations, appear on the constant energy transfer with the varying incident energy throughout the M5 edge. The energy separation between the intensity maxima of transitions to the 4f7/2135fn+1 (associated with Mα1) and 4f5/25fn+1 (associated with Mα2) components, defined by the 4f spin–orbit interaction, gradually increases from ∼9 eV to ∼18 eV when going from ThO2 to CfO2.
It has been shown22−24 for the 3d transition-metal (TM) compounds that the constant-incident-energy cut along the energy-transfer axis through the quadrupole part of the 1s-2p RIXS map of TM, which involves the 1s13dn+1 excitations, can provide ”TM-2p-edge-like” information, because the final state configuration includes the 2p53dn+1 multiplet. In our case, a constant-incident-energy cut through the RIXS maximum in panel (a) in these figures will not represent the XAS spectrum at the An 4f edge,7,25 which includes 4f136d1 multiplet, but rather the 4f → 5f transition part of the energy-electron-loss (EELS)26 or nonresonant inelastic X-ray scattering (NIXS)27 spectra at this edge.
For the An M4 edges, the 3d-4f RIXS maps (panel (a) in Figures 9–16) appear, overall, to be significantly different from those for the An M5 edges. While no separation into the two transition groups is expected, because of the 4f spin–orbit interaction (only the 4f5/2135fn+1 multiplet is involved), some calculated (although weak) transitions appear at a quite few eV below and above the main RIXS intensity maximum on the energy-transfer scale. For example, for UO2 (Figure 10), such transitions can be found at the energy transfer of around 385.9 and 398.8 eV, while the maximum is located at ∼390.5 eV. The ∼385.9 eV and ∼398.8 eV transitions are a result of the interaction of the 4f core hole with the 5f electrons in the final state of the spectroscopic process and are dependent on the values of exchange integrals Gk(4f,5f).
Figure 10.
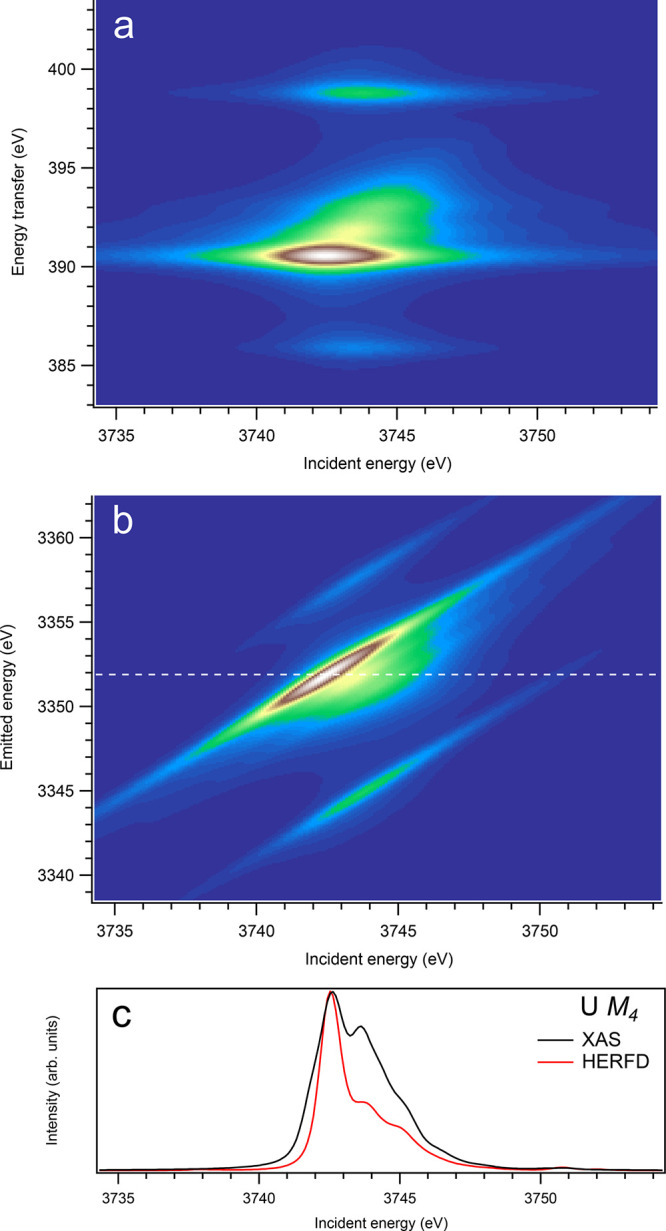
3d-to-4f RIXS map of UO2 with the incident energy on the x-axis and the (a) energy transfer or (b) emitted energy on the y-axis. The incident energy varies across the U M4 edge. (c) Comparison between the calculated conventional XAS spectrum (black curve) at the U M4 edge with a reduced core–hole lifetime broadening and a HERFD cut (red curve) of the 3d-to-4f RIXS map along the incidence energy axis at an emitted energy corresponding to the RIXS maximum. This cut is indicated by a dashed line in panel (b). The spectra in panel (c) are normalized to a main maximum.
By plotting the 3d-4f RIXS map on the emitted energy scale as in panel (b) in Figures 1–16, a connection is made to how the measurements of the HERFD-XAS spectra are performed, when the scattered photons are counted with a X-ray emission spectrometer at a fixed emitted energy while scanning the incident energy across the X-ray absorption edge. Horizontal cuts of the maps in panel (b) in these figures allow one to compare the RIXS profile with the conventional XAS spectrum. Panel (c) in Figures 1–16 provide such a comparison, using a cut through the RIXS intensity maximum (see horizontal white dashed lines in panel (b)), as a representation of the HERFD-XAS spectrum.
At the An M5 edges of dioxides, for actinides from Th to Cm, a clear trend in differences between calculated conventional XAS and HERFD is observed when the HERFD spectra are lacking some intensity on the low-incident-energy side of the main line and show the extra intensity on the high-incident-energy side, compared to conventional XAS spectral shapes. This becomes especially pronounced for CmO2 (see Figure 6). A lack of some intensity on the low-energy side can be understood from the considerations similar to those described in ref (28). The high-spin states of the 3d95fn+1 multiplet at the An M5 edge have a tendency to be at a lower energy than the low-spin states. Such high-spin states have a tendency to elastically scatter/decay to states at the low energy transfer, so that the inelastic scattering weight is minimized. This is, in a way, similar to an observation of the relatively lower intensity on the low-energy side of the fluorescence-yield spectra as compared to XAS (see ref (9)). On the other hand, the low-spin states have a tendency to scatter inelastically.
Figure 6.
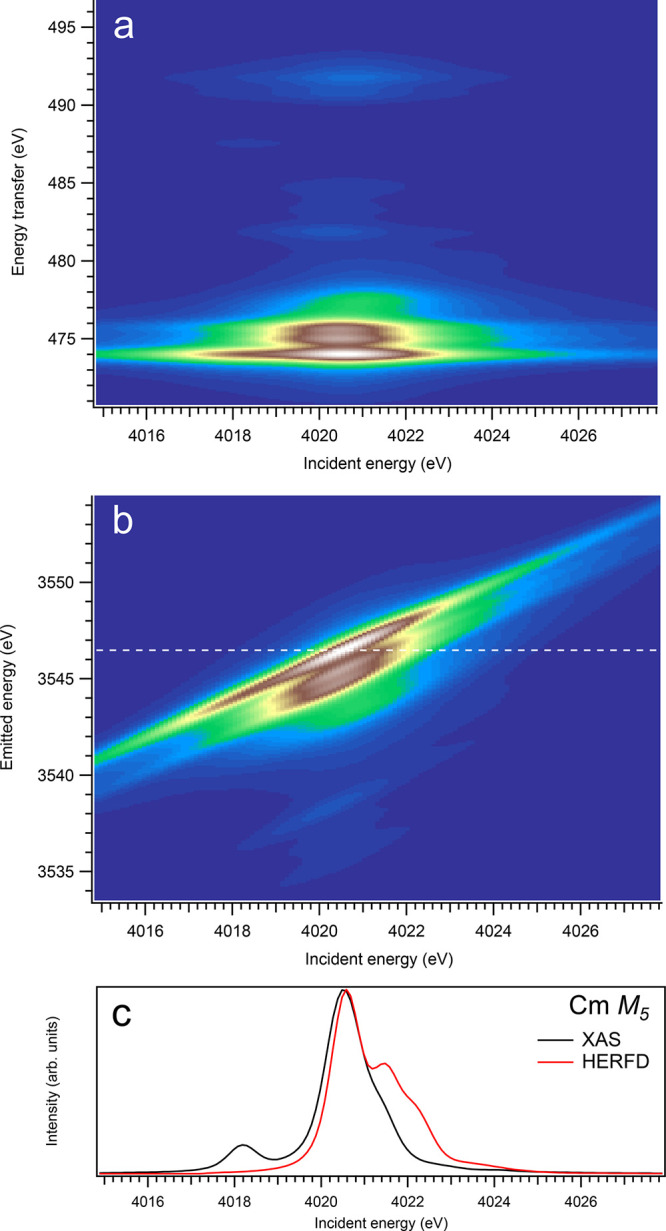
3d-to-4f RIXS map of CmO2 with the incident energy on the x-axis and the (a) energy transfer or (b) emitted energy on the y-axis. The incident energy varies across the Cm M5 edge. (c) Comparison between the calculated conventional XAS spectrum (black curve) at the Cm M5 edge with a reduced core–hole lifetime broadening and a HERFD cut (red curve) of the 3d-to-4f RIXS map along the incidence energy axis at an emitted energy corresponding to the RIXS maximum. This cut is indicated by a dashed line in panel (b). The spectra in panel (c) are normalized to a main maximum.
The origin of the extra intensity on the high-incident-energy side of the main line in the HERFD spectra can be understood from the analysis of the ThO2 spectra (Figure 1), as an example. In the calculated conventional Th M5 XAS spectrum of ThO2, the XAS transition to the highest state of the 3d95f1 multiplet is observed at 3341.5 eV and contributes to the main XAS peak, while the calculated Th M5 HERFD spectrum shows, in addition, some structure at ∼3343.0 eV. An inspection of Figure 17 can explain the appearance of this structure. The figure includes two 3d-4f RIXS spectra calculated at incident energies of 3341.5 and 3343.0 eV (spectra A and B, respectively), which are displayed on the emitted energy scale. The spectra represent transitions to the states of the 4f135f1 multiplet. Since the vertical line in Figure 17 corresponds the emitted energy of the M5 HERFD cut in Figure 1, one can see that spectrum B still has a significant intensity at this emitted energy when the incident energy is at 3343.0 eV. That is because the states of the 4f135f1 multiplet show a wider spread in energy than the states of the 3d95f1 multiplet, because of larger F2,4,6(4f,5f) and G2,4,6(4f,5f) integrals, thus still offering the possibility for the excited state to decay by emitting a photon with the energy used for the detection of the HERFD spectrum. Therefore, the ∼3343.0 eV structure in the calculated Th M5 HERFD spectrum of ThO2 (Figure 1) can be considered as the final state effect of the 3d-4f RIXS process.
Figure 17.
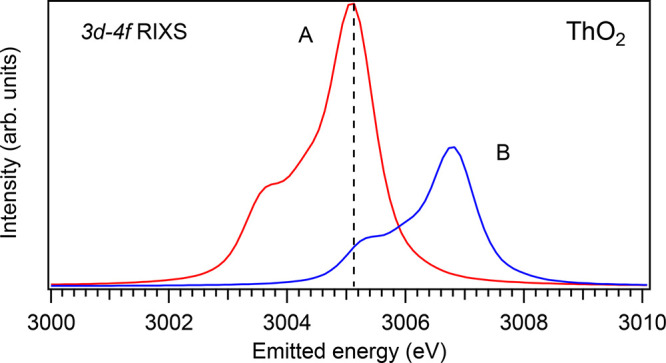
Two 3d-4f RIXS spectra of ThO2 calculated for incident energies of 3341.5 (curve A) and 3343.0 eV (curve B).
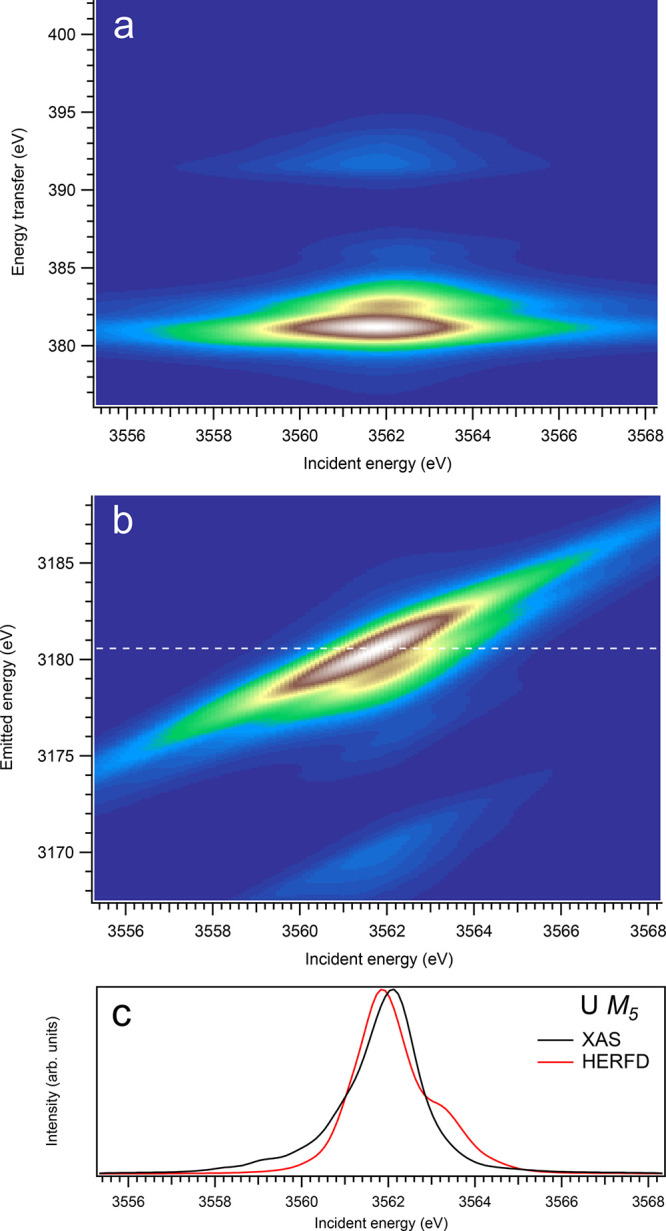
Overall, one can say that profiles of the An M5 HERFD spectra do not follow the X-ray absorption cross-section at the An M5 edges of An dioxides well and exhibit some extra structures, which are absent for the dipole transitions from the ground state to the states of the 3d95fn+1 multiplet. Furthermore, the Cf M5 HERFD spectrum of CfO2 was found to be very different from the Cf M5 XAS spectrum. The cuts of the calculated An 3d-4f RIXS maps for the M5 edge at several different emitted-photon energies were also checked, but they reveal no improvement in agreement with the calculated XAS spectra. Nevertheless, for most actinides, the M5 HERFD spectra can be used for studies of small variations in the chemical state (e.g., because of covalency), because the main maxima of the HERFD and XAS spectra coincide rather well (for UO2, noticeable shift of ∼0.3 eV is found between HERFD and XAS maxima), regardless of the CfO2 case.
On the other hand, at the An M4 edges of dioxides (Figures 9–16), the calculated HERFD spectra reproduce the main structures of the XAS spectra (except for AmO2), although the relative intensities of these structures vary between HERFD and XAS spectra for some dioxides. In particular, the main peak at ∼3742.5 eV in the U M4 HERFD spectrum of UO2 (Figure 10) is much stronger than other structures, while it is not the case for the U M4 XAS spectrum. Nevertheless, the results of calculations for the An M4 edges demonstrate overall better agreement between the HERFD and XAS spectra than that for the An M5 edges. At the M4 edge, the contribution of the states of the 3d95fn+1 multiplet (which are the intermediate states in the 3d-4f RIXS process) to the XAS spectrum is more rich, in terms of observable structures, and is spread over a larger energy range, compared to that at the M5 edge. Therefore, the final state effects due to the 4f135fn+1 multiplet involvement are less pronounced at the M4 edge in the HERFD-XAS spectra (except for the significantly separated-in-energy, weak structures appearing quite a few eV below and above of the main RIXS intensity maximum, which were discussed above). Furthermore, the high- and low-spin states of the 3d95fn+1 multiplet are more intermixed in energy at the M4 edge, compared to those at the M5 edge, where high-spin states have a tendency to group on the low-energy side. In addition, the high-spin states are even preferentially distributed to the 3d5/2 manifold, compared to the 3d3/2 manifold.
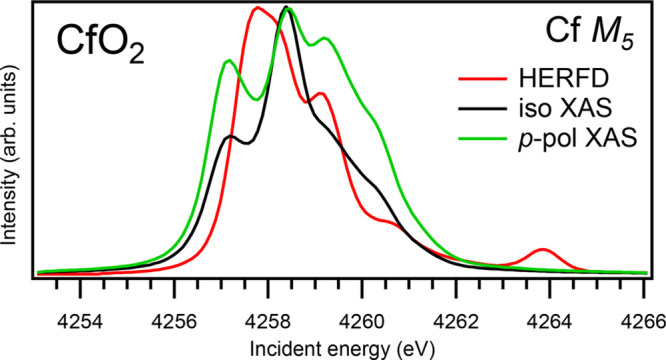
XAS for the π-polarized incident beam was also calculated, since such polarization was used in RIXS calculations. A large difference between π-polarized and isotropic XAS spectra was found only at the Cf M5 edge of CfO2 (see the graphical Table of Contents entry). Some visible changes were found for U M4, Np M4 and Bk M5 and M4 XAS spectra. The structures at ∼3743.6 eV and ∼3866.3 eV in the π-polarized U M4 and Np M4 XAS spectra of UO2 and NpO2, respectively, somewhat grow up, as compared to the isotropic XAS spectra, thus making the agreement with the corresponding HERFD spectra worse. On the other hand, the structure at ∼4375.2 eV in the π-polarized Bk M4 somewhat decreases, becomes more separated from the main peak and appears similar, shape-wise, to the corresponding (∼4375.3 eV) structure in the HERFD spectrum, thus improving an agreement with the HERFD spectrum, compared to the isotropic XAS spectrum. For other An M5 and M4 edges of An dioxides, negligible or no changes were found between the calculated π-polarized and isotropic XAS spectra.
The incident and emitted energy scales shown in all figures use the ab initio Hartree–Fock values obtained in the calculations. For comparison with experimental spectra, some uniform shifts in energy will be required since these Hartree–Fock calculations were performed for actinide ions and do not take into account all the solid-state effects. Considering the available experimental data, recorded with high resolution, we find a fairly good agreement in the spectral shape between calculated and measured HERFD spectra for the Th M4 edge of ThO2,3 for the U M5 and M4 edges of UO2,29 and for Np M5 edge of NpO2.30 However, all of the main structures of the experimental Pu M5 and M4 HERFD spectra of PuO25 are reproduced by the crystal-field multiplet calculations; the agreement between calculated and measured spectra becomes somewhat worse than that observed for dioxides of other early actinides. That is because, for PuO2, AmO2, CmO2, BkO2, and CfO2, the An 5f-O 2p charge-transfer effects become significant and must be taken into account in calculations of X-ray spectroscopic data.31 Furthermore, the calculations of the Slater integrals specifically for compounds in question, using, e.g., the density functional theory approach instead of using the scaled atomic values of the Slater integrals for actinide ions, should improve the agreement between RIXS/HERFD calculations and the experiment. Note that the Am dioxide is claimed32 to be hypostoichiometric without high oxygen pressure, which makes it difficult to perform a comparison using the results of present calculations.
Summary
The results of crystal-field multiplet calculations of 3d-4f RIXS of An dioxides indicate that the 3d-4f RIXS profiles significantly differ for the An M5 and M4 edges. Both of the selection rules, when the 4f7/2 and 4f5/2 components are involved in the 5fn → 3d95fn+1 → 4f135fn+1 excitation–de-excitation process at the M5 edge, whereas only the 4f5/2 component is involved at the M4 edge, and the final state effects of the RIXS process due to the 4f-5f interaction are contributing to the calculated differences.
The simulation of the HERFD spectra by making cuts across the 3d-4f RIXS maps along the incident energy axis at the emitted energy, corresponding to the maximum of the RIXS intensity, shows that the HERFD technique at the An M4,5 edges is indeed an efficient tool for the evaluation of the An chemical state. However, it was found that the An M5 HERFD profiles are departing from the X-ray absorption cross-section, in terms of the existence of additional transitions, whereas the results of calculations for the An M4 edges reveal overall better agreement between the HERFD and XAS spectra for most dioxides, keeping in mind the restricted HERFD resolution that is due to the core–hole lifetime broadening in the final state. Since the shape of the spectra is affected by both the An valency and the local symmetry at the An sites, our results indicate that, in some instances, it will be crucial to calculate the entire 3d-4f RIXS process in order to interpret the HERFD spectra.
Acknowledgments
The author acknowledges support from the Swedish Research Council (Research Grant No. 2017-06465).
The author declares no competing financial interest.
References
- Kvashnina K. O.; Butorin S. M.; Martin P.; Glatzel P. Chemical State of Complex Uranium Oxides. Phys. Rev. Lett. 2013, 111, 253002. 10.1103/PhysRevLett.111.253002. [DOI] [PubMed] [Google Scholar]
- Vitova T.; Denecke M. A.; Göttlicher J.; Jorissen K.; Kas J. J.; Kvashnina K.; Prüßmann T.; Rehr J. J.; Rothe J. Actinide and lanthanide speciation with high-energy resolution X-ray techniques. J. Phys.: Conf. Ser. 2013, 430, 012117 10.1088/1742-6596/430/1/012117. [DOI] [Google Scholar]
- Butorin S. M.; Kvashnina K. O.; Vegelius J. R.; Meyer D.; Shuh D. K. High-resolution X-ray absorption spectroscopy as a probe of crystal-field and covalency effects in actinide compounds. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, 8093–8097. 10.1073/pnas.1601741113. [DOI] [PMC free article] [PubMed] [Google Scholar]; Note that, because of the erroneous offset in energy, the RIXS map at the M5 edge instead of the M4 edge was used in Figure 2A of this reference. Therefore, the calculated XAS spectrum at the M4 edge in Figure 2B of this reference is erroneously compared with the HERFD-XAS cut of the RIXS map calculated at the M5 edge. The error does not affect the main conclusions of this reference, since they are based on the comparison of experimental data with calculations of XAS (not HERFD) spectra.
- Butorin S. M.; Kvashnina K. O.; Prieur D.; Rivenet M.; Martin P. M. Characteristics of chemical bonding of pentavalent uranium in La-doped UO2. Chem. Commun. 2017, 53, 115–118. 10.1039/C6CC07684J. [DOI] [PubMed] [Google Scholar]
- Kvashnina K. O.; Romanchuk A. Y.; Pidchenko I.; Amidani L.; Gerber E.; Trigub A.; Rossberg A.; Weiss S.; Popa K.; Walter O.; Caciuffo R.; Scheinost A. C.; Butorin S. M.; Kalmykov S. N. A Novel Metastable Pentavalent Plutonium Solid Phase on the Pathway from Aqueous Plutonium(VI) to PuO2 Nanoparticles. Angew. Chem., Int. Ed. 2019, 58, 17558–17562. 10.1002/anie.201911637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butorin S. M.; Kvashnina K. O.; Smith A. L.; Popa K.; Martin P. M. Crystal-Field and Covalency Effects in Uranates: An X-ray Spectroscopic Study. Chem. - Eur. J. 2016, 22, 9693–9698. 10.1002/chem.201505091. [DOI] [PubMed] [Google Scholar]
- Butorin S. M.; Modin A.; Vegelius J. R.; Kvashnina K. O.; Shuh D. K. Probing Chemical Bonding in Uranium Dioxide by Means of High-Resolution X-ray Absorption Spectroscopy. J. Phys. Chem. C 2016, 120, 29397–29404. 10.1021/acs.jpcc.6b09335. [DOI] [Google Scholar]
- Tanaka S.; Okada K.; Kotani A. Resonant X-Ray Emission Spectroscopy in Dy Compounds. J. Phys. Soc. Jpn. 1994, 63, 2780–2787. 10.1143/JPSJ.63.2780. [DOI] [Google Scholar]
- Kurian R.; Kunnus K.; Wernet P.; Butorin S. M.; Glatzel P.; de Groot F. M. F. Intrinsic deviations in fluorescence yield detected x-ray absorption spectroscopy: the case of the transition metal L2,3 edges. J. Phys.: Condens. Matter 2012, 24, 452201. 10.1088/0953-8984/24/45/452201. [DOI] [PubMed] [Google Scholar]
- Lynch D. W.; Cowan R. D. Effect of hybridization on 4d → 4f spectra in light lanthanides. Phys. Rev. B: Condens. Matter Mater. Phys. 1987, 36, 9228–9233. 10.1103/PhysRevB.36.9228. [DOI] [PubMed] [Google Scholar]
- Nakotte H.; Rajaram R.; Kern S.; McQueeney R. J.; Lander G. H.; Robinson R. A. Crystal fields in UO2 - revisited. J. Phys.: Conf. Ser. 2010, 251, 012002 10.1088/1742-6596/251/1/012002. [DOI] [Google Scholar]
- Amoretti G.; Blaise A.; Caciuffo R.; Cola D. D.; Fournier J. M.; Hutchings M. T.; Lander G. H.; Osborn R.; Severing A.; Taylor A. D. Neutron-scattering investigation of the electronic ground state of neptunium dioxide. J. Phys.: Condens. Matter 1992, 4, 3459–3478. 10.1088/0953-8984/4/13/010. [DOI] [Google Scholar]
- Magnani N.; Amoretti G.; Carretta S.; Santini P.; Caciuffo R. Unified crystal-field picture for actinide dioxides. J. Phys. Chem. Solids 2007, 68, 2020–2023. 10.1016/j.jpcs.2007.08.052. [DOI] [Google Scholar]
- Kern S.; Robinson R. A.; Nakotte H.; Lander G. H.; Cort B.; Watson P.; Vigil F. A. Crystal-field transition in PuO2. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 104–106. 10.1103/PhysRevB.59.104. [DOI] [Google Scholar]
- Hubert S.; Thouvenot P.; Edelstein N. Spectroscopic studies and crystal-field analyses of Am3+ and Eu3+ in the cubic-symmetry site of ThO2. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 48, 5751–5760. 10.1103/PhysRevB.48.5751. [DOI] [PubMed] [Google Scholar]
- Thouvenot P.; Hubert S.; Edelstein N. Spectroscopic study and crystal-field analysis of Cm3+ in the cubic-symmetry site of ThO2. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 9715–9720. 10.1103/PhysRevB.50.9715. [DOI] [PubMed] [Google Scholar]
- Cowan R. D.The Theory of Atomic Structure and Spectra; Los Alamos Series in Basic and Applied Sciences, Vol. 3; University of California Press: Berkeley, CA, 1981. [Google Scholar]
- Butler P. H.Point Group Symmetry Applications: Methods and Tables; Plenum Press: New York, 1981. [Google Scholar]
- Thole B.; Van Der Laan G.; Butler P. Spin-mixed ground state of Fe phthalocyanine and the temperature-dependent branching ratio in X-ray absorption spectroscopy. Chem. Phys. Lett. 1988, 149, 295–299. 10.1016/0009-2614(88)85029-2. [DOI] [Google Scholar]
- Campbell J.; Papp T. Width of the atomic K–N7 levels. At. Data Nucl. Data Tables 2001, 77, 1–56. 10.1006/adnd.2000.0848. [DOI] [Google Scholar]
- Ogasawara H.; Kotani A.; Thole B. T. Calculation of magnetic x-ray dichroism in 4 d and 5 d absorption spectra of actinides. Phys. Rev. B: Condens. Matter Mater. Phys. 1991, 44, 2169–2181. 10.1103/PhysRevB.44.2169. [DOI] [PubMed] [Google Scholar]
- Glatzel P.; Bergmann U.; Gu W.; Wang H.; Stepanov S.; Mandimutsira B. S.; Riordan C. G.; Horwitz C. P.; Collins T.; Cramer S. P. Electronic Structure of Ni Complexes by X-ray Resonance Raman Spectroscopy (Resonant Inelastic X-ray Scattering). J. Am. Chem. Soc. 2002, 124, 9668–9669. 10.1021/ja026028n. [DOI] [PubMed] [Google Scholar]
- de Groot F. M. F.; Glatzel P.; Bergmann U.; van Aken P. A.; Barrea R. A.; Klemme S.; Havecker M.; Knop-Gericke A.; Heijboer W. M.; Weckhuysen B. M. 1s2p Resonant Inelastic X-ray Scattering of Iron Oxides. J. Phys. Chem. B 2005, 109, 20751–20762. 10.1021/jp054006s. [DOI] [PubMed] [Google Scholar]
- Lundberg M.; Kroll T.; DeBeer S.; Bergmann U.; Wilson S. A.; Glatzel P.; Nordlund D.; Hedman B.; Hodgson K. O.; Solomon E. I. Metal–Ligand Covalency of Iron Complexes from High-Resolution Resonant Inelastic X-ray Scattering. J. Am. Chem. Soc. 2013, 135, 17121–17134. 10.1021/ja408072q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butorin S. M.; Modin A.; Vegelius J. R.; Suzuki M.-T.; Oppeneer P. M.; Andersson D. A.; Shuh D. K. Local Symmetry Effects in Actinide 4f X-ray Absorption in Oxides. Anal. Chem. 2016, 88, 4169–4173. 10.1021/acs.analchem.5b04380. [DOI] [PubMed] [Google Scholar]
- Moser H. R.; Delley B.; Schneider W. D.; Baer Y. Characterization of f electrons in light lanthanide and actinide metals by electron-energy-loss and x-ray photoelectron spectroscopy. Phys. Rev. B: Condens. Matter Mater. Phys. 1984, 29, 2947–2955. 10.1103/PhysRevB.29.2947. [DOI] [Google Scholar]
- Caciuffo R.; van der Laan G.; Simonelli L.; Vitova T.; Mazzoli C.; Denecke M. A.; Lander G. H. Uranium 5d–5f electric-multipole transitions probed by nonresonant inelastic x-ray scattering. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 81, 195104. 10.1103/PhysRevB.81.195104. [DOI] [Google Scholar]
- Thole B. T.; van der Laan G. Branching ratio in x-ray absorption spectroscopy. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 38, 3158–3171. 10.1103/PhysRevB.38.3158. [DOI] [PubMed] [Google Scholar]
- Kvashnina K.; Kvashnin Y.; Butorin S. Role of resonant inelastic X-ray scattering in high-resolution core-level spectroscopy of actinide materials. J. Electron Spectrosc. Relat. Phenom. 2014, 194, 27–36. 10.1016/j.elspec.2014.01.016. [DOI] [Google Scholar]
- Bahl S. P.Advanced Chemical and Structural Characterization of Nuclear Waste Materials Related to the Nuclear Fuel Cycle. Ph.D. Thesis, Karlsruhe Institut für Technologie, Karlsruhe, Germany, 2017. [Google Scholar]
- Kotani A.; Ogasawara H. Theory of core-level spectroscopy in actinide systems. Phys. B 1993, 186–188, 16–20. 10.1016/0921-4526(93)90485-O. [DOI] [Google Scholar]
- Epifano E.; Guéneau C.; Belin R. C.; Vauchy R.; Lebreton F.; Richaud J.-C.; Joly A.; Valot C.; Martin P. M. Insight into the Am–O Phase Equilibria: A Thermodynamic Study Coupling High-Temperature XRD and CALPHAD Modeling. Inorg. Chem. 2017, 56, 7416–7432. 10.1021/acs.inorgchem.7b00572. [DOI] [PubMed] [Google Scholar]
Figure 2.
3d-to-4f RIXS map of UO2 with the incident energy on the x-axis and the (a) energy transfer or (b) emitted energy on the y-axis. The incident energy varies across the U M5 edge. (c) Comparison between the calculated conventional XAS spectrum (black curve) at the U M5 edge with a reduced core–hole lifetime broadening and a HERFD cut (red curve) of the 3d-to-4f RIXS map along the incidence energy axis at an emitted energy corresponding to the RIXS maximum. This cut is indicated by a dashed line in panel (b). The spectra in panel (c) are normalized to a main maximum.


