AUTOMATIC SCORING OF A NONWORD REPETITION TEST

Abstract

In this study, we explore the feasibility of speech-based techniques to automatically evaluate a nonword repetition (NWR) test. NWR tests, a useful marker for detecting language impairment, require repetition of pronounceable nonwords, such as ”D OY F”, presented aurally by an examiner or via a recording. Our proposed method leverages ASR techniques to first transcribe verbal responses. Second, it applies machine learning techniques to ASR output for predicting gold standard scores provided by speech and language pathologists. Our experimental results for a sample of 101 children (42 with autism spectrum disorders, or ASD; 18 with specific language impairment, or SLI; and 41 typically developed, or TD) show that the proposed approach is successful in predicting scores on this test, with averaged product-moment correlations of 0.74 and mean absolute error of 0.06 (on a observed score range from 0.34 to 0.97) between observed and predicted ratings.

1. INTRODUCTION

Nonword repetition (NWR) tests require repetition of pronounceable nonwords of increasing length, such as “doyf”, presented aurally by an examiner or via a recording. Simple as this test is, it has proven to be a useful marker for detecting language impairment, especially deficits in phonological processing (e.g., [1, 2]). In addition, a recent study in our center has shown that this test can differentiate between children with specific language impairment (SLI) and children who have both autism spectrum disorder and language impairment (ALI), matched on a broad measure of language ability, with the latter group outperforming the former on NWR [3]. Thus, NWR tests are of interest both for clinical applications and for a broader understanding of speech production and understanding. However, while automating the administration of NWR tests is easy enough, scoring is not so simple. First, no training data are available in quantities comparable to what is available for a general-purpose large vocabulary speech recognizer. Second, typical instructions for NWR tests require scoring to ignore imperfect pronunciation, such as friction of voiceless stops or heavy nasalization of vowels, as long as this does not cause a phonetic segment to sound more like another phoneme. As far as we know, no successful automated scoring methods exist that use raw, untranscribed speech as input. Yet, the value of automated scoring for clinical practice and research is considerable.

In this paper, we propose a new method for automated NWR scoring, based on an ASR system that generates transcriptions of the verbal responses and a machine learning-based scoring algorithm that estimates scores from the transcription.

2. DATA

We used a NWR test developed by Dollaghan and Campbell [4]. Stimuli for this test vary between 1 and 4 syllables in length (see Table 1). Scoring ignores insertions and thus only counts omissions or substitutions. The total score is computed as the percentage of all phonemes correctly reproduced, in the correct order. Thus, a response of “foyd” to the stimulus “doyf” would have two errors even though no phoneme is omitted, and a response of “doyfs” would have no errors even though it contains an insertion error.

Table 1.

Phonemic transcriptions of the nonwords

(1) N AY B	(5) T EY V AA K	(9) CH IY N OY T AW B	(13) V EY T AA CH AY D OY P
(2) V OW P	(6) CH OW V AE G	(10) N AY CH OW V EY B	(14) D AE V OW N OY CH IY G
(3) T AW JH	(7) V AE CH AY P	(11) D OY T AW V AE B	(15) N AY CH OY T AW V UW B
(4) D OY F	(8) N OY T AW F	(12) T EY V OY CH AY G	(16) T AE V AA CH IY N AY G
consonant-vowel sequence
CVC	CVCVC	CVCVCVC	CVCVCVCVC

The NWR test was administered as part of a larger NIH-funded project on prosody in autism spectrum disorder. Subjects were children aged 5–8 years from the Portland, OR area. The sample comprised children with typical development (TD), Specific Language Impairment (SLI), and autism spectrum disorder (ASD). Exclusion criteria were: (1) identified metabolic, neurological, or genetic disorder; (2) gross sensory or motor impairment; (3) brain lesion; (4) orofacial abnormality (e.g., cleft palate); or (5) not speaking English as a native language. We required a mean length of utterance in morphemes of no less than three, and a performance IQ no less than 80. Although this paper will not present results broken down by diagnostic group, we describe these groups here to make the point that the subjects formed a quite heterogeneous group, thereby demonstrating that our methods, if successful, are robust.

Inclusion in the SLI group (N=18) required: (1) documented history of language impairments; (2) best estimate clinical consensus judgment of language impairment in the absence of ASD based on all available evidence; and (3) core language scores (CLS) on the Clinical Evaluation of Language Fundamentals (CELF) below 85 (1 SD below the mean). Inclusion in the autism spectrum (ASD) group (N=42) required: (1) an existing diagnosis of ASD; (2) a best estimate clinical consensus judgment of ASD using the DSM-IV-TR criteria; and (3) above cut-off scores for ASD on both the Autism Diagnostic Observation Schedule (ADOS-G Module 2 or 3) revised algorithm and the Social Communication Questionnaire (SCQ). We subdivided the ASD group into those with language impairment (ALI; N=22) and those with normally developing language (ALN; N=20) using the same criteria as for SLI. The remaining children were TD (N=41)

2.1. Manual Scores

The NWR responses were manually transcribed by linguists. The portions of the audio where the child was responding to the nonword stimuli were excised and paired with their transcriptions. Per-item errors are based on counts of phoneme deletions and substitutions seen in each response (as was mentioned, phoneme insertions are ignored). Per-subject scores are then computed based on per-item errors across all responses as follows:

$$e_i=S_i+D_i;i\in \{1,2,\cdots ,I\}$$ (1)

$$y^n=\frac{TP-{\sum }_{i=1}^I{e}_i}{TP};n\in \{1,2,\cdots ,N\}$$ (2)

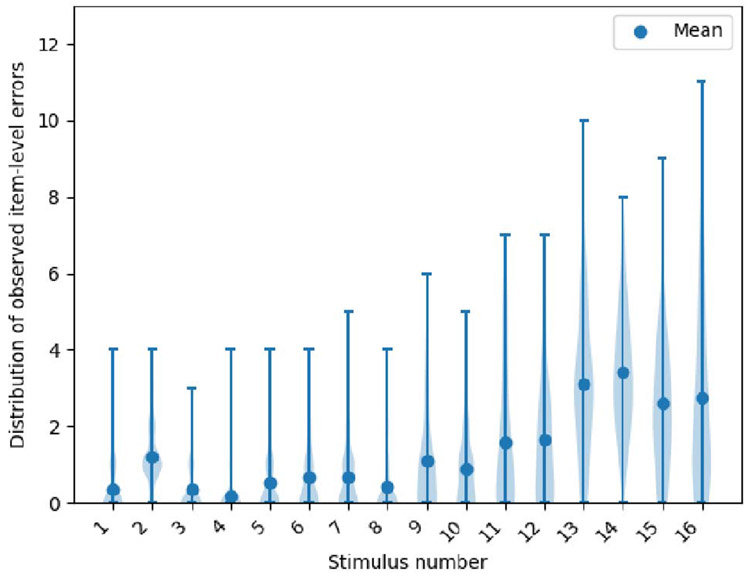
where e_i denotes the error in the i_th response, S denotes the number of incorrect phonemes substituted, and D denotes the number of phonemes deleted. Also, I and N denote the total number of stimuli in the test and participants, respectively. In Equ. (2), yⁿ stands for the true score of n_th participant and TP denotes the total number of phonemes in all stimuli in the test, i.e., 96 in our corpus. We employ violin plots to represent the probability distribution of item-level scores across participants. Violin plots are similar to box plots except that they use a kernel density estimation function to approximate the underlying distribution of the samples. Figure (2) illustrates probability distribution observed (“true”) item-level errors of 16 stimuli across 101 subjects, plotted separately for each stimulus. As it is seen in this figure, the number of deletion and substitution errors observed in the responses monotonically increase as a function of stimulus length, except for the second stimulus. The observed mean and standard deviation of per-subject scores are 0.77 and 0.11, respectively (observed score ranges from 0.34 to 0.97).

Fig. 2.

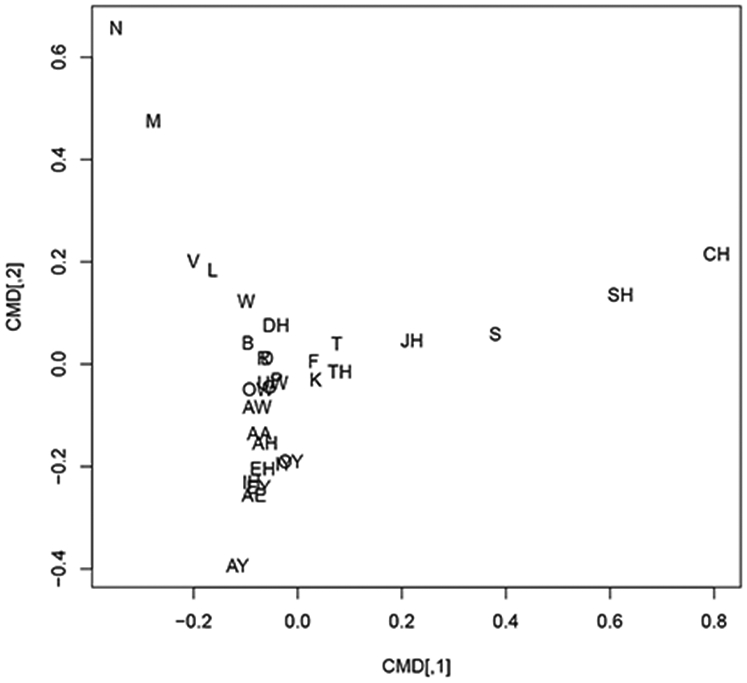
Two-dimensional representation of substitution error patterns

3. METHOD

Our proposed approach has two components: an automatic speech recognition (ASR) system that generates transcriptions of the verbal responses and a machine learning-based scoring algorithm that estimates scores from the transcription.

3.1. KALDI ASR system

For automatic transcription of the recordings, we adopt a GMM-HMM based model from the state-of-the-art Kaldi speech recognition toolkit [5]. With 39-dimensional mel-frequency cepsteral coefficients (MFCC) features with delta and delta-delta coefficients, we built a ASR system using the latest Kaldi recipe (egs/timit/s5). For training acoustic models, we divided subjects into five folds, using four folds for training and leaving the fifth one for testing. After cepstral mean and variance normalization and liner discriminative analysis (LDA), we employed model space adaptation using maximum likelihood linear regression (MLLR). Also, speaker adaptive training (SAT) of the acoustic models was performed by both vocal tract length normalization (VTLN) and feature-space adaptation using feature space MLLR (fMLLR). A four-gram phone model was built on the manual transcription of responses that were only available in the training set using the SRILM toolkit [6]. The average phoneme error rate (PER) computed via a five fold cross-validation schema was 20.13%. PER is defined as the number of phoneme insertions, deletions, and substitutions seen in the transcription divided by the total number of phonemes. Due to the very limited amount of training data at each fold, we decided to not din use Kaldi’s DNN based recipe for training purposes.

3.1.1. Stim-Rescore: Re-scoring the ASR lattice

Typically, an ASR system is used to produce the single highest-likelihood transcription of the spoken response. However, it is often the case that the most accurate transcript is not the one receiving the highest acoustic and language model likelihoods. Therefore, we use the nonword stimulus to rerank the ASR lattice and take the transcription that minimizes the PER with respect to the stimulus (often called oracle transcription).

3.2. Analysis of substitution error

Substitution errors on the NWR task could be random or systematic, and in the case of latter, exploring possible structure in the error space is valuable. Here, our assumption is that substitution errors are more likely between phonemes sharing similar phonetic characteristics such as place or manner of articulation. Figure 2 shows that phonetic characteristics may indeed be relevant. The coordinates of the phonemes were computed as follows. First, we computed a confusion matrix by counting the number of times a given phoneme in the stimulus was responded to (as determined via an alignment algorithm) by a given phoneme in the response, pooling data across all participants. The resulting confusion matrix (with rows corresponding to stimulus phonemes and columns to response phonemes) was normalized by dividing all elements by their corresponding row sums. Subsequently, we computed pairwise Euclidean distances between rows, and fed these into the “R” cmdscale program, based on Mardia et. al. [7], which maps phonemes into a k-dimensional space (we chose k=2) such that the distances in this space correspond as closely as possible to the distances between the rows. As can be seen, vowels and diphthongs cluster together, as do nasals, voiceless plosives, and voiceless fricatives. This open an avenue for future recherches on exploring methods to make use of phonetic characteristics in the analysis of NWR tasks.

4. SCORING ALGORITHMS

As a baseline method, we compute the subject-level scores from the ASR-based transcription of nonword stimuli using Equ. (2). We use Stim-Rescore generated oracle in addition to the 1-best transcription to independently evaluate the performance of each method. In the next section, we will describe machine learning based algorithms for predicting the final scores.

4.1. Learning Methods

Equ. (2) assumes that observed errors in responses to different stimuli contribute equally to the final scores. However, as can be seen in Figure (2), the distribution of true item-level errors are not uniformly distributed across stimuli. In fact, the number of errors seen in the responses is directly proportional to the length of the prompt, which suggests that errors made in longer stimuli make larger contributions to the final score. As an alternative to Equ. (2), we construct a long subject-level feature vector using ASR errors seen in generated transcriptions and a let learning algorithm predict the final score.

4.2. Subject-level Features

Per-subject features are computed across all 16 nonword stimuli by concatenating the per-item numbers of substitutions and deletions. This will generate a 32 dimensional feature vector (two features per item) representing a error distribution across all stimuli as follows:

$$F(n)=[{\widehat{S}}_1,{\widehat{D}}_1,{\widehat{S}}_2,\cdots ,{\widehat{S}}_I,{\widehat{D}}_I];i\in \{1,2,\cdots ,I\}$$ (3)

where F(n) represents the extracted feature vector of the n_th participant.

4.3. Learning Strategies

We investigate three forms of regularized regression models learned on item-level features extracted from subjects’ responses. The learned parameters of regression models will depend on the choice of the loss function and normalization term. We conducted three forms of regularization, L2-norm in Ridge regression, L1-norm in Lasso, and Hinge loss function in linear support vector regression (SVR). In Ridge regression, the loss function and regularizer are squared loss and L2-norm, respectively; in Lasso regression, the loss function is L2-norm but the regularization term is the L1-norm, and linear SVR uses a Hinge loss function and an L2-norm for regularization [8]. These three learning strategies were evaluated on our data set using cross-validation with the scikit-learn toolkit [9]

5. EXPERIMENTS

We evaluated the performance of our proposed methods by calculating the mean absolute error (MAE) in addition to product-moment correlation between the automatically computed and manually computed NWR scores.

In order to estimate the optimal set of acoustic and language model parameters for the ASR system, we used a fivefold cross validation scheme, setting four of the five sets as training set, and using the fifth ones only at the testing time. Data was split by subject to make subject-independent test and train sets.

Table 2 reports the performance of two ASR-based methods for predicting the subject-level scores in terms of MAE and product-moment correlations between observed and predicted scores across test folds. In this test, we used Equ. (2) to compute subject-level scores from ASR transcriptions. As can be seen in the table, re-scoring the ASR lattice using the target stimuli leads to the best automatic scoring results with an MAE of 0.51 and correlation of 0.78.

Table 2.

MAE and product-moment correlations (ρ) between observed and predicted scores, and PER across test folds. Here, we predict per-item scores and, as per Equ. (2), sum these to compute the predicted total scores.

Measure	1-best	Stim-Rescore
MAE	0.054	0.051
ρ	0.75	0.76
PER	20.13	19.76

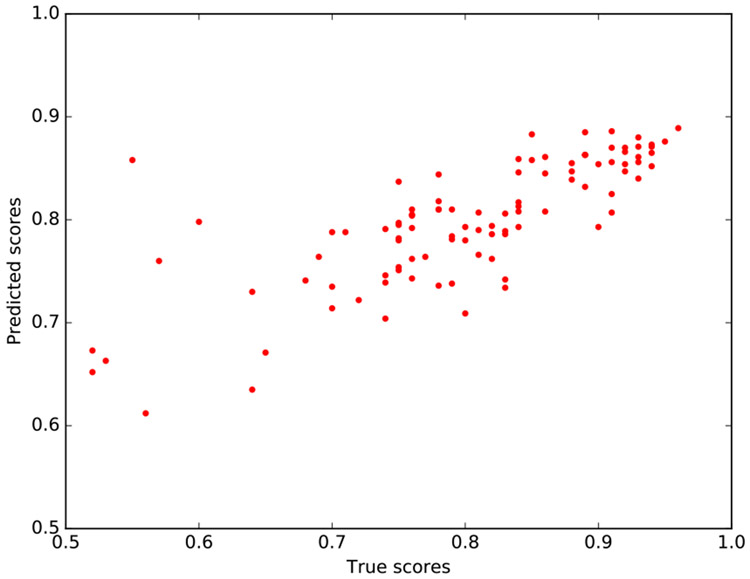
Next, we evaluated the performance of our proposed scoring method based on the three described regression models. For optimizing the parameters of the regression models, we used the same cross-validation folds used for ASR training and testing. Tables 3 and 4 report MAE and product-moment correlations computed via three regression models. We applied regression models over three types of subject-level features extracted from ASR transcriptions. In (Figure 3), we illustrate the correlation between the predicted and true scores obtained by Ridge regression with features extracted from transcriptions using Stim-Rescore approach.

Table 3.

Mean absolute error (MAE) between observed and predicted scores across test folds, using machine learning to optimally combine per-item deletion and substitution errors.

Model	1-best	Stim-Rescore
Ridge	0.052	0.040
Lasso	0.06	0.041
Linear SVR	0.066	0.058

Table 4.

product-moment correlations between observed and predicted scores across test folds, using machine learning to optimally combine per-item deletion and substitution errors.

Model	1-best	Stim-Rescore
Ridge	0.79	0.85
Lasso	0.73	0.74
Linear SVR	0.74	0.76

Fig. 3.

Observed and predicted scores, based on optimizing product-moment correlations using Ridge regression on features of Stim-Rescore transcriptions

From the results, it is clear that the use of regression models enhances the performance of scoring system in terms of correlation coefficients between observed and predicted scores. Also, results suggest that Ridge regression with L2-norm regularization term is more suitable for this task than the Lasso and SVR. Furthermore, comparing the results of Ridge regression with those presented in Table 2 suggests that a properly weighted combination of item-level errors effectively improves the performance.

6. CONCLUSION

In this paper, we showed that a nonword repetition test can be automatically scored with reasonable accuracy. The scoring system applies ASR to the verbal responses of children, construct a subject-level feature vector based on item-level errors, and optimally estimates true scores by applying regression models to extracted features. Confining the analysis to 101 children ( 42 with ASD, 18 with SLI, and 41 typically developed ) who had been given 16 nonword stimuli, and estimating their scores on these items, we found that the Mean Absolute Error of observed and estimated total scores was 0.04 ; the product moment correlation was 0.85. We expect that further improvements in performance can be expected, for example by using phonetic features based language models. Challenges remain, however, the most severe one being that while we used recordings in which irrelevant speech was removed manually, for real-world usage it will be necessary to do this automatically.

Fig. 1.

Distribution of errors over participants’ responses as a function of stimulus number