Abstract
Magnetic resonance imaging (MRI) is widely used for screening, diagnosis, image-guided therapy, and scientific research. A significant advantage of MRI over other imaging modalities such as computed tomography (CT) and nuclear imaging is that it clearly shows soft tissues in multi-contrasts. Compared with other medical image super-resolution methods that are in a single contrast, multi-contrast super-resolution studies can synergize multiple contrast images to achieve better super-resolution results. In this paper, we propose a one-level non-progressive neural network for low up-sampling multi-contrast super-resolution and a two-level progressive network for high up-sampling multi-contrast super-resolution. The proposed networks integrate multi-contrast information in a high-level feature space and optimize the imaging performance by minimizing a composite loss function, which includes mean-squared-error, adversarial loss, perceptual loss, and textural loss. Our experimental results demonstrate that 1) the proposed networks can produce MRI super-resolution images with good image quality and outperform other multi-contrast super-resolution methods in terms of structural similarity and peak signal-to-noise ratio; 2) combining multi-contrast information in a high-level feature space leads to a signicantly improved result than a combination in the low-level pixel space; and 3) the progressive network produces a better super-resolution image quality than the non-progressive network, even if the original low-resolution images were highly down-sampled.
Keywords: Magnetic resonance imaging (MRI), super-resolution (SR), multi-contrast, neural network, progressive neural network
I. Introduction
MAGNETIC resonance imaging (MRI) is one of the most widely used medical imaging modalities. Compared with other modalities such as computed tomography (CT) and nuclear imaging, MRI is advantageous in providing clear tissue structure and functional information without inducing ionizing radiation. With pulse sequences, the MRI system can be flexibly configured to generate multi-contrast images like T1, T2, and proton density (PD) weighted images, which contain important physiological and pathological features. However, a major shortcoming of current MRI system is that it is difficult to obtain high-resolution (HR) MR images in clinical applications due to the trade-off between the system cost-effectiveness and signal-to-noise ratio [1], [2]. Clinically, in order to obtain HR MR images, patients are required to remain stable in the gantry for long time, which intensifies patients’ discomfort and inevitably introduces motion artifacts that compromise image quality.
Super-resolution (SR) techniques improve image quality only through algorithms and without any hardware update, which have been extensively studied in the natural image domain. From model-based methods like interpolation algorithms [3] and iterative deblurring algorithms [4], [5] to learning-based methods such as dictionary learning methods [6]-[8], many impressive SR results were achieved yielding deblurred edges and contours. In recent years, deep learning has become a mainstream approach for super-resolution imaging, and a number of network-based SR models were proposed. Among the published model- or learning-based methods, convolutional neural networks produce superior SR results with better clarity and less artifacts. According to different designs, these network-based models can be categorized into convolutional models such as the image super-resolution convolutional network [9] and the very deep super-resolution network [10], residual models such as the cascading residual network [11] and the residual encoder decoder network [12], recursive models such as the deep recursive convolutional network [13] and the deep recursive residual network [14], densely connected models such as the residual dense network [15] and the dense deep back-projection network [16], the attention-based model that combines the convolutional network and selection units [17] and the so-called the residual channel attention network [18], progressive models such as the sparse coding-based network [19] and the deep Laplacian pyramid super-resolution network (LapSRN) [20], and generative adversarial network (GAN) representatives like the EnhanceNet [21] and the super-resolution generative adversarial network [22].
Inspired by the great success of deep learning in achieving SR of natural images, researchers developed neural networks to improve the quality of MR images without introducing any cost on hardware modification. The neural networks were proposed to implement MRI SR and shorten scan time [23]-[26]. However, these existing methods only used single contrast MRI images and did not make full use of multi-contrast information. Clinically, T1, T2 and PD weighted images are often generated together for diagnosis with complementary information. Although each weighted image is only good at showing certain types of tissues, they reflect the same anatomy, and can provide synergy when used in combination. Based on this consideration, here we propose an MRI multi-contrast super-resolution (MCSR) approach to use MRI multi-contrast images collectively for SR imaging superior to single-image super-resolution (SISR) results. Typically, MCSR imaging may achieve super-resolution results for a specific contrast image aided by HR images with other contrasts. Relevant information in those reference images is extracted to guide the recovery of details in an image of interest. Recently, MCSR has gradually become a hot topic in the MRI field. Rousseau et al. [27] and Khouzani et al. [28] both used non-local means to implement MCSR. Brudfors et al. [29] proposed a multi-channel total variation method to utilize multi-contrast information. Zheng et al. [30] proposed an MCSR method that utilizes a gradient-guided edge enhancement algorithm to estimate the similarity between image patches in different contrasts. Gong et al. [31] designed an algorithm called PROMISE to process shareable information between MRI images in different contrasts from parallel imaging. Song et al. [32] proposed a coupled dictionary learning method to implement MCSR. Lu et al. [33] declared a manifold regularized sparse learning algorithm for MCSR. Zeng et al. [34] designed a convolutional neural network which contains two sub-networks to implement MCSR.
In this paper, we propose a one-level non-progressive network for low up-sampling factor MCSR and a two-level progressive neural network for high up-sampling factor MCSR. The main contributions of this paper are: 1) the two-level progressive neural network based on the Wasserstein generative adversarial network with gradient penalty (WGAN-GP) architecture that can achieve excellent MCSR results in the case of a high up-sampling factor; 2) the finding that combining multi-contrast information in a high-level feature space leads to a significantly improved results over the combination in the low-level pixel space; and 3) a composite loss function including mean-squared-error (MSE), perceptual loss, and texture matching loss to ensure that generated images can recover texture details (due to the perceptual and texture matching losses) and are faithful to the ground truth (due to MSE).
II. Methodology
A. Overall Super-Resolution Process
Given an HR MR image of the size n×n, the LR image obtained after the down-sampling process with a factor s > 1 is of the size n/s × n/s. This down-sampling process f can be expressed as:
| (1) |
where φ denotes the down-sampling or blurring function, and ϵ represents the system noise. Theoretically, an SR process is to find the inverse solution f−1 of the original down-sampling function f. As SR imaging is an ill-posed problem, it is impossible to find the exact inverse solution, and only approximate solutions can be obtained. The goal of the SR imaging process is to find the most desirable inverse function g of the ideal inverse solution f−1. Then, the SR process can be expressed as:
| (2) |
To obtain such an approximate solution g, image priors should be used. In our previous single-image super-resolution (SISR) study [26], we proposed an ensemble-learning-based deep learning framework to achieve MRI SR imaging with complementary image priors. Although a dataset with rich image features was built for single-contrast images, the amount of prior information gathered from single-contrast images is still limited. Therefore, in this study we take advantage of multi-contrast images for MRI SR imaging, which should contain more prior information than single-contrast images. Specifically, we propose a deep learning-based MCSR method for SR T2 weighted imaging by incorporating high-resolution PD or T1 weighted images as reference images.
B. Down-Sampling and Zero-Filling
In our previous study [26], LR MRI images were obtained by down-sampling T2-weighted images in the frequency domain. We first converted the original T2 image of size 256 × 256 into the k-space. Then, we cropped data and only kept data points in a central low frequency region. For the down-sampling factors 2, 3 and 4, the central 25%, 11.1% and 6.25% data points were kept. All the peripheral data points were zeroed out, which is called zero-filling. Finally, we used the inverse Fourier transform to convert the modified data back into the image domain to produce LR images. Through such a down-sampling and zero-filling process, we degraded the image quality and kept the image size unchanged.
C. One-Level Non-Progressive Network
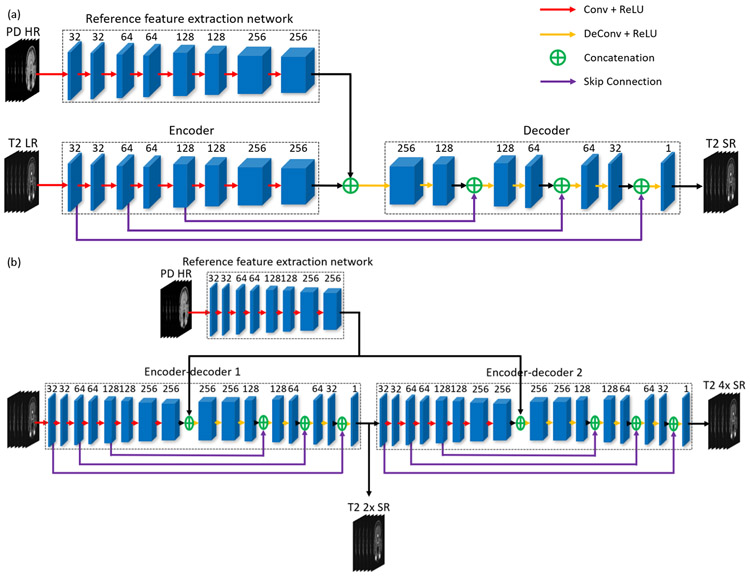
The proposed one-level non-progressive network is based on the Wasserstein generative adversarial network with gradient penalty (WGAN-GP) [35], which includes a generator and a discriminator. As shown in Fig. 1 (a), the generator consists of an encoder-decoder network and a reference feature extraction network.
Fig. 1.
Two proposed network architectures for MCSR. (a) The generator of the proposed onelevel non-progressive model, which contains an encoder-decoder network and a reference feature extraction network, and (b) the generator of the proposed two-level progressive model.
The encoder-decoder network [36] mainly contributes to the improvement of image quality. The encoder has 8 sequential convolutional layers, each of which is followed by a rectified linear unit (ReLU). The number of these convolutional filters are 32, 32, 64, 64, 128, 128, 256, and 256, respectively. Each convolutional layer uses 3 × 3 convolution kernels with a stride of 1. The encoder condenses information and extracts features layer by layer. The decoder consists of 8 sequential transposed convolutional layers, each of which is also followed by a ReLU. The numbers of filters in each transposed convolutional layer are 256, 128, 128, 64, 64, 32, 32, 1, respectively. Differing from convolutional layers, transposed convolutional layers enlarge feature maps through transposed convolution filters of kernel size 3×3 with a stride of 1. Note that zero-padding is not used in all layers. The decoder gradually dilates information layer by layer. Between the encoder and the decoder, there are three skip connections. Feature maps extracted in the encoder are transferred to the decoder through the skip connections. These skip connections can boost the training process through utilizing the similarity between input and output images. The discriminator includes three blocks followed by two fully-connected layers. Each block contains two convolutional layers, two ReLU activation functions, and a 2 × 2 max-pooling layer. Each convolutional layer contains 3 × 3 convolution kernels with a stride of 1. Zero-padding is used to keep feature-maps unchanged. The numbers of convolutional filters are 64, 64, 128, 128, 256, and 256, respectively. The numbers of neurons in the two fully-connected layers are 128 and 1, respectively.
The reference feature extraction network is utilized to extract feature maps from the reference images. These extracted features are then fed into the encoder-decoder network. The structure of the reference feature extraction network is the same as the encoder of the encoder-decoder network.
D. Objective Function
The objective function of the generator contains four parts: the adversarial loss , mean-squared error (MSE) , perceptual loss , and texture matching loss . Below we will introduce each loss term in detail and explain the reason why we choose these four loss terms.
1). Adversarial loss:
The adversarial loss in the generative adversarial network framework is used to train the generator to maximize the output of the discriminator for its fake instances. In combination with the discriminator loss, the adversarial loss guides the improvement of the generator to fool the discriminator and produce realistic fake results as compared to the corresponding real instances. In the WGAN-GP framework, the adversarial loss can be expressed as:
| (3) |
where G represents the generator, D stands for the discriminator, and ILR is the input LR image of the generator.
2). Mean-squared error:
The mean-squared error (MSE) is one of the most widely used fidelity measuring metrics in SR studies. It evaluates the difference between the output of the generator and the corresponding ground truth at the pixel-wise level. Using the MSE loss can greatly improve the signal-to-noise ratio of generated images [37]. The MSE can be expressed as
| (4) |
where ∥ · ∥F represents the Frobenius norm.
3). Perceptual loss:
Although MSE leads to a high signal-to-noise ratio in reference to the ground truth, it tends to produce over-smoothed SR results [38], [39]. As a result, some image details may be lost in the SR results. To overcome this problem and recover more details, the perceptual loss is included in the objective function. Different from the MSE loss that evaluates image differences in the image space, the perceptual loss measures image similarity in a high-level feature space. We used the VGG16 model [40] pretrained on ImageNet to extract features from a given image. Specifically, following [39], feature maps from the 2nd, 4th, 7th, and 10th convolutional layers were selected to compute the perceptual loss. All feature maps equally contribute to the perceptual loss. The perceptual loss can be expressed as the MSE of feature maps between the output of the generator and the corresponding ground-truth:
| (5) |
where ϕl represents extracted feature maps from the l-th selected convolution layer of VGG16.
4). Texture matching loss:
In addition to the MSE loss and perceptual loss, we also include another fidelity term called the texture matching loss. The texture matching loss proposed by Gatys et al. [41] contributes to generate an image with great similarity between the output of the generator and the ground truth by statistically matching extracted features. Sajjadi et al. [21] applied this loss to natural images for super-resolution. The texture matching loss calculates the Gram matrices between the output of the generator and the corresponding ground truth in a feature space. The Gram matrix measures feature correlations of multiple layers. Texture information can be kept by decreasing the Gram matrix difference. As the Gram matrix reflects the feature correlations and can be used to represent the style of an image, the texture matching loss measures the difference between two Gram matrices of two images, which is also called the style loss. This type of characteristics is suitable for MCSR studies. The MCSR imaging process can also be viewed as a style transfer between images of different contrasts. Using this loss term promotes the corresponding feature matching and ensures that features are fully utilized. Specifically, the texture matching loss is the MSE of the Gram matrices between the output of the generator and the corresponding ground truth in a feature space:
| (6) |
where stands for the Gram matrix defined as the outer product of feature map matrix and its transpose matrix F⊤. nl is the number of feature maps in the convolution layer, and ml stands for the height times the width of the feature map. In this study, feature maps involved in the texture matching loss are the same as those used for the perceptual loss.
In total, the objective function of the generator is:
| (7) |
where θG presents the trainable parameters of the generator, and λmse, λper, and λtxt are the trade-off parameters for , , and , respectively.
The objective function of the discriminator is the same as the objective function of the original WGAN-GP model, which is defined as follows:
| (8) |
where θD represents the trainable parameters of the discriminator. is a synthesis sample from real and fake samples: , ϵ is randomly drawn from a uniform distribution , and ∇ is the gradient operator.
E. Two-Level Progressive Network
Different from the neural networks that achieve SR imaging through one step, the progressive network splits an SR work into several sequential steps. In each step, the progressive network implements the image up-sampling by a small factor [20], [42]. Through the combination of several steps, it can implement the SR for a large up-sampling factor. LapSRN [20] is a good example of the progressive network, which contains three sequentially displaced subnets; each subnet can increase the image resolution by a factor of 2. Through such a neural network, LapSRN can finally improve image resolution by a factor of 8.
Here we propose a two-level progressive neural network to achieve MCSR for an up-sampling factor of 4. The proposed model is the combination of two one-level non-progressive networks. Its generator contains two encoder-decoder networks and a reference feature extraction network, as shown in Fig. 1(b). The discriminator is the same as the one for the one-level non-progressive network. To obtain 4-fold MCSR results, we trained the progressive network to ensure that it can progressively improve image quality level by level. In the first level, 2-fold MSCR results will be achieved. The other 2-fold MCSR results will be obtained in the second level. The input of the progressive network is the LR images through 4-fold down-sampling and zero-filling. The ground truth of the first level is the LR images through 2-fold down-sampling and zero-filling. The ground truth of the second level is the original HR images.
The objective function of the progressive network combines results of both the two levels. The modified equations of Eqs. (4), (5) and (6) are expressed as
| (9) |
| (10) |
| (11) |
where I4×LR stands for 4-fold down-sampled LR images, I2×LR for 2-fold down-sampled LR images, and IHR for original HR images. For simplicity, the subscripts of the summation notations in Eqs. (9), (10), and (11) are ignored.
F. Image Quality Evaluation Metrics
The structural similarity (SSIM), peak signal-to-noise ratio (PSNR) [37] and information fidelity criterion (IFC) [43] metrics are used to evaluate the image quality of MCSR results.
SSIM is a fidelity metric that compares images in the terms of luminance, contrast, and structural similarity. The SSIM is defined as follows:
| (12) |
where μX and μY stand for the average pixel intensities of images X and Y, and represent the pixel intensity variances of X and Y. σXY is the covariance of image X and Y, and c1 and c2 are two variables to stabilize the division. As SSIM measures the similarity at the patch level, in this work all SSIM scores will be given as the mean of SSIM values based on a window size of 7 × 7.
PSNR is another commonly used fidelity measure. It is related to MSE, and can be expressed as the ratio between the square of the maximum value and the MSE value:
| (13) |
IFC proposed by Sheikh [43] measures image quality based on natural scene statistics. While image information can be extracted by human visual system, IFC utilizes the mutual information between the reference and a distorted image to evaluate image quality. Compared with SSIM and PSNR, IFC takes the correlation between image and human visual perception into account. However, IFC is not the best at evaluating structural similarity.
III. Experiments
A. Datasets
IXI dataset: The IXI dataset [44] contains registered T2 weighted and proton density (PD) weighted magnetic resonance imaging (MRI) images of 578 patients. T2 weighted images were used for super-resolution (SR) with PD weighted images as the reference. 7,000 pairs of T2 and PD weighted images from randomly selected 56 subjects were used for training. Another 1,955 pairs from another randomly selected 16 subjects for testing. We adopted 10-fold cross-validation in this study. The size of original HR images of both T2 and PD weighted images is 256×256. 2-fold, 3-fold, and 4-fold down-sampled T2 weighted low-resolution (LR) images were created through down-sampling and zero-filling. Before training, all images were normalized into the range of [0, 1]. Each LR and high-resolution (HR) image pairs was cropped into 16 patch pairs with the patch size of 64 × 64.
NAMIC Dataset:
NAMIC brain multimodality dataset [45] includes registered T1 and T2 weighted MRI images scanned from 20 patients. 1,620 pairs from randomly selected 18 subjects were used for training, and 180 pairs from the other 2 subjects for testing. Similar to what we did with the IXI dataset, we chose T2 weighted images for SR with T1 weighted images as the reference. The size of the original HR image is 256 × 256. We down-sampled and zero-filled T2 weighted images for 2-, 3-, and 4-fold LR images. Before training, all images were normalized into the interval [0, 1]. Each LR and HR image pairs was cropped into 16 patch pairs with the patch size of 64 × 64.
B. Experimental Details
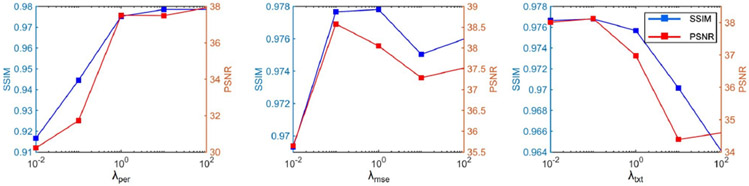
For training, 112K image patches of the size 64 × 64 were randomly selected with a batch size of 32. The training process continued for 50 epochs with the learning rate of 2×10−5. The discriminator was trained four times before the generator was trained once. Hyper-parameters λmse, λper, and λtxt in the objective function of the generator Eq. (7) were determined based on the result shown in Fig. 2. Only training data was involved in this hyper-parameter tuning process. We used a greedy method to tune each hyper-parameter in Eq. (7). The coefficient of the perceptual loss was first tuned. As shown in Fig. 2, both SSIM and PSNR scores get dramatically increased when λper goes up from 0.01 to 1.0. Some further SSIM and PSNR improvement can be obtained by increasing λper from 1.0 to 100. However, such an increment was far less than the increment in the range of 0.01 and 1.0. Considering a too large perceptual loss coefficient will overwhelm the contributions from other loss components, we finally set λper to 1.0. Next, we tuned λmse and λtxt. For the coefficient of the MSE loss, when λmse was set to 0.1, the highest PSNR and the second highest SSIM scores can be obtained. Based on these, we set λmse to 0.1. Similarly, we set λtxt to 0.1. To verify the effective of those tuned hyper-parameters and eliminate the concern that the order of tuning hyper-parameters may impact the result, we re-ran the hyper-parameter tuning process in the inverse order. That is, the hyper-parameter of the texture matching loss was first determined, and then followed by the hyper-parameter of the MSE loss. Finally, the hyper-parameter of the perceptual loss was obtained. The result is in the supplementary material Fig. 1. It can be found that the best value for each hyper-parameter remains the same as the results in Fig. 2. The value of λgp in the objective function of the discriminator Eq. (8) was 10, which was suggested by Ref [35]. The Adam optimization method [46] was used to train the neural network. All the work was implemented using PyTorch on a GTX 1080Ti GPU.
Fig. 2.
Results of tuning hyperparameters in the objective function (the x-axes are on the logarithmic scale).
IV. Results
A. Convergence Behavior
During the training process, the perceptual loss , MSE loss, and Wasserstein distance (Wdis) in each epoch were recorded for monitoring the convergence of the network model. Variations of the perceptual loss and MSE loss reflect the similarity between the generated result and the ground truth in the high-level feature space and low-level image space respectively. The Wasserstein distance is known as the earth-movers (EM) distance, which shows the probability distribution similarity between the generator output data and the true data. It is defined as
| (14) |
As shown in Fig. 3, all perceptual loss curves, MSE loss curves, and Wasserstein distance curves gradually decrease towards zero with the continuation of the training process, indicating that our model converged stably. After 40 epochs, all curves become stable and close to zero, which reflects the fact that the generator can stably bring about super-resolution results with great similarity relative to the corresponding HR ground truth.
Fig. 3.
Comparison between different models used in our ablation studies in terms of the perceptual loss, mean-squared-error (MSE) loss, Wasserstein distance, PSNR and SSIM.
B. Ablation Study
To find the best neural network structure for MCSR imaging, we built four models and conducted a systematic ablation evaluation. In this subsection, only IXI dataset was used. In the first study, to investigate the utility of the introduction of reference images, we removed the reference feature extraction network from the proposed network and only kept a single encoder-decoder network with only T2 weighted LR images as the input. In the second study, we were interested in directly converting PD weighted images into T2 weighted images through an image synthesis process. Hence, we used PD weighted HR images as the input to the same neural network in the first study, instead of T2 weighted LR images. In the third and fourth studies, we focused on how to effectively utilize the information in PD weighted HR images. In the third study, these two-contrast images were combined in a low-level image space and fed into the same neural network model used in the previous two studies. In the fourth study, two-contrast images were combined in a high-level feature space, which is the proposed network. The above four studies are illustrated in Fig. 4. For comparison, all input T2 weighted LR images used in the ablation study are 2-fold down-sampled LR images. Results from the ablation studies are shown in Fig. 5 and Table I.
Fig. 4.
Schematic views of the four ablation studies. (a)-(d) corresponds to the proposed four ablation studies. The blue block represents the encoder-decoder network and the orange block stands for the reference feature extraction network. (a) The first study is an SISR study in which the input is a T2 weighted LR image, and the output is an T2 weighted SR image. (b) The second study is an image synthesis study in which the input is a PD weighted HR image, and the output is a T2 weighted SR image. (c) The third study is an MCSR study in which the input is a T2 weighted LR image, with the PD weighted HR image as the reference, the output is the T2 weighted SR image. Multi-contrast information is combined in a low-level image space. (d) The fourth study is also an MCSR study in which the input is a T2 weighted LR image, with the PD weighted HR image as the reference, the output is the T2 weighted SR image. Multi-contrast information is combined in a high-level feature space. (d) is also the schematic view of the network shown in Fig. 1(a).
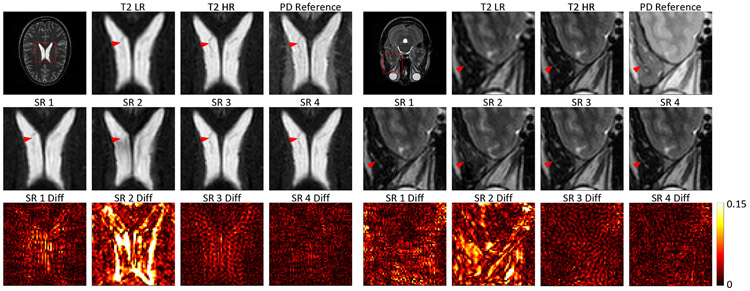
Fig. 5.
Results from the ablation-based evaluation. T2 LR, T2 HR, and PD stand for the input low-resolution T2-weighted image, high-resolution T2-weighted ground truth image, and high-resolution reference image in proton density contrast. SR1, SR2, SR3, and SR4 indicate the results from the four ablation studies respectively. The hot maps in the bottom row show the absolute pixel-value differences between the ablation study results and the corresponding ground truth T2 weighted HR image respectively.
TABLE I.
Statistic Results from the ablation studies based on the IXI dataset (MEAN±95%CI), where “MEAN” and “CI” represent the average value and the confidential intervals respectively.
| SR1 | SR2 | SR3 | SR4 | |
|---|---|---|---|---|
| SSIM | 0.960 ± 0.002 | 0.915 ± 0.040 | 0.975 ± 0.001 | 0.976 ± 0.001 |
| PSNR | 34.705 ± 0.205 | 28.282 ± 0.221 | 38.225 ± 0.236 | 38.513 ± 0.248 |
| IFC | 3.990 ± 0.037 | 1.890 ± 0.025 | 4.666 ± 0.042 | 5.058 ± 0.047 |
Fig. 3 shows that convergence curves in the second ablation study, with the highest Wasserstein distance, perceptual loss, MSE loss and the lowest SSIM and PSNR values. As shown in Fig. 5, the SR result obtained in the second study also has the worst image quality as it has the largest pixel-value difference from the ground truth. Taking the center white matter regions in the first three rows as an example, all other SR results show the fissure with clear shapes while the second SR result cannot. Quantitative results in Table I also indicate that the results from the second ablation study have the lowest SSIM, PSNR and IFC scores. All these results emphasize that the image synthesis study converting PD weighted HR images into T2 weighted HR images cannot obtain high-quality SR results.
When comparing results among the first, third and fourth ablation studies, MCSR results from the third and fourth ablation study beat the SISR results from the first study. MCSR results have higher PSNR, SSIM, and IFC scores and less pixel-value differences between MCSR results and the ground truths than SISR results. As an example, the dark curve highlighted by the red arrow in the T2 weighted LR image in the fourth row of Fig. 5 can be hardly distinguished from the background. However, this curve shows clearly in the corresponding PD weighted HR image. After the training, this curve is still hard to be seen in the SR result in the first ablation study but it became much clearer in the third and fourth ablation studies that utilized PD weighted HR images in the training process.
In the third and fourth ablation study, curves of the third study in Fig. 3 decrease quickly in the first several training epochs. However, after 10 epochs, curves of the fourth study are slightly lower than the third study. Fig. 5 demonstrates that the fourth study can achieve SR results with smaller pixel-value differences. Quantitative results in Table I also show that the fourth ablation study results beat the third ablation counterparts in terms of PSNR, SSIM and IFC scores.
C. Non-progressive Model MCSR Results with 2-fold, 3-fold and 4-fold Up-sampling
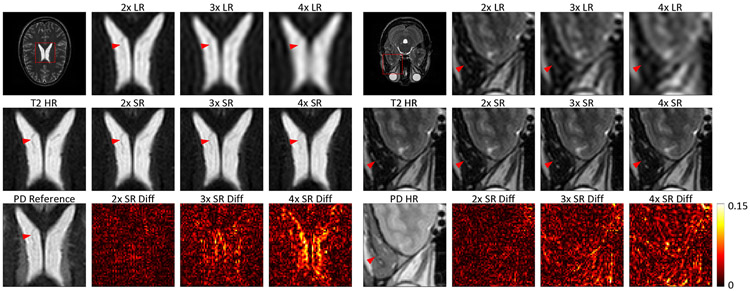
In the previous subsection, we demonstrated that our method can achieve 2-fold up-sampling MCSR results with good image quality. Now, let us study MCSR with a higher up-sampling factor. MCSR results for 2-, 3-, and 4-fold up-sampling rates based on the one-level model are shown in Figs. 6, 7, and Table II. It can be seen that when images are down-sampled by a larger factor, the down-sampled LR images become much more blurred with much less visible details. After training, we can obtain quite good MCSR results with clearer shapes and textual details, and these MCSR results are with great structural similarity with the corresponding HR image. For example, fissures in the white matter pointed by red arrows in Fig. 6 become gradually less clear and less detectable with the increment of down-sampling factors. However, in each MCSR result, these fissures become much clearer and detectable. Among all MCSR results, it can be found that MCSR results obtained from a smaller down-sampling factor have higher PSNR, SSIM, and IFC scores and less pixel-value differences with the HR ground truth, indicating that these MCSR results based on LR images with a small down-sampling factor have higher image qualities than those based on LR images with a larger down-sampling factor, as heuristically expected.
Fig. 6.
T2 weighted SR results with different down-sampling factors based on the IXI dataset. 2×LR, 3×LR, and 4×LR stand for low-resolution T2-weighted images with different down-sampling factors. T2 HR and PD stand for the input low-resolution T2-weighted image and high-resolution reference image in proten density contrast respectively. 2×SR, 3×SR, and 4×SR represent T2-weighted super-resolution results from the corresponding LR images respectively. The hot maps show the absolute pixel-value differences between MCSR results and the ground truth T2 weighted HR image.
Fig. 7.
T2 weighted SR results with different down-sampling factors based on the NAMIC dataset. 2×LR, 3×LR, and 4×LR stand for low-resolution T2-weighted images with different down-sampling factors. T2 HR and T1 stand for the input low-resolution T2-weighted image and high-resolution reference image in T1 contrast respectively. 2×SR, 3×SR, and 4×SR represent T2-weighted super-resolution results from the corresponding LR images respectively. The hot maps show the absolute pixel-value differences between the corresponding MCSR results and the ground truth T1 weighted HR images.
TABLE II.
Statistic Result of Larger-Factor MCSR Imaging Using The One-Level Non-progressive Model (MEAN±95%CI)
| 2×SR | 3×SR | 4×SR | ||
|---|---|---|---|---|
| IXI Dataset |
SSIM | 0.976 ± 0.001 | 0.960 ± 0.001 | 0.950 ± 0.002 |
| PSNR | 38.513 ± 0.248 | 35.215 ± 0.256 | 33.329 ± 0.297 | |
| IFC | 5.058 ± 0.047 | 3.304 ± 0.034 | 2.708 ± 0.030 | |
| NAMIC Dataset |
SSIM | 0.974 ± 0.001 | 0.954 ± 0.001 | 0.925 ± 0.002 |
| PSNR | 34.127 ± 0.137 | 31.562 ± 0.161 | 28.207 ± 0.165 | |
| IFC | 3.538 ± 0.023 | 2.504 ± 0.015 | 1.923 ± 0.016 |
D. Progressive Model Further Improves Image Quality with 4-fold Up-sampling
In the previous subsection, although quite good MCSR results based on the non-progressive model can be obtained from highly down-sampled LR images like 4-fold SR results, these results are still with lower image quality compared with those based on low down-sampling factor LR images. We hope to further improve the quality of 4-fold down-sampled LR images, and proposed a two-level progressive model to achieve this goal. In this subsection, we presented two 4-fold MCSR results from the proposed progressive model trained with different objective functions. One is called U-PRO, and the other one C-PRO. “U” and “C” mean unconstrained and constrained respectively. The unconstrained results are from the progressive model trained with the objective functions Eqs. (4), (5), and (6) that only considers the final 4-fold SR results. On the other hand, the constrained results are from the progressive model that trained with the objective functions Eqs. (9), (10), and (11) that considers both 2-fold and 4-fold SR results.
Fig. 8 shows the comparison between each subnets output and its corresponding ground truth based on the 4×PRO C SR model. As shown in Fig. 8, our two-level progressive network can generate two levels of MCSR results under a strong restriction. Compared with their ground truths, the network can produce very faithful results.
Fig. 8.
Comparison of the two-level progressive network outputs with their ground truths. 2×LR represents the ground truth at the first level, and T2 HR stands for the ground truth at the second level. 2×PRO SR shows the outputs of the first level, and 4×PRO SR the outputs of the second level.
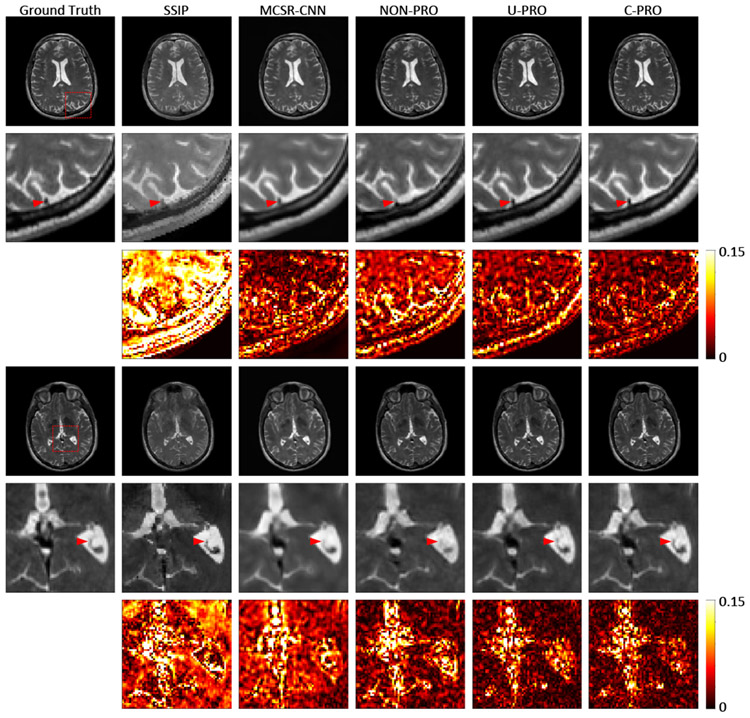
Figs. 9 and 10 show the comparison of 4-fold MCSR results based on the one-level non-progressive model (NON-PRO) and the two-level progressive model (U-PRO and C-PRO). It can be found that the progressive network produced MCSR results have sharper edges, clearer texture details, and less pixel-wise differences from the corresponding ground truths than the corresponding NON-PRO results. Table III statistically compares different methods. Both the U-PRO and C-PRO results are with higher SSIM, PSNR, and IFC scores than the NON-PRO results. Compared with the U-PRO results, the results of C-PRO have slightly higher SSIM, PSNR, and IFC scores, indicating the constrained progressive model can bring about SR imaging result with better image quality than the unconstrained model.
Fig. 9.
Comparisons of T2 weighted MCSR results from the our method and other state-of-the-art methods. Results are all based on the 4-fold down-sampled IXI dataset. SSIP and MCSR-CNN are two state-of-the art MCSR methods. NON-PRO indicates results obtained using the one-level non-progressive model. U-PRO and C-PRO denote MCSR results using the two-level progressive networks. The hot maps show the absolute pixel-value differences between the super-resolution results and the ground truth T2 weighted HR images.
Fig. 10.
Comparison of T2 weighted MCSR results obtained using the our method and other state-of-the-art methods. The results are all based on the 4-fold down-sampled NAMIC dataset. SSIP and MCSR-CNN are two state-of-the art MCSR methods. NON-PRO indicates the results from the one-level non-progressive model. U-PRO and C-PRO denote MCSR results using the two-level progressive networks. The hot maps show the absolute pixel-value differences between the super-resolution results and the ground truth T2 weighted HR images.
TABLE III.
Statistical Comparison of the MCSR results from the non-progressive model and progressive models respectively (MEAN±95%CI).
| 4×LR | NON-PRO | U-PRO | C-PRO | ||
|---|---|---|---|---|---|
| IXI Dataset | SSIM | 0.793 ± 0.004 | 0.950 ± 0.002 | 0.958 ± 0.002 | 0.961 ± 0.001 |
| PSNR | 27.151 ± 0.184 | 33.329 ± 0.297 | 34.814 ± 0.308 | 35.140 ± 0.310 | |
| IFC | 1.627 ± 0.150 | 2.708 ± 0.021 | 3.129 ± 0.038 | 3.354 ± 0.043 | |
| NAMIC Dataset | SSIM | 0.751 ± 0.003 | 0.925 ± 0.002 | 0.951 ± 0.002 | 0.953 ± 0.002 |
| PSNR | 26.827 ± 0.159 | 28.207 ± 0.165 | 30.763 ± 0.173 | 30.942 ± 0.222 | |
| IFC | 1.626 ± 0.120 | 1.923 ± 0.017 | 2.352 ± 0.017 | 2.385 ± 0.017 |
E. Comparing with State-of-the-art Methods
We also compared our results with some recently published state-of-the-art MCSR methods, including the self-similarity and image prior (SSIP) method [47] as the representatives of the model-based methods and the multi-contrast super-solution convolutional netweork (MCSR-CNN) method [34] as the deep-learning-based representative. These two methods were selected because they are both classic in each category, described in detail in the original papers, and can be accurately implemented. According to the results shown in Figs. 9 and 10, our two progressive model produced results superior to the SSIP and MCSR-CNN results, with less pixel-wise differences from the ground truth. Quantitative comparisons based on SSIM, PSNR, and IFC scores are shown in Table I in the supplementary material.
F. Reader Study Results
To evaluate the clinical effectiveness of our proposed method, three experienced medical doctors (3, 5, and 17 years of experience) were invited to conduct a double-blinded reader study. Totally 10 images from the IXI dataset and another 10 images from the NAMIC dataset were randomly selected for evaluation. Each selected image was processed by 5 different MCSR algorithms (SSIP, MCSR-CNN, NON-PRO, U-PRO, and C-PRO). All results were rated using the five-point scale. A score of 1 refers to a non-diagnostic image while a score of 5 means an excellent diagnostic image quality. The experts’ opinions are listed in Table IV. It can be found that our C-PRO results achieved the highest average scores among all the methods on both IXI and NAMIC datasets.
TABLE IV.
Double blind reader study comparing our methods with the other state-of-the-art MCSR methods (Mean±95%CI).
| SSIP | MCSR-CNN | NON-PRO | U-PRO | C-PRO | |
|---|---|---|---|---|---|
| IXI dataset | 2.47 ± 0.72 | 3.83 ± 0.75 | 3.90 ± 0.74 | 3.90 ± 0.74 | 4.03 ± 0.54 |
| NAMIC dataset | 1.77 ± 0.55 | 3.63 ± 0.58 | 3.23 ± 0.55 | 4.00 ± 0.73 | 4.07 ± 0.59 |
V. Discussions
In this study, we have jointly used the adversarial loss, MSE loss, perceptual loss, and textual matching loss in the objective function. Only using the adversarial loss, SSIM, PSNR and IFC scores are 0.823, 33.722 and 4.653 with 95% confidence interval (CI) of 0.003, 0.150 and 0.055. After the perceptual loss is added, SSIM, PSNR and IFC scores are 0.955, 36.943 and 4.927 with 95% CI of 0.003, 0.152 and 0.051. When all the four loss terms are included, the highest SSIM, PSNR and IFC scores are obtained (0.976, 38.513 and 5.058 with 95% CI of 0.003, 0.151 and 0.047). Since the statistical significance exists when comparing the results associated with different objective function, it suggests that all four loss terms contribute to the improvement of MCSR image quality. We also provide an example in the supplemental material (supplementary Fig. 2).
Inspired by the success of the perceptual loss that extracts features from a high-level feature space such as for image processing and reconstruction, we tend to investigate whether a combination of multi-contrast information in a high-level feature space can bring about results better than that based on the information combined in the low-level space. To achieve this, we conducted four ablation studies. According to the ablation results shown in Figs. 3, 5 and Table I, the use of only PD weighted HR images for image synthesis cannot generate good T2 weighted images, which indicates that PD weighted HR images cannot provide enough information or image priors for the neural network to reconstruct a T2 weighted image of high quality. Compared with the SISR method, MCSR methods show superior results, suggesting that multi-contrast images can provide much more image priors than single-contrast images for super-resolution imaging.
When comparing results of the third ablation study to that of the fourth study, the results from the fourth study slightly outperform that from the third one. With respect to different multi-contrast information combinations, the resultant SR imaging results indicate that multi-contrast image information combined in a high-level feature space can bring about better MCSR results than a low-level image space combination. These results may be appreciated from three aspects. First, adding such a reference feature extraction network splits the feature extraction process of two-contrast images, which facilities the neural network to flexibly extract features based on each contrast modalitys unique characteristics. Second, more parameters are used in the high-level combination strategy, which indicates that the neural network may have a stronger ability to extract more multi-contrast features for the SR imaging. Third, the high-level combination model only transfers features of T2 weighted images through skip connections to the decoder. Such a design enhances the contribution of T2 weighted features in the image restoration process happened in the decoder, and makes sure that the SR images are restored with more T2 characteristics.
To obtain good SR results with high up-sampling factors, we propose a two-level progressive network to progressively achieve MCSR level-/stage-wise. Compared with 4-fold MCSR results obtained from a one-level nonprogressive network (NON-PRO), the proposed two-level progressive network (U-PRO and C-PRO) shows better results. According to the image quality scores from three readers in Table IV, the progressive model produced 4-fold up-sampling MCSR results better than that from the non-progressive model. This can be explained at least in part by the fact that the progressive models are more complicated and have more parameters than the non-progressive model. When only comparing the results from the progressive models, the C-PRO results are better than the U-PRo results. Such an improvement of the C-PRO model attributes to the strong restriction on the model parameters. The parameters in the generator of the C-PRO model are strictly constrained during the training process guided by the objective function. At each level, the encoder-decoder network is trained to produce 2-fold up-sampling SR results. Compared with the U-PRO model that has a loosely constrained training process (only making sure that the final output is close to the ground truth, without any constraint on intermediate results), such a strong constriction for the C-PRO model can boost the optimization process and ensure parameters more reasonably adapted to generate good results.
To compare our results with state-of-the-art methods, we implemented two representative algorithms: SSIP representing model-based methods and MCSR-CNN standing for deep-learning methods, and tested them on the same dataset. According to the reader study results in Table IV, our U-PRO and C-PRO results outperformed these two competing methods, indicating a translational potential of our approach. In the future, we will optimize our method with a large dataset for clinical translation.
Our progressive model can be extended to perform larger factor up-sampling MCSR tasks. For example, our current two-level progressive model can be extended into a three-level model for 8-fold up-sampling MCSR. We believe that for 8-fold resolution improvement, more contrast mechanisms may be needed. For example, we may need to couple CT and MRI images together [48]. We have not implemented such an 8-fold MCSR because the limitation of the dataset. Also, the size of original HR images used in this study is 256×256, with 8-fold down-sampling the obtained LR images would be too blurry.
VI. Conclusion
In this paper, we have proposed a one-level non-progressive neural network for low factor up-sampling (such as 2×) and a two-level progressive neural network for large factor up-sampling (such as 4×). To achieve better results, multiple losses have been combined in a composite objective function. Our experimental results have demonstrated that MCSR results with high image quality can be generated when multi-contrast information is combined in a high-level feature space. The proposed progressive network could be extended for MCSR results with an even larger up-sampling factor if more different contrast images are available.
Supplementary Material
Acknowledgments
This work was partially support by NIH/NCI under award numbers R01CA233888, R01CA237267, R01CA194578, R37CA230451, and UGCA189824, and NIH/NIBIB under award number R01EB026646.
VII. Appendix
TABLE V.
List of all the acronyms in this paper
| Acronym | Full name |
|---|---|
| MRI | Magnetic Resonance Imaging |
| PD | Proton Density |
| SR | Super-Resolution |
| LR | Low-Resolution |
| HR | High-Resolution |
| MCSR | Multi-Contrast Super-Resolution |
| SISR | Single-Image Super-Resolution |
| WGAN-GP | Wasserstein Generative Adversarial Network with Gradient Penalty |
| MSE | Mean-Squared Error |
| SSIM | Structrual Similarity |
| PSNR | Peak Signal-to-Noise Ratio |
| IFC | Information Fidelity Criterion |
| SSIP | Self-Similarity and Image Prior method from Ref [47] |
| MCSR-CNN | Multi-Contrast Super-Resolution method using Convolutional Neural Networks from Ref [34] |
| NON-PRO | One-level Non-progressive Network |
| U-PRO | Unconstrained Two-level Progressive Network |
| C-PRO | Contrained Two-level Progressive Network |
Contributor Information
Qing Lyu, Department of Biomedical Engineering, Rensselaer Polytechnic Institute, Troy, NY, 12180, USA.
Hongming Shan, Department of Biomedical Engineering, Rensselaer Polytechnic Institute, Troy, NY, 12180, USA.
Cole Steber, Department of Radiation Oncology, Wake Forest School of Medicine, Winston-Salem, NC, 27101, USA.
Corbin Helis, Department of Radiation Oncology, Wake Forest School of Medicine, Winston-Salem, NC, 27101, USA.
Christopher T. Whitlow, Department of Radiology, Department of Biomedical Engineering, and Department of Biostatistics and Data Science, Wake Forest School of Medicine, Winston-Salem, NC, 27157, USA
Michael Chan, Department of Radiation Oncology, Wake Forest School of Medicine, Winston-Salem, NC, 27101, USA.
Ge Wang, Department of Biomedical Engineering, Rensselaer Polytechnic Institute, Troy, NY, 12180, USA.
REFERENCES
- [1].Plenge E, Poot DH, Bernsen M, Kotek G, Houston G, Wielopolski P, et al. , “Super-resolution methods in MRI: Can they improve the trade-off between resolution, signal-to-noise ratio, and acquisition time?” Magnetic resonance in medicine, vol. 68, no. 6, pp. 1983–1993, 2012. [DOI] [PubMed] [Google Scholar]
- [2].Van Reeth E, Tham IW, Tan CH, and Poh CL, “Super-resolution in magnetic resonance imaging: A review,” Concepts in Magnetic Resonance Part A, vol. 40, no. 6, pp. 306–325, 2012. [Google Scholar]
- [3].Park SC, Park MK, and Kang MG, “Super-resolution image reconstruction: a technical overview,” IEEE signal processing magazine, vol. 20, no. 3, pp. 21–36, 2003. [Google Scholar]
- [4].Hardie R, “A fast image super-resolution algorithm using an adaptive Wiener filter,” IEEE Transactions on Image Processing, vol. 16, no. 12, pp. 2953–2964, 2007. [DOI] [PubMed] [Google Scholar]
- [5].Manjón JV, Coupé P, Buades A, Fonov V, Collins DL, and Robles M, “Non-local MRI upsampling,” Medical image analysis, vol. 14, no. 6, pp. 784–792, 2010. [DOI] [PubMed] [Google Scholar]
- [6].Yang J, Wright J, Huang TS, and Ma Y, “Image super-resolution via sparse representation,” IEEE transactions on image processing, vol. 19, no. 11, pp. 2861–2873, 2010. [DOI] [PubMed] [Google Scholar]
- [7].Zeyde R, Elad M, and Protter M, “On single image scale-up using sparse-representations,” in International conference on curves and surfaces Springer, 2010, pp. 711–730. [Google Scholar]
- [8].Timofte R, De Smet V, and Van Gool L, “A+: Adjusted anchored neighborhood regression for fast super-resolution,” in Asian conference on computer vision Springer, 2014, pp. 111–126. [Google Scholar]
- [9].Dong C, Loy CC, He K, and Tang X, “Image super-resolution using deep convolutional networks,” IEEE transactions on pattern analysis and machine intelligence, vol. 38, no. 2, pp. 295–307, 2015. [DOI] [PubMed] [Google Scholar]
- [10].Kim J, Kwon Lee J, and Mu Lee K, “Accurate image super-resolution using very deep convolutional networks,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 1646–1654. [Google Scholar]
- [11].Ahn N, Kang B, and Sohn K-A, “Fast, accurate, and lightweight super-resolution with cascading residual network,” in Proceedings of the European Conference on Computer Vision (ECCV), 2018, pp. 252–268. [Google Scholar]
- [12].Mao X, Shen C, and Yang Y-B, “Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections,” in Advances in neural information processing systems, 2016, pp. 2802–2810. [Google Scholar]
- [13].Kim J, Kwon Lee J, and Mu Lee K, “Deeply-recursive convolutional network for image super-resolution,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 1637–1645. [Google Scholar]
- [14].Tai Y, Yang J, and Liu X, “Image super-resolution via deep recursive residual network,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 3147–3155. [Google Scholar]
- [15].Zhang Y, Tian Y, Kong Y, Zhong B, and Fu Y, “Residual dense network for image super-resolution,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 2472–2481. [Google Scholar]
- [16].Haris M, Shakhnarovich G, and Ukita N, “Deep back-projection networks for super-resolution,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 1664–1673. [Google Scholar]
- [17].Choi J-S and Kim M, “A deep convolutional neural network with selection units for super-resolution,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, 2017, pp. 154–160. [Google Scholar]
- [18].Zhang Y, Li K, Li K, Wang L, Zhong B, and Fu Y, “Image super-resolution using very deep residual channel attention networks,” in Proceedings of the European Conference on Computer Vision, 2018, pp. 286–301. [Google Scholar]
- [19].Wang Z, Liu D, Yang J, Han W, and Huang T, “Deep networks for image super-resolution with sparse prior,” in Proceedings of the IEEE international conference on computer vision, 2015, pp. 370–378. [Google Scholar]
- [20].Lai W-S, Huang J-B, Ahuja N, and Yang M-H, “Deep Laplacian pyramid networks for fast and accurate super-resolution,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 624–632. [Google Scholar]
- [21].Sajjadi MS, Scholkopf B, and Hirsch M, “Enhancenet: Single image super-resolution through automated texture synthesis,” in Proceedings of the IEEE International Conference on Computer Vision, 2017, pp. 4491–4500. [Google Scholar]
- [22].Ledig C, Theis L, Huszár F, Caballero J, Cunningham A, Acosta A, et al. , “Photo-realistic single image super-resolution using a generative adversarial network,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 4681–4690. [Google Scholar]
- [23].Chaudhari AS, Fang Z, Kogan F, Wood J, Stevens KJ, Gibbons EK, Lee JH, Gold GE, and Hargreaves BA, “Super-resolution musculoskeletal MRI using deep learning,” Magnetic resonance in medicine, vol. 80, no. 5, pp. 2139–2154, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Chen Y, Xie Y, Zhou Z, Shi F, Christodoulou AG, and Li D, “Brain MRI super resolution using 3D deep densely connected neural networks,” in 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018) IEEE, 2018, pp. 739–742. [Google Scholar]
- [25].Liu C, Wu X, Yu X, Tang Y, Zhang J, and Zhou J, “Fusing multiscale information in convolution network for MR image super-resolution reconstruction,” Biomedical engineering online, vol. 17, no. 1, p. 114, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Lyu Q, Shan H, and Wang G, “MRI super-resolution with ensemble learning and complementary priors,” IEEE Transactions on Computational Imaging, pp. 1–1, 2020. [Google Scholar]
- [27].Rousseau F, Initiative ADN, et al. , “A non-local approach for image super-resolution using intermodality priors,” Medical image analysis, vol. 14, no. 4, pp. 594–605, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Jafari-Khouzani K, “MRI upsampling using feature-based nonlocal means approach,” IEEE transactions on medical imaging, vol. 33, no. 10, pp. 1969–1985, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Brudfors M, Balbastre Y, Nachev P, and Ashburner J, “MRI super-resolution using multi-channel total variation,” in Annual Conference on Medical Image Understanding and Analysis Springer, 2018, pp. 217–228. [Google Scholar]
- [30].Zheng H, Zeng K, Guo D, Ying J, Yang Y, Peng X, et al. , “Multi-contrast brain MRI image super-resolution with gradient-guided edge enhancement,” IEEE Access, vol. 6, pp. 57 856–57 867, 2018. [Google Scholar]
- [31].Gong E, Huang F, Ying K, Wu W, Wang S, and Yuan C, “Promise: Parallel-imaging and compressed-sensing reconstruction of multicontrast imaging using sharable information,” Magnetic resonance in medicine, vol. 73, no. 2, pp. 523–535, 2015. [DOI] [PubMed] [Google Scholar]
- [32].Song P, Weizman L, Mota JF, Eldar YC, and Rodrigues MR, “Coupled dictionary learning for multi-contrast MRI reconstruction,” IEEE Transactions on Medical Imaging, 2019. [DOI] [PubMed] [Google Scholar]
- [33].Lu X, Huang Z, and Yuan Y, “MR image super-resolution via manifold regularized sparse learning,” Neurocomputing, vol. 162, pp. 96–104, 2015. [Google Scholar]
- [34].Zeng K, Zheng H, Cai C, Yang Y, Zhang K, and Chen Z, “Simultaneous single-and multi-contrast super-resolution for brain MRI images based on a convolutional neural network,” Computers in biology and medicine, vol. 99, pp. 133–141, 2018. [DOI] [PubMed] [Google Scholar]
- [35].Gulrajani I, Ahmed F, Arjovsky M, Dumoulin V, and Courville AC, “Improved training of Wasserstein GANs,” in Advances in neural information processing systems, 2017, pp. 5767–5777. [Google Scholar]
- [36].Shan H, Zhang Y, Yang Q, Kruger U, Kalra MK, Sun L, et al. , “3-D convolutional encoder-decoder network for low-dose CT via transfer learning from a 2-D trained network,” IEEE transactions on medical imaging, vol. 37, no. 6, pp. 1522–1534, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Wang Z, Bovik AC, Sheikh HR, Simoncelli EP, et al. , “Image quality assessment: from error visibility to structural similarity,” IEEE transactions on image processing, vol. 13, no. 4, pp. 600–612, 2004. [DOI] [PubMed] [Google Scholar]
- [38].Dosovitskiy A and Brox T, “Generating images with perceptual similarity metrics based on deep networks,” in Advances in neural information processing systems, 2016, pp. 658–666. [Google Scholar]
- [39].Johnson J, Alahi A, and Fei-Fei L, “Perceptual losses for real-time style transfer and super-resolution,” in European conference on computer vision Springer, 2016, pp. 694–711. [Google Scholar]
- [40].Simonyan K and Zisserman A, “Very deep convolutional networks for large-scale image recognition,” arXiv preprint arXiv:1409.1556, 2014. [Google Scholar]
- [41].Gatys LA, Ecker AS, and Bethge M, “Image style transfer using convolutional neural networks,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 2414–2423. [Google Scholar]
- [42].Anwar S, Khan S, and Barnes N, “A deep journey into super-resolution: A survey,” CoRR, vol. abs/1904.07523, 2019. [Online]. Available: http://arxiv.org/abs/1904.07523 [Google Scholar]
- [43].Sheikh HR, Bovik AC, and De Veciana G, “An information fidelity criterion for image quality assessment using natural scene statistics,” IEEE Transactions on image processing, vol. 14, no. 12, pp. 2117–2128, 2005. [DOI] [PubMed] [Google Scholar]
- [44].IXI. [Online]. Available: {https://brain-development.org/ixi-dataset/} [Google Scholar]
- [45].NAMIC. [Online]. Available: {http://insight-journal.org/midas/collection/view/190} [Google Scholar]
- [46].Kingma DP and Ba J, “Adam: A method for stochastic optimization,” arXiv preprint arXiv:1412.6980, 2014. [Google Scholar]
- [47].Manjón JV, Coupé P, Buades A, Collins DL, and Robles M, “MRI superresolution using self-similarity and image priors,” Journal of Biomedical Imaging, vol. 2010, p. 17, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Wang G, Kalra M, Murugan V, Xi Y, Gjesteby L, Getzin M, et al. , “Vision 20/20: Simultaneous CT-MRI – Next chapter of multimodality imaging,” Medical physics, vol. 42, no. 10, pp. 5879–5889, 2015. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.