Abstract
Per- and Polyfluoroalkyl Substances (PFAS) are emerging contaminants of critical concern. As surfactants, PFAS tend to accumulate at air-water interfaces and may stay in the vadose zone for long times before contaminating groundwater. Yet not well understood, the extent of retention in the vadose zone has critical implications for risk management and remediation strategies. We present the first mathematical model that accounts for surfactant-induced flow and solid-phase and air-water interfacial adsorption. We apply the model to simulate PFOS (a PFAS compound of primary concern) transport in the vadose zone at a model fire-training area site impacted by Aqueous Film-Forming Foam (AFFF). Air-water interfacial adsorption is shown to have a significant impact—amplified by the low water content due to gravity drainage—total retardation factors range from 233 to 1355 for the sand and 146 to 792 for the soil used in the study. The simulations illustrate it can take several decades or longer for PFOS to reach groundwater. Counterintuitively, the lower water content in the sand—due to stronger drainage and weaker capillary retention—leads to retardation factors greater than for the soil. Also, most PFOS is adsorbed at air-water interfaces with only 1–2% in the aqueous phase. The implications include 1) fine-texture materials could have lower retardation factors than sand due to higher retained water content, 2) soil PFAS concentrations are likely to be orders of magnitude higher than those in groundwater at source zones. Both implications are consistent with recent field observations at hundreds of AFFF-impacted sites.
1. Introduction
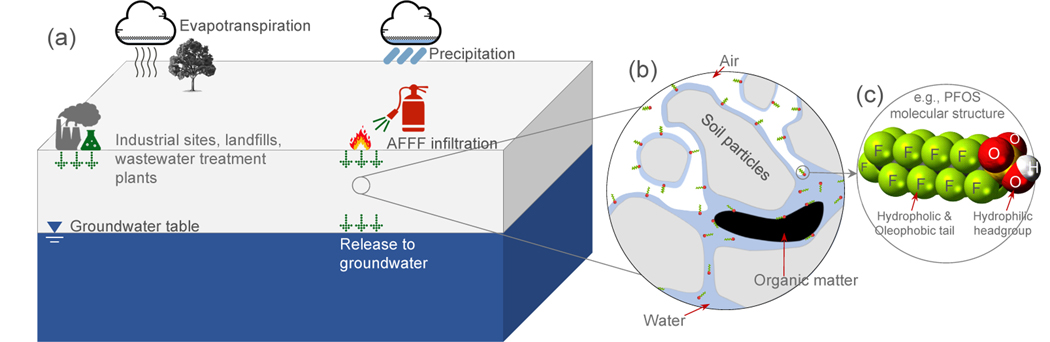
Per- and Polyfluoroalkyl Substances (PFAS)—a group of synthetic chemicals—have become emerging contaminants of critical concern. Since the late 1940s, PFAS have been used in a wide variety of products including non-stick coatings, textiles, paper products, and firefighting foams (Buck et al., 2011; Banks et al., 2013; Wang et al., 2017). Large-scale manufacturing and use of the PFAS compounds have resulted in their widespread presence in the environment. When released at the ground surface, PFAS can infiltrate into the shal low subsurface and transport through the vadose zone to contaminate groundwater (Fig. 1(a)). Many PFAS were created as surfactants—a property that distinguishes them from traditional contaminants—when released to the environment they tend to accumulate at air-water interfaces and may stay in the vadose zone for long periods of time (Fig. 1(b,c)). Except for PFAS precursors, the majority of PFAS are not known to degrade in the enviroment due to the strong carbon-fluorine bond (Wang et al., 2017; ITRC, 2018). While some progress on PFAS transport in groundwater has been made in the past decade, investigations in the vadose zone have only begun recently. A number of field studies have demonstrated that the vadose zone can serve as a source zone of PFAS (Filipovic et al., 2015; Xiao et al., 2015; Weber et al., 2017; Anderson et al., 2019; Dauchy et al., 2019; Høisæter et al., 2019). A major complexity of the vadose zone is the coexistence of air and water that form fluid-fluid interfaces in the soil materials. Additional complexity can be introduced when organic immiscible liquids (e.g., chlorinated solvents and hydrocarbon fuels) are present and form interfaces with air and water. The transport and fate processes of PFAS in the vadose zone in the presence of complex fluid-fluid interfaces are not well understood (SERDP, 2017). In particular, the time scale that PFAS may stay in the vadose zone due to fluid-fluid interfacial adsorption and the potential long-term release to groundwater are unknown.
Figure 1:
(a) Schematic of the sources of PFAS (AFFF-impacted fire training and fire response sites, industrial sites, landfills, and wastewater treatment plants) and the transport and migration in the subsurface. (b) A zoom-in cross-section of a configuration of soil grains, air, and water showing the distribution of PFAS in the vadose zone and the relevant transport processes (The figure is not to scale). (c) A PFAS molecular structure (PFOS is used as an example) showing a hydrophobic and oleophobic tail and a hydrophilic headgroup.
The impact of fluid-fluid interfacial adsorption on PFAS retention and transport in soil was examined initially by Brusseau (2018), who employed surface-tension data for PFAS including two of primary concern—perfluorooctanoic acid (PFOA) and perfluorooctane-sulfonic acid (PFOS)—and measured air-water interfacial areas along with a comprehensive retention model to conduct a theoretical assessment. Additional surface-tension-based theoretical analyses of PFAS retention have since been reported (Brusseau, 2019a, 2019b; Brusseau & Van Glubt, 2019; Costanza et al., 2019; Silva et al., 2019). Miscible-displacement laboratory experiments demonstrating that adsorption of PFAS at air-water and NAPL-water interfaces can be an important retention process in soil and sand materials have also been reported (Lyu et al., 2018; Brusseau, Khan, et al., 2019). A number of factors that can influence the magnitude of air-water interfacial adsorption were investigated in these studies, including water saturation, solution composition, different types of PFAS and their concentrations, and different porous media materials. To date, all of these theoretical and experimental studies employed or assumed steady-state flow conditions. The impact of transient variably saturated flow on the transport and retention of PFAS has not been considered. Yet, air-water interfaces can rapidly evolve under transient variably saturated flow driven by infiltration and evapotranspiration fluxes, which can then strongly influence the transport and retention of PFAS in the vadose zone. Conversely—as surfactants—PFAS present in solution can modify surface tension and hence impact flow. These interactive processes lead to a system where variably saturated flow and PFAS transport and adsorption are fully coupled. Mathematical formulations and computational frameworks that represent these coupled flow and transport processes are critical for improved understanding of PFAS transport and migration in the vadose zone.
Mathematical models for the transport of surfactants have been applied in the petroleum industry since the 1970s (Pope et al., 1978; UTCHEM, 2000). The application was driven by the design and evaluation of surfactant flooding technologies for enhanced oil recovery, which often requires solutions to a highly nonlinear system of three-phase flow coupled with complex phase behaviors of surfactant-oil-aqueous mixtures. Later on, surfactant-based technologies were introduced to enhance remediation of nonaqueous phase liquid (NAPLs) contaminants by solubilization or mobilization, i.e., surfactant enhanced aquifer remediation (SEAR) (e.g., Fountain et al., 1991; Pennell et al., 1993). Subsequently, mathematical models were developed in the environmental literature to quantify the impact of the physical and chemical processes in SEAR (Abriola et al., 1993; Delshad et al., 1996; Ji & Brusseau, 1998). Abriola et al. (1993) assumed immobile NAPLs—trapped in otherwise water-saturated pores—that dissolve into water at the NAPL-water interfaces. The transport of organic and surfactant components in a stationary configuration of NAPL and water fluid phases was simulated. Delshad et al. (1996) adopted from the surfactant-enhanced oil recovery literature the full compositional formulations with inclusion of surfactant-oil-aqueous phase behaviors. Concomitantly, models to quantify the effects of surfactants on unsaturated water flow and solute transport in the vadose zone were also developed (Smith & Gillham, 1994) by using a modified soil characteristic curve scaled by the change of surface tension based on Leverett et al. (1941). The formulation was shown to compare well with sand-packed column and flow cell experiments (Smith & Gillham, 1999; Henry et al., 2002; Henry & Smith, 2003; Karagunduz et al., 2015). A comprehensive review on the experimental data and numerical modeling of surfactant-induced flow in the vadose zone was provided by Henry and Smith (2003). The prior modeling studies incorporated solid-phase adsorption for the transport of surfactants, but not fluid-fluid interfacial adsorption. More recently, Costanza-Robinson and Henry (2017) modified HYDRUS-1D (Simunek et al., 2008) to simulate surfactant-induced flow to evaluate the aqueous air-water Interfacial Partitioning Tracer Test (IPTT) method. Both solid-phase and air-water interfacial adsorption were included. The adsorption coefficients—though varying among simulations—were kept constant during each simulation, and thus have underestimated the nonlinear responses of the adsorption processes under transient flow. In general, the above cited references have focused more on the impact of surfactants on fluid flow with less emphasis on the transport processes of surfactants themselves. Thus, to accurately simulate PFAS transport, there is a critical need to develop a flow and transport model that explicitly incorporates the full range of interfacial adsorption processes under transient conditions.
Compared to general surfactants, mathematical modeling studies of PFAS transport in the vadose zone are very limited. Shin et al. (2011, 2012) applied the US EPA Pesticide Root Zone Model Version 3 (PRZM-3) (EPA, 2001) to simulate PFOA transport in the vadose zone. Air-water interfacial adsorption was not considered in their model. Recently, a one-dimensional (1D) solute-transport model incorporating rate-limited solid-phase adsorption and air-water interfacial adsorption was applied to simulate the breakthrough curves of PFOS and PFOA in soil/sand-packed column experiments under unsaturated conditions (Brusseau, 2020). These simulations focused on the transport of PFAS at steady-state unsaturated flow with a uniform saturation—no transient effects of water flow were simulated. To the best of our knowledge, no models for PFAS transport to date have accounted for both transient variably saturated flow and solid-phase and fluid-fluid interfacial adsorption processes.
Here, we develop the first mathematical model for the transport of PFAS under transient variably saturated flow in the vadose zone. Our formulation explicitly accounts for the change of surface tension by dissolved PFAS as well as PFAS adsorption at both air-water interfaces and solid grain surfaces. The variably saturated flow is modeled by the Richards’ equation. An advection-dispersion equation coupled with process-specific adsorption terms is formulated to model the transport of PFAS. The air-water interfacial area is parameterized as a function of water saturation based on experimental measurements. The coupled flow and transport processes are solved in a fully implicit computational framework—water pressure head and the aqueous concentration of PFAS are solved simultaneously using Newton-Raphson iterations. We apply the new model to simulate the synthetic release of PFAS to a vadose zone resulting from the use of Aqueous Film-Forming Foam (AFFF) for fire-training practices over a period of 40 years. PFOS is used as a representative PFAS because of its dominance in AFFF solutions (Houtz et al., 2013; Høisæter et al., 2019). The simulations consider two PFOS concentrations (100 mg/L vs. 1000 mg/L), two types of porous media (sand vs. soil), and two climatic conditions (semi-arid vs. humid). Rainfall and evapotranspiration datasets from Arizona and New Jersey are used as examples of semi-arid and humid regions, respectively. Detailed data of hydraulic properties and air-water interfacial area for the sand and soil were measured by column experiments. Solid-phase adsorption, surface tension, and the air-water interfacial adsorption coefficients are all obtained from laboratory experiments.
The mathematical formulations of variably saturated flow and the transport processes of PFAS are presented in section 2. This is followed by a description of the numerical methods in section 3 to solve the mathematical formulations. Detailed data and parameters employed are presented in section 4. We then present the simulation results in section 5, which are followed by discussions (section 6) on the key factors that control the transport and retention of PFAS in the vadose zone. We close with concluding remarks in section 7.
2. Mathematical models
We formulate a mathematical model for transient variably saturated flow coupled with the transport processes of PFAS in the vadose zone in the following two subsections (sections 2.1 and 2.2).
2.1. Variably saturated flow
We consider 1D variably saturated ow in the vertical dimension of the vadose zone, which may be described by the mixed form of the Richards’ equation as (Richards, 1931; Pinder & Celia, 2006)
| (1) |
where is the volumetric water content is the porosity of the porous medium , and Sw is the water saturation . K is the unsaturated hydraulic conductivity (cm/s). h is the water pressure head (cm). z is the spatial coordinate (assuming positive downward) (cm). t is time (s). Here we assume that the capillary pressure head (−h) scales with surface tension σ following Leverett et al. (1941) and Smith and Gillham (1994) such that
| (2) |
where σ0 and σ are surface tensions of water without and with dissolved PFAS (dyn/cm). h0 is the water pressure head corresponding to σ0. For simplicity, the contact angle is assumed unchanged with dissolved PFAS. It is noted that our formulation can be extended to include a variable contact angle, for example, using the scalings summarized in Henry and Smith (2003).
θ is often approximated as an empirical function of h0 (based on laboratory measurements done using water without dissolved PFAS) and referred to as soil water characteristics. Here we use the functional form proposed by van Genuchten (Van Genuchten, 1980). After substituting , we obtain Eq. (3)
| (3) |
where α (1/cm) and n (−) are fitting parameters. and θs are the residual and saturated water content (−), respectively. Because surface tension σ is a function of the PFAS aqueous concentration, Eqs. (1) and (3) imply that the variably saturated flow and PFAS transport are fully coupled.
The unsaturated hydraulic conductivity K can also be approximated as an empirical function (Mualem, 1976; Van Genuchten, 1980) of h as
| (4) |
where Ks is the saturated conductivity (cm/s). is the effective water saturation (−).
2.2. Transport of PFAS
Transport of a PFAS compound in the vertical dimension of the vadose zone may be described by an advection-dispersion equation with adsorption terms (Kim et al., 1997; Brusseau, Yan, et al., 2019)
| (5) |
where C is the aqueous concentration (μmol/cm3). Caw is the adsorbed concentration at air-water interfaces (μmol/cm3). Cs is the solid-phase adsorbed concentration (μmol/g). ρb is the bulk density of the porous medium (g/cm3). v = q/θ is the interstitial pore water velocity (cm/s), where q = −K (∂h/∂z − 1) is the Darcy flux that will be computed from Eq. (1). Both v and q are positive downward. D = αLv + τD0 is the dispersion coefficient (cm2/s), where αL is the longitudinal dispersivity (cm), is the tortuosity factor for the water phase (Millington & Quirk, 1961), D0 is the molecular diffusion coefficient in free water. We note that other partitioning processes may be relevant for some PFAS such as partitioning to the air phase and organic immiscible liquids (when present) (Brusseau, 2018). Here we focus on two processes—solid-phase and air-water interfacial adsorption, that are the primary processes of concern for PFOS and similar PFAS.
We first present formulations of equilibrium isotherms for Cs and Caw. The solid-phase adsorption Cs can be modeled by the nonlinear Freundlich isotherm as suggested by prior experimental measurements (Higgins & Luthy, 2006; Wei et al., 2017; Brusseau, Khan, et al., 2019; Brusseau, 2020)
| (6) |
where Kf and N are fitting parameters to experimental data.
The adsorption at air-water interfaces Caw has the following form
| (7) |
where Aaw is the air-water interfacial area (cm2/cm3). Γ = KawC is the surface excess at the air-water interface (μmol/cm2). Kaw is the air-water interfacial adsorption coefficient (cm3/cm2). Air-water interfacial area comprises two general types—capillary interfaces associated with menisci between bulk air and water, and film-associated interfaces associated with wetting films surrounding grain surfaces. The combination of the two is considered the total air-water interfacial area, which is employed in the present study
The air-water interfacial area depends on capillary pressure head, water saturation, and the imbibition and drainage history. Here, we approximate Aaw as a function of water saturation Sw using equation (8), which is fitted to air-water interfacial area data measured in column experiments.
| (8) |
where x2, x1, and x0 are fitting parameters. The parameter values for the sand and soil used in the present work are reported in section 4. Hysteresis effects are not considered. The functional relationship between air-water interfacial area and water saturation will in general depend on the drainage and imbibition history (Hassanizadeh & Gray, 1993; Reeves & Celia, 1996; Schaefer et al., 2000). Quantifying the impact of hysteresis effects will require air-water interfacial area measurements for different drainage and imbibition processes.
The air-water interfacial adsorption coefficient Kaw can be calculated following Eq. (9) by relating the surface excess Γ to the aqueous concentration C using the Gibbs adsorption equation with the ideal dilute solution assumption (below the critical micelle concentration) (Chang & Franses, 1995; Adamson & Gast, 1997; Brusseau, 2018).
| (9) |
Surface tension σ (dyn/cm) is a function of the aqueous concentration C, which can be modeled by the Szyszkowski equation (Chang & Franses, 1995; Adamson & Gast, 1997)
| (10) |
where a (μmol/cm3) and b (−) are fitting parameters to experimental data. Substituting Eq. (10) into Eq. (9) yields
| (11) |
where R = 8.314 is the universal gas constant (J/K/mol) and T is temperature (K). Eq. (11) shows that Kaw monotonically increases as C decreases and asymptotically approaches a maximum value.
Substitutting Eqs. (6–7) to Eq. (5), we obtain an equation for the transport of a PFAS compound in the vadose zone with equilibrium adsorption processes.
| (12) |
where Aaw and Kaw follow Eqs. (8) and (11), respectively.
If the solid-phase and air-water interfacial adsorption are rate-limited, kinetic adsorption models need to be applied. Here we present an example formulation based on the simple two-domain sorption kinetics model (e.g., Cameron & Klute, 1977; Brusseau, 1995). More advanced models such as continuous-distribution, multirate models that incorporate a continuous distribution of domains and associated sorption/desorption rate coe_cient are also available in the literature (e.g., Chen & Wagenet, 1995, 1997; Culver et al., 1997; Li & Brusseau, 2000). In the two-domain model, the solid-phase adsorption Cs = Cs,1 + Cs,2, where Cs,1 is the adsorbed concentration (μmol/g) in the “instantaneous” sorption domain and Cs,2 is the adsorbed concentration (μmol/g) in the kinetic sorption domain. Cs,1 and Cs,2 are governed by Eqs. (13) and (14), respectively.
| (13) |
| (14) |
where Fs is the fraction of sorbent for which sorption is instantaneous (−). αs is the first-order rate constant for kinetic solid-phase adsorption (1/s). For air-water interfacial adsorption of PFAS, diffusion from the bulk to the air-water interface has been considered as the primary controlling factor for kinetic adsorption (e.g., Sekine et al., 2004; Valkovska et al., 2004; Day et al., 2007; Loppinet & Monteux, 2016; Miller et al., 2017; Brusseau, 2020).
In general, diffusive mass transfer needs to be included to model the air-water interfacial kinetic adsorption. Here we approximate using the two-domain approach by assuming that the sorption at a fraction of the air-water interfaces is instantaneous, while is kinetic (i.e., limited by diffusive mass transfer) at the rest of the air-water interfaces. Thus, the air-water interfacial adsorption Caw = Caw,1+Caw,2, where Caw,1 is the adsorbed concentration at the air-water interfaces wherein the adsorption is instantaneously (μmol/cm3) and Caw,2 is the adsorbed concentration at the air-water interfaces wherein adsorption is limited by diffusive mass transfer (μmol/cm3). Under this assumption, Caw,1 and Caw,2 have the following forms
| (15) |
| (16) |
where Faw is the fraction of air-water interfaces for which sorption is instantaneous (−). Substituting equations (13–16) to equation (5) gives the transport equation for a PFAS compound with kinetic adsorption processes
| (17) |
Eq. (17) needs to be coupled with Eqs. (14) and (16) to solve for the kinetic adsorbed concentrations Cs,2 and Caw,2. In the rest of the study, we only present simulations of PFAS transport using the equilibrium adsorption models, i.e., Eq. (12).
3. Numerical methods
We apply a fully implicit numerical framework to solve the mathematical formulations in section 2, i.e., Eqs. (1) and (12), subject to initial and boundary conditions. The Richards’ equation (1) is solved following the numerical scheme of Celia et al. (1990). Cell-centered finite difference and backward Euler approximations are used for the spatial and temporal discretizations. The nonlinear system of equations resulting from the discretization are solved using a Newton-Raphson iteration scheme (quadratic convergence) as opposed to the Picard iteration (linear convergence) in Celia et al. (1990). For the advection-dispersion equation (12), a first-order upwind scheme is used for the advection term and a central difference scheme is used for the diffusion term. The adsorption terms are all treated implicitly in the temporal discretization. A tolerance for the Newton updates of both Eqs. (1) and (12) is used as a criterion to determine convergence of the nonlinear system of equations. Our numerical implementation utilizes the gridding and automatic differentiation utilities of the Matlab Reservoir Simulation Toolbox (MRST) (Lie, 2019).
Flux and pressure head boundary conditions are both implemented for the top and bottom boundaries of the domain. The top boundary also considers surface evaporation and ponding conditions. Similar to the implementation in HYDRUS-1D, when the pressure head of the top numerical cell reaches below a critical value (hcr) (i.e., under very dry conditions), the flux condition at the top boundary switches to a fixed pressure head condition (htop = hcr). Ponding conditions are used when rainfall rate exceeds the rate of infiltration. When ponding occurs, the boundary condition at the top also switches from flux to pressure head. The pressure head is set to the ponding depth, which is determined by tracking the rates of rainfall and infiltration. For the transport equation, a flux condition (i.e., inward flux of PFAS) and a zero gradient of the aqueous PFAS concentration are used at the top and bottom boundaries, respectively. To verify our implementation of the Richards’ and advection-dispersion equations, we have compared our code with HYDRUS-1D for a simulation of water infiltration and solute transport (see the supporting information (SI)). Excellent agreement between the results from the two codes is observed (Fig. S1 in the SI).
4. Data and parameters
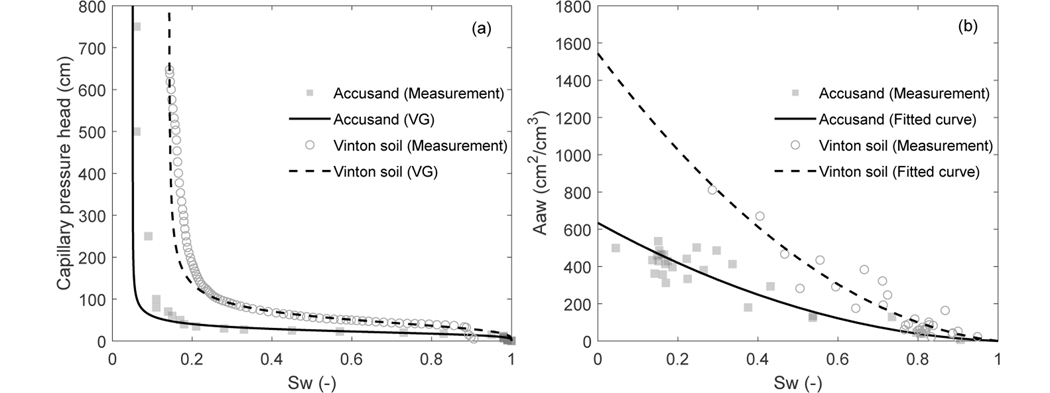
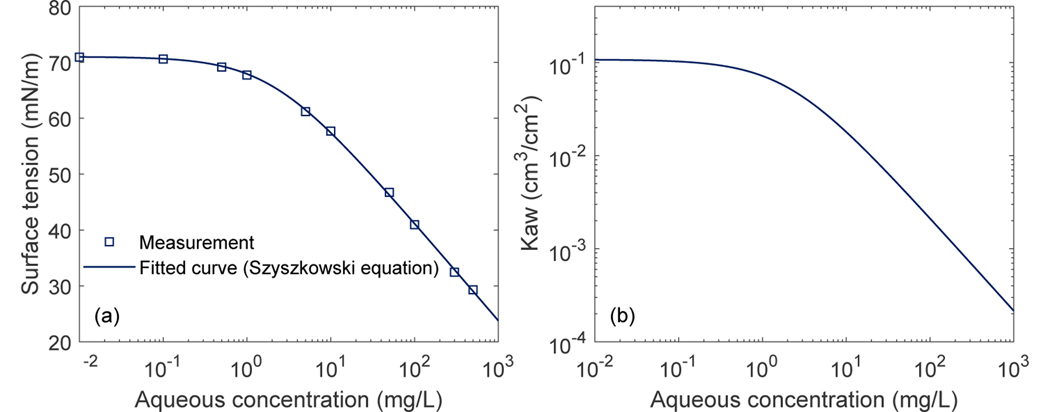
Parameters for two types of porous media (Accusand and Vinton soil) measured by prior experiments are used in the present work. The Accusand is a commercially available natural quartz sand (UNIMIN Corp.). It has a median grain diameter of 0.35mm and a total organic carbon content of 0.04%, Fe, Mn, and Al oxide contents of 14, 2.5, and 12 μg/g, respectively. Its clay content is negligible. The Vinton soil was collected locally in Tucson, Arizona. It consists of 54% silica, 36% feldspar, 3% amphibole, 4.7% clay minerals, and 0.1% organic carbon content. Parameters for the soil water characteristics (Fig. 2(a)) and relative permeability for the Accusand and Vinton soil were measured by Brusseau and colleagues (unpublished). The air-water interfacial area (Fig. 2(b)) was measured using the aqueous-IPTT method and a mass balance (aqueous) surfactant-tracer method reported in Brusseau et al. (2007), Brusseau et al. (2015), and Araujo et al. (2015). The measurements from the aqueous-IPTT and mass balance (aqueous) surfactant-tracer method are in general lower than those measured by the gas-IPTT method, especially at lower water saturations, while higher than X-ray microtomography measurements wherein roughness-impacted film-associated air-water interfaces are not accounted for (Brusseau et al., 2007). Air-water interfacial area using aqueous-based methods has been shown to be more representative for transport processes in the aqueous phase (Lyu et al., 2018; Brusseau, Yan, et al., 2019; Brusseau, 2019a). Saturated conductivity for the Accusand and Vinton soil were measured by Brusseau and colleagues (unpublished) and from Bagour (2001), respectively. The surface tension data for PFOS solutions (Fig. 3(a)) was reported in Brusseau (2019b). σ0 is 71dyn/cm, a = 4.00 × 10−3 μmol/cm3, and b = 0.107. The air-water interfacial adsorption coefficient is computed via Eq. (11) based on the fitted Szyszkowski equation of the surface tension data. A constant temperature T = 293.15 K is used. The parameters for the Freundlich isotherm for the Accusand and Vinton soil were reported in Brusseau (2020) and Brusseau, Khan, et al. (2019), respectively. Note that Kf in Brusseau (2020) and Brusseau, Khan, et al. (2019) was for PFOS aqueous concentrations in mg/L and solid-phase adsorption concentration in mg/kg. Here we have converted to the Kf values for PFOS aqueous concentrations in μmol/cm3 and solid-phase adsorption in μmol/g. The molecular weight of PFOS is 500.13g/mol. The value for the longitudinal dispersivity αL is estimated using the equation αL = 0.83(log L)2.414 proposed by Xu and Eckstein (1995), where L the apparent length scale. Here we take L as the length of the computational domain. The aqueous diffusion coefficient D0 is obtained from measured values reported in Schaefer et al. (2019). The above parameters employed for the simulations in the present work are summarized in Table 1.
Figure 2:
Measurements and fitted curves for (a) soil water characteristics, and (b) air-water interfacial area as functions of water saturation for two porous media: Accusand and Vinton soil. The markers are measurements and the lines are fitted curves. The soil water characteristics are fitted using the van Genuchten model and the air-water interfacial area are fitted using second-degree polynomials. The parameters for these curves are presented in Table 1.
Figure 3:
(a) Measured surface tension as a function of the aqueous concentration of PFOS. The solid line is a fitted curve using the Szyszkowski equation. (b) The computed air-water interfacial adsorption coefficient (Kaw) as a function of the aqueous concentration of PFOS.
Table 1:
A summary of the parameters for the Accusand and the Vinton soil that are used in the simulations.
| Parameter | Accusand | Vinton soil | unit |
|---|---|---|---|
| Ks | 2.10 × 10−2 | 1.17 × 10−3 | (cm/s) |
| θs | 0.294 | 0.395 | (−) |
| θr | 0.015 | 0.056 | (−) |
| ϕ | 0.294 | 0.395 | (−) |
| ρb | 1.65 | 1:627 | (g/cm3) |
| α | 0.04479 | 0.02178 | (cm−1) |
| n | 4 | 0.71 | (−) |
| m | 0.75 | 3.451 | (−) |
| αL | 34.96 | 34.96 | (cm) |
| D0 | 5.4 × 10−6 | 5.4 × 10−6 | (cm2/s) |
| x2 | 548.54 | 1305 | (−) |
| x1 | −1182.5 | −2848.6 | (−) |
| x0 | 633.96 | 1543.6 | (−) |
| Kf | 0.055 | 0.381 | (−) |
| N | 0.85 | 0.81 | (−) |
We consider two climatic conditions (semi-arid vs. humid) to examine the impact of climate on PFAS transport in the vadose zone. Here, by “semi-arid” and “humid” we focus specifically on precipitation and evapotranspiration for the climatic conditions. The site of Walnut Gulch Kendall Grasslands (Scott, 2004) in Arizona, US is used to represent a semi-arid region, while the site of Silas Little (Clark, 2004) in New Jersey, US is used to represent a humid region. Precipitation and evapotranspiration data at a 30-min resolution for a period of 10 years (Jan 1, 2005 to December 31, 2014) were downloaded from the AmeriFlux database (URL: https://ameriflux.lbl.gov) for both sites. The average annual precipitation during the 10 years are 293 mm and 1066 mm for the two sites, respectively. The gaps (~ 10%) in the data are filled using 14-day moving-average values suggested by Scott (2010). For each site, the 10-year data are repeated three times to generate a 40-year dataset of precipitation and evaportranspiration (see Fig. S2 in the SI). For simplicity, we treat all precipitation as rainfall and do not distinguish between rain and snow in our simulations. In addition, we approximate the evapotranspiration data as potential evapotranspiration to determine the surface evaporation fluxes. This should be a reasonable approximation given that we do not model transpiration through plants—the surface evaporation flux should always be smaller than the measured evapotranspiration.
PFAS can be released from various types of sources including fire-training area (FTA) sites, fire response sites, industrial sites, landfills, and wastewater treatment plants (ITRC, 2018). The release from the use of AFFF at FTA sites is considered as an example source in the present work. The fire training is assumed to occur every 10 days and last for 40 years (Moody & Field, 1999, 2000). Specific information about the fire training conditions is obtained from a report by the Federal Aviation Administration (FAA, 2010) and from the literature. The report suggests two categories for the burn area, which have an average area of 385 m2 and 1318 m2, respectively. For each training session, we assume that 50 to 150 gallons (189.3 to 567.8 L) of diluted AFFF aqueous solutions are applied. The volume range is consistent with values reported in Dauchy et al. (2019) at a French FTA site (400 to 800L per training session). We note that even larger volumes (1200 to 3200L) of aqueous AFFF solutions were reported elsewhere (Moody & Field, 2000). Assuming all of the AFFF solutions infiltrate into the vadose zone, it gives a total infiltration of 0.0458cm per training session. We use PFOS as a representative PFAS and consider two limiting concentrations of 100 mg/L and 1000 mg/L. The range is consistent with concentrations reported in the literature. Høisæter et al. (2019) reported that 1:100 dilution of an AFFF concentrate leads to a PFOS concentration of 100 mg/L; PFOS is the dominant PFAS accounting for 88.7% of the total PFAS. Houtz et al. (2013) analyzed AFFF concentrates manufactured between 1984–2010 from various manufacturers; PFOS concentration was reported to range from 4.9–11.4 g/L. Assuming these AFFF concentrates are either 3% or 6%, it leads to a PFOS concentration from 147 mg/L to 684 mg/L after dilution. Each training session is assumed to last for two hours from 9 AM to 11 AM during that day.
5. Results
5.1. Problem setup
We consider a 1D domain along the vertical (z) axis. The length of the domain is 500 cm. z = 0 cm is at the land surface and z = 500 cm is at the bottom of the domain. The groundwater table is assumed fixed at z = 482 cm. For water flow, an atmospheric boundary condition is used at z = 0 cm, namely time-dependent flux is given by the rainfall and evaporation data. The flux condition switches to a pressure head condition under surface ponding or a very dry condition (see section 3). In our simulations, the critical pressure head (hcr) corresponds to an effective water saturation of 0.002. The bottom boundary condition at z = 500 cm is set to a fixed pressure head h = 18 cm based on the location of the water table. A zero gradient of the aqueous PFOS concentration is used at the bottom boundary for the transport equation. In the numerical discretization, a uniform grid size is used (Δx = 0.5 cm). The time step size is adaptive and constrained by the maximum number of iterations and the tolerance for the Newton-Raphson iterations. Because the rainfall and evapotranspiration data have a temporal resolution of 30 mins, we enforce multiple time steps to be used for each 30 mins, i.e., the maximum time step size is smaller than 30 mins. Our simulations have converged for Δx and Δt. For the nonlinear Newton-Raphson iterations, we use absolute tolerances of 5×10−4 cm for the pressure head, 1×10−3 for the water content θ, 1×10−4 μmol/cm3 for the aqueous concentration, and 0.1 cm2/cm3 for the air-water interfacial area, all of which have to be met for convergence at every time step. The simulations are conducted in a homogeneous vadose consisting of the Accusand and the Vinton soil introduced in section 4. For each porous medium, we conduct 8 simulations: semi-arid vs. humid climates, low (100mg/L) vs. high (1000mg/L) PFOS concentrations, and with vs. without air-water interfacial adsorption.
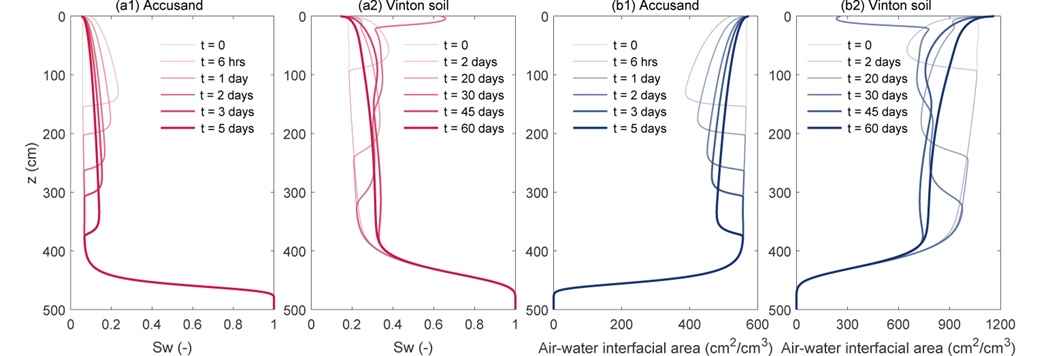
Before simulating the transport of PFOS, we first show some illustrative simulations for variably saturated water flow only to demonstrate the spatial distribution and temporal evolution of water saturation and air-water interfacial area. We select the largest rainfall event (60 mm of total rainfall within 4 hours) from the 10-year data at the semi-arid site and simulate a period of 5 days for the Accusand and a period of 60 days for the Vinton soil. The simulation starts at the same time when the largest rainfall event occurs; rainfall events following the largest one are also included if they are within the period of the simulation. The initial condition of the pressure head is set to the time-averaged pressure head over a period of 10 years computed in a separate simulation. The bottom boundary is set to a fixed pressure head at h = 18 cm. The temporal evolution of water saturation and air-water interfacial area are presented in Fig. 4.
Figure 4:
Illustrative results of the temporal evolution of water saturation and air-water interfacial area in space. (a1) and (a2) are water saturations, and (b1) and (b2) are air-water interfacial areas. (a1) and (b1) are for the Accusand, while (a2) and (b2) are for the Vinton soil.
The results show that it takes ~ 5 days for the wetting front to reach the groundwater table in the Accusand (Fig. 4(a)). For the majority of the time during the 5-day simulation, the water saturation stays below 0.25 (corresponding to a water content of 0.074) and the air-water interfacial area stays above 400 cm2/cm3 (Fig. 4(c)) despite the fact that the conditions represent the largest rainfall event. For Vinton, the wetting front propagation is considerably slower—it takes ~ 60 days for the wetting front to reach the groundwater table (Fig. 4(b)). For the majority of the time, the water saturation is below 0.35 (corresponding to a water content of 0.138) and the air-water interfacial area is above 700 cm2/cm3 (Fig. 4(d)). These distributions of water saturation (or water content) and air-water interfacial area have strong implications on the transport simulations in the following two sections, namely they amplify the impact of air-water interfacial adsorption on the retention of PFOS in the vadose zone.
5.2. Accusand
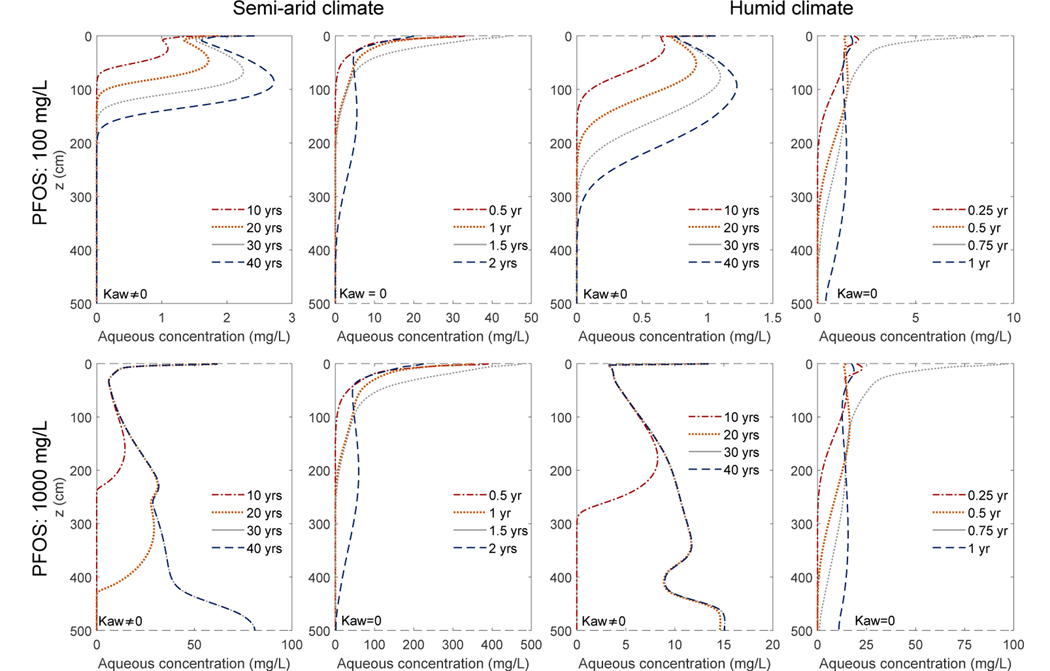
We present the simulations of PFOS release and migration in a homogeneous vadose 362 zone consisting of a sandy media represented by the Accusand. The vertical profiles of the 363 aqueous PFOS concentration for 10, 20, 30, 40 years are shown in Fig. 5. Comparing the 364 concentration profiles with and without interfacial adsorption (columns 1 & 3 vs. columns 2 & 4) shows that air-water interfacial adsorption greatly reduces the downward migration of PFOS. The overall time scale for PFOS to reach groundwater has increased by one to two orders of magnitude from 1 or 2 years to several decades or longer. The extent of retardation varies among different climates and PFOS concentrations. A higher PFOS concentration and a more humid climate both accelerate the migration of PFOS. Several factors are responsible for PFOS to move faster with a higher aqueous concentration. First, the air-water interfacial adsorption coefficient becomes smaller (see Fig. 3). Second, the solid-phase adsorption is nonlinear with an exponent N < 1 and thus the effective linear adsorption coefficient will decrease for a higher aqueous concentration. Under a more humid climate, it is expected that PFOS will migrate faster because: 1) more water is flowing through the vadose zone to groundwater with higher pore water velocities leading to more “leaching”, and 2) the water content is likely higher leading to less air-water interfacial adsorption. Among the four scenarios, PFOS propagates the slowest with the low PFOS concentration under a semi-arid climate—the front has only migrated down 2 meters after 40 years.
Figure 5:
Simulated temporal evolution of the PFOS aqueous concentration profiles over 40 years in a vadose zone beneath an FTA site consisting of the Accusand. The first and second rows are simulations with a PFOS concentration of 100 mg/L and 1000 mg/L, respectively. The first two columns are under a semi-arid climate. The third and fourth columns are under a humid climate. The first and third columns are with air-water interfacial adsorption, while the second and fourth columns are without air-water interfacial adsorption.
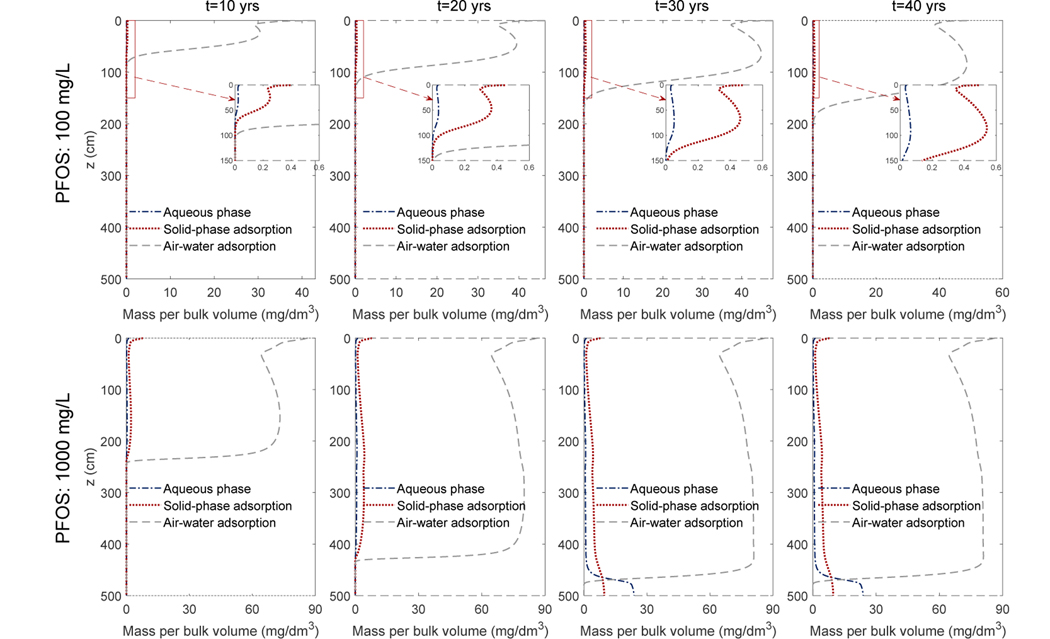
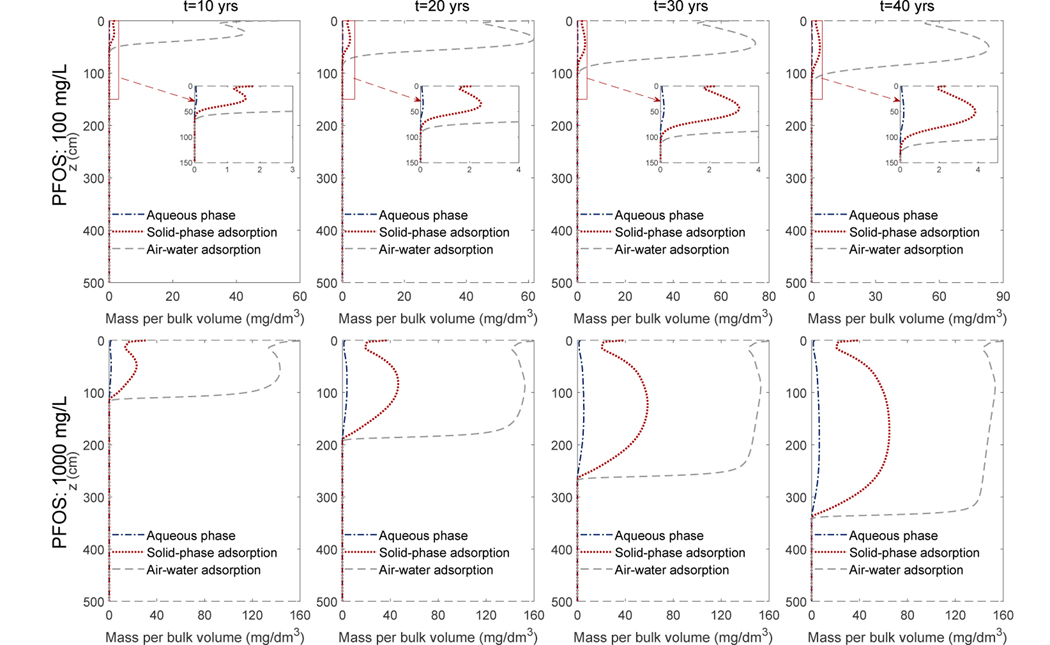
To show the distribution of PFOS in the different phases, we have computed the mass per bulk volume of porous medium for the aqueous phase, solid-phase adsorption, and the air-water interfacial adsorption. The results for the semi-arid climate scenarios are shown in Fig. 6 (the humid-climate scenarios have similar patterns and thus not shown here). The majority of the PFOS in the vadose zone is adsorbed at air-water interfaces. For example, at the maximum concentration of the plume, the air-water interfacial adsorption accounts for roughly 99% and 95% of the total PFOS in the low and high PFOS concentration scenarios, respectively. The fraction of the air-water interfacial adsorption is slightly less in the high PFOS concentration scenario because of a lower Kaw.
Figure 6:
The four columns are the profiles of the PFOS mass per bulk volume of the porous medium for the Accusand under the semi-arid climate scenario at 10, 20, 30, 40 years, respectively. The first and second rows are simulations with a PFOS concentration of 100 mg/L and 1000 mg/L, respectively.
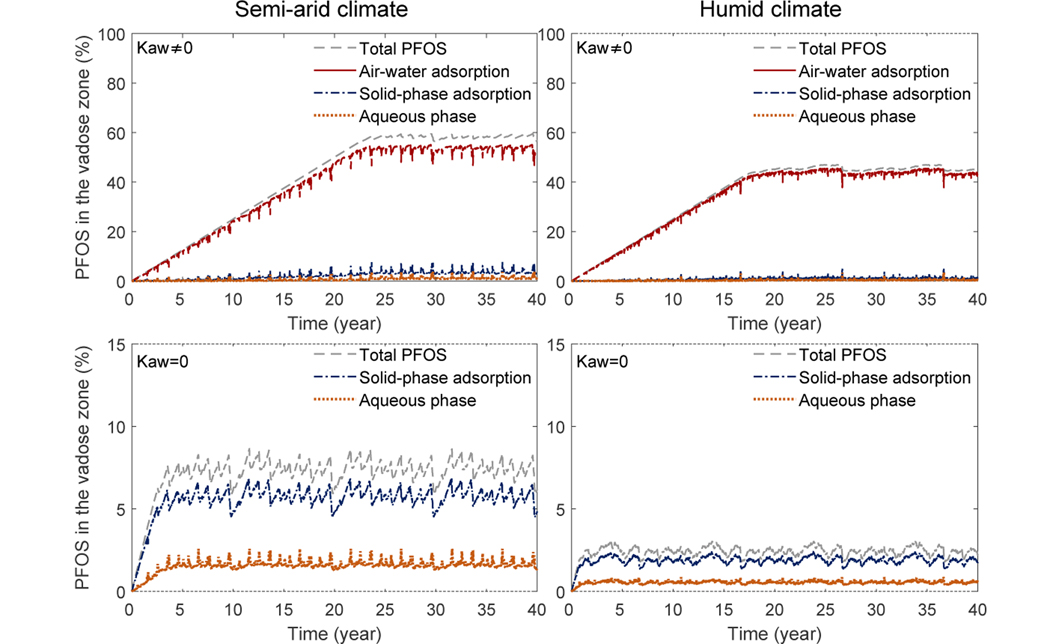
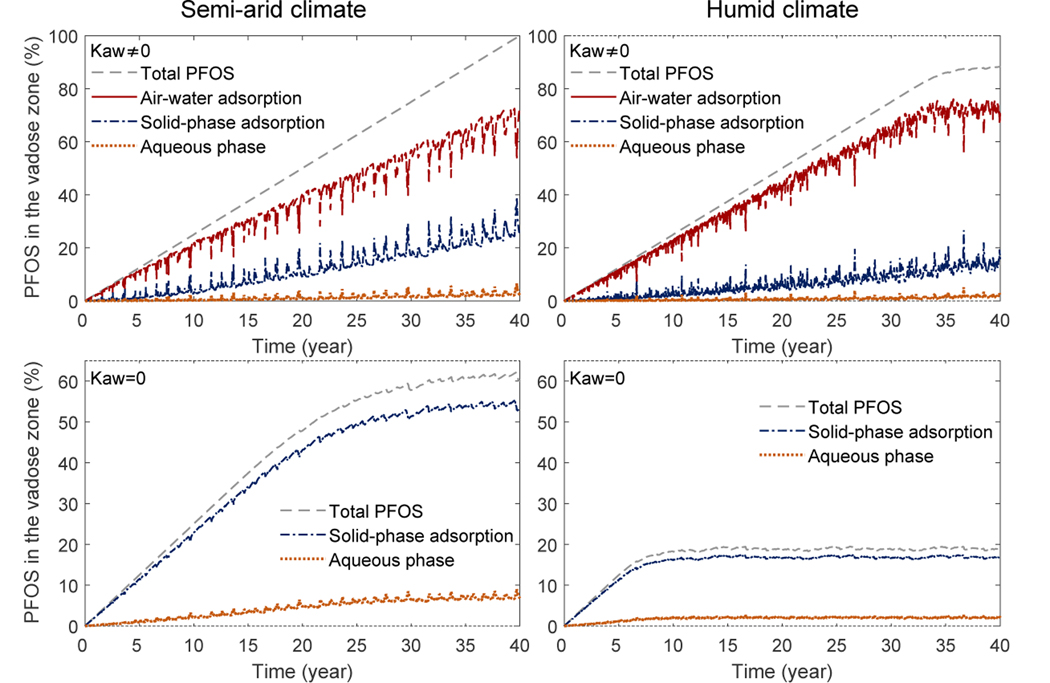
We have also computed the cumulative mass of PFOS in the vadose zone. As an example, we show the high PFOS concentration case in Fig. 7. The cumulative mass is normalized by the total mass of PFOS released over 40 years. Inspection of Fig. 7 gives the following four observations. 1) For all cases, the total cumulative mass of PFOS increases linearly before PFOS reaches groundwater. After PFOS reaches groundwater, the cumulative mass plateaus with slight variations driven by seasonal and interannual variations of rainfall. This implies that the amount of PFOS that goes into the vadose zone is comparable to the amount that is discharged to groundwater after this point. 2) The partitioning of mass between air-water interfacial adsorption, solid-phase adsorption, and aqueous phase varies over time, primarily driven by time-dependent rainfall events. When large infiltration occurs due to rainfall events, the water saturation increases leading to a decrease in air-water interfacial area. The PFOS adsorbed at the air-water interfaces is released to the aqueous phase and the majority of that is then adsorbed to the solid surface. 3) When air-water interfacial adsorption is considered, approximately 58% and 45% of the total released PFOS remains in the vadose zone at 40 years, for the semi-arid and humid climates, respectively. For the semi-arid case, more than 93% of the mass in the vadose zone is adsorbed at the air-water interfaces. Approximately 1.5% is in the aqueous phase, and the remaining 5.5% is in the solid-phase adsorption. For the humid-climate case, approximately 97% is adsorbed at the air-water interfaces, 1% is in the aqueous phase, and 2% is in the solid-phase. These fractions confirm the observations made in Fig. 6. 4) When air-water interfacial adsorption is not considered, the total mass left in the vadose zone is substantially lower—approximately 7% and 2% remain in the vadose zone for the semi-arid and humid climates, respectively.
Figure 7:
Cumulative mass of PFOS in the vadose zone for the case of high a PFOS concentration (1000 mg/L) for the Accusand. The total mass of PFOS and the mass in the aqueous phase, air-water interfacial adsorption, and solid-phase adsorption are all presented. The first column is under a semi-arid climate, while the second column is under a humid climate. The first and second rows are with and without air-water interfacial adsorption, respectively.
Another way to quantify the impact of the adsorption mechanisms is to use the concept of retardation factors. We compute the retardation factor for each numerical cell within the PFOS plume for the simulations that have included air-water interfacial adsorption. A numerical cell is considered inside the plume if its aqueous PFOS concentration is greater than 0.1% of the maximum aqueous concentration in the domain. The retardation factor is then averaged in space within the plume. Finally, we compute the mean values over 40 years for each simulation, which are reported in Table 2. The fractions of that are associated with air-water interfacial sorption (the KawAaw/θ term) and solid-phase adsorption (the ρbKfCN−1/θ term) are also reported; 420 they are referred to as and , respectively. ranges from 233 to 1355, and are mainly contributed by the air-water interfacial adsorption; it accounts for more than 97% of the retardation. The retardation factors are consistent with the results of the plume migration in Fig. 5. The large contributions of air-water interfacial adsorption are caused by the low water content and the corresponding high air-water interfacial areas. To demonstrate that, we have computed the average values of the water content, air-water interfacial area, and air-water interfacial adsorption coefficient in the plume over 40 years. The water content is down to 0.037 (corresponding to a water saturation of 0.126). It is slightly lower for higher PFOS concentration because of possibly greater surfactant-induced drainage caused by a greater decrease of surface tension at a higher aqueous PFOS concentration. For example, the surface tension drops from 65.7mN/m to 52.8mN/m when the aqueous concentration increases from 2mg/L to 20mg/L. The humid climate leads to higher average water content as expected. A major difference between low and high PFOS concentrations is the value of —it decreases by 5 to 10 times from low to high PFOS concentrations, which explains 434 the much smaller retardation factors in the high PFOS concentration scenarios.
Table 2:
Retardation factors for the Accusand for the simulations that have included air-water interfacial adsorption. The retardation factors are average values in the vadose zone over the entire simulation time; each and the fractions contributed by air-water interfacial adsorption () and solid-phase adsorption () correspond to one simulation. The corresponding average values of water content, air-water interfacial area, and air-water interfacial adsorption coefficient are also presented.
| Climates | PFOS (mg/L) |
(−) |
(cm2/cm3) |
(cm3/cm2) |
(−) |
(%) |
(%) |
|---|---|---|---|---|---|---|---|
| Semi-arid | 100 1000 |
0.039 0.037 |
505.0 510.1 |
0.0652 0.0069 |
1355 233 |
99.1 97.3 |
0.9 2.7 |
| Humid | 100 1000 |
0.048 0.046 |
472.3 476.3 |
0.0647 0.0151 |
1101 326 |
99.1 98.3 |
0.9 1.7 |
5.3. Vinton soil
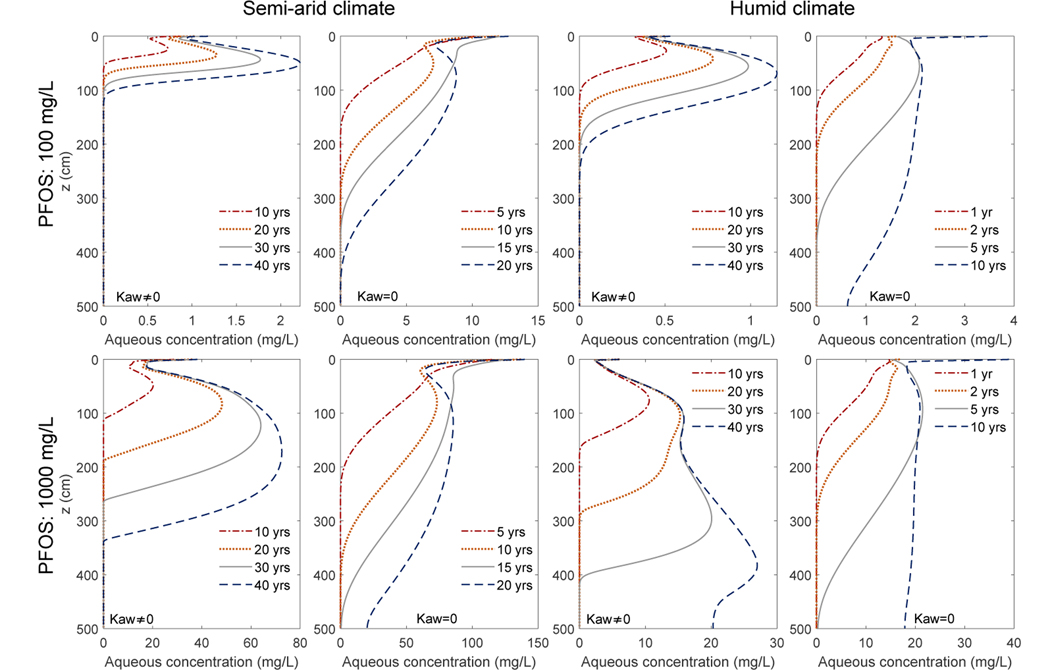
In this section, we perform simulations in a homogeneous vadose zone consisting of a soil media represented by the Vinton soil similar to those done on the Accusand in section 5.2. The results are presented in Figs. 8–10 and Table 3. They are generally similar to the Accusand results, but with three key differences. 1) The PFOS moves much slower when compared to the Accusand simulations. After 40 years, PFOS reaches groundwater for only the high PFOS concentration case under a humid climate. 2) PFOS migration is still substantially slower for the scenarios that considered the air-water interfacial adsorption compared to those with air-water interfacial adsorption turned off. However, the extent of retardation becomes smaller when compared to Accusand—the time scale to reach groundwater is only ~ 5 times greater when air-water interfacial adsorption is included. In addition, the scenarios without air-water interfacial adsorption also produce much slower PFOS migration than those in the Accusand simulations. It takes ~ 5 years (high PFOS concentration; humid climate) to ~ 20 years (low PFOS concentration; semi-arid climate) for the PFOS to reach groundwater. We attribute the two differences 1) and 2) to the following factors. First is that though Vinton has higher relative permeabilities because of the higher water content, its saturated hydraulic conductivity is much smaller (~ 18 times smaller; see Table 1). Second is that the solid-phase adsorption in Vinton is much greater (with a Kf that is ~ 9 times larger than Accusand). The stronger solid-phase adsorption is also evident when looking at the mass fractions in the aqueous phase, solid-phase adsorption, and the air-water interfacial adsorption in Figs. 9–10. The solid-phase adsorption accounts for about 30% and 17% of the total mass in the vadose zone for the semi-arid and humid climates, respectively (Fig. 10), which are much higher than the corresponding Accusand values. The fraction of the aqueous phase PFOS is still very small—one or two percent. The remainder are adsorbed at the air-water interfaces. 3) When air-water interfacial adsorption is turned off, the cumulative PFOS in the vadose zone plateaus at a much higher value than that of the Accusand case. Approximately 60% and 20% of the total released PFOS remain in the vadose zone for the semi-arid and humid climates respectively, which are almost 10 times greater than those in the Accusand scenarios.
Figure 8:
Simulated temporal evolution of the PFOS aqueous concentration profiles over 40 years in a vadose zone beneath an FTA site consisting of the Vinton soil. The first and second rows are simulations with a PFOS concentration of 100 mg/L and 1000 mg/L, respectively. The first two columns are under a semi-arid climate. The third and fourth columns are under a humid climate. The first and third columns are with air-water interfacial dsorption, while the second and fourth columns are without air-water interfacial adsorption.
Figure 10:
Cumulative mass of PFOS in the vadose zone for the case of high PFOS concentration (1000 mg/L) for the Vinton soil. The total mass of PFOS and the mass in the aqueous phase, air-water interfacial adsorption, and solid-phase adsorption are all presented. The first column is under a semi-arid climate, while the second column is under a humid climate. The first and second rows are with and without air-water interfacial adsorption, respectively.
Table 3:
Retardation factors for the Vinton soil for the simulations that have included air-water interfacial adsorption. The retardation factors are average values in the vadose zone over the entire simulation time; each and the fractions contributed by air-water interfacial adsorption () and solid-phase adsorption () correspond to one simulation. The corresponding average values of water content, air-water interfacial area, and air-water interfacial adsorption coefficient are also presented.
| Climates | PFOS (mg/L) |
(−) |
(cm2/cm3) |
(cm3/cm2) |
(−) |
(%) |
(%) |
|---|---|---|---|---|---|---|---|
| Semi-arid | 100 1000 |
0.123 0.122 |
842.1 844.2 |
0.0714 0.0264 |
792 153 |
95.6 90.5 |
4.4 9.5 |
| Humid | 100 1000 |
0.152 0.150 |
686.0 690.5 |
0.0699 0.0089 |
478 146 |
94.3 91.7 |
5.7 8.3 |
Figure 9:
The four columns are the profiles of the PFOS mass per bulk volume of the porous medium for the Vinton under the semi-arid climate scenario soil at 10, 20, 30, 40 years, respectively. The first and second rows are simulations with PFOS concentration of 100 mg/L and 1000 mg/L, respectively.
Similar to the Accusand case, we have also computed the average retardation factors for the simulations that have included air-water interfacial adsorption to quantify the impact of the adsorption processes on the transport of PFOS (Table 3). The average values of water content, air-water interfacial area, and air-water interfacial adsorption coefficient are also computed. The retardation factors are on the order of several hundreds—though still very large—they are lower compared to the Accusand retardation factors. This is rather counterintuitive because the Vinton soil has larger interfacial areas and also stronger solid-phase adsorption. A closer inspection reveals that the Accusand has much lower water content than the Vinton soil (more than 3 times lower), which is the main reason responsible for the Accusand’s greater retardation factors. The retardation factors decrease from low to high PFOS concentration scenarios, similar to Accusand, due to the reduction in the air-water interfacial adsorption coefficients caused by the increase in the aqueous PFOS concentration. When looking at the contributions to the retardation factors associated with the solid-phase adsorption alone (), they are ~ 4 times that of the Accusand values because Vinton has a solid-phase adsorption capacity that is almost 9 times greater.
To examine the impact of surfactant-induced flow on the transport of PFOS, we have also performed simulations wherein we kept the surface tension constant (i.e., the PFOS does not impact fluid flow) and have compared the results to those that have included the feedback of PFOS to flow. The comparison shows that PFOS-induced flow has a relatively minor impact on PFOS transport and migration in the vadose zone for both Accusand and Vinton soil, especially before PFOS reaches groundwater (see Fig. SI3 in the SI). A closer inspection reveals that the simulated water saturation above the groundwater table is generally small, and for Accusand and Vinton soil, saturation (and thus air-water interfacial area) is not sensitive to capillary pressure head (or water pressure head) at low saturations (see Fig. 2). After PFOS reaches the higher water saturation zone near the groundwater table, saturation and air-water interfacial area become more sensitive to capillary pressure head. As such, the presence of PFOS surfactant—by modifying the capillary pressure head and the soil water characteristic curve—has a more noticeable impact, though still not significant, on PFOS transport. The above observation also implies that surfactant-induced flow will likely have a greater impact on PFOS transport in fine-texture porous media wherein the water saturation is higher as can be seen in Fig. SI3 that the impact is slightly greater for Vinton soil than that for Accusand.
Finally, we report the global mass conservation errors. For all simulations performed in the present work, the relative global mass conservation error (at the end of 40 years) is less than 0.1% for water and less than 0.005% for PFOS, respectively. These errors are small enough with no impact on PFOS transport in the vadose zone and can be further reduced if more restricted tolerances are used for the nonlinear Newton-Raphson iterations.
6. Discussion
We have developed mathematical formulations and a fully implicit computational framework for the transport processes of PFAS under transient variably saturated flow. To the best of our knowledge, this is the first mathematical model for PFAS transport in the vadose zone that explicitly accounts for the solid-phase and air-water interfacial adsorption processes. Though we have not compared our model directly to experimental data (such data does not yet exist), the individual components of the formulations have been validated by prior experiments. The model for surfactant-induced flow has been validated by application to sand-packed column and flow cell experiments (Smith & Gillham, 1999; Henry & Smith, 2002; Henry et al., 2002; Karagunduz et al., 2015). The solid-phase and air-water interfacial adsorption formulations have been used to model PFAS transport in soil/sand-packed columns under steady-state unsaturated flow. Good agreement of breakthrough curves between simulation and experiment were reported (Brusseau, Yan, et al., 2019; Brusseau, 2020).
By applying the model to simulate PFAS (using PFOS as a representative PFAS) transport in a vadose zone beneath a synthetic FTA site, we show that adsorption at air-water interfaces has a significant impact on the transport and retention of PFAS. The retardation factors—though varying with PFOS concentrations, climates, and different types of porous media—are always on the order of several hundreds to more than one thousand. We have demonstrated that such large retardation factors are mainly caused by the low water content resulting from gravity drainage. A low water content increases the retardation factor because: 1) it is in the denominator of the expression for the retardation factor, and 2) it leads to a large interfacial area and thus more interfacial adsorption. We note that though our simulations used laboratory measured parameters, the computed water content is consistent with measured water content in large lysimeters (4 m deep and 2.5 m in diameter) packed with the Vinton soil at The University of Arizona’s Karsten Center for Turfgrass Research (Young et al., 1996; Carlson et al., 2003). The water content in the lysimeters was 528 observed to reach as low as 0.035. We expect that vadose zones with deeper groundwater 529 tables (4.82m is set in our simulations) will have similar or even lower water contents. A 530 shallower groundwater table may increase the overall water content if the porous medium 531 has a thick capillary transition zone.
The other critical finding from our simulations is that the majority of the PFOS in the vadose zone is retained at the air-water interfaces—only one or two percent is in the aqueous phase. This implies that the total PFAS concentration in the vadose zone is likely orders of magnitude higher than that in groundwater beneath source zones. Recent field investigations have shown that measured PFAS concentrations in the soil were up to six or seven orders of magnitude higher than the concentrations in the groundwater (Anderson et al., 2019; Dauchy et al., 2019). In particular, the study by Anderson et al. (2019) was based on an analysis of 324 Air Force sites across the continental US impacted by AFFF, and higher soil PFAS concentrations were observed in the vast majority (87%) of the data collected.
Because water content and air-water interfacial areas have a major impact on the retention of PFAS transport in the vadose zone, other factors that can influence water content and the amount of air-water interfacial area will thus also have an impact on the retention. For example, a humid climate leads to a higher water content and a lower air-water interfacial area than a semi-arid climate. Another important factor is the properties of the porous medium. Our simulations show rather counterintuitively that the Vinton soil has lower PFOS retardation factors compared to the Accusand. The reason is that though the Vinton soil has a larger interfacial area than the Accusand for the same water saturation, it retains much higher water saturation than the Accusand does in the vadose zone due to stronger capillary forces. Though more comprehensive analysis for a wider range of porous media is needed to generalize the findings, our results appear to imply that a fine-texture porous medium that can retain more water in the vadose zone, for example silt or clay, could have a lower retardation factor than sand materials similar to the scenarios of the Vinton soil vs. Accusand in the present work. This is supported by several prior field observations. Through the analysis of 324 Air Force sites across the continental US impacted by AFFF, Anderson et al. (2019) showed that the ratio between the PFAS concentration in the soil and groundwater decreases with increasing clay content, which they hypothesized is due to the higher water saturation in the presence of higher clay content. In another field investigation, Dauchy et al. (2019) showed that PFAS were detected 15m below ground despite the presence of clay layers implying that the retardation factors in clay may not be as great as what is usually thought for other contaminants. Our modeling framework and the detailed simulations can be used to test the above hypotheses at field sites, and more generally to provide fundamental insights into the primary factors controlling the transport, migration, 565 and retention of PFAS in the vadose zone.
Finally, we recognize that there are a few factors that are not considered in the current study that may impact PFAS transport in the vadose zone. For example, the seasonal and interannual variability of the groundwater table may influence the water saturation in the vadose zone and hence the air-water interfaces, especially when the vadose zone is relatively shallow. In that case, not including the groundwater table dynamics will likely overestimate the retention of PFAS in the vadose zone. Also, our current simulations did not consider transpiration of water through plants. For the low PFOS concentration scenarios, surface evaporation only accounts for approximately 16% of the total rainfall in the Accusand simulations. It is larger for Vinton, which accounts for approximately 44% of the total rainfall. For the high PFOS concentration scenarios, the surface evaporation is slightly lower due to more induced drainage caused by a greater reduction in surface tension. Thus, not accounting for transpiration fluxes due to plant uptake will likely overestimate the water content and thus underestimate the time-scale of retention in the vadose zone. For the adsorption processes, we have presented mathematical formulations for both equilibrium and kinetic solid-phase and air-water interfacial adsorption, but we have not simulated the impact of kinetics on the transport and retention of PFAS in the vadose zone. Thus, it remains unclear whether kinetics are important under transient flow conditions, which requires further investigation. Several other factors that can add additional complexities are soil heterogeneity, multiple components of PFAS, and the transformation of PFAS precursors in the source zone. Geological heterogeneities such as macropores and fractures can generate preferential flow paths, which can accelerate the migration of PFAS in the vadose zone. Transport of multiple PFAS compounds can generate interesting interactions among the components both in terms of modifying surface tension as well as adsorption at the air-water interfaces. Though these processes are not simulated in the present work, our mathematical formulations and the computational framework can be extended to include these additional processes to examine their quantitative impact on the migration of PFAS in the vadose zone.
7. Conclusion
We have developed a novel mathematical model for the release and migration of PFAS in the vadose zone under dynamic flow conditions. The mathematical formulation accounts for transient variably saturated flow, advective and dispersive transport, and adsorption at soil grain surfaces and air-water interfaces. We have applied the model to a model source zone impacted by AFFF due to fire trainings over a period of 40 years. A series of scenarios covering a wide range of conditions are constructed, which include two porous media (sand vs. soil), two AFFF concentrations (low vs. high), and two climates (semi-arid vs. humid). PFOS is used as a representative PFAS in the AFFF solutions.
The detailed simulations show that adsorption at air-water interfaces has a strong impact on the migration and retention of PFOS in the vadose zone. More importantly, air-water interfacial adsorption is amplified by the low water content (and hence large air-water interfacial areas) in the vadose zone caused by gravity drainage. The retardation factors—though vary among the different scenarios—are always on the order of several hundred to more than one thousand. The lower water content caused by greater gravity drainage and weaker capillary retention in the sand has also led to a counterintuitive result that the retardation factors for the sand (233 to 1355) are larger than those for the soil (146 to 792). A direct implication is that fine-texture materials such as silt or clay could have lower PFAS retardation factors compared to sand due to the higher retained water content in the vadose zone. This is supported by field evidence of decreasing soil to groundwater PFAS concentrations with increasing clay content. The large retardation factors lead to long time scales for PFOS to reach groundwater. For the conditions we simulate, it takes several decades or longer to reach a groundwater table at ~ 5m below the land surface. In addition, the results show that the majority of the PFOS in the vadose zone is retained at the air-water interfaces (70% or more) and the solid surfaces (5% to 30%) leaving only one or two percent in the aqueous phase. This implies that PFAS concentrations in the vadose zone are likely orders of magnitude higher than those in the groundwater in source zones, which is consistent with recently reported data at hundreds of AFFF-impacted FTA sites in the US and elsewhere. Overall, the present study has provided fundamental insights into the primary factors controlling the transport and retention of PFAS in the vadose zone. More generally, the mathematical model provides a quantitative framework that can be extended to examine the complex interactions between dynamic flow and adsorption processes at field sites.
Supplementary Material
Key Points:
We develop a mathematical model for the transport and retention of PFAS in the vadose zone.
Air-water interfacial adsorption leads to retardation factors of several hundreds or greater.
Retardation factors for fine-texture media can be lower than for sand due to greater retained water content.
Acknowledgments
This work is in part supported by the Water, Environmental, and Energy Solutions (WEES) Initiative at the University of Arizona to B. Guo and J. Zeng, and by the NIEHS Superfund Research Program (grant # P42 ES 4940) to M.L Brusseau. We note that no new measured data were reported in this study, and that all literature data used in the study have been provided in the manuscript except for the rainfall and evapotranspiration data, which can be downloaded from the AmeriFlux database (URL: https://ameriflux.lbl.gov).
Footnotes
Publisher's Disclaimer: This article has been accepted for publication and undergone full peer review but has not been through the copyediting, typesetting, pagination and proofreading process, which may lead to differences between this version and the Version of Record. Please cite this article as doi: 10.1029/2019WR026667
References
- Abriola LM, Dekker TJ, & Pennell KD (1993). Surfactant-enhanced solubilization of residual dodecane in soil columns. 2. Mathematical modeling. Environmental Science & Technology, 27(12), 2341–2351. [Google Scholar]
- Adamson AW, & Gast AP (1997). Physical Chemistry of Surfaces. John Wiley & Sons, Inc, New York. [Google Scholar]
- Anderson RH, Adamson DT, & Stroo HF (2019). Partitioning of poly-and perfluoroalkyl substances from soil to groundwater within aqueous film-forming foam source 640 zones. Journal of Contaminant Hydrology, 220, 59–65. [DOI] [PubMed] [Google Scholar]
- Araujo JB, Mainhagu J, & Brusseau ML (2015). Measuring air–water interfacial area for soils using the mass balance surfactant-tracer method. Chemosphere, 134, 199–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bagour MH (2001). Measuring and predicting steady state infiltration rates for arizona irrigated soils. [Google Scholar]
- Banks RE, Smart BE, & Tatlow J (2013). Organofluorine chemistry: principles and commercial applications. Springer Science & Business Media. [Google Scholar]
- Brusseau ML (1995). The effect of nonlinear sorption on transformation of contaminants during transport in porous media. Journal of Contaminant Hydrology, 17(4), 277–291. [Google Scholar]
- Brusseau ML (2018). Assessing the potential contributions of additional retention processes to PFAS retardation in the subsurface. Science of the Total Environment, 613, 176–185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brusseau ML (2019a). Estimating the relative magnitudes of adsorption to solid-water and air/oil-water interfaces for per-and poly-fluoroalkyl substances. Environmental Pollution, 254, 113102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brusseau ML (2019b). The influence of molecular structure on the adsorption of PFAS to fluid-fluid interfaces: Using qspr to predict interfacial adsorption coefficients. Water Research, 152, 148–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brusseau ML (2020). Simulating PFAS transport influenced by rate-limited multi-process retention. Water Research, 115179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brusseau ML, El Ouni A, Araujo JB, & Zhong H (2015). Novel methods for measuring air–water interfacial area in unsaturated porous media. Chemosphere, 127, 208–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brusseau ML, Khan N, Wang Y, Yan N, Van Glubt S, & Carroll KC (2019). Nonideal transport and extended elution tailing of pfos in soil. Environmental Science & Technology. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brusseau ML, Peng S, Schnaar G, & Murao A (2007). Measuring air- water interfacial areas with x-ray microtomography and interfacial partitioning tracer tests. Environmental Science & Technology, 41(6), 1956–1961. [DOI] [PubMed] [Google Scholar]
- Brusseau ML, & Van Glubt S (2019). The influence of surfactant and solution composition on PFAS adsorption at fluid-fluid interfaces. Water Research. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brusseau ML, Yan N, Van Glubt S, Wang Y, Chen W, Lyu Y, ... Holguin FO (2019). Comprehensive retention model for pfas transport in subsurface systems. Water research, 148, 41–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buck RC, Franklin J, Berger U, Conder JM, Cousins IT, De Voogt P, ... van Leeuwen SP (2011). Perfluoroalkyl and polyfluoroalkyl substances in the environment: terminology, classification, and origins. Integrated Environmental Assessment and Management, 7(4), 513–541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cameron D, & Klute A (1977). Convective-dispersive solute transport with a combined equilibrium and kinetic adsorption model. Water Resources Research, 13(1), 183–188. [Google Scholar]
- Carlson T, Costanza-Robinson M, Keller J, Wierenga P, & Brusseau ML (2003). Intermediate-scale tests of the gas-phase partitioning tracer method for measuring soil-water content. Soil Science Society of America Journal, 67(2), 483–486. [Google Scholar]
- Celia MA, Bouloutas ET, & Zarba RL (1990). A general mass-conservative numerical solution for the unsaturated flow equation. Water Resources Research, 26(7), 1483–1496. [Google Scholar]
- Chang C-H, & Franses EI (1995). Adsorption dynamics of surfactants at the air/water interface: a critical review of mathematical models, data, and mechanisms. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 100, 1–45. [Google Scholar]
- Chen W, & Wagenet R (1997). Description of atrazine transport in soil with heterogeneous nonequilibrium sorption. Soil Science Society of America Journal, 61(2), 360–371. [Google Scholar]
- Chen W, & Wagenet RJ (1995). Solute transport in porous media with sorption-site heterogeneity. Environmental science & technology, 29(11), 2725–2734. [DOI] [PubMed] [Google Scholar]
- Clark K (2004). AmeriFlux US-Slt Silas Little-New Jersey (Tech. Rep.). AmeriFlux; United States Department of Agriculture Forest Service. [Google Scholar]
- Costanza J, Arshadi M, Abriola LM, & Pennell KD (2019). Accumulation of PFOA and PFOS at the air–water interface. Environmental Science & Technology Letters, 6(8), 487–491. [Google Scholar]
- Costanza-Robinson MS, & Henry EJ (2017). Surfactant-induced flow compromises determination of air- water interfacial areas by surfactant miscible-displacement. Chemosphere, 171, 275–283. [DOI] [PubMed] [Google Scholar]
- Culver TB, Hallisey SP, Sahoo D, Deitsch JJ, & Smith JA (1997). Modeling the desorption of organic contaminants from long-term contaminated soil using distributed mass transfer rates. Environmental science & technology, 31(6), 1581–1588. [Google Scholar]
- Dauchy X, Boiteux V, Colin A, Hémard J, Bach C, Rosin C, & Munoz J-F (2019). Deep seepage of per-and polyfluoroalkyl substances through the soil of a firefighter training site and subsequent groundwater contamination. Chemosphere, 214, 729–737. [DOI] [PubMed] [Google Scholar]
- Day JP, Campbell RA, Russell OP, & Bain CD (2007). Adsorption kinetics in binary surfactant mixtures studied with external reflection ftir spectroscopy. The Journal of Physical Chemistry C, 111(25), 8757–8774. [Google Scholar]
- Delshad M, Pope G, & Sepehrnoori K (1996). A compositional simulator for modeling surfactant enhanced aquifer remediation, 1 formulation. Journal of Contaminant Hydrology, 23(4), 303–327. [Google Scholar]
- EPA. (2001). Pesticide Root Zone Model—Release 3 (PRZM) Version 3.12.1. EPA: Washington, DC. [Google Scholar]
- FAA. (2010). Advisory circular: Aircraft Rescue and Fire Fighting (ARFF) training facilities Federal Aviation Administration, U.S. Department of Transportation. [Google Scholar]
- Filipovi M., Woldegiorgi A., Norströ K., Bib M., Lindber M., & Österå A-H.¨ (2015). Historical usage of aqueous film forming foam: A case study of the widespread distribution of perfluoroalkyl acids from a military airport to groundwater, lakes, soils and fish. Chemosphere, 129, 39–45. [DOI] [PubMed] [Google Scholar]
- Fountain JC, Klimek A, Beikirch MG, & Middleton TM (1991). The use of surfactants for in situ extraction of organic pollutants from a contaminated aquifer. Journal of Hazardous Materials, 28(3), 295–311. [Google Scholar]
- Hassanizadeh SM, & Gray WG (1993). Thermodynamic basis of capillary pressure in porous media. Water resources research, 29(10), 3389–3405. [Google Scholar]
- Henry EJ, & Smith J (2002). The effect of surface-active solutes on water flow and contaminant transport in variably saturated porous media with capillary fringe effects. Journal of Contaminant Hydrology, 56(3–4), 247–270. [DOI] [PubMed] [Google Scholar]
- Henry EJ, Smith J, & Warrick A (2002). Two-dimensional modeling of flow and transport in the vadose zone with surfactant-induced flow. Water Resources Research, 38(11), 33–1. [Google Scholar]
- Henry EJ, & Smith JE (2003). Surfactant-induced flow phenomena in the vadose zone. Vadose Zone Journal, 2(2), 154–167. [Google Scholar]
- Higgins CP, & Luthy RG (2006). Sorption of perfluorinated surfactants on sediments. Environmental Science & Technology, 40(23), 7251–7256. [DOI] [PubMed] [Google Scholar]
- Høisæter Å, Pfaff A, & Breedveld GD (2019). Leaching and transport of PFAS from aqueous film-forming foam (AFFF) in the unsaturated soil at a firefighting training facility under cold climatic conditions. Journal of contaminant hydrology, 222, 112–122. [DOI] [PubMed] [Google Scholar]
- Houtz EF, Higgins CP, Field JA, & Sedlak DL (2013). Persistence of perfluoroalkyl acid precursors in afff-impacted groundwater and soil. Environmental science & technology, 47(15), 8187–8195. [DOI] [PubMed] [Google Scholar]
- ITRC. (2018). Environmental fate and transport for per- and polyfluoroalkyl substances (Tech. Rep.). Washington, D.C.: Interstate Technology & Regulatory Council. [Google Scholar]
- Ji W, & Brusseau ML (1998). A general mathematical model for chemical-enhanced flushing of soil contaminated by organic compounds. Water Resources Research, 34(7), 1635–1648. [Google Scholar]
- Karagunduz A, Young MH, & Pennell KD (2015). Influence of surfactants on unsaturated water flow and solute transport. Water Resources Research, 51(4), 1977–1988. [Google Scholar]
- Kim H, Rao PSC, & Annable MD (1997). Determination of effective air-water interfacial area in partially saturated porous media using surfactant adsorption. Water Resources Research, 33(12), 2705–2711. [Google Scholar]
- Leverett M, et al. (1941). Capillary behavior in porous solids. Transactions of the AIME, 142(01), 152–169. [Google Scholar]
- Li Z, & Brusseau ML (2000). Nonideal transport of reactive solutes in heterogeneous porous media: 6. microscopic and macroscopic approaches for incorporating heterogeneous rate-limited mass transfer. Water Resources Research, 36(10), 2853–2867. [Google Scholar]
- Lie K-A (2019). An introduction to reservoir simulation using MATLAB/GNU Octave. Cambridge University Press. [Google Scholar]
- Loppine B., & Monteu C. (2016). Dynamics of surfactants and polymers at liquid interfaces In Soft Matter at Aqueous Interfaces (pp. 137–157). Springer. [Google Scholar]
- Lyu Y, Brusseau ML, Chen W, Yan N, Fu X, & Lin X (2018). Adsorption of PFOA at the air–water interface during transport in unsaturated porous media. Environmental Science & Technology, 52(14), 7745–7753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller R, Aksenenko E, & Fainerman V (2017). Dynamic interfacial tension of surfactant solutions. Advances in colloid and interface science, 247, 115–129. [DOI] [PubMed] [Google Scholar]
- Millington R, & Quirk J (1961). Permeability of porous solids. Transactions of the Faraday Society, 57, 1200–1207. [Google Scholar]
- Moody CA, & Field JA (1999). Determination of perfluorocarboxylates in groundwater impacted by fire-fighting activity. Environmental Science & Technology, 33(16), 2800–2806. [Google Scholar]
- Moody CA, & Field JA (2000). Perfluorinated surfactants and the environmental implications of their use in fire-fighting foams. Environmental Science & Technology, 34(18), 3864–3870. [Google Scholar]
- Mualem Y (1976). A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resources Research, 12(3), 513–522. [Google Scholar]
- Pennell KD, Abriola LM, & Weber WJ Jr (1993). Surfactant-enhanced solubilization of residual dodecane in soil columns. 1. experimental investigation. Environmental Science & Technology, 27(12), 2332–2340. [Google Scholar]
- Pinder GF, & Celia MA (2006). Subsurface hydrology. John Wiley & Sons. [Google Scholar]
- Pope GA, Nelson RC, et al. (1978). A chemical flooding compositional simulator. Society of Petroleum Engineers Journal, 18(05), 339–354. [Google Scholar]
- Reeves PC, & Celia MA (1996). A functional relationship between capillary pressure, saturation, and interfacial area as revealed by a pore-scale network model. Water Resources Research, 32(8), 2345–2358. [Google Scholar]
- Richards LA (1931). Capillary conduction of liquids through porous mediums. Physics, 1(5), 318–333. [Google Scholar]
- Schaefer C, DiCarlo D, & Blunt M (2000). Experimental measurement of air-water interfacial area during gravity drainage and secondary imbibition in porous media. Water Resources Research, 36(4), 885–890. [Google Scholar]
- Schaefer C, Drennan DM, Tran DN, Garcia R, Christie E, Higgins CP, & Field JA (2019). Measurement of aqueous diffusivities for perfluoroalkyl acids. Journal of Environmental Engineering, 145(11), 06019006. [Google Scholar]
- Scott RL (2004). AmeriFlux US-Wkg Walnut Gulch Kendall Grasslands (Tech. Rep.). AmeriFlux; United States Department of Agriculture. [Google Scholar]
- Scott RL (2010). Using watershed water balance to evaluate the accuracy of eddy covariance evaporation measurements for three semiarid ecosystems. Agricultural and Forest Meteorology, 150(2), 219–225. [Google Scholar]
- Sekin M., Campbel RA., Valkovsk DS., Da JP., Curwe TD., Marti LJ., ... Bain CD (2004). Adsorption kinetics of ammonium perfluorononanoate at the air–water interface. Physical Chemistry Chemical Physics, 6(21), 5061–5065. [Google Scholar]
- SERDP. (2017). SERDP and ESTCP workshop on research and demonstration needs for management of AFFF-impacted sites. [Google Scholar]
- Shin H-M, Ryan PB, Vieira VM, & Bartell SM (2012). Modeling the air–soil transport pathway of perfluorooctanoic acid in the mid-ohio valley using linked air dispersion and vadose zone models. Atmospheric Environment, 51, 67–74. [Google Scholar]
- Shin H-M, Vieira VM, Ryan PB, Detwiler R, Sanders B, Steenland K, & Bartell SM (2011). Environmental fate and transport modeling for perfluorooctanoic acid emitted from the Washington Works Facility in West Virginia. Environmental Science & Technology, 45(4), 1435–1442. [DOI] [PubMed] [Google Scholar]
- Silva JA, Martin WA, Johnson JL, & McCray JE (2019). Evaluating air-water and napl-water interfacial adsorption and retention of perfluorocarboxylic acids within the vadose zone. Journal of Contaminant Hydrology, 223, 103472. [DOI] [PubMed] [Google Scholar]
- Simunek J, Sejna M, Saito H, Sakai M, & Van Genuchten MT (2008). The HYDRUS-1D software package for simulating the one-dimensional movement of water. Heat, and Multiple Solutes in Variably-Saturated Media, Version, 4, 281. [Google Scholar]
- Smith JE, & Gillham RW (1994). The effect of concentration-dependent surface tension on the flaw of water and transport of dissolved organic compounds: A pressure head824 based formulation and numerical model. Water Resources Research, 30(2), 343–354. [Google Scholar]
- Smith JE, & Gillham RW (1999). Effects of solute concentration–dependent surface tension on unsaturated flow: Laboratory sand column experiments. Water Resources Research, 35(4), 973–982. [Google Scholar]
- UTCHEM. (2000). UTCHEM-9.0: A three-dimensional chemical flood simulator. University of Texas at Austin. [Google Scholar]
- Valkovska DS, Shearman GC, Bain CD, Darton RC, & Eastoe J (2004). Adsorption of ionic surfactants at an expanding air-water interface. Langmuir, 20(11), 4436–4445. [DOI] [PubMed] [Google Scholar]
- Van Genuchten MT (1980). A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal, 44(5), 892–898. [Google Scholar]
- Wang Z, DeWitt JC, Higgins CP, & Cousins IT (2017). A never-ending story of per-and polyfluoroalkyl substances (PFASs)? Environmental Science & Technology, 51(5), 2508–2518. [DOI] [PubMed] [Google Scholar]
- Weber AK, Barber LB, LeBlanc DR, Sunderland EM, & Vecitis CD (2017). Geochemical and hydrologic factors controlling subsurface transport of poly-and perfluoroalkyl substances, cape cod, massachusetts. Environmental Science & Technology, 51(8), 4269–4279. [DOI] [PubMed] [Google Scholar]
- Wei C, Song X, Wang Q, & Hu Z (2017). Sorption kinetics, isotherms and mechanisms of pfos on soils with different physicochemical properties. Ecotoxicology and Environmental Safety, 142, 40–50. [DOI] [PubMed] [Google Scholar]
- Xiao F, Simcik MF, Halbach TR, & Gulliver JS (2015). Perfluorooctane sulfonate (PFOS) and perfluorooctanoate (PFOA) in soils and groundwater of a us metropolitan area: migration and implications for human exposure. Water Research, 72, 64–74. [DOI] [PubMed] [Google Scholar]
- Xu M, & Eckstein Y (1995). Use of weighted least-squares method in evaluation of the relationship between dispersivity and field scale. Groundwater, 33(6), 905–908. [Google Scholar]
- Young M, Wierenga P, & Mancino C (1996). Large weighing lysimeters for water use and deep percolation studies. Soil Science, 161(8), 491–501. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.