Increasing riverine heat influx triggers Arctic sea ice decline and oceanic and atmospheric warming

Positive river heat–sea ice feedback doubles the river heat effect on declining Arctic sea ice.

Abstract

Arctic river discharge increased over the last several decades, conveying heat and freshwater into the Arctic Ocean and likely affecting regional sea ice and the ocean heat budget. However, until now, there have been only limited assessments of riverine heat impacts. Here, we adopted a synthesis of a pan-Arctic sea ice–ocean model and a land surface model to quantify impacts of river heat on the Arctic sea ice and ocean heat budget. We show that river heat contributed up to 10% of the regional sea ice reduction over the Arctic shelves from 1980 to 2015. Particularly notable, this effect occurs as earlier sea ice breakup in late spring and early summer. The increasing ice-free area in the shelf seas results in a warmer ocean in summer, enhancing ocean–atmosphere energy exchange and atmospheric warming. Our findings suggest that a positive river heat–sea ice feedback nearly doubles the river heat effect.

INTRODUCTION

River discharge transports large volumes of relatively warm freshwater into the Arctic Ocean (1), affecting the heat budget and potentially enhancing sea ice decline. Observations show high riverine heat (Q_rh) in spring and early summer when the shelf seas are still covered by ice (2). The entrained Q_rh is difficult to measure, however, since it remains invisible to satellite observations and is largely decoupled from the atmosphere (3). Meanwhile, its effect becomes clearly visible in spring when Q_rh triggers ice breakup in the vicinity of river mouths (4, 5). Subsequent warming of ocean surface waters in summer further delays sea ice formation in autumn (6), although the relationship between Q_rh and autumn sea ice is less defined compared to the well-established strong impact of Q_rh on spring sea ice retreat (3, 4). There are, however, reasons to believe that the impacts of Q_rh are not confined to seasonal changes of sea ice in the shelf seas. Enhanced offshore sea ice retreat in spring caused by Q_rh likely results in further increase of net solar radiation loading during summer, which is closely linked to seasonal heat cycling in the upper ocean and energy exchange with the atmosphere linked to climate (7, 8). However, more comprehensive information needed to quantify the various impacts of Q_rh in the Arctic has been lacking.

There is now no alternative to numerical modeling for quantifying Q_rh transport over the Arctic shelves and further offshore to the deep-sea areas and the associated impacts on Arctic sea ice variability. Most state-of-the-art climate models have incorporated riverine freshwater (volume) influxes to the Arctic Ocean (9–13). However, Q_rh has been rarely included in these models. Recently, Q_rh has been simulated in fully coupled climate models incorporating more sophisticated land surface modules, namely, CM2M and CM2G from the Geophysical Fluid Dynamics Laboratory. Another state-of-the-art model, Nucleus for European Modeling of the Ocean (NEMO), has an optional parameterization of Q_rh in which river water temperature (T_w) was represented by sea surface temperature (T_s) observed at river mouths (14), although this parameterization does not realistically account for the seasonal change of T_w. Whitefield et al. (15) developed a new pan-Arctic climatological dataset of river discharge and T_w based on observed records from 30 Arctic rivers and used this dataset in regional sea ice–ocean model simulations, showing that riverine heat fluxes to the Arctic shelves reduced September sea ice extent by ~10% from 1979 to 2012. While these prior studies have made notable advances in clarifying the influence of river heat on Arctic ocean–sea ice–atmosphere dynamics, previous model studies have not deeply evaluated impacts of interannually variable Q_rh. In this study, we combined a pan-Arctic coupled sea ice–ocean model [Center for Climate System Research Ocean Component Model (COCO), version 4.9] (16) with an Arctic land surface model [A coupled hydrological and biogeochemical model (CHANGE)] and distributed hydrological model (1, 17) to quantify the Q_rh impact on decreasing Arctic sea ice within the six major Arctic shelf regions (Fig. 1C) in the recent decades (1980–2015). The coupled land–ocean–sea ice model framework provides capabilities for clarifying the influence of Q_rh seasonal and interannual variability and longer-term warming trends on Arctic sea ice dynamics in the recent decades. The experimental design also represents a substantial advance toward more realistic simulation and attribution of Arctic sea ice variability, feedbacks, and underlying drivers.

Fig. 1. Riverine heat release causes anomalous sea ice thickness and volume.

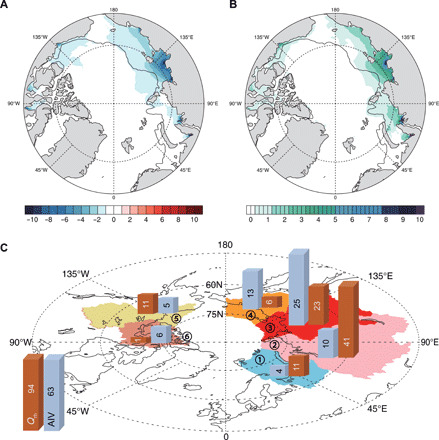
(A) The anomaly of annual mean sea ice thickness (centimeters) caused by riverine heat, Q_rh from 1980 to 2015. (B) The proportion (%) of the ice thickness reduction shown in (A) relative to annual mean sea ice thickness. (C) The mean Q_rh (×10¹⁸ J) produced by the six largest river drainages and the annual anomalous sea ice volume (AIV, cubic kilometer, positive indicates reduction) caused by Q_rh from 1980 to 2015 for the six individual shelf regions. In (A) and (B), only values with a mean sea ice thickness anomaly exceeding 0.5 cm are shown. The colored areas in (C) represent the six targeted shelf regions in this study, including the major river drainage areas producing Q_rh. The circled numbers in (C) represent ① Barents Sea, ② Kara Sea (Ob and Yenisey Rivers), ③ Laptev Sea (Lena River), ④ Eastern Siberian Sea (Kolyma River), ⑤ Beaufort Sea (Mackenzie River), and ⑥ Canadian Archipelago. Thin black contours in (A) and (B) show the 200-m isobath.

RESULTS AND DISCUSSION

Spatiotemporal variability of riverine heat

According to the CHANGE simulations, an average of 94.4 × 10¹⁸ J year⁻¹ of Q_rh was delivered to the Arctic river mouths from 1980 to 2015 (Fig. 1C), which is equivalent to an annual heat flux of 3.0 TW. This estimate is similar to the 3.2 TW estimate obtained by Whitefield et al. (15) based on observations from 30 Arctic rivers. Our analysis showed an increasing Q_rh trend of 0.25 ± 0.09 × 10¹⁸ J year⁻¹ during this period (Fig. 2A). This Q_rh contribution to the Arctic Ocean energy budget is sizable, constituting about 6.8% of oceanic heat inputs from the Atlantic and Pacific oceans (18)—enough to melt 0.31 × 10⁶ km² of 1-m-thick ice. The Q_rh is characterized by strong seasonal variability; whereby, approximately 65% of the annual Q_rh input occurs from May to July (Fig. 2B) when the Arctic shelf is mostly covered by sea ice, thus warming the shelf waters (4). Independent observations of melting dates derived from the satellite record show a 10- to 30-day delay in seasonal retreat of the ice cover over the shelf seas relative to thawing of nearby Arctic land areas from 1980 to 2015 (fig. S1). The spring thaw signal over Arctic land areas coincides with seasonal snowmelt and the freshwater runoff pulse to Arctic rivers (19, 20); the earlier terrestrial thaw onset indicates a Q_rh contribution to ocean warming under the ice cover, whereby Q_rh is an important heat source for preconditioning sea ice melt in spring and early summer.

Fig. 2. Seasonal and interannual variability of riverine heat and anomalous sea ice volume.

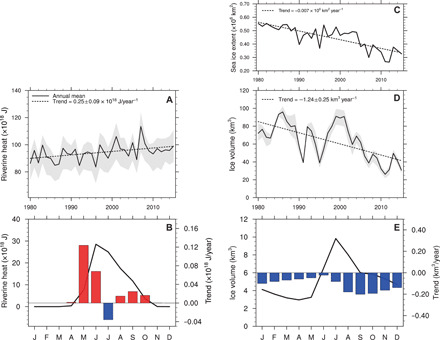
Impact of riverine heat Q_rh on Arctic sea ice decay in the six Arctic shelf regions (see Fig. 1c for their definition). (A) Time series of Q_rh discharged into the Arctic Ocean, (B) seasonal cycle of Q_rh (line); 1980–2015 trends are shown by red and blue bars, (C) satellite summer (15–31 July) sea ice extent, (D) AIV interannual variation, and (E) seasonal cycle with trends (bars) of ice volume reduction caused by Q_rh over the six Arctic regions. Gray shading in (A) and (D) denotes uncertainties indicated from model sensitivity experiments (Supplementary Materials). Linear trends in (A), (C), and (D) are shown by dotted lines.

Decay of sea ice under impact of riverine heat

The simulated annual sea ice thickness decay caused by Q_rh indicates that the largest sea ice reduction impact occurs around the mouths of the largest Arctic rivers (Fig. 1, A and B). An overall maximum annual reduction in the estimated regional mean sea ice thickness of more than 10% (~10 cm) occurred in near-shore part of the Laptev Sea and was associated with a relatively large Q_rh input from local rivers (mostly the Lena River). In this region, the impact of Q_rh on sea ice can be traced as far as 80°N during summer, demonstrating that Q_rh eventually causes sea ice decay over the outer shelf rather than being only confined to a narrow coastal zone (Fig. 1, A and B).

Our analysis shows that from 1980 to 2015, Q_rh caused a sea ice extent retreat of 0.05 × 10⁶ km² over the six Arctic shelf regions in September (fig. S2). Anomalous ice volume (AIV), representing the annual sea ice reduction driven by Q_rh over the Arctic shelves (Fig. 1C), averaged 63.3 km³ from 1980 to 2015 (Fig. 2D). The linear AIV trend suggests a sea ice volume decay rate of 1.24 ± 0.25 km³ year⁻¹ (P < 0.01) from 1980 to 2015 (Fig. 2D). Seasonally, the maximum AIV is found in July (Fig. 2E). The AIV shows strong interannual variability ranging from 25 to 100 km³ and large regional differences (Fig. 1C). The largest AIV of 25 km³ is found in the Laptev Sea, which has the highest Q_rh among the six shelf regions (Fig. 1C) (compared, for example, with AIV = 5 km³ in the Beaufort Sea).

However, the relationship between AIV and Q_rh is complex; for instance, AIV in the East Siberian Sea, despite relatively low Q_rh, is larger than the AIV in the Kara Sea (Fig. 1C). This provides important evidence indicating why AIV was higher in the 1980s and 1990s compared with the more recent decades (Fig. 2D), despite having lower Q_rh (Fig. 2A). Consolidated sea ice conditions near riverine heat sources (river mouths) in the 1980s and 1990s (Fig. 2C) led to an enhanced Q_rh impact on sea ice through intensive lateral and bottom sea ice melt (3, 6), while earlier ice retreat and more extensive ice-free area in recent decades (Fig. 2C) decreased the direct contact of Q_rh with sea ice during the melting season, hence lowering AIV (Fig. 2D). Significant correlation (r = 0.60, P < 0.01) between simulated AIV and observed sea ice extent in early summer supports this finding (Fig. 2C). However, according to our model simulations, the increasing Q_rh trend (Fig. 2A) and decrease in heat expenditures on sea ice melt in the vicinity of river mouths enhanced ocean warming and additional heat released to the atmosphere. The consequences of these changes are discussed in the following sections.

Warming of shelf waters caused by riverine heat

The anomalous ocean warming resulting from the increasing impact of Q_rh averaged over 1980–2015 was estimated as Q_ow = 48.2 × 10¹⁸ J year⁻¹. This warming spreads from the river mouths toward the outer shelf and also vertically, occupying the entire water column, with greater spread in the recent decades relative to the 1980s (Fig. 3). For example, the anomalous warming of the ocean surface layer reached 76°N in August in the Laptev Sea, where the thin (~5 m) surface layer showed anomalous warming (+1.5°C) from 2006 to 2015 (Fig. 3). Whitefield et al. (15) simulated a ~150-km spread of warm surface riverine water into the Beaufort Sea, which was associated with intensive mixing with deeper water layers at the shelf break. Our analysis shows a similar lateral Q_rh spread of up to ~200-km offshore from the Mackenzie River outlet (Fig. 1B). The associated warming resulted in earlier breakup of sea ice by ~5 to 14 days over the coastal shelf and by ~3 days over the outer shelf for the 2006–2015 period relative to 1981–1990 (fig. S3). Both satellite records (fig. S1) and model simulations (fig. S3) also show a widespread lengthening of the ice-free season from 1981–1990 to 2006–2015, consistent with the earlier ice breakup and later freezing. The anomalous warming of the water column toward the outer shelf and bottom layer persists until September, as shown for the 2006–2015 period (Fig. 3), although the impact of Q_rh on sea ice reduction in the outer shelves is not as large (Fig. 1, A and B) because the sea ice has already retreated further northward (Fig. 3). Further details of the heat contributed to ocean warming are discussed in the next section.

Fig. 3. Riverine heat increases oceanic temperatures over the Arctic shelves.

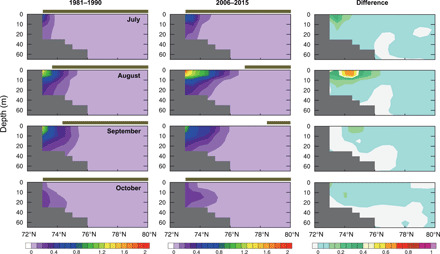
Latitude-depth sections of monthly anomalous ocean temperatures (°C) caused by Q_rh along the 127°E section of the Laptev Sea averaged for periods (left) 1981–1990, (middle) 2006–2015, and (right) their difference (positive values denote recent warming). The upper horizontal bars in each panel indicate the maximum sea ice extent in individual months.

Ocean–sea ice–atmosphere heat balance change under riverine heat impacts

Our results provide compelling evidence that Q_rh contributes to sea ice decay (Fig. 2D) and ocean warming (Q_ow; Fig. 3) over the six Arctic shelf regions (Fig. 1C). However, we also found that the sea ice retreat triggered feedbacks resulting from the sensitivity of the Arctic ocean–sea ice–atmosphere system to the state of the sea ice cover. A representative example is the ice-albedo feedback. By comparing the two numerical experiments, we found that sea ice decay and associated changes in surface albedo (21, 22) resulted in anomalous absorption of additional shortwave radiation (Q_sw), which also led to further ocean warming and sea ice melt. In addition, sea ice retreat prompted the release of ocean heat into the atmosphere (Q_ao) through ice-free areas via contributions of upward longwave radiation and sensible and latent heat fluxes. Furthermore, we quantify the consequences of this increasing Q_rh influx. Since the outer boundaries of the shelf regions are far away from the area where impact of Q_rh is significant, heat losses through lateral exchanges between the shelves and deeper ocean areas were assumed to be negligible.

The ocean–sea ice–atmosphere system heat balance, including sources (Q_rh + Q_sw) and sinks (Q_im + Q_ow + Q_ao) induced by riverine heat influx, averaged for 1980–2015 in the six Arctic shelf regions (Fig. 1C) is summarized in Fig. 4. Here, the ice-albedo feedback triggered by sea ice retreat resulted in 60.6 × 10¹⁸ J year⁻¹ of radiative heat (Q_sw) pumped into the system in addition to the 94.4 × 10¹⁸ J year⁻¹ of Q_rh delivered by warm riverine waters. Q_sw represents the difference in net solar radiation between the two model experiments over the six Arctic shelf regions. Together, Q_rh + Q_sw represent total system sources in annual heating of 155.0 × 10¹⁸ J year⁻¹—an astonishing 64% increase in net energy inputs due to the positive ice-albedo feedback.

Fig. 4. Heat balance change over Arctic shelf regions caused by influx of riverine heat.

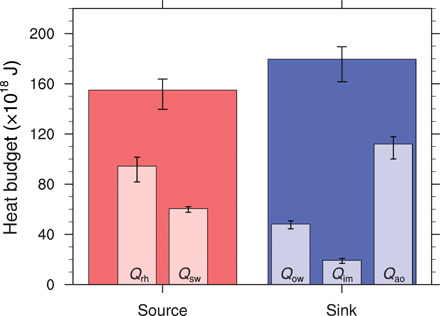
Mean annual energy budget, including heat sources and sinks over the six Arctic shelf regions (Fig. 1). The heat sources are constituted by influx of riverine heat (Q_rh) and additional absorption of solar radiation at the ocean surface caused by the sea ice–albedo feedback (Q_sw). The heat sinks are formed by ocean warming (Q_ow), sea ice melting (Q_im), and heat release from ocean to atmosphere (Q_ao). All values are averaged for the 1980–2015 period. The vertical lines at the top of the bars represent uncertainties of the estimates, defined by the three sensitivity experiments (Supplementary Materials).

The ocean–sea ice–atmosphere system heat sources were balanced by several sinks, including heat sinks to sea ice melt (Q_im) estimated as L_f ∙ ρ_i ∙ A ∙ h_i, where L_f is the latent heat of fusion (333.7 × 10³ J kg⁻¹), ρ_i is the ice density (917 kg m⁻³), A is the ice area (5.18 × 10¹² m²), and h_i is the melted ice thickness (meters). The resulting Q_im estimate of 19.4 × 10¹⁸ J year⁻¹ constituted 12% of Q_rh + Q_sw (Fig. 4). Most notable, the effect of the Q_im heat sink occurred in spring and early summer, accounting for 9% of Q_rh during May and August (Fig. 2E). The sea ice reduction by Q_rh in winter (Fig. 2E) represents an amplified impact of summer ocean warming across the season (6) and is corroborated by observations showing a thinning shelf ice thickness trend in winter (23).

The anomalous heat sink for ocean warming (Q_ow) was estimated as 48.2 × 10¹⁸ J year⁻¹ (Fig. 4) for the upper 100-m ocean layer (or surface to bottom layer, whichever is shallower) averaged over the six Arctic shelf regions, with an increasing Q_ow heat sink trend of 0.16 ± 0.09 × 10¹⁸ J year⁻¹ from 1980 to 2015 (fig. S4A). The maximum Q_ow occurred in late summer (i.e., August or September; fig. S5B), which is a seasonally delayed manifestation of the increased ice melt in spring and early summer due to the peak of Q_rh. In addition, the ocean warming caused a ~4-day delay of freezing during sea ice formation around large river mouths (fig. S3). The later freezing and earlier breakup trend yielded a longer open water period of up to 15 days in the inner parts of the shelf seas (fig. S3).

Most of the heat stored in the upper ocean in summer is lost to the atmosphere during autumn and winter by the upward propagation of longwave radiation and sensible/latent heat fluxes (fig. S5A). Annual ocean-to-atmosphere heat fluxes contributed 112.0 × 10¹⁸ J (0.68 W m⁻²), or 62%, to the overall heat sinks, thus constituting the largest of the energy sink components. The anomalous heat release to the atmosphere was strongest in late summer and autumn due to ocean surface warming (fig. S5). The three ocean–atmosphere heat flux components (net upward longwave radiation, sensible, and latent heat) contributed almost equally to the ocean heat sink (fig. S4B). Q_ao showed a significant increasing trend of 0.70 ± 0.18 × 10¹⁸ J year⁻¹ from 1980 to 2015, which is well expressed by the three Q_ao constituents and dominated by increasing latent and sensible heat fluxes in the recent decade (fig. S4B). Our simulations captured the effects of the ice-albedo feedback via reduction of sea ice cover and the ocean temperature increase caused by Q_rh, resulting in enhanced ocean–atmosphere energy transfer. Thus, our simulations provide a conservative estimate of atmospheric warming caused by Q_rh and associated ocean warming.

Average warming of the 300-m atmospheric surface layer (24) in summer (JJAS) over the six Arctic shelf regions from the anomalous Q_ao increase was estimated to be 0.34 K (Supplementary Materials), contributing 0.003 K per year to the increasing air temperature trend from 1980 to 2015 (fig. S6). This regional air temperature increase constitutes a sizable part (~5%) of the overall Arctic surface air temperature warming trend of 0.064°C year⁻¹ documented from maritime meteorological stations from 1979 to 2008 (25). The temperature increase further amplifies the Q_rh effects on sea ice retreat and ocean warming, although these secondary effects were not addressed by our study.

The model estimated components (Q_im + Q_ow + Q_ao) indicate a combined annual heat sink of approximately 179.5 × 10¹⁸ J from the influx of riverine heat into the Arctic shelf regions (Fig. 4). The apparent imbalance between annual heat sources and sinks of ~24.6 × 10¹⁸ J (expressed as a difference between sources and sinks in Fig. 4) characterizes an uncertainty of the estimated heat balance in the system. We note, however, that this imbalance is well within the range of model uncertainty due to the formulated forcing (i.e., indicated by vertical uncertainty lines in Fig. 4). Split evenly between energy sources and sinks, this uncertainty represents only ~8% of the total amount of heat sources or sinks annually by the system. This uncertainty can be explained by nonstationarities in the heat budget of the system, which are difficult to distinguish. For example, the residence time of riverine water and heat in the deeper water column may exceed 1 year in the shelf seas (26), resulting in overestimated annual Q_ow. Additional information about uncertainties in our estimates of the heat balance components is provided by the sensitivity experiments derived from three different atmospheric forcing datasets and represented by the uncertainty lines in Fig. 4. For example, the Q_rh uncertainty of 19.7 × 10¹⁸ J year⁻¹ (table S1) is mainly driven by the difference in precipitation between the three forcing datasets. Overall, these uncertainties do not preclude a meaningful analysis of the heat balance in the ocean–sea ice–atmosphere system (Fig. 4).

Our results indicate that riverine heat influx from the six major river drainage systems is having an important effect on the state of Arctic sea ice and, more generally, the ocean–sea ice–atmosphere system. Q_rh enforced shelf sea ice decay in the melt season is triggering additional ocean absorption of shortwave radiation associated with the ice-albedo feedback. Increasing riverine heat influxes in the recent decade have warmed extensive areas of the Arctic shelves, promoting stronger ocean–atmosphere heat exchanges and thinner winter sea ice relative to the 1980s (Fig. 5).

Fig. 5. Schematic showing changes in the Arctic atmosphere–sea ice–ocean system caused by riverine heat.

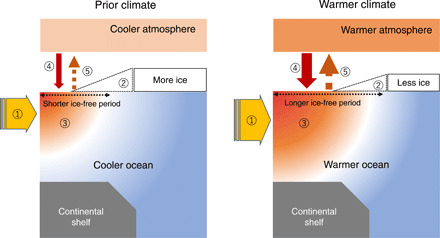
Anomalous riverine heat Q_rh influx ① results in ② sea-ice reduction including loss of ice area, thickness, and longer ice-free periods, ③ ocean warming, ④ positive feedback caused by additional sea ice retreat and enhanced absorption of atmospheric heat, and ⑤ additional atmospheric warming caused by anomalous release of ocean heat into the atmosphere. The thicker vertical and horizontal arrows indicate larger heat fluxes or inflows.

The important role of riverine heat inputs on the Arctic ocean–sea ice–atmosphere system revealed by this study is lacking in the current generation of Earth system models. Thus, model improvements to better represent Q_rh are needed to provide more realistic projections of future Arctic climate system trajectories. A considerable area of the Siberian shelf is underlain by submarine permafrost vulnerable to thawing. Increasing trends in Q_rh may facilitate additional thawing of bottom permafrost and the release of greenhouse gases (27, 28) that further amplify Arctic warming. The warming ocean likely affects the shelf ecosystem that preserves large amounts of organic matter discharged from terrestrial rivers (29). Increasing ocean temperatures over the broad Arctic shelves may result in enhanced decomposition of benthic organic matter through enhanced bacterial activity and the microbial loop (30), consequently altering nutrient cycling and affecting food availability associated with changes in sea ice, stratification, and vertical mixing (31). Thus, implications of increasing Q_rh influx in the Arctic may be far reaching, contributing to and potentially triggering multidisciplinary changes in the Arctic climate system.

MATERIALS AND METHODS

We used the COCO-CHANGE model framework to assess impacts of Q_rh on the Arctic sea ice variability. The COCO model, with 25-km horizontal resolution and 28 hybrid σ-z vertical levels, covers the pan-Arctic region from the Bering Strait to 45°N latitude in the Atlantic side. The atmospheric forcing components are constructed from the Climate Forecast System Reanalysis (32). The CHANGE model includes two modules. The first module represents land surface processes simulating explicit water and energy fluxes and vegetation dynamics in the atmosphere-soil-vegetation system. The second module includes a river discharge scheme adopting a storage-based distributed water routing algorithm with 0.5° (latitude/longitude) resolution (1, 17). Discharge and river water temperatures, simulated using the CHANGE model forced by three different meteorological datasets (Supplementary Materials), were used as riverine freshwater and heat fluxes in the COCO model experiments, which makes it possible to quantify the sensitivity of sea ice to the associated fluxes. Both COCO and CHANGE have been extensively used to simulate changes in sea ice–ocean processes associated with the Arctic sea-ice retreat (12) and long-term changes in river discharge and water temperatures from the pan-Arctic river system (1, 17), respectively.

Two sets of model experiments using the COCO-CHANGE framework were performed. The first (control) experiment used river discharge without consideration of riverine heat: Riverine heat flux referenced to T_s at each river mouth was kept to zero. In other words, T_w is assumed to be the same as the simulated T_s at each model time step so that the simulated ocean temperature is not changed directly by river discharge. This experimental setting is typical for the traditional model design [e.g., (9–13)]. The second experiment used the same atmospheric forcing and model configuration as the control, except that the COCO model used variable T_w derived from CHANGE [i.e., the riverine heat flux defined by ρ_wC_wv(T_w – T_s) is positive in most periods, ρ_w is the water density (kg m⁻³), C_w = 4187 J kg⁻¹ K⁻¹ is the specific heat of water, and v is the volume flux (m³ s⁻¹)]. The second experimental design is advanced in that the model realistically represents seasonal and interannual changes of Q_rh and the associated impacts on the Arctic sea ice and heat budget compared with previous modeling efforts that used more simplistic parameterizations (14) and climatological data (15). We note that this approach is valid only when the mass transport in a basin with open boundaries is balanced so that the heat fluxes have unambiguous physical interpretation (33). However, we used this approach in our study as it is a standard one for modeling simulations. Differences between the two experiments were used to quantify the effect of the Q_rh -induced heat flux anomaly on the state of the Arctic ocean–sea ice–atmosphere system in the defined six Arctic shelf regions (Fig. 1C). Full descriptions of the model approach are given in the Supplementary Materials.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/45/eabc4699/DC1