Thresholds in Origin of Life Scenarios

Summary

Thresholds are widespread in origin of life scenarios, from the emergence of chirality, to the appearance of vesicles, of autocatalysis, all the way up to Darwinian evolution. Here, we analyze the “error threshold,” which poses a condition for sustaining polymer replication, and generalize the threshold approach to other properties of prebiotic systems. Thresholds provide theoretical predictions, prescribe experimental tests, and integrate interdisciplinary knowledge. The coupling between systems and their environment determines how thresholds can be crossed, leading to different categories of prebiotic transitions. Articulating multiple thresholds reveals evolutionary properties in prebiotic scenarios. Overall, thresholds indicate how to assess, revise, and compare origin of life scenarios.

Graphical Abstract

Chemistry; Biological Sciences; Biochemistry; Evolutionary Biology; Evolutionary Processes; Astrobiology; Astrochemistry

Introduction

The transition from non-living to living matter is usually formulated in a historical manner, aiming to address the origin of life on Earth (Oparin, 1938; de Duve, 1991). However, the sparsity of historical evidence suggests that the “origin of life cannot be discovered; it has to be reinvented” (Eschenmoser and Loewenthal, 1991). This view, together with increasing experimental possibilities and the question of life on exoplanets (Rimmer et al., 2018), broadens the field of investigation to synthetic systems with lifelike properties (Solé, 2016), such as metabolism, reproduction, and evolution (Attwater and Holliger, 2014).

Origin of life scenarios consist of successions of transitions. Major transitions have been outlined (Smith and Szathmáry, 1995; Szathmáry, 2015) but there are so far few empirical validations. Indeed, experiments may face huge parameter spaces and waiting times. Furthermore, studying transitions requires inputs from many disciplines, including chemistry, biochemistry, molecular biology, evolutionary biology, physics, astrophysics, geology, or geochemistry (Preiner et al., 2019). Thus, it remains a challenge to decompose scenarios at a sufficiently fine-grained scale for experimental tests to be possible, while allowing articulation of elementary steps and overall plausibility estimates.

Here, we propose thresholds to be an operational notion that can be used to decompose origin of life scenarios, articulate theory and experiment, and assess scenario plausibility by coordinating interdisciplinary efforts. A threshold can be defined as a major qualitative change undergone by a physical-chemical system upon relatively minor changes in the values of systemic or environmental control parameters. One of the most studied thresholds is Eigen's “error threshold,” which constrains replication-based scenarios of early genetic polymers (Eigen, 1971; Kun et al., 2015; Takeuchi et al., 2017). A number of other prebiotic transitions invoke thresholds explicitly or implicitly: for instance, the appearance of homochirality (Budin and Szostak, 2010, Hawbaker and Blackmond, 2019), replication (Kauffman, 1986; Szathmáry, 2006), compartmentalization (Hargreaves et al., 1977), or Darwinian evolution (Goldenfeld et al., 2017).

Here, we first sample the diversity of thresholds found in origin of life research. Thresholds are encountered at different stages and levels of organization. In the second section, as a case study, we examine the original formulation of the “error threshold” for template-based replication, highlighting its interdisciplinary nature. In the third section, we analyze revisions to the error threshold that aim at establishing more precise or more plausible models. In the fourth section, we generalize the threshold approach to properties of prebiotic systems other than replication. Introducing a phase diagram representation allows us to categorize different types of threshold transitions as a function of the relationship between systems and their environment. In the fifth section, we investigate how to articulate multiple thresholds toward building complete scenarios. In turn, we determine qualitative relationships between transitions, such as entrenchment, contingency, or transience. These relationships are typically used in evolutionary biology but are more generally applicable to prebiotic threshold transitions. Finally, we discuss how thresholds can be used to coordinate research efforts to study the origin of life.

The Diversity of Thresholds in Origin of Life

To set the context, we illustrate the diversity of threshold-type transitions in origin of life research with a non-exhaustive list of examples taken from chemistry and thermodynamics all the way up to evolutionary and Darwinian dynamics (Table 1).

Table 1.

Examples of Thresholds in Origin of Life Scenarios

Threshold Examples	System State before Threshold	System State after Threshold	Variables Triggering the Transition (in Model or Experiment)	Naturalized Variables Posited to Have Triggered the Transition in an Origin of Life Scenario
Chirality symmetry breaking (Budin and Szostak, 2010; Hawbaker and Blackmond, 2019)	Racemic state of a solution	Homochiral state of a solution	Enantiomeric excess	Presence of circularly polarized light, stereospecific crystallization, isotopic enantioselective initiators, auto-catalysis
Spontaneous polymerization (Monnard et al., 2003; Baaske et al., 2007; Lambert, 2008)	Solution of monomers	Solution of polymers	Concentrations of monomers, chemical activation	Ponds evaporation, freeze-thaw cycle, mineral surfaces, thermophoresis in hydrothermal vents, in situ closure in vesicles
Self-assembly of compartments (Bachmann et al., 1992; Todisco et al., 2018)	Solution of free constituents	Solution of molecular self-assembled compartments	Concentration of the constituents, salinity, pH, temperature, molecular crowding	Increase of CO2 concentration, day-night temperature variations, wet-dry cycles
Catalytic closure threshold (Kauffman, 1986)	Solution of polymers with few catalysts	Closed collective autocatalytic sets	Number of catalysts and reactions catalyzed	Spontaneous and effective synthesis of diverse polymers
Error threshold (Eigen, 1971; Takeuchi et al., 2017)	Unreplicated polymers	Polymers copied by template-based replication	Selective advantage, copying error rate, polymers length	Selection of compartments, genotype-phenotype redundancy, mineral surfaces
Decay threshold (King, 1977; Szathmáry, 2006; Vasas et al., 2012)	No autocatalysis	Autocatalytic set	Kinetics, network topology, feedstock concentration	Transient depletion in reactants or rare product of pre-existing reactions
Darwinian threshold (Woese, 2002; Goldenfeld et al., 2017)	Progenotes with high Horizontal Gene Transfer (HGT)	Speciated individuals with high Vertical Gene Transfer	HGT strength (i.e., competence), fitness	Decrease in cell density, nutrient limitation, alkaline shift, toxic chemicals release

Systems states before and after crossing the threshold are listed, along with corresponding physico-chemical variables and prebiotically relevant phenomena.

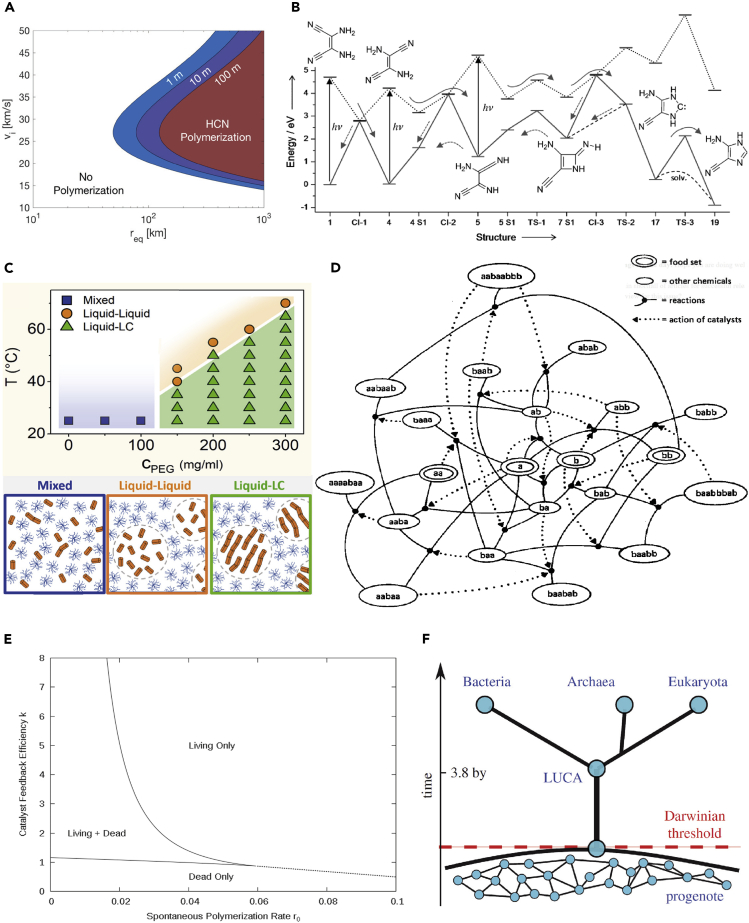
The prebiotic synthesis of the building blocks of life (i.e., amino acids, nucleic acids, sugars, fatty acids) requires reactants to reach sufficient concentrations for the reactions to take place, hence the existence of concentration thresholds. Concentration thresholds can be overcome by acting on physical-chemical conditions resulting from enclosure into vesicles (Luisi et al., 2014), wet-dry cycles (Nelson et al., 2001), freeze-thaw cycles (Monnard et al., 2003; Trinks et al., 2005), adsorption on mineral surfaces (Lambert, 2008), or thermophoresis effects in hydrothermal vents (Baaske et al., 2007). Eutectic ice and meteoritic impacts have been pointed out to overcome a concentration threshold of hydrogen cyanide for its polymerization into purines (Miyakawa et al., 2002; Parkos et al., 2018) (Figure 1A). This pathway to purines includes yet another threshold that concerns free-energy barriers for the formation of intermediate compounds, which could be overcome through exposition to light (Boulanger et al., 2013) (Figure 1B). Since Miller's famous experiment (Miller, 1953), lightning is often considered to overcome such energy thresholds as well. The subsequent polymerization of building blocks (e.g., nucleotides) must also overcome energy thresholds (Dickson et al., 2000), through chemical activation (Wachowius and Holliger, 2019) or adsorption on mineral surfaces (Hazen and Sverjensky, 2010). More generally, when it comes to forming the chemical bonds of biomolecules, a kinetic barrier has been estimated to be around 100 kJ/mol at moderate temperature (Pascal, 2012). Another threshold transition in prebiotic chemistry concerns the emergence of homochirality among biomolecules, i.e., the fact that in extant life amino acids are left-handed and sugars right-handed (Hawbaker and Blackmond, 2019).

Figure 1.

A Sample of Thresholds in Origin of Life Research

(A) Phase diagram representing necessary conditions for a meteoritic impact to deliver a quantity of HCN above a threshold value of 10 mM (required for its polymerization into nucleobases, assuming an oxidizing early Earth atmosphere). Diagram obtained by mathematical modeling; meteorite radius represented on the x axis; impact velocity on the y axis; several mixing depths below water surface are represented (from Parkos et al. (2018) with permission).

(B) Diagram of the photoactivated reactions from cis-DAMN to AICN compounds, which are key intermediates in the prebiotic synthesis of purine nucleotides. Ground and excited states, respectively, represented in solid and dotted lines; dashed arrows indicate backward reactions. This pathway reveals different free-energy barriers of at least 52 kcal/mol that can be overcome thanks to light energy (from Boulanger et al. (2013) with permission).

(C) Liquid-crystal phase diagram delimiting three areas: a homogeneous phase of mixed RNA and polyethylene glycol (PEG) (in blue), a liquid-liquid phase separation of RNA-rich droplets in PEG solution (in orange), and a liquid-liquid crystals (LC) microdomains phase separation (in green). Going from one area to another is made possible by varying temperature or molecular crowding (i.e., PEG concentration) (from Todisco et al. (2018) with permission).

(D) Graph describing an autocatalytic set of theoretical polymers that has reached catalytic closure (threshold). The reactions are represented by nodes connecting reactants and products of ligation and cleavage reactions. Dashed lines indicate catalysis and point from catalyst to catalyzed reaction (from Farmer et al. (1986) with permission).

(E) Phase diagram for an RNA polymerization model as a function of catalyst feedback efficiency k and spontaneous polymerization rate r₀. So called “dead” state characterized by slow spontaneous rate of RNA synthesis, “living” state by rapid autocatalytic rate of RNA synthesis (from Wu and Higgs (2012) with permission).

(F) Diagram representing the conjectured transition from a state of progenote cells (genetic transfer mainly achieved horizontally) to a state of speciated individuals (lineages resulting from vertical genetic transfer). Passed the Darwinian Threshold, individuals go from a communal evolution to a Darwinian evolution. Such a transition can be triggered by a decrease in competence initiated by environmental parameters or selected mutations (from Goldenfeld et al. (2017) with permission).

The emergence of prebiotic compartments can be studied as a phase transition in the thermodynamic sense. Several thresholds that separate phases of dissociated components from self-assembled structures have been identified. Self-assembly thresholds controlling compartments formation can be overcome by varying physical-chemical parameters such as pH, temperature, or molecular crowding. It has been studied for the formation of vesicles (Bachmann et al., 1992), coacervates (Jiang et al., 2015), or microdomains in liquid crystals (Todisco et al., 2018) (Figure 1C). For finite-size structures, such as peptide nanospheres (Carny and Gazit, 2005), mathematical models have established a threshold separating the self-assembled state from a “yield catastrophe phase” where constituents nucleate without stabilizing into final structures, controlled by activation and dimerization rates (Gartner et al., 2020).

Transitions toward self-organization in reaction networks require the spontaneous formation of autocatalytic networks (Kauffman, 1993) (Figure 1D). A first threshold concerns catalytic closure, initially formulated for a model of networks of ligation and fragmentation reactions between peptides (Kauffman, 1986). Catalytic closure implies the existence of a set of peptides such that the formation of any member of the set is catalyzed by another member of the set. In this model, the transition happens when $\frac{E}{N}>\frac{1}{2}$, with $E$ being the number of catalyzed reactions and $N$ the number of peptides (respectively, edges and nodes of the network) (Cohen, 1988). Other models have simulated autocatalytic transitions in the context of template-based replication (Chen and Nowak, 2012; Mathis et al., 2017). Wu and Higgs (2012) for instance examined how variations in catalytic feedback efficiency and spontaneous polymerization rate could induce the crossing of a threshold delimiting a regime of slow spontaneous RNA synthesis from a regime of rapid autocatalytic RNA synthesis (Figure 1E). This transition is stochastic, meaning that the systems explore random chemical compositions in a fixed environment before undergoing the transition.

Once formed, autocatalytic networks need to be sustained. For this, catalysts within autocatalytic networks should exhibit high enough specificity toward the reactions of the network to overcome degradation and losses due to side reactions. Given an autocatalytic set of $p$ reactions, each catalyzed with a specificity $s_i$ (where $i=0,\mathrm{..},p)$, disappearance can be avoided, provided $\prod _{i=1\dots p}{s}_i>\frac{1}{2}$, thereupon revealing a “decay threshold” (Szathmáry, 2006; Vasas et al., 2012; Blokhuis et al., 2020a). Furthermore, for survival to be possible, the concentration of feedstock compounds must stay above a specific value most of the time. For a single autocatalytic reaction, this condition is fulfilled if $R>\frac{a}{k}$, with $R$ being the concentration of reactants, $a$ the degradation kinetic coefficient of the autocatalyst and the kinetic rate of autocatalyst production (King, 1977).

Later stages in origin of life concern the emergence of template-based replication of genetic polymers, which is discussed in detail in the next section, and the emergence of protocells. Early compartments and genetic polymers may not have been strictly associated in lineages. Indeed, compartments provide a way for multilevel selection (Poole, 2009) even when genes are submitted to pooling and mixing (Matsumura et al., 2016). The “progenote stage” has been described as a stage where genes heavily exchange between dividing protocells via horizontal gene transfer (HGT) (Woese and Fox, 1977). The transition from dominant HGT to lineages where genetic polymers and compartments are strongly correlated has been coined the “Darwinian threshold” (Woese, 2002) (Figure 1F). Mathematical models (Arnoldt et al., 2015; Goldenfeld et al., 2017) show that such a threshold can be crossed when the progenotes HGT rate decreases below a specific value. This decrease might result from mutations and environmental changes such as protocell density, alkaline shifts, or nutrient limitation (Claverys et al., 2006; Kovács et al., 2009). In contrast, other authors posit the advent of Darwinian evolution before the appearance of protocells. This is the case of Eigen's theory of template-based replication of genetic polymers (Eigen, 1971; Eigen and Schuster, 1977; Eigen et al., 1988), which we detail in the coming section.

The Error Threshold and the Replicase

The error threshold, introduced by Eigen (1971), has certainly been the most studied threshold in origin of life theories. We draw here on the main findings to make a case study and highlight the usefulness of studying thresholds, the replicase scenario being reviewed elsewhere (Kun et al., 2015; Takeuchi et al., 2017). In the RNA world hypothesis, an RNA capable of catalyzing the polymerization of its own sequence as well as others (Cheng and Unrau, 2010), a generalist self-replicase, is regarded as a primordial replicator capable of Darwinian evolution. The appearance and maintenance of such a replicase regime—a process that we will refer to as the “replicase scenario”—is constrained by the error threshold, which imposes upper bounds on the length of the copied reference sequences given an error rate during replication. More specifically, to avoid the disappearance of the sequence to be copied across rounds of replication, called the “error catastrophe,” the following condition must be fulfilled:

$$l\le \frac{ln\left(s\right)}{e}$$ (Equation 1)

where e is the replicase copying error rate and s the selective advantage, defined as the ratio of the replication rate of the reference sequence to that of the erroneous sequences. Note that Equation (1) was initially derived by Eigen et al. assuming that a polymerase is present and non-limiting or that replication is non-enzymatic (see next section for more precise models). Equation (1) is valid for $s>1$, otherwise this model forbids any reference sequence, including the replicase, to be sustainable. From (Equation 1), we deduce a function $e_{max}=\frac{ln\left(s\right)}{l}$ (red curve on Figure 2A). Owing to the minimum structure complexity required for replicase activity, replicases of a given length $l$ cannot reach perfect fidelity and their error rate must be above a certain value $e_{min}\left(l\right)$ (blue curve on Figure 2A). Bounds $e_{min}$ and $e_{max}$ delineate a domain in the space parametrized by $(l,e)$ so that above $e_{min}$ there exist replicases, and under $e_{max}$, replicase copying can be sustained through faithful replication. If these domains overlap, i.e., if there exists an $l$ such that $e_{max}\left(l\right)\ge e_{min}\left(l\right)$, then the replicase regime is possible in the intersection domain (green zone in Figures 2A and 2B; note that the sheer possibility of the replicase regime does not imply its plausibility). Otherwise, $e_{max}\left(l\right)<e_{min}\left(l\right)$ for all $l$, and the replicase regime has no existence domain (Figure 2C). The latter case corresponds to the so-called Eigen's paradox: no long replicases without replication fidelity, but no fidelity without long replicases.

Figure 2.

Phase Diagrams for the Replicase Scenario

(A–D) (A) Phase diagram showing the areas where the replicase regime is possible (green area delimited by the red and blue curves) in the parameter space (e, l), where $e$ is the error rate of the replicase and $l$ the length of the copied sequences, including the replicase itself. The red curve represents the function $e_{max}$ that sets the maximal replicase error rate $e_{max}$ for each given length $l$ of the copied sequence, and for a given selective advantage (s in Equation (1)); it gives the maximal length of copied sequences, for each given error rate $e$. When $e$ is low enough, $e_{max}\left(l\right)\sim \frac{1}{l}$; when $e$ is close to 1, Equation (1) is no longer valid and $l$ exponentially tends toward 0 (Eigen, 1971). Above the red curve, the copied sequences vanish in the error catastrophe. The blue curve represents the function $e_{min}$ that sets the minimal error rate $e_{min}$ a replicase can reach due to biochemical considerations. As first approximation, higher fidelity needs to be encoded in longer sequences. When $e$ tends toward 1, the blue curve reaches a plateau corresponding to the minimum length that a replicase must have to catalyze a phosphodiester bond between two nucleotides. For a given length, there is no existing replicase under $e_{min}$. Note that $l$ stands for the length of any copied sequence in the case of the red curve, whereas it only stands for the length of the replicase in the case of the blue curve; the representation of the two lengths on the same graph is possible thanks to the fact that the replicase regime assumes that the replicase is itself subjected to replication as well. The blue and red curves are obtained by merging models and experiments; their shape can therefore change. For example, in (B), the existence zone is wider than in (A). In (C), there is no existence zone at all; as a consequence, the replicase scenario must be revised or abandoned in this case. Figure (D) represents the distribution $f$, i.e., the number of available replicases as a function of their copying error rate (at a given illustrative length of 200 nucleotides, as in B). The purple zone bounded between $e_{min}$ and $e_{max}$ depicts the total number of possible sustainable replicases.

If the replicase regime is possible, the next step is to study the plausibility of emergence of a sustainable replicase. First needed is the number $N_l$ of sequences of length $l$ that have a replicase activity with an error rate $e$. The higher this number, the greater the chances of reaching at least one such replicase by a pre-existing generative process. The distribution $f(e,l)$ of these sequences is depicted in Figure 2D for a given length $l$. Second, the pre-existing generative process also determines the plausibility of the transition. A typical model for this regime is random polymerization, where every sequence is generated with equal probability for a given length. There, the fraction of generated polymers of a certain length $g\left(l\right)$ in the polymer population decreases rapidly with $l$. From the distributions $f(e,l)$ and $g\left(l\right)$, we estimate the probability for a sustainable replicase to appear to be:

$$P_r={\sum }_{l}g\left(l\right){\int }_{e_{min}\left(l\right)}^{e_{\max }\left(l\right)}f\left(e,l\right)de$$ (Equation 2)

This probability can be used in the context of an environmental scenario supplying estimates of the total number $N$ of random oligomers present at any moment, their global renewal rate $\rho$ resulting from sequence generation and destruction dynamics. The typical time $t$ required for one replicase to appear then obeys:

$$\rho tN{P}_r\sim 1$$ (Equation 3)

The parameters found in Equations (2) and (3) highlight the highly interdisciplinary nature of the question: the threshold $e_{max}$ is determined by replication dynamics studied in theoretical biology; the distribution $f$ and threshold $e_{min}$ arise from genotype-to-function relationships obtained from biochemical considerations; $g$ depends on the chemistry of spontaneous polymerization; $\rho$ and $N$ depend on geochemical processes, and $t$ should be compared with estimates from geology and planetary system stability analysis.

The analysis leading to (3) is only part of the answer for the replicase scenario: for the replication dynamics to actually start, a replicase needs to encounter either a copy of its own sequence or a complementary sequence. This should probably take place in a compartmentalized setting, where only replicase sequences are present, since otherwise the copying of other sequences would immediately take over the population. Furthermore, the analysis presented so far may be questioned, given that Equations (1, 2, and 3) rely on a number of strong assumptions. We examine some of these considerations in the coming section.

Refining and Revising the Replicase Scenario

The error threshold of Equation (1) relies on a number of simplifying assumptions that have been refined in subsequent models presented here. Such models may lead to lower $e_{max}$, thus reducing the size of the green zone in Figure 3, which goes to the detriment of the replicase scenario. For instance, Eigen's original model ignores the effects of changes in replicase concentration, whereas the latter is impacted by replication. Including this aspect greatly lowers $e_{max}$ (Obermayer and Frey, 2009). Experimental data about RNA replication highlight another required model revision, because replication errors typically lead to shorter sequences rather than to point mutations (Ichihashi and Yomo, 2016). As a result, mutants tend to replicate faster than the original sequence, which means $s<1$ by definition of the selective advantage, so that replicase regimes cannot be sustained (see Section The Error Threshold and the Replicase). Note, however, that it is still unclear whether results obtained with protein replicases used in these experiments extrapolate to hypothetical RNA replicases. In contrast, other model refinements tend to increase $e_{max}$, thus broadening the range of viable replicases. This is the case when considering the abundance of neutral mutations in the neighborhood of the replicase sequence, leading to a “relaxed” error threshold that is significantly lower than Eigen's (Kun et al., 2005; Takeuchi et al., 2005).

Figure 3.

Different Ways of Crossing Thresholds

The y axis represents a relevant environmental variable, whereas the x axis represents a variable of the system itself, in (A), (B), and (C). The phase diagrams are divided into two: a green region β where the system displays a specific property p and a region α where it does not.

(A) The system, initially in point A, acquires the property p in point B thanks to an environmental change from E₁ to E₂, i.e., via an extrinsic transition. Vesicle formation from a micellar solution can be so described, where E would be, for instance, the concentration of dissolved CO₂ (Bachmann et al., 1992).

(B) The system undergoes a transition from A to B because of an internal variation of the system, in a given environment, i.e., via an intrinsic transition. Stochastic transitions from random polymerization to replicating polymers fit in this representation, where X could describe the diversity of generated polymers (Mathis et al., 2017).

(C) The system acquires p (from A to B) thanks to an environmental change. It keeps this property in B” while the environmental variable goes back to its initial value E₁. This is made possible thanks to a transitory change of a variable of the system itself in environment E₂ (from B to B′). For instance, the property p could be the ability to sustain an autocatalytic network, the transient environmental change the shift between dry and rainy periods, and the transition from B to B′ the accumulation of autocatalysts. The y variable would then be environmental hygrometry and the x variable catalyst concentration.

(D) Here, two independent systems in A and B fuse into a single one in C that displays p, in environment E₁. This is the case when autocatalytic networks get encapsulated into compartments, endowing the novel system with the property to evolve through natural selection (Vasas et al., 2012).

Other modifications are revisions of the scenario. So-called hypercycles were first proposed as a way to increase the robustness of the system to replication errors (Eigen and Schuster, 1977). This model is based on a network with multiple molecular species, each species being replicated in a template-based manner while helping the replication of other members of the network. The resulting cooperative dynamics can raise the error threshold, thereby increasing the replicase regime zone (Takeuchi et al., 2017). Other scenarios introduce compartments and more generally spatial structure. The Stochastic Corrector Model (SCM) considers lineages of compartments which grow, are selected, and divide (Szathmáry and Demeter, 1987; Gray et al., 1995). Transient Compartmentalization (TC) assumes simpler cycles consisting of compartmentalization, selection, and pooling (Matsumura et al., 2016; Blokhuis et al., 2020b). Unlike the original model and its Equation (1), SCM and TC authorize the presence of parasite sequences that replicate faster than the reference sequence. This was experimentally demonstrated for TC with replicated RNA (Matsumura et al., 2016). Indeed, in both cases, erroneous copies only locally invade compartments and are removed from the population by compartment-level selection. Surface clusters are an even less constrained setting that allows the maintenance of replication, although less efficiently than non-permeable compartments (Szabó et al., 2002; Shah et al., 2019). These mechanisms increase $e_{max}$, thus also increase the plausibility of the replicase scenario. However, this comes at the cost of assuming the existence of spatial structures and introducing additional parameters (number of molecules per compartment, compartment lifetime, selection process, etc.).

Once the error threshold is determined, the next question is to estimate the fraction of viable replicases in the sequence space. This corresponds to determining the distribution $f$ in Equation (2), which depends on the relationship between sequence and catalytic function, including the minimum possible error rate $e_{min}$ given a certain replicase length. This problem cannot be solved computationally yet and heavily relies on experimental data. Experiments on synthetic replicases show that processivity—the ability to copy long templates is a limiting factor even before considering fidelity. Processivity is notably hampered when copying folded RNAs, which is the case for replicase templates. Consistently, replicases synthesized in the laboratory can copy other RNAs as long as themselves but cannot copy themselves (Horning and Joyce, 2016; Attwater et al., 2018). Another issue is that the sequence space cannot be covered experimentally owing to its astronomical size (∼10¹¹⁴ for a typical 190 nucleotides long replicase [Johnston et al., 2001]). Consequently, experimental data need to be combined with theory and computation in order to estimate $f$. For instance, the diversity of RNA secondary structures is predicted to increase as $1.4848\times n^{-\frac{3}{2}}{\left(1.8488\right)}^n$ where $n$ is the sequence length (Schuster et al., 1994). This is consistently smaller than the $4^n$ possible sequences. Taking structure similarity as a proxy for function indicates an average redundancy in sequences with similar catalytic properties, potentially reducing the size of the space to characterize. A complementary approach is to estimate the tail of distribution $f$ between $e_{min}$ and $e_{max}$ (Figure 2D) using laws of extreme statistics (Gumbel, 1958). Indeed, replicases are rare sequences for which statistics are expected to follow extreme value theory. The latter restricts distributions of rare properties to functional forms (among the Weibull, Gumbel, and Fréchet laws) with few parameters. Such approach has been tested experimentally for proteins (Boyer et al., 2016) and ribozymes (Pressman et al., 2017). Despite the complexity of the genotype-to-phenotype relationship, the limited number of parameters involved in these laws may allow estimates of $f$ from a restricted sample of replicases.

Finally, the transition scenario toward existence of a sustainable replicase may be revised by considering different polymer generation processes anterior to the replicase regime. Polymer generation could have been enhanced by catalysis of polymerization (Hazen and Sverjensky, 2010), ligation (Mutschler et al., 2018), or recombination (Blokhuis and Lacoste, 2017), as well as by size selection (Mizuuchi et al., 2019). An alternative is that autocatalytic sets could have preceded template-based replication and biased polymer populations toward longer and more functional sequences (Vasas et al., 2012). All these processes can add weight to the distribution $g$ in Equation (2) in the length categories corresponding to replicases and contribute to the plausibility of their emergence.

Generalizing the Threshold Approach

We have seen that the error threshold sets a number of requirements on polymerases for them to sustain replication. We now generalize the threshold approach to other properties of prebiotic systems. In Figure 3, the axes correspond to relevant parameters of the system and its environment, and regions α and β, respectively, correspond to systems without and with a property of interest (regions separated by a threshold line). We call this representation a phase diagram, by analogy with equilibrium thermodynamics, extending its use to non-equilibrium regimes as well. In the replicase scenario, region α corresponds to a regime of randomly produced RNAs and region β to sustainable template-based RNA replication, the boundary between the two being the error threshold. In contrast with Figure 2 where the axes stand for system parameters only, the x axis in Figure 3 captures system parameters (e.g., replicase error rate) and the y axis environment variables (e.g., temperature). Note that it is not always obvious to distinguish prebiotic systems from their environment, and choosing a variable as being either part of the system or of the environment may be a matter of choice. Note also that the x axis represents chosen control parameters of the system; other parameters of the system may lie in other dimensions, in particular as encoded by the green shading of β in Figure 3, which indicates the presence of a specific property of the system. A point in the diagram then represents a system with certain fixed properties in a given environment. Such phase diagrams allow us to classify modes by which a system overcomes a threshold and acquires a novel property, i.e., moves from region α to region β. We classify transitions into four modes.

Extrinsic Transition

The acquisition of a new property is here solely driven by the environment. In Figure 3A, the system is initially located at point A in region α and environment E₁; a change from E₁ to E₂ brings the system to B in region β. Since this transition is not caused by any change in the system control parameters, there is no variation along the x axis. Transitions in prebiotic chemistry are typically framed in the context of extrinsic transitions (Kawamura and Maurel, 2017; Kitadai and Maruyama, 2018; Benner et al., 2019), where concentration thresholds are overcome during wet-dry cycles in ponds (Campbell et al., 2019), where steps of nucleobase synthesis occur at the junction of interconnecting streams (Patel et al., 2015), or where hydrogen cyanide is synthesized upon meteorite impacts (Parkos et al., 2018). This mode can also be applied to the appearance of vesicles triggered by CO₂ (Bachmann et al., 1992).

Intrinsic Transition

The novel property here results from changes in parameters of the system while the environment remains unchanged. In Figure 3B, the system is initially located at point A in α with environment E₁ and moves to B in β without any environmental change, simply moving along the x axis. This is the case when a replicase appears from random polymerization as described in the section Refining and revising the replicase scenario (Mathis et al., 2017). Another example is the appearance of autocatalytic sets as modeled by Jain and Krishna (1998). This model assumes that catalytic species only are limiting and follow a dynamic where the least fit species tend to disappear and be randomly replaced by novel catalytic species. Under these assumptions, an autocatalytic set inevitably emerges and fixes. Note that, in the examples cited above, extrinsic transitions are deterministic, whereas intrinsic transitions are stochastic, but this need not always be the case. For a discussion on contingency versus determinism in the origin of life see Luisi (2003).

Scaffolding Transition

The environment changes only transiently, and fixing a novel property requires a combination of the environmental change with a system-driven change. Here, the environment plays the role of a scaffold in the sense that it transiently supports the emergence of a property that is then internalized, i.e., becomes an intrinsic property of the system (Caporael et al., 2014). In Figure 3C, the system starts at point A in region α in environment E₁, then moves to point B in region β via an extrinsic transition triggered by an environmental change to E₂. At this stage, returning to E₁ would bring the system back into α. However, if the property acquired in β allows exploration of neighboring areas along the x axis, the system may reach B′ in β while in environment E₂. Then, an environmental change from E₂ back to E₁ would bring the system from B′ to B,” yet still within β. Such scaffolding transition could be observed when a dilute solution of polymers in a pond (system in A) is submitted to partial evaporation (from E₁ to E₂), thereby reaching a concentration threshold above which autocatalysis becomes possible (system in B), leading it to accumulate enough catalysts (from B to B′) so that once back to wet conditions, autocatalysis is maintained (from B′ to B″).

Symbiotic Transition

Two distinct systems aggregate into a new system thereby acquiring a novel property. In Figure 3D, systems A and B both in α merge into a new system C located in β in a constant environment. Such transition is hypothesized when compartments meet autocatalytic chemistries (Hordijk et al., 2018; Joyce and Szostak, 2018). Both may pre-exist separately, but evolution by natural selection requires autocatalytic chemistries to be compartmentalized in order to provide a collective level of selection (Vasas et al., 2012).

Articulating Series of Thresholds

So far, we have analyzed single threshold transitions. However, origin of life scenarios combine multiple transitions (Szathmáry, 2015; Solé, 2016). There are to date only a few attempts to assemble complete detailed scenarios (Martin et al., 2003; Damer and Deamer, 2020). Research efforts have focused on combining transitions for specific stages, such as the synthesis of building blocks (Patel et al., 2015; Kitadai and Maruyama, 2018; Becker et al., 2019), the emergence of functional RNAs from random ones (Briones et al., 2009; Higgs and Lehman, 2015), or the emergence of evolution from catalytic micelles (Lancet et al., 2018), to cite a few. Below, we apply the phase diagram representation to multiple thresholds. This analysis reveals different types of articulations between threshold transitions: accumulation, entrenchment, contingency, transience, facilitation. These concepts are borrowed from evolutionary biology but are used here to analyze systems that do not necessarily evolve in a Darwinian manner. We indeed consider these concepts to be generally applicable to successions of threshold transitions, heritable transitions through Darwinian evolution only being a particular case.

We first consider the crossing of two successive thresholds. In Figures 4A–4C, the green and blue regions β and γ indicate systems that possess properties p_β and p_γ, respectively; in region α, the system does not possess any of them. Here, the x- and y axes depict relevant variables that can be environmental, systemic, or both. For accumulation of properties p_β and p_γ to be possible, regions β and γ must intersect. Figures 4A–4C depict systems that start from region α, then cross the threshold leading to β, followed by a second threshold-crossing to region γ. A notion stronger than accumulation is entrenchment, where any property p_γ posterior to p_β requires p_β and fixes that property irreversibly. This is illustrated in Figure 4A, where region γ is entirely included in region β. For example, p_β could stand for the existence of catalytic RNAs and p_γ of autocatalytic RNAs. Another threshold articulation is when β and γ intersect without inclusion. Such a situation is characterized by contingency in the sense that p_γ may exist independently of p_β (and vice versa) so that any of the two properties may appear first (Figure 4B, from points A to B or points A to b). This would be the case with the appearance of RNAs (p_γ) together with other genetic polymers (p_β) (Cleaves et al., 2019). Alternative polymers further illustrate transience, where a property is acquired and then lost (Figure 4B, any path from point A to point D). For instance, TNA may have appeared, coexisted with RNA, then disappeared (Yu et al., 2012). Finally, a threshold transition can make a subsequent transition more plausible when acquiring p_β lowers the threshold to acquire p_γ (Figure 4C); this is referred to as facilitation. For example, compartmentalization (p_β) lowers the error threshold that delineates sustainable replication (p_γ) (Matsumura et al., 2016).

Figure 4.

Articulating Different Thresholds

Figures (A), (B), and (C) represent combinations of two phase diagrams, with x- and y axes describing relevant systemic and environmental variables (the representation is simplified to fit a 2D illustration). The green region β and the blue region γ represent two regions where properties p_β and p_γ can be acquired, respectively. The arrows show different ways to cross a succession of two thresholds.

(A) Entrenchment. Region γ is included into region β so that the system must acquire p _β before acquiring p_γ. In this configuration, p_β could stand for the ability to generate random polymers and p_γ for the property of having an autocatalytic set of polymers (Mathis et al., 2017).

(B) Contingency and transience. Region γ partially intercepts region β so that the system can combine p_β and p_γ in C by first acquiring either one of the two properties. Here p_β and pγ could stand for the ability to generate one type of genetic polymer or the other. The system in C would therefore generate both types of polymers at the same time, such as RNA and TNA. Transition from C to D, through a second threshold, shows that a specific property can be lost across phase transitions. It could be the loss of TNA that is not present in the actual living world (Cleaves et al., 2019).

(C) Facilitation. Getting p_β first lowers the threshold delineating p_γ. This is the case when compartmentalization (p_β) raises the error-threshold of a replicating system (p_γ) making it more likely to appear (Matsumura et al., 2016).

(D) This Venn diagram shows different ways of crossing a series of thresholds. Colored edges represent thresholds that delimit domains with novel properties. Each domain is denoted with a Greek letter. Points denoted with a capital Latin letter stand for a given system state. Arrows between points represent possible trajectories of a prebiotic system across successive domains. The figure exhibits contingency (the system can reach C or D from B), enabling constraint (the system in D can reach F but not E), accumulation (the system in C has accumulated properties gained in A and B), entrenchment (the property acquired in B remains in all other locations), and transience (the system in F has lost the property acquired in A).

(E) This graph illustrates how crossing successions of thresholds may account for an increase in lifeness over time.

Consider now the articulation between more than two thresholds as depicted in Figure 4D as a Venn diagram, where thresholds delineate regions corresponding to different properties. For example, a chemical system may start in region α where it has the ability to synthetize random RNAs. By reaching β, it gains the ability to synthesize random peptides as well. Next, reaching γ allows autocatalysis among sets of peptides. Furthermore, in these examples, the system is allowed to accumulate the properties that define α, β, and γ because they all intersect. An example of entrenchment here is RNA oligomer synthesis (α) that is a necessary condition for the existence of autocatalysis in RNA sets (δ is fully included in α). Transience happens if the system loses its ability to synthesize random RNAs (α) but acquires protein RNA replicases (ϕ), as it allows replication of long RNAs from single nucleotides.

The notion of entrenchment can be further refined. As we have seen, it occurs when a system cannot get rid of a feature because too many features have evolved on that basis. As a result, the entrenched feature can narrow down the access to other properties as well as open up other possibilities. The former is known as “contingent irreversibility” (Smith and Szathmáry, 1995) and the latter as “generative entrenchment” (Schank and Wimsatt, 1986) or “enabling constraint” (Kauffman, 2014). In Figure 4D, reaching region δ allows transition to region ε but not ϕ. The advent of homochirality illustrates these notions. Indeed, a racemic mixture of oligonucleotides (region β in Figure 4D) could break its symmetry because of a triggered small enantiomeric excess amplified by an autocatalytic reaction leading either to L-ribose RNA only (region γ) or to D-ribose RNA only (region δ) (Hawbaker and Blackmond, 2019). Entrenchment would follow with peptide synthesis: L-ribose RNA systems could imply D-amino acids peptides only (region ϕ), whereas D-ribose RNA systems could imply L-amino acids peptides only (region ε) (Illangasekare et al., 2010).

Such threshold articulations in origin of life scenarios also make sense in light of the concept of lifeness (also referred to as aliveness or life index) proposed by several authors (Bruylants et al., 2010; Sutherland, 2017; Malaterre and Chartier, 2019). Lifeness stands for a scale where so-called infrabiological systems (Szathmáry, 2005) are positioned between a non-living state and a living state. It remains debated which quantities or measures best account for lifeness. For instance, Bedau (2012) proposes a discrete scale from 0 to 9 depending on the number of interactions between three subsystems: container, metabolism, and program, whereas Malaterre and Chartier (2019) propose a multidimensional gradual scale that integrates system and environment-related functions. In any case, projecting the paths of Figure 4D on any such measure would make threshold transitions appear as sequential jumps, the directionality of paths toward a living state corresponding to increasing lifeness (Figure 4E). In this view, we propose that lifeness corresponds, at first order, to the number of thresholds crossed relative to the total number of thresholds in a given scenario. This suggests a way toward formalizing the notion of chemical evolution: early prebiotic systems may not yet evolve in a canonically Darwinian manner, but in the sense of acquiring and sustaining qualitatively novel properties by crossing thresholds, thereby increasing their lifeness before getting a chance to increasing their fitness.

Discussion

Thresholds define conditions of existence for particular states along the path from inanimate matter to life. Although not all prebiotic transitions are threshold transitions, thresholds pose well-defined problems that can structure interdisciplinary efforts to understand the origin of life (Figure 5). Thresholds may initially be deduced from apparent paradoxes, so-called catch-22 or chicken-and-egg situations stated as: “without X, no Y, and without Y, no X” (Benner, 2018). For instance, from a bird's-eye view of life, metabolism, genetics, and compartments appear so intertwined that there is no obvious scenario for their gradual emergence. As we have seen, thresholds are also detected when taking a closer look at molecular processes, such as template-based replication, or from computer simulations and experiments. Their signatures are discontinuities, hysteresis, and waiting time distributions, as observed with first order phase transitions in physics.

Figure 5.

Threshold Transitions in Origin of Life Research

Identifying a threshold in an origin of life scenario allows the formalization of a parameterized theoretical model. This model can be refined by the output of appropriate experiments, which reciprocally benefit from a refinement of the theoretical model. These back-and-forth relations make it possible to refine the threshold model. The parameters of the threshold model help to integrate several disciplines, among which are physics, chemistry, or molecular biology. If the threshold is such that the transition from one state to another is possible, it can be used as a basis for modeling such a transition within a broader scenario for the transition from non-living to living matter. Transition possibilities are then constrained by hypothesized environments as determined by Earth sciences, geochemistry, astronomy, etc. Plausibility estimates of such transitions allow one to build and estimate multi-stage scenarios articulated around well-identified thresholds. If a scenario reaches a dead-end, it needs to be revised and novel thresholds identified.

Quantitatively characterizing a threshold requires back-and-forth adjustments between theory and experiment. Interestingly, thresholds pose conditions of existence of a given state without referring to any anterior nor posterior state. Thus, their study is independent of a particular transition or scenario in the first place. The starting point is typically a simplified model establishing relationships between parameters. Such a “toy model” has been highly productive in the case of the error threshold, notably pointing to the disciplinary diversity of its parameters. From this point, thorough theoretical investigations of the parameter space and regimes help elaborating hypotheses testable with synthetic experiments in chemistry, systems chemistry, physical-chemistry, soft matter physics, etc. (Solé, 2016; Preiner et al., 2019). In turn, models may be refined until convergence. A possible outcome is that the proposed regime is impossible owing to multiple incompatible thresholds, resulting in a true paradox and the revision of the scenario with alternative regimes. Otherwise, the regime is possible and then comes the question of its plausibility.

To assess plausibility, transition from an anterior state must be accounted for (Orgel, 2008; Schwartz, 2013). Theory, possibly again with back-and-forth adjustment with experiments, estimates the probability of crossing the threshold given the anterior state and environmental conditions as determined by geology, geochemistry, or planetary dynamics (Stüeken et al., 2013; Sasselov et al., 2020). Comparing the crossing probability from different anterior states and environments selects between transitions (e.g., random polymerization or autocatalytic sets before to template-based replication). The plausibility of scenarios finally results from the probability of successions of such transitions. If this total probability is deemed too low, alternative scenarios may lead to consider novel thresholds (e.g., error thresholds with compartment instead of without).

So far, there is no consensus on whether any scenario is devoid of true paradoxes (impossibilities). However, the threshold approach outlined above can establish firm building blocks on the way to constructing scenarios. For this to be effective, studies on the origin of life ought to be explicit with the thresholds they address, the parameters involved, and the relationships between these parameters, following the example of the error threshold.