A Benchmark Open-Source Implementation of COSMO-SAC

Abstract

The COSMO-SAC modeling approach has found wide application in science as well as in a range of industries due to its good predictive capabilities. While other models for liquid phases, as for example UNIFAC, are in general more accurate than COSMO-SAC, these models typically contain many adjustable parameters and can be limited in their applicability. In contrast, the COSMO-SAC model only contains a few universal parameters and sub-divides the molecular surface area into charged segments that interact with each other. In recent years, additional improvements to the construction of the sigma profiles and evaluation of activity coefficients have been made. In this work, we present a comprehensive description how to postprocess the results of a COSMO calculation through to the evaluation of thermodynamic properties. We also assembled a large database of COSMO files, consisting of 2261 compounds, freely available to academic and noncommercial users.

We especially focus on the documentation of the implementation and provide the optimized source code in C++, wrappers in Python, sample sigma profiles calculated from each approach, as well as tests and validation results. The misunderstandings in the literature relating to COSMO-SAC are described and corrected. The computational efficiency of the implementation is demonstrated.

Graphical Abstract

1. Introduction

The calculation of thermodynamic properties of multi-component mixtures is of great importance for the chemical industry. The reason for this is that experimental measurements of mixtures are very time-consuming, costly or involve a high risk when measuring in extreme conditions or considering toxic fluids. In the past, many successful models have been developed. The accuracy of results of predictive models such as the Group Contribution Method (GCM) is based on numerous adjustable parameters which have to be fitted to experimental data. If no adjusted parameters for specific group interactions exist, the model cannot be used. A more predictive alternative to GCM’s such as UNIFAC,^1–6 are models based on quantum mechanical conductor-like screening model (COSMO) calculations, originally proposed by Klamt et al. (conductor-like screening model for real solvents, COSMO-RS).^7–9 Based on the COSMO-RS model, Lin and Sandler¹⁰ developed the COSMO segment activity coefficient model (COSMO-SAC). In these models, the interactions of molecules in a mixture are not modeled as pairwise molecular group interactions, but rather as pairwise interactions of charged surface segments of the molecule that can be obtained from quantum mechanical calculations when the molecule is placed in a perfect conductor. COSMO-based models are models for liquid mixtures which typically depend on temperature and composition only, i.e., the pressure-dependency is usually neglected. However, note that pressure-dependency can be introduced to the model by either combining COSMO-based models with equations of state (see, e.g., refs 11–20) or by modifying the model itself (see, e.g., refs 21,22). While COSMO-based models are useful tools for predicting properties of mixtures, their correct implementation can be tricky and time-consuming. The purpose of this work is therefore to provide a reference implementation of three COSMO-SAC models, which are: the original COSMO-SAC model by Lin and Sandler¹⁰ and the modifications of this model by Hsieh et al.^23,24. These models will be discussed in more detail in section 3.1 (the original model COSMO-SAC-2002¹⁰), section 3.2 (COSMO-SAC-2010²³), and section 3.3 (COSMO-SAC-dsp²⁴). The COSMO-SAC model can in principle be applied to all types of liquid mixtures. Fingerhut et al. examined thoroughly its performance for over ten thousand binary mixtures based on 2295 compounds, including water.²⁵ The method can also be used for polymers²⁶ and, when combined with the Pitzer-Debye-Hückel model, for electrolyte^27,28 and ionic liquids.^29,30 The article is organized thematically by addressing the following aspects of the COSMO-SAC model:

Preprocessing:

1. Generate sigma profile(s) from the results of the COSMO quantum mechanical calculation

2. Split the profile into hydrogen bonding parts if desired

3. Calculate dispersive contributions

Use:

1. Calculate activity coefficients and the excess Gibbs energy

2. Calculate phase equilibria by combining COSMO-SAC with the ideal gas law

2. Part I: COSMO file processing

The COSMO file obtained as the output of a quantum mechanical density-functional-theory calculation is a text file of non-standardized format containing the results of the calculation and information about the molecule. The information needed for creating the sigma profile (see section 2.2) in order to conduct a COSMO-SAC calculation is essentially:

• Volume and surface area of the molecule

• Positions of all nuclei

• Location of each segment patch of the molecule, together with its area and charge

The units of the parameters in the COSMO files are frequently not specified. This un-fortunate historical design decision has led to many mistakes in publications and implementations (see for instance Section 2.2). Therefore, users must be exceptionally careful to ensure that a consistent set of units is used. The most frequent source of confusion is the length unit, which is sometimes given in Bohr radius (atomic units), and sometimes in Ångstroms (Å). The conversion factor from Bohr radius to Å is not large in magnitude (1 Bohr radius a₀ ≈ 0.52918 ų¹), further muddying the waters.

2.1. Atoms, Bonds, and Dispersion

The structural information of the molecules is not required for the original model COSMO-SAC-2002 (see section 3.1). However, the structure of the molecule is important for the more advanced models COSMO-SAC-2010 (see section 3.2) and COSMO-SAC-dsp (see section 3.3).

Position data of all nuclei are read from the COSMO file and converted to the Ångstrom scale by multiplying with the conversion factor 0.52917721067 Å/(Bohr radius) as given by CODATA.³¹ These nuclei position data are used to determine: a) which atoms are bonded to each other, and b) what type of hybridization of the electron orbitals is present in the atom, used in the analysis of dispersion.

The pairwise distance between each pair of nuclei m and n, in Å, is calculated from

$$d_{mm}=\sqrt{{\left(x_m-x_n\right)}^2+{\left(y_m-y_n\right)}^2+{\left(z_m-z_n\right)}^2}.$$ (1)

Whether atoms m and n are covalently bonded is determined by comparing their distance and the sums of the covalent radii of the atoms of the pair. If the distance between atoms is less than the sum of the covalent radii, the atoms are assumed to be bonded together. Covalent radii were obtained from Ref.,³² and these values are also used in the OpenBabel (v2.3.1) cheminformatics library. The covalent radius for carbon was taken to be 0.76 Å (equal to that of the sp³ hybridization).

2.1.1. Hydrogen bonding

COSMO-SAC-2010 and COSMO-SAC-dsp take different types of hydrogen bonding into account. The molecular surface is separated into segments that are non-hydrogen-bonding (nhb) and segments that form hydrogen bonds. The hydrogen-bonding segments are further divided into hydrogen bonds of an hydroxyl group (OH) and other hydrogen bonds (OT). Other hydrogen bonds (OT) consider surface segments of the atoms nitrogen (N), oxygen (O), and fluorine (F) as well as hydrogen (H) atoms bonded to N or F. Therefore, information about bonding needs to be obtained from the COSMO file. The source code for determining nhb, OT, and OH segments is organized as follows: Once it has been determined which atoms are bonded to each other, the hydrogen bonding class of each atom is determined. If the atom is not in the set of (O, H, N, F), the atom is not considered to be a candidate for hydrogen bonding in the COSMO-SAC framework, and is given the hydrogen bonding flag of ”NHB” (non-hydrogen-bonding). If the atom is an N or an F, the atom is considered to hydrogen bond, but is not in the OH family, and therefore, it is given the ”OT” designation (hydrogen bonding, but not OH). If the atom is O or H, the hydrogen bonding class of the atom is:

1. OH: if the atom is O and is bonded to an H, or vice versa

2. OT: if the atom is O and is bonded to an atom other than H, or if the atom is H and is bonded to N or F

3. NHB: otherwise

2.1.2. Dispersion

The models COSMO-SAC-dsp²⁴ and COSMO-SAC 2013³³ take the dispersion contribution to the activity coefficient into account. The dispersive interactions have been considered by Hsieh et al.²⁴ by assuming equally sized atoms with a size parameter σ = 3 Å of the Lennard-Jones potential and assigned a dispersion parameter ϵ_Atom to each atom forming a molecule. They proposed to compute the dispersion parameter of the molecule ϵ_Molecule from the relation

$$\frac{{ϵ}_{\text{Molecule}}}{k_{\text{B}}}=\frac{1}{N_{\text{Atom}}}\sum _{i=1}^n\frac{{ϵ}_{\text{Atom},i}}{k_{\text{B}}},$$ (2)

where ϵ_Atom,i/k_B is the dispersion parameter of atom i, n is the number of atoms in molecule i, and N_Atom is the total number of atoms for which $\left|{ϵ}_{\text{Atom},i}/k_{\text{B}}\right|>0$. The molecular dispersion parameter for the molecule ϵ_Molecule/k_B depends on the atomic structure of the molecule and on the dispersion parameters of each atom ϵ_Atom,i/k_B. A dispersion parameter is attached to each atom, depending on its orbital hybridization. The orbital hybridization of an atom in a molecule is determined by the number of atoms that are bonded to it. In the case of carbon, sp³ hybridization corresponds to four, sp² to three, and sp to two bonded neighbor atoms. In the case of nitrogen, sp³ and sp² hybridization corresponds to three and two bonded neighbor atoms, respectively, and sp to one bonded neighbor atom.

In addition, the w parameter for the COSMO-SAC-dsp model contains additional molecule specific information (see section 3.3). To calculate w, the dispersive nature of the molecules are classified into categories:

• DSP_WATER indicates water

• DSP_COOH indicates a molecule with a carboxyl group

• DSP_HB_ONLY_ACCEPTOR indicates that the molecule is only a hydrogen bonding acceptor

• DSP_HB_DONOR_ACCEPTOR indicates that the molecule is a hydrogen bonding acceptor and donor

• DSP_NHB indicates that the molecule is non-hydrogen-bonding

If the molecule is a water molecule or if the molecule contains a COOH-group, the molecule is tagged as DSP_WATER or DSP_COOH, respectively. Following the implementation of COSMO-SAC-dsp,²⁴ a molecule is treated as DSP_HB_ONLY_ACCEPTOR if the molecule contains any of the atoms O, N, or F but no H-atoms bonded to any of these O, N, or F. Molecules with NH, OH, or FH (but not OH of COOH or water) functional groups are treated as DSP_HB_DONOR_ACCEPTOR. If the molecule meets neither of the hydrogen-bonding criteria and is not water and does not contain a COOH group, it is handled as a non-hydrogen bonding molecule and tagged as DSP_NHB. For the COSMO-SAC-dsp model, if an atom other than C, H, O, N, F, Cl is included, the associated value of ϵ_Atom,i/k_B is set to an undefined value and the calculation is aborted.

2.1.3. Example

The block of the COSMO file with atom locations looks something like the example in Fig. 2 taken from the database of Mullins et al.³⁴ In case of a .cosmo file from DMol³, the location of the atoms (x, y, z) are given in Å. For in stance, the x, y, z position of the first hydrogen nucleus (H1) is (0.888162953 Å, −1.326789759 Å, −0.880602803 Å).

Figure 2:

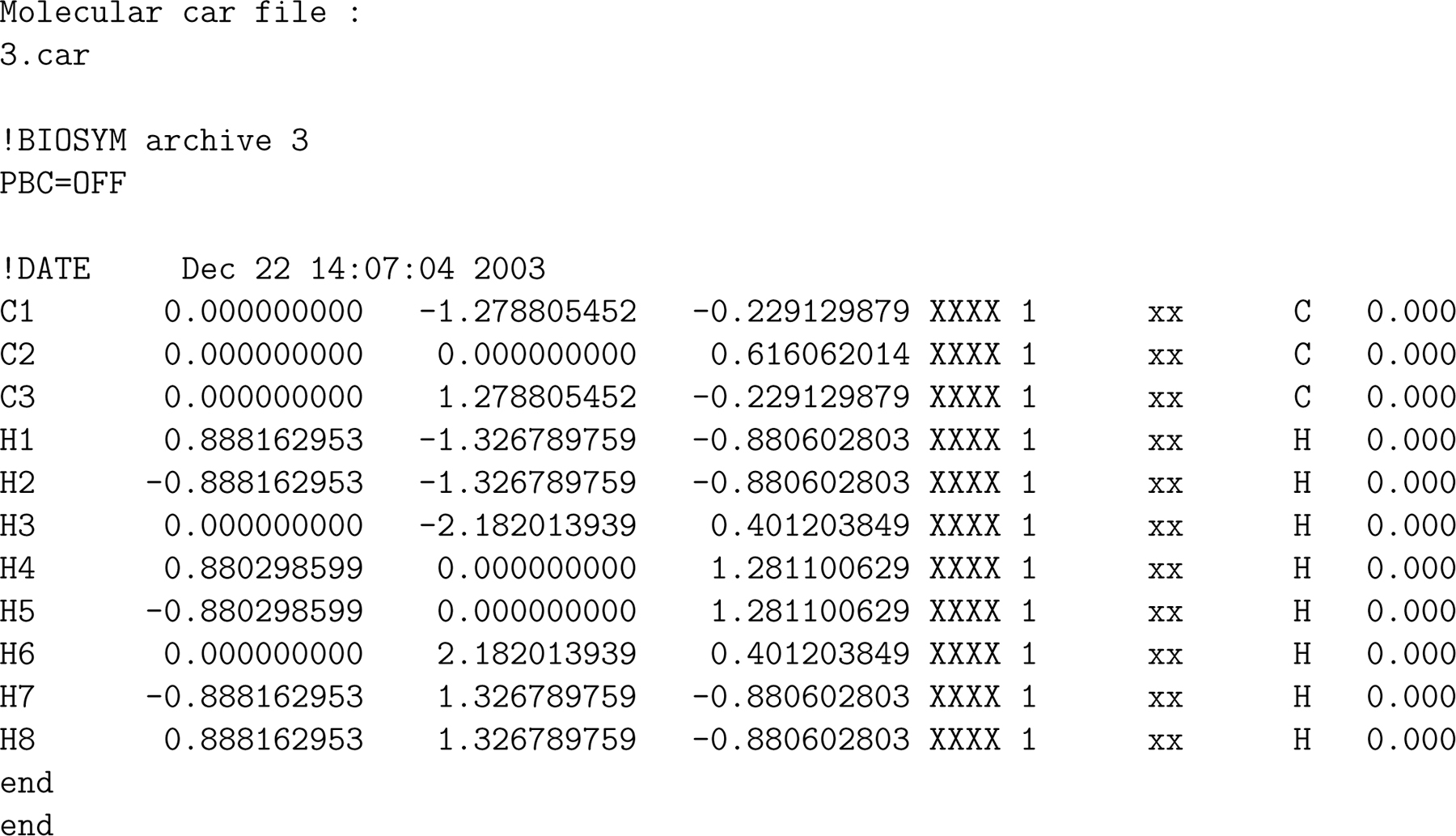
The atom locations (in Å) from the .cosmo file for propane (C₃H₈) from DMol³.

2.2. Sigma Profile Construction

When doing a quantum mechanical COSMO calculation, the output file supplies a charge density ${\sigma }_m^{*}$ on each surface element with area a_n as well as its charge. These numerical values for the surface charge density are truncated to a few significant digits in the COSMO file. When using the charge density values as given in the COSMO file instead of recalculating the charge density by dividing the charge by the surface area of the segment, the differences can be on the order of a few percent. Therefore, for full replicability of numerical values with the values in this work, the charge density of each segment must be calculated from the charge given in the COSMO file divided by the area given in the COSMO file.

The following averaging equation was originally used by Klamt et al.⁸ for COSMO-RS

$${\sigma }_m=\frac{{\sum }_n{\sigma }_n^{*}\frac{r_n^2{r}_{\text{av}}^2}{r_n^2+r_{\text{av}}^2}\exp \left(-\frac{d_{mn}^2}{r_n^2+r_{\text{av}}^2}\right)}{{\sum }_n\frac{r_n^2{r}_{\text{av}}^2}{r_n^2+r_{\text{av}}^2}\exp \left(-\frac{d_{mn}^2}{r_n^2+r_{\text{av}}^2}\right)},$$ (3)

where ${\sigma }_n^{*}$ is the original, non-averaged, surface charge of the n-th segment given in elementary charge e coming directly from the COSMO file, r_n = (a_n/π)^0.5, r_av = 0.5 Å, and d_mn is the distance (in Å) between the centers of the surface segments n and m in Å.

Lin and Sandler¹⁰ used an effective radius for averaging of r_eff = (a_eff /π)^0.5 with a_eff = 7.5 Ų , but otherwise applied a similar methodology as Klamt. Due to a confusion of units in the COSMO file generated by DMol³ (Lin and Sandler¹⁰ thought the coordinates of the centers of the segments used to calculate the distances were in Å but they were in Bohr radii), in the erratum³⁵ to their original article Lin and Sandler¹⁰ had to provide a unit conversion parameter f_decay to correct the distance d_mn from Å to Bohr radius (1 Bohr radius a₀ ≈ 0.52918 Å,³¹ thus f_decay = 0.52918⁻² ≈ 3.57). The corrected equation is given as

$${\sigma }_m=\frac{{\sum }_n{\sigma }_n^{*}\frac{r_n^2{r}_{\text{eff}}^2}{r_n^2+r_{\text{eff}}^2}\exp \left(-f_{\text{decay}}\frac{d_{mn}^2}{r_n^2+r_{\text{eff}}^2}\right)}{{\sum }_n\frac{r_n^2{r}_{\text{eff}}^2}{r_n^2+r_{\text{eff}}^2}\exp \left(-f_{\text{decay}}\frac{d_{mn}^2}{r_n^2+r_{\text{eff}}^2}\right)},$$ (4)

where d_mn is the distance (in Å) between the centers of the surface segments n and m, r_eff = (a_eff /π)^0.5 in Å. Nonetheless, this equation remains dimensionally inconsistent (the argument of the exponential function has units of bohr²/Ų); the parameter f_decay should therefore be thought of as a dimensionless scaling quantity (only). Hence, the practical interpretation of f_decay is that, first, the coordinates of the segments given in bohr are converted to Å and, second, f_decay is used to scale the values given in Å back to the numerical values of bohr (keeping Å as unit).

The model of Lin and Sandler^10,35 was made available as a Fortran source code together with a comprehensive sigma-profile database in the very useful work of Mullins et al.³⁴ They computed the sigma profiles with density-functional-theory calculations using the software DMol³. Note that the parametrization and the results of COSMO models in general depend on the underlying method and software with which the sigma profiles are calculated.³⁶ Hence, it is very important for the comparability and evaluation of these models to use exactly the same set of sigma profiles.

It is furthermore important to note that in the Fortran code for the computation of the sigma profiles, Mullins et al.³⁴ used the same averaging equation as Klamt (Eq. (3)), but with r_av = 0.81764 Å. The use of an averaging radius of r_av = 0.81764 Å and f_decay = 1 is equivalent (when assuming $r_n^2<<r_{\text{av}}^2$) to the assumption of dividing numerator and denominator by f_decay, such that the f_decay correction is applied to the averaging radius.

Once the averaged value of σ_m has been obtained for each segment m, the p(σ)A_i values (probability p(σ) of finding a given segment with specified value of σ multiplied with the entire surface area A_i of molecule i, which gives the surface areas A_i(σ_m) of molecule i with charge densities σ_m) need to be obtained on gridded values. The values of σ for which the p(σ)A values are to be obtained is generally - 0.025 e/Ų to 0.025 e/Ų in increments of 0.001 e/Ų, forming a set of 51 points.

Subsequently for each value of σ (in e/Ų), the (0-based) index corresponding to the left of the value is obtained from

$$i_{\text{left}}=\lfloor \frac{\sigma -\left(-0.025\hspace{0.17em}\text{e}/{\AA }^2\right)}{0.001\hspace{0.17em}\text{e}/{\AA }^2}\rfloor ,$$ (5)

the fractional distance of the value between the left and right edges of the cell are given by

$$w=\frac{\sigma \left[i_{\text{left}}+1\right]-\sigma }{0.001\hspace{0.17em}\text{e}/{\AA }^2},$$ (6)

which is by definition between 0 and 1. The area of the segment is then distributed between the gridded sigma values above and below the value, according to the weighting parameter w:

$$p\left(\sigma \right)A_i\left[i_{\text{left}}\right]+=w{A}_n$$ (7)

$$p\left(\sigma \right)A_i\left[i_{\text{left}}+1\right]+=\left(1-w\right)A_n.$$ (8)

Figure 3 illustrates the construction of the sigma profile for ethanol. For each patch, the value of sigma is obtained, and from that, the value of sigma is then distributed amongst the gridded values. As can be seen in this plot, the histogram is constructed from a relatively small number of patches.

Figure 3:

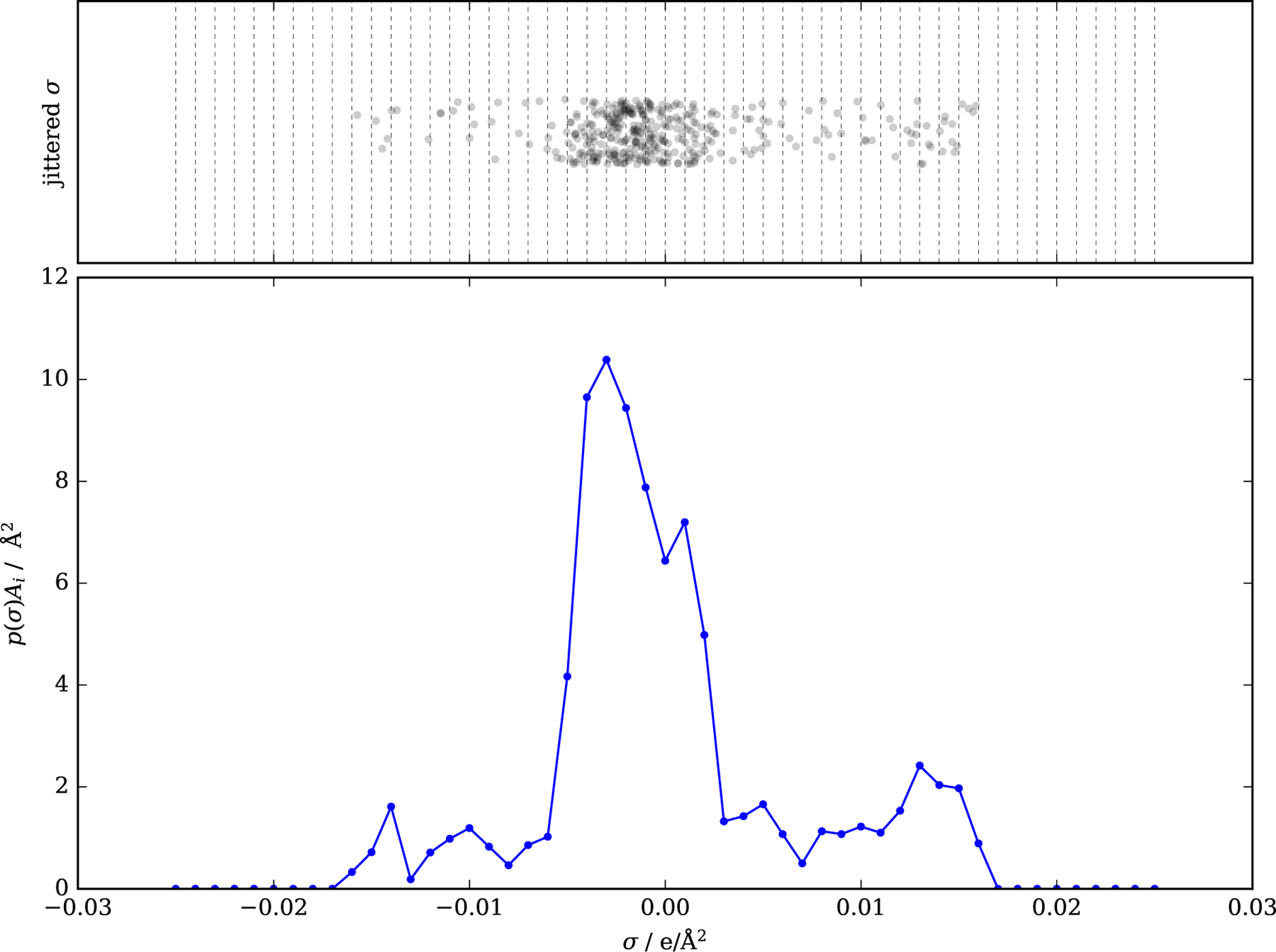
Sigma values for ethanol (single profile, with averaging scheme of Mullins) Top: Values of averaged charge densities on segments (randomly jittered in the vertical direction). Vertical lines correspond to the nodes at which the sigma profile will be generated. Bottom: Sigma profile generated from these σ values.

2.2.1. Example

Figure 4 gives an example of a COSMO file from DMol³. It is important to note that the units are not specified for the areas or the charge. It is especially problematic that the length units differ within the same line of the file (the area in units of Ų, and segment positions are in Bohr radius (from the atomic units (a.u.) system of measurement)), a source of confusion for many authors, ourselves included. Nonetheless, this is a standard file format.

Figure 4:

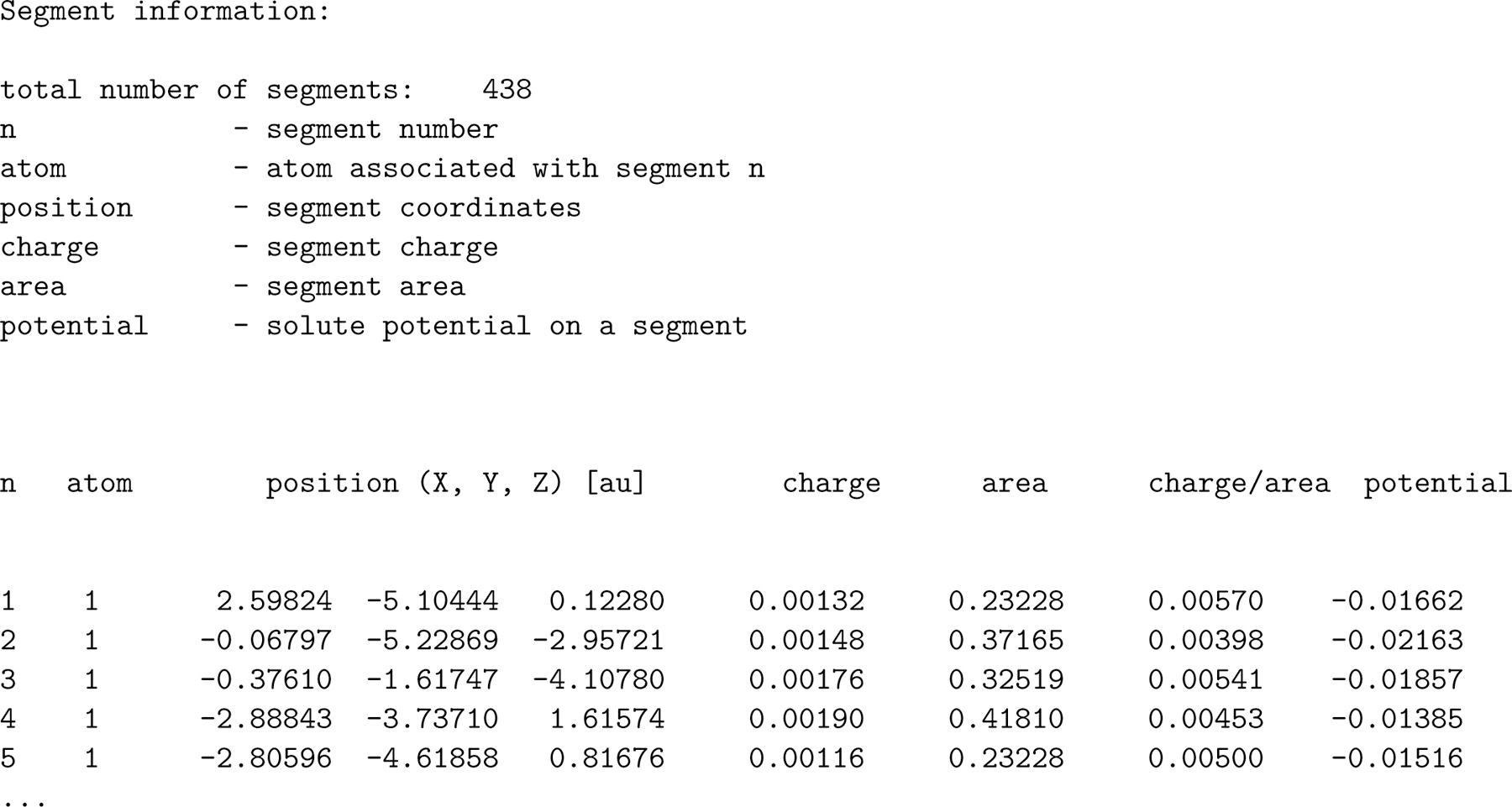
The first five segments of a COSMO file from DMol³. The charge is in units of e, the area in units of Ų, and segment positions are in Bohr radius (from the atomic units (a.u.) system of measurement)

2.3. Splitting of Profiles

Lin et al.³⁷ proposed to split the sigma profile into hydrogen-bonding (hb) and non-hydrogen-hydrogen-bonding (nhb) segments with $p_i\left(\sigma \right)=p_i^{\text{nhb}}\left(\sigma \right)+p_i^{\text{hb}}\left(\sigma \right)$. Hydrogen-bonding atoms were defined to be oxygen, nitrogen, and fluorine atoms as well as hydrogen atoms bound to one of oxygen, nitrogen, or fluorine. Hence, all surfaces belonging to the aforementioned atoms contribute to the sigma profile $p_i^{\text{hb}}\left(\sigma \right)$ and the other atoms forming molecule i contribute to the sigma profile $p_i^{\text{nhb}}\left(\sigma \right)$. Hsieh et al.²³ suggested to further split the hydrogen-bonding sigma profile into interactions of surfaces belonging to groups of oxygen and hydrogen (OH) and surfaces belonging to other groups (OT).

Each atom of the molecule is assigned to be in one of the hydrogen-bonding classes:

• NHB: the atom is not a candidate to hydrogen bond

• OH: the atom is either the oxygen or the hydrogen in a OH hydrogen-bonding pair

• OT: the atom is N, F, or an oxygen that is not part of an OH bonding group

Though these classes are consistent with the work of Hsieh et al.,²³ they do not consider the fact that the H of a COOH group (likewise for other similar groups) is delocalized between the two oxygens of the group.

$$p\left(\sigma \right)=p^{\text{nhb}}\left(\sigma \right)+p^{\text{OH}}\left(\sigma \right)+p^{\text{OT}}\left(\sigma \right).$$ (9)

A currently undocumented feature of the profile splitting is that the contribution for a given segment is deposited into the NHB, OH, or OT sigma profiles depending on its averaged charge density in the following manner:

• If the segment belongs to an O atom, and the hydrogen-bonding class of the atom is OH, and the averaged charge density value of the segment is greater than zero, the segment goes into the OH profile.

• If the segment belongs to an H atom, and the hydrogen-bonding class of the atom is OH, and the averaged charge density value of the segment is less than zero, the segment goes into the OH profile.

• If the segment belongs to an O, N, or F atom, and the hydrogen-bonding class of the atom is OT, and the averaged charge density value of the segment is greater than zero, the segment goes into the OT profile.

• If the segment belongs to an H atom, and the hydrogen-bonding class of the atom is OT, and the averaged charge density value of the segment is less than zero, the segment goes into the OT profile.

• Otherwise, the segment goes into the NHB profile.

By definition, the superpositioned profiles (NHB + OH + OT) must equal the original profile (see Eq. (9)). Wang et al.³⁸ proposed the use of a Gaussian-type function for the probability P of a hydrogen-bonding segment to indeed form a hydrogen bond

$$P^{\text{hb}}\left(\sigma \right)=1-\exp \left(-\frac{{\sigma }^2}{2{\sigma }_0^2}\right)$$ (10)

with σ₀ = 0.007 e/Ų . This probability function considers that not all surfaces belonging to potentially hydrogen-bond forming atoms in fact form hydrogen bonds. With the probability function for hydrogen bonding according to Eq. (10), it follows

$$p^{\text{nhb}}\left(\sigma \right)=\frac{A_i^{\text{nhb}}\left(\sigma \right)}{A_i}+\frac{A_i^{\text{hb}}\left(\sigma \right)}{A_i}\left[1-P^{\text{hb}}\left(\sigma \right)\right],$$ (11)

$$p^{\text{OH}}\left(\sigma \right)=\frac{A_i^{\text{OH}}\left(\sigma \right)}{A_i}{P}^{\text{hb}}\left(\sigma \right),$$ (12)

$$p^{\text{OT}}\left(\sigma \right)=\frac{A_i^{\text{OT}}\left(\sigma \right)}{A_i}{P}^{\text{hb}}\left(\sigma \right),$$ (13)

where $A_i^{\text{nhb}}\left(\sigma \right)$ is the surface area of non-hydrogen-bonding atoms of molecule i, $A_i^{\text{hb}}\left(\sigma \right)=A_i^{\text{OH}}\left(\sigma \right)+A_i^{\text{OT}}\left(\sigma \right)$ is the surface area of hydrogen-bonding segments of molecule i, $A_i^{\text{OH}}\left(\sigma \right)$ is the surface area of hydrogen-bonding segments of OH-groups of molecule i, and $A_i^{\text{OT}}\left(\sigma \right)$ is the surface area of hydrogen-bonding segments other than OH.

2.4. Implementation, Validation and Verification

A Python script profiles/to_sigma.py was written that fully automates the process of reading in a COSMO file from a DMol³ calculation and generates the split profiles as well as calculates the dispersion parameters. The output file with sigma profiles is a space-delimited text file with additional metadata stored in JSON (JavaScript Object Notation) format in the header of the sigma profile. In case of discrepancies between the description above and the Python code, the latter should be used as the reference. This Python script makes heavy use of vectorized matrix operations of the numpy matrix library, especially in case of the sigma averaging, the computationally most expensive part of sigma profile generation. Furthermore, the sigma profile generation from COSMO files is automated with the Python script profiles/generate_all_profiles.py, which generates sigma profiles in parallel. All of these scripts are available in the provided code.

The sigma profiles, dispersion flags, and dispersion parameters are available in the supplemental material for 2261 molecular species. Parameters to carry out the sigma profile averaging (r_av, f_decay) are documented in the header of each sigma profile for reproducibility. All parameters are specified along with their units (where appropriate).

Before carrying out any COSMO-SAC calculations, users should first verify that their implementation yields exactly the same sigma profiles compiled in the supplemental material when processing the provided COSMO files. Values of p(σ) A should agree to within at least 10⁻¹⁵.

Finally, a segment charge visualization tool was written with the three.js javascript library. This tool, driven by a Python-based script, reads the COSMO file and generates an HTML file with the data of the locations and orientations of the segments (and the atoms). The visualization scene is constructed with three.js and behind the scenes, WebGL powers the 3D visualization, allowing for a seamless visualization in three dimensions, even for rather large molecules. This approach is cross-platform, fully open-source, and while intended to be rudimentary, could easily be extended by users for their own application. An example of the visualization tool is provided in Fig. 1, and other examples are available.

Figure 1:

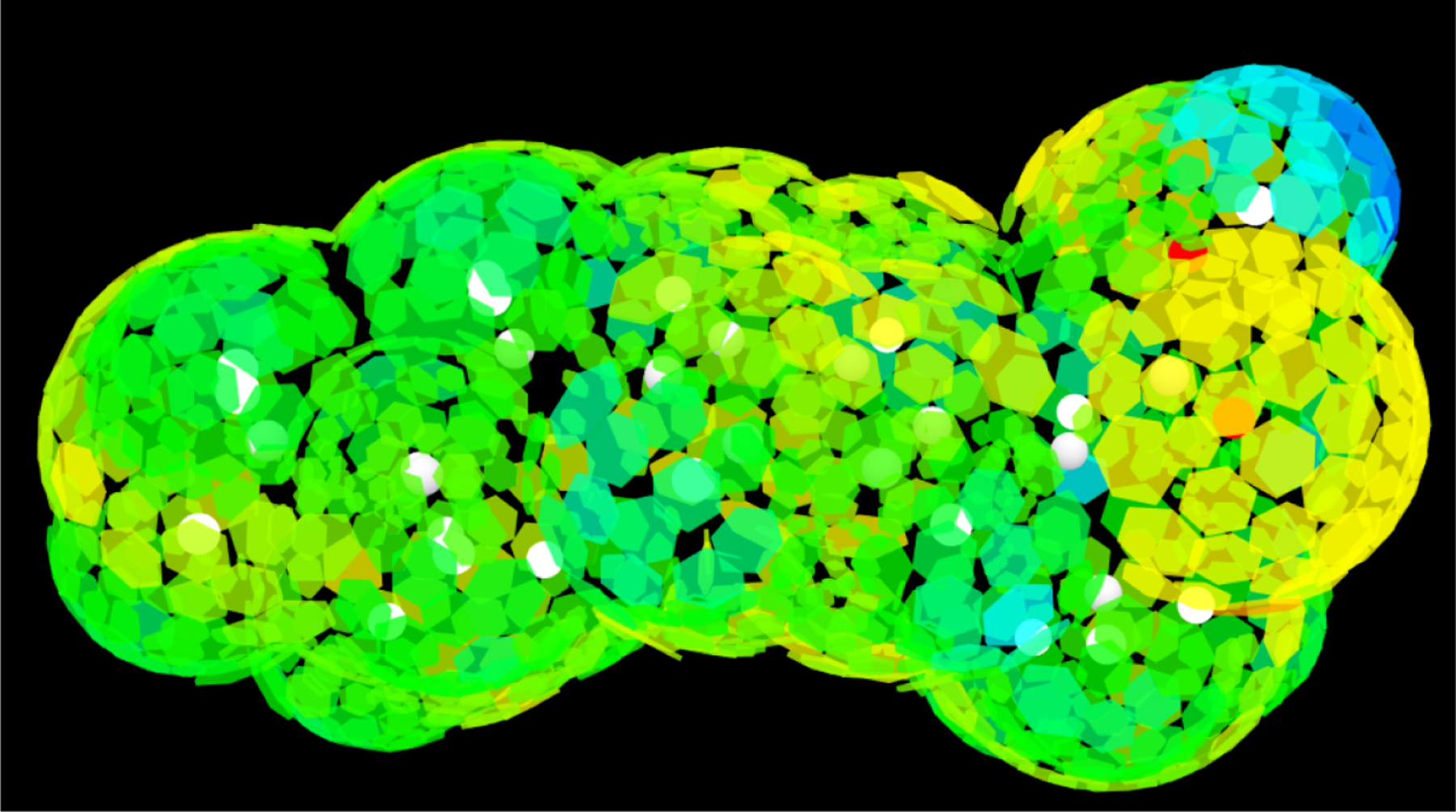
A three-dimensional view of ibuprofen and its segment charge densities (not averaged charge densities) with the visualization tool developed in this work. An interactive HTML file is available in the supplemental material.

3. Part II: Activity Coefficient Calculation

3.1. Model of Lin and Sandler – COSMO-SAC 2002

To generate the sigma profile, in accordance with the work of Mullins et al.,³⁹ we have used the equation from Klamt (Eq. (3)) with the value of effective radius defined by r_av = 0.81764 Å, and all radii in Å. The model parameters are summarized in Table 1.

Table 1:

Parameters of COSMO-SAC 2002 as implemented by Mullins et al.³⁴ and their SI equivalents. The value for the charge of the electron is e = 1.602176634 × 10⁻¹⁹ C.

Parameter	Value	Value (SI)
q0	79.53 Å2	79.53 × 10−20 m2
r0	66.69 Å3	66.69 × 10−30 m3
z	10	10
rav	0.81764 Å	8.1764 × 10−11 m
aeff	7.5 Å2	7.5 × 10−20 m2
chb	85580 kcal Å4 mol−1 e−2	1.3949003091892562 × 106 J m−4 mol−1 C−2
σhb	0.0084 e Å−2	0.134582837256 C m−2
α′†	16466.72 kcal Å4 mol−1 e−2	2.6839720518033312 × 105 J m−4 mol−1 C−2
R	0.001987 kcal mol−1 K−1	8.313608 J mol−1 K−1

^†: Mullins et al. used an erroneous value in their Table 1. The correct value for the misfit energy parameter¹⁰ is obtained from $\left(0.3f_{\text{pol}}\cdot a_{\text{eff}}^{3/2}\right)/{\epsilon }_0$, with ε₀ = 2.395 × 10⁻⁴ (e² mol)/(kcal Å), ϵ = 3.667, f_pol = (ϵ – 1)/(ϵ + 0.5), and a_eff = 7.5 Ų, according to the FORTRAN code of Mullins et al.

According to Lin and Sandler,¹⁰ the activity coefficient γ_i,S of component i in the liquid mixture S can be obtained from the equation

$$\ln \left({\gamma }_{i,\text{S}}\right)=\ln \left({\gamma }_{i,\text{S}}^{\text{c}}\right)+\ln \left({\gamma }_{i,\text{S}}^{\text{r}}\right),$$ (14)

where the combinatorial part $\ln \left({\gamma }_{i,\text{S}}^{\text{c}}\right)$ accounts for the size and shape differences of the molecules. This quantity is usually described by the Staverman-Guggenheim combinatorial term

$$\ln \left({\gamma }_{i,\text{S}}^{\text{c}}\right)=\ln \left(\frac{{\varphi }_i}{x_i}\right)+,\frac{z}{2}{q}_i\ln \left(\frac{{\theta }_i}{{\varphi }_i}\right)+l_i-\frac{{\varphi }_i}{x_i}\sum _j{x}_j{l}_j,$$ (15)

with

$${\theta }_i=\frac{x_i{q}_i}{{\sum }_j{x}_j{q}_j},$$ (16)

$${\varphi }_i=\frac{x_i{r}_i}{{\sum }_j{x}_j{r}_j},$$ (17)

$$l_i=\frac{z}{2}\left(r_i-q_i\right)-\left(r_i-1\right),$$ (18)

and

$$r_i=V_i/r_0,$$ (19)

Here r₀ = 66.69 ų denotes the normalized volume parameter and

$$q_i=A_i/q_0,$$ (20)

where q₀ = 79.53 Ų denotes the normalized surface area parameter and z is the coordination number, which was chosen to be 10. Note that r₀ is not needed to calculate the combinatorial term as it cancels out internally in Eq. (15), see, e.g., Ref. 33. V_i is the molecular volume of component i and A_i is the molecular surface area of component i coming from the COSMO calculations. Note that in the article by Lin and Sandler,¹⁰ there are misplaced parentheses in the equation for l_i, which was corrected in Eq. (18) (compare, e.g., Ref.¹).

In the case of infinite dilution, when one of the mole fractions goes to zero, Eqs. (16) and (17) are ill-defined because division by zero occurs. The terms in Eq. (15) leading to division by zero can be rewritten as

$$\frac{{\theta }_i}{x_i}=\frac{q_i}{{\sum }_j{x}_j{q}_j},$$ (21)

$$\frac{{\varphi }_i}{x_i}=\frac{r_i}{{\sum }_j{x}_j{r}_j},$$ (22)

$$\frac{{\theta }_i}{{\varphi }_i}=\frac{x_i}{\frac{{\varphi }_i}{x_i}},$$ (23)

and were used throughout.

The residual part $\ln \left({\gamma }_{i,\text{S}}^{\text{r}}\right)$, which is also called the restoring free energy part, mainly accounts for electrostatic interactions between the molecules in the mixture. According to a statistical mechanical derivation by Lin and Sandler,¹⁰ the residual part of the activity coefficient can be obtained as follows

$$\ln \left({\gamma }_{i,\text{S}}^{\text{r}}\right)=n_i\sum _{{\sigma }_m}{p}_i\left({\sigma }_m\right)\left[\ln \left({\Gamma }_{\text{S}}\left({\sigma }_m\right)\right)-\ln \left({\Gamma }_i\left({\sigma }_m\right)\right)\right],$$ (24)

where n_i denotes the number of surface segments of molecule i with a standard segment surface area a_eff and can be calculated according to:

$$n_i=\frac{A_i}{a_{\text{eff}}}$$ (25)

σ_m is the screening charge density of segment m, which is the average screening charge of the surface segment divided by a_eff , p_i (σ_m ) denotes the probability of finding a segment with screening charge density σ_m on the surface of component i, Γ_S (σ_m) is the activity coefficient of segment m in the mixture, and Γ_i (σ_m) is the activity coefficient of segment m in the mixture of segments of only pure component i. The quantity p_i (σ_m) is called the sigma profile of pure component i and is defined as

$$p_i\left({\sigma }_m\right)=\frac{A_i\left({\sigma }_m\right)}{A_i},$$ (26)

where A_i(σ_m) is the surface area with screening charge density σ_m of a molecule of species i and A_i is again the entire surface area of the molecule of species i. The sigma profile of the mixture S can then be obtained by

$$p_{\text{S}}\left({\sigma }_m\right)=\frac{{\sum }_{i=1}^N{x}_i{A}_i{p}_i\left({\sigma }_m\right)}{{\sum }_{i=1}^N{x}_i{A}_i},$$ (27)

where x_i is the mole fraction of component i. The segment activity coefficient in the mixture can be calculated from

$$\ln \left({\Gamma }_{\text{S}}\left({\sigma }_m\right)\right)=-\ln \left\{\sum _{{\sigma }_n}{p}_{\text{S}}\left({\sigma }_n\right)\hspace{0.17em}{\Gamma }_{\text{S}}\left({\sigma }_n\right)\exp \left[-\frac{\Delta W\left({\sigma }_m,{\sigma }_n\right)}{RT}\right]\right\}$$ (28)

where the sum on the right hand side goes over all charge densities σ_n in the mixture. Note that Eq. (28) needs to be solved numerically for the segment activity coefficients Γ_S (σ_m). The quantity ∆W (σ_m, σ_n) is called the exchange energy and can be calculated from

$$\Delta W\left({\sigma }_m,{\sigma }_n\right)=\left(\frac{{\alpha }^{\prime }}{2}\right){\left({\sigma }_m+{\sigma }_n\right)}^2+c_{\text{hb}}\max \left[0,{\sigma }_{\text{acc}}-{\sigma }_{\text{hb}}\right]\min \left[0,{\sigma }_{\text{don}}+{\sigma }_{\text{hb}}\right]$$ (29)

where the first term on the right hand side is the misfit energy, accounting for the electrostatic interactions, and the second term on the right hand side accounts for hydrogen-bonding interactions. The values of the generalized parameters are: α′ = 16466.72 kcal Å⁴ mol⁻¹ e⁻², c_hb = 85580 kcal Å⁴ mol⁻¹ e⁻², and σ_hb = 0.0084 e Å⁻² (with 1 kcal = 4184 J). Note that – in accordance with the FORTRAN code supplied by Mullins et al.³⁴ – the value for α′ given in the article of Lin and Sandler¹⁰ was used rather than the different value provided in the article by Mullins et al.³⁴ Furthermore, σ_acc = max(σ_m, σ_n) and σ_don = min(σ_m, σ_n)) holds. Γ_i (σ_m) and Γ_S (σ_m) have a similar form

$$\ln \left({\Gamma }_i\left({\sigma }_m\right)\right)=-\ln \left\{\sum _{{\sigma }_n}{p}_i\left({\sigma }_n\right)\hspace{0.17em}{\Gamma }_i\left({\sigma }_n\right)\exp \left[-\frac{\Delta W\left({\sigma }_m,{\sigma }_n\right)}{RT}\right]\right\}.$$ (30)

3.2. Model of Hsieh et al. – COSMO-SAC 2010

In 2010, Hsieh et al.²³ suggested an improvement of COSMO-SAC for phase equilibrium calculations based on the modifications published by Lin et al.³⁷ and Wang et al.³⁸ Hsieh et al. proposed two modifications for Eq. (29), which in their model reads

$$\Delta W\left({\sigma }_m^t,{\sigma }_n^s\right)=c_{\text{ES}}\left(T\right)\cdot {\left({\sigma }_m^t+{\sigma }_n^s\right)}^2-c_{\text{hb}}\left({\sigma }_m^t,{\sigma }_n^s\right){\left({\sigma }_m^t-{\sigma }_n^s\right)}^2,$$ (31)

where the superscripts t and s denote different types of sigma profiles. The first modification concerns the electrostatic interaction parameter c_ES, which was made temperature dependent

$$c_{\text{ES}}=A_{\text{ES}}+\frac{B_{ES}}{T^2},$$ (32)

with A_ES = 6525.69 kcal Å⁴ mol⁻¹ e⁻² and B_ES = 1.4859 × 10⁸ kcal Å⁴ K² mol⁻¹ e⁻². The second modification concerns the hydrogen-bonding term given in Eq. (31). With this distinction, the parameter c_hb is defined as follows

$$c_{\text{hb}}\left({\sigma }_m^t,{\sigma }_n^s\right)=\{\begin{array}{ll}{c}_{\text{OH-OH}}\hfill & \text{if}\hspace{0.17em}s=t=\text{OH}\hspace{0.17em}\text{and}\hspace{0.17em}{\sigma }_m^t\cdot {\sigma }_n^s<0\hfill \\ c_{\text{OT-OT}}\hfill & \text{if}\hspace{0.17em}s=t=\text{OT}\hspace{0.17em}\text{and}\hspace{0.17em}{\sigma }_m^t\cdot {\sigma }_n^s<0\hfill \\ c_{\text{OH-OT}}\hfill & \text{if}\hspace{0.17em}s=\text{OH,}\hspace{0.17em}t=\text{OT,}\hspace{0.17em}\text{and}\hspace{0.17em}{\sigma }_m^t\cdot {\sigma }_n^s<0\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array},$$ (33)

where c_OH−OH = 4013.78 kcal Å⁴ mol⁻¹ e⁻², c_OT−OT = 932.31 kcal Å⁴ mol⁻¹ e⁻², and c_OH−OT = 3016.43 kcal Å⁴ mol⁻¹ e⁻². Due to the separation of the sigma profiles into nhb, OT, and OH contributions, an additional sum over the different sigma-profiles needs to be introduced in Eqs. (24), (28), and (30). Equation (24) becomes

$$\ln \left({\gamma }_{i,\text{S}}^{\text{r}}\right)=n_i\sum _{\text{t}}^{\text{nhb,OH,OT}}\sum _{{\sigma }_m}{p}_i^t\left({\sigma }_m^t\right)\left[\ln \left({\Gamma }_{\text{S}}^t\left({\sigma }_m^t\right)\right)-\ln \left({\Gamma }_i^t\left({\sigma }_m^t\right)\right)\right],$$ (34)

and Eq. (29) becomes

$$\ln \left({\Gamma }_{\text{S}}^t\left({\sigma }_m^t\right)\right)=-\ln \left\{\sum _s^{\text{nhb,OH,OT}}\sum _{{\sigma }_n}{p}_{\text{S}}^s\left({\sigma }_n^s\right){\Gamma }_{\text{S}}^s\left({\sigma }_n^s\right)\exp \left[-\frac{\Delta W\left({\sigma }_m^t,{\sigma }_n^s\right)}{RT}\right]\right\}.$$ (35)

Equation (30) can again be obtained by changing the index S to i in Eq. (35). For COSMO-SAC 2010, Hsieh et al.²³ used the sigma profile database of Mullins et al.³⁴

Furthermore the value for a_eff was changed to 7.25 Ų and the sigma profile averaging equation according to Eq. (4) was used. A summary of the model parameters is given in Table 2.

Table 2:

Parameters of COSMO-SAC 2010 and their SI equivalents. The value for the charge of the electron is e = 1.602176634 × 10⁻¹⁹ C

Parameter	Value	Value (SI)
q0	79.53 Å2	79.53 ×10−20 m2
r0	66.69 Å3	66.69 × 10−30 m3
z	10	10
aeff	7.25 Å2	7.25 × 10−20 m2
reff	(aeff/π)0.5
fdecay	3.57	3.57
cOH−OH	4013.78 kcal Å4 mol−1 e−2	6.542209585204081 × 104 J m4 mol−1 C−2
cOT-OT	932.31 kcal Å4 mol−1 e−2	1.5196068091379239 × 104 J m4 mol−1 C−2
cOH-OT	3016.43 kcal Å4 mol−1 e−2	4.916591656517583 × 104 J m4 mol−1 C−2
σ0	0.007 e Å−2	0.11215236437999998 C m2
AES	6525.69 kcal Å4 mol−1 e−2	1.06364652940795 × 105 J m4 mol−1 C−2
BES	1.4859 108 kcal Å4 K2 mol−1 e−2	2.421923778247623 × 109 J m4 K2 mol−1 C−2
NA	6.022140758 × 1023 mol−1	6.022140758 × 1023 mol−1
kB	1.38064903 × 10−23 J K−1	1.38064903 × 10−23 J K−1
R	kBNA/4184 kcal mol−1 K−1	kBNA J mol−1 K−1

3.3. Model of Hsieh at el. – COSMO-SAC-dsp

On the basis of their model modification summarized in section 2.2, Hsieh et al.²⁴ proposed to also take dispersive interactions between the molecules into account, which were entirely neglected before. The activity coefficient of component i in the mixture S then becomes

$$\ln \left({\gamma }_{i,\text{S}}\right)=\ln \left({\gamma }_{i,\text{S}}^{\text{c}}\right)+\ln \left({\gamma }_{i,\text{S}}^{\text{r}}\right)+\ln \left({\gamma }_{i,\text{S}}^{\text{dsp}}\right),$$ (36)

with ${\gamma }_{i,\text{S}}^{\text{dsp}}$ being the contribution to the activity coefficient due to dispersion. The combinatorial part $\ln \left({\gamma }_{i,\text{S}}^{\text{c}}\right)$ and the residual part ln $\ln \left({\gamma }_{i,\text{S}}^{\text{r}}\right)$ are calculated in the same way and with the same parameters as given in sections 2.1 and 2.2, respectively. Hsieh et al.²⁴ suggest the use of the one-constant Margules equation for the calculation of the dispersive interaction and give the following equations for a binary mixture of components 1 and 2

$$\ln \left({\gamma }_{1,\text{S}}^{\text{dsp}}\right)=A{x}_2^2\hspace{0.17em}\text{and}\hspace{0.17em}\ln \left({\gamma }_{2,\text{S}}^{\text{dsp}}\right)=A{x}_1^2.$$ (37)

As given in the article by Hsieh et al.,²⁴ the parameter A can be calculated according to

$$A=w\left[0.5\left({ϵ}_1+{ϵ}_2\right)-\sqrt{{ϵ}_1{ϵ}_2}\right],$$ (38)

with the definition of w given in a corrigendum by Hsieh et al.⁴⁰

$$w=\{\begin{array}{ll}-0.27027\hfill & \text{if}\hspace{0.17em}\text{water+hb-only-acceptor}\hfill \\ -0.27027\hfill & \text{if}\hspace{0.17em}\text{COOH+}\left(\text{nhb}\hspace{0.17em}\text{or}\hspace{0.17em}\text{hb-only-acceptor}\right)\hfill \\ -0.27027\hfill & \text{if}\hspace{0.17em}\text{water+COOH}\hfill \\ 0.27027\hfill & \text{otherwise}\hfill \end{array}.$$ (39)

Hsieh et al.²⁴ define substances as hb-only-acceptor, if they are able to form a hydrogen-bond by accepting a proton from its neighbor and hb-donor-acceptors as substances that are able to form hydrogen-bonds by either providing or accepting a proton from its neighbors. All substances containing a carboxyl group are denoted with COOH. Note that there is a typographical error in the corrigendum, where the value w = −0.27027 is proposed for the combination of “COOH + nhb or hb-only-acceptor”, whereas in the article, this value for w is given for the combination of “COOH + nhb or hb-donor-acceptor”. Furthermore, note that there also is a confusion of units in the original article, as the constant A should be dimensionless and the dispersion parameters are usually divided by Boltzmann’s constant k_B = 1.380649 × 10⁻²³ J K⁻¹ (value taken from⁴¹). Therefore, we implemented Eq. (38) and Eq. (39) as follows

$$A=w\left[0.5\left(\frac{{ϵ}_1}{k_{\text{B}}}+\frac{{ϵ}_2}{k_{\text{B}}}\right)-\sqrt{\frac{{ϵ}_1}{k_{\text{B}}}\frac{{ϵ}_2}{k_{\text{B}}}}\right],$$ (40)

and

$$w=\{\begin{array}{ll}-0.27027\hspace{0.17em}{\text{K}}^{-1}\hfill & \text{if}\hspace{0.17em}\text{water+hb-only-acceptor}\hfill \\ -0.27027\hspace{0.17em}{\text{K}}^{-1}\hfill & \text{if}\hspace{0.17em}\text{COOH+}\left(\text{nhb}\hspace{0.17em}\text{or}\hspace{0.17em}\text{hb-only-acceptor}\right)\hfill \\ -0.27027\hspace{0.17em}{\text{K}}^{-1}\hfill & \text{if}\hspace{0.17em}\text{water+COOH}\hfill \\ 0.27027\hspace{0.17em}{\text{K}}^{-1}\hfill & \text{otherwise}\hfill \end{array}.$$ (41)

The dispersion parameters of the atoms have been fitted to experimental data by Hsieh et al.²⁴ and are listed in Table 3 (already considering the corrigendum⁴⁰). The other model parameters stayed the same as already given in Table 2.

Table 3:

Dispersion parameters for atom types in COSMO-SAC-dsp as implemented by Hsieh et al.²⁴

Atom type i	(ϵAtom,i/kB) / K	Note
C (sp3)	115.7023	bonded to four others
C (sp2)	117.4650	bonded to three others
C (sp)	66.0691	bonded to two others
N (sp3)	15.4901	bonded to three others
N (sp2)	84.6268	bonded to two others
N (sp)	109.6621	bonded to one other
–O–	95.6184	bonded to two others
=O	−11.0549	double-bonded O
F	52.9318	bonded to one other
Cl	104.2534	bonded to one other
H (water)	58.3301	H in water
H (OH)	19.3477	H-O bond (not water)
H (NH)	141.1709	H bonded to N
H (other)	0
other	invalid

The QM/COSMO calculation results from the University of Delaware database³³ were used for the development of COSMO-SAC-dsp model. This database can be considered as a revised and extended version of the VT-database^34,39 and was developed with the co-operation of Stanley Sandler’s research group at the University of Delaware and Dr. S. Lustig, formerly at DuPont. The basis set used in Dmol³ was the GGA/VWN-BP/DNP functional with double numerical basis with polarization functions (DNP). The detailed procedure for obtaining the equilibrium geometry and the screening charges can be found in Ref. 34. The effects from using different combination of DFT methods and basis set were studied by Chen et al.⁴² More details are available in Xiong et al.³³ A fully-open-source set of sigma profiles generated from an open-source quantum chemical tool is available⁴³ at https://github.com/lvpp/sigma for the release 18.07,⁴⁴ and their use in a COSMO approach has been investigated previously.^45,46

4. Implementation Details for the COSMO-SAC Models

The numerical method used to solve the non-linear system of Eqs. (28) and (35) is the successive substitution method. This method is the solver used in the code of Mullins et al.³⁴ forming the basis of this implementation. Successive substitution is characterized as being both reliable and slowly convergent. Analysis of the successive substitution method and a comparison with the Newton-Raphson method is provided in Possani and de P. Soares.⁴⁷

To solve the segment activity coefficient of Eqs. (28) and (35), initial values have to be specified for Γ_S (σ_n) and ${\Gamma }_{\text{S}}^s\left({\sigma }_n^s\right)$, respectively. Therefore all values of Γ are set to unity before initiating the calculation for all intervals of the considered pure molecule or mixture. After the first iteration, the newly calculated Γ will be averaged with the previous values and the differences between the averaged and former values ∆Γ will serve as convergence criteria. Only when ∆Γ of every interval reaches the convergence criterion (here, that the maximum absolute difference between values of Γ is less than 10⁻⁸), the successive substitution will be terminated, otherwise the iteration starts again with the averaged Γ substituting the previous initial values.

Furthermore, the equations can be rewritten to remove the evaluation of the logarithm, as the evaluation of log(exp(x)) is computationally much more expensive than division. Therefore, a slightly more efficient implementation (here, demonstrated for the case of the mixture segment activity coefficients with one sigma profile) is

$${\Gamma }_{\text{S},\text{new}}={\left\{\sum _{{\sigma }_n}{\text{A}}^{(+)}{\Gamma }_{\text{S},\text{old}}\left({\sigma }_n\right)\right\}}^{-1}.$$ (42)

In the present C++ code, the sum on the right hand side is carried out in a vectorized form with matrix-vector operations from the Eigen library. Furthermore, the matrix

$${\text{A}}^{(+)}=\exp \left[-\frac{\Delta W\left({\sigma }_m,{\sigma }_n\right)}{RT}\right]p_{\text{S}}\left({\sigma }_n\right)$$ (43)

can be precalculated, as it does not depend on the current value of Γ_S,old. This operation can be carried out by multiplying each row of the matrix exp(−∆W/(RT )) by p_S (σ_n) in a coefficient-wise sense.

In the code by Mullins et al.,³⁴ the sum in Eq. (42) contains all elements of the sigma profile, but this is not necessary as charge densities which do not exist in a molecule do not contribute to the sum. Especially in the case of relatively nonpolar molecules (e.g., the alkanes), only a small fraction of the range of σ is populated. Therefore, it is necessary to, at the time of loading the model, determine the range of σ that is found in any molecule. The range of σ is obtained by considering the non-hydrogen-bonding profile of an equimolar mixture of components. It is not necessary to consider the OT or OH profiles because the NHB will at least have a small contribution from each of the other profiles, according to Eq. (10). The minimum and maximum values of σ with a contribution p(σ)A greater than zero are retained, and only these elements are evaluated.

5. Vapor-Liquid Equilibrium Calculations

Pressure-composition diagrams are created by calculating boiling and dew pressures for a selection of compositions to generate the complete boiling and dew point curves. In order to calculate phase equilibria, the fugacity of the vapour phase $f_i^{\text{vap}}$ for each component i has to be equal to the fugacity of the liquid phase $f_i^{\text{liq}}$ of the same component in a mixture with given mole fractions x_i

$$f_i^{\text{vap}}=f_i^{\text{liq}}.$$ (44)

The fugacity is defined as f_i = φ_ix_ip and the activity coefficient for the liquid phase as ${\gamma }_i^{\text{liq}}={\phi }_i^{\text{liq}}/{\phi }_{i,0}^{\text{liq}}$, so that Eq. (44) becomes

$${\phi }_i^{\text{vap}}\hspace{0.17em}{x}_i^{\text{vap}}\hspace{0.17em}p={\gamma }_i^{\text{liq}}\hspace{0.17em}{x}_i^{\text{liq}}\hspace{0.17em}{\phi }_{i,0}^{\text{liq}}\hspace{0.17em}p,$$ (45)

with ${\phi }_{i,0}^{\text{liq}}$ being the fugacity coefficient of the liquid phase of pure component i, ${\phi }_i^{\text{vap}}$ the fugacity coefficient of the vapor phase of component i in the mixture and ${\gamma }_i^{\text{liq}}$ the activity coefficient of the liquid phase of component i. The first assumption is ${\phi }_i^{\text{vap}}=1$ for the vapor phase as it is assumed to be an ideal gas. The second assumption is ${\phi }_{i,0}^{\text{liq}}\left(T\right)$ being independent of pressure p. Equating the fugacity of pure component i in the liquid phase $f_{i,0}\left(T,p\right)={\phi }_{i,0}^{\text{liq}}\hspace{0.17em}p$ to that of the pure fluid at saturation, and then also to that of the vapor phase

$$f_{i,0}\left(T,p\right)=p{\phi }_{i,0}^{\text{liq}}\approx p_{\text{sat},i}{\phi }_{i,0,\text{sat}}^{\text{liq}}\approx p_{\text{sat},i}$$ (46)

$p{\phi }_{i,0}^{\text{liq}}$ becomes the vapor pressure p_sat,i of the pure component i. Equation (45) is now given by

$$x_i^{\text{vap}}\hspace{0.17em}p={\gamma }_i^{\text{liq}}\hspace{0.17em}{x}_i^{\text{liq}}\hspace{0.17em}{p}_{\text{sat},i}.$$ (47)

For a binary mixture this leads to

$$x_1^{\text{vap}}\hspace{0.17em}p={\gamma }_1^{\text{liq}}\hspace{0.17em}{x}_1^{\text{liq}}\hspace{0.17em}{p}_{\text{sat},1},$$ (48)

$$x_2^{\text{vap}}\hspace{0.17em}p={\gamma }_2^{\text{liq}}\hspace{0.17em}{x}_2^{\text{liq}}\hspace{0.17em}{p}_{\text{sat},2},$$ (49)

Their sum is equal to

$$p={\gamma }_1^{\text{liq}}\hspace{0.17em}{x}_1^{\text{liq}}\hspace{0.17em}{p}_{\text{sat},1}+{\gamma }_2^{\text{liq}}\hspace{0.17em}{x}_2^{\text{liq}}\hspace{0.17em}{p}_{\text{sat},2},$$ (50)

so that the equilibrium pressure p can be directly calculated once the activity coefficients ${\gamma }_1^{\text{liq}}$ and ${\gamma }_2^{\text{liq}}$ are known. Then, the mole fraction of component i in the vapor phase is given by

$$x_i^{\text{vap}}=\frac{{\gamma }_i^{\text{liq}}\hspace{0.17em}{x}_i^{\text{liq}}\hspace{0.17em}{p}_{\text{sat},i}}{p}.$$ (51)

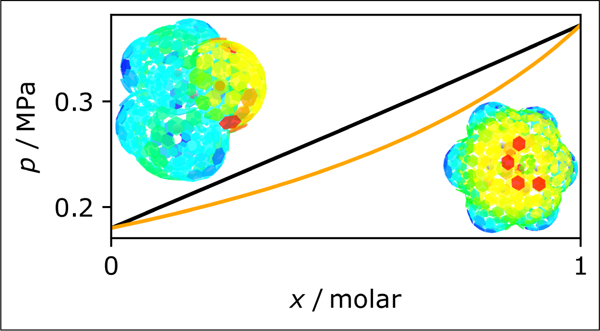
The same process is repeated for a range of mixture compositions to create the boiling and dew point curves. An example of an isothermal phase-equilibrium calculation is presented in Fig. 5. Two isotherms are plotted for the mixture ethanol + water, overlaid with experimental data. The code used to generate the figure is in the jupyter notebook COSMO-SAC.ipynb in the repository (and in the archive).

Figure 5:

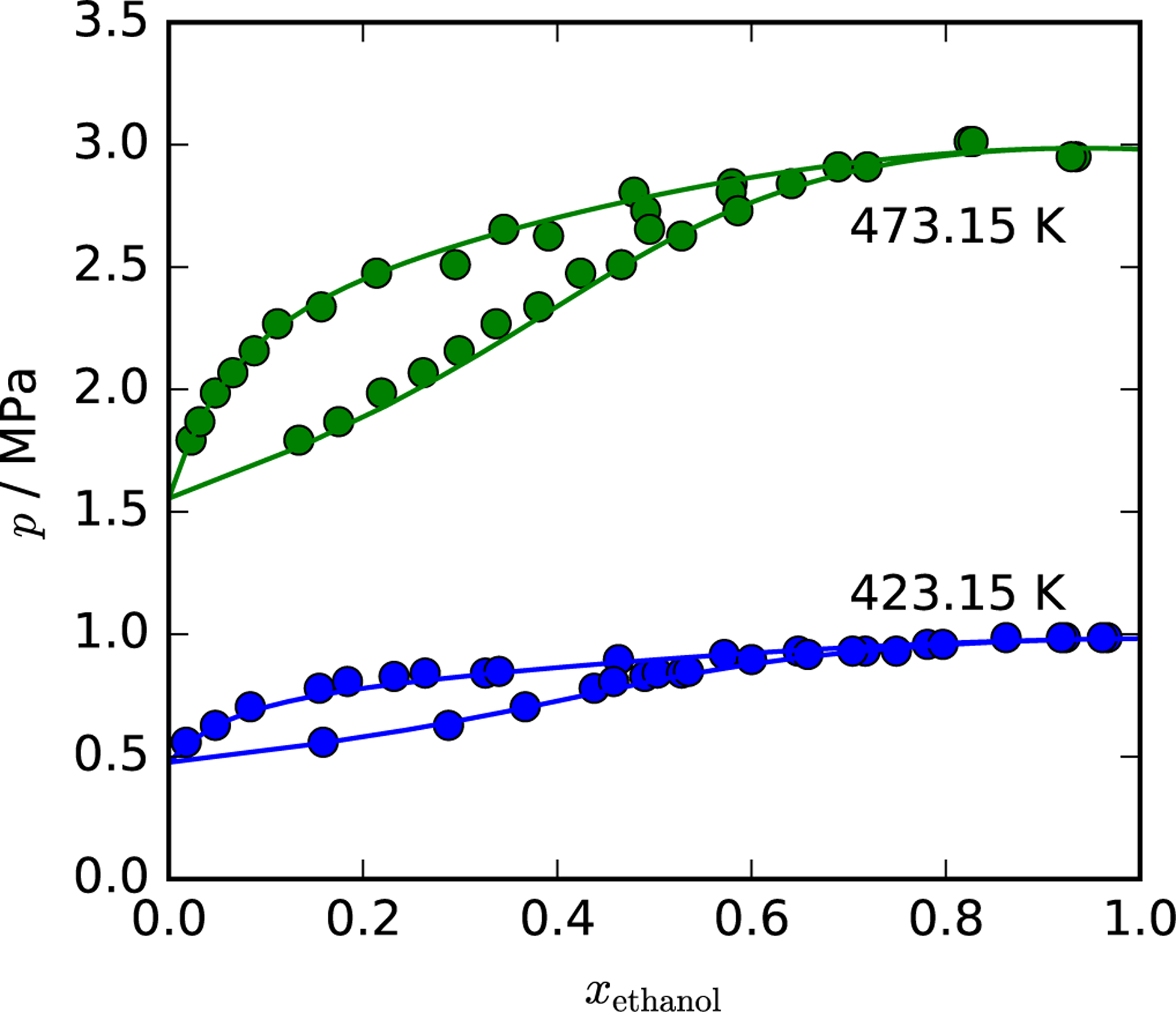
A p-x diagram for the mixture ethanol + water. The experimental data are from Barr-David and Dodge,⁴⁸ and the vapor pressure of the pure components are obtained from the ancillary equations of the respective fluid⁴⁹

6. Code and Validation

The development code including the sigma profiles and COSMO-SAC post-processing is contained in a git repository at https://github.com/usnistgov/COSMOSAC. The archival version of the code used in this paper is furthermore stored at the DOI of https://doi.org/10.5281/zenodo.3669311. Permission from BioVia was obtained to make the .cosmo files available for academic and non-commercial use. Additional information about the .cosmo file database is given in a README file in the file profiles/UD/README.txt relative to the root of the code.

The code workflow mirrors the analysis described in this paper. As a pre-processing step, the sigma profiles are generated from each of the .cosmo files according to the Python script in profiles/to_sigma.py. This script has a command-line interface that allows for selection of the charge averaging scheme, how many contributions the sigma profiles should be subdivided into (1 or 3), and from this script a single .sigma profile is generated.

Once the sigma profile has been generated, the COSMO-SAC analysis is applied. This code allows for the calculation of the activity coefficients, among other outputs. Either the C++ or Python interfaces may be used, according to the user’s preference. A wide range of other numerical analysis programming environments now support calling Python in a nearly-native fashion, so between C++ and Python most users should be able to find a way to call the COSMO code.

Examples of the use of the COSMO-SAC implementation are provided in jupyter notebooks provided with the code, along with the calculation of phase equilibrium calculations, for which the saturation pressure curves for the pure fluids provided by CoolProp⁴⁹ are used. A limitation of this method is that vapor pressure curves must be available for the given fluid. Alternatively, vapor pressure curves could be obtained with the consistent alpha function parameters for the Peng-Robinson equation of state of Bell et al.⁵⁰

Further verification is provided by a large set of calculated values from our model. Users should first ensure that they can precisely regenerate these values prior to making use of the library. The script that generates the verification data is in the file profiles/generate_validation_data.py relative to the root of the code.

7. Conclusions

Since Lin and Sandler¹⁰ proposed the original COSMO-SAC model, many modifications and improvements for this model have been proposed. The reproduction of COSMO-SAC models from the literature is often challenging, because on the one hand the model results strongly depend on the sigma profiles, which themselves depend on the program used to calculate them. Therefore, it is crucial to use the same sigma profiles as the authors of the COSMO-SAC model in order to reproduce their model. On the other hand, some misunderstandings regarding the description of COSMO-SAC models exist in the literature, which further complicate the reimplementation of COSMO-SAC models. In this work, we provide an open source C++ and python implementation of three different COSMO-SAC models^10,23,24, together with a detailed documentation of the implemented models. Furthermore, we provide a consistent set of sigma profiles calculated with the software DMol³ based on the database provided by Mullins et al.³⁴. The corresponding COSMO output files and computer code to calculate the sigma-profiles from the COSMO output files is also provided. Thus, this work intends to provide an open-source reference implementation of state-of-the-art COSMO-SAC models.