Applicability of QCM-D for Quantitative Measurements of Nano- and Microparticle Deposition Kinetics: Theoretical Modeling and Experiments

Abstract

A new theoretical model is formulated for the quantitative analysis of quartz crystal microbalance (QCM) response for heterogeneous loads consisting of nano- and microparticles. The influence of particle coverage and structure is described using a universal correction function in an ab initio manner. Explicit analytical expressions for the frequency and dissipation shifts are derived for the entire range of particle size under the rigid contact regime. The solvent coupling functions are also calculated to determine the dry coverage using the QCM measurements. These expressions furnish the upper limit of the QCM signal, which can be attained for a sensor providing perfect adhesion of particles. Correction functions accounting for the finite adhesion strength (soft contact regime) are also derived. The theoretical results are confronted with QCM and atomic force microscopy measurements of positively charged polymer particle deposition on silica sensors. The main features of the theoretical model are confirmed, especially the abrupt decrease in the QCM wet mass with the particle coverage and the overtone number. The latter effect is especially pronounced for microparticles under the soft contact regime, where the higher-number overtones produce a negligible QCM signal. These results represent a useful reference data for the interpretation of protein and bioparticles, for example, virus and bacteria attachment processes to various substrates.

The information about nano-sized solute adsorption kinetics on solid substrates and their adhesive contact strength is essential for colloid, analytical sciences, catalysis, biology, medicine, and for a plethora of practical applications.

Protein molecule adsorption is a prerequisite for their separation and purification, for the formation of biosensors, and for numerous immunological assays.¹⁻³ Undesired protein adsorption can result in implant failure, plaque formation, and fouling of artificial organs and ultrafiltration units.

Predicting attachement rate of viruses, for example, the coronavirus MHV-A59 of size ca. 100 nm^4,5 attached to various substrates (e.g., metals), is essential for devising strategies of their efficient deactivation and removal.

Noble metal nanoparticles and their monolayers on solid substrates, play an important role in catalysis, analytical science, and medicine.⁶⁻¹² Because of the pronounced biocidal properties, silver nanoparticles are also used to modify surfaces of various materials, in particular, fibers and polymers, applied in manifold consumer products such as surgical gowns, dressing bandages, masks,^10,11 and so forth. They also serve as analytical sensors in SERS⁸ and metal-enhanced fluorescence.⁹

Other nanoparticles such as Au, SiO₂, TiO₂, and ZnO are applied in biosensing devices in heterogeneous catalysis (especially photocatalysis) and as biocidal agents.¹³

On the other hand, from the investigations of microparticle deposition, one can acquire reference data facilitating the interpretation of bioparticle adhesion, for example, bacteria and living cells¹⁴ comprising the cancerous ones.

Because of its significance, nanoparticle (protein) adsorption kinetics was studied using reflectometry, ellipsometry,¹⁵⁻¹⁷ light mode waveguide spectroscopy (OWLS),¹⁸⁻²⁰ surface plasmon resonance (SPR),²¹ atomic force microscopy (AFM),²² and electrokinetic methods.²³ However, these techniques become less accurate or inadequate for larger particles, especially for the microparticle size range. Another deficiency of these methods is the inability to furnish valid information about the adhesive contact strength.

In this respect, the quartz crystal microbalance (QCM) exhibits pronounced advantages because it enables precise, real-time measurements of protein nano- and microparticle adsorption/desorption kinetics in liquid phases under flow conditions.^{15,18,24−35} On the other hand, the electrochemical QCM method can be applied to simultaneously monitor the current and the frequency change. Such measurements were performed in ref (36) to investigate the formation of polypyrrole aggregates on a gold-plated QCM sensor.³⁶

In refs (16) and (17), modified QCM-D cells were used to simultaneously determine the surface coverage (dry mass) of protein molecules using ellipsometry, reflectometry, and SPR.

An alternative method was applied in refs (28) and (29), where the dry mass of adsorbates is derived from the solution of the continuity (mass transfer) equation. This allows to determine the amount of coupled solvent as the difference between the wet QCM mass and the dry mass calculated in this way. Recently, this approach was used to determine the kinetics of positively charged amidine polymer nanoparticle deposition on a silica sensor.³⁵

Interesting investigations of soft liposome deposition of the size equal to 78 nm on a titanium oxide QCM sensor were reported in refs (33) and (34) and theoretically interpreted in terms of lattice Boltzmann numerical modeling. A unique procedure was elaborated to determine the aspect ratio of adsorbed liposomes under in situ conditions. Additionally, in ref (34), extensive modeling of the influence of particle hydrodynamic interactions on the QCM-D signal was performed using a cell model for a broad range of particle coverage.

Other factors that should be considered by the interpretation of QCM measurements are the mechanical compliance of the contact area between the adsorbed particle and the sensor that can induce their sliding or oscillatory motions. These effects were analyzed by applying the finite element modeling^{25−27,30,33,37} and some phenomenological approaches.^16,17,27,31

Tarnapolsky and Freger¹⁴ measured using the QCM method for the attachment of polystyrene and silica microparticles to gold and silica sensors. Experimental results were interpreted in terms of a soft adhesive contact model, which was used to derive valid information about the contact impedance. These investigations confirmed the essential role of the particle adhesive contact whose strength governs the damped oscillations of attached particles. For low contact strength (work of adhesion), an increase in the sensor frequency was observed upon particle attachment, yielding negative QCM mass. A similar effect, confirming the appearance of negative QCM mass, was previously reported by Pomorska et al.³⁷

However, a quantitative interpretation of QCM experimental data obtained for the nano- and microparticles^13,14 is hindered because, surprisingly, there are no theoretical results for the perfectly rigid contact regime valid for all overtones and particle coverage range.

Therefore, the primary goal of this work is to formulate such a model yielding useful analytical expressions for the frequency and dissipation shifts. Additionally, several functions characterizing the coupled solvent mass are introduced, enabling a proper interpretation of particle deposition kinetics derived from QCM measurements. A universal function is also formulated, which characterizes the influence of particle coverage and their monolayer structure on the QCM-D signal. The theoretical results are compared with QCM and AFM measurements of particle adsorption kinetics. Monodisperse polymer particles of well-controlled positive surface charge are used, which enables their irreversible adsorption at negatively charged silica sensors.

These results represent a useful reference data for the interpretation of protein and bioparticles, for example, virus and bacteria attachment processes to various substrates.

Theoretical Section

Modeling QCM Response to Particle Load

For the small-load regime pertinent to the nano- and microparticles, the complex QCM response Δf* is given by^14,38

1

where Δf is the frequency shift, n₀ is the overtone number, f_F is the fundamental frequency, ΔD is the dissipation shift, and i is the imaginary number.

The frequency and dissipation shifts are explicitly given by

2

where ΔZ_L^*, defined as the ratio of the tangential stress (force per unit area) to the crystal surface velocity, is the complex load impedance expressed relative to a reference state and Z_q is the acoustic impedance of the quartz sensor equal to 8.8 × 10⁶ kg m^–2 s^–1.

It should be mentioned that the force exerted on the crystal surface differs from the force acting on the attached particle layer and depends on the rigidity of the adhesive contact, governed by specific surface interactions. Only for firmly fixed particles, which cannot neither translate nor rotate relative to the surface, the net force on the interface is equal (and opposite in direction) to the force acting on particles. Under such situation, the net force exerted on particles consists of the inertia and hydrodynamic contributions

3

where ΔF* is the complex hydrodynamic force, N_p is the number of deposited particles, ΔF_h^* is the excess hydrodynamic force per particle that depends on the particle coverage and the structure of the particle layer, V_i is the sensor tangential velocity, ω = 2πf_F·n₀ is the angular velocity of the sensor oscillations, and m_p is the particle mass.

Considering eq 3, the frequency and dissipation shifts become (Supporting Information)

4

where N is the surface concentration of particles. One can also express eq 4 in the following form useful for the interpretation of experimental data pertinent to nanoparticle deposition kinetic

5

where Γ_Q can be interpreted as the QCM (wet) coverage, that is, the particle mass per unit area, Γ = Nm_p is the dry mass per unit area of particles and

6

is the Sauerbrey constant equal to 0.177 (mg m^–2) s for f_F = 5 × 10⁶ Hz.

As one can deduce, calculation of the frequency change for f_F=5 × 10⁶ Hz and the QCM mass from eqs 4 and 5 requires the scaled hydrodynamic force, which depends on the particle surface concentration (coverage). It is shown in the Supporting Information that the complex force on spherical particles attached to the oscillating sensor is given by

7

with

8

where δ̅ = δ/a and δ is the hydrodynamic boundary layer thickness

9

and a is the particle radius.

A_i is the universal function shown in Figure S1

10

where C_i^o = 10.21 is the dimensionless constant and

11

is the absolute coverage of particles.

Interestingly, eq 10 indicates that for particle coverage above 0.2, the asymptotic form of the A_i(θ) function is given by 1/θ.

One should mention that eqs 7–11 are strictly valid for δ̅ ≫ 1.

The results derived from numerical modeling by Gillissen et al.³⁴ confirm that for δ̅ > 2, there appears a significant decrease in the normalized frequency shift with the particle coverage fully analogous to that predicted by eq 10. On the other hand, for δ̅ < 2, a decrease in the frequency shift is shown to be less pronounced.

It is interesting to observe that the A_i(θ) function is practically independent of the structure of particle monolayers.³⁹ This function also describes the effect of the streaming current reduction and is often used for the interpretation of the experimental data derived from electrokinetic measurements for nanoparticles⁴⁰ and protein molecules²³ adsorbed on solid substrates.

Using eqs 4 and 7, one obtains

12

For δ̅ ≫ 1 and for vanishing particle coverage, the QCM mass is given by

13

This formula indicates that the QCM mass increases with δ̅/a, that is, inversely proportional to the square root of the overtone number n₀.

Analytical solution was derived in ref (14) for the opposite limit where the hydrodynamic boundary layer becomes comparable with the particle radius, which occurs for larger particles and overtone number. In consequence, one can assume that the particle attached to the interface effectively oscillates in a stagnant fluid. In consequence, one can derive the following expressions for Δf, Γ_Q and ΔD (Supporting Information)

14

Equation 14 indicates that the frequency change and the QCM coverage Γ_Q should linearly increase with δ̅, that is, inversely proportional to the square root of the overtone number n₀ with the slope equal to 9/4 = 2.25 analogously, as for the above case of the sphere in the shear flow.

However, one should mention that eq 14 only remains accurate in the limit of negligible particle coverage.

Using the expressions for the QCM mass, one can define several functions commonly used in the literature.^17,27,35 Primarily, it is useful to define the following function referred to for aqueous media as the water factor w

15

This function reflects the ratio of the total force to the inertia force acting on an adsorbed particle. In the literature, it is interpreted as the ratio of the total (wet) mass m_s + m_p to the particle mass m_p (where m_s corresponds to the hydrodynamically coupled solvent mass).

Another function H often used in the literature represents the ratio of the coupled mass to the QCM wet mass and is given by

16

It is also convenient to define another function representing the ratio of the coupled solvent volume v_s to particle volume v_p,³⁴ which is proportional to the hydrodynamic force on particle

17

Using eqs 12 and 14, the v® functions derived for the above two regimes can be expressed as

18

It should be underlined that these functions, shown in Figure 1, comprise no adjustable parameters and are, therefore, valid for arbitrary size of particles and frequencies (overtone numbers) under the rigid contact regime.

Figure 1.

(1) The function (this work); (2) the function;¹⁴ and (3) the function numerically calculated by Gillissen et al.,³³ that is, .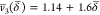

From eq 18, one can also infer that v̅₁(δ̅) linearly increases with δ̅ without showing any leveling off effect. This seems quite unexpected but directly stems from the definition of this function as the ratio of the hydrodynamic to the inertia force acting on the particle (sensor). Because the hydrodynamic force in a shear flow increases as the square and the inertia force as the cube of the particle radius, one can predict that v̅₁(δ̅) ∼ 1/a ∼δ̅, for a fixed oscillation frequency.

On the other hand, for δ̅ = 2 (where the hydrodynamic boundary layer is equal to the particle diameter), the v̅₁(δ̅) function becomes equal to v̅₂(δ̅), which can be treated as a valid estimate of its range of applicability. Thus, for δ̅< 2, the v̅₂(δ̅) function becomes more accurate, yielding a proper asymptotic value of 1/2 for δ̅ tending to zero. It is also seen in Figure 1 that the theoretical results numerically calculated by Gillissen et al.³³ reasonably agree with the analytical results for δ̅ < 4.

Soft Contact Model

The soft contact model was formulated in refs^14,31,32,38 considering that the particle attached to the surface can undergo lateral and angular displacements, the latter referred to as the rolling or rocking motion, governed by the complex spring constant κ_c^*

19

where κ_s^* is the shearing (complex) spring constant, κ_b is the bending spring constant, κ_c is the real component of the spring constant, ξ is the damping coefficient, and ξ̅ = ξ/κ_c.

This model allows to specify the following expression for the complex mechanical impedance¹⁴

20

where

21

Considering that the term 1 – F_r^*/F_t remains fairly constant and equal to c_f, eq 20 simplifies to the following form (Supporting Information)

22

where the C constant is given by

23

with

24

Combining eqs 21 and 22, one can derive the expressions for the QCM mass

25

where

26

Experimental Section

Materials

Sodium chloride, sodium hydroxide, and hydrochloric acid were commercial products of Sigma-Aldrich used without additional purification. Ultrapure water was obtained using the Milli-Q Elix&Simplicity 185 purification system from Millipore. Fibrinogen in the form of crystalline powder was supplied by Sigma.

Suspensions of positively charged amidine and negatively charged sulfate polystyrene microparticles (latexes) were supplied by Invitrogen.

The fibrinogen/sulfate microparticle complex was prepared according to the procedure described in ref (41), consisting in physical adsorption of fibrinogen carried out under controlled pH and ionic strength (3.5 and 0.01 M, respectively). The irreversibly adsorbed fibrinogen coverage on the microparticles was equal to 2.5 mg m^–2.

Dynamic light scattering (DLS) was used to determine the diffusion coefficient of particles. The hydrodynamic diameter was calculated using the Stokes–Einstein relationship.

The laser Doppler velocimetry (LDV) was applied to determine the electrophoretic mobility of particles. The zeta potential was calculated using the Henry and Smoluchowski formulae.

Quartz/silicon dioxide (SiO₂) sensors used in the experiments were supplied by Q-Sense, Gothenburg, Sweden. Before every measurement, the sensors were cleaned in a mixture of 96% sulfuric acid (H₂SO₄), hydrogen peroxide (30%) and ultrapure water in volume ratio 1:1:1 for 3 min. The topography of sensors and their root-mean-square (rms) factor were determined by AFM imaging under ambient conditions. The sensors exhibited the rms roughness below 1 nm.

Methods

The QCM measurements were carried out according to the procedure described in refs^28,42,43 using the Q-Sense QCM Instrument (Biolin Scientific, Stockholm, Sweden).

The kinetics of particle deposition was independently determined using the AFM as previously described in refs (42) and (43). Accordingly, the QCM adsorption runs were stopped after discrete time intervals, the sensors were removed from the suspension, and examined by AFM. The absolute (dimensionless) coverage of particles was calculated as Θ = N S_g, where S_g is the characteristic cross-sectional area of the particle and N is the surface concentration of particles determined by AFM.

Results and Discussion

Particle and Substrate Characteristics

In the investigations, five amidine microparticle suspensions were used with the DLS diameter d_p equal to 67, 140, 360, 810, and 820 nm denoted as A70 and A140, A350, A800, and LSfi800 (fibrinogen covered), respectively (see Table S1).

The zeta potentials of the particles derived from the LDV measurements are collected in Table S1. It is confirmed that all suspensions exhibit a large and positive zeta potential varying between 74 and 97 mV (at pH 4 and an ionic strength of 0.01–0.001 M), whereas the zeta potential of the LSfi800 sample was lower and equal to 25 mV.

The zeta potential of the oxidized Si/SiO₂ substrate was determined by the streaming potential measurements.²⁰ It was equal to −20 and −32 mV for an ionic strength of 10^–2 and 10^–3 M, respectively, at pH equal to 4.

Kinetics of Particle Deposition

The use of the polymer nanoparticles in the QCM studies is advantageous because of their large and positive zeta potential opposite to the sensor zeta potential that promotes a barrierless deposition regime.³⁸ A primary QCM kinetic run performed for the A70 particles is shown in Figure 2 as the dependence of Δf/n₀ on the deposition time.

Figure 2.

(a) Primary nanoparticle deposition run shown as the dependence of the overtone normalized frequency change Δf/n₀ (for the overtones 1, 3, 5, and 7) on the deposition time; silica sensor, ionic strength 0.01 M, pH 4, volumetric flow rate 2.5 × 10^–3 cm³ s^–1, A70 particle suspension, and bulk concentration 10 mg L^–1. (b) Kinetics of particle deposition expressed as the dependence of the coverage on the deposition time for the same parameters as in (a). The solid lines represent the results calculated from Eq.(5) using the frequency shift constant, the points represent the experimental dry coverage derived from AFM, and the dashed line shows the theoretical results derived from the RSA model. The inset shows the AFM image of the particle monolayer at the sensor.

One can observe that Δf/n₀ abruptly decreases with the time for all overtones attaining stationary values at the time of ca. 40 min. In accordance with theoretical predictions, eq 12, the decrease in Δf/n₀ is the most significant and is equal to −400 Hz for the first overtone (fundamental frequency), whereas for the seventh overtone, it is only −290 Hz. Afterward, the desorption run was initiated at a time of 60 min. As can be seen in Figure 2 the changes in Δf/n₀ were negligible, which confirms that there was no desorption of particles. It is interesting to mention that the kinetic run shown in Figure 2 is analogous to the one previously observed for protein molecule adsorption.^26,28

The primary results shown in Figure 2a are converted to the QCM coverage Γ_Q expressed in mg m^–2 using the Sauerbrey constant C_s defined by eq 6. One can observe in Figure 2b that the QCM coverage abruptly increases with the deposition time, initially in a linear manner. Afterward, the stationary values of the coverage are attained, which systematically decrease from 70 to 50 mg m^–2 for the first and seventh overtone, respectively. These plateau remain practically unchanged after initiation of the desorption run where pure electrolyte flow was flushed through the cell.

The results shown in Figure 2a are compared with the theoretical calculations derived from the hybrid random sequential (RSA) approach described in the Supporting Information where the coupling of the bulk particle transfer with the surface transfer through the particle monolayer governed by blocking effects is considered.³⁸

The theoretical results calculated from the RSA model are shown in Figure 2b as dashed lines. One can observe that the QCM coverage is considerably larger than the RSA coverage with the Γ_Q/Γ ratio attaining ca. 10 for short times and the first overtone. However, for longer times, where the coverages attain saturation (maximum) values, the Γ/Γ_Q ratio significantly decreases to 3.5. For the seventh overtone, this effect was significantly smaller.

One should mention that our results are analogous to those previously reported by Bingen et.al.¹⁷ using simultaneously the reflectometry and QCM methods. The Γ_Q/Γ ratio was equal to 11 and 6 in the limit of low coverage for streptavidin and avidin, respectively.

The theoretical RSA results presented in Figure 2 are compared with the experimental data stemming from the direct AFM measurements. As can be seen, the AFM results agree with the RSA theoretical data, which validate the use of this model for predicting the adsorption kinetics. Therefore, for the sake of convenience, the dry mass derived from RSA was used to calculate the experimental values of the water factor and the derivative functions H and v® defined by eqs 15–17. The obtained results are shown in Figure 3a (the H function) and Figure 3b (the v® function). As can be seen, the H function in the limit of zero coverage approaches 0.89 ± 0.02 and 0.84 ± 0.02 for the first and the seventh overtone, respectively. These values correlate with those previously reported by Bingen et al.,¹⁷ which were equal to 0.89, 0.8, and 0.8 for CPMV (virus), streptavidin, and avidin, respectively. Analogously, Gillissen et al.³³ reported H = 0.9 for liposomes adsorbing on titania in the limit of low coverage.

Figure 3.

(a) The hydration function vs the dry coverage of particles Θ for various overtones 1, 3, 5, and 7; the points show the experimental data for the A70 suspension; silica sensor, pH 4, ionic strength 0.01 M, and the solid lines denote the theoretical results calculated from eqs 8,16 and 25. (b) The hydration function v® vs the dry coverage of particles Θ with the same parameters and for various overtones 1, 3, and 7; the points show that the experimental data and the solid lines denote the theoretical results calculated from eqs 8, 17 and 25.

For larger coverages, the hydration function monotonically decreases, attaining for Θ = 0.45 the values of 0.69 ± 0.02 and 0.57 ± 0.02 for the first and the seventh overtone, respectively.

The experimental data shown in Figure 3 were interpreted using the QCM response model given by eq 12, with the H function calculated from eq 16. In the limit of negligible particle coverage, one obtains 0.95 and 0.89 for the first and seventh overtone, respectively, which is close to the above experimental values. However, one should remember that the H function is rather insensitive to the water factor if it considerably exceeds unity and is specific because it comprises the particle density. Therefore, the v® function, which is independent of the particle density, is more universal. The experimental results pertinent to this function are presented in Figure 3b. It is seen that the experimental v® values (points) approach in the limit of low coverage, 9.2 ± 0.3, 7.0 ± 0.3, 6.0 ± 0.2, and 5.5 ± 0.2 for the first, third, fifth, and seventh overtone, respectively. These experimental data agree with those previously reported by Reimhult et al.⁴⁴ for streptavidin who obtained v® = 9.0 in the limit of low coverage. Analogously Bingen et al.¹⁷ obtained v® = 9.0 and 6.0 for streptavidin and avidin, respectively. As can be seen in Figure 3a, the v® function decreases with the particle coverage, attaining for Θ = 0.45 the values of 2.3 ± 0.1 and 1.6 ± 0.1 for the first and seventh overtone, respectively. It is interesting to mention that Gillissen et al.³⁴ theoretically predicted an analogous decrease in the v® function from 8.2 to ca. 2.4 for Θ equal to 0 and 0.45, respectively, for a similar δ̅ value of 4.6.

The experimental data shown in Figure 3b were interpreted using the theoretical function using the QCM response model given by eq 12, with the v® function calculated from eq 17, which gives the following expression

27

It is predicted from this formula that for the A70 suspension, v® should be equal to 24 and 9 in the limit of low coverage for the first and seventh overtone, which considerably exceeds the experimental data. The most obvious of this discrepancy is the finite adhesion strength that may allow particle rocking motion. The significance of this effect is controlled by the given adhesion constant c_a given by eq 24, that is, for a fixed particle size by the work of adhesion, see eq S41. Assuming a plausible value of the Hamaker constant for the polystyrene/water/silica interactions equal to 1.4 × 10^–20 kT and the minimum approach distance equal to 1 nm for smooth sensors,³⁵ one can calculate that for the A70 suspension and the first overtone, c_a = 0.0082. For the minimum approach distance equal to 2 nm pertinent to rough surfaces, one obtains c_a = 0.033. Using these values, one can predict from eqs 17 and 25 that in the limit of low coverage, v® should be equal to ca. 9 for c_a = 0.0082, whereas for c_a = 0.033, a negative value of v® is predicted. This estimate shows that the sensor roughness is expected to play a significant role in QCM measurements of nanoparticle deposition. In consequence, as suggested in ref (14), after exceeding a critical adhesion constant value, the particles can freely oscillate around the equilibrium position transferring negligible force to the sensor. Given that the roughness distribution is heterogeneous in the microscale, one can expect that there is always a statistical distribution of the adhesion constant over the sensor, indicating that there also exist areas where the particles produce no QCM signal. This hypothesis was previously formulated by Tarnapolsky and Freger,¹⁴ who observed analogous behavior for polymer microparticles adsorbing on silica and gold sensors. Indeed, the experimental data shown in Figure 3 can be theoretically accounted for using eqs 17 and 25 with c_a = 0.0082 and assuming that only a fraction of the sensor promotes an adhesive contact (see solid lines in Figure 3).

As suggested by eq 24, the c_a constant increases proportionally to particle mass; therefore, the soft contact effect is expected more pronounced for larger particles because of their increased inertia. To verify this prediction, deposition kinetic experiments were performed for the larger particle suspensions. In Figure 4, representative results are presented for A800 particles. One can observe that for the first overtone, Δf/n₀ abruptly decreases with the time, attaining a plateau value of −2230 Hz after the time of 400 min. The frequency shift decreases (in absolute terms) proportionally to the overtone number, amounting to only −760 and −235 Hz for the third and fifth overtone.

Figure 4.

(a) Primary nanoparticle deposition run shown as the dependence of the overtone-normalized frequency change Δf/n₀ (for overtones 1, 3, 5, and 7) on the deposition time, A800 suspension, bulk concentration 500 mg L^–1, and other parameters as in Figure 2. (b) Kinetics of particle deposition expressed as the dependence of the coverage on the deposition time; the solid lines represent the QCM results calculated using the Sauerbrey constant for various overtones (1, 3, 5, and 7) for the A800 suspension and the same conditions as mentioned above, the dry coverage derived from AFM measurements is shown by the square points, and the dashed lines show the theoretical results derived from the RSA model. The inset shows the AFM image of the particle monolayer.

In Figure 4b, the dependence of the QCM coverage of the A800 particles for various overtones, calculated as previously using the Sauerbrey constant, is plotted as a function of deposition time. One can observe that the QCM coverage for the first overtone exceeds the coverage derived from the RSA and AFM measurements, which agree with each other. However, for the higher overtones, the QCM coverage significantly decreases and becomes smaller than the dry (inertia) mass of the monolayer. This indicates that the w factor becomes smaller than unity and the H function becomes negative. This apparently physically incorrect result is a direct manifestation of the soft contact effect, which diminishes the force transferred to the sensor below the inertia force exerted on the particle monolayer.

One should mention that the analogous behavior was previously reported in the literature for microparticle size range albeit without performing a direct interpretation in terms of the solvent coupling functions. Thus, Tarnoplsky and Freger¹⁴ determined for 1 μm in diameter polystyrene particle deposition on a gold sensor that the absolute frequency shift in the limit of low coverage was practically independent of the overtone number, indicating that the overtone-normalized frequency shift decreased as 1/n₀. An analogous effect was observed by Olsson et al.³¹ for the same size of silica particles adsorbing on a bare silica sensor where the larger overtone number harmonics produced a constant or even increasing frequency shift (normalized to the particle coverage).

The experimental kinetic data obtained for all particle suspensions comprising the fibrinogen latex complex L800fi microparticles are transformed using eqs 17 and 25 to the v® versus the particle coverage dependencies and are presented in Figure 5 (for the first overtone). One can observe that the experimental v® values in the limit of low coverage rapidly decrease for increasing size of the particles from 9.2 ± 0.3 to 0.4 ± 0.1 for the A70 and A350 suspensions, respectively. Interestingly, for the A800 suspension, the v® function in the limit of low particle coverage vanishes, which indicates that the Γ_Q/Γ ratio approaches unity. For the L800fi complex, the v® function even becomes negative for the Θ < 0.1. Another unexpected feature is that for these microparticles, the function increases with the coverage attaining for Θ = 0.45 the values close to unity.

Figure 5.

The hydration function v® vs the dry particle coverage for various particle suspensions: 1. A70, 2. A 140, 3. A350, 4. A800, and 5. L800fi; the points show the experimental data obtained for the first overtone; the solid lines show the theoretical results calculated from the damped oscillator model using eqs 10, 17, and 26.

This behavior, which has been reported before in the literature, is a direct manifestation of the soft contact regime allowing for damped rocking motion of attached particles, as predicted in ref (14). On the other hand, the increase in the v® and w functions with the particle coverage is caused by the damping of the flow within the particle monolayer as predicted by the A_i function. This decreases the hydrodynamic shearing forces on particles, enhancing the role of surface adhesion interactions. This hypothesis is confirmed by the fact that the theoretical results calculated using eqs 17 and 25 with the damping function described by eq 10 (solid lines in Figure 5) reasonably well reflect the experimental data for various particle sizes and the entire coverage range available experimentally.

It should be underlined, however, that reproducible experimental data for the microparticle size range characterized by adequate precision are obtained for the first overtone, with the higher overtones yielding a practically negligible QCM signal.

Conclusions

A quantitative analysis of QCM response for heterogeneous loads comprising nano- and microparticles is performed. Explicit analytical expressions for the frequency and dissipation shifts are derived in terms of the normalized hydrodynamic boundary layer thickness δ̅ = δ/a under the rigid contact assumption. The influence of particle coverage is described via a universal correction function given by eq 10 derived without adjustable parameters. These results represent the upper limit of the QCM signal attainable for sensors providing perfect adhesion of particles.

Using the approach formulated in ref (14), the correction function accounting for the finite adhesion strength, pertinent to the soft contact regime, is also derived.

These theoretical results allowed a thorough analysis of experimental data derived from QCM and AFM measurements pertinent to positively charged polymer nano- and microparticle deposition kinetics. The main features of the theoretical model are confirmed, especially the abrupt decrease in the solvent coupling function v® with the particle coverage and the overtone number. It is also shown that the latter effect is especially pronounced for microparticles under the soft contact regime. In this case, the larger number overtones produce a negligible QCM signal, yielding the water factor below unity and negative values of the H function.

This behavior, which is a direct manifestation of the soft contact regime allowing for damped rocking motion of the attached particles, was adequately interpreted by introducing a correction for the finite adhesion strength given by eq 25.

These results represent useful reference data for the interpretation of protein and bioparticles, for example, viruses and bacteria adsorption kinetics on rough surfaces.

Another conclusion of practical implications is that the sensor quality, especially its roughness and homogeneity, governing the adhesion strenght, plays a crucial role in the QCM measurements of both micro- and nanoparticle-sized solutes. Therefore, reproducible QCM measurements are feasible for a sensor characterized by the rms factor below 1 nm and a homogeneous surface charge being opposite to the adsorbing solute charge.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.analchem.0c03115.

• Modeling QCM response, basic characteristic of polymer particles, and modeling adsorption kinetics of particles (PDF)

The authors declare no competing financial interest.