Start and Turn Performances of Competitive Swimmers in Sprint Butterfly Swimming

Abstract

The purposes of this study were to establish relationships between selected underwater kinematics and the starting and turning performances and to quantify kinematic differences between these segments in sprint butterfly swimming. Fourteen male swimmers performed 50 m maximal butterfly swimming in a short course pre-calibrated pool. The entire race was filmed by a multi-camera system, which quantified the forward head displacement and velocity (vx_head) throughout the race with a sampling frequency of 50 Hz. The time taken between 0-15 m (T_0-15) and 25-35 m (T_25-35) as well as 16 kinematic variables were acquired from the data provided by the system and manual video processing for further analysis. The mean underwater velocity (UW-vx_mean) was related to both T_0-15 and T_25-35 (r = -0.70 and -0.95, respectively; p < 0.01). UW-vx_mean was positively correlated with vx_head during the first kick (r = 0.84, p < 0.001) in the start segment and with vx_head during the last kick in the turn segment (r = 0.68, p < 0.01), but other kinematic variables such as kick frequency, body angle, deceleration during kicks (Dec_kick), and glide time were not related to UW-vx_mean. Swimmers had larger vx_head at the beginning of the segment and during the first kick in the start than in turn segment (p < 0.001). However, vx_head during the last kick was similar due to the larger Dec_kick (p < 0.05) in the start than in turn segment. The underwater time was similar between the segments despite a longer underwater distance (p < 0.01) and a larger kick count and frequency (p < 0.01) in the start than turn segment. In conclusion, UW-vx_mean is an important factor for start and turn performances, but swimmers select individual kinematic strategies to achieve a large UW-vx_mean. Results also highlighted the importance of the different parts within the underwater segment in each segment.

Key points.

• In 50 m butterfly swimming, few kinematic variables were linearly related to start and turn performances due to a large inter-individual variability.

• The mean forward velocity during the underwater phase was largely correlated with start and turn time. The mean velocity was related to the first kick velocity in the start segment and to the last kick velocity in the turn segment.

• In 50 m butterfly swimming, the initial forward velocity (the velocity at the feet-entry and the push-off) was larger in the start than in the turn segment, but the forward velocity at the last kick before the breakout was not different between the segments.

• In 50 m butterfly swimming, the underwater distance is longer in the start than in the turn segment, but the underwater time is similar between the segments. Despite the similarity in the underwater time, swimmers perform a larger number of kicks with higher kick frequency in the start than the turn segment.

Introduction

Competitive swimming races consist of four different segments – namely the start, clean swimming, turn, and finish (Smith et al., 2002; Veiga et al., 2013). The definition of the start and turn segments varies among the extant literature mainly due to changes in Fédération Internationale de Natation (FINA) competition rules such as restricting the underwater locomotion after the start and turns over 15 m (Smith et al., 2002). Currently, these segments are commonly defined as 15 m from the starting block for the start segment and 15 m around the push-off for the turn segment such as 5 m turn-in and 10 m turn-out or 7.5 m turn-in and -out (Garland Fritzdorf et al., 2009; Veiga et al., 2013). This means that more than 60 % of the short course swimming event is covered by these two segments. Since the goal of competitive swimming is to finish the distance in the shortest possible time, the start and turn performances are also often defined as the time spent during the segment (Morais et al., 2019).

In the start and turn segments, the mean distance of breakout (the point at which the swimmer emerges from the water) of elite male swimmers in 100 m races is 9-13 and 7-11 m for the start and turn, respectively, (Morais et al., 2019; Veiga et al., 2014), which shows that the underwater swimming covers the majority of these segments. The distance and time of the underwater swimming during the start and turn segments must be adjusted to maximize the average velocity (Veiga et al., 2014), meaning that good start and turn performances cannot simply be explained by a single parameter (only underwater time or the distance). Indeed, Nicol et al. (2019) established that the breakout distance is a good predictor of the turn performance, whereas another study has reported that a long underwater distance is not necessarily related to a fast finishing time and suggested that some fast swimmers might prioritize to emerge from the water quickly to maximize the mean forward velocity (Veiga et al., 2016).

It is currently unknown how swimmers maximize the underwater velocity to achieve fast start and turn time since race analysis in real competitions are usually limited to analyzing video footage recorded only from above the water (Morais et al., 2019; Veiga et al., 2016). Therefore, an approach that employs a similar condition as a real race (a maximal effort trial in accordance with the FINA regulation without any testing equipment attached on the body) with analyzing underwater kinematic information is useful to better understand the start and turn performances in swimming. Factors that affect the start and turn segments include the initial forward velocity and deceleration during the underwater swimming (Takeda et al., 2020), gliding (Naemi and Sanders, 2008; Tor et al., 2015), body posture (Houel et al., 2013), and kick frequency (Connaboy et al., 2009). These kinematic variables have been widely studied, but not examined in a race condition.

To investigate those factors in a race condition, focusing on butterfly start and turn techniques would be beneficial as an initial step. The start and turn in butterfly swimming are unique since the majority of the underwater locomotion consists of a single propulsive technique – undulatory swimming. On the other hand, swimmers perform other techniques in addition such as flutter kicking in front crawl and backstroke (Trinidad et al., 2020) and whip kicking and arm pull-out in breaststroke (Seifert et al., 2007). This means that analyzing start and turn segments in butterfly is much simpler compared with the other techniques since the underwater locomotion in these three techniques involves complex factors such as inter-limb coordination and the timing of the transition of motions.

To summarize, it is well understood how competitive swimmers perform underwater swimming during competitions, but there is a lack of knowledge about the selected kinematic parameters that affect the underwater distance, time, and velocity in a race condition. Due to its simplicity, analyzing butterfly swimming would be beneficial to investigate which kinematic factors are affecting the start and turn performances. The primary purpose of this study was to establish relationships between selected underwater kinematics and the start and turn performances. The second purpose of this study was to investigate the differences in these kinematics between the start and turn segments. Relating to the second purpose, it was hypothesized that swimmers would show a higher velocity throughout the segment in the start than in turn due to a different initial velocity and similar deceleration as swimmers have different segment initiation (diving and wall push-off) but perform the same kicking technique in both segments.

Methods

Participants

Fourteen male national-level butterfly swimmers (19.8 ± 2.5 years, 1.89 ± 0.05 m and 82.5 ± 7.8 kg) volunteered to participate in the present study. All swimmers were specialized in butterfly swimming and qualified for national championships with the mean short course 50 m butterfly personal best record of 24.8 ± 1.0 s, corresponding to the FINA point of 686.0 ± 85.7. The local ethics committee and the National Data Protection Agency for Research approved the procedures in accordance with the Declaration of Helsinki. Benefits and potential risks of participating in the study were explained in detail to each participant before they provided written informed consent.

Data collection

Participants underwent their personal warm-up routines on land and in the water (approximately 45-60 minutes) and were required to perform 50 m butterfly swimming with maximal effort with a diving start. The entire 50 m race was recorded and analyzed by the AIM race analysis system (AIMSys Sweden AB, Lund, Sweden), which is an automatic race analysis system that does not require swimmers to equip with any device except for a yellow silicon cap. The system consists of five underwater cameras perpendicular to the swimming direction and five above water cameras at the side of the pool. In both underwater and above the water, the five cameras were set alongside the pool with a between-camera distance of approximately 5 m. The cameras were calibrated in the manner established by Haner et al. (2015). The mean calibration errors were 0.025 degrees and 0.006 m of angular and linear error, respectively. The system contained an automatic yellow color tracking algorithm, based on a support vector machine and a non-linear color transformation. The algorithm detected instantaneous displacement of the head (due to the yellow color of the cap) with a sampling frequency of 50 Hz. The system was also synchronized with an electronic Omega timing system (Swiss Timing, Bienne, Switzerland) that provided the time of each lap and the whole race. The two-dimensional global coordinates were defined as X (forward direction) and Y (upward direction), respectively. The origin of the global coordinates was the wall where swimmers started the lap (X) and the water surface (Y). Detailed calibration algorithm and procedures are reported in Haner et al. (2015).

Data analysis

Temporal X- and Y-velocity of the head (vx_head and vy_head, respectively) were defined as the rate at which X- and Y-displacement of the head changed with time. The underwater time was defined as the time between the feet-entry (start) or push-off from the wall (turn) and the point where Y-displacement of the head changed from negative to positive (the head breakout). The underwater distance was calculated as the X-displacement of the head during the underwater time, and the mean underwater vx_head (UW-vx_mean) was obtained by calculating the average of vx_head throughout the period. For the turn segment, the duration of the feet being on the wall was not considered for the underwater time and distance quantification.

The time to 15 m after the start (T_0-15) and to the 10 m after the turn (T_25-35) were determined as the time when the X-displacement of the head reached the respective points after the start signal or the end of the first lap, and the time of each lap was derived from the Omega timing system. Even though a short distance before the turning motion (5 m or 7.5 m turn-in) is often included in the turn segment, the turn-in was excluded from the analysis as this is more related to the clean swimming segment in the preceding lap (Veiga et al., 2013).

The underwater video footage provided by the AIM software was used to manually identify the timing of feet-entry and push-off as well as the start and the end of each kick cycle that was defined as the beginning of each downward kick motion. The time between the feet-entry or push-off and the beginning of the first kick was defined as the glide time, and the mean kick frequency during the underwater phase was determined as the inverse of the mean kick cycle time. The shoulder and hip of swimmers were also manually digitized to obtain the angle of the upper body (body angle; BA) as the arctangent of the ratio of X and Y camera coordinates (Figure 1). The timestamp of the video footage was synchronized with the timeline of the head displacement data in the software, thereby enabled us to calculate the mean vx_head, vy_head, and BA during each kick cycle. The three kinematic variables at the instant of the feet entry and the push-off were also calculated and defined as Initial-vx_head, Initial-vy_head, and Initial-BA for each segment.

Figure 1.

The definition of the coordinate axes and the angle of the upper body (An image obtained from a pilot study).

The last kick motion before the breakout without the arm pull was considered as the last kick during the underwater phase to avoid potential effects of the transition arm pull on the results. The mean vx_head, vy_head, and BA during the first and the last kick were quantified (First-vx_head, Last-vx_head, First-vy_head, Last-vy_head, First-BA, and Last-BA, respectively). The mean deceleration during the undulatory kicks (Dec_kick) was calculated as the difference between the First- and Last-vx_head divided by the time taken for all kicks. The number of kicks performed from the first to the last kick (Kick count) was also quantified. The detection of the start/end of each kick cycle was based on the video observation, rather than the coordinate data. Therefore, intra-investigator reliability of the timing detection was assessed by analyzing one trial for ten times, which showed an excellent agreement (ICC > 0.999, p< 0.001) with the mean coefficient of variation of 0.11 %.

Statistical analysis

The data distribution was checked using the Shapiro-Wilk test and confirmed as normal in all variables. Relationships between obtained variables were assessed using Pearson’s correlation coefficient. The threshold values representing small, moderate, large, very large, and extremely large correlations were defined as 0.1, 0.3, 0.5, 0.7, and 0.9, respectively (Hopkins et al., 2009). In the correlation analysis, there were around 120 variable combinations in both the start and turn segment, due to many kinematic variables analyzed. This large number of statistical procedures raised the risk of having at least one type I error among the observed variables up to almost 100 %. Therefore, for the correlation analysis, the level of significance was set at p < 0.01 to reduce this risk.

A paired sample t-test was used to compare the underwater distance, underwater time, UW-vx_mean, kick frequency, kick count, glide time, and Dec_kick between the start and turn segments. Since vx_head, vy_head, and BA at different times are not independent but related to each other, a two-way repeated-measures ANOVA was used to compare these variables between the start and turn segments with the segments and the events where the velocity was quantified (entry or push-off, first-kick, and last-kick) as two within-participant factors. Simple main effects were assessed when an interaction between the factors was observed using a paired sample t-test with the Bonferroni adjustment. For those hypothesis-driven statistics, the level of significance was set at p < 0.05. For the segment comparison, Cohen’s d, as well as 95 % confidence intervals (95% CIs), were also calculated to assess the magnitude of the differences. According to Cohen (1988), d value of 0.20, 0.50, and 0.80 were considered as small, medium, and large effects, respectively.

Results

Relationships between kinematic variables and start and turn performance

In both start and turn segment, T_0-15 and T_25-35 had an extremely large correlation with the lap time (r = 0.93 and 0.90, respectively; both p < 0.001), and they were largely or extremely largely correlated with UW-vx_mean (r = -0.70 and -0.95; p < 0.01 and < 0.001, respectively). In the start segment, other kinematic variables associated with T_0-15 were kick count (r = -0.70; p < 0.01), First-vx_head (r = -0.86; p < 0.001), First-vy_head (r = 0.69; p < 0.01), and First-BA (r = 0.70; p < 0.01). On the other hand, only Initial-BA had a moderate correlation (r = 0.69; p < 0.01) with T_25-35 in the turn segment (Table 1). Detailed correlation analysis results showing the relationships between all kinematic variables are presented in Table 2 (start segment) and Table 3 (turn segment).

Table 1.

Mean ± standard deviation (SD) and statistical results obtained in the present study.

Variables	Start segment	Turn segment	Correlation coefficient		T-test Difference	ANOVA
			Start (vs. T0-15)	Turn (vs. T25-35)		Main effect (Segments)	Main effect (Events)	Interaction
Lap time (s)	11.51 ± 0.43	13.71 ± 0.59	0.93†	0.90†	n.a.	n.a.
T0-15 and T25-35 (s)	6.24 ± 0.25	5.35 ± 0.25	n.a.	n.a.	n.a.	n.a.
UW-vxmean (m·s-1)	2.26 ± 0.11	1.98 ± 0.08	-0.70#	-0.95†	0.28 ± 0.92†	n.a.
UW Time (s)	3.23 ± 0.61	3.18 ± 0.81	-0.51	-0.41	0.46 ± 0.61	n.a.
UW Distance (m)	7.26 ± 1.42	6.29 ± 1.68	-0.64	-0.57	0.97 ± 1.12#	n.a.
Kick frequency (Hz)	2.52 ± 0.23	2.16 ± 0.19	-0.16	-0.46	0.36 ± 1.55†	n.a.
Kick count (times)	7.00 ± 1.56	5.71 ± 2.09	-0.70#	-0.55	1.29 ± 1.49#	n.a.
Deckick (m·s-2)	-0.51 ± 0.23	-0.36 ± 0.27	0.33	0.43	-0.16 ± 0.21*	n.a.
Glide time (s)	0.40 ± 0.13	0.59 ± 0.27	0.56	0.33	-0.20 ± 0.20#	n.a.
Initial-vxhead (m·s-1)	4.60 ± 0.33	3.04 ± 0.16	0.03	-0.48	n.a.	F = 476.71† η2P = 0.97	F = 438.07† η2P = 0.97	F = 137.95† η2P = 0.91
First-vxhead (m·s-1)	2.70 ± 0.27	2.13 ± 0.21	-0.86†	-0.59	n.a.
Last-vxhead (m·s-1)	1.81 ± 0.15	1.70 ± 0.11	-0.55	-0.51	n.a.
Initial-vyhead (m·s-1)	-1.51 ± 0.52	-0.39 ± 0.22	0.57	0.66	n.a.	F = 121.08† η2P = 0.90	F = 49.47† η2P = 0.79	F = 70.67† η2P = 0.85
First-vyhead (m·s-1)	0.11 ± 0.24	0.002 ± 0.16	0.69#	0.39	n.a.
Last-vyhead (m·s-1)	0.34 ± 0.10	0.25 ± 0.10	-0.50	-0.65	n.a.
Initial-BA (˚)	-14.63 ± 8.42	-6.93 ± 5.58	0.48	0.69#	n.a.	F = 60.26† η2P = 0.82	F = 1.12 η2P = 0.08	F = 14.71† η2P = 0.53
First-BA (˚)	7.57 ± 7.02	3.44 ± 6.78	0.70#	0.46	n.a.
Last-BA (˚)	12.62 ± 5.34	11.43 ± 6.09	-0.29	-0.15	n.a.

T_0-15, 0-15 m time; T_25-35, 25-35 m time; UW, underwater; vx_mean, forward velocity; Dec_kick, the mean deceleration from the first to the last kick; Initial-vx_head, the forward head velocity at the feet entry or push-off; First-vx_head, the mean forward velocity during the first kick; Last-vx_head, the mean forward velocity during the last kick; Initial-vy_head, the upward head velocity at the feet entry or push-off; First-vy_head, the mean upward velocity during the first kick; Last-vy_head, the mean upward velocity during the last kick; Initial-BA, the angle of the upper body at the feet entry or push-off; First-BA, the mean angle of the upper body during the first kick; Last-BA, the mean angle of the upper body during the last kick; η²_P, Partial eta squared.

*, p < 0.05;

#, p < 0.01;

†, p < 0.001; n.a., not applicable

Table 2.

Correlation coefficients between analyzed kinematic variables in the start segment.

	UW Time	UW Distance	KF	Kick count	Deckick	Glide time	Initial-vxhead	First-vxhead	Last-vxhead	Initial-vyhead	First-vyhead	Last-vyhead	Initial-BA	First-BA	Last-BA
UW-vxmean	0.005	0.21	0.21	0.19	-0.19	-0.27	-0.24	0.84†	-0.55	-0.34	-0.31	0.51	-0.32	-0.26	0.56
UW Time		0.98†	-0.28	0.84†	-0.12	-0.15	-0.06	0.58	0.18	-0.48	-0.76#	-0.008	-0.55	-0.70#	0.01
UW Distance			-0.22	0.87†	-0.16	-0.23	-0.15	0.68#	0.35	-0.62	-0.81†	0.12	-0.60	-0.74#	0.10
KF				0.24	-0.57	-0.70#	-0.09	0.39	-0.04	0.55	-0.15	-0.003	0.51	-0.28	-0.49
Kick count					-0.47	-0.60	-0.22	0.86†	0.19	-0.36	-0.85†	0.12	-0.36	-0.88†	-0.16
Deckick						0.59	-0.16	-0.51	0.08	-0.11	0.31	0.21	-0.003	0.45	0.38
Glide time							0.23	-0.82†	-0.19	-0.12	0.57	-0.25	0.04	0.69#	0.26
Initial-vxhead								-0.23	-0.27	0.02	0.25	0.06	0.25	0.17	0.09
First-vxhead									0.38	-0.36	-0.81†	0.26	-0.37	-0.86†	-0.08
Last-vxhead										-0.44	-0.35	0.60	-0.43	-0.33	0.32
Initial-vyhead											0.32	-0.31	0.84†	0.20	-0.45
First-vyhead												-0.34	0.29	0.89†	-0.12
Last-vyhead													-0.25	-0.29	0.35
Initial-BA														0.25	-0.28
First-BA															0.24

UW, underwater; vx_mean, forward velocity; KF, Kick frequency, Dec_kick, the mean deceleration from the first to the last kick; Initial-vx_head, the forward head velocity at the feet entry; First-vx_head, the mean forward velocity during the first kick; Last-vx_head, the mean forward velocity during the last kick; Initial-vy_head, the upward head velocity at the feet entry; First-vy_head, the mean upward velocity during the first kick; Last-vy_head, the mean upward velocity during the last kick; Initial-BA, the angle of the upper body at the feet entry; First-BA, the mean angle of the upper body during the first kick; Last-BA, the mean angle of the upper body during the last kick;

#, p < 0.01;

†, p < 0.001

Table 3.

Correlation coefficients between analyzed kinematic variables in the turn segment.

	UW Time	UW Distance	KF	Kick count	Deckick	Glide time	Initial-vxhead	First-vxhead	Last-vxhead	Initial-vyhead	First-vyhead	Last-vyhead	Initial-BA	First-BA	Last-BA
UW-vxmean	0.18	0.36	0.57	0.38	-0.38	-0.43	0.35	0.55	0.68#	-0.59	-0.27	0.68#	-0.53	-0.37	0.07
UW Time		0.98†	0.11	0.89†	-0.04	-0.13	0.44	0.41	-0.39	-0.56	-0.59	0.29	-0.76#	-0.60	0.42
UW Distance			0.17	0.92†	-0.14	-0.18	0.49	0.50	-0.24	-0.65	-0.61	0.40	-0.82†	-0.63	0.43
KF				0.49	-0.42	-0.82†	0.23	0.79#	0.50	-0.23	-0.69#	0.21	-0.12	-0.62	-0.20
Kick count					-0.40	-0.52	0.49	0.72#	-0.11	-0.58	-0.82†	0.35	-0.71#	-0.78#	0.34
Deckick						0.56	-0.29	-0.64	-0.16	0.08	0.53	-0.29	0.24	0.56	-0.07
Glide time							-0.32	-0.80#	-0.46	0.14	0.70#	-0.16	0.13	0.59	-0.04
Initial-vxhead								0.59	0.04	-0.57	-0.36	0.43	-0.45	-0.32	0.39
First-vxhead									0.36	-0.39	-0.77#	0.42	-0.47	-0.80#	0.03
Last-vxhead										-0.12	-0.05	0.38	-0.10	-0.18	-0.27
Initial-vyhead											0.33	-0.76#	0.66	0.35	-0.62
First-vyhead												-0.35	0.50	0.85†	-0.14
Last-vyhead													-0.61	-0.40	0.42
Initial-BA														0.67#	-0.23
First-BA															0.12

UW, underwater; vx_mean, forward velocity; KF, Kick frequency, Dec_kick, the mean deceleration from the first to the last kick; Initial-vx_head, the forward head velocity at the feet entry; First-vx_head, the mean forward velocity during the first kick; Last-vx_head, the mean forward velocity during the last kick; Initial-vy_head, the upward head velocity at the feet entry; First-vy_head, the mean upward velocity during the first kick; Last-vy_head, the mean upward velocity during the last kick; Initial-BA, the angle of the upper body at the feet entry; First-BA, the mean angle of the upper body during the first kick; Last-BA, the mean angle of the upper body during the last kick;

#, p < 0.01;

†, p < 0.001

Differences in the kinematic variables between the start and turn segment

Swimmers showed 14.4 % longer underwater distance (p < 0.001; d = 0.87; 95% CI = 0.33 – 1.62 m), 35.6 % larger (in magnitude) deceleration (p < 0.05; d = 0.73; 95% CI = -0.28 – -0.03 m·s^-2), 16.7 % higher kick frequency (p < 0.001; d = 1.62; 95% CI = 0.27 – 0.45 Hz) with 1.3 times more kicks (p < 0.01; d = 0.70; 95% CI = 0.43 – 2.15 times), and 33.9 % shorter glide time (p < 0.01; d = 0.89; 95% CI = -0.31 – -0.08 s) in the start than in turn segment. Main effects of segments (start and turn) and events (entry or push-off, first-kick, and last-kick) on vx_head, vy_head, BA and the interaction between the factors were all significant except the effect of the events on BA (Table 1).

Simple main effect tests showed that Initial-, First-, and Last-vx_head were all different (p < 0.001) with swimmers showing smaller velocity as moving forward in both segments. The start segment exhibited larger Initial-vx_head (p < 0.001; d = 5.07; 95 % CI = 1.38 – 1.73) and First-vx_head (p < 0.001; d = 3.12; 95 % CI = 0.47 – 0.68) than the turn segment by 69.9 % and 24.2 %, respectively. On the other hand, no difference was observed in Last-vx_head between the segments (Figure 2). Initial-vy_head was smaller, meaning that swimmers travelled more downward, in the start than in the turn segment (p < 0.001; d = 2.81; 95 % CI = -1.39 – -0.84). On the other hand, First- and Last-vy_head were larger (p< 0.05; d = 0.54; 95 % CI = 0.01 – 0.23, and p < 0.01; d = 0.88; 95 % CI = 0.04 – 0.14, respectively) in the start than the turn segment (Figure 3).

Figure 2.

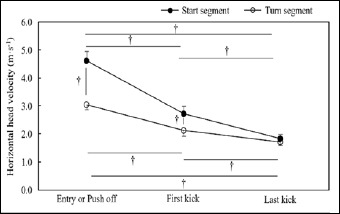
Differences in the forward head velocity between three different timings and between the start and turn segment (results from simple main effect tests.; † shows a difference with p < 0.001).

Figure 3.

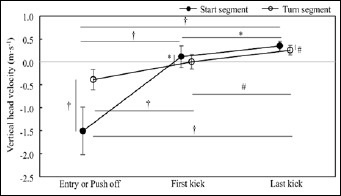
Differences in the vertical head velocity between three different timings and between the start and turn segment (results from simple main effect tests; †, #, and * show differences with p < 0.001, 0.01, and 0.05, respectively).

Initial-, First-, and Last-BA also showed differences between each other (p < 0.05) with BA becoming larger as the swimmers travelled forward, except between First- and Last-BA in the start segment. Swimmers had a smaller Initial-BA and larger First-BA in the start than the turn segment (p < 0.01; d = 1.04; 95 % CI = -11.82 – -3.58, and p < 0.05; d = 0.58; 95 % CI = 0.98 – 7.27, respectively) with BA during the turn being closer to 0˚ compared with the start. This means that swimmers had steeper BA in both timings (with their head pointing down- and up-ward, respectively) in the start than in the turn segment. On the other hand, they showed no difference between the segments in Last-BA (Figure 4).

Figure 4.

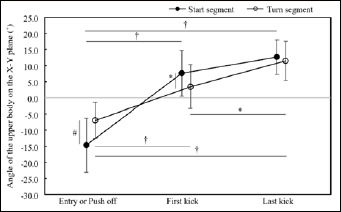
Differences in the upper body angle between three different timings and between the start and turn segment (results from simple main effect tests; †, #, and * show differences with p < 0.001, 0.01, and 0.05, respectively).

Discussion

The primary purpose of the present study was to establish relationships between selected underwater kinematics and the start and turn performances, and the second purpose was to assess the differences in the kinematics between the start and turn segments. In the current study, UW-vx_mean had large and extremely large relationships with T_0-15 and T_25-35, but no relationships were observed between UW-vx_mean and Initial-vx_head or between UW-vx_mean and Dec_kick . These results were surprising from a technical perspective, as swimmers should aim to maximize the initial velocity and minimize the deceleration during the underwater locomotion to achieve fast start and turn time (Takeda et al., 2020; Veiga et al., 2014).

Given the high impact of underwater kicks on the start and turn time (Takeda et al., 2020; Veiga et al., 2016), UW-vx_mean should be related to vx_mean during the whole, or a part of, underwater kicks. Notably, the timing where swimmers showed related vx_head with UW-vx_mean was different between the start and turn segment (the first kick in the former and the last kick in the latter segment), suggesting that the strategy for achieving a large UW-vx_mean was different between the two segments. The positive relationship between UW-vx_mean and First-vx_head in the start segment suggests that a large vx_head during the first kick (regardless of the Initial-vx_head) results in a large UW-vx_mean, which contributes to a fast T_0-15. First-vx_head was also negatively associated with First-vy_head and First-BA that had the mean value of 0.11 ± 0.24 m·s^-1 and 7.57 ± 7.02˚, respectively. These results mean that swimmers who had a large First-vx_head tended to have a negative BA (head pointing downward with the back facing forward) or BA close to the horizontal.

There are several explanations of why having small First-BA and First-vy_head contribute to large First-vx_head. Firstly, the relationships might have reflected that fast swimmers controlled their swimming direction and BA to maximize the horizontal component of the swimming velocity, as suggested by previous studies (Houel et al., 2013; Tor et al., 2015). The second possibility is that fast swimmers tried not to change their BA much after the entry to minimize the drag. Given that the mean Initial-vx_head and Initial-vy_head were 4.60 and -1.51 m·s^-1, the resultant velocity was around 4.84 m·s^-1. Since the hydrodynamic resistance at passive streamline condition is proportional to the square of the velocity (Vennell et al., 2006), the hydrodynamic resistance is critical after the entry, and the slight posture change would cause a severe deceleration. Considering that Initial-BA was smaller (steeper with the back facing forward) than First-BA and that Initial-BA was not correlated with either First-vx_head or First-BA, it is logical that fast swimmers tended to have a small change in BA from the entry until they performed their first kick.

These explanations can also support why UW-vx_mean was largely related to Last-vx_head but not with First-vx_head in the turn segment. The change in BA from the entry or push-off to the first kick was approximately 21 and 8.5˚ in the start and turn segment, which suggests that the potential effect of the change in BA on First-vx_head in the turn segment is not as great as in the start segment. Because of potentially smaller BA effect on First-vx_head in the turn than in the start segment, the impact of First-vx_head on UW-vx_mean is relatively less critical (consequently, the relative importance of Last-vx_head is higher) in the turn segment compared with the start segment.

In the present study, underwater time and distance were not related to T_0-15 and T_25-35, despite the association of UW-vx_mean with T_0-15 and T_25-35, which suggest that swimmers select their individual strategy to maximize the underwater velocity, as suggested by Veiga et al. (2014; 2016). This could also explain why there were no correlations of Dec_kick with T_0-15 and T_25-35 despite the correlations between First- or Last-vx_head and these times, because Dec_kick obtained in the present study was the mean value, meaning that this variable was affected not only by the difference between First- and Last-vx_head, but also the duration spent between the first and last kick.

Kick count was largely related to T_0-15 in the start segment, but not to T_25-35 in the turn segment. Kick count should be determined by the glide time, kick frequency, and the underwater time; however, none of these variables was correlated with T_0-15 and T_25-35. Thus, the relationship between kick count and T_0-15 cannot be explained by a single factor and could only be explained by, once again, individual strategies of swimmers. In other words, fast swimmers tend to perform a large number of kicks in the start segment, but the reason for it is individually different.

A number of results in the current study showed a lack of associations between kinematics and start and turn performances due to large inter-individual variability. However, it should be stressed that this does not necessarily mean that there are no relationships between the investigated kinematics and the start and turn performance, but the current study merely rejected the linear relationship possibility. It is still possible that there are non-linear relationships between those kinematic measures and T_0-15 or T_25-35. To explore more possibilities, further studies are necessary with non-linear approaches, such as cluster analysis (Simbana-Escobar et al., 2018).

Underwater time was similar between the start and turn segment despite vx_head being faster at the beginning of the segment in the start than in turn. Assuming that swimmers tried to breakout with an individually optimal forward velocity(that was supported by the similar Last-vx_head between the segments), the difference in the underwater time was probably due to the larger Dec_kick in the start compared with the turn segment. One explanation for the difference in Dec_kick was simply because of the higher Initial- and First-vx_head in the start than the turn segment; in other words, due to a larger resistive force that increases with the forward velocity exponentially (Vennell et al., 2006). However, if the velocity differences were the primary reason for the difference in Dec_kick, swimmers should have followed the same deceleration pattern. In such a case, swimmers should spend longer time underwater in the start than turn segment to reach the same breakout velocity. Therefore, even though the difference in Initial- and First-vx_head should have affected the difference in Dec_kick, this cannot be the only source of the difference.

Therefore, differences in other kinematics should have affected the distinct Dec_kick between the segments. Because of the different segment initiation (taking-off from a starting block and wall push-off in the water), swimmers showed smaller Initial-vy_head and Initial-BA in the start than in the turn segment, meaning that they travelled more downwards in the start segment. Because of the difference in the initial downward motion, swimmers had to travel upward to a larger extent (194 % and 30 % during the first and last kick, respectively) with a 70 % larger First-BA in the start than turn segment. This means that swimmers had to make a greater effort on travelling upward in the start than in the turn segment, that might have caused the larger Dec_kick in the start segment as suggested in a previous study that investigated different underwater trajectories after the start (Tor et al., 2015).

Despite the similar underwater time, swimmers performed 1.3 times more kicks in the start than in the turn segment, which was likely due to the higher kick frequency and shorter glide time in the start than in the turn segment. However, the glide time difference was only 0.2 s, which corresponds to 40-50 % of one kick cycle time (0.4 and 0.46 s in the start and turn segment). Therefore, the primary source of the difference in kick count was probably the kick frequency. One explanation for the difference in kick frequency between the segments is fatigue. There has been no research comparing the underwater kinematics between the start and turn segment in a race condition; therefore, it is difficult to examine the result in comparison with the literature. However, it has been reported that swimmers decreased their stroke frequency due to fatigue from the first to the last lap of the short course 100 m front crawl and butterfly swimming (de Jesus et al., 2012; Toussaint et al., 2006), which shows the effect of fatigue on the limb speed during swimming.

Another explanation is the effect of the water flow speed relative to the body. In the start segment, swimmers had higher Initial- and First-vx_head than in the turn segment, meaning that the backward flow speed relative to the body was much faster in the start segment. Therefore, swimmers might have experienced a smaller drag force on their feet when they kicked backwards, which could potentially affect kick frequency. In future studies, it would be of interest to investigate if the fast flow speed relative to the body affects kick kinematics of swimmers using both kinematic and hydrodynamic analyses.

Conclusion

This was the first study that investigated underwater kinematics in a condition equivalent to competitions and therefore provided important insights into underwater locomotion during the start and turn segments. In male 50 m butterfly swimming, performance in the start and turn (fast T_0-15 and T_25-35) was related to a large UW-vx_mean regardless of Initial-vx_head, Dec_kick, and other kinematic variables such as kick frequency, suggesting a wide range of individual strategies to achieve a large UW-vx_mean. On the other hand, UW-vx_mean was associated with different factors in the start and turn segment; First-vx_head was important in the start segment, whereas Last-vx_head was essential in the turn segment.

Biographies

Tomohiro GONJO

Employment

Post-doctoral researcher at Norwegian School of Sport Sciences.

Degree

PhD

Research interests

Biomechanics and performance analysis in aquatic sports with specific emphasis on elite swimmers’ skills.

E-mail: tomohiro.gonjo@nih.no

Bjørn Harald OLSTAD

Employment

Associate professor at Norwegian School of Sport Sciences.

Degree

PhD

Research interests

Swimming and aquatic activities from beginner to elite levels, with a particular interest in coaching science, technology and performance analysis in swimming.

E-mail: b.h.olstad@nih.no