Abstract
The neurovascular unit (NVU) underlines the complex and symbiotic relationship between brain cells and the cerebral vasculature, and dictates the need to consider both neurodegenerative and cerebrovascular diseases under the same mechanistic umbrella. Importantly, unlike peripheral organs, the brain was thought not to contain a dedicated lymphatics system. The glymphatic system concept (a portmanteau of glia and lymphatic) has further emphasized the importance of cerebrospinal fluid transport and emphasized its role as a mechanism for waste removal from the central nervous system. In this work, we outline a novel multiporoelastic solver which is embedded within a high precision, subject specific workflow that allows for the co-existence of a multitude of interconnected compartments with varying properties (multiple-network poroelastic theory, or MPET), that allow for the physiologically accurate representation of perfused brain tissue. This novel numerical template is based on a six-compartment MPET system (6-MPET) and is implemented through an in-house finite element code. The latter utilises the specificity of a high throughput imaging pipeline (which has been extended to incorporate the regional variation of mechanical properties) and blood flow variability model developed as part of the VPH-DARE@IT research platform. To exemplify the capability of this large-scale consolidated pipeline, a cognitively healthy subject is used to acquire novel, biomechanistically inspired biomarkers relating to primary and derivative variables of the 6-MPET system. These biomarkers are shown to capture the sophisticated nature of the NVU and the glymphatic system, paving the way for a potential route in deconvoluting the complexity associated with the likely interdependence of neurodegenerative and cerebrovascular diseases. The present study is the first, to the best of our knowledge, that casts and implements the 6-MPET equations in a 3D anatomically accurate brain geometry.
Keywords: Glymphatic system, multiple-network poroelastic theory, neurovascular unit, finite element method, Alzheimer’s disease
Introduction
Although the brain only accounts for approximately 2% of the body’s total mass, it has the capacity to consume approximately one fifth of its resting energy production.1 The high metabolic demand of this organ is driven by a constant flow of blood supplied through a widespread and densely packed network of microvasculature (the sensitivity of the vascular tone is essential in regulating the cerebral blood supply) comprising of arterioles, capillaries and venules. The architectonics of the microvasculature in the cerebral cortex allows for the adequate supply of oxygen and nutrients2 and is also unique in its ability to form a blood–brain barrier (BBB). This barrier regulates homeostasis of the central nervous system (CNS) by tightly regulating the transport of ions, molecules and cells. The BBB does not function independently, as it is a constituent of a multi-cellular neurovascular unit (NVU). The NVU comprises of neurons, astrocytes, pericytes, microglia and blood vessels. In this work, a highly integrated workflow that can capture the broad spectrum of biological flows within complex three-dimensional, deformable and permeable brain tissue is presented. The core numerical template that sits at the epicentre of this state-of-the-art precision medicine pipeline was largely developed within the VPH-Dementia Research Enabled by IT Project.3 In this project, the focus was to extend the understanding of Alzheimer’s Disease (AD) in addition to promoting earlier differential diagnosis through a unified multiscale modelling platform that accounts for a subjects’ environment and lifestyle. In the work presented here, the original four-compartment poroelastic model presented as part of this precision medicine pipeline is extended to six-compartments. This extension is important, since the four-compartment model made an implied assumption regarding cerebrospinal fluid (CSF): it amalgamated all fluid outside the vascular tree into a single entity, or one compartment, within the multiporoelastic model. A physiologically more accurate representation requires the intracellular and extracellular fluid to be separated, in addition to incorporating distinctive extracellular fluid pathways, like the glymphatic system,4 which require special treatment in order to more faithfully represent both the complex hypotheses and the pathophysiological processes allied to neurodegenerative diseases such as AD.
The neurovascular unit: Origins and composition
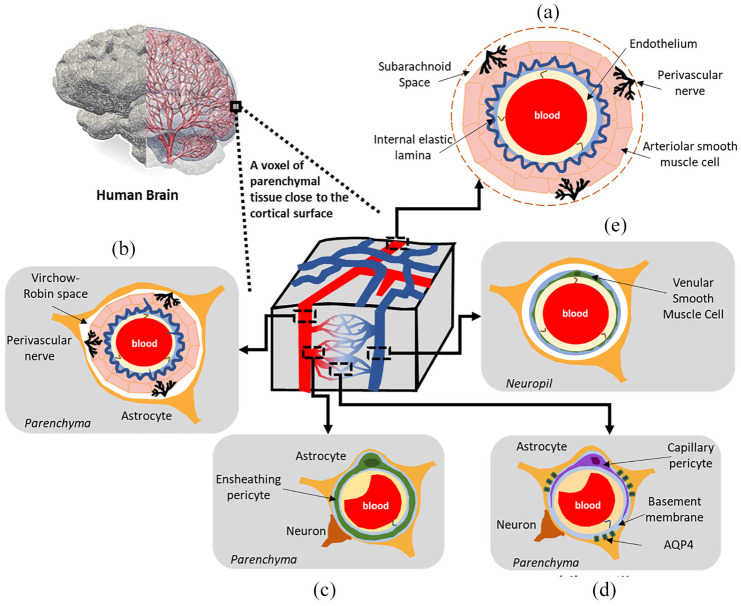
The conceptual understanding of the neurovascular unit (NVU) underlines the complex and symbiotic association between brain cells and the cerebral vasculature. More specifically, the NVU dictated the need to consider both neurodegenerative and cerebrovascular diseases under the same mechanistic umbrella, by offering the opportunity for important discussions revolving around the brain and its vessels in both healthy and diseased states.5 Figure 1(a)–(e) depicts the range of vessels that are situated within parenchymal tissue. For a thorough treatment of the architecture of these vessels along with the important roles these play in fluid transport in the brain, the reader is referred to the work of Iadecola, McConnell et al. and Coelho-Santos and Shih.5–7
Figure 1.
A schematic representation of the mature (adult) neurovascular unit (NVU) within a rodent cerebral cortex. A range of vessels are situated within parenchymal tissue. The vascular wall composition at the level of (a) the pial arterioles on the cortical surface, (b) the penetrating arterioles, (c) pre-capillary arterioles, (d) capillaries, and (e) the ascending venules.
AQP4: aquaporin 4.
Understanding dementia and Alzheimer’s Disease
By 2050, it is estimated that over 150 million people will be living with dementia.8 Alzheimer’s Disease (AD) is acknowledged as a progressive multifarious neurodegenerative disorder. It is the most prevalent form of dementia (accounting for around 50%–70% of cases) and is the main cortical neurodegenerative disease.9 With an ageing global population, AD is projected to generate a major a public health crisis in the coming decades.10 A more detailed understanding of the mechanisms driving AD necessitates the redefinition of the disorder as a mixture of dysfunctions rather than one defining pathology.
The vascular hypothesis of AD and the role of hypoperfusion
From a pathophysiological perspective, several hypotheses allied to AD have been studied to help understand this multifactorial disorder (amyloid cascade, cholinergic and the vascular hypotheses).11,12 The well documented pathological hallmarks of AD incorporate amyloid-β peptide (Aβ) plaques, tau tangles, neuroinflammation, and subsequent neurodegeneration.10 Aβ can be found both in the brain parenchyma, or in and around blood vessels (cerebral amyloid angiopathy).13 A competing hypothesis (to the amyloid cascade hypothesis) is the vascular hypothesis of AD. This hypothesis is reinforced by increasing evidence that relates vascular dysfunction and AD development.9,14 The latter is very often associated with cerebrovascular pathologies12,14–18 (such as microinfarcts, haemorrhage, decreased cerebral blood flow, small vessel disease and white matter abnormalities).19,20 It has been observed in recent studies that there is a correlation between cognitive dysfunction and vascular disease.18,21 Additionally, numerous investigations fortify the association between various vascular risk factors (such as arterial hypertension,22 obesity,23 atherosclerosis24 and genetic risk factors (for example the APOE ε4 allele))25 and the heightened probability of developing AD. Recent studies postulate that cerebral hypoperfusion (CH) precedes AD.26,27 CH triggers a metabolic energy crisis (via the promotion of a hypoxic state and the accumulation of Aβ and aggravation of vascular disease) which ultimately leads to neuronal degradation.9,28–33
Clearance pathways for unwanted molecules in the brain: The glymphatic system concept
Research into cerebral health and disease has attracted increasing attention, yet, the exact clearance mechanisms responsible are yet to be identified. Unlike peripheral organs, the brain was thought not to contain a dedicated lymphatics system.
The glymphatic system concept has given new impetus to the field of CSF fluid transport and underscored its role as a process for waste clearance from the CNS.34 This hypothesis involves CSF being continuously transported from the basal cisterns and into the subarachnoid space (SAS) at the periphery of the cerebral hemispheres, to the periarterial spaces. Subsequently, CSF is driven from the periarterial network into the interstitial fluid (ISF) space. This transport of fluid is seemingly facilitated via aquaporin-4 (AQP4) water channels. The latter are predominantly localised on astroglia end-feet (see Figure 1(d)).35 The latter process enables the mixing of both CSF and ISF in addition to waste solute removal. Lastly, the CSF and ISF mixes with interstitial waste solutes, and is transported towards the perivenous compartment of the larger central veins, ultimately entering the systemic circulation. 34,36
Recent studies on the downstream lymphatic network, and how this interconnect with the glymphatic pathway have become important areas of consideration.37–39 As described by Benveniste et al., the glymphatic system may be viewed as a waste processing unit,34,40 with the key constituents being: perivascular AQP4 water channels, hydraulic forces associated with arterial pulsation, respiratory effort, and body position,34,41–43 regular CSF production and transport, and a state of arousal.44,45
The convoluted nature of the glymphatic system along with the visibly complex, and broad spectrum of disorders that constitute dementia requires the use of a biomechanistic model that is both accurate and general enough to define clinically relevant biomarkers allied to the multiscale cerebral environment. A precision medicine workflow is presented here, which allows for a previously unexplored understanding of the disease trajectory (from mild cognitive impairment [MCI] to AD) through the lens of the physiologically accurate definition and interplay of both the NVU and the glymphatic pathway (by treating this pathway as a separate compartment within a multiporoelastic system). The in-silico model presented here requires the use of a surrogate model that outputs arterial blood flow waveforms (that are used as boundary conditions) whilst taking into account lifestyle and environmental factors (LEFs) and subject profiles. Additionally, an imaging pipeline is used to further personalize the workflow via the acquisition of: (i) a subject-specific atlas of CSF/extracellular fluid (ECF) permeability within the cerebral parenchymal tissue; (ii), the accurate representations of the cerebroventricular geometries; and (iii), the partitioning of white and grey matter which is complemented by a field of varying parenchymal tissue stiffness. The reader is referred to3,46–48 for further details.
Outline of the article
The methodology behind the full implementation of the novel six compartment poroelastic model follows in the ‘Methodology’ section, which also briefly describes the extension (spatial variation of the region-specific mechanical properties of brain tissue) of a recently developed high precision workflow.3 The results, discussion and limitations are given in the ‘Results and discussion’ section, where 6-MPET results at the level of the neurovascular unit for five separate regions of the brain (cortical grey matter, hippocampus, amygdala, thalamus and brainstem) are presented. The conclusions and perspectives for future work are given in the ‘Conclusion’ section.
Methodology
The six-compartment multiporoelastic model for perfused parenchymal tissue
The underlying conservation equations allied to multiple network poroelastic theory (MPET), have been described in previous publications by the same authors.47–53 In this section, the novel six-compartment (6-MPET) formulation (and its FEM-based discretisation) is concisely described. This 6-MPET extension is embedded within a larger workflow and replaces the 4-MPET template developed by the same authors.3,46–48 Methodologically, the work presented here builds upon previous work47–53 by: (i) defining two additional compartments (reflecting the glial cells and perivascular space/glymphatic system) within the multiple network poroelastic framework in order to more accurately mimic the physiology of the neurovascular unit; and (ii), by partitioning white and grey matter within the cerebral cortex and enforcing a field of weakly varying parenchymal tissue stiffness for the white matter.
In this work, the consolidated workflow is used on one cognitively healthy control subject. This allows one to acquire a biomechanistic understanding into the basic mechanisms of the neurovascular unit (pial/penetrating arterioles, capillaries, ascending venules/veins, see Figure 1) and glymphatic system in the whole parenchyma, in addition to focusing on five important regions of the brain (cortical grey matter (CGM), hippocampus, thalamus, amygdala and brainstem) through key derivative 6-MPET solution fields (perfusion associated with the capillary compartment, tissue swelling and drainage associated with the capillary, CSF/ECF, glymphatic, glial and paravenous spaces).
The newly developed 6-MPET model utilises the following primitive variables in the governing equations (solid matrix/cerebral tissue displacement, u, and the pore pressures of six fluid compartments: pa, pc, pe, pv, pl, pg):
| (1a-g) |
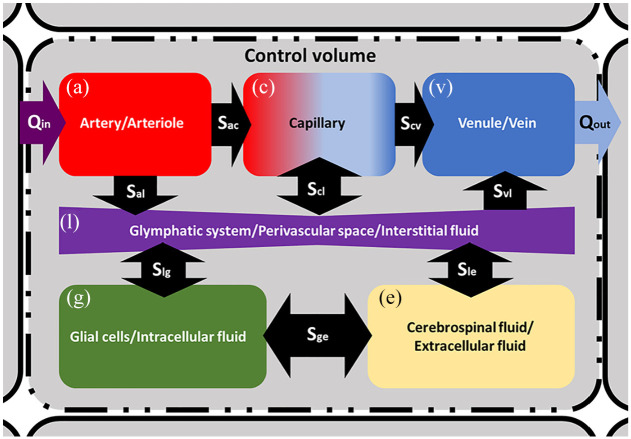
From equation (1a–g), α is the Biot-Willis coefficient (which satisfies ϕ≤αa+αc+αe+αv+αl+αg≤ 1, where ϕ is the total porosity), c the constrained specific storage, ε denotes the dilatational strain, the Sxy terms in equation (1b–g) define spatially varying source (Sxy > 0) or sink (Sxy < 0) densities (rate of fluid transfer between networks driven by a hydrostatic pressure gradient) incorporating the intercompartmental transfer coefficient (ωyx, which scales the flow between network y and x). Qin and Qout represent the flux entering, and leaving the control volume, K is the hydraulic permeability tensor (equal to κ(μ−1), where κ is the permeability tensor and μ is the viscosity) for each of the six fluid compartments. In this work, the CSF/ECF compartment is anisotropic, whilst the remaining fluid compartments are assumed isotropic. For more details, the reader is referred to previous work by the same authors.47,48,49,54 Figure 2 depicts the nature of the control volume in which the 6-MPET model operates within. Table 1 lists the parameters used to run the 6-MPET model.
Figure 2.
A schematic representation of the 6-MPET model within a control volume. Directional flow constraints are applied between the CSF/ECF (e) and the arterial/arteriole (a), capillary (c) and venule/venous (v) network, as dictated by the physiology of these compartments. The glymphatic system (l) mediates the transfer of fluid between the blood networks associated with the neurovascular unit, the CSF/ECF and the glial cells (g). Directional flow transfer is depicted by the black arrows, and the spatially varying source/sink terms associated with the conservation equations are depicted in the form Sxy.
Table 1.
6-MPET parameters used in this study.
| Parameters | Values | Units | Parameters | Values | Units |
|---|---|---|---|---|---|
| αa,v | 0.1 | cv,l,g | 1.5 × 10−5 | m2N−1 | |
| αl,g,c,e | 0.2 | ce | 3.9 × 10−4 | m2N−1 | |
| λg | 505 | Pa | ka ,e,v | 1.0 × 10−10 | m2 |
| Gg | 216 | Pa | kl | 2.0 × 10−11 | m2 |
| λw | 1010 | Pa | kg | 5.0 × 10−8 | m2 |
| Gw | 433 | Pa | kc,white | 1.0 × 10−10 | m2 |
| L | 70 × 10−3 | m | kc,grey | 1.0 × 10−8 | m2 |
| d | 3 × 10−3 | m | ωac,cv | 1.5 × 10−19 | m2N−1s−1 |
| pls | SSBF | Pa | ωal | 2.8 × 10−14 | m2N−1s−1 |
| plv | 2445 | Pa | ωcl,vl,el,gl,eg | 4.1 × 10−9 | m2N−1s−1 |
| pgv | 1767 | Pa | R | 8.5 × 1013 | m−3 |
| pbp | 650 | Pa | Qp | 5.8 × 10−9 | m3s−1 |
| ca ,c | 2.9 × 10−4 | m2N−1 | Δt | 0.1 | s |
Values of shear modulus, G, and Lamé’s constant λ for the white matter (with subscript w) than the grey matter (with subscript g) are given. The reader is referred to Vardakis et al., Guo et al. and Chou3,47,48,54–56 for further details.
SSBF: subject-specific blood flow profile derived arterial pressure.
The 6-MPET numerical template
The 6-MPET system of partial differential equations has been discretised using the finite element method (FEM). The FEM code was written in FORTRAN 90/95. In previous work, the authors conducted grid-independence studies, verified the multiporoelastic system against analytical solutions,47,57,58 in addition to the system being recently validated with respect to data arising from both a CSF infusion test54 and ASL based values.55
In line with previous work, grid-independence of the 6-MPET system was conducted, and converged solutions fell within a specified percentage band of numerical error estimates. For details regarding the discretisation of the conservation equations, the reader is referred to Guo et al. and Vardakis et al.47,48,54,55 Finally, the discretised form of the 6-MPET system is solved using the PETSc library.59,60
Subject-specific dataset, 6-MPET parameters and boundary conditions
Subject-specific dataset
The details regarding the subject-specific dataset used in the execution of the 6-MPET model presented here, along with further details can be found in previous publications by the same authors.3,47,48 Subject and region-specific geometries of the cortical tissue and cerebroventricular system, permeability tensor maps of the cerebral tissue and subject-specific flow waveforms were acquired using the protocol in Vardakis et al. and Guo et al.3,47,48 From this combined dataset, a 72-year-old cognitively healthy female subject (whilst undergoing a period of high activity) was used to execute the high-precision workflow.
Parameters of the 6-MPET system
As in previous work,55 the differentiation between grey and white matter is adopted, as the segmentation of the of T1w MR images defines 28 separate regions in both hemispheres, including the grey and white matter. This partitioning of the parenchymal volume allows for different values to be assigned for the mechanical properties (such as Young’s modulus) of the grey (584 Pa)47–51 and white matter (1168 Pa).55 In order to further extend the state-of-the-art, this numerical template also allows for the perturbation of the Young’s modulus field within the white matter, of the order of ±10 Pa. It has been observed that a decrease in brain viscoelastic parameters is associated with ageing,61 and in AD, the overall brain stiffness is observed to decrease.62,63 To be able to account for these key characteristics within the presented numerical template, the 6-MPET code was augmented with the capability of capturing a spatially varying elasticity field in the white matter. Additionally, the permeability of the arteriole/capillary compartment is assigned partitioned values for white (kc,white) and grey matter (kc,grey), and reflects the calibration of the capillary compartment with respect to the validation of the filtration velocity via CBF data acquired from ASL images.55 In this manuscript, a new set of Biot-Willis constants were used, reflecting the theoretical nature of this study. In previous studies (see Vardakis et al.48 for example), the value of the CSF/ISF compartment in the 4-MPET framework was almost double (0.49) that of the feeding blood compartments (arterial and capillary compartments were set at 0.25), and approached small values for the less compliant venous system (10−2). In this work, the larger calibre vessels (arteries/arterioles and venules/veins) that feed and drain the representative elementary volume of the 6-MPET system are scaled to be lower than the constituents of the NVU (see Table 1), in order to simplify the study of the 6-MPET system, and also to reflect the need to physiologically define the low resistance pathways facilitating CSF flow (paravascular spaces surrounding leptomeningeal arteries).64 The intercompartmental transfer coefficients (ωal, ωcl, ωvl. ωel, ωgl, ωeg) associated with the two additional compartments (glial cells/intracellular fuid and glymphatic system/perivascular space/ISF) are calculated by incorporating parameters associated with hydraulic conductivity, a bidirectional constrained specific storage coefficient and the surface to volume ratio. These terms also possess the ability to incorporate aquaporin expression (see Chou56 for further details). The remaining intercompartmental flux terms (ωac, ωcv) are the same as in previous studies (see for instance Vardakis et al. and Guo et al.).3,47,48,54,55
Boundary conditions of the 6-MPET numerical template
In the work conducted here, the outer/inner boundary of the cerebral tissue represents the cortical surface/cerebroventricular wall respectively. Table 2 lists the Dirichlet, Neumann and Robin boundary conditions used in this model. The details and physiological significance of the boundary conditions associated with the 4-MPET model are explained in previous publications.3,47–50,52,55 In this section, only the boundary conditions associated with the two additional compartments (glial and glymphatic system) are described in further detail. In the 6-MPET compartment associated with the glymphatic system, it is assumed that a peak arterial pressure on the cortical surface prevails (∼100 mmHg, in line with previous studies),47,48,55 whilst on the surface of the cerebral ventricles, the pressure is equal to that of the average pressure associated with the capillary compartment (∼18 mmHg).55 This is not an unreasonable assumption to make, since it is assumed that the perivascular space maintains its pressure throughout the parenchymal volume in order to maintain cerebral homeostasis and the integrity of the BBB. For the glial cell compartment, it is assumed that a Dirichlet condition equal to the average of the CSF/ECF and capillary pore pressure exists on the surface of the cerebral ventricles, whilst the skull has the CSF/ECF pore pressure as a boundary condition. These assumptions are made on the premise that within the parenchymal tissue, a continuous CSF compartment exists, spanning from the SAS, cisterns, and paravascular spaces, whilst simultaneously considering the parenchymal vasculature.41
Table 2.
Boundary conditions used in the 6-MPET model. The reader is referred to Vardakis et al., Guo et al. and Chou3,47,48,54–56 for further details. ∂Γs and ∂Γv are boundaries at the skull and cerebroventricular wall respectively, n is the outward unit normal vector and u1 is the maximum ventricular displacement at each time increment.
| 6-MPET variable | Cortical surface | Cerebroventricular wall |
|---|---|---|
| u | u = 0 | |
| pa | ||
| pc | ||
| pe | ||
| pv | ||
| pl | ||
| pg |
The reader is referred to previous work3,46–48 regarding the methodology behind the implementation of the boundary conditions, including the Neumann application of the CBF waveforms associated with the driving compartment (the arterial compartment) of the 4-MPET (and by extension, the 6-MPET) system. The solutions of the 6-MPET system are acquired from the final periodic steady state (spanning 50 simulation cycles). It should be noted that for this subject, the internal carotid artery (ICA) profiles between left and right hemisphere were closely aligned (unlike the variation present for other subjects studied in work by the same authors).47,48 The VA profiles are identical for both hemispheres, in line with previous work.47,48 This implies a greater degree of morphological symmetry to the developing solution fields (as the arterial compartment is the driving compartment of the system) and allows the compartmental interrogation of the 6-MPET model to be conducted according to the aforementioned extensions to the high precision workflow.
Results and discussion
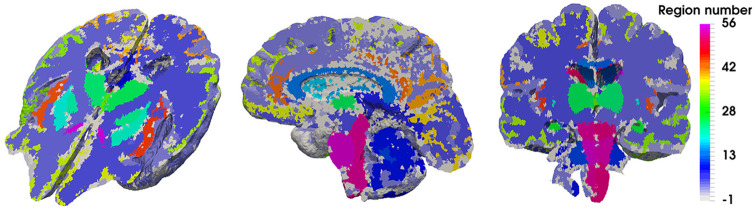
Figure 3 depicts the 28 regions (spanning the two hemispheres, so a total of 56 separate regions) that this precision medicine pipeline can stratify results for (like the hippocampus, brainstem and thalamus), in addition to the outputs of the 6-MPET system for the chosen subject (72-year-old female cognitively healthy control subject).
Figure 3.
Representation of the regional parenchymal specificity incorporated in the high precision workflow. A sagittal, coronal and perspective representation of the axial plane is shown in this figure, highlighting the 56 regions (28 for each hemisphere) of the parenchyma that can assist in stratifying the 6-MPET results.
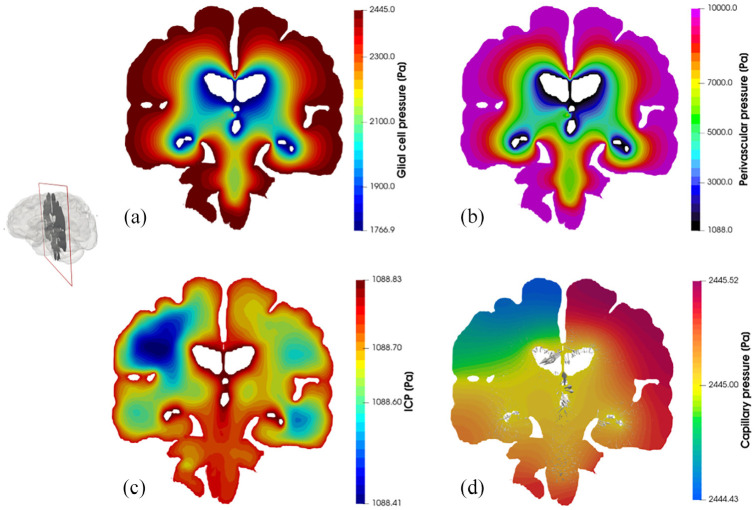
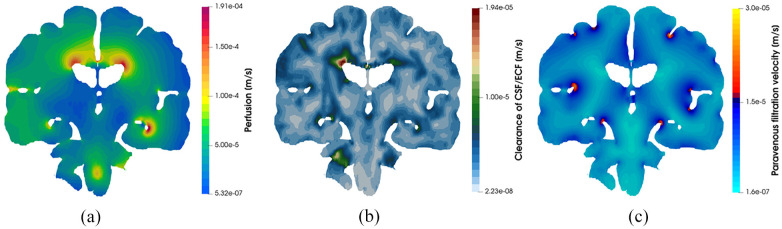
Figure 4 depicts core pore pressure solution fields garnered from executing this workflow, including glial and perivascular pressure (Figure 4(a) and (b)), intracranial pressure (ICP) (Figure 4(c)), and capillary pressure within the parenchymal volume (Figure 4(d)). Figure 5 depicts additional derivative solution fields (obtained at the post-processing stage of the workflow)47,48,55 of interest, namely perfusion (Darcy velocity of the capillary compartment, Figure 5(a), clearance of CSF/ECF (Darcy velocity of the CSF/ECF compartment, Figure 5(b) and paravenous filtration velocity (Darcy velocity of the venule/venous compartment, Figure 5(c). Clearance of CSF/ECF emphasizes the intertwined nature of the 6-MPET compartments, as it incorporates the effects of the subject-specific permeability tensor maps.
Figure 4.
Coronal slices of the 6-MPET solution fields allied to the parenchymal volume of the 72-year-old cognitively healthy female subject undergoing a period of high activity. Both the pore pressure of the glial cell compartment (a) and the perivascular/glymphatic system (b) is symmetric in morphology, reflecting the nature of the boundary conditions imposed for these compartments whilst also considering the intercompartmental influences of the remaining compartments. The latter influences are more prevalent in the compartments describing the (c) intracranial pressure (CSF/ECF compartment) and (d) capillary pressure, since the former superimposes a highly distinctive permeability tensor map which can capture the underlying parenchymal microstructure (see Guo et al. and Vardakis et al.47,48 for more details). The capillary compartment and its accompanying pore pressure reflect the asymmetric nature associated with the arterial flow variability being applied on the partitioned parenchymal surface, as it is in direct communication to the high transmantle pressure gradient present in that compartment. The superimposed velocity vectors associated to the paravascular/glymphatic system filtration velocity assist in attenuating the level of detail associated with this rich dataset.
Figure 5.
Coronal slices of the 6-MPET solution fields allied to (a) perfusion, (b) clearance of CSF/ECF and (c) paravenous filtration velocity. Some quantitative similarities for these solution fields can be found in Vardakis et al., Croci et al. and Thomas.48,65,66 It can be seen that the impact of the cerebroventricular geometry (in terms of its concavity) influences the localisation of the areas of peak perfusion, paravenous filtration, and clearance of CSF/ECF. These areas could play a role in AD progression.
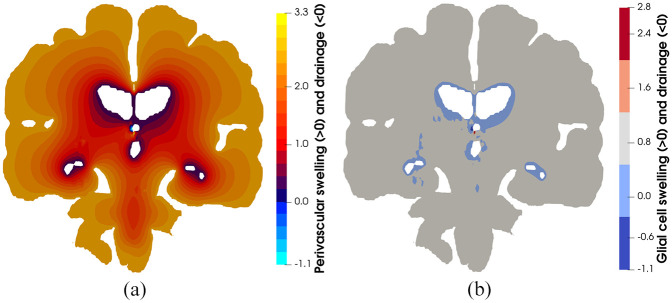
Figures 4 and 5 highlight the asymmetric nature of the primary solution fields allied to ICP, and capillary pressure, in addition to the derivative fields associated with fluid content and Darcy filtration velocity for the capillary, CSF/ECF, venous, and glial cell compartments. Derivative solution fields can be seen to capture the inherent concavity of the cerebral cortex and cerebroventricular system (especially in the periventricular regions), and in doing so, highlight the ability of the numerical template to incorporate areas of accumulating strain and scaled pore pressure fields with high qualitative accuracy. Periventricular lucency (PVL)67 (accompanied by localized cerebroventricular rupture)68 is a common neuroradiological finding, yet its pathogenesis and clinical significance remains inconclusive.69 It is postulated that the relief of excess pressure within the cerebroventricular system is facilitated by the tactical breakdown of the ependymal surface which is thought to also involve AQP4 (see Figure 1d).70 Additionally, the concavity of the cerebroventricular system47,48,52,69,71 is a constituent of PVL, and may also involve CSF/ECF clearance (see Figure 5) which may utilise stretch/swelling-activated Cl− channels (and therefore the extent to which the microglia can monitor the cerebral parenchyma).72 In this work, PVL is calculated as the increased fluid content in the periventricular regions and can be seen to reflect the aforementioned hallmark characteristics (see Figure 6, perivascular and glial cell swelling and drainage solution fields). Both the anterior and posterior horns of the lateral ventricles portray the focal areas of peak PVL, and these areas coincide with the cerebroventricular regions of pronounced concavity. Previous work by the same authors fortify these qualitative findings.47,48,50,52
Figure 6.
(a) Perivascular and (b) glial cell swelling and drainage. Swelling in depicted from positive values of the respective compartmental fluid content, whilst drainage is depicted with negative values. It is interesting to note the influence of the cerebroventricular system (as it possesses a high concavity) in accumulating strain, which is reflected in the highly accurate qualitative depiction of periventricular lucency, a potential inhibitor to the transport pathways associated with the glymphatic system (perivascular and glial cell swelling). On the contrary, drainage in these solution fields may be representative ependymal cell breakdown (which is assumed to be fused with the surrounding glial cells), forcing fluid to leave the ventricles in order to relieve the underlying pressure burden in these cavities.
Table 3 provides a snapshot of the additional capabilities of this consolidated pipeline. Derivative quantities of interest (perfusion, and degree of swelling and drainage for the perivenous, glial, glymphatic, CSF/ECF and capillary compartment) are given for five important regions of the brain (cortical grey matter,3 hippocampus,48 thalamus, amygdala and brainstem) that are important in the trajectory of AD progression. Developing protein pathology in the medial temporal lobe triggers cognitive deficit in AD, hence the focus on hippocampal73 dysfunction and how memory symptomology74 can be alleviated by therapies targeting this region. In this work, the thalamus is analysed for its perfusion and fluid content variability over key compartments of the 6-MPET system, since interrogating this region is deemed to provide a more balanced understanding of the transition between MCI and AD.74 Regional thalamic degeneration in AD is emerging as an important area of consideration alongside the hippocampus and amygdala.75 There is MRI evidence linking internal medullary lamina atrophy which is thought to promote thalamic degeneration in AD patients.75 The results in Table 3 show that although this region neighbours the hippocampus, its location and geometrical structure promotes peak perfusion values that vary (∼62 µm/s compared to ∼84 µm/s in the hippocampus) and is accompanied by a high proportion of paravenous drainage and swelling, whilst solely portraying swelling characteristics for the glial and capillary compartments. Like the thalamus, the amygdala is also affected in the nascent stages of AD, and evidence exists linking a reduced intrinsic functional connectivity in this region.76 It was observed that this region portrayed swelling characteristics in the capillary and glial compartments, and also maintained a large perfusion range (∼25 µm/s–0.2 mm/s), which could prove to be an interesting biomechanistic biomarker considering imaging studies have consistently shown evidence of atrophy in this region.75 The consistent swelling in the NVU in all regions considered may also signify an increased likelihood of BBB breakdown/dysregulation, which may ultimately lead to enhancing the malignantly progressive burden of neurodegeneration. This can include the perivascular accumulation of neurotoxic products and the promotion of small vessel disease–related brain tissue injury.77
Table 3.
6-MPET results for derivative quantities for five different regions of the brain.
| Region | Perfusion (min, max) | Fluid swelling (>0) & drainage (<0) for different compartments | |||||
|---|---|---|---|---|---|---|---|
| Capillary | CSF/ECF | Glymphatic | Glial | Paravenous | |||
| CGM | 4.3 µm/s, 0.7 mm/s | [−0.3,1.1] | [−0.7,0.8] | [−0.7,3.0] | [−0.5,1.1] | [−0.4,0.3] | |
| Hippocampus | 0 m/s, 0.19 mm/s | [−0.6,1.1] | [−0.9,0.8] | [−0.9,2.9] | [−0.7,1.0] | [−0.7,0.3] | |
| Thalamus | 0 m/s, 62.2 µm/s | [0.2.1.1] | [−0.2,0.8] | [−0.04,2.7] | [0.1,0.9] | [−0.7,0.3] | |
| Amygdala | 25.6 µm/s, 0.2 mm/s | [0.2,0.8] | [−0.2,0.5] | [−0.2,2.6] | [0.005,0.8] | [−0.2,0.3] | |
| Brainstem | 5.3 µm/s, 0.2 mm/s | [0.2,1.0] | [−0.1,0.7] | [−0.1,2.9] | [0.03,1.0] | [−0.1,0.3] | |
CGM: cortical grey matter.
Brainstem nuclei regulate autonomic, cognitive, and behavioural functions. Therefore, this region may be playing an important role in AD progression.78 Throughout the developmental stages of AD, brainstem neurodegeneration has been linked to a disruption in sleep patterns,79 respiration and blood pressure.80 Additionally, it is known that the proportion of 3R tau in the brainstem neurofibrillary changes increases with disease progression.81 Considering its location (its close proximity to the cerebellum), it is unsurprising that this region occupies a broad perfusion range (∼5 µm/s–0.2 mm/s), as the partitioned arterial boundary conditions (in Neumann form) on the cortical surface of the parenchyma approach 100 mmHg,3,47,48 reflecting the driving flow rates of over 700 ml/min for the left and right ICA, and approaching 200 ml/min for the left and right VA during peak systole within the fifty simulated cycles. Interestingly, the brainstem portrays evidence of paravenous drainage, but at the expense of predominant swelling in the paravascular space, glial cells, CSF/ECF and the capillary compartments.
The cortical grey matter (CGM) displays similar characteristics, with the notable exception of additional measurable drainage in the CSF/ECF and a larger peak perfusion velocity of 0.7 mm/s, as opposed to 0.2 mm/s in the brainstem. The blood perfusion results obtained from the 6-MPET model presented here lie within a similar quantitative range as the perfusion results obtained from a simpler multiporoelastic model that adhered to ranges that mimicked arterial spin labelling (ASL)-derived perfusion.55 Focusing on the CGM in this study, one is able to gain theoretical insight into the glymphatic system in this region, and its interplay with the other constituent compartment that define the representative elementary volume of parenchymal tissue. The enlarged perivascular space during AD postulated by a recent study82 can be given further consideration, since this work relaxes the assumption that the enlarged perivascular space occurs as a direct result of the periarterial swelling,3 and instead allows a similar statistical analysis to be conducted on the compartments that reflect these intertwined alterations most accurately (glymphatic and capillary compartment).
Limitations of the study
In this extensive, yet preliminary study, only one subject from the Lido study cohort was analysed (execution of the pipeline for the remaining cases is currently in progress). The emphasis has been placed on being able to associate some of the resulting outputs of the consolidated framework outlined in §2, with a potential setup to acquire AD specific biomarkers that respect the theoretical underpinning of the neurovascular unit in its entirety. Importantly, the work presented here will form part of a broader study, which will involve the assessment of the consolidated pipeline utilising the entire Lido dataset.3,47,48
Important limitations include the omission of cross-storage effects from the MPET formulation.49,83 The components of cerebroventricular displacement were constrained (rigid skull boundary condition) on the cortical surface (thereby omitting the cortical SAS), and the 6-MPET field equations are formulated by using a linear-elastic constitutive law (which is not unreasonable for chronic neurodegenerative diseases, but it is a limitation nonetheless). Regarding the additional compartments of the poroelastic model, the lack of additional experimental data to validate the full spectrum of model parameters required for all six compartments of the poroelastic model is a limitation of this study. Additionally, the numerical template omits body forces and inertial terms in the conservation equations since the acceleration frequencies are low in biological flows.49,51 Further limitations are discussed in Guo et al., Vardakis et al., Tully and Ventikos and Chou et al.47–53
Conclusion
This work outlines a novel 3D six-compartment poroelastic system for modelling the neurovascular unit by incorporating glial cells and the newly discovered glymphatic pathway. Additionally, this model is embedded within a high precision workflow3 that has been extended by allowing for the variation in mechanical properties (parenchymal tissue stiffness) in important regions of the brain (white matter). This paves the way for detailed studies allied to ageing induced neurodegeneration (such as AD) and allows for the probing and exploration of the highly dynamic and multifactorial fluid transport system that exists within the brain. This workflow is used on one cognitively healthy control subject in order to explore the underlying mechanisms of the neurovascular unit in five important regions of the brain (cortical grey matter, hippocampus, thalamus, amygdala and brainstem) through the regional differences in derivative solution fields of the multiporoelastic model (such as perfusion, swelling and drainage of the neurovascular unit).
Interesting and useful extensions to this numerical template include the coupling of this high precision workflow with a robust fluid flow solver that will help capture the ageing, lifestyle and neurodegenerative influences on cerebroventricular flow complexity, and incorporate novel boundary conditions on the inner surface of the cerebroventricular wall that capture cilia-driven flow within these important cavities. Finally, incorporating the Donnan effect within the 6-MPET numerical formulation (see Vardakis et al.52 for references therein) is also considered an important extension to the current numerical template.
Acknowledgments
We want to thank Dr A Sarrami-Foroushani, Dr N Ravikumar, Dr T Lassila, Mr Milton Hoz de Vila, Prof ZA Taylor and Prof AF Frangi from the University of Leeds for developing the models to generate subject-specific boundary conditions and meshes with permeability information, and the integrated workflows. We would like to thank Dr M Mitolo from Policlinico S. Orsola e Malpighi in Bologna and Prof A Venneri from the University of Sheffield for providing the clinical data for the subject-specific application.
Footnotes
Authors’ note: John C Vardakis is now affiliated with Laboratory for Vascular Translational Science (LVTS), Institut National de la Santé et de la Recherche Médicale (INSERM), University Paris Diderot, Paris, France.
Declaration of conflicting interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship and/or publication of this article.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship and/or publication of this article: This work was supported by the European Commission FP7 project VPH-DARE@IT (FP7-ICT-2011-9-601055).
Ethical approval: The following ethical protocols have been approved for the Alzheimer’s Disease study: This prospective data collection was approved by the joint ethics committee of the Health Authority Venice 12 and the IRCCS San Camillo (Protocol number 2014.08), and all participants gave informed consent prior to participation in the study.
ORCID iDs: John C Vardakis  https://orcid.org/0000-0003-2391-5257
https://orcid.org/0000-0003-2391-5257
Liwei Guo  https://orcid.org/0000-0001-5576-4559
https://orcid.org/0000-0001-5576-4559
References
- 1. Mink JW, Blumenschine RJ, Adams DB. Ratio of central nervous system to body metabolism in vertebrates: its constancy and functional basis. Am J Physiol 1981; 241(3): R203–R212. [DOI] [PubMed] [Google Scholar]
- 2. Blinder P, Tsai PS, Kaufhold JP, et al. The cortical angiome: an interconnected vascular network with noncolumnar patterns of blood flow. Nat Neurosci 2013; 16: 889–897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Vardakis JC, Bonfanti M, Franzetti G, et al. Highly integrated work flows for exploring cardiovascular conditions: exemplars of precision medicine in Alzheimer’s disease and aortic dissection. J Morphol 2019; 103(343): 148–160. [DOI] [PubMed] [Google Scholar]
- 4. Iliff JJ, Wang M, Liao Y, et al. A paravascular pathway facilitates CSF flow through the brain parenchyma and the clearance of interstitial solutes, including amyloid β. Sci Transl Med 2012; 4(147): 147ra111–147ra111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Iadecola C. The neurovascular unit coming of age: a journey through neurovascular coupling in health and disease. Neuron 2017; 96: 17–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. McConnell HL, Kersch CN, Woltjer RL, et al. The translational significance of the neurovascular unit. J Biol Chem 2017; 292: 762–770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Coelho-Santos V, Shih AY. Postnatal development of cerebrovascular structure and the neurogliovascular unit. Wiley Interdiscip Rev Dev Biol 2020; 9(2): e363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Patterson C. World Alzheimer’s report 2018. London: Alzheimer’s Disease International, 2018. [Google Scholar]
- 9. Rius-Pérez S, Tormos AM, Pérez S, et al. Vascular pathology: cause or effect in Alzheimer disease? Neurología (English Edition) 2018; 33: 112–120 [DOI] [PubMed] [Google Scholar]
- 10. Strickland S. Blood will out: vascular contributions to Alzheimer’s disease. J Clin Invest 2018; 128: 556–563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. de la Torre JC. Is Alzheimer’s disease a neurodegenerative or a vascular disorder? Data, dogma, and dialectics. Lancet Neurol 2004; 3: 184–190. [DOI] [PubMed] [Google Scholar]
- 12. Gottesman RF, Schneider AL, Zhou Y, et al. Association between midlife vascular risk factors and estimated brain amyloid deposition. Jama 2017; 317: 1443–1450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Yamada M. Cerebral amyloid angiopathy: emerging concepts. J Stroke 2015; 17: 17–30 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Di Marco LY, Marzo A, Munoz-Ruiz M, et al. Modifiable lifestyle factors in dementia: a systematic review of longitudinal observational cohort studies. J Alzheimers Dis 2014; 42: 119–135. [DOI] [PubMed] [Google Scholar]
- 15. Drachman DA. The amyloid hypothesis, time to move on: amyloid is the downstream result, not cause, of Alzheimer’s disease. Alzheimer’s & dementia: J Alzheimers Dis Assoc 2014; 10: 372–380. [DOI] [PubMed] [Google Scholar]
- 16. Austin BP, Nair VA, Meier TB, et al. Effects of hypoperfusion in Alzheimer’s disease. J Alzheimers Dis 2011; 26(Suppl 3): 123–133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Thomas T, Miners S, Love S. Post-mortem assessment of hypoperfusion of cerebral cortex in Alzheimer’s disease and vascular dementia. Brain 2015; 138: 1059–1069. [DOI] [PubMed] [Google Scholar]
- 18. Mazza M, Marano G, Traversi G, et al. Primary cerebral blood flow deficiency and Alzheimer’s disease: shadows and lights. J Alzheimers Dis 2011; 23: 375–389. [DOI] [PubMed] [Google Scholar]
- 19. Tarasoff-Conway JM, Carare RO, Osorio RS, et al. Clearance systems in the brain-implications for Alzheimer disease. Nat Rev Neurol 2015; 11: 457–470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Jack CR, Jr, Knopman DS, Jagust WJ, et al. Tracking pathophysiological processes in Alzheimer’s disease: an updated hypothetical model of dynamic biomarkers. Lancet Neurol 2013; 12: 207–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Ruitenberg A, den Heijer T, Bakker SL, et al. Cerebral hypoperfusion and clinical onset of dementia: the Rotterdam study. Ann Neurol 2005; 57: 789–794. [DOI] [PubMed] [Google Scholar]
- 22. Launer LJ, Ross GW, Petrovitch H, et al. Midlife blood pressure and dementia: the Honolulu-Asia aging study. Neurobiol Aging 2000; 21: 49–55. [DOI] [PubMed] [Google Scholar]
- 23. Xu WL, Atti AR, Gatz M, et al. Midlife overweight and obesity increase late-life dementia risk: a population-based twin study. Neurology 2011; 76: 1568–1574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Hofman A, Ott A, Breteler MM, et al. Atherosclerosis, apolipoprotein E, and prevalence of dementia and Alzheimer’s disease in the Rotterdam study. Lancet (London, England) 1997; 349: 151–154. [DOI] [PubMed] [Google Scholar]
- 25. Rodriguez GA, Burns MP, Weeber EJ, et al. Young APOE4 targeted replacement mice exhibit poor spatial learning and memory, with reduced dendritic spine density in the medial entorhinal cortex. Learn Memory (Cold Spring Harbor, NY) 2013; 20: 256–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Johnson KA, Albert MS. Perfusion abnormalities in prodromal AD. Neurobiol Aging 2000; 21: 289–292. [DOI] [PubMed] [Google Scholar]
- 27. Zhao Y, Gong CX. From chronic cerebral hypoperfusion to Alzheimer-like brain pathology and neurodegeneration. Cell Mol Neurobiol 2015; 35: 101–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Gorelick PB, Scuteri A, Black SE, et al. Vascular contributions to cognitive impairment and dementia: a statement for healthcare professionals from the American Heart Association/American Stroke Association. Stroke 2011; 42: 2672–2713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. de la Torre JC. Cerebrovascular and cardiovascular pathology in Alzheimer’s disease. Int Rev Neurobiol 2009; 84: 35–48. [DOI] [PubMed] [Google Scholar]
- 30. Roher AE, Debbins JP, Malek-Ahmadi M, et al. Cerebral blood flow in Alzheimer’s disease. Vasc Health Risk Manag 2012; 8: 599–611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Nishimura T, Hashikawa K, Fukuyama H, et al. Decreased cerebral blood flow and prognosis of Alzheimer’s disease: a multicenter HMPAO-SPECT study. Ann Nucl Med 2007; 21: 15–23. [DOI] [PubMed] [Google Scholar]
- 32. Moreira PI, Smith MA, Zhu X, et al. Oxidative stress and neurodegeneration. Ann NY Acad Sci 2005; 1043: 545–552. [DOI] [PubMed] [Google Scholar]
- 33. Cermakova P, Eriksdotter M, Lund LH, et al. Heart failure and Alzheimer’s disease. J Intern Med 2015; 277: 406–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Benveniste H, Liu X, Koundal S, et al. The glymphatic system and waste clearance with brain aging: Rev Gerontol 2019; 65: 106–119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Hirt L, Price M, Benakis C, et al. Aquaporins in neurological disorders. Clin Transl Neurol 2018; 2(1): 2514183X17752902. [Google Scholar]
- 36. Abbott NJ, Pizzo ME, Preston JE, et al. The role of brain barriers in fluid movement in the CNS: is there a ‘glymphatic’ system? Acta Neuropathol 2018; 135: 387–407. [DOI] [PubMed] [Google Scholar]
- 37. Patel TK, Habimana-Griffin L, Gao X, et al. Dural lymphatics regulate clearance of extracellular tau from the CNS. Mol Neurodegener 2019; 14: 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Da Mesquita S, Fu Z, Kipnis J. The meningeal lymphatic system: a new player in neurophysiology. Neuron 2018; 100: 375–388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Shibata-Germanos S, Goodman JR, Grieg A, et al. Structural and functional conservation of non-lumenized lymphatic endothelial cells in the mammalian leptomeninges. Acta Neuropathol 2019; 139(2): 383–401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Iliff JJ, Wang M, Zeppenfeld DM, et al. Cerebral arterial pulsation drives paravascular CSF-interstitial fluid exchange in the murine brain. J Neurosci 2013; 33: 18190–18199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Bedussi B, van der Wel NN, de Vos J, et al. Paravascular channels, cisterns, and the subarachnoid space in the rat brain: a single compartment with preferential pathways. J Cereb Blood Flow Metab 2017; 37: 1374–1385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Antila S, Karaman S, Nurmi H, et al. Development and plasticity of meningeal lymphatic vessels. J Exp Med 2017; 214: 3645–3667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Lee H, Xie L, Yu M, et al. The effect of body posture on brain glymphatic transport. J Neurosci 2015; 35: 11034–11044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Mestre H, Hablitz LM, Xavier ALR, et al. Aquaporin-4-dependent glymphatic solute transport in the rodent brain. eLife 2018; 7: e40070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Hauglund NL, Pavan C, Nedergaard M. Cleaning the sleeping brain–the potential restorative function of the glymphatic system. Curr Opin Phys 2019; 15: 1–6 [Google Scholar]
- 46. Lassila T, Marco LYD, Mitolo M, et al. Screening for cognitive impairment by model-assisted cerebral blood flow estimation. IEEE Trans Biomed Eng 2018; 65: 1654–1661. [DOI] [PubMed] [Google Scholar]
- 47. Guo L, Vardakis JC, Lassila T, et al. Subject-specific multi-poroelastic model for exploring the risk factors associated with the early stages of Alzheimer’s disease. Interface Focus 2018; 8: 20170019–20170019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Vardakis JC, Guo L, Peach TW, et al. Fluid–structure interaction for highly complex, statistically defined, biological media: homogenisation and a 3D multi-compartmental poroelastic model for brain biomechanics. J Fluid Struct 2019; 91: 102641. [Google Scholar]
- 49. Tully B, Ventikos Y. Cerebral water transport using multiple-network poroelastic theory: application to normal pressure hydrocephalus. J Fluid Mech 2011; 667: 188–215. [Google Scholar]
- 50. Vardakis JC, Tully BJ, Ventikos Y. Exploring the efficacy of endoscopic ventriculostomy for hydrocephalus treatment via a multicompartmental poroelastic model of CSF transport: a computational perspective. PLoS One 2014; 8: e84577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Chou D, Vardakis JC, Guo L, et al. A fully dynamic multi-compartmental poroelastic system: application to aqueductal stenosis. J Biomech 2016; 49: 2306–2312. [DOI] [PubMed] [Google Scholar]
- 52. Vardakis JC, Chou D, Tully BJ, et al. Investigating cerebral oedema using poroelasticity. Med Eng Phys 2016; 38: 48–57. [DOI] [PubMed] [Google Scholar]
- 53. Tully B, Ventikos Y. Coupling poroelasticity and CFD for cerebrospinal fluid hydrodynamics. IEEE Trans Biomed Eng 2009; 56: 1644–1651. [DOI] [PubMed] [Google Scholar]
- 54. Guo L, Vardakis JC, Chou D, et al. A multiple-network poroelastic model for biological systems and application to subject-specific modelling of cerebral fluid transport. Int J Eng Sci 2020; 147: 103204. [Google Scholar]
- 55. Guo L, Li Z, Lyu J, et al. On the validation of a multiple-network poroelastic model using arterial spin labeling MRI data. Front Comput Neurosci 2019; 13: 60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Chou D. Computational modelling of brain transport phenomena: application of multicompartmental poroelasticity. PhD Thesis, University of Oxford, Oxford, United Kingdom, 2016. [Google Scholar]
- 57. Terzaghi K. Erdbaumechanik auf bodenphysikalischer grundlage. Vienna, Austria: Leipzig u. Wien, F. Deuticke, 1925. [Google Scholar]
- 58. Mandel J. Consolidation des sols (étude mathématique). Géotechnique 1953; 3: 287–299. [Google Scholar]
- 59. Balay S, Abhyankar S, Adams MF, et al. PETSc Web page 2019a, http://www.mcs.anl.gov/petsc. (accessed 18 November 2019)
- 60. Balay S, Abhyankar S, Adams MF, et al. PETSc users manual, ANL-95/11 – revision 3.9. Lemont, IL: Argonne National Laboratory, 2019. [Google Scholar]
- 61. Sack I, Beierbach B, Wuerfel J, et al. The impact of aging and gender on brain viscoelasticity. NeuroImage 2009; 46: 652–657. [DOI] [PubMed] [Google Scholar]
- 62. Murphy MC, Huston J, III, Jack CR, Jr, et al. Decreased brain stiffness in Alzheimer’s disease determined by magnetic resonance elastography. J Magn Reson Imaging 2011; 34: 494–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Murphy MC, Jones DT, Jack CR, et al. Regional brain stiffness changes across the Alzheimer’s disease spectrum. NeuroImage: Clin 2016; 10: 283–290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Bedussi B, Almasian M, de Vos J, et al. Paravascular spaces at the brain surface: low resistance pathways for cerebrospinal fluid flow. J Cereb Blood Flow Metab 2017; 38: 719–726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Croci M, Vinje V, Rognes ME. Uncertainty quantification of parenchymal tracer distribution using random diffusion and convective velocity fields. Fluids Barriers CNS 2019; 16(1): 32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Thomas JH. Fluid dynamics of cerebrospinal fluid flow in perivascular spaces. J R Soc Interface 2019; 16(159): 20190572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Naidich TP, Epstein F, Lin JP, et al. Evaluation of pediatric hydrocephalus by computed tomography. Radiology 1976; 119: 337–345. [DOI] [PubMed] [Google Scholar]
- 68. Hopkins L, Bakay L, Kinkel W, et al. Demonstration of transventricular CSF absorption by computerized tomography. Acta Neurochir (Wien) 1977; 39: 151–157. [DOI] [PubMed] [Google Scholar]
- 69. Kim H, Jeong E-J, Park D-H, et al. Finite element analysis of periventricular lucency in hydrocephalus: extravasation or transependymal CSF absorption? J Neurosurg 2016; 124(2): 334–341. [DOI] [PubMed] [Google Scholar]
- 70. Gleiser C, Wagner A, Fallier-Becker P, et al. Aquaporin-4 in astroglial cells in the CNS and supporting cells of sensory organs-a comparative perspective. Int J Mol Sci 2016; 17: 1411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. Pena A, Bolton MD, Whitehouse H, et al. Effects of brain ventricular shape on periventricular biomechanics: a finite-element analysis. Neurosurgery 1999; 45: 107–116. [DOI] [PubMed] [Google Scholar]
- 72. Pagani F, Paolicelli RC, Murana E, et al. Defective microglial development in the hippocampus of Cx3cr1 deficient mice. Front Cell Neurosci 2015; 9: 111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Halliday G. Pathology and hippocampal atrophy in Alzheimer’s disease. Lancet Neurol 2017; 16: 862–864. [DOI] [PubMed] [Google Scholar]
- 74. Aggleton JP, Pralus A, Nelson AJ, et al. Thalamic pathology and memory loss in early Alzheimer’s disease: moving the focus from the medial temporal lobe to papez circuit. Brain: J Neurol 2016; 139: 1877–1890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Zarei M, Patenaude B, Damoiseaux J, et al. Combining shape and connectivity analysis: an MRI study of thalamic degeneration in Alzheimer’s disease. NeuroImage 2010; 49: 1–8. [DOI] [PubMed] [Google Scholar]
- 76. Ortner M, Pasquini L, Barat M, et al. Progressively disrupted intrinsic functional connectivity of basolateral amygdala in very early Alzheimer’s disease. Front Neurol 2016; 7: 132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Freeze WM, Bacskai BJ, Frosch MP, et al. Blood-brain barrier leakage and microvascular lesions in cerebral amyloid angiopathy. Stroke 2019; 50: 328–335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Lee JH, Ryan J, Andreescu C, et al. Brainstem morphological changes in Alzheimer’s disease. Neuroreport 2015; 26: 411–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79. Montplaisir J, Petit D, Lorrain D, et al. Sleep in Alzheimer’s disease: further considerations on the role of brainstem and forebrain cholinergic populations in sleep-wake mechanisms. Sleep 1995; 18: 145–148. [DOI] [PubMed] [Google Scholar]
- 80. Rub U, Del Tredici K, Schultz C, et al. The autonomic higher order processing nuclei of the lower brain stem are among the early targets of the Alzheimer’s disease-related cytoskeletal pathology. Acta Neuropathol 2001; 101: 555–564. [DOI] [PubMed] [Google Scholar]
- 81. Uematsu M, Nakamura A, Ebashi M, et al. Brainstem tau pathology in Alzheimer’s disease is characterized by increase of three repeat tau and independent of amyloid β. Acta Neuropathol Commun 2018; 6: 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82. Boespflug EL, Simon MJ, Leonard E, et al. Targeted assessment of enlargement of the perivascular space in Alzheimer’s disease and vascular dementia subtypes implicates astroglial involvement specific to Alzheimer’s disease. J Alzheimers Dis 2018; 66: 1587–1597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83. Vardakis JC, Chou D, Guo L, et al. Response to letter to the editor concerning “a fully dynamic multi-compartmental poroelastic system: application to aqueductal stenosis”. J Biomech 2017; 58: 243–246. [DOI] [PubMed] [Google Scholar]