Simulation of Copper Electrodeposition in Through-Hole Vias

Abstract

Copper electrodeposition processes for filling metallized through-hole (TH) and through-silicon vias (TSV) depend on spatially selective breakdown of a co-adsorbed polyether-chloride adlayer within the recessed surface features. In this work, a co-adsorption-dependent suppression model that has previously captured experimental observations of localized Cu deposition in TSV is used to explore filling of TH features. Simulations of potentiodynamic and galvanostatic TH filling are presented. An appropriate applied potential or current localizes deposition to the middle of the TH. Subsequent deposition proceeds most rapidly in the radial direction leading to sidewall impingement at the via center creating two blind vias. The growth front then evolves primarily toward the two via openings to completely fill the TH in a manner analogous to TSV filling. Applied potentials, or currents, that are overly reducing result in metal ion depletion within the via and void formation. Simulations in larger TH features (i.e., diameter = 85 μm instead of 10 μm) indicate that lateral diffusional gradients within the via can lead to fluctuations between active and passive deposition along the metal/electrolyte interface.

For more than four decades, advancement in microelectronic device performance and functionality has been primarily driven by miniaturization of transistors, resulting in chips with more than 10 billion transistors, each of which is as small as 7 nm in dimension. As the industry approaches physical limitations in transistor size, new efforts are underway exploring alternative avenues to advance device capabilities. One such effort involves three-dimensional integration of electronic chips, or chip stacking, to provide greater performance in a smaller footprint with improved power consumption and bandwidth associated with shorter interconnects. Copper electrodeposition in high-aspect ratio cavities is an essential processing step in fabricating the interconnects for electronic devices, with length-scale requirements ranging from tens of nanometers for interconnects between individual transistors to hundreds of micrometers for through-siliconvias (TSV) connecting stack levels and through-hole (TH) structures in printed circuit boards (PCBs). As TSV and TH features are orders of magnitude larger than damascene-type metallization, optimization of plating time, as well as the continued need for fabrication of robust and void-free features, is essential to industry. Void-free copper electrodeposition in high-aspect ratio features has been demonstrated for both damascene on-chip metallization and TSV/TH filling using a variety of organic additive combinations, often categorized as either two additive (suppressor-accelerator) or three additive (suppressor-accelerator-leveler) chemistries.^1–11 More recently, electrolytes with a single polyether additive (suppressor) have enabled almost ideal bottom-up electrodeposition of copper in TSV^12–14 features. Using a variation on the suppressor chemistry, this approach has been demonstrated for void-free TSV filling with Ni,^15,16 Co,¹⁷ and Au.^18,19 Electrolytes using a single organic additive have also been employed in the filling of TH structures.^20–23

Electroanalytical measurements in suppressor containing copper electrolytes clearly indicate that formation of a halide adlayer prior to co-adsorption of the polymeric suppressing additive is essential to void-free filling; the resulting halide-polyether adlayer inhibits copper deposition by limiting Cu²⁺ access to the metal surface.^24–41 Possible factors contributing to enhanced suppressor adsorption on halide include: multiplicity of halide-polyether binding sites,²⁴ halide perturbation of the water structure making a more hydrophobic interface that favors polyether adsorption,²⁵ or stabilized Cu⁺ as an ether-halide binding agent.^26–28 Polarization to sufficiently negative potentials disrupts the adlayer, allowing Cu²⁺ access to the electrode followed by its electrodeposition.^{12–14,26,29,42–45} Breakdown of the polyether-halide suppression layer is a critical phenomenon that depends on both additive concentration and electric potential. Recent studies indicate that the breakdown potential that marks the onset of electrodeposition in voltammetry follows a −60 mV/log[Cl⁻] dependence in dilute chloride systems (≤ 80 μmol/L).¹⁴ Suppressor deactivation entails some combination of desorption and/or consumption of its components. In the case of polymer desorption, either the state of the molecule or interface must change such that the polymer is unable to re-adsorb. Incorporation of suppressor and/or halide into the growing metal film, on the other hand, establishes a sustained concentration gradient within the unfilled volume of a recessed feature.^29,34,42,43 Suggested mechanisms for suppression breakdown include reduction of a Cu⁺ halide-ether binding agent,^26–28 potential driven order-disorder transitions in the halide adlayer,⁴⁶ and disruption of the polymer adsorption process by the metal deposition process itself that, amongst other variants, can involve a change in the hydrophilicity of the interface.^{12,24,39–41,44,47,48} Significant research is underway to link electroanalytical results with metallurgical and spectroscopic measurements of deposit microstructure and residual additive components incorporated in the growing deposit both during and following suppression breakdown.

Potential-driven suppression breakdown is accompanied by positive feedback from copper deposition that leads to significant hysteresis in voltammetry. Following correction for losses associated with electrolyte resistance, an S-shaped negative-differential-resistance (S-NDR) is revealed.¹² S-NDR electrochemical systems exhibit a multiplicity of stable states that often manifest as a bifurcation of the electrode into regions of passive and active electrodeposition.^{12–14,26,49,50} On planar electrodes, random Turing-like patterns form, their pattern size and shape being intrinsically related to the differing time scales for chemical transport and electrode polarization.^12,51,52 On topographically engineered electrodes such as TSV, the concentration gradients within the via related to suppression breakdown allow for optimization of processing conditions such that sustained localized bottom-up filling occurs. Conditions that produce suppression breakdown on the sidewalls in the via can result in superconformal, conformal, or subconformal deposition depending on the depth of the suppression breakdown and the extent of metal cation and additive depletion. The observation of S-NDR induced bifurcation and patterning is dependent on external resistances related to the electrolyte or contacts. In high conductivity systems, the Turing patterns associated with critical systems do not develop under potential control.^53,54 At the other limit, a high electrolyte resistivity that obscures S-NDR in voltammetry actually provides a nominally stable control point for bifurcating deposition/passivation on any electrode under potential control.

Several computational models describing the dynamics of suppressor breakdown and copper electrodeposition in single organic additive (suppressor) systems have been proposed. They rely on either a non-linear relationship between suppressor coverage and deposition or additive consumption at the metal/electrolyte interface to capture the voltammetric hysteresis observed experimentally.^{14,24,43,44,47,55,56} Simulations exploring TSV filling have focused on a sustained consumption derived chemical gradient of additives within the recessed feature that serve to localize deposition near the bottom.^{14,43,44,55,56} Models of feature filling in electrolytes with high chloride concentrations (>80 μmol/L) have assumed formation of the polyether-halide adlayer and consequent suppression of copper deposition depend only on the flux and adsorption/consumption kinetics of the suppressor.^43,55 In solutions more dilute in halide (≤ 80 μmol/L), transport and adsorption/consumption kinetics of both additives influence formation of the suppressor surface phase. To capture experimental observations of co-adsorption dynamics, a two-additive halide-suppressor model¹⁴ that limits suppressor coverage to chloride coverage (θ_P ≤ θ_Cl) has been proposed, showing favorable comparison to both voltammetry and TSV filling experiments.

In parallel with 3D-integration of microprocessors and memory chips, printed circuit board (PCB) manufacturers are shifting to high-density interconnect (HDI) technology to further increase circuit density and improve thermal management and high frequency signal transmission.^22,57,58 Among the key features are laser or mechanically drilled vias known as through-holes (TH) ranging from tens to hundreds of micrometers in diameter and tens of micrometers to millimeters in height that are filled with Cu to function as multilevel interconnects. The THs are distinct from “blind” microvias in that they are open at both ends. The same phenomenon enabling bottom-up filling in TSV underlies “butterfly” filling in TH; optimal additive concentrations and potential/current waveforms induce localized electrodeposition of copper at the most recessed area of the feature, specifically the bottom in TSV and the middle in TH. Electrolytes analogous to those used in TSV and damascene metallization have also been successfully employed in butterfly TH filling,^10,11,20 including solutions with a single organic, rate-suppressing additive^20–23 similar to those enabling the S-NDR mechanism detailed for TSV. The hysteretic voltammetric response of these electrolytes on a planar surface is similar to that previously detailed for electrolytes yielding bottom-up TSV filling. Likewise, inspection of the published data reveals significant contribution of electrolyte resistance to the voltammetry.^20,21,59

In this study, a two-additive halide-suppressor S-NDR computational model explores the mechanism of “butterfly” filling of through-hole features by both potentiodynamic and galvanostatic operation. A subset of applied potential programs and fixed current densities yield selective deposition in the TH middle, with outward growth of the deposit occurring after impingement of the sidewalls at the via center consistent with experimental filling. Simulated potential and current transients provide insight into the dynamic response of potential drop in solution and comparison between local current density at the TH middle versus on the neighboring field. An approximation based on the symmetry of the problem enables use of a front-tracking computational approach to enable simulation beyond impingement of the sidewall deposits, which otherwise would require implementation of level-set methods that more generally deal with such topological changes.

Computational Methods

Finite element method (FEM) computations are used to simulate cyclic voltammetry and through-hole filling during copper electrodeposition. Simulations of the 1-D geometry used to model cyclic voltammetry (Figure 1a) assume a fixed boundary layer thickness (δ) of 25 μm and a reference/counter electrode distance (L) of 0.25 cm from the working electrode. The value of L was chosen to yield a simulated cell resistance of 5 Ω, similar to that previously measured during voltammetry of copper electrodeposition.^13,14 The 2-D axisymmetric geometry used for simulating deposition in TH features is depicted in Figure 1b; a fixed boundary layer thickness of 25 μm and reference/counter electrode distance of 0.25 cm from the electrode field are used in these simulations as well. The concentration of each species is set equal to that of the bulk solution $\left(C_i^o\right)$ at the top of the boundary layer and the electric potential is set equal to zero at the reference/counter electrode. In the 2-D axisymmetric simulations, the concentration and flux N_i of each species (Cu²⁺, Cl⁻, and polymer) in the electrolyte domain is described by the Nernst-Planck equation, capturing both diffusion and electromigration by

$$\frac{d{C}_i}{dt}=-\nabla \cdot {\stackrel{\rightharpoonup }{N}}_i=-\nabla \cdot \left(-z_i{u}_{m,i}F{C}_i\nabla \mathrm{\varphi }-D_i\nabla C_i\right)$$ [1]

given charge z_i and the mobility u_m,i calculated by the Einstein relationship

$$u_{m,i}=\frac{D_i}{RT}.$$ [2]

The simulated electrolyte consists of 0.88 mol/L CuSO₄, 0.18 mol/L H₂SO₄, 20 μmol/L NaCl, and 40 μmol/L polyether suppressor, consistent with experimental systems reported in literature.^20,22,23 Full dissociation of CuSO₄ and NaCl is assumed for the concentrations of Cu²⁺ and Cl⁻. The suppressing polyether molecule (P) is assumed to be neutral in charge (z_P = 0). Diffusion coefficients listed in Table I for Cu²⁺, Cl⁻, and polyether are taken or estimated from literature sources.^14,60–64 Conductivity of the electrolyte (κ) is 7.5 S/m based on reference literature.⁶⁵

Figure 1.

Schematic of (a) 1-D and (b) 2-D axisymmetric geometries used in the S-NDR model to simulate cyclic voltammetry and through-hole via filling, respectively. Relevant domains and boundaries are indicated with r_i(z, t) and z_i(r, t) defining the spatially and temporally dependent location of the metal/electrolyte interface. For through-hole simulations, once the radial growth of the deposit reaches r_i(0, t) ≤ 0.01R_TH the equations governing the boundary at z = 0 () are changed to those of the electrode ().

Table I.

Parameters for voltammetry and through-hole filling simulations.

Parameter	Name	Units	Value	Source
Through-Hole Cell Geometry
TH Radius	Rth	μm	5
TH Height	H	μm	40
Cell Radius	Rc	μm	3 × Rth
Boundary layer thickness for rotation rate ω = 320π rad/min (160 rpm)	δ	μm	25
Distance to reference electrode	L	cm	0.25
Electrolyte Parameters
Bulk concentration Cu2+	$C_{Cu}^o$	mol/L	0.88
Bulk concentration Cl−	$C_{Cl}^o$	μmol/L	20
Bulk concentration polyether	$C_P^o$	μmol/L	40
Diffusion coefficient Cu2+	DCu	cm2/s	2.65 × 10−6	Ref. 60
Diffusion coefficient Cl−	DCl	cm2/s	9 × 10−6	Ref. 14
Diffusion coefficient polyether	DP	cm2/s	1 × 10−6	Refs. 62–64
Adsorbate Parameters
Saturation chloride coverage	ΓCl	mol/m2	1.62 × 10−5	Ref. 14
Saturation suppressor coverage	ΓP	mol/m2	9.2 × 10−8	Ref. 67
Chloride adsorption kinetics	$k_{Cl}^{+}$	m3/mol·s	20	Ref. 14
Chloride deactivation kinetics	$k_{Cl}^{-}$	1/m	1.5 × 107	Ref. 14
Suppressor adsorption kinetics	$k_P^{+}$	m3/mol·s	2500	Ref. 14
Suppressor deactivation kinetics	$k_P^{-}$	1/m	1 × 107	Ref. 14
Electrochemical Kinetics
Unsuppressed Cu exchange current density	$j_0^o$	A/m2	20	Ref. 14
Suppressed Cu exchange current density	$j_1^o$	A/m2	0.13	Ref. 14
Unsuppressed charge transfer coefficient	α0	–	0.5	Ref. 14
Suppressed charge transfer coefficient	α1	–	0.5	Ref. 14
Cu ionic charge	n	–	2
Cu molar volume	Ω	m3/mol	7.1 × 10−6
Electrolyte conductivity	κ	S/m	7.5	Ref. 65
Temperature	T	K	298
Miscellaneous
Cyclic voltammetry ramp rate	Vramp	mV/s	1
Applied current density (TH)	japp	mA/cm2	−2.4
Projected through-hole electrode area	Acell	m2	πRc2

Due to the high concentration of CuSO₄ and the H₂SO₄ supporting electrolyte, potential in the electrolyte (ϕ) is defined by Laplace’s equation

$${\nabla }^2\mathrm{\varphi }=0,$$ [3]

which neglects potential variation in the solution arising from ionic gradients. The current density j associated with the Cu²⁺ flux through the electrolyte is given by ohms law

$$\stackrel{\rightharpoonup }{j}=-\mathrm{\kappa }\nabla \mathrm{\varphi }.$$ [4]

Zero flux conditions at the side of the cell (R_c) are imposed in terms of gradients of the solution potential (ϕ)

$$\frac{\partial \mathrm{\varphi }}{\partial r}=0$$ [5]

and the chemical species in solution

$$\frac{\partial C_i}{\partial r}=0.$$ [6]

Accumulation of adsorbates on the electrode follows Langmuir adsorption kinetics with deactivation related to metal deposition involving a combination of desorption and/or incorporation into the growing metal deposit. Evolution of the fractional chloride coverage θ_Cl, defined as the surface concentration divided by the saturation coverage, is described by

$$\frac{d{\mathrm{\theta }}_{Cl}}{dt}=k_{Cl}^{+}{C}_{Cl}\left(1-{\mathrm{\theta }}_{Cl}\right)-k_{Cl}^{-}{\mathrm{\theta }}_{Cl}v$$ [7]

where $k_{Cl}^{+}$ is the adsorption rate constant, C_Cl is the chloride concentration at the evolving metal/electrolyte interface, $k_{Cl}^{-}$ is the deactivation rate constant and ν is the metal deposition rate. Likewise, evolution of the fractional polyether coverage θ_P is described by

$$\frac{d{\mathrm{\theta }}_P}{dt}=k_P^{+}{C}_P\left({\mathrm{\theta }}_{Cl}-{\mathrm{\theta }}_P\right)-k_P^{-}{\mathrm{\theta }}_P\mathrm{\upsilon }$$ [8]

where the polyether is restricted to adsorption on top of halide covered sites and thereby implicitly subject to the requirement that θ_P cannot exceed θ_Cl through adsorption. Fractional chloride and polyether coverage are both further limited to values between 0 and 1. Values for $k_i^{+}$ and $k_i^{-}$ listed in Table I are estimated from model fits to the S-NDR voltammetry with the fitting procedure focused on capturing the onset potential for suppressor breakdown as a function of suppressor and halide concentration.^14,43

The metal deposition rate is assumed to be a function of the suppressor coverage θ_P (or equivalently, coverage of the polyether-chloride bi-layer), metal ion concentration C_Cu, and overpotential η at the interface, thus

$$v\left({\mathrm{\theta }}_P,C_{Cu},\mathrm{\eta }\right)=\frac{\mathrm{\Omega }}{nF}\frac{C_{Cu}}{C_{Cu}^o}\left[j_{\mathrm{\theta }=0}(\mathrm{\eta })\left(1-{\mathrm{\theta }}_P\right)+j_{\mathrm{\theta }=1}(\mathrm{\eta }){\mathrm{\theta }}_P\right]$$ [9]

The current densities on unsuppressed (j_{θ= 0}) and suppressed (j_{θ= 1}) surfaces are only associated with metal deposition (i.e., ignoring parasitic contributions) and directly reflect the growth velocity, ν, using Faraday’s constant (F = 96485 C/mol), the ionic charge n, and the molar volume Ω of solid copper. This simple form captures suppression arising from the polyether coverage (as limited by chloride coverage). The current densities (j_{θ= 0,1}) are assumed to exhibit the conventional exponential dependence on overpotential η by

$$j_{\mathrm{\theta }=0,1}(\mathrm{\eta })=j_{\mathrm{\theta }=0,1}^o\left(e^{\frac{\left(1-{\mathrm{\alpha }}_{\mathrm{\theta }=0,1}\right)F}{RT}\mathrm{\eta }}-e^{-\frac{{\mathrm{\alpha }}_{\mathrm{\theta }=0,1}F}{RT}\mathrm{\eta }}\right).$$ [10]

The applied potential V_app is related to the overpotential at the working electrode through

$$V_{app}=\mathrm{\eta }+\mathrm{\varphi }+E_{rev}$$ [11]

where the potential ϕ within the electrolyte, evaluated at the electrolyte/deposit interface, captures the potential drop from the reference due to electrolyte resistivity and the overpotential driving electrodeposition is referenced to the reversible Nernst potential for the reaction. As defined using Eq. 9, the exchange current densities $j_{\mathrm{\theta }=0,1}^o$ for the bare, θ_P = 0, and fully inhibited, θ_P = 1, surfaces are for bulk metal ion concentration $C_{Cu}^o$ at the interface. The values of $j_{\mathrm{\theta }=1}^o$ and α_{θ = 1} are obtained by fitting the suppressed negative-going voltammetric sweeps up to the onset of suppression breakdown.¹⁴ The kinetics of metal deposition on polymer-free surfaces are known to be a function of halide coverage; however, for simplicity, the present work uses a single set of $j_{\mathrm{\theta }=0}^o$ and α_θ = 0 for deposition on the polymer-free surface.

The local current density at the electrode is equated to the Cu²⁺ flux from the electrolyte onto the interface (outward surface normal $\widehat{n}$) according to

$$\frac{1}{nF}{\stackrel{\rightharpoonup }{j}}_{Cu}\cdot \widehat{n}=-\left(z_{Cu}{u}_{m,Cu}F{C}_{Cu}\nabla \mathrm{\varphi }+D_{Cu}\nabla C_{Cu}\right)\cdot \widehat{n}.$$ [12]

Similarly, the normal fluxes of chloride and polyether from the electrolyte onto the interface are equated to the rates of their adsorption yielding

$$-\left(z_{Cl}{u}_{m,Cl}F{C}_{Cl}\nabla \mathrm{\varphi }+D_{Cl}\nabla C_{Cl}\right)\cdot \widehat{n}={\mathrm{\Gamma }}_{Cl}{k}_{Cl}^{+}{C}_{Cl}\left(1-{\mathrm{\theta }}_{Cl}\right)$$ [13]

and

$$-D_P\nabla C_P\cdot \widehat{n}={\mathrm{\Gamma }}_P{k}_P^{+}{C}_P\left({\mathrm{\theta }}_{Cl}-{\mathrm{\theta }}_P\right)$$ [14]

for saturation coverages Г_i estimated from literature.^14,66–68 As stated previously, the (θ_Cl – θ_P) term captures the requirement that the suppressor only adsorbs on chloride.

The full system of equations is solved numerically using a finite element method employing the COMSOL Multiphysics version 5.3 software package implementing the following modules: secondary current distribution, transport of dilute species, separate coefficient form boundary partial differential equations for both chloride and suppressor, and deformed geometry. Significantly, the deformed geometry module in COMSOL typically cannot handle topological variation, such as formation of a void or sidewall impingement (i.e. sealing of the radius in through-hole filling). However, in the case of the simulations included here, just prior to impingement an artificial ‘bridge’ boundary is inserted into the geometry that enables approximation of the “butterfly” through-hole filling mechanism using this module. This approximation is implemented by stopping the time-dependent simulation when the radial growth of the depositing interface reaches 0.99R_TH (i.e., the radial gap at the TH mid-line ≤ 1% of the initial TH radius) and activating a pre-existing boundary that connects the opposing sidewalls at the location of thickest deposit growth. Governing equations for the metal/electrolyte interface (Eqs. 7–14) are then imposed at this boundary as well, with adsorbate coverages on the new boundary set to those of the nearest mesh node on the metal/electrolyte interface. The simulation is then reinitialized using the conditions immediately prior (at t = t_bridge) as initial conditions for the relevant domain equations and boundary conditions. This procedure requires creation of a deformed configuration of the geometry at t = t_bridge and re-meshing the model after insertion of the new ‘bridge’ boundary. A metric of 0.999R_TH instead of 0.99R_TH yielded negligible variation in the final results but more than tripled the computational time, a result caused by requiring more refined mesh in the gap for the solution to progress. In fact, the time of sidewall impingement differed by less than 1% for the simulations, consistent with a relatively constant growth rate at the TH mid-height and suggesting that the reported impingement times (taken at 0.99R_TH) can be extrapolated by 1% to give more accurate estimations.

The above procedure allows for an approximation of topological changes of moving interfaces using a front-tracking computational approach. An alternative is the use of level-set equations to follow the geometry change during the collision of opposing growth fronts during through-hole filling, a method that has previously been employed to explore feature filling in through-silicon-via^43,44 and damascene⁶⁹ structures. That said, level-set simulations require equivalent sized mesh throughout the domain over which the interface transits. In contrast, front-tracking models can use a graded mesh, with smaller nodes limited to the regions of higher chemical/potential gradients (i.e., near the metal/electrolyte interface), reducing the computational times substantially. Selective mesh refinement in the regions of highest gradient is used in this work to reduce computational burden without loss of model accuracy. Through-hole deposition is modeled using triangular mesh nodes in the refined regions of 0.1 μm (smaller vias) or 0.7 μm (larger vias) and a total of between 4000 and 7000 mesh elements. The overall charge balance error (the fractional difference between the total integrated currents at the counter electrode and the substrate) is less than 0.1% throughout all simulations. Computations were performed on a Dell Optiplex 980 desktop computer with an Intel Core i5 CPU@ 3.20 GHz and 8 GB RAM using a Windows 7 Enterprise 64-bit operating system. A moving boundary smoothing parameter of 1, geometry shape order of 2, and hyperelastic mesh smoothing type are used in the deformed geometry module (see COMSOL documentation for detailed explanation on how these conditions impact moving boundary convergence). Individual simulations took on the order of hours to compute.

Results and Discussion

Simulations on planar electrodes

The kinetic relationship for copper electrodeposition without any organic additives follows a conventional Butler-Volmer construct, with current being exponentially dependent on overpotential. A simulation of cyclic voltammetry (1 mV/s scan rate) in additive-free 0.88 mol/L CuSO₄ and 0.18 mol/L H₂SO₄ is shown in Figure 2; the forward and reverse sweeps superimpose due to the slow scan rate. With the combined addition of micromolar polyether (40 μmol/L) and chloride (20 μmol/L), substantial inhibition of the deposition rate is evident on the negative-going sweep due to the formation of a polyether-halide overlayer (θ_Cl = θ_P ≈ 1) that blocks access of Cu²⁺_aquo to the underlying Cu surface. The layer forms rapidly and provides strong suppression toward the metal deposition reaction at low overpotentials. However, as the overpotential advances to larger values a critical potential is reached where the polyether-chloride adlayer is disrupted, and a steep rise in the metal deposition current is evident. The previously noted −60 mV/decade relationship of experimental breakdown potential with logarithmic chloride concentration¹⁴ is consistent with the reported potential-dependent structural phase transition in the chloride adlayer, although a process that involves reduction of Cu⁺-Cl⁻-polymer binding sites cannot be excluded at this juncture.^22,44 During the return sweep, copper electrodeposition proceeds at an elevated current level, the value reflecting the average across active and passive regions on the bifurcated electrode^12,45 as metal deposition continues to disrupt reformation of the adlayer on the former. However, the blocking layer rebuilds as the overpotential decreases, passivating the electrode fully near ≈ −0.1 V.

Figure 2.

Simulations of cyclic voltammetry at 1 mV/s using a 2-additive (halide-suppressor) S-NDR model for Cu electrodeposition in solution containing 0.88 mol/L CuSO₄ and 0.18 mol/L H₂SO₄ without additives (···) and with 20 μmol/L NaCl and 40 μmol/L polyether suppressor (─). Post experimental iR-correction is for an electrochemical cell with 5 Ω total resistance. The 1-D simulation assumes a fixed boundary layer of 25 μm and electrode area of 0.196 cm² with other parameters from Table I.

The positive feedback associated with critical breakdown of the polyether-chloride adlayer is characteristic of electrochemical systems exhibiting additive-derived S-shaped negative-differential-resistance (S-NDR).^12,52 The hysteretic region between −100 mV and −180 mV defines the domain where bi-stable reaction states (passive and active) can coexist on a planar macroelectrode surface. Development of the spatial patterns depends on the coupling between forces controlling inhibition (additive transport) and catalytic activation (potential). Thus, the potential gradient in solution and its influence on chemical transport, including electromigration, greatly influence the bifurcation of the electrode surface. As potential is the control variable during cyclic voltammetry, the inversion associated with S-NDR is typically only revealed upon post-experimental correction for the resistive losses in solution.¹² Indeed, S-NDR is evident in Fig. 2 only following correction for the 5 Ω solution resistance across the simulated electrochemical cell. Importantly, the hysteretic regime defined by the S-NDR also corresponds to the potential range where bottom-up TSV feature filling occurs.^12–14 Fitting such simulations from the model equation to experimental data across a range of additive concentrations allows the $k_i^{+}$ and $k_i^{-}$ values to be evaluated either universally or for a given additive concentration.

Simulations of through-hole filling

Predictions obtained from the 2-additive S-NDR model detailed herein have previously compared favorably to experimental Cu filling of annular though-silicon vias in electrolytes with a poloxamine concentration of 40 μmol/L and chloride concentrations ranging from 20 μmol/L to 80 μmol/L.¹⁴ The model captures the position of a passive-active transition on the sidewalls of the via as a function of applied potential and chloride concentration as well as a shift to bottom-up growth at higher chloride concentrations (≥ 80 μmol/L). The position of the passive-active transition was determined to be defined by the balance between the transport-limited additive (Cl⁻) flux and its deactivation by metal deposition, allowing its position to be tailored using the additive concentration, hydrodynamics, and applied potential in the system. Simulations indicated that void-free Cu filling of TSV could be achieved using potential-stepped waveforms to progressively shift the threshold location of suppression breakdown up the feature; the method was demonstrated for filling of millimeter scale vias, although quantitative comparison to the halide consumption model will require modeling of the forced hydrodynamics involved.⁷⁰ A similar additive flux balance approach has also been demonstrated for filling Ni and Co TSV based on consumption of a polyethyleneimine suppressor within the growing solid.^15,17

The above approach can be applied to through-hole features, with conditions selected to initially yield the highest rate of deposition at the through-hole mid-height (z = 0). Figure 3 shows a simulation of potential-controlled copper electrodeposition in a through-hole using the two-additive (polyether-halide) S-NDR model. The electrolyte composition is 0.88 mol/L CuSO₄, 0.18 mol/L H₂SO₄, 20 μmol/L NaCl, and 40 μmol/L polyether suppressor (used throughout this study unless noted otherwise). The additive concentrations are such that suppressor adsorption is constrained by halide transport. The TH dimensions (10 μm in diameter and 40 μm in height) are similar to those of annular TSV previously simulated with this S-NDR model. The simulation assumes a fixed boundary layer distance (δ) of 25 μm above the TH field. The applied potential stepped waveform is: −0.12 V for 12 min followed by −0.14 V for 10 min, −0.16 V for 8 min, and finally −0.18 V for 10 min. Growth contours in the rightmost image, colorized to indicate local current density at the metal/electrolyte interface, are spaced at 2 min intervals. Initially, deposition is uniform across the entire TH via at −0.12 V. As time progresses, however, chloride and polyether additives adsorb to form the suppressor phase at the metal/electrolyte interface. This occurs most readily on the field due to a significant Cl⁻ depletion gradient within the via that is captured in the isoconcentration lines overlaid on the unfilled volumes in the partially filled THs in Fig. 3. Consequently, metal growth proceeds most rapidly at mid-height, reaching a local current density between 10 mA/cm² and 15 mA/cm². The resulting geometry change entails a systematic decrease in TH radius within the plane of the workpiece. With time, the shape and aspect ratio of the evolving growth front begins to favor accumulation of chloride and polyether additives even along the active regions toward the center of the TH, slowing deposition; this is reflected in a shift to current density magnitude below 5 mA/cm² at 12 min, immediately prior to the next potential step. Stepping the potential to −0.14 V re-activates copper electrodeposition near the TH middle (local current density exceeding 20 mA/cm²) by increasing adsorbate consumption/deactivation as per Eqs. 7–8. The sidewalls impinge at 15 min 32 s, forming the butterfly shape and transforming the unfilled geometry into that of two blind vias, after which feature filling dynamics may be viewed as analogous to filling in conventional TSV. Subsequent potential steps to −0.16 V at 22 min and −0.18 V at 30 min are necessary to achieve complete filling. Otherwise the increased additive transport closer to the TH opening passivates the surface as seen in the growth contour at 30 min, where current density has fallen below −5 mA/cm² everywhere on the metal/electrolyte interface. The potential step to −0.18 V activates deposition both within the TH as well as on the field, resulting in a fully filled through-hole. A variety of potential steps and dwell times may result in simulation of a completely filled TH, the waveform presented here demonstrating only a single example.

Figure 3.

Simulations of potential stepped copper electrodeposition in a through-hole via of aspect ratio 4 at the indicated times. Isocontours of chloride concentration normalized by the bulk concentration are overlaid in the electrolyte domain. The rightmost image shows filling contours at 2 min intervals colorized to indicate local current density at the evolving metal/electrolyte interface. Applied potential steps, relative to the reversible Cu/Cu²⁺ electrode are: −0.12 V to 12 min, −0.14 V to 22 min, −0.16 V to 30 min, and −0.18 V to 40 min; contours at 12 min, 22 min, and 30 min are concurrent with the potential steps. Via radius is 5 μm, via height is 40 μm, and simulated cell radius is 15 μm (full cell domain is not shown). The boundary layer is fixed at 25 μm from the TH field.

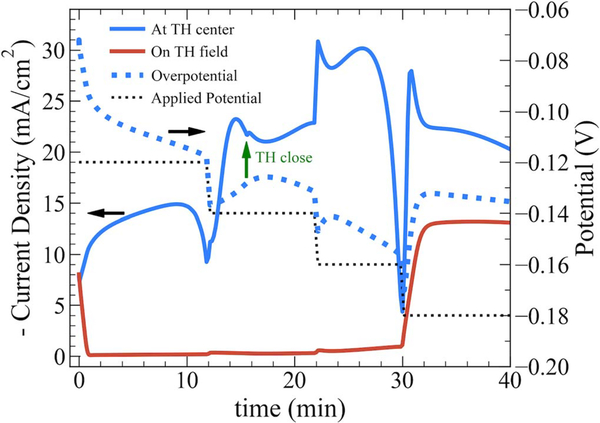
Figure 4 shows the applied potential program and resulting current transients during the simulated filling of the TH in Figure 3. The local current density on the free surface (field) and at the TH mid-height position, that later corresponds to the center of the via bottom after sidewall impingement, are tracked in response to changes in the applied potential. The calculated overpotential available for driving the deposition reaction at the mid-height position, or center of the via bottom, is also shown. At t = 0 s, current density across the work piece is uniform and the overpotential is substantially below the applied value due to potential drop in the electrolyte. As time progresses, current density on the field quickly falls toward zero due to formation of the polyether-chloride adlayer facilitated by relatively low overpotential and rapid additive transport. At the middle of the TH, however, the current density increases both because polyether and chloride adsorption is comparatively limited by transport within the via and because passivation of the majority of the metal/electrolyte surface decreases the total current driven through the cell, weakening the iR-drop in solution and consequently increasing the electrode overpotential driving deposition. As the suppressor adlayer builds at the TH mid-height the local current density (and total current) drops sharply and the overpotential merges with the applied potential. Complete passivation is prevented only by stepping the applied potential to −0.14 V at t = 12 min; a sharp increase in current density at the TH middle is accompanied by a negligible change in current density on the field. This local reactivation/acceleration of metal growth, and corresponding increase in global current, leads to a measurable ≈ 15 mV decrease in the overpotential from the applied potential. Sidewall impingement at the TH center occurs at 15 min and 32 s; merging of the sidewalls is followed by a relaxation of the v-notch angle and associated decrease in total current due to the shrinking active area, the variation of current density at the TH center after impingement mirroring the overpotential profile for the same reason. At 22 minutes the applied potential is advanced to −0.16 V, yielding a current density at the TH center of −30 mA/cm² while current density on the field remains near zero. The current density at the center after this potential step again mirrors the evolving overpotential due to the changing potential-drop across the cell until t = 27 min. At this point current density begins to fall off sharply because higher additive flux closer to the via openings overwhelms deactivation/consumption of the adsorbed suppressor. The final potential step to −0.18 V at 30 min re-activates deposition not only at the TH center but also on the field. As current density on the field rises to −13 mA/cm², before reaching a plateau at around 32 min, the current density at the TH center decreases, the two values converging as the deposit at the TH center approaches the via opening. The higher total current through the cell that accompanies complete activation of the field depolarizes the overpotential by 40 mV from the applied potential. The interplay between the transport limited flux of halide required to form the passivating suppressor layer and the coupling of spatially varying suppression with the electrical response of the system is clearly demonstrated in these simulations.

Figure 4.

Applied potential (···) program and selected local current density transients (─) for potential-controlled copper electrodeposition in the through-hole via depicted in Fig. 3. Current densities are sampled on the sidewall at mid-height of the via (defined as r = r_i(0, t) until impingement of the sidewall deposits and z = z_i(0, t) thereafter) and on the field at the cell edge (z = z_i(R_c, t)). The applied potential and overpotential are sampled at the via middle. The elapsed time for via closure upon impingement of the sidewall deposits, corresponding to the simulation in Fig. 3 (t = 15 min 32 s), is indicated by the green arrow. Black arrows are used to indicate corresponding axes to line types (solid or dashed).

While advancing the applied potential with stepped or ramped waveforms reveals the detailed coupling between mass transport and electrical response in feature filling, significant and rapid variations in the local deposition rate accompany the process. These variations might be expected to impact the microstructure. In contrast, a galvanostatic approach offers simplicity in process control and is consistent with industrial practice that is frequently based on a 2-electrode configuration for electroplating. Accordingly, Figure 5 presents simulations of galvanostatic copper electrodeposition in through-hole vias with aspect ratios of 2 and 4 (diameter = 10 μm for both). In both simulations the boundary layer distance is 25 μm from the field and the applied current density (the imposed current divided by the projected area πR_c²) is −2.4 mA/cm². Growth contours spaced at 3 min intervals and reflecting the local current density at the evolving metal/electrolyte interface show that, for both aspect ratios, deposition localizes within the TH by 3 min. Interestingly, the current density localizes further toward the middle of the TH, increasing as it does, until the sidewalls impinge at 12 min 40 s and 16 min 57 s for the aspect ratio 2 and 4 THs, respectively. Isocontours of fractional chloride concentration (normalized by $C_{Cl}^o$) overlaid in the electrolyte domain make clear that additive depletion in the increasingly narrow unfilled region is key to this enhancement. Deposition after impingement of the deposits on the sidewalls results in upward filling exhibiting the cusped u-shaped growth front that is observed experimentally and reflects the gradient of additives (and thus suppression) within the via. Deposition delocalizes as the growth-front approaches the TH opening, with metal growth within the feature slowing considerably as the applied current distributes more evenly across the remaining surface. The time to achieve complete TH filling is 60 min and 80 min for the aspect ratio 2 and 4 vias, respectively. The simplicity of the galvanostatic filling operation is evident.

Figure 5.

Simulations of galvanostatic copper electrodeposition in through-hole vias of an aspect ratio of 2 (upper) and 4 (lower) at the indicated times. Isocontours of chloride concentration normalized by the bulk concentration are overlaid in the electrolyte domain. The rightmost image in each row shows filling contours at 3 min intervals with the lines colorized to indicate local current density values at the evolving metal/electrolyte interface. Via radius is 5 μm and simulated cell radius is 15 μm for both aspect ratios (full cell domain is not shown). The boundary layer (δ) is fixed at 25 μm from the field and applied current density is −2.4 mA/cm² (defined current imposed using projected area πR_c²) for both aspect ratios.

The potential and local current density transients that accompany galvanostatic filling of the two different aspect ratio through-holes are shown in Figure 6. The local current density is again sampled at the TH mid-height and on the field, whereas the applied electrode potential and deposition overpotential are sampled only at the TH middle. For the shorter TH via (AR = 2), current density at the TH middle and on the field are, as under potential control, equal at the start of the simulation. Also as before, the field and side walls near the openings passivate due to enhanced flux of chloride and polyether, the current density on the field falling to near zero while current at the TH center rises to compensate, reaching −14 mA/cm² by 100 s. The current density at the TH mid-height continues to rise thereafter as the electrode polarizes, reaching a maximum when the deposits on the sidewalls impinge at 12 min and 40 s. Current density at the center then falls rapidly while the current density on the field increases, the two values converging toward that of the applied current density (−2.4 mA/cm²) as the interface levels out due to a more uniform Cl⁻ flux. After 30 min, the difference in current density between the TH center and the field is less than 3 mA/cm², the reduced deposition rate on all surfaces captured in the closely spaced filling contours in Fig. 5. Because the total current remains constant, the potential-drop through the cell remains fixed throughout the computation, yielding the time-independent offset of the applied potential and overpotential profiles in Fig. 6.

Figure 6.

Selected local current density (─) and potential (···) transients for galvanostatic copper electrodeposition in the (a) AR = 2 and (b) AR = 4 through-hole vias simulated in Fig. 5. Current densities are sampled on the sidewall on the midline of the via (defined as r = r_i(0, t) until impingement of the sidewall deposits and z = z_i(0, t) thereafter and on the field at the cell edge (z = z_i(R_c, t)). Applied potential and overpotential are sampled at the via middle. The elapsed time for via closure upon impingement of the sidewall deposits, corresponding to the simulations in Fig. 5 (t = 12 min 40 s and t = 16 min 57 s), are indicated by the green arrow. Black arrows are used to indicate corresponding axes to line types (solid or dashed).

The potential transients and localized current densities for the higher aspect ratio through-hole exhibit broadly similar behavior, albeit with some differences. Current density at the TH mid-height initially rises rapidly as the current density on the field falls toward zero. Deposition slows just prior to rising slightly upon impingement of the sidewall deposits at 16 min 57 s. The slowing is caused by cupric ion depletion down the increasingly long and narrow unfilled central region of the TH that is followed by acceleration as the fixed current is coupled with the reduction of active area immediately following impingement. The current density at the TH center subsequently declines to a local minimum near 21 min before rising once again between 22 min and 34 min, apparently reflecting the convolution of increased polarization and changing concentration gradients as the growth front moves up the via. After 34 min, the current density at the TH center falls while the current density on the field increases, both converging toward the applied current density as the blind via bottoms approach the free surfaces. As with the AR = 2 feature, activation of the field necessarily slows the upward growth of the deposit within the TH, resulting in the closely spaced growth contours in Fig. 5.

Both potentiodynamic and galvanostatic through-hole feature filling yield localization of deposition at the TH middle because the field is more readily passivated by the higher flux of suppressing additives. However, the potential-controlled simulations require a stepped waveform to initiate deposition at the TH middle and then progressively advance the threshold breakdown location outwards to achieve full feature filling. Potentiostatic deposition limited to a single value, e.g. −0.12 V in Fig. 3, results in a partially filled TH as the metal/electrolyte interface becomes fully passivated prior to complete TH filling. Nonetheless, both operating modes require optimization to achieve complete and void-free filling. Figure 7 shows simulations of potentiostatic (−0.16 V) and galvanostatic (−9.6 mA/cm²) conditions that result in voiding during deposition in the AR = 4 through-hole. The lefthand images depict the deposit at the time of side-wall impingement while the right-hand images show growth contours spaced 1 min apart. Scaled chloride concentrations (limiting suppressor adsorption) are overlaid in the unfilled volume on the former while the growth contours on the latter reflect the coverage of adsorbed suppressor. In both cases inappropriate values of the control parameter (i.e., applied potential or current) result in breakdown of the polyether-chloride adlayer that extends well away from the center of the TH; the extent of the active range is evident from the transition between electrode passivation and active growth where suppressor coverage shifts from 1 to 0. Narrowing of the overly long active region during deposition leads to sufficient depletion of cupric ion toward the TH middle that a pinch-off void forms.

Figure 7.

Simulations of copper electrodeposition in through-hole vias resulting in void formation under potentiostatic (−0.16 V) and galvanostatic (−9.6 mA/cm²) operating conditions. Isocontours of chloride concentration normalized by the bulk concentration are overlaid in the electrolyte domain. The right hand images show filling contours at 1 min intervals with the lines colorized to show local suppressor coverage at the evolving metal/electrolyte interface. Via radius is 5 μm, aspect ratio is 4, and simulated cell radius is 15 μm for both simulations (full cell domain is not shown). The boundary layer (δ) is fixed at 25 μm from the TH field.

The through-hole dimensions simulated thus far are ≈ 5 × smaller than what is commonly described for industrial PCB applications.^20,59 From one perspective this is forward looking, but it also allows exploration of the S-NDR behavior in features where the hydrodynamics can be effectively approximated by a uniform boundary layer. Experimental deposition of Cu in substantially larger (125 μm diameter and 625 μm deep) through-silicon vias has established that convective transport can greatly impact feature filling, affecting not only the dynamics of the superconformal filling process but even the symmetry of the growth surface.^45,70 Full computational fluid dynamic calculations must be added to electrodeposition models in order to quantitatively capture how convective transport impacts deposition in larger features. Nevertheless, simulations using a fixed boundary layer provide a foundation for modelling filling in S-NDR based systems, with coupled fluid dynamics to be explored in the future.

Accordingly, Figure 8 shows a galvanostatic simulation of incremental filling of an 85 μm diameter and 150 μm deep through-hole at −1.5 mA/cm². The boundary layer is fixed 6.25 μm above the TH field, comparable to that for a rotating disk electrode spinning at 2600 rpm (5200π rad/min). As a result of the small boundary layer, the majority of concentration variation (92%) is predicted to occur within the via itself. Isocontours of chloride concentration normalized by the bulk concentration are overlaid in the electrolyte domain of the partially filled features. Growth profiles of the evolving deposit are shown at 20 min intervals in the right-most image, the lines colorized to capture the local current density. Deposition is already localized to the TH middle by the first contour (20 min), with sidewall impingement occurring after 2.75 hr of deposition. Deposition proceeds outward after impingement, the growth front leveling out approximately 45 min later. Nonetheless, the peak current density at the TH center occurs only as the growth front nears the via outlet after 5 hr of deposition with the alleviation of cupric ion depletion. Shortly thereafter, the deposition current redistributes and, with current now also going to the field, deposition within the feature slows considerably, filling only 22 μm over the final 5 hr as compared to 110 μm over the first 5 hr. A wide variety of TH dimensions, electrolyte compositions, additive combinations, and convective flow techniques are present in the literature. Direct comparison of experiments to these simulations is not possible in the absence of well-defined kinetics and hydrodynamics for the electrolyte-additive systems used. Experimental filling of a TH with the same dimensions in a similar electrolyte to that presented in Fig. 8 is reported in Figure 5 of Ref. 20, although that study uses a higher sulfuric acid concentration (0.54 mol/L), a different organic suppressor, and a higher applied current density (−2.4 mA/cm²). In that case, optical micrographs indicate sidewall impingement occurs between 1.5 hr and 3 hr of deposition with complete filling in 5 hours. While the simulations indicate a similar time to impingement, the time for total filling is 2 × longer than observed experimentally. One likely explanation (beyond the study differences already listed above) is the approximation of convective transport by a fixed boundary layer in the simulations.

Figure 8.

Simulations of galvanostatic copper electrodeposition in an 85 μm diameter and 150 μm deep through-hole via at −1.5 mA/cm² (defined current imposed using projected area πR_c²) at the indicated times. Isocontours of chloride concentration normalized by the bulk concentration are overlaid in the electrolyte domain. The rightmost image shows filling contours at 20 min intervals with the lines colorized to indicate local current density at the metal/electrolyte interface. The boundary layer is fixed at 6.25 μm from the TH field and simulated cell radius is 127.5 μm (full cell domain is not shown).

The potential transients and sampled current densities predicted during filling of the 85 μm diameter and 150 μm deep through-hole are shown in Figure 9. Current density is again tracked at the TH mid-height and on the field, while the applied potential and overpotential are sampled only at the TH middle. As in to the previous simulations, the current density is uniform initially, the field quickly passivating and deposition localizing to the TH middle. Current at the TH middle reaches −10 mA/cm² within 10 min as the electrode overpotential polarizes to −0.11 V. The current density profile at the TH middle exhibits a series of minor inversions, ranging from −15 mA/cm² to −10 mA/cm², prior to sidewall impingement. These mirror the overpotential profile, reflecting the sensitive dynamics between additive adsorption and deactivation, area change, gradients within the unfilled region of the TH, and the resulting rate of metal deposition across the evolving metal/electrolyte interface. Comparison to the growth profiles in Fig. 8 shows the highest current density occurring at 100 min (before sidewall impingement), with active deposition occurring primarily over a fixed central region of the TH in the radial direction. The growth contours show deposition proceeding toward the TH openings (in the z-direction) as well at 120 min, the substantial increase of active area over this time period being responsible for the decreased current density at the midline evident in Fig. 9. The deposits on the sidewalls impinge after 2.75 hr of deposition, the current density then briefly increasing before falling steadily until 4.75 hr. Over the same time interval the overpotential increases monotonically from −0.10 V to −0.12 V. At this point, the corresponding growth front within the TH in Fig. 8 is flat. Interestingly, two sharp oscillations in current density at the TH center are seen over the next ≈ 1 hr of deposition. The first peaks at −19 mA/cm² then falls to −0.4 mA/cm² and the second rises to −20.5 mA/cm² before stabilizing at −1.2 mA/cm². Current density on the field begins to increase during the same time period, with the two values converging toward the global applied current density over the final 4 hours of deposition. As in the other simulations, activation of the field slows upward growth within the via, yielding the closely spaced filling contours seen in Fig. 8.

Figure 9.

(a) Local current density (─) and potential (···) transients for galvanostatic copper electrodeposition (−1.5 mA/cm²) and (b) magnified growth contours in the through-hole via simulated in Fig. 8. Current densities are sampled on the sidewall on the midline of the via (r = r_i(0, t)) and on the field at the cell edge (z = z_i(R_c, t)). Overpotential and applied potential are sampled at the via middle. The elapsed time for via closure upon impingement of the sidewall deposits, corresponding to the simulation in Fig. 8 (t = 2.75 hr) is indicated by the green arrow. Black arrows are used to indicate corresponding axes to line types (solid or dashed). Contour lines are the same as in Fig. 8, spaced 20 min apart and colorized to indicate local current density.

The dramatic current density cycling between active and passive deposition at the TH center between 4.75 hr and 6 hr in the growth contours in Figure 8 is replotted at higher resolution in Figure 9b. The oscillations reflect the sensitivity and thus instability of the S-NDR system, with history, as much as local conditions, impacting present evolution. In the present case, the oscillations occur as the growth front approaches the free surface, nearing the imposed hydrodynamic boundary layer; the changing profile of the diffusion field offers new avenues for dissipation. At 4 hr and 40 min of deposition the growth contour is nearly flat within the via, albeit with a faster deposition rate in the center than at the edges. The higher deposition rate leads to greater additive deactivation that, despite comparable chemical flux given the flat growth profile, promotes further acceleration of the central region. Thus, the contour at 5 hr shows an even greater enhancement in current density. Consequently, the growth front develops a convex profile by 5 hr 20 min, at which point sufficiently increased additive flux to the higher central region inhibits deposition there and current localization shifts to the edges lower down within the via. After an additional 20 min the deposit profile becomes flat again, and current localization shifts back to the center. It is only the redistribution of current over the far larger surface area of the field toward 6 hr that halts the oscillations in the system and relatively uniform deposition rate is achieved everywhere. The oscillatory behavior speaks to the critical nature of the passive-active transition and its sensitivity to perturbation of local interface roughness relative to the neighboring boundary layer thickness.

Conclusions

A model based on the formation and breakdown of a polyether-chloride suppressor adlayer that underlies bottom-up electrodeposition of Cu in TSV has been shown to successfully explain void-free “butterfly” filling of TH previously detailed in the experimental literature.^20–23 Breakdown of suppression that occurs at higher over-potentials gives rise to hysteretic cyclic voltammetry that, under closer analysis, reveals a hidden additive-derived S-shaped negative differential resistance. The potential-driven disruption of the suppressing phase allows Cu²⁺ to access the electrode, stimulating metal deposition and consequently higher currents during the reverse sweep in the voltammograms. The non-linear system gives rise to bifurcation of planar electrodes into passive and active regions of deposition known as Turing patterns. In the case of topographically patterned substrates, such as TSV and TH, deposition parameters can be tuned such that the bifurcation leads to void-free bottom-up deposition with the highest deposition rate occurring, absent significant metal ion depletion, farthest from the feature opening(s) where the additive concentration is lowest. Nevertheless, optimization of the additive concentration and applied potential/current is necessary to ensure that suppression breakdown initiates at the TSV bottom and the TH middle. Filling was explored in simulations based on the S-NDR model using both potential and current control. For potentiostatic deposition, application of a suitable potential leads to the onset of deposition localized to the most recessed section of the TH. However, as the growth front advances the increased flux of suppressor components, in particular Cl⁻ in the present work, leads to deceleration of the growth front and its eventual passivation. By progressively advancing the applied potential to more negative values (i.e., potentiodynamic control) the bottom up growth modality can be maintained, as the location of the passive-active transition advances, or even accelerates, toward the via opening(s) and the free surface. The resistive losses that accompany current flow in the electrolyte lead to dynamic changes in the overpotential available for the metal deposition process. When convolved with the workpiece geometry, and the slower response of mass transport, the combination of effects leads to sustained bottom-up filling proceeding from the most recessed location in the feature. Selecting an initial potential that is too negative results in an active area that is too large, leading to depletion of the metal ion at the TH middle and formation of a central void.

In contrast to potential-stepped waveforms, galvanostatic Cu deposition can sustain bottom-up deposition using a single value of applied current(density). The process leads to a smoother advance of the active growth front with time as compared to the potential step methods. That said, use of a suitable potential ramp or potentiodynamic protocol would also be expected to smooth the filling process as previously demonstrated in other metal systems.¹⁵ As with potentiostatic deposition, a more rapid increase of polyether-chloride coverage on the TH field at early times due to enhanced additive flux directs localization of copper deposition to the TH middle. As the growing metal/electrolyte interface approaches the TH openings, deposition on the field activates, spreading the applied current over the entire workpiece and thereby slowing the final outward growth from the recessed feature. Analogous to potential-controlled deposition, selection of too large a current density results in an overly large active region and metal ion depletion near the TH center that causes void formation. Simulations of galvanostatic deposition in larger through-holes also show preferential localization of deposition to the TH middle followed by outward growth after sidewall impingement. However, unlike the smaller features, the formation of significant diffusional gradients in the radial direction with the TH via can yield dynamic fluctuations between passive and active deposition on the metal/electrolyte interface in the via similar to those observed during voltammetry on a macro planar electrode.