Efficiency evaluation of Brazilian airlines operations considering the Covid-19 outbreak

Abstract

In this paper we evaluate the operational efficiency of the Brazilian airlines considering the novel coronavirus Covid-19 outbreak. This novel coronavirus was first reported end of 2019 in Wuhan, China, however the powerful contamination spread among people forced the World Health Organization to characterize the Covid-19 as a pandemic in March of 2020. Here we analyze the main Brazilian airlines operations response due to lower demand because Covid-19 outbreak in first quarter of 2020 comparing with first quarter of 2019. The analysis here aims to verify the efficiency of airlines in domestic air transport market in Brazil through Multicriteria Data Envelopment Analysis (MCDEA) model. We used MCDEA to avoid limitations of classical DEA models for the case, especially the numbers of decision units and variable. In this paper we used an improvement of the MCDEA model to seek benchmarks considering a dual model all objective functions of MCDEA. The results highlight the challenges for the airlines, due to flight restriction and demand dropping. And also, the evaluation exposes the different company configuration of aircrafts age and network reconfiguration which was reflected by the efficiency difference on the period. The assessment shows the company with a better mix of aircraft models has a leverage on efficiency response due to unpredictable period as the pandemic Covid-19 outbreak.

1. Introduction

The air transport industry performs one third, in value, of global cargo trade. On the other hand, in Brazil, this sector responsible for only 1.4% of the country's GDP IATA (2016). In this industry, airlines and airports play a strategic role to both government and private companies (Bel and Fageda, 2008; Doganis, 1992). In addition, Zook and Brunn (2006) show air transport connectivity as a crucial factor in influencing the position of a region on a global scale.

Thus, air transport largely facilitates human mobility worldwide which includes in this case the frequency spread of infectious disease epidemics. Findlater and Bogoch (2018) described the world witness of several infectious diseases spread as in recent cases of Zika and Chikungunya virus in Latin America and types of coronavirus as Middle Eastern respiratory syndrome (MERS-CoV) in 2012 and the severe acute respiratory syndrome (SARS-CoV) outbreak in 2002.

The first report of Covid-19 was on December 30th^, 2019 at province Wuhan, China, since then the World Heath Organization (WHO) started working to response this outbreak. Due to the rapid spread transmission of Covid-19, WHO declared it on March 11th^, 2020 a world pandemic. Thus, at final of first quarter of 2020 there were 750,890 contaminated people and 35,405 deaths worldwide (Who, 2020).

The novel coronavirus (Covid-19) outbreak is a reminder how powerful the diseases spread worldwide by travellers (Wang et al., 2020), especially in this case when we consider the air transport connectivity and the good environment inside of an aircraft for virus respiratory transmission (Wilson, 2020).

Considering that airport infrastructure highly influence air transport efficiency (Assis et al., 2017), Pereira et al. (2018) informed connectivity has a direct impact on financial results of the airlines companies.

Green (2007) and Bruechner (2013) consider studies in air traffic area important because of their relation to the economic development of any country. Regarding novel Covid-19 outbreak, many countries started adopting on their population movements restrictions, in some cases lockdown, which include also borders to air transport operation (Quilty et al., 2020).

The air transport demand significantly dropped due to Covid-19 outbreak first news, impacting first quarter of 2020 of air companies worldwide. To face this scenario, the companies started to adjust their air network to this new condition. In South America, for example, daily departures dropped more 90% in March 2020 (IATA, 2020).

There are approximately 2498 airports (including landing areas) in Brazil, i.e., the second largest number of airports in the world, only behind the United States. When we consider the Brazilian air transport case, the coverage of domestic air network reflects population concentration according to McKinsey and Company (2010). The largest number of airports and flight availability is in the Southeast region, where the biggest cities São Paulo and Rio de Janeiro are located (Pereira and Soares de Mello, 2019; Pereira and Soares de Mello, 2020).

However, the Brazilian air transport market for domestic passengers is high concentrated in three big air companies (Azul, Gol and Latam) with more than 90% of RTK (Revenue tonne kilometer) market share. Due to novel Covid-19, in March 2020 only theses three companies were operating in Brazilian domestic air network (Anac, 2020).

The aim of the paper is to evaluate the company's efficiency response due to novel Covid-19 outbreak in first quarter of 2020 comparing together with first quarter of 2019 for the main three Brazilian airlines. The efficiency model used herein seeks to improve the discrimination of the units analyzed, since Data Envelopment Analysis (Charnes et al., 1978) classical models (i.e. DEA CCR) have limitation regarding number of units versus variables in the assessment (Pishgar-Komleg et al., 2020).

Therefore, we used a Multiple Criteria Data Envelopment Analysis (MCDEA) model, proposed by Li and Reeves (1999) which refines discrimination and provide relevant information on airport efficiency. We calculate the MCDEA Efficiency to obtain an efficiency value for each three main Brazilian airlines at each month of first quarter of 2019 and 2020.

MCDEA model only provides efficiency on the evaluation missing the benchmarks assessment, as we could check in DEA classical model. We needed to consider A MCDEA dual model to seek benchmarks for each decision unit, then we used the novel Pereira and Soares de Mello (2019) model since this considers the three objective functions in the same dual analysis, different development from previous studies.

In the next section, we present a literature review regarding air transport for DEA studies, then detailing the theoretical MCDEA background which supports our current analysis. Here in model and the methodology that calculates efficiencies based on. In results, we describe the study case of the three main Brazilian airlines, presenting and discussing the analysis with the MCDEA model. In the last section, we present conclusions of this paper.

2. Theoretical bases

Data Envelopment Analysis (DEA) is a nonparametric mathematical programming problem (Charnes et al., 1978) that calculates the efficiencies of Decision Making Units (DMUs), considering their resources (inputs) and products (outputs). These DMUs are homogeneous as they use the same multiple resources, called inputs, and produce the same multiple products, called outputs, and operate under similar conditions (Dyson et al., 2001). A DMU is efficient if its index is 1 and otherwise inefficient. Further details on the characteristics, properties and different DEA models can be found in Cooper et al. (2007).

Considering DEA models evaluation for air transport system, there are various papers on airlines efficiency (Rubem et al., 2017; Gomes Júnior et al., 2016) or airports assessment (Wanke and Barros, 2016). For a comprehensive survey on airport productivity and efficiency studies, see for instance Liebert and Niemeier (2013), who surveyed methods, data and findings of empirical research. Although Pels et al. (2001), who studied efficiency of European airports, obtained similar results from both methodologies, still, they present different strengths and weaknesses.

In Brazil, Pacheco & Fernandes (2003) used a BCC input-oriented model to analyze 35 airports with predominant domestic traffic in 1998. The authors considered as outputs domestic passengers, tons of cargo and mail, operating revenue, commercial revenue, and other revenues; and as inputs average number of employees, payroll, and operating expenses. Their studies found 10 efficient airports, including in São Paulo, Belo Horizonte and Rio de Janeiro.

Perelman and Serebrisky (2012) considered as outputs number of passengers, tons of freight and number of aircraft movements, and as inputs number of employees, number of runways and terminal size. Results show that two airports from São Paulo (VCP and CGH) are efficient in both time periods (2000–2003 and 2004–2007), even in the DEA model with constant returns to scale (CCR – Charnes et al., 1978).

Adler and Berechman (2001) developed a model to verify the quality and relative efficiency from a set of European and non-European airports. In this line, Lin and Hong (2006) assess the operational performance from of twenty major airports around the world. Another approach Liu (2016) analysis the global and operational efficiencies for the ten major Asian airports, using a sub process model of DEA. Meanwhile, Lozano et al. (2013) use the sub process DEA model to analyze Spain airport considering the aircrafts movements comparing with passengers and cargo for each flight.

Standard DEA models calculate the multipliers for inputs and outputs of each DMU, so that its efficiency is maximized, following the model's restrictions. Although this is a central characteristic in DEA models, it could lead to distorted results, such as efficient DMUs that attribute null multipliers for several inputs and/or outputs. Another consequence of such benevolence is the low discriminatory power of standard DEA, particularly for problems with few DMUs, compared to the number of inputs and outputs.

Although the problems of discrimination of classical DEA, the Li and Reeves (1999) model uses a resolution by the multiobjective function to consider additional measures of efficiency by the minisum criteria (minimizes the sum of the deviations) and the minimax (minimizes the maximum deviation) (Pereira et al., 2018), considering characteristics in analysis for equality of the units and overall optimization for a dual approach (Soares de Mello et al., 2009). The Formulation (1) presents the Li and Reeves, 1999 model with the additional objective functions.

$$\begin{array}{l}Min{d}_o\\ Min\sum _{k=1}^n{d}_k/n\\ MinM\\ Subjectto\\ \sum _{i=1}^r{v}_i{x}_{io}=1\\ \sum _{j=1}^s{u}_j{y}_{jk}-\sum _{i=1}^r{v}_i{x}_{ik}+d_k=0,k=1,\dots ,n\\ M-d_k\ge 0,k=1,\dots ,n\\ u_j,v_i\ge 0,\forall j,i\end{array}$$ (1)

Where $M$ is minimax for deviation, $d_k$ is deviation for the DMU k, $x_{ik}$ is the value for input i for DMU k, $y_{jk}$ is the value for outpu j for DMU k, $u_j$ is the calculated weight for output j and $v_i$ is calculated weight for input i.

Li and Reeves (1999) model is also used to improve the discrimination and dispersion of weights (Chang and Chen, 2007; Ghasemi et al., 2014 and Bal et al., 2010). However, Soares de Mello et al. (2009) used a model of Li and Reeves to analyze a small number of DMU's, while Carrillo et al. (2016) verified the ranking of alternatives with multiobjective DEA. Additionally, Lins et al. (2004) verified the targets using a multiobjective DEA model.

The Li and Reeves (1999) model is applied in different areas. Bostian et al. (2015) apply the multiobjective DEA optimization model to verify methods in the agricultural area where they perform an analysis with fertilizers. Lo, 2007, Lu and Lo (2012) and Liang et al. (2004) use environmental variables in environmental assessment models involving multiobjective techniques in DEA.

To solve multicriteria model we used the TRIMAP software (Clímaco and Antunes, 1987, 1989) which is a free program that provides the combination of non-dominated solutions in tri-criteria linear programming problems, as a solution generator and a tool for weight space analysis (Soares de Mello et al., 2009), which can be used to find MCDEA non-dominated solutions.

The primal model (Li and Reeves, 1999) is originally a multiobjective method and did not present benchmarks evaluation for DMUs. First concept for dual model to MCDEA (Chaves et al., 2016) used a methodology of duality for multiobjectice function considering pairs of functions, as original MCDEA is a tri-objective model.

In this case, Chaves et al. (2016) split the MCDEA into two different models (R12 and R13), where the first function $Min{d}_o$ is optimized in both model, which one model considers the minisum function as constraint and the other model considers minimax function as constraint as well. The dual model of the R12 and R13 models are presented by the set of equation (2) and the set of equation (3), respectively:

$$\begin{array}{l}\text{R}12-\text{dual model}\\ Minz=h+\Psi \theta \\ \text{Subject to}\\ \sum _{j=1}^n{y}_{rj}{\lambda }_j-\sum _{j=1}^n{y}_{rj}\theta \ge y_{r0}\\ x_{i0}h-\sum _{j=1}^n{x}_{ij}{\lambda }_j-\sum _{j=1}^n{x}_{ij}\theta \ge 0\\ u_r,v_i,{\lambda }_j\ge 0\end{array}$$ (2)

$$\begin{array}{l}\text{R}13-\text{dual model}\\ Mink=h+\varphi \theta \\ \text{Subject to}\\ \sum _{j=1}^n{y}_{rj}{\lambda }_j-\sum _{j=1}^n{y}_{rj}{\delta }_j\ge y_{r0}\\ x_{i0}h-\sum _{j=1}^n{x}_{ij}{\lambda }_j-\sum _{j=1}^n{x}_{ij}{\delta }_j\ge 0\\ \sum _{j=1}^n\left(-1\right){\delta }_j+\theta \ge 0\\ {\lambda }_{j,}{\delta }_j\ge 0\end{array}$$ (3)

Chaves et al. (2016) used the ψ to solve R12 in order to find the optimal (minimum) value of the minisum function, and the ϕ to reduce the maximum inefficiency of the DMUs. Despite of Chaves et al. (2016) could present benchmarks for MCDEA, they considered and optimize the model separated which did not consider the MCDEA full characteristics.

Pereira and Soares de Mello (2019) novel model for MCDEA duality considered the original tri-objective MCDEA model (Li and Reeves, 1999) and transformed into a mono objective function linear programming model. This novel duality model improves the MCDEA benchmarks analysis with inclusion of all characteristics in the same programming. Among the different methods to linearize a multiobjective (Antunes et al., 2016) in a mono objective model, the weighted sum method was used to transform the formulation of (Li and Reeves, 1999) as presented in Formulation (4).

$$\begin{array}{l}Min({\alpha }_1{d}_o+{\alpha }_{2}M+{\alpha }_3\sum _{k=1}^n{d}_k/n)\\ \text{Subject to}\\ \sum _{i=1}^r{v}_i{x}_{io}=1\\ \sum _{j=1}^s{u}_j{y}_{jk}-\sum _{i=1}^r{v}_i{x}_{ik}+d_k=0,k=1,\dots ,n\\ M-d_k\ge 0,k=1,\mathrm{\dots },n\\ u_j,v_i\ge 0,\forall j,i\end{array}$$ (4)

In cases where the DMU presents more than one region of non-dominated solutions, the model Rubem et al. (2017) is followed where the choice of the set of weights (${\mathrm{\alpha }}_1,{\mathrm{\alpha }}_2$ e ${\mathrm{\alpha }}_3$) is done by the largest region presented by TRIMAP. This methodology of efficiency assessment is applicable in different business area, as Pereira and Soares de Mello (2019) used to evaluate central airports in Brazil. For the benchmarks analysis we shall use Formulation (5) which describes a dual model for Formulation (2).

$$\begin{array}{l}Max{b}_o\\ \text{Subject to}\\ b_o{x}_{io}-\sum _{\text{k}=1}^n{w}_k{x}_{ik}\le 0,\forall i=1,\dots ,r\\ \sum _{k=1}^n{w}_k{y}_{jk}\le 0,\forall j=1,\dots ,s\\ w_o-m_0\le {\alpha }_1+{\alpha }_3/n\\ w_k-m_k\le {\alpha }_3/n,\forall k=1,\dots ,n\ne o\\ \sum _{k=1}^n{m}_k\le {\alpha }_2,\forall k=1,\dots ,n\\ m_k\ge 0,k\\ b_o,w_k,\text{free }\forall k\end{array}$$ (5)

The variable $b_o$ means an efficiency for the DMU in analysis considering all aspects of the objective functions aggregated from Li and Reeves (1999) model. Analysing (5) and comparing with dual for CCR classical model (Cooper et al., 2007), we verify that variables $w_k$ provides the benchmarks. However, as $w_k$ is as free variable we could find negative numbers. This benchmark analysis is proved comparing the results to CCR classical dual (Charnes et al., 1978) by Formulation (6).

$$\begin{array}{l}Min\theta \\ Sujectto\\ \sum _{j=1}^n{x}_{ik}{\lambda }_k-\theta x_{ik}\le 0i=1,\dots ,r\\ \sum _{j=1}^n{y}_{jk}{\lambda }_k\ge y_{jo}j=1,\dots ,s\\ {\lambda }_k\ge 0\forall k=1,\dots ,n\end{array}$$ (6)

Where θ = Efficiency; λk = DMUk participation in the target goal of the analyzed DMU; xjk = Input j of DMU k; yik = Output i of DMU k; xj0 = Input j of analyzed DMU; yi0 = Output i of analyzed DMU; n = Number of units of the sample; s = Number of Outputs; and, m = Number of Input. Considering that deviations is opposite from efficiency we verify that $\theta =1-b_o$. In this case we see $Min\left(1-b_o\right)=Max{b}_o$, without losing properties.

From the definition (Charnes et al., 1978) in Formulation (6) of the variable${\lambda }_k$ is also defined as the participation of the efficient DMUj in the target goal DMUk under analysis. The benchmarks are defined from the values found in${\lambda }_k$, if they are greater than zero ranging up to one, the value will be the ratio that the DMUj is a reference for the DMUk. Assuming that ${\lambda }_k=-{\mu }_k\forall k\ne o$ and ${\lambda }_o=1-{\mu }_{o}k=o$, in this case ${\lambda }_o$ and ${\mu }_o$ is regarding the DMU under analysis, we could substitute the constrains from Formulation (4) as following:

• -First constrain$\sum _{j=1}^n{x}_{ik}{\lambda }_k-\theta x_{ik}\le 0$ could be re-written as $(1-b_o)x_{io}-(1-{\mu }_o)x_{io}+\sum _{j=1}^n{x}_{ik}{\mu }_k\ge 0$, or simplifying as $b_o{x}_{io}-\sum _{j=1}^n{x}_{ik}{\mu }_k\le 0$, considering $i=1,\dots ,r$;
• -Second constrain $\sum _{j=1}^n{y}_{jk}{\lambda }_k\ge y_{jo}$ could be re-written as $\left(1-{\mu }_o\right)y_{jo}-\sum _{j=1}^n{y}_{jk}{\mu }_k\ge y_{jo}$, or simplifying as $\sum _{j=1}^n{y}_{jk}{\mu }_k\le 0$, considering $j=1,\dots ,\text{s}$;
• -Third constrain ${\lambda }_k\ge 0$ could be re-written split in two considerations where ${\lambda }_k\ge 0\text{ on }\forall k\ne o$ we verify ${\mu }_k\le 0$ and also where ${\lambda }_o\ge 0\text{ on }k=o$ we have ${\mu }_o\le 1$

After proceeding with the substitutions on objective function and constrains in Formulation (6) we could verify the Formulation (5) as result. The association between positive ${\lambda }_k$ from Formulation (6) and negative ${\mu }_k$ from Formulation (5) provides us benchmarks considering the respective method in use (i.e. classical CCR or MCDEA).

We used the TRIMAP software, developed by Clímaco and Antunes (1989), to solve the MCDEA model, an also to provide set of weights (${\mathrm{\alpha }}_1,{\mathrm{\alpha }}_2$ e ${\mathrm{\alpha }}_3$). This softwareis a free search method that provides the set of non-dominated solutions in tri-criteria linear programming problems, through a learning process. Despite its interactive environment, TRIMAP could be used for MCDEA problems, as a generator of solutions and a tool for weights space analysis (Soares de Mello et al., 2009).

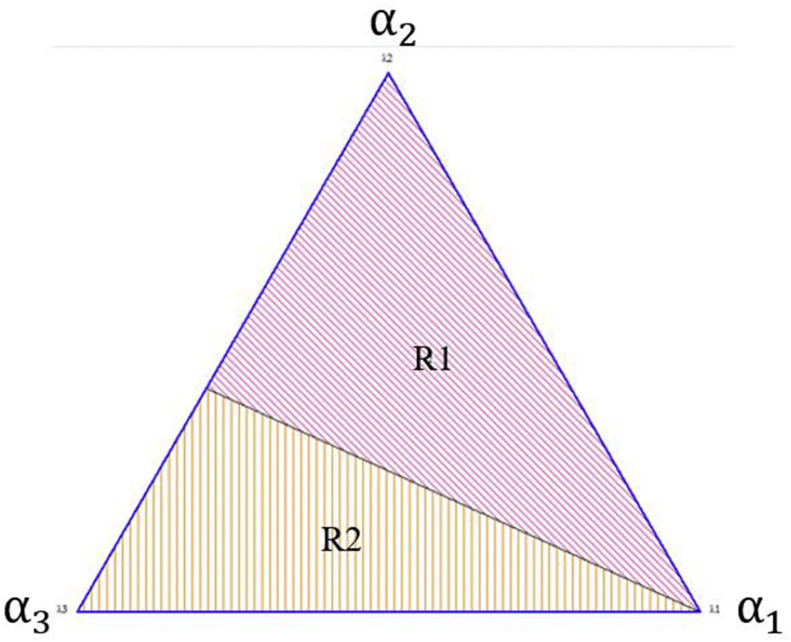
In addition on computing all optimal solutions for MCDEA's three objective functions, TRIMAP also presents graphical representations, one of which is very useful for MCDEA, namely the weights space decomposition. This representation shows the indifference regions of the weights space that correspond to the non-dominated basic solutions. Fig. 1 presents an example from TRIMAP triangle solutions result.

Fig. 1.

Regions with set of solutions from TRIMAP.

We should highlight that such weights refer to the multipliers of the objective functions, and that, in indifference regions, these weights could vary without altering the solution. The weights space is represented in a triangle, whose corners correspond to the optimization of each objective function.

With such tool, it is possible to evaluate whether the DMUs’ optimal evaluations have stable solutions or if they depend on specific multipliers. Large indifference regions indicate that the solution remains the same even with moderate changes of the objective function's weights. For instance, if the same indifference region contains two triangle corners, one associated with the classic objective function and the other associated with the minimax or minisum objective functions, the observed DMU is therefore minimax or minisum efficient, respectively.

Moreover, it is also possible to identify potentially good solutions, which improve results for the second and third objective functions, even if they do not confer the DMU's maximum efficiency, for instance. For the MCDEA efficiency region is influenced by of solution chose from TRIMAP. Nevertheless, among from same region of solution is indifference the set of weights ${\alpha }_k$ chosen.

3. Case study

We use for this article data based on Brazilian regular commercial domestic from ANAC (in Portuguese from Agência Nacional de Aviação Civil - the national regulation agency for air sector). Moreover, we considered for passenger and cargo transportation during first quarter of 2019 and 2020 (January, February and March).

Therefore, in order to evaluate the efficiency of the main three Brazilian airlines (Azul Linhas Aéreas Brasileiras – AZU; Gol Linhas Aéreas – GLO; Latam Airlines Brasil - TAM). We considered for each DMU the data from the respective air company in a specific month forming a total of 18 DMUs.

We considered for each DMU as input variables the numbers of take-offs, the Available tonne kilometer -ATK and the fuel consumed. As output for each DMU we verified the Revenue tonne kilometer – RTK. The values ATR and RTK consider tonnage for average passengers’ weight and cargo load, thus we analyzed the market response of the airlines. These variables are in line with studies of air transport assessment based in DEA methods (Lozano and Guitiérrez, 2011).

Regarding the fuel consumed, the treatment as input implies in valuation for production model with the lowest impact coupled with the lower use of resources then we considered it as undesirable output (Liu and Sharp, 1999) due to environmental impact. Moreover, in air transport evaluation the fuel consumption is related to efficiency improvements on technology and operating costs (Morrel, 2009).

Table 1 shows the differences on performance of each company in 2019 and 2020, for example the number of take offs in January for all companies raised from 2019 to 2020. However, in February 2020 we could see the droppage of numbers on the begging of novel Covid-19, and the worst level in March 2020 once the WHO pandemic declaration.

Table 1.

Data information for airline per month.

Com/Y/M	Takeoff	ATK	Fuel	RTK
AZU-2019/1	23,850	235,601,371	80,221,730	168,594,247
AZU-2019/2	21,649	197,412,037	67,430,776	140,929,071
AZU-2019/3	22,381	208,962,669	70,451,261	146,853,613
GLO-2019/1	22,957	476,521,593	119,365,213	326,427,451
GLO-2019/2	17,987	351,686,234	89,152,352	235,150,338
GLO-2019/3	18,836	363,036,813	91,740,480	233,614,628
TAM-2019/1	18,146	380,448,704	101,362,199	254,801,421
TAM-2019/2	15,632	323,335,401	86,480,332	210,967,082
TAM-2019/3	16,674	345,984,079	90,149,738	222,266,798
AZU-2020/1	26,401	294,578,478	87,997,903	214,122,675
AZU-2020/2	22,703	243,378,622	73,084,766	170,279,197
AZU-2020/3	16,462	178,061,337	52,313,862	115,045,741
GLO-2020/1	24,199	484,206,154	121,085,536	307,734,488
GLO-2020/2	19,862	392,598,263	99,180,133	240,103,199
GLO-2020/3	14,884	293,917,608	72,500,594	161,198,652
TAM-2020/1	21,768	452,239,712	120,764,282	312,825,746
TAM-2020/2	19,353	400,721,106	106,640,332	264,018,192
TAM-2020/3	14,817	318,845,098	81,574,692	181,444,844

Collected data from ANAC.

Each company operates different aircrafts configuration, i.e. TAM uses Airbus models, GOL uses Boeing models while Azul operates a mix of ATR, Embraer and Airbus models. This characteristic shows the performance for each one on comparing the take offs for offering availability and fuel consumption.

Due to Covid-19 outbreak, the flights cancellations raised since governmental restrictions or passenger cancellations. Despite of the passenger decreasing, the Brazilian air transport authority defined a minimum essential air network to airlines in order to connect the states with at least on flight, which could also help the Brazilian health system response to the Covid-19 outbreak (ANAC, 2020).

The Brazilian air transport authority also allowed the companies to change the aircrafts configurated to passengers to operation for cargo flight. This allowance helped airliners to leverage the usage of the aircrafts and revenue for the period.

4. Results

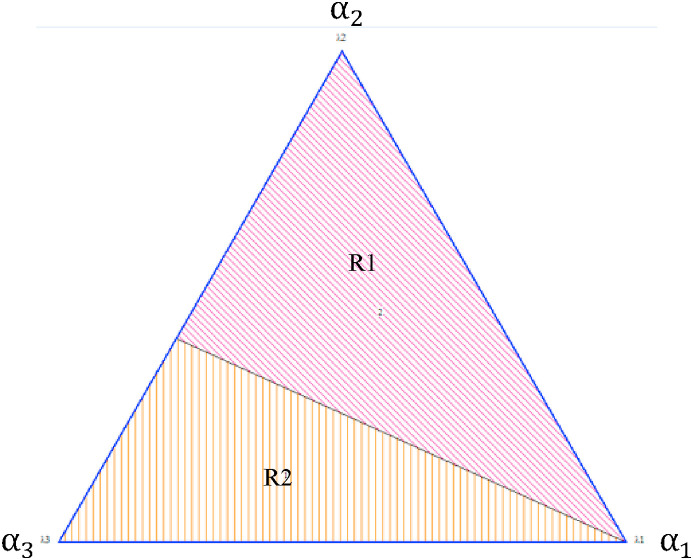
For each DMU we use the TRIMAP software to calculate results for the MCDEA model of Formulation (1) and obtain the weight space decomposition. As an example, we extracted in TRIMAP the set of non-dominated solution for DMU AZUL-2020/1 where we identified two regions (R1 and R2), as shown in Fig. 2 .

Fig. 2.

TRIMAP result for AZUL-2020/1.

Then, following Rubem et al. (2015), we selected from Fig. 2 the central point of the largest region (R1) to obtain a set of weights ${\mathrm{\alpha }}_1,{\mathrm{\alpha }}_2$ e ${\mathrm{\alpha }}_3$ that represent a non-dominated solution for the multiobjective problem of DMU AZUL-2020/1. The extracted set of weight for DMU AZUL-2020/1 (${\mathrm{\alpha }}_1$= 0.166039, ${\mathrm{\alpha }}_2$ = 0.15827 and ${\mathrm{\alpha }}_3$ = 0.675691) to apply Formulation (4).

Considering Formulation (4), we verified for each DMU the respective deviation value ($d_o$). As a definition, the efficiency value is the deviation complementary number. Thus, for AZUL-2020/1 the deviation as zero, then the efficiency for this DMU is 1.000. Hence, we calculated the Formulation (4) for all DMUS from Table 1 to evaluation the deviations. With the deviation complementary values, Table 2 presents the result of the efficiency for each DMU considered.

Table 2.

Efficiency for airline per month.

Com/Y/M	Eff
AZU-2019/1	0.954
AZU-2019/2	0.945
AZU-2019/3	0.935
GLO-2019/1	1.000
GLO-2019/2	0.972
GLO-2019/3	0.937
TAM-2019/1	0.969
TAM-2019/2	0.943
TAM-2019/3	0.932
AZU-2020/1	1.000
AZU-2020/2	0.961
AZU-2020/3	0.894
GLO-2020/1	0.928
GLO-2020/2	0.890
GLO-2020/3	0.805
TAM-2020/1	1.000
TAM-2020/2	0.953
TAM-2020/3	0.829

For the three companies the lowest values efficiency occurred in March of 2020, when the novel Covid-19 outbreak was considered by WHO a global pandemic. Even with an average drop of 25% from takeoffs and 32% from RTK comparing February and March of 2020, the companies could not reflect it in better efficiency response to the Covid-19 outbreak restrictions.

The DMU GLO-2019/1, AZU-2020/1 and TAM-2020/1 presented the top results regarding the better utilization of offering inputs with the demand output, considering the January is a month with a strong demand for travels during summer vacation in Brazil.

Regarding the DMU from 2020, in January the novel Covid-19 was starting the spread in Asia, and there were not any case in South America at that moment. The results also reflect the companies’ position related to aircrafts configuration and age. For example, TAM and Gol performed in March less flights than Azul, the fuel consumption was higher for both cases.

The number of variables compared to the number of DMUs were not issues to discrimination of the DMUs because the MCDEA presents more restrictive characteristics to overcome this problem and avoid many efficient DMUs that would difficult to rank the results. When we apply Formulation (5) for the case data information, we shall seek for benchmarks to each DMU Table 3 presents the benchmark for each DMU operation period.

Table 3.

Airlines operation period benchmark.

Com/Y/M	Benchmarck
AZU-2019/1	GLO-2019/1	AZU-2020/1	TAM-2020/1
AZU-2019/2	GLO-2019/1	AZU-2020/1
AZU-2019/3	GLO-2019/1	AZU-2020/1	TAM-2020/1
GLO-2019/1	GLO-2019/1	AZU-2020/1
GLO-2019/2	GLO-2019/1	AZU-2020/1
GLO-2019/3	GLO-2019/1	AZU-2020/1
TAM-2019/1	GLO-2019/1	AZU-2020/1	TAM-2020/1
TAM-2019/2	GLO-2019/1	AZU-2020/1	TAM-2020/1
TAM-2019/3	GLO-2019/1	AZU-2020/1	TAM-2020/1
AZU-2020/1	GLO-2019/1
AZU-2020/2	GLO-2019/1	AZU-2020/1
AZU-2020/3	GLO-2019/1	AZU-2020/1
GLO-2020/1	GLO-2019/1	AZU-2020/1
GLO-2020/2	GLO-2019/1	AZU-2020/1
GLO-2020/3	GLO-2019/1	AZU-2020/1
TAM-2020/1	GLO-2019/1	AZU-2020/1
TAM-2020/2	GLO-2019/1	AZU-2020/1	TAM-2020/1
TAM-2020/3	GLO-2019/1	AZU-2020/1	TAM-2020/1

From Table 3 we verify for each DMU its benchmark, because the results from Formulation (5) for each DMU show the respective $w_k$ negative which is referenced to DMUk. Even we are evaluating multiobjective method with more restrictive constraints, the benchmark evaluation considers the importance of any DMU which we could check the best practices.

Each DMU seek to a benchmark from the top efficient DMUs (GLO-2019/1, AZU-2020/1 and/or TAM-2020/1) checking the best practices and utilization for the fleet. However, the restrictions from Government due to Covid-19 strongly dropped the demand in March of 2020 while a minimum flight attendance was determined by authorities.

The benchmarks analysis shows the best practices shall follow the operation from January, since this month is the higher period of school vacations in Brazil due to summer, when the companies see the best occupation on their flights.

5. Conclusion

The United Nations agency for civil aviation (ICAO – International Civil Aviation Organization) expects in the worst scenario US$ 253 billion potential loss of gross revenue of airlines worldwide (ICAO, 2020). This potential loss depends the spread magnitude of Covid-19 outbreak, economics conditions due to government restrictions or passenger confidence.

As the air transport system smooths people mobility worldwide, the air transport is also a speed motor for diseases spread to different location. Due to Covid-19 outbreak spread the passenger confidence or government restrictions impacted directly in operations and demand for airlines worldwide.

The response from airlines to this pandemic is limitation the availability offer for air transport whenever is possible. However, even with this response as we could checked for the Brazilian case herein the operation efficiency of the airlines is not suitable in analysis with 2019 first quarter. These non-efficiency values are impacting directly the financial results and reflected the operation position for each company (i.e. aircraft models) and also government minimum offer definition. However, the cargo flights allowance on aircrafts configurated prior to passengers helped the companies to minimize the revenue loss and helped also the aircrafts better usage.

The MCDEA model provide efficiency analysis improvements as the DMUs on results could be better discriminated comparing to DEA classical models. The novel duality model on Formulation (5) extended the evaluation to obtain benchmarks better than prior dual studies.

The benchmarks verified during the highest demand in summer period, indicates to airlines to improve the politics and negotiate with authorities some alternatives to survive to unpredictable period. The possibility to transport cargo inside the cabin, which was authorized in Brazil during the outbreak, is way to increase the output RTK numbers.

Nevertheless, for the inputs we check that airlines with new aircrafts in their fleet tend to save fuel to perform the minimum flight required, as the passengers demand confidence is stronger. Moreover, the aircraft size impacts the occupation rate, in this case for development of future studies we suggest to include financial aspects in this analysis.