Shared Decision Making: From Decision Science to Data Science

Abstract

Background.

Accurate diagnosis of patients’ preferences is central to shared decision making. Missing from clinical practice is an approach that links pretreatment preferences and patient-reported outcomes.

Objective.

We propose a Bayesian collaborative filtering (CF) algorithm that combines pretreatment preferences and patient-reported outcomes to provide treatment recommendations.

Design.

We present the methodological details of a Bayesian CF algorithm designed to accomplish 3 tasks: 1) eliciting patient preferences using conjoint analysis surveys, 2) clustering patients into preference phenotypes, and 3) making treatment recommendations based on the posttreatment satisfaction of like-minded patients. We conduct a series of simulation studies to test the algorithm and to compare it to a 2-stage approach.

Results.

The Bayesian CF algorithm and 2-stage approaches performed similarly when there was extensive overlap between preference phenotypes. When the treatment was moderately associated with satisfaction, both methods made accurate recommendations. The kappa estimates measuring agreement between the true and predicted recommendations were 0.70 (95% confidence interval = 0.052–0.88) and 0.73 (0.56–0.90) under the Bayesian CF and 2-stage approaches, respectively. The 2-stage approach failed to converge in settings in which clusters were well separated, whereas the Bayesian CF algorithm produced acceptable results, with kappas of 0.73 (0.56–0.90) and 0.83 (0.69–0.97) for scenarios with moderate and large treatment effects, respectively.

Limitations.

Our approach assumes that the patient population is composed of distinct preference phenotypes, there is association between treatment and outcomes, and treatment effects vary across phenotypes. Findings are also limited to simulated data.

Conclusion.

The Bayesian CF algorithm is feasible, provides accurate cluster treatment recommendations, and outperforms 2-stage estimation when clusters are well separated. As such, the approach serves as a roadmap for incorporating predictive analytics into shared decision making.

In clinical settings with multiple treatment options, sharing treatment decisions is essential for optimal care.¹ This tailored approach increases patients’ medical knowledge, promotes treatment adherence, and improves overall satisfaction with care.^2–6 Nevertheless, health providers often make educated guesses regarding patients’ values rapidly and under stressful conditions. Likewise, for patients, it is often challenging to compare multiple treatment options and choose the one that best aligns with their values.

A fundamental aspect of shared medical decision making is the diagnosis of patients’ preferences.^7,8 Preference diagnosis requires an understanding of how patients weigh the risks and benefits associated with treatments and uses this information to arrive at an appropriate treatment decision. A key challenge in diagnosing patient preferences is to accurately measure preferences in a way that does not burden patients and, at the same time, improves patient-reported outcomes, such as treatment satisfaction and quality of life. One promising machine-learning approach is to first divide (or “segment”) a large population into meaningful preference groups comprising patients with shared values. Segmentation underscores the variability in patients’ values while identifying subgroups with clinically important differences in values.⁸ Moreover, if these subgroups can be accurately defined, the treatment experience of one member can be used to recommend treatments for other members in the same group. This approach, commonly referred to as collaborative filtering (CF),⁹ has been widely used in online marketing to make product recommendations for new consumers based on the experiences of like-minded consumers.¹⁰

Recently, segmentation has been applied to medical decision making, which Fraenkel and colleagues⁸ refer to as “preference phenotyping.” However, even when appropriately performed, preference phenotyping alone may not be enough to improve shared decision making. Most notably, the current use of preference phenotyping to inform medical decisions does not account for the potential change in values that patients experience as they undergo illness and its treatment. Therefore, pretreatment preferences—if precisely diagnosed—might identify the optimal pretreatment decision, but they might not align with posttreatment satisfaction and overall experience with care.

In this article, we discuss a data science approach to shared decision making in which pretreatment preference phenotyping is coupled with posttreatment satisfaction to inform medical decisions. Specifically, we propose a data-driven approach that accomplishes 3 tasks: 1) eliciting patient preferences in a way that minimizes the burden to patients, 2) clustering patients into well-defined preference phenotypes using relevant demographic and clinical information, and 3) making evidence-based treatment recommendations for a novel set of patients based on the posttreatment satisfaction of patients with shared phenotypes. The last 2 tasks are performed iteratively as part of unified Bayesian algorithm. We illustrate the approach in the context of anticoagulant therapies following hip and knee replacement surgery. We also conduct simulation studies to illustrate the method and its feasibility and features and to compare it to a conventional 2-stage estimation approach.^11–13

Method

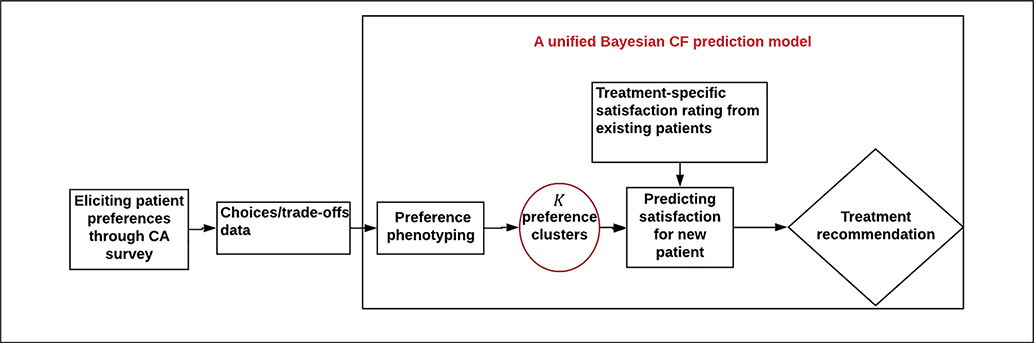
Overview: CF Algorithm for Shared Medical Decision Making

Our proposal can be broadly construed as a CF algorithm, a process by which information from a shared community is used to make evidence-based recommendations for like-minded users.¹⁰ CF is a type of online “recommender system” by which known preferences of an existing group of individuals are used to recommend products for a new group with shared values.¹⁰ Perhaps the most recognizable industry example of CF is Netflix, which uses consumers’ viewing history to identify individuals with similar tastes and preferences. The site then makes recommendations for new content based on the experiences of similar users. Thus, CF is a natural self-learning system: with every use, the system updates its information about the population, resulting in more precise recommendations.

Recently, CF has been proposed for use in medical settings to help select educational materials and to recommend future orders for hospitalized patients.¹⁴ However, this method has not been used to generate recommendations for treatments from similar patients’ experiences, primarily because traditional consumer-based preference models rely on extensive purchasing and rating histories to accurately characterize consumer preferences. In health care settings, however, there is often only a 1-time treatment decision, and repeated experiences with different treatments are not available. Consequently, for CF to work in health care settings, we first need to collect patient preference data in a reliable way. We accomplish this using a survey methodology known as conjoint analysis (CA).

CA for Eliciting Patient Preferences

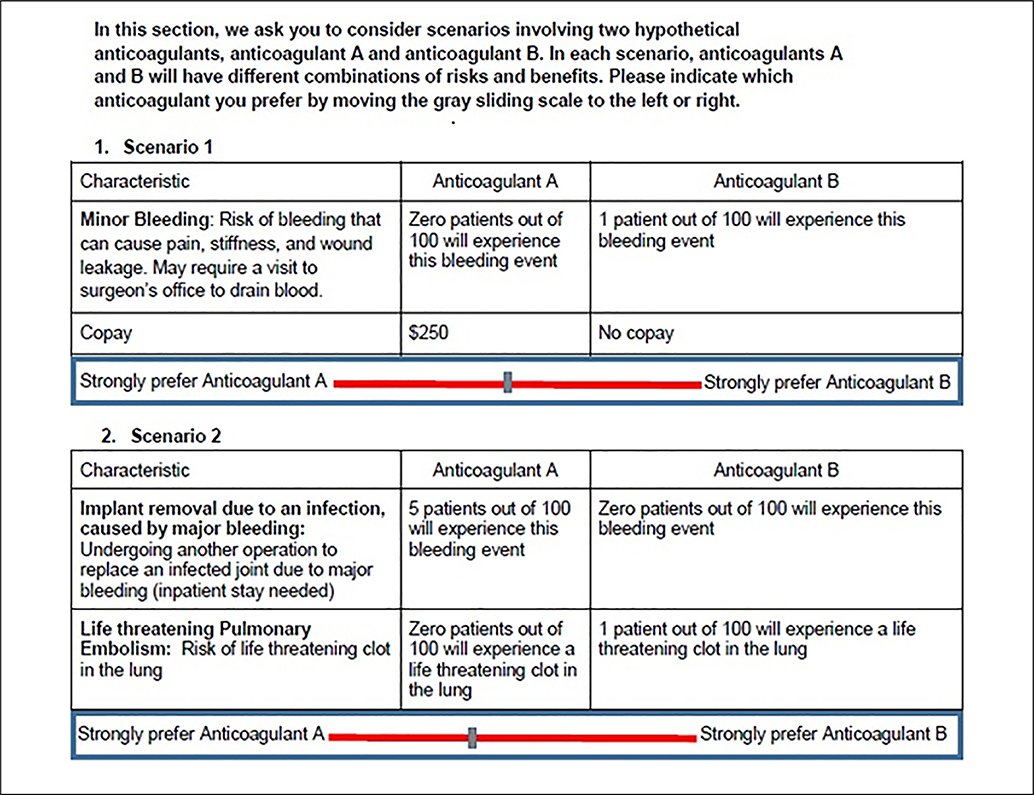
As illustrated by the left-most box of Figure 1, the proposed approach begins by eliciting patient pretreatment preferences through a CA survey exercise. Originally developed to assess consumer preferences, CA evaluates tradeoffs between hypothetical treatments to determine which treatment features patients most prefer.¹⁵ In the conjoint exercise, the analyst designs a set of hypothetical situations based on a limited number of relevant treatment attributes (e.g., risk of side effects, cost, etc.). Respondents then rate, rank, or choose treatments in each scenario, indicating their relative preference of each treatment. Answers to the responses are subsequently used to quantify how patients value specific treatment attributes. Different CA designs have been proposed to capture individuals’ values.¹⁵ A popular choice is the numeric scale, pairwise design,^16,17 whereby patients rate 2 competing treatments on a continuous numeric scale from, say, −10 to 10, with −10 representing strong preference for treatment A and 10 representing strong preference for treatment B. Numeric scales provide more information than binary (prefer A v. prefer B) responses and hence allow for more precise measurement of patient preferences. For example, patients may tend to prefer more costly treatments with fewer side effects. However, the degree of preference might vary, with some patients narrowly preferring treatments with increased costs and fewer side effects and others strongly preferring such treatments. Numeric scales allow investigators to differentiate the degree of preference in such cases.

Figure 1.

Conceptual framework for a collaborative filtering system for medical decision making.

Figure 2 presents a hypothetical pairwise conjoint exercise in the context of anticoagulant treatment following hip and knee replacement. The figure includes 2 excerpts from a 10-scenario, pairwise survey originally developed in consultation with investigators from an ongoing anticoagulant trial. Orthopedic patients undergoing elective hip or knee surgery are recommended to take anticoagulant medication for at least 7 days following surgery to prevent life-threatening blood clots. Orthopedic surgeons typically opt for 1 of 3 anticoagulants: aspirin, warfarin, or rivaroxaban. The ideal choice will balance, among other things, the risk of fatal pulmonary embolism with the risk of excessive bleeding leading to secondary infection and follow-up surgery. In scenario 1, anticoagulant A is associated with no risk of bleeding following surgery but has a copay of $250, whereas anticoagulant B is associated with a 1% risk of bleeding with no copay. In scenario 2, anticoagulant A is associated with a 5% risk of major infection but no risk of pulmonary embolism, while anticoagulant B carries no risk of infection but a 1% risk of a pulmonary embolism. Patients indicate their preference by sliding the cursor at the bottom of Figure 2 either to the left, indicating a preference for treatment A, or to the right, indicating a preference for treatment B. This simple example illustrates a clinical setting in which patient preferences play a critical role in achieving an evidence-based shared treatment decision. In fact, anticoagulants provide a classic example in which CA surveys have been commonly used to report patient preferences.¹⁸ More broadly, CA has the potential for use in a wide array of clinical applications, including cancer therapies,¹⁹ reproductive health,²⁰ and quality-of-life assessments.²¹

Figure 2.

Example of a pairwise conjoint analysis survey applied to anticoagulant therapy.

Bayesian CF

Once the preference data have been collected, a Bayesian CF model is used to quantify patient preferences, cluster patients into distinct subpopulations defined by shared preferences, and make evidence-based treatment recommendations in consultation with health care providers. These “preference clusters,” or “preference phenotypes,” represent patient subgroups with shared values based on data from the CA survey. For example, one cluster might represent patients who prefer treatments with lower risks of pulmonary embolism even if they increase the risk of bleeding and have higher costs. In contrast, patients in a second cluster might be willing to tolerate higher risks of blood clots if treatments are less costly and result in fewer bleeding complications.

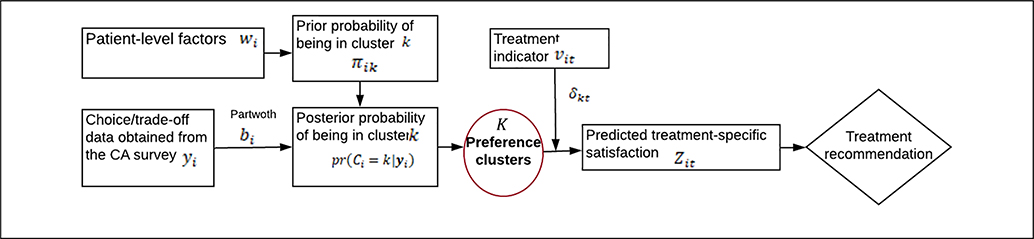
As illustrated in Figure 3, the model first assigns patients to preference clusters as part of an iterative computational algorithm known as Markov chain Monte Carlo (MCMC).²² In practice, the number of clusters, K, is derived from the data using Bayesian information criteria,²³ specially designed computational algorithms,²⁴ or advanced Bayesian nonparametric clustering methods.²⁵ Next, for patients within cluster k(k = 1, … , K), the model quantifies how patients value various aspects of treatment (cost, side effects, etc.). These relative values are commonly referred to as “partworths,” that is, the part of patients’ total value that they ascribe to specific attributes. The partworths for patient i are denoted by the numeric-valued vector b_i in Figure 3. If a patient’s partworth for attribute j is equal to 0, then the patient assigns “average” importance to the attribute; if the partworth is greater than 0, the patient assigns more importance to the attribute than does an average patient in cluster k; and if the partworth is less than 0, the patient assigns below-average importance. We typically assume that the partworths follow a multivariate normal distribution characterized by a cluster-specific mean and variance, although this assumption can be relaxed if needed. This flexibility represents a key advantage of the proposed method compared with existing “black-box” software packages that offer only a limited number of modeling options.

Figure 3.

The unified Bayesian collaborative filtering algorithm to predict satisfaction and make treatment recommendations.

Because the preference clusters are not explicitly observed but are instead latent variables in the model, we can only estimate the probability that patient i belongs to cluster k, denoted in Figure 3 by the parameter π_ik. The cluster-membership probabilities can subsequently be used to make decision rules for allocating patients to a particular cluster. For instance, we might assign patients to their most likely cluster based on the cluster probabilities. In practice, it is reasonable to assume that these cluster membership probabilities vary as a function of patient, clinical, and system-level covariates, such as age, type of provider, and comorbidity burden, which are denoted by w_i in Figure 3. For example, older patients or patients with elevated comorbidity might have a higher probability of being assigned to a “risk-averse” cluster than younger patients with fewer comorbid complications. These covariates are incorporated into the model by introducing for each patient a latent cluster indicator variable, C_i, such that C_i = k (patient i belongs to cluster k) with probability π_ik. We then link the cluster probabilities π_ik to w_i using a multinomial logit model. The online supplement provides a formal mathematical description of the models used in the simulation study below.

At each iteration of the MCMC algorithm, the model assigns each patient to one of the K clusters. Once these cluster allocations have been made, the next step is to make treatment recommendations. This step is illustrated in the right-most diamond of Figure 1. The goal is to use the satisfaction data for existing patients within cluster k to predict the missing satisfaction data for new patients in the cluster. We then recommend the treatment associated with the highest satisfaction level. Details of the recommendation phase are illustrated in the right-most section of Figure 3. At each iteration of the MCMC algorithm, patient i’s satisfaction with treatment t, denoted Z_it, is determined by the patient’s current cluster allocation, C_i = k, and the strength of the treatment effects for that cluster. For each treatment t, the treatment regression coefficient, δ_kt, can be estimated in a number of ways. A straightforward supervised learning approach is to fit a regression model of the form

$$Z_{it}={\mathrm{\delta }}_{k1}+\sum _{t=2}^T{\delta }_{kt}{v}_{it}+{ϵ}_{it},$$

where δ_k1 is an intercept term corresponding to the “reference” treatment (treatment 1 in this case), v_it is a binary indicator taking the value 1 if patient i receives treatment t(t = 2, … T), and ε_it is a normally distributed error term. At each MCMC cycle, we obtain posterior estimates ${\widehat{\mathrm{\delta }}}_{kt}$ using the data for existing patients in cluster k. Next, for a new patient i′ in cluster k, we use the expression ${\widehat{\mathrm{\delta }}}_{k1}+\sum _{t=2}^T{\widehat{\delta }}_{kt}{v}_{i^{\prime }t}$ to predict the satisfaction scores, ${\widehat{Z}}_{i^{\prime }t}$, under each treatment. We then recommend the treatment with the highest ${\widehat{Z}}_{i^{\prime }t}$ value. Over the course of the MCMC algorithm, the value of ${\widehat{Z}}_{i^{\prime }t}$ will vary, as will the recommended treatment. As a final recommendation, we select the treatment that occurs most often during the MCMC algorithm. The degree of confidence in recommending treatment t is captured by the proportion of iterations in which t is selected as the preferred treatment. For a given patient, if treatment t is sampled frequently during the MCMC procedure, we have high confidence in recommending treatment t for that patient. Conversely, if all treatments are sampled with the same frequency, we have little confidence in recommending any one treatment. Of note, the preference clustering, partworth estimation, satisfaction prediction, and treatment recommendation are performed iteratively as part of a unified computational algorithm; thus, the uncertainty associated with each step is incorporated into the entire recommendation process.

Simulation Study

To examine features of the approach in a controlled setting, we undertook a simulation study that paralleled the anticoagulant study described above. Specifically, we assumed 3 anticoagulant treatments characterized by 6 attributes: the risk of pulmonary embolism (PE), the risk of deep vein thrombosis (DVT), the risk of a major bleeding event, the risk of a minor bleeding event, copay, and the requirement of a routine international normalized ratio test (a simple blood test to monitor the anticoagulant level throughout the treatment uptake period). Table 1 describes the attributes and levels in detail. The first 4 attributes have 3 levels corresponding to an increased risk of occurrence, and the last 2 attributes have 2 levels representing whether the attribute was present or not.

Table 1.

Attributes and Levels Used to Generate the Conjoint Responses in the Simulation Study

Attribute	Level 1	Level 2	Level 3
Risk of pulmonary embolism	No risk	1%	2%
Risk of deep vein thrombosis	No risk	5%	10%
Risk of minor bleeding	No risk	5%	10%
Risk of major bleeding	No risk	2%	5%
Copay	No copay	$200
Routine international normalized ratio test	Not required	Required

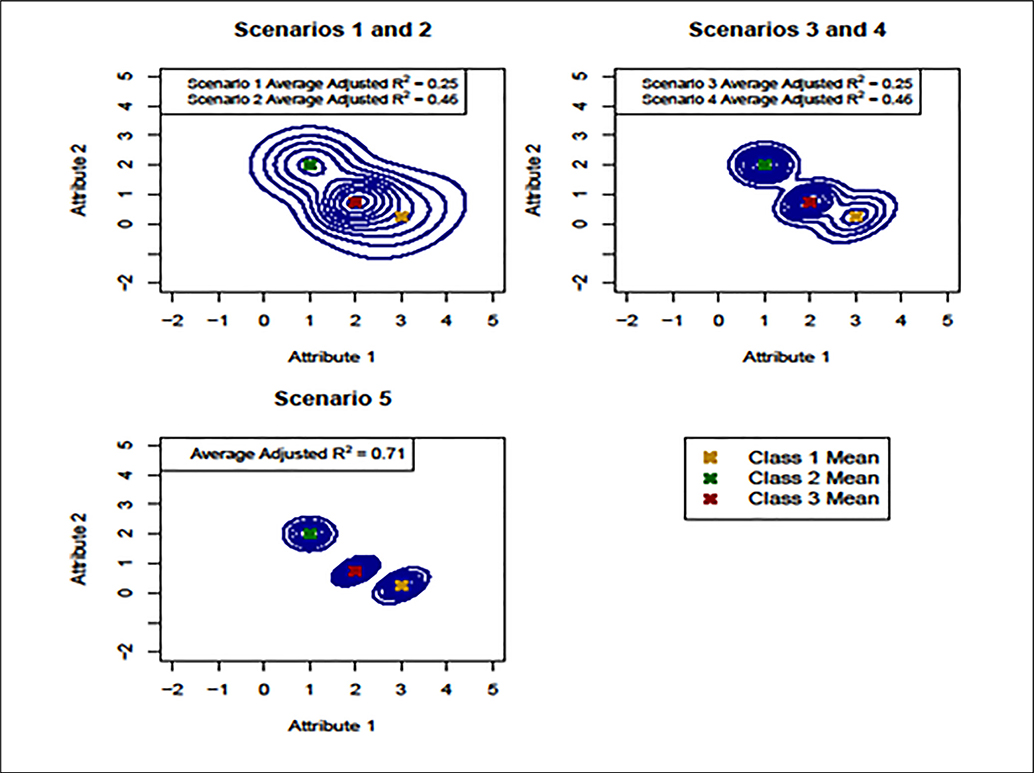
Given this basic design, we simulated conjoint responses and satisfaction data for 500 patients under 5 scenarios likely to arise in practice. The preference partworths were generated from a multivariate normal mixture model with 3 clusters. We chose 3 clusters based on previous studies identifying a small number of preference phenotypes in the context of anticoagulant therapy.⁸ For illustrative purposes, we assumed here a fixed number of clusters, but in general, one would leave this unspecified and allow the data to determine the optimal number of clusters using one of the approaches described above. Conditional on the partworths, the conjoint responses were assumed to follow a normal distribution on a sliding numeric scale, as described in Figure 2. Finally, satisfaction scores for each patient were generated according to equation 1. Figure 4 presents contour plots of the partworth distribution for the first 2 attributes (PE and DVT) under each scenario. Adjusted R² values measuring the association between treatment and satisfaction are given in the legends. For each scenario, we assumed that patients in cluster 1 were most satisfied with treatment 1, those in cluster 2 were most satisfied with treatment 2, and that those in cluster 3 were most satisfied with treatment 3. Because the accuracy of the recommendations depends in part on the association between treatment and satisfaction within each cluster, we varied the adjusted R² values across scenarios to accommodate different strengths of association.

Figure 4.

Partworth contour plots for the first 2 attributes—pulmonary embolism (PE) and deep vein thrombosis (DVT)—in each scenario. The upper left panel corresponds to homogenous clusters and average adjusted R² values of 0.25 (scenario 1) and 0.46 (scenario 2). The upper right panel corresponds to more heterogeneous clusters and average adjusted R² values of 0.25 (scenario 3) and 0.46 (scenario 4). Scenario 5 (lower left) corresponds to well-defined clusters and an average adjusted R² of 0.71.

As shown in the upper left panel of Figure 4, scenarios 1 and 2 corresponded to low between-cluster heterogeneity, resulting in poorly defined preference clusters. For scenario 1, we assumed an adjusted R² of 0.25 on average across clusters. Details regarding the R² values for each cluster and scenario are provided in online Supplementary Table S1. Scenario 2 maintained the same level of cluster heterogeneity but increased the average adjusted R² to 0.46, implying that more of the uncertainty in the recommendation process was due to incorrect cluster assignments. For scenarios 3 and 4 (upper right panel of Figure 4), we simulated data with increased between-cluster heterogeneity and average adjusted R² values of 0.25 and 0.46, respectively. This resulted in more well-defined clusters, particularly for cluster 2, which is pulled away from the other clusters in the upper right panel of Figure 4. Finally, scenario 5 corresponded to distinct clusters with an average adjusted R² of 0.71, implying a stronger association between treatment and satisfaction (lower left panel of Figure 4). For each scenario, we modeled the cluster probabilities π_ik as a function of 3 simulated patient-level covariates.

To determine how well our method predicted satisfaction (and corresponding recommendations) for new patients, we withheld satisfaction data for 50 patients (10% of the sample) when fitting the model. We then used our model to predict the missing satisfaction scores and to make subsequent treatment recommendations for this holdout sample. To evaluate the performance of the method, we compared true and predicted cluster assignments, as well as true and predicted recommendations for the 50 “new” patients in the holdout sample. We used unweighted kappa statistics to indicate the level of agreement between the true and the estimated values. To implement the model, we ran an MCMC algorithm for 2500 iterations, discarding the first 500 iterations as a “burn-in” period to ensure convergence. We assumed noninformative conjugate priors for all model parameters. Finally, we compared our model to a conventional 2-stage approach in which the partworths are first estimated via a generalized linear mixed model that ignores clustering.^11–13 Then, in stage 2, k-means was used to identify preference clusters, and the mean satisfaction scores within each cluster were used to make treatment recommendations. We conducted the simulation using R code²⁶ developed by the second author, which is available as supplementary material accompanying this article.

Results

Tables 2 and 3 show a cross-tabulation of the true and predicted cluster allocations for the Bayesian CF algorithm (Table 2) and the 2-stage approach (Table 3). For each method, the results are identical for scenarios 1 and 2 because they assume the same level of cluster heterogeneity. For both scenarios, 94% of the 500 patients were correctly clustered under the proposed method (Table 2), and 95% were correctly clustered under the 2-stage approach (Table 3). The corresponding kappa estimates were 0.91 (95% confidence interval [CI]: [0.88–0.94]) and 0.92 (95% CI: [0.89–0.95]), respectively. Thus, for both approaches, there was strong agreement between the true and predicted cluster assignments, even in this setting where the patient population was relatively homogeneous with respect to its underlying preferences (i.e., attribute partworths).

Table 2.

Cross-Tabulation of True and Predicted Cluster Allocations for the Bayesian Collaborative Filtering Algorithm under Each Scenario (N = 500 Patients per Scenario)

Scenarioa		True Class 1	True Class 2	True Class 3	Kappa (95% CI)
Scenarios 1 and 2	Predicted class 1	122	4	7	0.91 (0.88–0.94)
	Predicted class 2	4	214	0
	Predicted class 3	10	3	136
Scenarios 3 and 4	Predicted class 1	134	0	4	0.98 (0.97–0.99)
	Predicted class 2	0	221	0
	Predicted class 3	2	0	139
Scenario 5	Predicted class 1	135	0	1	>0.99 (0.99–1.0)
	Predicted class 2	0	221	0
	Predicted class 3	1	0	142

^aScenarios 1 and 2 correspond to high within-cluster heterogeneity and low between-cluster heterogeneity, resulting in poorly defined clusters. Scenarios 3 to 5 correspond to lower within-cluster heterogeneity and increased between-cluster heterogeneity, leading to more well-defined clusters. Average adjusted R² across clusters is 0.25 for scenarios 1 and 3, 0.46 for scenarios 2 and 4, and 0.71 for scenario 5.

Table 3.

Cross-Tabulation of True and Predicted Cluster Allocations for the 2-Stage Approach under Each Scenario (N = 500 Patients per Scenario)

Scenarioa		True Class 1	True Class 2	True Class 3	Kappa (95% CI)
Scenarios 1 and 2	Predicted class 1	117	2	3	0.92 (0.89–0.95)
	Predicted class 2	4	218	0
	Predicted class 3	15	1	140
Scenarios 3–5	Did not converge

^aScenarios 1 and 2 correspond to high within-cluster heterogeneity and low between-cluster heterogeneity, resulting in poorly defined clusters. Scenarios 3 to 5 correspond to lower within-cluster heterogeneity and increased between-cluster heterogeneity, leading to more well-defined clusters. Average adjusted R² across clusters is 0.25 for scenarios 1 and 3, 0.46 for scenarios 2 and 4, and 0.71 for scenario 5.

Scenarios 3 to 5 increased the between-cluster heterogeneity, leading to more well-defined clusters. Of note, the 2-stage approach failed to converge for these scenarios, as it assumes a single population (albeit with heterogeneity across patients) when estimating the partworths in stage 1 of the procedure. When this assumption is violated, the generalized linear mixed model used in stage 1 fails to converge. In contrast, the proposed method provided accurate cluster allocations in all cases. For scenarios 3 and 4, 99% of the patients were correctly classified in each case, with a corresponding kappa estimate of 0.98 (95% CI: [0.97–0.99]). Scenario 5 increased the separation between clusters even further, leading to almost perfect clustering and a kappa exceeding 0.99.

Tables 4 and 5 present cross-tabulations of the true and predicted treatment recommendations for the Bayesian CF algorithm (Table 4) and the 2-stage procedure (Table 5). In scenario 1, 52% of the patients received correct recommendations under the Bayesian CF model (kappa = 0.25 [0.03–0.44]), compared with 54% under the 2-stage approach (kappa = 0.28 [0.07–0.48]), indicating the 2 methods performed similarly when the population was relatively homogenous and the treatments were weakly associated with patient satisfaction. For both methods, the level of agreement exceeded the 33% expected by chance under random recommendation assignment. Although these kappa estimates indicate “fair” agreement according to the scale proposed by Landis and Koch,²⁷ their modest values are not surprising given the poorly defined clusters and moderate adjusted R² values under this scenario.

Table 4.

Cross-Tabulation of True and Predicted Recommendations for the Bayesian Collaborative Filtering Algorithm under Each Scenario for 50 Holdout Patients^a

			True Recommendation
			Treatment 1	Treatment 2	Treatment 3	Kappa (95% CI)
Predicted recommendation	Scenario 1	Treatment 1	4	6	2	0.25 (0.03–0.44)
		Treatment 2	2	15	9
		Treatment 3	4	1	7
	Scenario 2	Treatment 1	8	4	0	0.70 (0.52–0.88)
		Treatment 2	1	23	2
		Treatment 3	1	1	10
	Scenario 3	Treatment 1	4	6	2	0.28 (0.07–0.48)
		Treatment 2	2	16	9
		Treatment 3	4	0	7
	Scenario 4	Treatment 1	8	4	0	0.73 (0.56–0.90)
		Treatment 2	1	24	2
		Treatment 3	1	0	10
	Scenario 5	Treatment 1	9	3	0	0.83 (0.69–0.97)
		Treatment 2	0	26	1
		Treatment 3	1	0	10

^aScenarios 1 and 2 correspond to high within-cluster heterogeneity and low between-cluster heterogeneity, resulting in poorly defined clusters. Scenarios 3 to 5 correspond to lower within-cluster heterogeneity and increased between cluster heterogeneity, leading to more well-defined clusters. Average adjusted R² across clusters is 0.25 for scenarios 1 and 3, 0.46 for scenarios 2 and 4, and 0.71 for scenario 5.

Table 5.

Cross-Tabulation of True and Predicted Recommendations for the 2-Stage Approach under Each Scenario for 50 Holdout Patients^a

			True Recommendation
			Treatment 1	Treatment 2	Treatment 3	Kappa (95% CI)
Predicted recommendation	Scenario 1	Treatment 1	4	6	2	0.28 (0.07–0.48)
		Treatment 2	2	16	9
		Treatment 3	4	0	7
	Scenario 2	Treatment 1	8	4	0	0.73 (0.56–0.90)
		Treatment 2	1	24	2
		Treatment 3	1	0	10
	Scenarios 3–5	Did not converge

^aScenarios 1 and 2 correspond to high within-cluster heterogeneity and low between-cluster heterogeneity, resulting in poorly defined clusters. Scenarios 3 to 5 correspond to lower within-cluster heterogeneity and increased between cluster heterogeneity, leading to more well-defined clusters. Average adjusted R² across clusters is 0.25 for scenarios 1 and 3, 0.46 for scenarios 2 and 4, and 0.71 for scenario 5.

Scenario 2 increased the average adjusted R² across clusters to 0.46, indicating a stronger association between treatment and satisfaction. Here, 82% and 84% of the holdout sample received the correct recommendation under the Bayesian CF and 2-stage approaches, respectively, with corresponding kappa estimates of 0.70 (95% CI: [0.52–0.88]) and 0.73 (95% CI: [0.56–0.90]). As noted above, the 2-stage analysis failed to converge for scenarios 3 to 5. The Bayesian CF model, on the other hand, produced kappa estimates of 0.28 (95% CI: [0.07–0.48]) and 0.73 (95% CI: [0.56–0.90]) under scenarios 3 and 4, respectively. These estimates are similar to those from scenarios 1 and 2, which is not surprising because the 2 sets of scenarios differ only in terms of the separation between clusters. Because scenarios 1 and 2 already provide accurate cluster allocations, there is only slight improvement in the cluster assignments in scenarios 3 and 4, and hence, the recommendation results are similar across the 2 pairs of scenarios.

Scenario 5 increased the average adjusted R² even further to 0.71, leading to 90% accuracy in recommendations under the proposed method, with a kappa of 0.83 (95% CI: [0.69–0.97]). Thus, as the clusters become more defined and the within-cluster treatment effects increase, the proposed method provides correct recommendations for the vast majority of patients.

Discussion

Implications for Clinical Processes and Shared Decision Making

Shared decision making brings patient preferences into care settings when deliberation between patient and provider is required.²⁸ In this context, we have described a Bayesian CF approach that clusters patients into preference phenotypes as a tool to assist with shared decision making. We first described how CA can be used to elicit patient preferences in medical settings. We then outlined a Bayesian machine-learning approach that combines elements of unsupervised learning (in the form of preference clustering) and supervised learning (in the form of satisfaction prediction) to identify preference phenotypes, estimate partworths, predict satisfaction, and recommend appropriate treatments as part of an iterative MCMC computational algorithm. Results from our simulation studies suggest that the method is feasible and provides accurate recovery of the true treatment recommendations when there are distinct preference phenotypes in the population and treatments are well aligned with patient-reported outcomes such as satisfaction. Of these 2 conditions, our simulations suggest that the alignment between treatment and satisfaction is the most critical to the recommendation process, as the model accurately identified clusters even when the patient population was relatively homogeneous. We compared the approach to a 2-stage estimation method, in which the preference partworths were first estimated assuming a homogeneous population, and then ad hoc clustering algorithms such as k-means were used to cluster patients and predict satisfaction. The 2 approaches performed comparably when the preference phenotypes overlapped substantially. When the phenotypes were distinct, however, the 2-stage approach broke down because of its reliance on a homogeneous population when fitting the generalized linear mixed model in stage 1. Thus, in practice, investigators might first try the 2-stage approach, and if that fails to converge due to cluster separation, they might then move to the proposed Bayesian integrated approach.

More generally, the methods developed here raise the possibility of new types of decision support for patients in clinical environments. Under the proposed data-driven approach, the clinician’s role shifts from full elicitation of values, followed by deliberation on choices, to confirmation and communication of evidence obtained through the proposed model. For example, a provider might confirm results suggesting that a patient belongs to a phenotype that prefers convenience of medication over low risks of adverse effects. This phenotype might, in turn, be more satisfied with a certain therapy (e.g., rivaroxaban) than with other therapies (e.g., warfarin). After confirmation of a preferred treatment, decision support methods such as alerts might be used to help ensure patients receive the treatment that is most consistent with their preferences.²⁹ The goal is not to replace the essential communication and deliberation process between patients and their providers but to systematically support this process by providing analytic tools to predict which treatment most likely aligns with patients’ preferences.

Is such an approach feasible in practice? The above sections suggest that the approach rests on a sound theoretical foundation and is validated by simulation studies. Further, Lenert and Soetikno³⁰ have shown that collecting large numbers of preference measurements and outcomes at a community level is possible and could drive systems of care based on data rather than decision analysis. Ultimately, one could envision automating the process and incorporating relevant CA surveys into Web-based applications such as patient portals or other online devices, so that patients could complete the conjoint survey prior to their clinic visit, upload their data into the CF algorithm in real time, and then review the results and recommendations with clinicians during the visit. While we are at the beginning of such a path, our findings provide promising evidence that a data-driven approach to shared decision making is not only desirable but also attainable in the near future.

Limitations

There are several limitations to this work. To date, we have applied the method only to simulated data. A case study using clinical data is forthcoming upon completion of an ongoing clinical trial. Although we attempted to make the simulation as realistic as possible, it is not feasible to simulate the full complexity of a real-world application. Moreover, for illustrative purposes, we assumed a fixed number of clusters in our simulation; future work might instead apply data-driven approaches to estimate the number of clusters. Finally, our approach is specifically designed for cases in which there are well-defined preference phenotypes, there is an observable association between treatment and outcomes, and the treatment effect varies across phenotypes. When these assumptions are not met, the method is not appropriate. For example, patient preferences elicited prior to treatments may not be consistent with a model-based treatment recommendation because of other stated preferences discovered in the shared decision making process. In addition, treatments may not align with satisfaction (e.g., none of the treatments are appealing). However, this may not be a shortcoming in the performance of the method per se but rather a limitation to the scope of its applicability. For example, if treatments are not predictive of posttreatment satisfaction, then patients and providers might wish to rely on other approaches to shared decision making. Finally, for illustrative purposes, we used simple linear regression to predict patient satisfaction. Future work might consider more advanced machine-learning approaches, such as tree-based methods or neural networks, to improve recommendation accuracy when effect sizes are limited.

Conclusion

Data science offers new approaches to the problem of diagnosing patients’ preferences for health outcomes. By linking preference models empirically to measurements of satisfaction and other patient-reported outcomes, we can create evidence-based recommender systems to identify appropriate treatments for patients in a wide array of clinical settings. The proposed Bayesian CF algorithm provides a starting point for incorporating predictive analytics into shared decision making, paving the way for data-driven tools to be used alongside other decision aids in the context of shared decision making.