Increased Dissociation of Adamantanamines in Influenza A M2 S31N with Partial Block by Rimantadine

Abstract

The ubiquitous mutation from serine (WT) to asparagine at residue 31 (S31N) in the influenza A M2 channel renders it insensitive to amantadine (AMT) and rimantadine (RMT) block, but it is unknown whether the inhibition results from weak binding or incomplete block. Two-electrode voltage clamp (TEVC) of transfected Xenopus oocytes revealed that the M2 S31N channel is essentially fully blocked by AMT at 10 mM, demonstrating that, albeit weak, AMT binding in a channel results in complete block of its proton current. In contrast, RMT achieves only a modest degree of block in the M2 S31N channel at 1 mM, with very little increase in block at 10 mM, indicating that the RMT binding site in the channel saturates with only modest block. From exponential curve fits to families of proton current wash-in and wash-out traces, the association rate constant (k₁) is somewhat decreased for both AMT and RMT in the S31N, but the dissociation rate constant (k₂) is dramatically increased compared with WT. The potentials of mean force (PMF) from adaptive biasing force (ABF) molecular dynamics simulations predict that rate constants should be exquisitely sensitive to the charge state of the His37 selectivity filter of M2. With one exception out of eight cases, predictions from the simulations with one and three charged side chains bracket the experimental rate constants, as expected for the acidic bath used in the TEVC assay. From simulations, the weak binding can be accounted for by changes in the potentials of mean force, but the partial block by RMT remains unexplained.

Significance

The influenza A M2 channel is insensitive to AMT and RMT block because of the mutation of serine to asparagine at residue 31. The change in M2-AMT or M2-RMT interactions in the mutant channel has not been thoroughly studied. It is unclear whether the insensitivity is from weak binding or incomplete block. The results presented here demonstrate that the mutation reduces binding for both, but when bound, AMT completely inhibits proton flow, whereas RMT only inhibits 25%. This observation has significant implications for novel M2 blockers and should be considered during new drug design and development.

Introduction

The influenza A M2 channel is a proton channel responsible for the acidification of the viral interior required for effective release of the viral RNA into the host cytoplasm. The influenza virus is taken up by endocytosis. The M2 channel is activated when the pH drops in the late-stage endosome. There are four His37 side chains in the hometetrameric M2 channel. It is believed that three of the imidazoles need to be protonated before M2 is activated (1), and studies have investigated the pKa-values for the M2 His37 protonation states (2). The late-stage endosome reaches a pH low enough to protonate the three imidazoles required for M2 activation. Once activated, the His37 complex transports protons through one of two proposed models: the gating model (3, 4, 5) or the shuttle model (6,7). This acid activation is ideal for using the two-electrode voltage-clamp (TEVC) electrophysiology method to study the M2 channel.

The M2 channel has been demonstrated to be a feasible target for organic compounds, including amantadine (AMT) and rimantadine (RMT) (Fig. 1). However, a mutation at residue 31 from serine to asparagine caused the M2 channel to become insensitive to AMT and RMT block. It is not well understood why this mutation caused the insensitivity. One important question that needs to be answered is whether there is AMT or RMT binding without block or whether the mutation reduces the binding rate constants of AMT and RMT.

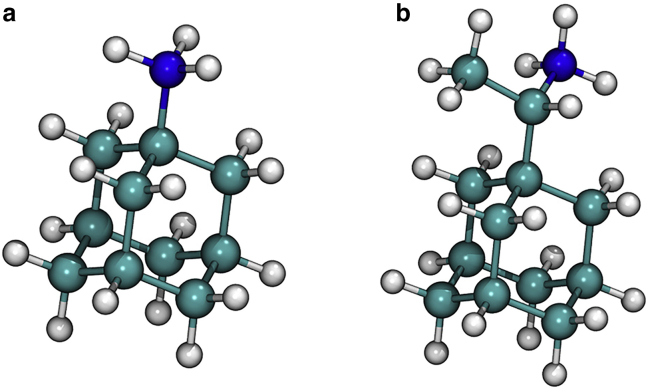
Figure 1.

AMT⁺ (a) and RMT⁺ (b) structures.

Previous estimates of association (k₁) and dissociation (k₂) rate constants for AMT binding in WT M2 were based on curve fitting of the wash-in and wash-out trace at a selected bath drug concentration with data collected using TEVC (8). They estimated k₁ to be 900 M⁻¹ s⁻¹ and k₂ to be 3 × 10⁻⁴ s⁻¹.

Here, we use the same method but extended it to a family of traces at different drug concentrations to evaluate the kinetics of AMT or RMT binding to WT or M2 S31N. From these traces, a global nonlinear least-squares curve fit kinetic model, with one drug binding site having a variable degree of current block when occupied, was used to obtain k₁ and k₂ rate constants. Rate constants for AMT or RMT binding to WT or M2 S31N are compared. Most notably, k₂-values are dramatically increased in the M2 S31N, and there, RMT binds with minimal block of proton transport.

Adaptive biasing force (ABF) molecular dynamics simulations (9) were used along lines similar to those previously implemented (10) to elucidate AMT or RMT binding to M2 S31N. Potential of mean force (PMF) plots are used to show free energy differences between AMT⁺ or RMT⁺ binding to WT or M2 S31N for three M2 His37 tetrad charge states: neutral, +1, and +3. From the PMFs, k₂ is estimated based on an expression from Kramers’ theory for diffusion over a barrier, and k₁ is based on an adaptation of Arrhenius theory with an estimated diffusion-limited reaction rate constant as a prefactor. The selectivity filter charge is exquisitely impactful on the rate constants, probably because of electrostatic repulsion between the selectivity filter and the cationic drug. We report the sensitivity of these rate constant predictions to the drug type, channel type, and selectivity filter charge, identifying the probable selectivity filter charge as near +1 for the WT but as yet indeterminate for the M2 S31N.

Materials and Methods

A/Udorn/72 H3N2 M2 S31N mRNA synthesis

The A/Udorn/72 H3N2 plasmid, a gift from Dr. Larry Pinto, and its homolog with S31N produced by site-directed mutagenesis in the Busath laboratory, were transformed into chemically competent Escherichia coli by standard methods. The plasmid was harvested using the Zymo Miniprep Kit (Zymo Research, Irvine, CA). To confirm that no mutations were introduced, the M2 DNA segment was PCR amplified and Sanger sequenced (Fig. S1). After confirmation, the PCR product was transcribed using the mMESSAGE mMACHINE T7 Ultra Transcription Kit (Thermo Fisher Scientific, Waltham, MA) to prepare mRNA for oocyte injections.

Electrophysiology

Oocytes from Xenopus laevis (EcoCyte Bioscience, Austin, TX) were maintained in ND-96²⁺ (96 mM NaCl, 2 mM KCl, 1.8 mM CaCl₂, 1 mM MgCl₂, 2.5 mM sodium pyruvate, 5 mM HEPES-NaOH (pH 7.4)) solution at 17°C until injection of ∼40 ng of A/Udorn/72 H3N2 M2 or A/Udorn/72 H3N2 M2 S31N mRNA using a Nanoject II (Drummond Scientific, Broomall, PA). After injection, the oocytes were maintained at 4°C in ND96²⁺ (pH 7.4) until electrophysiological recording. 72 h after mRNA injection, whole-cell currents were recorded with a TECV apparatus at Vm = −20 mV, room temperature, in Barth’s solution (0.3 mM NaNO₃, 0.71 mM CaCl₂, 0.82 mM MgSO₄, 1.0 mM KCl, 2.4 mM NaHCO₃, 88 mM NaCl, 15.0 mM HEPES (pH 7.5)). Inward current was induced by perfusion with Barth’s (pH 5.3) (15.0 mM MES instead of 15.0 mM HEPES). The oocytes were then perfused by Barth’s (pH 5.3) with AMT or RMT hydrochloride at concentrations 10 μM, 100 μM, 500 μM, 1 mM, or 10 mM. A wash-out was done using Barth’s (pH 5.3) without drug. Current traces were obtained from each of three oocytes for each of the concentrations.

Noninjected oocytes were also tested with the same acid perfusion protocols and concentrations of drug to assess the possible native acid-activated channel and AMT- or RMT-induced leak current (LC) in the oocytes.

Global nonlinear least-squares curve fit

Because the Hill coefficient for AMT-WT binding has been assessed as 0.91 (8) and considering the shape of the channel lumen, analysis of AMT or RMT block for each channel type was done using the one-site binding model shown here:

$$\text{O}\underset{k_2}{\overset{k_1}{\rightleftarrows }}\text{C.}$$

The open state O is the unblocked M2 channel, in which proton conductance is unimpeded. The closed state C is the fully or partially blocked M2 proton current. The fractional leakage around the drug (i.e., the channel current with drug bound/channel current without drug bound) is denoted as f. For convenience in discussing the results, we will also refer to the fraction of proton current blocked by drug as 1-f.

It has been established (8) that Xenopus oocytes naturally have small amounts of acid-activated current without transfection. These native channels are not AMT sensitive and are immediately active upon acid exposure without observable time-dependent gating. Furthermore, the application of hydrophobic amine drugs, especially at high concentrations, could transport current across the cell membrane in parallel with channel currents. Because each cell varies in the amount of native acid-activated current (plus drug-mediated current), which from our control experiments varied between −5 and −20 nA (generally <2.5% of the total acid-activated M2 current), a preliminary global fit was done using Eq. 1, in which LC was allowed to vary in that range independently for each cell before normalizing the M2 current in wash-in and wash-out traces to range from 0 to 1.

In addition, for wash-in, the drug concentration near the channel mouth was treated as rising with time because of the diffusion of the drug in the bulk solution, measured to change around the egg rapidly (on the millisecond timescale), through the unstirred layer. Knowing the diffusion coefficient of the drug in bulk, it was possible to estimate the thickness of the unstirred layer, L, from the initial lag in current blocking by the drug. This is captured in Eq. 1 as a time dependence to the concentration of drug, [D](t), elucidated by Eq. 3. No similar phenomenon was observable in the wash-out trace, and the unstirred layer effect was considered negligible for them.

Finally, the data traces for the three cells were averaged pointwise, and Eqs. 1 and 2 were used simultaneously on all of the averaged, normalized wash-in (Eq. 1) and wash-out (Eq. 2) traces for the global Levenberg-Marquardt (11) curve fit with the electrophysiology data to obtain rate constants k₁ and k₂ and the leakage parameter f. In this final fit, LC was set to 0.

$$I_{washin}=(1-\text{LC})\times (\text{f}+(1-\text{f})\times \left(\left(1-\frac{{\text{k}}_2}{{\text{k}}_1\times \left[\text{D}\right]\left(\text{t}\right)+{\text{k}}_2}\right)\times {\text{e}}^{-\left({\text{k}}_1\times \left[\text{D}\right]\left(\text{t}\right)+{\text{k}}_2\right)\times \text{t}}+\left(\frac{{\text{k}}_2}{{\text{k}}_1\times \left[\text{D}\right]\left(\text{t}\right)+{\text{k}}_2}\right)\right)+\text{LC}$$ (1)

and

$$I_{washout}=\text{f}+\left(1-\text{f}\right)\times \left(1-\text{A}\times {\text{e}}^{-{\text{k}}_2\times \text{t}}\right).$$ (2)

A in Eq. 2 is the final probability of occupancy from the wash-in calculated during the global fit and incorporates the LC. [D](t) is bulk drug concentration, D is the diffusion coefficient of the drug in the unstirred layer outside of the channel entry, and L is the thickness of the unstirred layer which was assumed to fill as a slab in contact with the bulk, thus modulating the drug concentration at the channel entry (Eq. 3; (12)):

$$\left[\text{D}\right]\left(\text{t}\right)=\left[\text{D}\right]-\left(\frac{4\times \left[\text{D}\right]}{\pi }\right)\times {\text{e}}^{-\left(\frac{\text{D}\times {\pi }^2\times \text{t}}{4\times {\text{L}}^2}\right)},$$ (3)

where [D] is the bulk drug concentration. A weighted reduced χ² (11) was calculated to determine the quality of the curve fit. All curve fits and statistical analyses were done using MATLAB R2018a (The MathWorks, Natick, MA) (13).

Molecular dynamics simulations

The simulations reported here were performed using NAMD (9), and the results were analyzed using VMD (9). The CHARMM37b1 force field (14) was used for protein and lipid molecules. The ligand parameters were developed using the CHARMM-GUI ligand reader and modeler, which uses CGENFF (14,15), and are shown in Tables S3 and S4. The protein-bilayer system, consisting of the solid state NMR (ssNMR) 2KQT structure (16) centered in a 2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) bilayer (182 lipid molecules) orientated normal to the z axis, was solvated with a tetragonal 60 Å × 60 Å × 90 Å water box (z being the long axis) using 9145 TIP3 water molecules. The total system charge was neutralized with 98 Cl and 70 Na ions, representing 150 mM NaCl. The ion parameters used are from the CHARMM37b1 force field. The nonbonded van der Waals interaction cutoff was set to 12.0 Å. The particle mesh Ewald sums long-range electrostatics method was used. A constant area barostat parameter was used to keep the unit cell in the x-y plane constant while allowing fluctuations in the z axis. The target Langevin piston was set to 1.01325 bar (atmospheric pressure at sea level). The system was minimized for 1000 steps and equilibrated for 1 ns, restraining the protein center of mass (COM) to the COM of the DMPC bilayer harmonically. The temperature was kept near 300 K with Langevin dynamics, and the default NAMD relaxation rate parameter was used. The equations of motion were integrated with a time step of 0.5 fs.

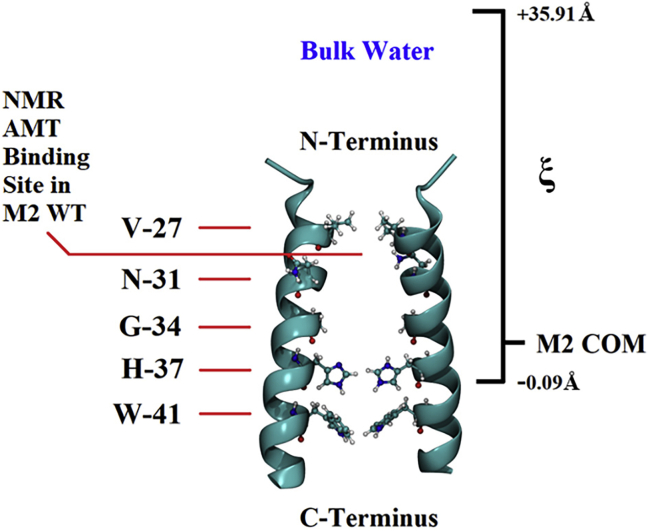
The ABF method was used to obtain a free energy profile for AMT or RMT in the 2KQT M2 model, which consists of a homotetramer of the transmembrane domain (residues 22–46) having the same sequence as A/Udorn/72 WT. A homology model for the M2 S31N was created from 2KQT with the VMD Mutator plugin. This compared favorably (root mean-square deviation ∼1 Å) to the structure of 5CO2, a crystal structure M2 S31N transmembrane domain (TMD), after it was relaxed in the same bilayer system as described above. To explore the free energy landscape of M2 with AMT or RMT, the reaction coordinate, ξ (used in PMFs), was chosen as the distance N-ward along the channel separating the COM of the M2 channel (Fig. 2) and the COM of AMT or RMT. 11 ABF simulation windows were used for each of the four cases of peptide and drug. The first ABF window placed the COM of AMT or RMT at the COM of 2KQT with the amine of AMT or RMT ∼2 Å from the COM of the His37 cluster. Each window was 3 Å along the channel axis in width, with 100 kcal/mol ⋅ Ų constraints at each end of the window to keep the ligand from leaving. The other 10 windows placed AMT or RMT at 3-Å intervals along the channel axis above (N-ward) the first. The total reaction coordinate ranged from −0.09 Å below the COM of 2KQT to 35.91 Å above the COM of 2KQT, well into bulk water. All restraints were removed for the ABF simulations. The protein-bilayer system was free to diffuse in the water box. The water box was large enough to allow for diffusion without interacting with the periodic boundaries. Each window simulation time was 100 ns. The fullSamples command was used to obtain an estimate of the bias force to avoid sudden jumps in the biasing force (17). The value 2000 was used for the fullSamples command, which is sufficient to obtain a reasonable estimate of the biasing force. A good estimate of the biasing force and millions of counts collected in the bins during the 100 ns simulations was sufficient to reach convergence. Counts were collected for each window in bins of size 0.1 Å, resulting in 30 bins per window. After a total of 1.1 μs simulation time for the entire reaction coordinate, counts in all the bins were between 2 × 10⁶ and 3 × 10⁶, sufficient for adequate biasing force equilibration in each of the windows (18).

Figure 2.

M2 S31N (+1) ABF reaction ξ coordinate. The reaction coordinate begins 0.09 Å below the M2 COM (0 Å on the reaction coordinate) and ends at 35.91 Å above the M2 COM and 15 Å into bulk water on the N-terminus side of M2. The H37 (cluster) COM is at −0.09 Å, the G34 COM is at 2.91 Å, the N31 (or S31 in WT) COM is at 5.91 Å, and the V27 COM is at 8.91 Å on the reaction coordinate. The M2 WT reaction coordinate is identical.

Rate constants from the simulated PMFs

The modified Arrhenius equation (Eq. 4) was used to calculate k₁, the second-order reaction rate constant for collision of a solute with a site, from the simulated PMFs. The diffusion-limited reaction rate constant k_c was assigned the value of 10⁹/Mol ⋅ s, a commonly cited value for maximal association rate constants for small solutes diffusing in aqueous solution (19), with the assumption that if there is no energy barrier, then AMT⁺ or RMT⁺ would diffuse as in bulk water and collide with the channel entrance with that rate constant k_c times the bulk drug concentration. The Boltzmann factor associated with the entry barrier free energy, ΔG^‡, governs the fraction of collisions leading to successful channel entries.

$$k_1=k_c{e}^{-\frac{\text{Δ}{G}^{‡}}{RT}}.$$ (4)

An expression from Kramers’ theory for a first-order reaction involving diffusing over a barrier (Eq. 5) was used to extract exit rate constants k₂ from the ABF free energy profiles as follows:

$$k_2=\frac{D\sqrt{{\Phi }_A{\Phi }^{†}}}{\pi kT}{e}^{-\frac{\text{Δ}{G}^{‡}}{kT}}.$$ (5)

The diffusion coefficient inside the channel, D, was obtained for each ABF window using the VMD Diffusion Coefficient Tool (20) and averaged for ABF windows 1–8 (M2 interior, Fig. S4). The simulations are converged after a microsecond of sampling. Therefore, the last 5 thousand frames (after 1 μs of sampling) of the simulations were used to calculate the diffusion coefficient in the VMD Diffusion Coefficient Tool. The free energy barrier height and shape were evaluated for Eq. 5 by manually fitting a parabola to the binding site energy well and an intersecting inverted parabola to the entry barrier (Figs. S2 and S3; (21)). ΔG^‡ is the difference between the minimum of one parabola and the maximum of the other; Φ_A is the inverse width of the potential energy well, a parabola breadth parameter, and Φ^‡ is the inverse width of the barrier, an inverted parabola breadth parameter (22).

Results

Global nonlinear least-squares curve fit

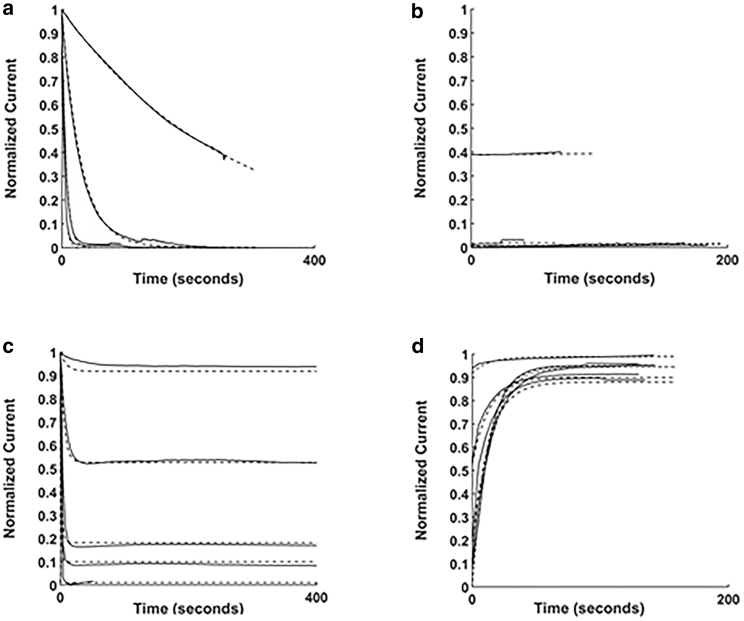
Binding kinetics were evaluated for blocking and wash-out traces for M2 WT or S31N exposed to various concentrations of AMT (Fig. 3). The normalized current traces are each pointwise averages of traces from three different cells. At 500 μM, 1 mM, or 10 mM for AMT, the M2 WT current is completely blocked by 200 s (3.5 min) (Fig. 3 a). No significant wash-out was observed for AMT in M2 WT by 190 s (Fig. 3 b). The rate constants from the global fit of these blocking and wash-out traces are 372 M⁻¹ s⁻¹ for the association and 1.58 × 10⁻⁴ s⁻¹ for dissociation (Table 1), corresponding to an equilibrium constant for the dissociation reaction of K_d = 0.42 μM, similar to previous reports (23). Unexpectedly, the M2 S31N current is more quickly blocked (Fig. 3 c) than the M2 WT, rapidly reaching an equilibrium block state at all concentrations tested. AMT block does not wash out appreciably from the WT channel (Fig. 3 b) but rapidly washes out in M2 S31N at all tested concentrations (Fig. 3 d). Surprisingly, the wash-out, though rapid, is incomplete; current levels never return to their original levels. It is unknown whether this is due to channel rundown, pH gradient rundown, a small amount of irreversible block by AMT in the S31N channel, or some other factor. Because each trace seemed to achieve a constant level, we chose to add a constant block parameter to the exponential wash-out model such that the theoretical prediction would not be forced to relax to 1.0 for the cases in Fig. 3 d. These allowed for better estimates of the wash-out relaxation time constant, which for the kinetic model must necessarily all be the same value, regardless of the starting (and ending) open state probability. It is notable that even though the theoretical curves (dashed lines) in Fig. 3 d appear to have different time constants because they cross each other, the crossovers are due to differing start amplitudes (represented in Eq. 2 by the parameter A) and ending amplitudes (due to the differing run-down/permanent block constants included in each of the fits).

Figure 3.

AMT wash-in traces (left) and wash-out traces (right) for M2 WT (upper) and S31N (lower). Each trace is the average of three normalized traces. For wash-in traces, the traces with more rapid and complete block were those at higher concentrations. The predictions of the global least-square fits for the one-site partial-block model with different parameters for WT and S31N channels are the dashed curves. (a) M2 WT is shown exposed with 100 μM, 500 μM, 1 mM, and 10 mM AMT. (b) Corresponding AMT wash-out traces in M2 WT are shown. (c) M2 S31N is shown exposed with 100 μM, 500 μM, 1 mM, and 10 mM AMT. (d) Corresponding AMT wash-outs in M2 S31N are shown. The wash-out is incomplete for four of the five concentrations. Thus, Eq. 2 was adjusted to include a constant representing the observed incomplete return to the original acid-induced current level.

Table 1.

Association and Dissociation Rate Constants from Global Nonlinear Least-Squares Fit for AMT or RMT in M2 WT or S31N

Global Fit Results
Compound	k1 (M−1 s−1)	k2 (s−1)	Fraction of Block (1-f)	Weighted Reduced χ2
AMT (WT)	372 ± 1.07	1.6 × 10−4 ± 2.5 × 10−5	0.993 ± 3.4 × 10−3	0.002
AMT (S31N)	3150 ± 49.5	0.35 ± 5.4 × 10−2	0.992 ± 2.2 × 10−3	0.23
RMT (WT)	659 ± 1.48	2.3 × 10−4 ± 4.2 × 10−5	0.978 ± 6.2 × 10−3	0.0123
RMT (S31N)	3622 ± 978	2.73 ± 0.74	0.25 ± 1.1 × 10−3	0.0132

The fraction of drug-occupied channel proton current block (1-f) is based on the third fitting parameter.

These features of the AMT traces can be accounted for by changes in the kinetics of blocker entry into the binding site, where the association rate constant k₁ is higher in M2 S31N by nearly 10-fold (3150 vs. 372 M⁻¹ s⁻¹) and the dissociation rate constant k₂ is higher by 1500-fold (0.348 vs. 1.58 × 10⁻⁴ s⁻¹) (Table 1). The calculated equilibrium constant for AMT in M2 S31N is above the therapeutic range: K_d = 110 μM, consistent with the observed insensitivity of modern influenza A to AMT. The potential for complete block at high doses (Fig. 3 a) and the cohesiveness of the global fit with just three parameters for each channel type confirms that the simple model is sufficient. In particular, the accurate prediction of intermediate equilibrium block levels consistent with the same pair of rate constants that predict the equilibrium relaxation during wash-in (esp. Fig. 3 c) and the dissociation rate constant, which alone predicts the wash-out (Fig. 1, b and d), implies that the fractional block for the bound state (1-f) is nearly complete, 0.993 in M2 WT and 0.992 in M2 S31N (Table 1).

RMT blocks M2 WT (Fig. 4, a and b) with kinetics similar to that of AMT, with k₁ higher (659 vs. 372 M⁻¹ s⁻¹) and k₂ slightly higher (2.3 × 10⁻⁴ vs. 1.58 × 10⁻⁴ s⁻¹), corresponding to a higher binding affinity (K_d = 0.35 μM), consistent with RMT’s commonly reported increased binding affinity and antiviral efficacy (e.g., (24)). The wash-out for 10 μM RMT in Fig. 4 b is faster than the fitted k₂ would predict, perhaps suggesting that the wash-out has fast and slow stages, hinting of a second binding site. However, the use of a single wash-out rate constant gives an adequate fit for the other wash-out traces and for the wash-ins, in which it comes into play in both the time constant and steady state occupancy.

Figure 4.

RMT wash-in traces (left) and wash-out traces (right) for M2 WT (upper) and S31N (lower). Each trace is the average of three normalized traces. The predictions of the global least-square fits for the one-site partial-block model with different parameters for WT and S31N channels are the dashed curves. (a) M2 WT is shown exposed with 10, 100, 500 μM, and 1 mM RMT. (b) Corresponding RMT wash-outs in M2 WT are shown. (c) M2 S31N is shown exposed with 100 μM, 500 μM, 1 mM, and 10 mM RMT. The inset shows the binding curve for RMT in M2 S31N. The solid curve is the probability of occupancy by RMT, assuming K_D = 754 μM. Circles are positioned at points on the curve corresponding to concentrations tested in (c). M2 S31N binding is essentially saturated at 10 mM RMT. (d) Corresponding RMT wash-outs in M2 S31N are shown.

Like AMT, RMT blocks (Fig. 4 c) and washes out (Fig. 4 d) more rapidly in M2 S31N than in M2 WT, essentially instantaneously on the timescale of the experiment. k₁ increases by 5.5-fold and k₂ increases by 17,000-fold (Table 1). But unlike AMT, the block is incomplete at all concentrations tested. The fitted rate constants are higher for RMT than for AMT in M2 S31N (3622 M⁻¹ s⁻¹ and 2.73 s⁻¹), corresponding to K_d = 754 μM, which is too high to be therapeutically useful. From these results, we expect virions with M2 S31N to be RMT insensitive, too (25). Despite applying saturating drug concentrations (i.e., concentrations of 1 and 10 mM, both higher than K_d) and despite rapid onset of block, RMT block is incomplete for M2 S31N at all drug concentrations (Fig. 4 c). In the Fig. 4 c inset, a plot of the expected probability of occupancy for the observed K_d emphasizes the point that, at the highest concentrations used, channel occupancy was apparently complete, so complete block was expected but not observed. Because of this observation, we included the third parameter in all the fits (f) and report the fractional block (1-f) for the occupied channels. Unlike the other three cases, in which the block of the occupied channel is complete (≥0.978), the proton current block of the RMT-occupied M2 S31N channel is very low, just 25% (Table 1). This low fractional block cannot be RMT-induced LC through the oocyte membrane because controls were done to know how much LC might be induced by high concentrations of drug, and amounts within the range observed in the control experiments were subtracted out as LC in the preliminary cell-wise fit before the final fit of the normalized, average traces.

Molecular dynamics

ABF simulations were done to evaluate AMT⁺ or RMT⁺ binding to M2 WT or the homology model for M2 S31N (Fig. 5).

Figure 5.

Adaptive biasing force (ABF) simulation results for AMT⁺ or RMT⁺ in M2 WT or S31N. Dotted lines represent neutral, dashed lines represent +1, and solid lines represent +3 charge state of M2. Each ABF plot represents 1.1 μs of total simulation time. (a) WT M2 with AMT⁺ is shown. (b) M2 S31N with AMT⁺ is shown. (c) WT M2 with RMT⁺ is shown. (d) M2 S31N with RMT⁺ is shown.

Each of the complete free energy profiles show an energy well N-ward to the H37 tetrad, between 2 and 8 Å, near the serine (or asparagine) in the M2 WT (or S31N). The energy barriers observed between 8 and 14 Å are nearest the Val27 luminal stricture. The flattening of the energy curve beyond 20 Å in the reaction coordinate represents AMT⁺ or RMT⁺ in bulk water.

As the M2 H37 tetrad charge is increased from neutral to +1 or +3, the energy well is increasingly shallower, as expected from increasing electrostatic repulsion between the tetrad and the charged drug, except in one case: the neutral-to-+1 case for AMT⁺ in the M2 S31N, in which the energy wells are unchanged (Fig. 5 b, dotted and dashed lines). Generally, the energy well between 2 and 8 Å is deeper in the WT (Fig. 5, left panels) than in S31N (right panels), except in the case of AMT⁺ in the +1 WT M2 (Fig. 5 a, dashed line) compared with AMT⁺ in the +1 M2 S31N (Fig. 5 b, dashed line). Entry barriers are modestly higher for AMT⁺ or RMT⁺ in WT (Fig. 5, left panels) than S31N (right panels). This corresponds to the higher rate of entry in M2 S31N seen in electrophysiology (Table 1).

Table 2 shows selected results of calculated rate constants from the PMFs using Eq. 4, the diffusion-limited rate constant reduced by the Boltzmann factor according to the entry barrier height (height of inverted parabola relative to bulk), for k₁ and, using Eq. 5, shows diffusion over the exit barrier according to the expression from Kramers’ theory for k₂. The parabolas fitted to the PMF for use with (4), (5) are shown in Figs. S2 and S3.

Table 2.

Association and Dissociation Rate Constants Calculated from ABF Simulations for AMT⁺ or RMT⁺ in WT or M2 S31N

ABF Rate Constant Results
	k1 (M−1 s−1) = kc × e−ΔG/kT	k2 (s−1)	EP k1 (M−1 s−1)	EP k2 (s−1)
WT M2(+1) AMT+	380.9	1.11 × 10−4	372	2.3 × 10−4
WT M2(+1) RMT+	617.6	1.27 × 10−4	659	1.58 × 10−4
S31N M2(+1) RMT+	1.61 × 105	24.9	3622	2.73

Electrophysiologically measured rate constants (EP) are included for reference.

The models with differing His37 charge states varied dramatically in predicted entry and exit rate constants (see Table S1 for complete results). Nevertheless, it is clear that the neutral tetrad would bind both drugs much too tightly, with Eq. 5 k₂ exit rate constants 14–42 orders of magnitude too low compared with those measured here (Table S1), as suggested previously (26). Uncertainties in the PMFs were not calculated, but because we were able to obtain a large number of sample points (millions), the error in the force estimation per bin is expected to be low (27). Table S2 is an example case for a parameter sensitivity test to show that the well and barrier width parameters have a small effect on the k₂-values and the barrier height parameter has a significant effect on k₂.

Clearly, the higher exit rate constants in the charged-tetrad models are more consistent with measured values, suggesting that electrostatic repulsion between the charged His37 tetrad, and the charged drug plays an important role in facilitating drug exit. For WT M2, the His37 tetrad with a total charge of +1 produced k₁- and k₂-values very similar to the electrophysiology-measured values for both AMT⁺ and RMT⁺ (Table 2). In contrast, none of the M2 S31N PMFs predicted k₁- or k₂-values similar to the measured values for the three tetrad charge states examined. The best case was the +1 charge state for the tetrad, which, with RMT⁺_, predicted a k₂ within a factor of 10 of the measured k₂-value (Table 2), but the predicted k₁ is too high because the entry barrier is too low. As noted above, the barrier to entry is uniformly low for all of the M2 S31N PMFs, and the predicted k₁-values are all dramatically too high as a consequence (Table S1), suggesting that the model channel is too open at the Val27 stricture. As noticed previously (28), we found the M2 S31N homology model to draw more water into the channel than M2 WT. Perhaps the force field parameters for Asn as they relate to TIP3 water parameters overexaggerate this effect to some degree. Finally, for the AMT⁺ exit rate constant, the observed k₂ is bracketed by the predictions of the +1 and +3 tetrad charge states, suggesting that it might be possible to identify intermediate tetrad charge states for both AMT⁺ and RMT⁺ that would account for the two-drug exit rate constants in M2 S31N, but we felt it unwise to explore these possibilities in view of the lower barriers than expected, given the rate constants, which also impact the exit rate constants because they depend on the difference between the well depth and the entry barrier height. Admittedly, this somewhat undermines the use of the PMFs for the S31N construct. Examination of these results for a mechanism for partial block of M2 S31N by RMT⁺ will be discussed below.

Discussion

The kinetics of current block and wash-out for WT and M2 S31N are presented for a broad range of AMT and RMT bath concentrations. The traces technically represent relaxations of the equilibrium binding state after abrupt alteration of the boundary condition (bath concentration) for the conditions that we assumed to be well described by a first-order ordinary differential equation. The onset of block has a time constant for the equilibrium relaxation equal to the inverse of the sum of the effective entry rate constant and the first-order exit rate constant, where the effective entry rate constant is the second-order entry reaction rate constant times the drug concentration. The final equilibrium occupancy state probability (after an infinitely long wash-in) is the exit rate constant times the relaxation time constant. The time constant for wash-out is the same as the time constant for onset of block but with the bath drug concentration set to zero, making it the inverse of the exit rate constant for the first-order chemical reaction. The global fit of the single-site model with possible fractional block, with the parameters of association rate constant, dissociation rate constant, and fraction of current blocked in the drug-occupied channel state, in which all of the features for the whole family of traces are modeled simultaneously, yielded secure estimate of the rate constants as well as the fractional occupied-state current parameter, f, for each of the four different cases in this two-drug, two-channel study.

The one-site binding model equation used includes parameters for diffusion of AMT or RMT through the unstirred layer that surrounds the oocyte. The model also includes a LC subtraction for current that produced by the oocyte’s native current-carrying channels. The use of a global fit (simultaneous optimization of the parameters for both wash-out and wash-in traces at each of several concentrations) allowing for partial block and corrected with the unstirred layer parameters and LC subtraction have not been included, traditionally, when extracting rate constants from the TEVC electrophysiology current traces.

New, to our knowledge, AMT or RMT binding insights were obtained from the curve fit. Both k₁-values for AMT and RMT in the M2 S31N channel were increased 10-fold, suggesting a faster entry rate and binding to M2 S31N. However, both k₂-values increased even more drastically, by 1500-fold for AMT and 17,000-fold for RMT. In the mutant channel, the two drugs spend less time in the bound state.

Also, a novel, to our knowledge, insight for RMT binding to M2 S31N was discovered. The fraction of block is very low, meaning that, because saturating test concentrations were used, RMT did not completely block proton transport. This is not true for AMT, in which the fraction of block is high in the mutant channel and the current is completely blocked when saturating test concentrations are used. However, we were unable to identify the mechanism for partial block with molecular dynamics simulations.

ABF simulations for AMT⁺ or RMT⁺ in WT M2 using the ssNMR 2KQT structure for the model did allow us to obtain free energy profiles for the binding reaction. The simulations were done with neutral, +1, or +3 M2 charge states. Rate constants were extracted from the profiles, projecting for the first time that the +1 His37 charge state agreed strongly with the measured rate constants. This success may have derived from fairly accurate structural models for the channel and drug binding orientation, which were deduced from NMR observables. Admittedly, because the diffusion-limited constant used to estimate k₁ is only an order-of-magnitude estimate, the predicted k₁-values are not to be considered accurate. However, a relative analysis between the k₁-values for different situations allows for ratiometric comparisons between them that would be due to differences in the entry barrier, insofar as the channel entryway with missing N-terminal amino acids is realistic. The charge state of the His37 tetrad, both in the absence (29) and presence (30) of AMT⁺, has been the subject of many NMR studies and simulation studies (31,32), including another study that used umbrella sampling to obtain PMFs for RMT in the +2 charge state of the 3LBW (WT) and 2LY0 (S31N) structures (33), but this is the first electrophysiology study attempting to relate AMT⁺ or RMT⁺ binding kinetics to interactions between the His37 tetrad charge and the drug charge. Throughout this report, the drugs are referred to as monovalent cations. This is the rational approach, considering that they have a single protonation state with pKa-values (10.1 for AMT, (34)) well above the bath pH, even in the somewhat hydrophobic channel.

An S31N homology model was made from the WT 2KQT structure, and free energy profiles were obtained for the neutral, +1, or +3 M2 charge states. Rate constants were extracted from the profiles. Neither of the k₁-values for the M2 S31N agreed with the measured k₁-values. We observed more water molecules in the M2 S31N channel homology model. The complexity of luminal water molecule configuration space may have created difficulty in adequate sampling of water configurations and drug orientation, leading to erroneous rate constant calculations from the free energy profiles. However, the k₂-value for RMT⁺ in the +1 M2 S31N channel was within a factor of 10 of the experimentally measured k₂-value. Qualitatively, the free energy profiles more closely matched expectations for changes in AMT⁺ or RMT⁺ binding to the +1 His37 of M2 S31N than to other charged states. Based on the calculated rate constants from the ABF results for the +1 M2 charge state and the measured rate constants from the TEVC data presented here, we propose the following model of binding for AMT and RMT:

The M2 channel is in the open state at pH 5.3, when three of the imidazoles are protonated (+3 state), but when AMT or RMT (both +1 charge) enters the channel, the charge on the His37 complex is destabilized by the positively charged AMT or RMT, reducing the M2 charge state to +1. Based on NMR measurements of the protonation state of the His37 cluster (7), we calculated a charge of ∼1 (specifically +1.3) on the His37 cluster at pH 5.2 when AMT is present. This is close to the +1 state simulated here, and the simulations at 0 and +3 were selected to bracket that case. It is reasonable to think of the drug remaining primarily in the +1 state during the binding process because its pKa (e.g., 10.1 for AMT) is so much higher than the pKa for initial protonation of the His37 cluster (≤7.6 in the apo state (7)), meaning the AMT and RMT amine have higher proton affinities. The conversion of the M2 His37 cluster from +3 to +1 would presumably occur as the drug enters the channel. In future work, it may be interesting to explore this part of the reaction coordinate more carefully, perhaps using His37 charges that are a function of drug amine proximity. Also, for M2 S31N, a more realistic reaction coordinate for the drug entry might include a more thorough examination of the binding orientation, which for larger drugs with secondary amines, such as RMT, appears from simulations (35) and, in one case, an NMR structure (36), is amine-out (pointing toward the N-terminus) throughout the narrow entryway rather than amine-in as simulated here. Perhaps either or both of these approaches could reveal the partially blocking bound state for RMT in M2 S31N reported here.

Conclusions

An accurate mathematical model using a family of traces was used to extract rate constants from TEVC experiments for AMT and RMT in WT or M2 S31N. The on- and off-rate constants for both AMT and RMT are increased dramatically in M2 S31N compared with WT M2. The significant increase of k₂ is likely responsible for the AMT and RMT insensitivity in M2 S31N. The most intriguing result from the global fit shows that RMT binds without block in the M2 S31N, whereas AMT, albeit binding weakly, blocks all proton transport when in the binding site. Molecular dynamics simulations show that AMT⁺ can easily change binding conformation with its amine out in M2 S31N instead of down as in the WT M2, whereas RMT⁺ most often remains in the binding site with its amine in the downward-pointing conformation. Simulated potentials of mean force are most consistent with binding of monovalent cation drugs near a monovalent His37 tetrad selectivity filter.

Editor: Alan Grossfield.