Should Virus Capsids Assemble Perfectly? Theory and Observation of Defects

Abstract

Although published structural models of viral capsids generally exhibit a high degree of regularity or symmetry, structural defects might be expected because of the fluctuating environment in which capsids assemble and the requirement of some capsids for disassembly before genome delivery. Defective structures are observed in computer simulations, and are evident in single-particle cryoelectron microscopy studies. Here, we quantify the conditions under which defects might be expected, using a statistical mechanics model allowing for ideal, defective, and vacant sites. The model displays a threshold in affinity parameters below which there is an appreciable population of defective capsids. Even when defective sites are not allowed, there is generally some population of vacancies. Analysis of single particles in cryoelectron microscopy micrographs yields a confirmatory ≳15% of defective particles. Our findings suggest structural heterogeneity in virus capsids may be under-appreciated, and also points to a nontraditional strategy for assembly inhibition.

Significance

Structural biology technologies have enabled the visualization of virus capsid structures at high resolution, showcasing the beauty and symmetry of spherical capsids. However, viral capsids form in fluctuating environments and often must disassemble in the infection process. This report shows that both mathematical modeling and direct electron microscopy evidence indicate that defects in capsid structures may be substantially under-appreciated and could play an important role in basic and translational virology.

Introduction

Capsid assembly is a critical step in the life cycle of all viruses (1,2). During each infection cycle, capsids must assemble for each new viral replicate before it leaves the cell, and often must go through maturation steps that involve significant changes in conformation as well. One consequence of the dynamic and intrinsically stochastic nature of viral capsid assembly is that the process does not always proceed to a precise end point and that, occasionally, defective capsids form. For example, there are three forms of the herpesvirus capsid that have been isolated in the nucleus, two of which do not proceed to form fully infectious virions (3,4). The human hepatitis B virus (HBV) capsid can assemble in vivo into two structures with different numbers of quasiquivalent subunits (5). The symmetry may be either $T=3$ (with 90 subunits per capsid) or $T=4$ (with 120 subunits per capsid) depending on the conformational behavior of seven amino acid residues on the C-terminal region of the HBcAg capsid subunit (6, 7, 8). The nature of the structures that form may also depend strongly on the ambient conditions. For example, the cowpea chlorotic mosaic virus can form a variety of structures, including multiwalled shells, tubes, and “rosettes,” depending on the pH and ionic strength (9).

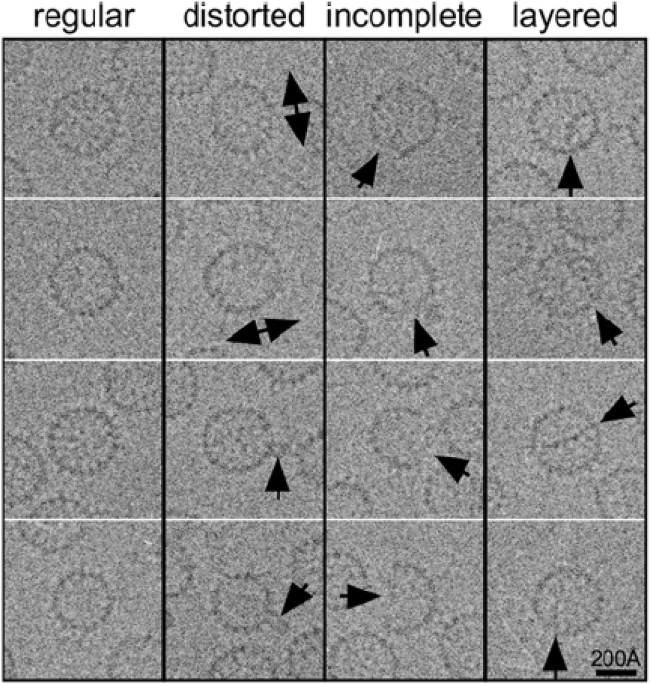
The limitations of conventional structural biology techniques make it very difficult to verify the formation of defective capsid structures directly. Although structures of individual viral capsid subunits can be obtained by x-ray crystallography, most structures of complete capsids are obtained using cryoelectron microscopy (cryo-EM) (10,11). Cryo-EM images often include capsids that are distorted or incomplete, or that have additional layers of subunits (Fig. 1; (12)). However, the signal/noise ratio of individual cryo-EM images is low, so obtaining atomistic structures requires collecting, filtering, reorienting, and averaging many such images (13, 14, 15, 16). This in turn requires discarding images of capsids that appear to be defective and exploiting symmetry in the averaging process, which artificially imposes a corresponding symmetry on the resulting structure. Because defective capsids are not uniform, this method cannot be applied to calculate high-resolution structures of defective capsids. Similarly, x-ray crystallography exploits the perfect repetition of the crystal lattice, thus excluding observation of irregular or infrequent capsids resulting from defects in assembly.

Figure 1.

Heterogeneity in raw cryo-EM data. Shown are selected cryo-EM images of hepatitis B capsid particles. Arrows indicate structural variation.

Computer simulations can enable detailed examinations of the mechanism of virus capsid assembly and the types of structures that can form (17, 18, 19, 20, 21). Several simulations produced unusual, malformed structures, such as oblate capsids lacking icosahedral symmetry or aggregates composed of several partially formed capsids joined together in an irregular fashion (22, 23, 24, 25, 26). A recent study of the assembly of the $T=4$ form of the HBV capsid using a semi-atomistic model yielded trajectories with persistent defects, despite the lowest energy conformation corresponding to a defect-free fully symmetrical structure (27).

Defective capsid formation can also be studied from a more theoretical perspective via thermodynamics and statistical mechanics (1,2,28, 29, 30, 31, 32, 33). A still-influential early model of equilibrium assembly for icosahedral capsids used 12 pentagonal subunits that unite to form a dodecahedron following a single, minimal-energy pathway for assembly (28). This 12-pentamer model indicated that, for a range of plausible concentrations of free subunits, the population of intermediates was very low compared to that of either free subunits or complete capsids—i.e., two-state behavior: fully formed or monomeric. However, capsid subunits were considered rigid and able to exist in only two states: either fully attached to the capsid or completely detached from it. Consequently, the only possible defects were vacancies. In addition, the assumption of a single minimal-energy pathway breaks down for large viruses because of the increased complexity of the structure and the larger number of sites in which a subunit can be attached to a growing capsid.

To develop an improved understanding of potential defects in capsids, we use the HBV capsid as a demonstration system because cryo-EM images of this capsid available to us show a variety of defects. Some of the defects represented include distorted, nonspherical capsids; incomplete capsids with gaps in their surface; and layered capsids with subunits forming additional surfaces inside an otherwise fully formed capsid. Several instances of these defects are shown in Fig. 1. Importantly, HBV capsids assemble spontaneously from a solution of their subunit proteins, without genetic material, and have been the subject of extensive study (12,34, 35, 36).

Extensive experimental studies of the thermodynamics and kinetics of HBV capsid assembly have been performed (28,35,37). At low salt concentration, significant concentrations of species with molecular masses intermediate between individual subunits and complete capsids were not reported, apparently confirming the two-state picture of (28). However, the resolution of size exclusion chromatography and light scattering as mass-measurement techniques is insufficient to distinguish between complete, perfect capsids and those that have small defects or vacancies. Furthermore, at high salt concentrations, charge depletion mass spectrometry (CDMS) experiments suggest the presence of significant numbers of trapped intermediates with ∼90 dimers. These experiments also suggest the presence of defective, overgrown capsids whose masses are greater than that of a perfect capsid (38,39). However, these experiments likewise do not have the resolution to identify small vacancies and do not provide detailed structural information. A study of the assembly of woodchuck HBV capsids using both CDMS and cryo-EM identified significant numbers of capsids with more than 120 dimers, where the additional dimers result in elongation along a fivefold axis or spiral-like deformities (40).

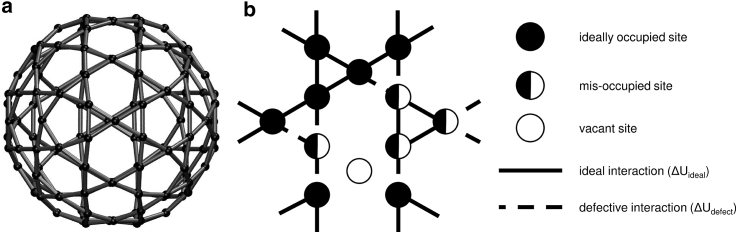
Here, we take a statistical-mechanical approach to the problem of determining the equilibrium distribution of capsid states, defining a lattice model (Fig. 2). Our model is similar to the lattice gas model for studying phase transitions in critical fluids (41,42) but defined on a contact graph that reflects the geometry of the HBV capsid. Unlike prior studies, this model incorporates the possibility of capsid subunits being partially attached or being in a conformational state such that their interactions with a partially formed capsid are not as strong as the intersubunit interactions in a fully formed capsid. The model can be simulated numerically using the Metropolis Monte Carlo method (43) and also solved analytically under the approximation that defects in capsids are isolated. Because of our primary interest in near-perfect capsids, the approximate calculation is highly useful.

Figure 2.

Lattice model for Hepatitis B virus capsid. (a) The perfect capsid, with all sites ideally occupied. (b) Close-up view of a subset of sites showing one possible mixture of ideally occupied sites (black circles), misoccupied sites (black half-circles), and vacant sites (white circles). The interaction energy between ideally occupied sites or between misoccupied sites is $\mathrm{\Delta }{G}_{\text{ideal}}$ (solid line), whereas the interaction energy between an ideally occupied and a misoccupied site is $\mathrm{\Delta }{G}_{\text{mixed}}$ (dashed line).

Materials and Methods

Model for capsid formation

We construct a statistical-mechanical model for capsid assembly and examine its equilibrium behavior, which depends only on the energy function via its parameters. Given a constant chemical potential for free subunits, we can determine the distribution of sizes of partially formed capsids. We emphasize that we are not estimating the free-energetic parameters of the model, but rather exploring the consequences of a physically plausible range of parameter choices.

Physically, each discrete state of our model represents a “set” of continuum configurations in the underlying configuration space. Therefore, all state energies are intrinsically free energies that account for both energetic and entropic characteristics of the underlying configurational subensembles (44). The entropic interactions include both configurational entropy due to minor structural fluctuations as well as solvation entropy changes including hydrophobic effects.

We employ a simple lattice-like graphical model with N sites (Fig. 2), in which each site i can be in one of three states: unoccupied, “ideally” occupied (i.e., in the orientation suitable for the symmetric capsid), or misoccupied (i.e., occupied but misoriented compared to the symmetric configuration). A contact graph $\mathcal{G}$ (Fig. 2) shows which sites interact with each other. Thus, the free energy of a capsid configuration $\mathbf{x}$ is given by

$$G\left(\mathbf{x}\right)=\sum _{\text{edges}ij\in \mathcal{G}}\mathrm{\Delta }{G}_{\text{int}}\left(x_i,x_j\right),$$ (1)

where $\mathrm{\Delta }{G}_{\text{int}}\left(x_i,x_j\right)$ is an interaction free energy that depends on the occupation states $x_i$ and $x_j$ of the two sites i and j as given below.

The interaction energy $\mathrm{\Delta }{G}_{\text{int}}$ can take on one of three possible values: $\mathrm{\Delta }{G}_{\text{ideal}}$ for interactions between ideally occupied sites, $\mathrm{\Delta }{G}_{\text{mixed}}$ for interactions between a ideally occupied site and a misoccupied site, or $\mathrm{\Delta }{G}_{\text{defect}}$ for interactions between misoccupied sites. In general, we expect that interactions between ideally occupied and misoccupied sites will be weaker than those between ideally occupied sites. We defined the difference $\mathrm{\Delta }\mathrm{\Delta }G=\mathrm{\Delta }{G}_{\text{mixed}}-\mathrm{\Delta }{G}_{\text{ideal}}$ to be the difference between the two interaction energies and is always assumed positive, i.e., mixed interactions are weaker than ideal. We also assumed that the interaction between two adjacent misoccupied sites $\left(\mathrm{\Delta }{G}_{\text{defect}}\right)$, which in principle could include ideal pair geometry, would overall be slightly weaker than that between ideally occupied sites $\left(\mathrm{\Delta }{G}_{\text{ideal}}\right)$, so that $\mathrm{\Delta }{G}_{\text{defect}}=\mathrm{\Delta }{G}_{\text{ideal}}+1.0k_{B}T$. Our results were not sensitive to this choice. Note that all of these interaction energies account for average effects of configurational fluctuations and hence represent effective free energies.

The probability of any given configuration $\mathbf{x}$ can be calculated based on its free energy. To probe the distribution of the number of occupied sites both in terms of energetic parameters and concentration effects, we work in the grand-canonical ensemble, in which the chemical potential of capsid subunits μ is fixed and the number of assembled subunits self-adjusts accordingly. This corresponds to considering any partially formed capsid as being in equilibrium with an ideal solution of free subunits. The probability of a given configuration $\mathbf{x}$ is given by

$$p\left(\mathbf{x}\right)\propto \text{exp}\left[-\beta G\left(\mathbf{x}\right)\right]\text{exp}\left[-\beta \mu N\left(\mathbf{x}\right)\right]=\text{exp}\left\{-\beta \left[G\left(\mathbf{x}\right)-\mu N\left(\mathbf{x}\right)\right]\right\},$$ (2)

where $N\left(\mathbf{x}\right)$ is the number of occupied sites for configuration $\mathbf{x}$. The total probability of having M subunits in the capsid is obtained by summing over all configurations having M occupied sites:

$$p\left(N\right)=\frac{{\sum }_{\mathbf{x}\text{s}.\text{t}.N\left(\mathbf{x}\right)=M}\text{exp}\left\{-\beta \left[G\left(\mathbf{x}\right)-\mu N\left(\mathbf{x}\right)\right]\right\}}{{\sum }_{\mathbf{x}}\text{exp}\left\{-\beta \left[G\left(\mathbf{x}\right)-\mu N\left(\mathbf{x}\right)\right]\right\}}$$ (3)

The chemical potential μ is usually approximated by an ideal relation to concentration

$$\mu =k_{B}T\text{ln}\frac{\left[\text{subunit}\right]}{{\left[\text{subunit}\right]}_{\text{ref}}},$$ (4)

though the true dependence is generally more complicated (45). The functional form of μ does not affect the results presented below.

Application to the hepatitis B virus capsid

We apply the lattice model described above to describe the thermodynamics of defective configurations of the HBV $T=4$ capsid to a first approximation. The capsid is composed of 120 dimers, each of which consists of a pair of sequentially identical subunits, each contributing a pair of helices to the 4-helix bundle interface and further linked by a disulfide bridge (46). Experimentally, these dimers have been found to be quite robust (35) and act as building blocks for the capsid. Consequently, we considered each dimer to constitute a site in our model. Furthermore, individual missing dimers seem to be a common feature in both the cryo-EM micrographs presented here and the defective conformations produced in our previous simulations (27). In the simulations, we also observed partially attached dimers which retained a significant degree of orientational freedom. Although no clear examples of partially attached dimers were observed in the cryo-EM images, this motivated our choice to define three possible states for each site: fully occupied, empty, or misoccupied.

Each of the dimers that constitute the HBV capsid is a sequentially identical homodimer, with very slight structural differences between dimers. Furthermore, estimates of the free energy of interactions between individual subunits show that they are approximately similar in strength (35). Consequently, as a first order approximation, we chose to define only one chemical potential μ and set of interaction strengths $\mathrm{\Delta }{G}_{\text{ideal}}$ and $\mathrm{\Delta }{G}_{\text{mixed}}$ for our model. We also assumed only local interactions between neighboring dimers, constructing the contact graph $\mathcal{G}$ for the virus from the structure of the capsid given in the Protein Data Bank (PDB: 1QGT) (46) by including an edge for each pair of dimers in which there is at least one pair of α-carbons within 10 Å of each other in the complete structure of the capsid. In this graph, there are four nearest neighbors for each site.

Analysis of defective images in cryo-EM micrographs of HBV capsids

Three historical micrographs of the HBV capsid assembled in vitro from expressed HBcAg truncated at residue 147 (6,12) were analyzed to identify and classify images of defective capsids. Briefly, samples were rapidly vitrified on copper grids with lacey carbon film, transferred on a Gatan 626 cryoholder (Gatan, Pleasanton, CA) into a Phillips CM200 cryoelectron microscope (FEI/Thermo Fisher Scientific, Portland, OR) operating at 120 kV, and imaged by low-dose techniques at 38,000x on film. The data were digitized on an SCAI flatbed scanner (Z/I Imaging, Huntsville, AL) to yield a pixel size at the sample of 1.84 Å. Scans of the three micrographs (which included one used in (12)) were then trimmed and processed using ImageMagick (https://imagemagick.org) to remove the edges and to eliminate the data window imprinted on the micrograph to reduce spurious regions of high contrast that would otherwise interfere with subsequent particle picking and extraction. The modified micrograph scans were then converted to MRC format using em2em (Image Science Software, Berlin, Germany) for further processing.

Images of capsids were then picked and extracted from the micrographs using RELION (14,47,48). An initial set of 89 particles was manually picked and extracted from the micrographs, and subjected to two-dimensional (2D) classification into five classes; one of the class means was then used as a template for template-based autopicking. A threshold value of −0.6 was used to maximize the number of particles selected while excluding unwanted debris as much as possible. This resulted in a first stack of 17,790 particle images, which was subjected to 2D classification into 10 classes to remove partial capsids and other debris. Two of the classes were selected to provide a final filtered stack of 4940 images. A random sample of 100 images was then drawn (without replacement) from this stack and examined manually to identify any visible defects. Statistics on the types of defects visible in the sample of images were then collected. The filtered stack was also subjected to 2D classification with 50 initial clusters and 50 iterations of the expectation-maximization (E-M) algorithm used by RELION.

Approximate analytical approach to the model based on assuming isolated defects

It is possible to obtain an analytical expression for the partition function of the above model if we make the approximation that all defects (either empty sites or misoccupied sites) are isolated from each other. This is a good approximation if there are few defects, which is the regime of primary interest in which capsids are generally stable.

The free energy change for each type of defect, a vacancy, or misoccupied site, can easily be obtained for a model with N sites, each of which has k nearest neighbors. Starting from a perfect capsid of free energy $G_{\text{perf}}=-N\mu +\left(Nk/2\right)\mathrm{\Delta }{G}_{\text{ideal}}$, changing one site to empty removes the interactions along k edges, and the free energy change is $\mathrm{\Delta }{G}_{\text{vac}}=\mu -k\mathrm{\Delta }{G}_{\text{ideal}}$. If instead we change one site to a misoccupied site, the free energy difference is $\mathrm{\Delta }{G}_{\text{mis}}=k\mathrm{\Delta }{G}_{\text{ideal}}-k\mathrm{\Delta }{G}_{\text{mixed}}\equiv -k\mathrm{\Delta }\mathrm{\Delta }G$.

The partition function can now be obtained from straightforward combinatorics. The number of configurations with $N_v$ vacant sites and $N_m$ misoccupied sites is $\left(N!/N_v!N_m!\left(N-N_v-N_m\right)!\right)$. When all defects are assumed to be isolated (not neighboring another defect), the free energy difference from the perfect capsid is simply additive,

$$N_v\mathrm{\Delta }{G}_{\text{vac}}+N_m\mathrm{\Delta }{G}_{\text{mis}}.$$ (5)

The grand-canonical partition function is then given by

$$\text{Ξ}=e^{-G_{\text{perf}}/k_{B}T}\sum _{N_v,N_m=0}^N\frac{N!}{N_v!N_m!\left(N-N_v-N_m\right)!}\text{exp}\left[-\left(N_v\mathrm{\Delta }{G}_{\text{vac}}-N_m\mathrm{\Delta }{G}_{\text{mis}}\right)/k_{B}T\right]$$ (6)

which is a trinomial form that can be evaluated exactly:

$$\text{Ξ}=e^{-G_{\text{perf}}/k_{B}T}{\left(1+e^{-\text{Δ}{G}_{\text{vac}}/k_{B}T}+e^{-\text{Δ}{G}_{\text{mis}}/k_{B}T}\right)}^N$$ (7)

With the partition function in hand, the probability of the “single” perfect capsid configuration is given by

$$p_{\text{perf}}=\frac{e^{-G_{\text{perf}}/k_{B}T}}{\text{Ξ}}={\left(\frac{1}{1+\text{exp}\left[-\left(\mu -k\mathrm{\Delta }{G}_{\text{ideal}}\right)/k_{B}T\right]+\text{exp}\left[-k\mathrm{\Delta }\mathrm{\Delta }G/k_{B}T\right]}\right)}^N,$$ (8)

which is used below to study more general spherical capsids, beyond HBV. Importantly, the only structural properties of the capsid on which this expression depends are the number of sites N and number of nearest neighbors k. A plot of Eq. 8 is given in Fig. S5.

The approach outlined here may be extended to conditions where defects are not isolated by using additional virial-like corrections to the isolated defect approximation are described in Appendix 2 in the Supporting Material. At higher defect concentrations, other structural properties of the capsid besides N and k, such as the overall topology of the capsid, may become relevant.

Monte Carlo simulations of the model

In addition to the analytical approximation just given, we study the full model described in Model for capsid formation below using Metropolis Monte Carlo (MC) simulation. In Metropolis MC, trial moves attempt to change the configuration and are accepted with probability $\text{min}\left(1,\text{exp}\left[-\beta \mathrm{\Delta }H\left(\mathbf{x}\right)\right]\right)$, where $H\left(\mathbf{x}\right)$ is the appropriate grand-canonical potential corresponding to Eq. 2) defined by

$$H\left(\mathbf{x}\right)=G\left(\mathbf{x}\right)-\mu N\left(\mathbf{x}\right)=-\mu N\left(\mathbf{x}\right)+\sum _{\text{edges}ij\in \mathcal{G}}{\mathrm{\Delta }G}_{\text{int}}\left(x_i,x_j\right),$$ (9)

where N is the total number of subunits and ΔH is the change in H in going from an old to a new configuration.

We performed a set of MC simulations for our model as applied to the HBV capsid, using the contact graph $\mathcal{G}$ constructed from its structure as described above. MC simulations of the model were performed with varying values of μ, $\mathrm{\Delta }{G}_{\text{ideal}}$, and $\mathrm{\Delta }{G}_{\text{mixed}}$ to map out a “phase diagram” for the system. The MC moves for these simulations consisted of choosing a site i at random and changing its state. Each simulation lasted for 1 billion trial moves, and the average number and distribution of the number of occupied sites were computed. The simulations were performed on a grid in μ-$\mathrm{\Delta }{G}_{\text{ideal}}$−$\mathrm{\Delta }{G}_{\text{mixed}}$ space in which μ ranged from $-6k_{B}T$ to $6k_{B}T$ in steps of $0.2k_{B}T$, $\mathrm{\Delta }{G}_{\text{ideal}}$ ranged from $-5k_{B}T$ to 0 in steps of $0.25k_{B}T$, and $\mathrm{\Delta }{G}_{\text{mixed}}$ ranged from $\mathrm{\Delta }{G}_{\text{ideal}}$ to 0 in steps of $0.25k_{B}T$. Only simulations in which $\left|\mathrm{\Delta }{G}_{\text{mixed}}\right|\le \left|\mathrm{\Delta }{G}_{\text{ideal}}\right|$ were run.

To be considered a “partially formed capsid,” a collection of subunits must be touching each other, so that they would be expected to move together because of the forces holding them together but independently of any other collection of subunits. Consequently, for the purposes of analyzing this simulation, a “partially formed capsid” was defined as a set of occupied sites (either ideally occupied or misoccupied) that span a connected subgraph of the contact graph $\mathcal{G}$. Therefore, after each trial move of the simulation, the subgraph of $\mathcal{G}$ spanned by the occupied sites was determined and divided into connected components. The distribution of the sizes of these subcomponents was then used for further analysis. The probability of perfect capsids (in which every site is ideally occupied) was determined separately.

Results

Defective capsids in cryo-EM images

Analysis of cryo-EM image data by random sampling of single-particle images yields populations of different types of defects and provides strong motivation for the theoretical analysis to follow. We collected images from three cryo-EM micrographs of HBV capsids, and examined samples of images manually to determine whether they contained defects and what kinds of defects they were. We examined both the entire stack of images obtained by template-based autopicking in RELION (14,47,48), as well as a filtered stack (subset) obtained by 2D classification. We note that only 600 of 1618 total T = 4 capsid particles were used in the original structure publication (12) due primarily to technological constraints, but likely resulting in a selection of the best one-third of the particle data set and avoiding defective capsids.

About one-sixth of the images from the filtered stack have visible defects (Table 1). A larger proportion of the images in the original stack also show defects; some of these images were filtered out by the classification steps that were used to create the filtered stack. The samples of images themselves are shown in Figs. S1 and S2 and descriptions of which images exhibit what kinds of defects are shown in Tables S2 and S3. The template-based autopicker selected a large number of image centers that were located midway between several capsid particles, resulting in images that consisted of parts of multiple capsids. Almost all of these images were filtered out by the 2D classification.

Table 1.

Classification of Defective Capsids Identified from Inspection of Electron Micrographs of the HBV Capsid

Stack	Entire	Filtered
Total number of images in stack	17,790	4940
Sample size	100	100
Images containing parts of multiple capsids	64	0
Images not containing a visible capsid, or partially obscured	3	1
Images showing extra lines, additional dimers, or “buds”	0	8
Images with one missing dimer	8	7
Images with multiple missing dimers	2	0
Images with an elongated or noncircular capsid	2	0
Images with unusually small capsids	4	0
Images with small capsids that also have a missing dimer	5	0
Total fraction of defective capsids	17%	16%

Descriptions of individual images are shown in Fig. S2 for the entire stack and Fig. S3 for the filtered stack. The images themselves are shown in Fig. S2 for the entire stack and Fig. S2 for the filtered stack.

The cluster mean images obtained by automatic 2D classification of the filtered stack are shown in Fig. 3 and the distribution is shown in Table S1. During the classification, some of the clusters became empty so that RELION produced a total of 22 clusters at the end of the E-M iterations. Almost all the images (98.5%) were classified into a set of clusters representing “perfect” capsids (clusters 11, 16, 24, 26, 29, 30, 32, 41, and 46) despite visual evidence to the contrary. RELION did identify a few clusters that appear to represent defective capsids. For example, cluster 47 appears to contain HBV capsids that are missing a dimer along the outer edge as seen in the micrograph, whereas cluster 42 appears to contain incomplete capsids that are missing multiple such dimers, similar to those shown in the “incomplete” column of Fig. 1. Clusters 35 and 45 appear to contain elongated capsids similar to those portrayed in the “distorted” column of Fig. 1. However, these clusters together account for only 1.5% of the filtered stack.

Figure 3.

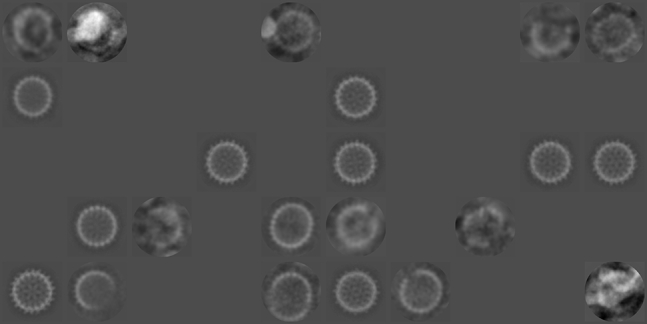
Cluster means obtained from automatic 2D classification of the filtered stack. During the classification, some of the clusters became empty so that RELION produced a total of 22 clusters at the end of the E-M iterations.

Calculated structural heterogeneity in a hepatitis B viral capsid lattice model

To assess the propensity for defects in a tractable model suited to distinguishing perfect capsids from those with moderate defects, we analyze the lattice model described above in the Model for capsid formation section (Fig. 2).

In brief, each discrete site of the model can either be empty, occupied ideally as in a perfect capsid, or “misoccupied” in a deviated conformation or orientation. Each site interacts only with its nearest neighbors. Semimicroscopic free energy parameters account for average atomistic interactions: $\mathrm{\Delta }{G}_{\text{ideal}}$ is the interaction energy between two ideally occupied sites, $\mathrm{\Delta }{G}_{\text{mixed}}$ for ideal-misoccupied neighbors, and $\mathrm{\Delta }{G}_{\text{defect}}$ for two misoccupied neighbors. As our analysis shows, the dominating parameter is the difference between ideal and ideal-misoccupied pairs: $\mathrm{\Delta }\mathrm{\Delta }G=\mathrm{\Delta }{G}_{\text{mixed}}-\mathrm{\Delta }{G}_{\text{ideal}}$, which generally will be positive because of weaker nonideal interactions. The chemical potential μ controls the overall subunit concentration, and we confirmed the expected increased favorability of larger (partial) capsids with higher subunit concentration and stronger ideal interactions (data not shown).

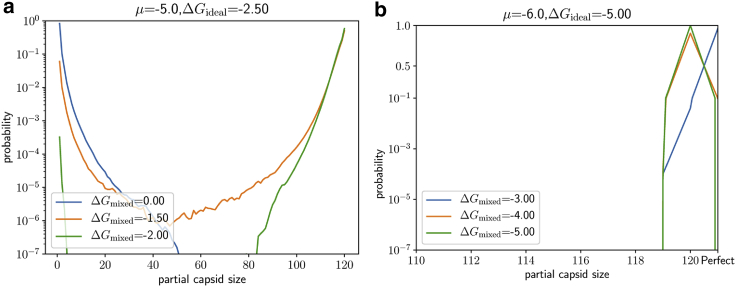
The model makes informative predictions regarding structural heterogeneity. Fig. 4 shows the distribution of the number of occupied sites, and importantly, there is always some population of imperfect capsids, which becomes dominant in some regions of parameter space. For the chosen sets of parameters, the distributions have two peaks, one corresponding to a nearly fully formed capsid, the other corresponding to an isolated subunit. In a model with fewer sites, or in typical experiments, the heterogeneity within each peak might not be resolved, depending on the experimental technique used.

Figure 4.

The distribution of partial capsid sizes from Monte Carlo simulation. (a) When $\left(\mu ,\mathrm{\Delta }{G}_{\text{ideal}}\right)=\left(-5.0,-2.5\right)$, the distribution of capsid sizes shows two peaks corresponding to nearly complete capsids and isolated dimers. Once $\mathrm{\Delta }\mathrm{\Delta }G=\mathrm{\Delta }{G}_{\text{mixed}}-\mathrm{\Delta }{G}_{\text{ideal}}\underset{\sim }{<}2k_{B}T$, as holds for all three curves, there is an appreciable population of partially formed capsids and even a depletion of full capsids for weaker interaction strengths. (b) When $\left(\mu ,\mathrm{\Delta }{G}_{\text{ideal}}\right)=\left(-6.0,-5.0\right)$, which roughly corresponds to experimental value of $\mathrm{\Delta }{G}_{\text{ideal}}$, the distribution consists primarily of larger partial and full capsids, shown here in magnified view. Note that ∼10% of capsids remain imperfect even for $\mathrm{\Delta }{G}_{\text{mixed}}=-3k_{B}T$.

Interestingly, the probability minimum between these peaks increases with $\mathrm{\Delta }\mathrm{\Delta }G$, which we ascribe to entropic effects, echoing recent work (49,50). Adding a third state increases the number of possible configurations, and in particular for larger capsids, there are more ways to mix fully occupied and misoccupied states. For example, when $\mathrm{\Delta }\mathrm{\Delta }G$ is very high the model will effectively be a two-state model, with only empty and fully occupied sites. In adding a third state to the model, the number of possible configurations with M sites occupied will be multiplied by $2^M$ because there are now two possible ways to occupy each site. If $\mathrm{\Delta }\mathrm{\Delta }G=0$ each of these $2^M$ configurations will have the same energy and consequently the overall probability of observing M sites occupied will be multiplied by $2^M$ and the entropy of this state will be increased by $k_{B}M\text{log}2$. If $\mathrm{\Delta }\mathrm{\Delta }G$ is low but greater than zero, the additional configurations will have higher energy than those in the two-state model, so the entropy will still increase but not by as much. Therefore, the entropy associated with large capsids is greater when there is a misoccupied state whose energy is close to that of the fully occupied state, and hence larger capsids will be favored.

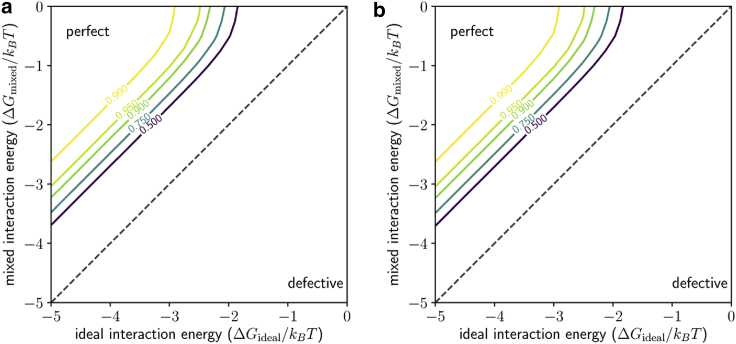
When do structurally “perfect” capsids predominate, and when are defective capsids significant? Fig. 5 shows the proportion of perfect capsids in which all sites are ideally occupied based on both MC simulations and analytical results obtained using the isolated-defect approximation Eq. 8. The proportion of perfect capsids depends predominantly on the difference $\mathrm{\Delta }\mathrm{\Delta }G=\mathrm{\Delta }{G}_{\text{mixed}}-\mathrm{\Delta }{G}_{\text{ideal}}$, and shows a critical threshold of $\mathrm{\Delta }\mathrm{\Delta }G\approx 2.5k_{B}T$. Below this threshold (stronger nonideal interactions), the fraction of defective capsids can become significant, whereas above it, and for a sufficient interaction strength, structurally perfect capsids predominate, although the fraction is below this threshold. At $\mathrm{\Delta }\mathrm{\Delta }G\approx 2k_{B}T$, the fraction of defective capsids is ∼10%, roughly matching what was observed in the cryo-EM images. As $\mathrm{\Delta }\mathrm{\Delta }G$ decreases, the many imperfect but complete capsid configurations in which some sites are misoccupied, but no sites are vacant, come to have the same energy and hence entropically dominate the system, as described above. The threshold of $2.5k_{B}T$ represents the point at which the lower energy of an ideally occupied site outweighs this entropic effect. We have also confirmed that the value of $\mathrm{\Delta }{G}_{\text{defect}}$ has little impact on the probability of perfect capsids, as demonstrated by plots of the perfect capsid probability for various values of $\mathrm{\Delta }{G}_{\text{defect}}$ (Fig. S6). We also note that the approximation is akin to a dilute fluid of noninteracting defects, and matches MC results extremely well because it is accurate in the “near-perfect” regime of interest.

Figure 5.

When are perfect capsids expected? (a) Contour plots are shown of the fraction of perfect capsids $p_{\text{perf}}$ as determined from Eq. 8 and (b) $p_{\text{perf}}$, as determined from MC simulations, both in the $\left(\mathrm{\Delta }{G}_{\text{ideal}},\mathrm{\Delta }{G}_{\text{mixed}}\right)$ plane (chemical potential and ideal interaction energy) for $\mu =-2.0k_{B}T$. To see this figure in color, go online.

Model prediction for arbitrary spherical capsids

Because the model is specific to HBV only based on the number of sites (subunits) N and the number of nearest neighbors per site k (Materials and Methods), theoretical analysis can readily be extended to arbitrary spherical viral capsids based on those two parameters. Although extending our lattice strategy to nonspherical shapes/defects is not difficult in principle, here, we prioritize tractability in an effort to quantify expectations for defects in the important class of spherical viruses.

In the presumably high-concentration milieu (large chemical potential μ) in which capsids assemble, we can develop an analytical expression Eq. 8, for fractional population of perfect capsids $p_{\text{perf}}\left(N,k,\mathrm{\Delta }\mathrm{\Delta }G\right)$ solely in terms of the two geometric parameters and the difference $\mathrm{\Delta }\mathrm{\Delta }G$ between mixed and ideal interactions. As before, we have fixed as constant the unimportant parameter $\mathrm{\Delta }{G}_{\text{defect}}$. To graphically interpret the equation, we invert it to obtain the threshold value of $\mathrm{\Delta }\mathrm{\Delta }G$ below which the fraction of defective capsids $p_{\text{perf}}$ exceeds a specified threshold:

$$\mathrm{\Delta }\mathrm{\Delta }G/k_{B}T=-\frac{1}{k}\text{log}\left(p_{\text{perf}}^{-1/N}-1\right)$$ (10)

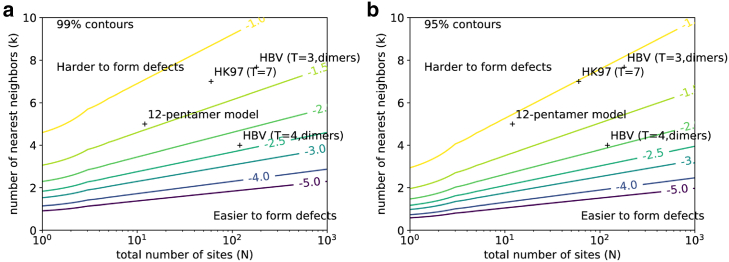
The analysis allows a theoretical characterization of whether defects should be expected based on geometric considerations. Fig. 6 shows the minimal ΔΔG value needed for an arbitrary spherical virus, defined by N and k, to exhibit an overwhelming population of perfect (defect-free) capsids. Below the $\mathrm{\Delta }\mathrm{\Delta }G$ threshold, defective interactions are competitive with ideal interactions given the entropic characteristics of the particular lattice. Above the threshold for a particular $\left(N,k\right)$ pair, perfect capsids predominate. Hence, if the threshold is smaller, a bigger range of ΔΔG values leads to a near-perfect population and fewer defects should be anticipated. Conversely, a larger $\mathrm{\Delta }\mathrm{\Delta }G$ threshold requires stricter structural selectivity for ideal versus mixed neighbor interactions. Based on this analysis, perfect capsids are seen to be most favorable at smaller N and larger k, and defects more to be expected at larger N and smaller k.

Figure 6.

Tolerance of defects for arbitrary spherical viruses. Shown are contour plots of the minimal ΔΔG-value needed to ensure a high proportion of capsid formation, given the total number of subunits N and the number of nearest neighbors k. If $\mathrm{\Delta }\mathrm{\Delta }G$ is above the minimal threshold for a given $\left(N,k\right)$ pair, perfect capsids predominate; below the threshold, there will be a substantial fraction of defects. Contours are based on 5. (a) 99% capsid formation is shown; (b) 95% capsid formation is shown. Values of N and k for selected viruses are plotted as well. The “12-pentamer model” refers to (28). To see this figure in color, go online.

We note that graph structure enters Eq. 10 only via N and k values for a given $\mathrm{\Delta }\mathrm{\Delta }G$. This stems from the dilute defect assumption, which is directly pertinent to examining perfect and near-perfect capsids.

Discussion

Our study questions the conventional wisdom that assembled virus capsids are essentially defect-free. A close review of HBV micrographs and analysis of a physiologically motivated statistical-mechanical model suggests significant fractions of defects can indeed be present and are likely under a range of conditions. The defective particles present in cryo-EM micrographs are usually rejected for being quite variable in structure and presumed to be physiologically off-pathway. Consistent with our findings, one previous study of woodchuck HBV capsid assembly using both CDMS and cryo-EM identified several types of defects similar to those seen here, including elongated particles and broken particles with spiral-like morphologies; ∼20% of the images showed elongated particles (40). Likewise, defects are a hallmark of computational models where defects are possible (22, 23, 24, 25, 26).

The analysis presented in this work, relying on visual inspection of cryo-EM images, is necessarily somewhat subjective because of the high level of noise in the images, and it is possible that, for example, variations in the noise level across the images could make it appear that a dimer is missing when in fact it is not. Because of the limited number of images and the diversity of possible defects, RELION was only able to classify a small proportion of the defective images together in a class. Even if not every image of a defective capsid is genuine, however, defective capsids may constitute a sizable proportion of the sample under study reflecting the innate assembly fidelity of the complex as well as aspects of sample preparation, and may offer insights into assembly that could be exploited for antiviral or other therapeutic purposes. Such heterogeneity in cryo-EM structures is now taken to be a fundamental part of structural biology (51, 52, 53, 54), and we hope that our findings will motivate similar analyses of other systems and other data sets.

Our theoretical model, although still greatly simplified, advances prior theoretical work in several ways. Generally speaking, our model incorporates more realistic and combinatoric possibilities than the seminal early model of Zlotnick (28) and follow-up work (30). We also find two-state behavior, mostly assembled and mostly disassembled, but the greater granularity of our model clearly shows that what appeared to be a uniform assembled state in the prior work consists of an “ensemble” of nearly fully assembled configurations in large parts of parameter space. That is, defects are common, both as vacancies and/or misassembled sites. A model somewhat similar to ours, though without misoccupied sites, also found a substantial imperfect population (32,33) Our theoretical analysis indicates that, in the dilute-defects limit appropriate to analyzing the degree of perfect capsid formation, the number of nearest neighbors (edges per node) and graph size (number of nodes) govern the likelihood of perfect capsid formation for a given set of thermodynamic parameters.

Our model has implications for the design of inhibitors of virus capsid assembly, which have received significant interest as a novel class of therapeutics for HIV (55, 56, 57) as well as for HBV (58, 59, 60). The model suggests that it is possible to design two distinct types of inhibitors: ones that block or destabilize ideal interactions between capsid subunits, and ones that stabilize nonideal interactions. In the case of HIV, both of these kinds of inhibitors have been developed (55, 56, 57). Coarse-grained simulations of the HIV-1 capsid protein suggest that the capsid assembly inhibitor PF74, a tripeptide mimic (61), works by stabilizing trimers of dimers, which then interact with partially assembled capsids in such a way as to encourage them to form incorrect assemblies (57). For HBV, the focus has been on developing modulators of capsid assembly that may either accelerate or inhibit functional capsid assembly, depending on circumstances. For example, the inhibitor BAY-41-4109 exhibits different behaviors depending on the stoichiometric ratio relative to the capsid dimers. At a low ratio, it accelerates capsid growth, whereas at a higher ratio, it causes capsids to misassemble into “voids” or polymers (62). There is a binding site on the capsid for assembly modulators that can either trigger assembly or disassembly, depending on how the modulator is bound and what conformation it adopts (63). Knowledge of the principles behind assembly should be useful for guiding the design of inhibitors that block or hijack the capsid assembly process.

One limitation of the statistical-mechanical model described here is that it considers the formation of only one capsid at a time from an ideal solution of free subunits. The possible defects are limited to vacant sites or sites with partially attached subunits. In other simulations, using structurally more realistic models, more complex structures were formed. For example, the Brooks group obtained a variety of irregular capsids, including twisted, tubular, prolate, and conical capsids, as well as partially formed capsids with missing subunits and open misaggregates consisting of two partial capsids joined together (23,24). Furthermore, the model described here is a thermodynamic model and implicitly assumes that all configurational transitions are reversible. Consequently, it cannot be used to study defective capsids occurring as a result of kinetic trapping or irreversible transitions, as has been observed in other simulations (1,18,25,64, 65, 66). This could be remedied by defining kinetic laws for transitions between configurational states.

The parameter $\mathrm{\Delta }{G}_{\text{ideal}}$, the interaction free energy, must include all environmental factors, including temperature and ionic strength. The experimental values for the interaction strength among HBV capsid subunits range from approximately −3.2 to −4.4 kcal/mol (35), which correspond to values of $\mathrm{\Delta }{G}_{\text{ideal}}$ from approximately −5 to −7 $k_{B}T$, on the upper end of the values considered here. The lower values are more consistent with physiological conditions; the strength of the intersubunit interaction increases with increasing temperature and ionic strength because of the primarily hydrophobic nature of the forces that hold the capsid together. Experimental studies comparing woodchuck and human HBV also demonstrate that the two capsid proteins, despite having ∼65% sequence identity and forming very similar assembled capsid structures, have very different thermodynamics of assembly, with that of woodchuck HBV having a stronger entropic contribution to assembly (36).

There are also many ways in which our model can be modified to accommodate other viruses with protein capsids besides HBV that have different capsid compositions or geometries. For example, the model may be extended to capsid geometries with different T values by specifying different contact graphs $\mathcal{G}$. Also, many capsids have two or more types of subunits with different sequences, although usually, the number of types is limited, and the different types have similar folds (31). To accommodate this, a separate value of the chemical potential μ could be defined for each type of subunit and a separate set of interaction parameters $\mathrm{\Delta }{G}_{\text{ideal}}$, $\mathrm{\Delta }{G}_{\text{mixed}}$, and $\mathrm{\Delta }{G}_{\text{defect}}$ could be used for each possible interactions between different types of subunits within the capsid.

Conclusions

To investigate systematically the potential for defect formation in virus capsids, we developed a statistical-mechanical model that incorporates more realistic capsid geometry than prior work, as well as taking into account the possibility of weaker intersubunit interactions due to partial attachment of subunits. The model, which is applicable to arbitrary spherical capsids, is motivated by the substantial fraction of defective particles (∼1 in 6) occurring in a re-analyzed set of HBV capsid micrographs.

Both analytical approximations and Monte Carlo simulations of the model reveal that significant proportions of defective capsids can form when the difference in interaction strengths between ideal and defective subunits is below a threshold that depends only on geometric properties of the capsid. This implies that capsid assembly can be inhibited equally well by blocking ideal interactions or by stabilizing nonideal ones. Although significant work remains to be done in extending the model to allow a greater variety of defects, and in clarifying the physical meaning of the parameters, these results demonstrate that the concentration of defective capsids can be more significant under certain conditions than previously appreciated. We believe the proposed model provides a paradigm that will be useful in understanding and designing a wide range of experiments.

Author Contributions

J.S. performed research, analyzed data, wrote computer code, analyzed cryo-EM images, and wrote initial draft of manuscript. J.F.C. designed and oversaw research, analyzed cryo-EM images, and edited manuscript draft. D.M.Z. designed and oversaw research and revised manuscript.

Editor: Yuji Sugita.