Mechanical Forces Regulate Asymmetric Vascular Cell Alignment

Abstract

Mechanical forces between cells and their microenvironment critically regulate the asymmetric morphogenesis and physiological functions in vascular systems. Here, we investigated the asymmetric cell alignment and cellular forces simultaneously in micropatterned endothelial cell ring-shaped sheets and studied how the traction and intercellular forces are involved in the asymmetric vascular morphogenesis. Tuning the traction and intercellular forces using different topographic geometries of symmetric and asymmetric ring-shaped patterns regulated the vascular asymmetric morphogenesis in vitro. Moreover, pharmacologically suppressing the cell traction force and intercellular force disturbed the force-dependent asymmetric cell alignment. We further studied this phenomenon by modeling the vascular sheets with a mechanical force-propelled active particle model and confirmed that mechanical forces synergistically drive the asymmetric endothelial cell alignments in different tissue geometries. Further study using mouse diabetic aortic endothelial cells indicated that diseased endothelial cells exhibited abnormal cell alignments, traction, and intercellular forces, indicating the importance of mechanical forces in physiological vascular morphogenesis and functions. Overall, we have established a controllable micromechanical platform to study the force-dependent vascular asymmetric morphogenesis and thus provide a direct link between single-cell mechanical processes and collective behaviors in a multicellular environment.

Significance

Exploring the coordinated roles of traction and intercellular forces in regulating cell asymmetric arrangement in a multicellular environment has critical implications during tissue development, embryogenesis, and vasculogenesis. However, a comprehensive understanding of the mechanistic basis of these forces and vascular asymmetric morphogenesis remains incomplete. This study has specifically addressed the critical impact of mechanical forces on vascular asymmetric alignment within a micropatterned endothelial cell sheet and established a controllable micromechanical platform to study tissue asymmetric morphogenesis, which may further contribute to reversing physiological morphogenesis and functions in organ developments.

Introduction

Asymmetric morphogenesis is a common biological phenomenon in organismal bodies, tissues, and even in individual cells (1). Conventional studies treat the vascular network as a uniform network of vessels. However, the vascular system is, in fact, a highly asymmetric cellular system (2). Asymmetric cell alignment, also termed polarized alignment, represents the unidirectional cell arrangement in a multicellular environment, which is different from the symmetric or nondirectional cell alignment. Recent studies implied that the asymmetric alignment of vascular endothelial cells (ECs) would be critical to maintain vascular functions such as endothelial multicellular permeability (3,4). Changes in the asymmetric vascular cell alignment due to genetic or environmental factors, such as diabetes (5) and nanomaterial toxicity (6), can lead to vascular maladaptation and dysfunction, which are the initial step in the pathogenesis of cardiovascular diseases, stroke, chronic kidney failure, cancer, and infectious diseases (3). For instance, high concentrations of glucose can disrupt vascular junctional proteins via protein kinase C (7) and increase vascular cell permeability with impaired asymmetric cell alignments (4). Genetic deficiency in SMAD4, which is usually present in hereditary hemorrhagic telangiectasia patients, can induce loss of asymmetric vascular cell alignments (8) and abnormal blood vessel structures and functions (9).

Although the asymmetric morphogenesis of organs and tissues has been extensively studied, little is known about the mechanisms at cellular and multicellular levels. To date, a variety of mechanisms have been reported for the multicellular asymmetric morphogenesis (1,10,11). The most popular and well-accepted theory is the “two-cilia hypothesis” (12), a mechanical sensing organelle that can sense the mechanical force. In the periphery, mechanosensitive channels on non-lrd-containing immotile cilia sense the force and give rise to imbalance signals, which leads to the asymmetric development (13). Although this hypothesis can explain several aspects of physiological behaviors (12), increasing evidence suggests that other signaling and mechanism should be involved to explain the asymmetric cell arrangement behaviors (1,10), especially in confined microenvironments (14, 15, 16). Recent studies found that the asymmetric cell alignments both in two-dimensionality and three-dimensionality depend on the cell phenotype and mechanical forces (14,16). For instance, cell actomyosin activity is considered important in this phenomenon because inhibition of actin assembly and actomyosin activity abolished the asymmetric rearrangements in stagnalis (17), zebrafish heart (18), and micropatterned tissues (15). However, how different mechanical forces regulate the asymmetric cell alignment in these processes remains unknown.

In the in vivo environment, cells encounter various mechanical signals transmitted by the surrounding extracellular matrix (ECM) and neighboring cells (19). For instance, during development, the specification and self-organization of migrating cells are mediated by physical boundaries imposed by the ECM and the surrounding tissues. Therefore, the forces from cell-matrix interaction (traction force) (20,21) and cell-cell interaction (intercellular force) (22,23) individually and collaboratively play vital roles in regulating cell arrangement and cell/tissue homeostasis (24, 25, 26). Recent studies demonstrate that the in-plane maximal shear stress drives cell alignment in confined micropatterns (27), although whether the cell alignment is asymmetric is unknown. Hence, exploring the coordinated roles of traction and intercellular forces in regulating the asymmetric cellular arrangement in a multicellular environment has critical implications during tissue development, embryogenesis, and vasculogenesis.

Here, we investigated how the traction and intercellular forces impact vascular asymmetric alignment and arrangement. Using an integrated mechanobiology platform, we mapped the single-cell traction and intercellular force profiles as well as the degree of asymmetric cell alignment within micropatterned endothelial ring-shaped monolayers. We highlight the interplay of traction and intercellular forces in regulating asymmetric cell alignment in a multicellular environment and thus provide a direct link between single-cell mechanical processes and collective behaviors in vascular morphogenesis.

Materials and Methods

Cell culture and reagents

Mouse ECs (C166-GFP; American Type Culture Collection, Manassas, VA) derived from mouse yolk sac were cultured in Dulbecco’s Modified Eagle Medium (Sigma-Aldrich, St. Louis, MO) supplemented with 10% fetal bovine serum (Sigma-Aldrich) and 0.2 mg/mL Geneticin (Gibco Laboratories, Gaithersburg, MD). Diabetic mouse aortic ECs (MD-6052; Cell Biologics, Chicago, IL) were cultured in endothelial cell medium (GPF1168; Cell Biologics).

Preparing polyacrylamide gel substrate for traction force microscopy measurement

Polyacrylamide (PAA) gels with an elastic moduli of 16.2 kPa were manufactured by mixing 40% acrylamide (Sigma-Aldrich), 2% bis-acrylamide (Sigma-Aldrich), and 0.4% fluorescent beads (F8833; Thermo Fisher Scientific, Waltham MA) as previously reported (28). To initiate the reaction, 10% ammonium persulfate (Sigma-Aldrich) and 0.1% tetramethylethylenediamine (Sigma-Aldrich) were added to the acrylamide and bis-acrylamide mixtures with orange fluorescent (540/560) microbeads (Thermo Fisher Scientific). After creating the gel solution, it was coated onto an aminosilane (Sigma-Aldrich)-activated cover glass substrate and covered with another coverslip pretreated with dichlorodimethylsilane (Sigma-Aldrich) to facilitate the release of the gel from the glass. The gel-coated coverslips were flipped upside down to allow the fluorescent beads to settle to the top of the gel layer and left to fully polymerize for 30 min at room temperature. After polymerization and cover glass removal, the gel was treated with 0.2 mg/mL sufosuccinimidyl-6-(4′-azido-2′-nitrophenylamino)-hexanoate (Pierce Biotechnology, Waltham, MA) diluted using phosphate-buffered saline (pH 7.4) (Thermo Fisher Scientific), to facilitate the bonding of fibronectin (50 μg/mL; Sigma-Aldrich) to the PAA gel under ultraviolet light (UVM-57; Analytik Jena, Jena, Germany) exposure for 30 min.

Microcontact printing of EC monolayers

Mouse vascular ECs were micropatterned into ring-shaped monolayers on the PAA gel substrate to mimic vascular lumens using a microcontact printing approach (14,16). Briefly, master micropatterns were fabricated using SU-8 (MicroChem, Westborough, MA) photolithographic technique on silicon wafers. Polydimethylsiloxane (Dow Corning, Midland, MI) stamps were made by replica molding of the SU-8 mask for the subsequent microcontact printing of adhesive molecules onto the PAA gel substrates. The polydimethylsiloxane stamp was then coated with fibronectin (50 μg/mL) and Alexa Fluor 647-conjugated fibrinogen (Thermo Fisher Scientific) for 1 h. After washing, the stamp was pressed onto the PAA gel for 10 min to transfer the adhesive molecules onto the PAA gel substrate. Finally, the PAA gel substrate was blocked with 0.2% Pluronic solution (Sigma-Aldrich) to prevent adhesion between cells and the nonpatterned region. After the microcontact printing, the PAA gel substrate was put in a 60-mm confocal dish, and 10⁵ ECs were then plated onto each micropatterned substrate and cultured for 24 h to form a cell colony monolayer within the defined patterns before imaging.

Live-cell imaging and cell alignment quantification

The live-cell nuclei were stained with Hoechst 33342 (2 μg/mL; Thermo Fisher Scientific) for live-cell imaging with an inverted fluorescent microscope (ZEISS Microscopy) at ∼37°C. The nucleus images were processed in ImageJ (National Institutes of Health, Bethesda, MD), and a customized MATLAB (The MathWorks, Natick, MA) code was used to determine the alignment angle for each cell based on the angle of the nucleus long axis in the vascular patterns.

Traction force measurement

The traction forces generated by individual cells in the EC monolayer were measured using a standard traction force microscopy (TFM) method on PAA gel substrates with embedded fluorescent beads (Fig. S1 a; (26,28)). After cells were patterned on the PAA gel substrates, fluorescent images were first taken to record the locations of the fluorescent beads underneath the cells using an inverted fluorescent microscope (ZEISS Microscopy) with a 40× objective and an sCMOS camera (Hamamatsu, Hamamatsu City, Japan). Postimaging cell lysis was then performed by adding 100 μL of 1 N NaOH (Sigma-Aldrich) to the cell culture dish to remove the cells. Postlysis fluorescent images of the same study areas were taken to record the locations of the fluorescent beads after cell removal. The postlysis images, along with the prelysis images, were used for calculating the displacements of each fluorescent bead underneath the cells using particle image velocimetry. Displacements calculated using particle image velocimetry were then used to calculate the local traction force exacted by the cell using fast Fourier transform cytometry (29).

Intercellular force calculation

A previous finite element method (FEM) was used to calculate the intercellular force (Fig. S1 b; (26,30)). Briefly, the confined micropatterns were modeled as a thin, deformable, linearly elastic, and isotropic plate by assuming all cells were connected perfectly with neighbors. The plate internal stress field was first solved using a customized MATLAB code, which was related to the experimentally obtained displacement field in TFM. The intercellular force was then calculated by integrating the plate internal stress along the junctional boundary of neighboring cells. Cellular boundaries and cell positions were drawn by hand using the phase-field images of the cells to achieve the highest reliability. For details, see Supporting Materials and Methods.

Computational modeling of the force-mediated asymmetric cell alignment

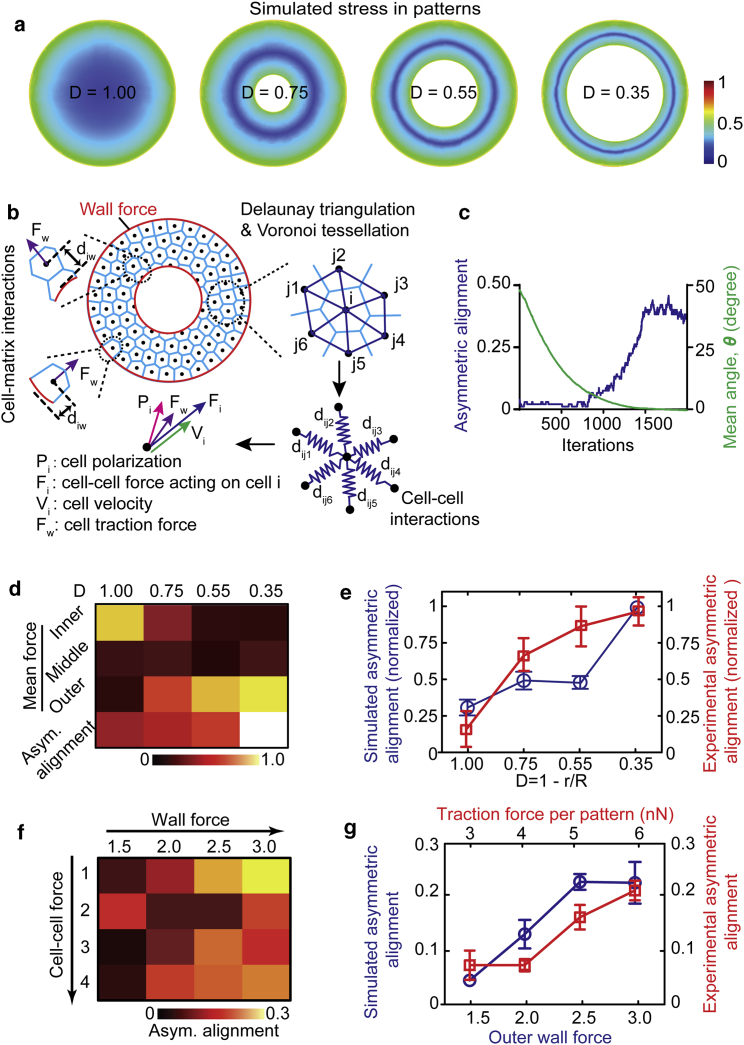
A previously established coherent angular movement (CAM) model was used to simulate the force-dependent asymmetric cell alignment behaviors in the ring-shaped vascular sheets (31). Briefly, as shown in Fig. 3 b, cells were assumed to be self-propelled active particles represented as discrete points at their center of mass with their inherent migration speed when moving with any external force. The confined vascular sheet was represented as a continuous sheet with cell-cell junctions and cell-matrix interactions. Cell-cell interactions were modeled as a spring system with conditions specified for repulsion, attraction, and neglection, based on the distance of two neighboring cells, to determine the forces (F_i) applied on the cell due to neighboring cells. Two wall forces (F_wall) were applied to both boundaries to ensure the confinement of the cell in the pattern, whereas an inward wall force on the outer pattern boundary and an outward wall force on the inner pattern boundary were set to stop the cell from leaving the outer pattern boundary. The cell-matrix traction force (F_w) at different position in the pattern was varied as a negative exponential function of the distance between cells from each boundary. Cells in the patterns were generated at random locations with random directions of initial cellular velocity at the start of the simulation. With the presence of surrounding cells, the cell migration velocity (V_i) was determined by the total force applied by the surrounding cells. The cell’s polarization vector (P_i) was assumed to orient with the direction of cell’s motion. The polarization coordination constant (nondimensional value of 0.5) was used to determine the tendency of cell’s polarization to rotate and align with the migration velocity vector. Note that all parameters are nondimensional, and no cell proliferation was considered for all the simulations. To analyze the asymmetric cell alignment index in a pattern in the simulation, all the cell’s polarization orientations were used to calculate the cell alignment angle and overall asymmetric alignment index. The force and polarization orientations per cell at different radial difference to pattern centers were analyzed to investigate the dynamic of force changes over the iteration time. For details, see Supporting Materials and Methods.

Figure 3.

Biophysical modeling of the force-dependent asymmetric cell alignment in the micropatterned vascular monolayer. (a) Simulated stress in different micropatterns is shown. The simulated micropatterns have the same sizes of the expertimental systems. The color coding represents the normalized magnitude of total von Mises stress on the bottom fixed surface, where 0 represents the minimal stress and 1 relates to the maximal stress. (b) A schematic shows an active particles model to simulate the micropatterned ring-shaped vascular sheets. Cells are represented as points (black dots) at their centers. Cell-cell interactions are mimicked by Delaunay triangulation (deep blue), which finds the closest nearby cell points and determines the forces (F_i) applied on the cell and the movement speed (V_i) accordingly. Voronoi tessellation (light blue) is used to visualize cells. Wall force is applied at the inner and outer boundaries of ring cell pattern (red circles) using exponential functions. Note that all parameters are nondimensional for all the simulations. (c) Quantified results are given, showing progression and stabilization of asymmetric alignments (blue line) as the mean angle (θ) of cells in the ring pattern (D = 0.55) decreasing to 0° (green line) along the iteration times. (d) Calculated total force magnitude and overall asymmetric alignments in different micropatterns (D = 1, 0.75, 0.55, 0.35) at iteration time of 2000 in the simulation model are given. It shows that the narrower the ring pattern with smaller value of “D,” the higher the asymmetric vascular cell alignment and relative force. Wall force was set as 0.5 for the inner wall and 3.0 for the outer wall. (e) Simulated (blue) asymmetric alignments in different patterns are consistent with the experimental (red) overall asymmetric alignments (normalized to maximum) in different micropatterns. (f) Calculated asymmetric alignment indexes from simulation models with different wall force (1.5–3.0) and cell-cell force (1–4) conditions in the ring patterns (D = 0.55) are shown. (g) Simulated results (blue) show the asymmetric cell alignment index correlates with the outer wall force in the ring pattern (D = 0.55, n ≥ 3), and experimental results (red) show the asymmetric cell alignment index correlates with the traction force magnitude in each pattern. In simulation, outer wall force was screened from 1.5 to 3.0 while keeping inner wall force constant as 0.5, and cell-cell force was kept consistent as 1. For the curve of the experimental results, each data point 3.0, 4, 5, 6 nN represents the group of traction forces per pattern in the range of 3–3.5, 1.5–4.5, 4.5–5.5, or 5.5–6.0 nN. Error bars represent ± standard errors. To see this figure in color, go online.

Statistics

All experiments were repeated in at least three independent experiments and ≥11 patterns for each condition. All data shown with error bars represent the mean values, and the error bars are the standard errors. Data were compared using one-way analysis of variance followed by Tukey’s post hoc test in Prism (GraphPad Software, San Diego, CA) or an unpaired, two-tailed Student’s t-test in Excel (Microsoft, Redmond, WA). For all comparisons, p < 0.05 was considered statistically significant and marked with an asterisk.

Results

Vascular asymmetric morphogenesis in micropatterned endothelial cell sheets

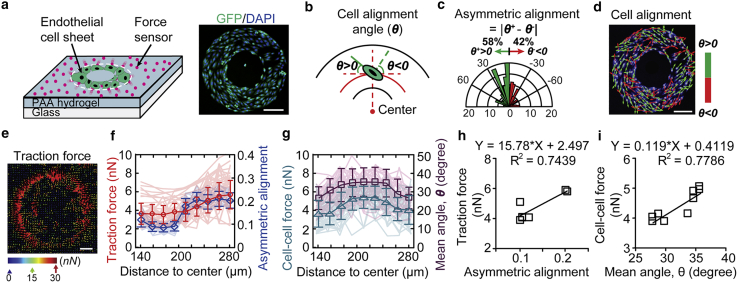
To study the vascular asymmetric morphogenesis, mouse vascular ECs (C166-GFP) were micropatterned into ring-shaped monolayers to mimic vascular lumens on force-sensing PAA gel substrates with an elastic modulus of 16.2 kPa using a microcontact printing approach (Figs. 1 a and S1; details in Materials and Methods; (14,16)). The ring-shaped vascular EC micropatterns had an inner diameter of 250 μm and an outer diameter of 550 μm. To visualize cellular arrangements, the nuclei of live ECs were labeled with Hoechst 33342 (Fig. 1 d, white) in fluorescent images and used to quantify the alignment angle (θ) of each cell in the micropatterns after a 24-h culture (Fig. 1, b–d). The cell alignment angle (Fig. 1 b, green lines) of each cell was defined as either positive (θ⁺ > 0; Fig. 1 d, green) or negative (θ⁻ < 0; Fig. 1 d, red), based on the deviation of the nucleus from the tangent direction (Fig. 1 b, red dashed line tangent to the red circle) (16). The asymmetric cell alignment index was defined between 0 and 1 as the absolute ratio difference of positive and negative cell alignment angles |θ⁺% − θ⁻%| in the pattern or the select region (Fig. 1 c).

Figure 1.

Vascular cells exhibit asymmetric morphogenesis on micropatterned geometries. (a) Schematic and staining images are shown, illustrating the platform for asymmetric vascular cell alignment and morphogenesis study with micropatterned ring-shaped vascular tissues (C166-GFP) on a mechanical-force sensing PAA hydrogel substrate. Scale bar, 100 μm. (b) The angle of cell alignment (green line) is defined as either positive or negative, based on the deviation from the tangent direction (red dash line tangent to the red circle). (c) A histogram of the mean angles of vascular cells and the definition of asymmetric alignment index based on the pattern in (b) is shown. (d) The alignment angle is illustrated as either green (positive angle) or red (negative angle) arrows. Note that the cell nuclei were stained with Hoechst 33342 (white) for angle quantification. Scale bar, 100 μm. (e) A representative color-coded force vector map in a micropatterned vascular sheet is shown. Scale bar, 50 μm. (f) Consistent trends between radial asymmetric alignments and traction force magnitude and (g) between cell alignment angles and cell-cell force magnitude at different radial positions on the ring (n = 35) are shown. Error bars represent ± standard errors. (h) A strong dependence of radial asymmetric cell alignments on traction force magnitude is shown. (i) A linear correlation of mean alignment angle with cell-cell force magnitude (n = 35) is shown.

We first investigated the morphological asymmetric alignments of cells in the micropatterns. A histogram of cell alignment angles in the micropatterned cell sheets in Fig. 1 c showed an overall asymmetric cell alignment index of 0.16, demonstrating the asymmetric morphogenesis in these ring patterns. A position-dependent analysis indicated a radial distribution of morphological alignments of cells in these ring patterns (Fig. 1 f, blue and Fig. 1 g, brown). We observed variable degrees of asymmetric cell alignment at different radial positions in the ring patterns, with stronger asymmetric cell alignment and lower mean cell alignment angles close to the inner and outer ring boundaries, whereas misalignments and weak asymmetric cell alignment were at the center of the ring patterns, which is consistent with previous studies (16).

Mechanical forces regulate vascular asymmetric morphogenesis in micropatterned endothelial cell sheets

To explore how the mechanical forces regulate the asymmetric cell alignments, traction forces exerted by individual cells in the micropatterns were measured using an established TFM method by tracking the displacements of the embedded fluorescent beads in the PAA substrates (Figs. 1 e and S1 a; (28)). Intercellular (cell-cell) forces between neighboring cells in the monolayer were further calculated based on the measured traction force data, using a previously established FEM model of a cellular monolayer as a thin sheet (Fig. S1 b; (26,30)). A position-dependent analysis revealed positive correlations of traction force magnitude with the asymmetric cell alignment index (Fig. 1, f and h) and intercellular force magnitude with the mean cell alignment angle at different radial positions (Fig. 1, g and i). Overall, cells closer to the outer ring boundary had a larger traction force value (∼6 nN) compared with those in the middle (Fig. 1, e and f, red), whereas a relatively stronger intercellular force occurred in the middle region of the ring pattern (Fig. 1 g, cyan). Hence, these results indicate that both the traction and intercellular forces are involved in regulating the vascular asymmetric morphogenesis.

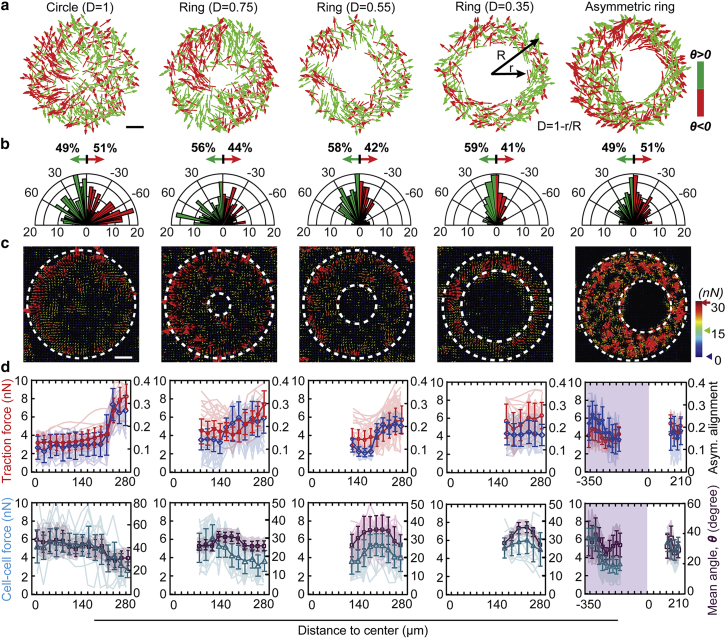
We further examined and compared the mechanical forces and asymmetric cell alignment in different micropatterns (Fig. 2). To illustrate the topographical features of micropatterns, parameter “D” was defined as D = 1 − r/R to indicate the width of the ring pattern, where r and R are the radii of inner and outer ring boundaries, respectively. We studied different topographic ring patterns with different inner diameters of 140, 250, and 360 μm, as well as a circular and an asymmetric ring patterns, while consistently maintaining the outer diameter as 550 μm to induce different cell force profiles (D = 1, 0.75, 0.55, and 0.35; Fig. 2 a) (32). We found that the overall asymmetric cell alignment index of the ring pattern decreased from 0.18 to 0.12 when the width of ring pattern increased from D = 0.35–0.75, whereas the circular pattern (D = 1) showed the lowest asymmetric cell alignment index of 0.02 (Fig. 2 b). Further radial cell alignment analysis indicated that cells exhibited similar trends in all patterns; that is, the closer to the pattern edge, the larger the radial asymmetric cell alignment (Figs. 2 d and S2, a and b). However, the radial asymmetric cell alignment index increased significantly in the inner and outer regions of narrow ring patterns (D = 0.35) as compared with wide ring patterns (D = 0.75) or circular patterns (D = 1), as shown in Fig. S2 a.

Figure 2.

Asymmetric vascular cell alignment correlates with traction and cell-cell forces in different geometric micropatterns. (a) The cell alignments within different geometric micropatterns are illustrated as either positive (green) or negative (red) arrows. Scale bar, 100 μm. (b) The histogram of the mean alignment angles of vascular cells demonstrated a stronger asymmetric cell alignment in the narrow ring patterns (D = 0.35) compared with the wide ring patterns (D = 0.75) or the circle pattern (D = 1). (c) Heat maps of traction force magnitude in different micropatterns are shown. Scale bar, 100 μm. (d) Quantified traction force magnitude (red curves), radial asymmetric cell alignment index (blue curves), cell-cell force magnitude (cyan curves), and mean alignment angle (purple curves) at different radial positions in different micropatterns are shown. Note that the consistent trends between traction force magnitude and radial asymmetric cell alignments and cell-cell force magnitude and mean alignment angle (n ≥ 22). Error bars represent ± standard errors.

To distinguish whether there is any preference for clockwise (CW) and counterclockwise (CCW) alignments, we quantified and compared the cell chirality, which is defined as the ratio difference of positive and negative cell alignment angles (θ⁺% − θ⁻%) (Fig. S3), of different types of patterns. Our results demonstrated different levels of asymmetric cell alignments in different patterns, and a preference of alignment toward negative angles (CCW) was observed in narrow rings (D = 0.35), but no obvious preference toward positive (CW) or negative (CCW) angles was observed in wide patterns of D = 1, 0.75, and 0.55.

We further examined and compared the radial distributions of traction (Fig. 2 c, red) and intercellular (Fig. 2 d, green) forces in different topographic patterns and observed similar trends in different ring patterns. However, the traction force magnitude in the middle regions of narrow ring patterns (D = 0.35; ∼6 nN) increased more significantly as compared with that in wide ring patterns (D = 0.75; ∼4 nN) and circular patterns (D = 1; ∼3.6 nN), as shown in Figs. 2 d and S2 c. Also, the intercellular force magnitude in the middle regions of ring patterns increased with the decrease of the of ring width and D parameter (Figs. 2 d and S2 d). Furthermore, along with similar force distributions, positive correlations between the traction force magnitude and the radial asymmetric cell alignment, the intercellular force magnitude and mean alignment angle were also demonstrated in all patterns (Fig. S4). Together, these findings suggested that cells at the ring boundaries prefer to align along the circumferential direction and exhibit larger radial asymmetric cell alignment, whereas cells in the middle region exhibit more random arrangements, which are likely dependent on the local traction and intercellular forces.

Moreover, we designed an asymmetric ring shape (Fig. 2 a) with features of both wide (D = 0.62) and narrow (D = 0.35) rings in one pattern to examine the impact of topographic features on asymmetric cell arrangement. Distinct force distributions and radial asymmetric cell alignments and chirality were observed in the two halves of narrow and wide regions (Fig. 2 d, purple region). The radial asymmetric cell alignment and chirality in the narrow region (Figs. 2 d and S5) were comparable with that in the symmetric ring patterns of the similar D parameter (D = 0.35). A negative (CCW) chirality of −0.12 was observed in the narrow region (D = 0.35), but no significant preference toward CCW was observed in the wide region of the asymmetric patterns (Fig. S5 b). In addition, a strong correlation between radial asymmetric cell alignment and traction force was observed as well (Fig. S4).

Biophysical modeling of the force-dependent asymmetric cell alignment in the micropatterned vascular monolayer

We next theorized the machinery of the force-dependent asymmetric cell alignment in the micropatterned vascular monolayer using analytical modeling (Fig. 3). We simulated the monolayer mechanics using a model of monolayer contraction against a fixed compliant substrate, which is used for replicating bulk tissue mechanical force in the micropatterns of the same sizes of the expertimental systems, as described in a previous study (details in Supporting Materials and Methods) (32). Consistent with the experimental results (Fig. 2 c), we found that the forces in the simulated system were concentrated along the edges of the micropatterns, with the outer edge experiencing a higher magnitude of force as compared with the middle edge in different patterns (Fig. 3 a). In particular, the narrower the ring is, the higher the mean of overall force exhibited on substrates. When compared with our experimental results (Fig. 2 c), the high mean overall force in the narrow ring patterns (D = 0.35) likely corresponds to the high asymmetric cell alignment.

Studies of cellular behaviors in confined micropatterned geometries have demonstrated the CAM and the emergence of cell alignments (31). Here, we further adopted a model based on the concept of CAM as described in a previous study (31) to explore the effect of mechanical forces upon guiding the asymmetric cell alignment in the confined vascular monolayer patterns (Fig. 3 b). Cell polarization orientations were supposed to orient to the cell movement direction. Delaunay triangulation and Voronoi tessellations were used to connect the cell populations and visualize each cell body (31). To simplify the modeling, the polarization angle (P_i) was represented by the preferential direction of the cell’s movements, which tend to align with its velocity vector (V_i). This model uses the inherent mobility of cells to simulate the cell-ECM traction forces and uses intercellular interactions and an arresting wall force to simulate the cellular motion in a confined cellular monolayer (details in Materials and Methods and Supporting Materials and Methods). Wall forces (F_wall) were applied both at the inner and outer boundaries of the ring cell pattern to ensure the cell confinement (Fig. 3 b, red circles). The cell-matrix traction force (F_w) at different position along the radial direction in the pattern was varied as a negative exponential function of the distance between cells from each boundary. Depending on the distance between cells, cells in the pattern experienced adhesive, repulsive, or no force along the vector connecting the cells. Thus, the overall imbalance (F_i) between intercellular and traction forces drive the cell movement in the sheet. Note that nondimensional parameters were used in all simulations to simplify the alignment angle analysis.

Ideally, cells in the pattern showed a progression and stabilization of asymmetric cell alignment as the mean angle (θ) of cells decreased to 0° along the iteration in the ring pattern (D = 0.55; Figs. 3 c and S6, a and b). Consistent with our experimental data, as shown in Fig. 2 d, the closer to the pattern edges, the larger the observed radial asymmetric cell alignment (Fig. S6 c). Force analysis indicted that at the initial iteration of 1, no obvious force difference was found along the distance to pattern center (Fig. S6 d). However, at an iteration of 1000 and 1500, the force of cells closer to the outer ring boundary exhibited an increased trend, which is consistent with the trend of radial asymmetric cell alignments (Fig. S6 b).

As expected, a strong asymmetric cell alignment in narrow rings (D = 0.35) as compared with wide rings (D = 0.75) and circular patterns (D = 1) is shown in Fig. 3, d and e, which is consistent with our experimental results (Fig. 2 b). To further examine whether asymmetric cell alignment would correspond to the mechanical force magnitude, we screened the asymmetric cell alignment index, traction, and intercellular force magnitudes at different radical positions in the ring patterns (D = 0.55) in both experimental measurements and simulation. We found that the larger the wall force applied at the outer boundary of the ring cell pattern, the stronger the asymmetric cell alignment (Fig. 3, f and g). Our experimental results indicated that the overall asymmetric cell alignment index of the pattern corelated with the traction force in the pattern (Fig. 3 g). Together, these results demonstrated that the asymmetric cell alignment phenomenon can be simulated in a mechanical force-propelled active particle model and further implicated that mechanical forces drive the asymmetric cell alignment in the confined micropatterns.

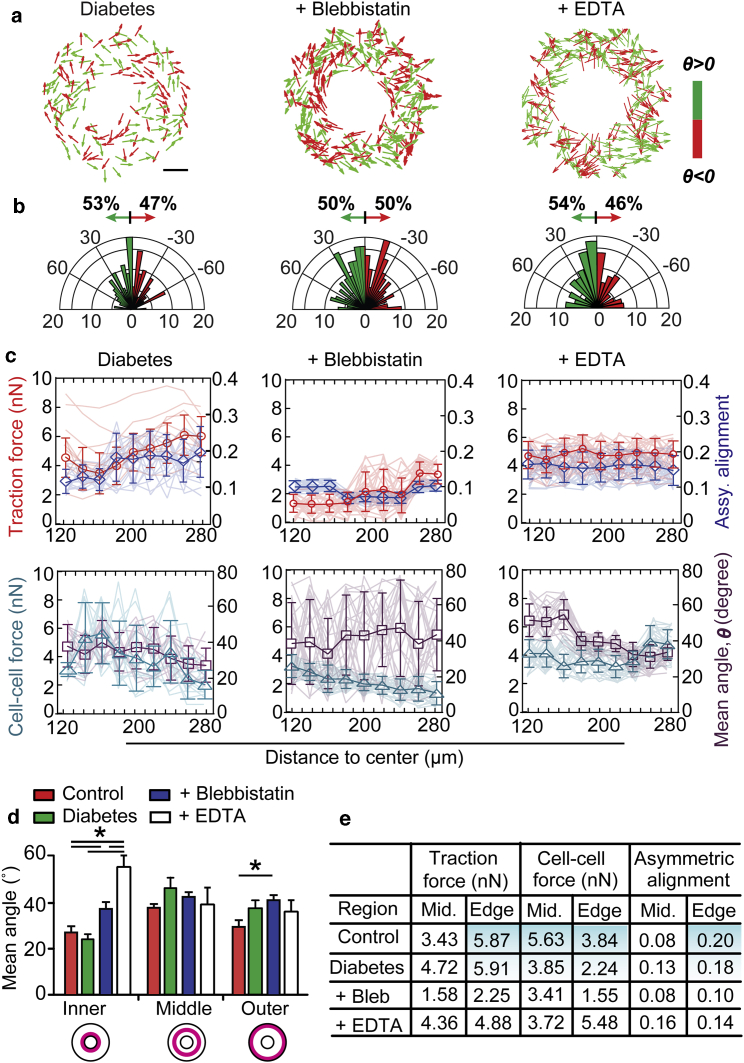
Cells with diabetes and dysfunctions in traction force and intercellular adhesion show disrupted asymmetric cell alignments

We next investigated the asymmetric cell alignment behaviors for diabetic aortic ECs (MD-6052; Cell Biologics) and ECs with abnormal traction and intercellular forces (Fig. 4). We found that the micropatterned diabetic EC sheets (D = 0.55) showed an overall asymmetric cell alignment index of 0.06 (Fig. 4 b), demonstrating a weaker asymmetric cell alignment in these diabetic EC ring patterns compared with the normal EC-formed patterns (0.16; Fig. 1 c). A position-dependent analysis of these diabetic EC ring patterns showed similar correlations of traction force magnitude with the asymmetric cell alignment index and intercellular force magnitude with the mean cell alignment angle at different radial positions (Fig. 4 c) with the normal EC ring patterns (Fig. 1, f and g). However, more misalignments and weaker asymmetric cell alignment in the inner and middle regions of the diabetic EC ring patterns were observed as compared with the normal EC ring patterns, which is largely due to the changes in the radial distributions of the traction and intercellular forces in these patterns (Fig. 4, d and e). These results indicate the potential pathological roles for mechanical forces and asymmetric cell alignment in vascular dysfunctions and diseases.

Figure 4.

Cells with diabetes and dysfunctions in traction force and intercellular adhesion show disrupted asymmetric cell alignments. (a) The cell alignments and (b) histogram of the mean alignment angles of diabetic aortic ECs and ECs treated with blebbistatin (10 μM) and EDTA (50 μM) to inhibit actomyosin activity or intercellular adhesion, respectively, in micropatterned vascular sheets (D = 0.55) are shown. The angles of cell alignment within different micropatterns are illustrated as either positive (green) or negative (red) arrows in (a). Scale bar, 100 μm. Note the decreased asymmetric cell alignment in micropatterns with diabetic ECs and treatments with blebbistatin and EDTA. (c) Quantified traction force magnitude (red curves), asymmetric cell alignment (blue curves), cell-cell force magnitude (cyan curves), and mean alignment angle (purple curves) at different radial positions in micropatterns with diabetic ECs and different drug treatments are shown. Note the disturbed correlation between traction force and radial asymmetric cell alignments or cell-cell force and mean alignment angle after drug treatments. Error bars represent ± standard errors. (d) Quantified mean alignment angles in micropatterns with diabetic ECs and under different pharmacological treatments are shown. Note that inhibiting traction force or intercellular adhesion decreased cell alignment with larger mean alignment angles in the inner and outer regions of the ring patterns, whereas there was no significant difference observed in the middle regions. P-values were calculated using one-way ANOVA. *, P < 0.05. (e) A table shows the quantified mechanical force magnitude and asymmetric cell alignment in micropatterns with diabetic ECs (n = 11) and under different pharmacological treatments (n ≥ 20). Note the decreased traction force and asymmetric cell alignment in diabetic ECs and micropatterns treated with blebbistatin.

To further examine the effects of abnormal interplay of traction and intercellular forces on asymmetric vascular cell alignment, we suppressed the cell traction force with a nonmuscle myosin II inhibitor, blebbistatin (10 μM; Sigma-Aldrich) (33), and disrupted intercellular adhesion using disodium EDTA (50 μM; Sigma-Aldrich) (34), a calcium chelator that blocks cadherin-mediated adhesion for 24 h (Fig. 4, a and b). Our experiments showed that when cell traction force was inhibited (Fig. 4 c), the degree of asymmetric cell alignment decreased in regions near the inner and outer edges, whereas no obvious change was observed in middle regions (Fig. 4, c–e). When the cell-cell adhesion was disrupted, the intercellular forces in the middle region decreased (Fig. 4 e), and the overall asymmetric cell alignment was slightly abolished (Fig. 4, b and e), which is consistent with our simulation predictions, as shown in Fig. 3, f and g. In addition, correlation analysis (Fig. S7) indicted that the dependence of asymmetric cell alignment on traction and intercellular forces were disturbed after pharmacological treatments. Taken together, these results confirm that mechanical forces are critically involved in vascular asymmetric alignment and morphogenesis.

Conclusion

Asymmetric cell alignments were increasingly discovered in various in vitro models using microfabrication techniques (4,16), but the understanding of the mechanistic basis of mechanical forces on multicellular asymmetric arrangement behaviors remains incomplete. Recent studies implied that in-plane maximal principal stress drives the cell alignments in a confined ring-like micropatterns (27). However, it has not been directly determined whether the cell alignments are asymmetric or symmetric and how cell mechanical forces directly drive the asymmetric cell alignments in vascular morphogenesis. In this study, we have demonstrated that the asymmetric vascular cell alignments in different micropatterns could be driven by the local traction and cell-cell forces via investigating the bias of cell alignments and cellular mechanical forces simultaneously. We systematically analyzed traction and intercellular forces, as well as cellular alignments in a confined vascular monolayer, using TFM measurement and FEM models. Specifically, we quantitatively calculated the cell-cell forces based on a previous method (26,30,35) using the force-balancing principle of cell-matrix force and intercellular force within neighboring cell clusters but not using in-plane stresses to represent intercellular force that are calculated based on homogeneous elastic membrane theory (27). Furthermore, our computational studies successfully demonstrated the possibility of using CAM models to predict the behaviors of asymmetric multicellular alignments in confined micropatterns by tuning both cell-cell interaction within connected single cells and traction force magnitude at pattern boundaries. However, cells are contractile in a confined microenvironment. Future work will be directed toward improving current models by considering the effect of actomyosin contractility and subcellular cytoskeleton.

Recent studies observed varied cell chirality, defined as CW and CCW cell alignments, in different in vitro models. In our study, we found different levels of asymmetric cell alignments but no obvious preference toward positive (CW) or negative (CCW) angles in wide ring patterns. However, a negative chirality was observed in narrow ring patterns or the narrow regions of asymmetric patterns. Our work demonstrates that the cellular forces regulate the asymmetric cell alignments and shed light on dictating cell chirality, but the cell chirality response is less sensitive than the cell alignments in our system. One possible reason is that we used a soft PAA substrate with an elastic modulus of 16.2 kPa in our system, which would generate lower mechanical forces in the cell sheets, as shown in a previous study (27). Thus, future efforts are needed for a detailed analysis of the effects of traction force and cell-cell force as well as ECM rigidity on regulating vascular chirality.

Impaired asymmetric cell alignments were previously observed in physiological vascular functions such as increased vascular cell permeability in diabetics and hereditary hemorrhagic telangiectasia patients (4,7). Our results demonstrated disrupted traction and intercellular forces in diabetic aortic EC patterns and ECs treated with force inhibitors lead to abnormal asymmetric cell alignments, which suggested the implication roles of mechanical forces and asymmetric cell alignments in vascular physiological functions. Hence, this study can provide new, to our knowledge, insight on the mechanoresponsive mechanisms in vascular morphogenesis.

Author Contributions

X.C., J.T., and W.C. designed research. X.C., J.T., J.Y., A.B., J.Y., Y.P., M.S., W.Q., and X.M. performed experiments and modeling. X.C., J.T., A.B., X.M., and W.C. analyzed data and wrote the manuscript. W.C. supervised the project. All authors edited and approved the final manuscript.

Editor: Guy Genin.