PathwayPCA: an R/Bioconductor package for pathway based integrative analysis of multi-omics data

Abstract

We present pathwayPCA, an R/Bioconductor package for integrative pathway analysis that utilizes modern statistical methodology, including supervised and adaptive, elastic-net, sparse principal component analysis. pathwayPCA can be applied to continuous, binary, and survival outcomes in studies with multiple covariates and/or interaction effects. It outperforms several alternative methods at identifying disease-associated pathways in integrative analysis using both simulated and real datasets. In addition, we provide several case studies to illustrate pathwayPCA analysis with gene selection, estimating and visualizing sample-specific pathway activities, identifying sex-specific pathway effects in kidney cancer, and building integrative models for predicting patient prognosis. pathwayPCA is an open-source R package, freely available through the Bioconductor repository. We expect pathwayPCA to be a useful tool for empowering the wider scientific community to analyze and interpret the wealth of available proteomics data, along with other types of molecular data recently made available by CPTAC and other large consortiums.

1. Introduction

Pathway analysis has become a valuable strategy for analyzing high-throughput omics data. By integrating with prior biological knowledge, such as those in KEGG database^[1], these pathway-based approaches test coordinated changes in functionally-related genes. In addition to improving power by combining associated signals from multiple genes within the same pathway, these systems approaches can also shed more light on the underlying biological processes involved in diseases^[2]. As technology advances, multiple types of omics data have also become increasingly available for the samples. For example, the Cancer Genome Atlas (TCGA) and the Clinical Proteomic Tumor Analysis Consortium (CPTAC) have generated comprehensive proteomic, genomic, and epigenomic profiles for multiple types of human tumors ^[3].

Given the large amount of available molecular information, Principal Component Analysis (PCA) is a popular technique for reducing data dimensionality to capture variations in individual genes or subjects. In particular, principal components (PCs) have previously been used as sample-specific summaries of gene expression values from multiple genes ^[4]. However, when the number of genes in the pathway is moderately large, genes unrelated to the phenotype may introduce noise and obscure the gene set association signal. Typically, only a subset of genes from an a priori defined pathway participates in the cellular process related to variations in phenotype, where each gene in the subset contributes a modest amount. Therefore, gene selection is an important issue in pathway analysis.

Previously, we developed a supervised PCA approach (SuperPCA)^{[5, 6]} and an unsupervised approach (Adaptive, Elastic-net, Sparse PCA or AES-PCA) ^[4] for gene selection in PC-based pathway analysis. Both approaches perform gene selection to remove irrelevant genes before estimating pathway-specific PCs, and were shown to have superior performance when compared to popular pathway analysis approaches such as Fisher’s exact test ^[7], GSEA ^[8], globalTest ^[9] in the analysis of gene expression data ^[5], GWAS data ^[6], and DNA methylation data ^[10].

Here we present a new R/Bioconductor package, pathwayPCA, which makes these methodologies available to the wider research community. We provide several case studies to illustrate pathwayPCA analysis with gene selection, estimation and visualization of sample-specific pathway activities, and analysis of sex-specific pathway effects. In addition, we proposed a new global test statistic that extends the AES-PCA approach for integrative analysis of two omics datasets with matched samples. We evaluated the performance of the global test for integrative analysis using both simulated and real datasets. Finally, we illustrate the power of integrative pathway-based prediction model for predicting cancer prognosis.

2. Materials and methods

2.1. An overview of pathwayPCA analysis

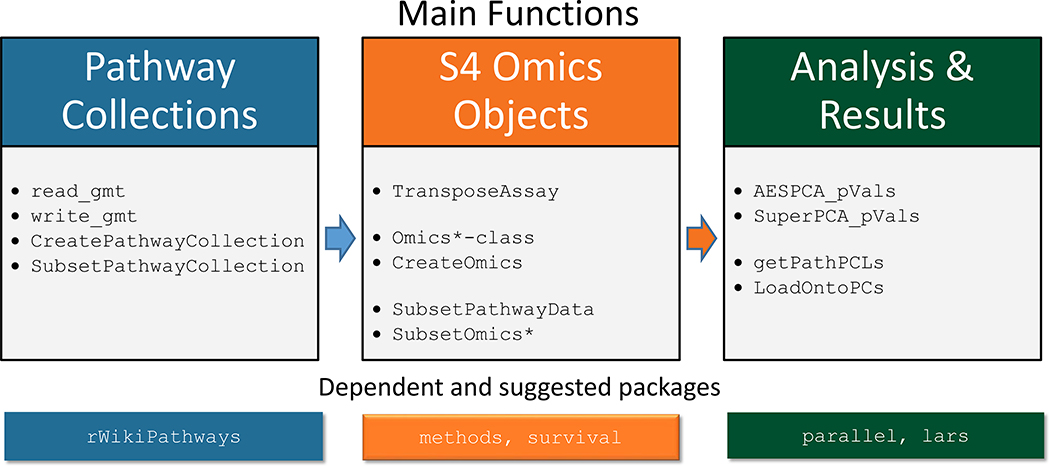
pathwayPCA is freely available at https://doi.org/10.18129/B9.bioc.pathwayPCA ^[11]. Figure 1 shows a schematic overview of pathwayPCA. The webpage (https://gabrielodom.github.io/pathwayPCA/) includes in-depth tutorials on each step of the analyses, as well as visualization of analysis results. We describe the major functionalities in pathwayPCA next.

Figure 1.

An overview of pathwayPCA functions.

Creating data objects for pathway analysis

The CreateOmics function creates an S4 data object of class Omics based on several user input datasets: (1) an assay dataset, (2) a collection of pathways from gene matrix transpose format which can be imported by the read_gmt function, and (3) phenotype information for each sample, which can be binary, continuous, or survival outcome. Extensive data checking is performed to ensure valid data are imported. For example, the CreateOmics function checks for matched samples between assay and response, proper feature names, features with near-zero variance, overlap between features and the given pathway collection, and complete cases in the response.

Testing pathway association with phenotype

Once we have a valid Omics-class object, we can perform pathway analysis using the AES-PCA or SuperPCA methods, which are implemented in the AESPCA_pVals and SuperPCA_pVals functions, respectively. Both functions return a table of the analyzed pathways sorted by p-values with additional fields including pathway name, description, number of included features, and estimated False Discovery Rate. These functions also return lists of the PCs and corresponding loadings for each pathway.

Briefly, in the AES-PCA method, we first extract latent variables (PCs) representing activities within each pathway using a dimension reduction approach based on adaptive, elastic-net, sparse PCA ^[4]. The estimated latent variables are then tested against phenotypes using an appropriate regression model g(phenotype) = α + β PC1 (default) or a permutation test that permutes sample labels, where the link function g() varies according to the response variable (i.e. Cox Proportional Hazards, identity, and logit link functions for survival, continuous, and binary response variables, respectively). Note that the AES-PCA approach does not use response information to estimate pathway PCs, so it is an unsupervised approach.

On the other hand, SuperPCA is a supervised approach: the subset of genes most associated with disease outcome are used to estimate the latent variable for a pathway. Because of this gene selection step, the test statistic in SuperPCA model can no longer be approximated well using the Student’s t-distribution. To account for the gene selection step, pathwayPCA estimates p-values from a two-component mixture of Gumbel extreme value distributions instead ^{[5, 6]}.

Extracting relevant genes in significant pathways

Because pathways are defined a priori (independently of the data), typically only a subset of genes within each pathway are relevant to the phenotype and contribute to a pathway’s significance. In our analyses, these relevant genes are the genes with nonzero loadings in the PCs extracted by AES-PCA or SuperPCA. To allow for easy inspection of data and further in-depth analysis, the SubsetPathwayData function can be used to extract assay data for genes within a particular pathway, merged with the phenotype information. In addition, given results from the AESPCA_pVals and SuperPCA_pVals functions and a specific pathway name, the getPathPCLs function returns the loadings for each gene in the particular pathway.

Estimating subject-specific pathway activities

In the study of complex diseases, there is often considerable heterogeneity among different subjects with regard to underlying causes of disease and the benefit of a particular treatment. Therefore, in addition to identifying disease-relevant pathways for the entire patient group, successful (personalized) treatment regimens will also depend upon knowing if a particular pathway is dysregulated for an individual patient. To this end, the getPathPCLs function also extracts sample estimates for the PCs, which allow users to assess pathway activities specifically for each patient.

A global test for integrative analysis of multiple omics datasets with matched samples

Consider two omics datasets for a particular pathway, for example from protein and gene expression data. For each data platform, first we estimate PC1 (the PC that accounts for most variations in data) representing activities in the pathway, that is, PC1_protein and PC1_RNA, respectively. With these PCs, we next fit the regression model g(phenotype) = α + β₁PC1_protein + β₂PC1_RNA and perform a global test of the null hypothesis H₀:β = (β₁ β₂)^t = 0. The link function g() varies according to the response variable (i.e. Cox Proportional Hazards, identity, and logit link functions for survival, continuous, and binary response variables, respectively). The joint effect of proteins and gene expressions in the pathway can then be tested using a two degrees of freedom likelihood ratio test.

Pathway based prediction analysis

There are two steps for building prediction models based on pathways: (1) for each pathway, estimate the latent variable that corresponds to pathway activities and (2) construct a prediction model using the latent variables as predictors. In the first step, we can use the getPathPCLs function described above to estimate subject-specific pathways activities for each sample. In the second step, we can use any prediction models that are capable of handling a large number of predictors.

2.2. Simulation study

To assess and compare the statistical properties of the global test with existing state of the art methods, we conducted a simulation study similar to that of Pucher et al. (2019) ^[12], which compared several integrative analysis methods for multi-omics data. Briefly, first we simulated two data matrices, from normal distribution and beta distribution respectively, using the same formula as in equations (1) and (2) of Pucher et al. (2019)^[12]. These two datasets represented two types of molecular profiles, for example, gene expressions and DNA methylation levels, respectively. The dimensions of these data matrices were set at 1600 features (genes) x 200 samples and 2400 features (DNA methylation probes) x 200 samples, respectively. Next, we divided the features in these datasets into 20 non-overlapping pathways, where each feature is assigned to one pathway.

Among the 200 samples, 100 are controls and 100 are treated samples. To simulate true positive pathways with differential expressions in both simulated gene expression and methylation datasets, we selected 5 pathways randomly and added treatment effects to samples in the treated group for a selected subset of features (parameter p_path) within each pathway. There are a total of 16 simulation scenarios, corresponding to different percentage of true positive features within a selected pathway (p_path = {10%, 15%, 20%, 50%}) and different effect sizes added to these features (δ = (0.2, 0.3,0.4, 0.6) relative to scaled standard deviation (see details in Pucher et al. (2019)^[12]). For each simulation scenario, a total of 100 pairs of two datasets were simulated.

We compared our proposed global test with the NMF ^[13] and sCCA ^[14] methods, which are the two methods that performed best in the Pucher et al. (2019) simulation study. For each set of simulated datasets, both NMF and sCCA return a set of selected features. To compute pathway p-values, we mapped these selected features to simulated pathways and computed over-representation p-values using one-tailed Fisher’s exact test (see details in Pucher et al. (2019)). For each method, power was estimated as the proportion of pathways with p-values less than 0.05 in pathways with added treatment effects. Type I error rate was estimated as the proportion of pathways with p-values less than 0.05 in pathways without added treatment effects. The R scripts for this simulation study can be accessed at https://github.com/gabrielodom/IamComparison.

3. Results

3.1. pathwayPCA outperforms alternative methods for integrative analysis

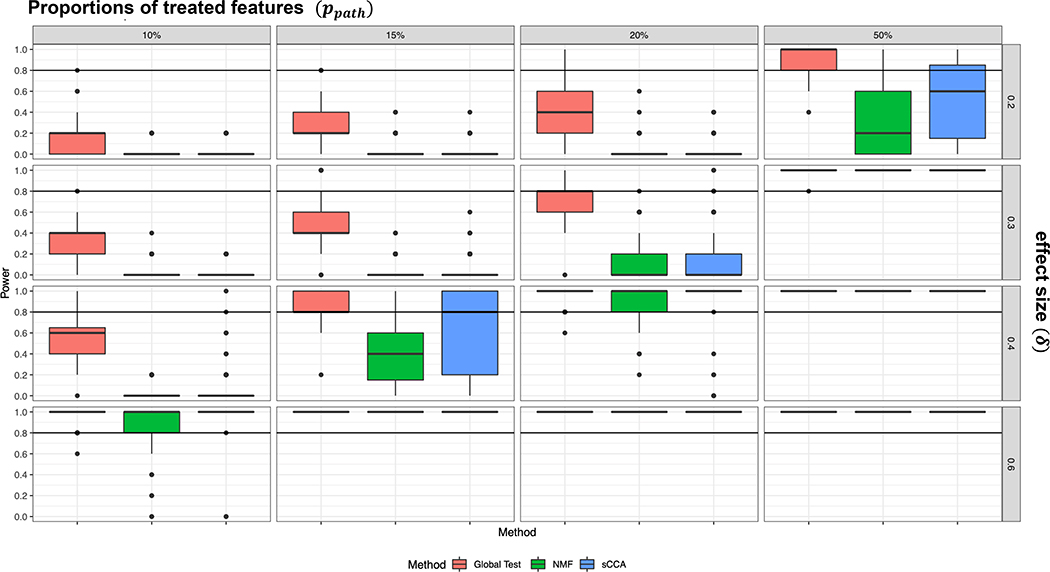
When no treatment effects were added to the pathways, Type I error for global test was close to nominal level at 5%, while NMF and sCCA appeared to be conservative. More specifically, the type I error rates were 0.0493, 0.0156, and 0.0148, for global test, NMF and sCCA, respectively. Figure 2 shows the power comparison of the three methods. Across all simulation scenarios, the global test performed best, followed by sCCA. We note that for global test, when effect size is small (δ = 0.2), good power (more than 80%) can still be achieved if there is a large percent of true positive features (p_path = 50%) in the pathways. On the other hand, when the percent of true positive features is small (p_path = 15%), a good power can be achieved with moderate effect size for the features (δ ≥ 0.4). In terms of computing time, NMF and sCCA took about 11.6 and 11.9 minutes, respectively, while pathwayPCA took about 0.7 minutes for each simulated dataset (Windows 7 64-bit; Intel Xeon E5–2640 v4 at 2.40Ghz, 64GB RAM).

Figure 2.

Comparison of power for global test, NMF and sCCA methods using simulated datasets. Each box corresponds to estimated power over 100 simulated datasets. The rows of the figures show effect sizes, the columns of figures show proportions of treated features. Within each figure, the vertical axis represents statistical power. The horizontal axis are the three methods: global test, Non-negative Matrix Factorization (NMF), and Sparse Canonical Correlations Analysis (sCCA).

3.2. A WikiPathways analysis of CPTAC ovarian cancer protein expression data

For this example, we downloaded a mass-spectrometry based global proteomics dataset generated by the CPTAC. The normalized protein expression dataset for ovarian cancer was obtained from the LinkedOmics database at http://linkedomics.org/data_download/TCGA-OV/. We used the dataset “Proteome (PNNL, Gene level)” which was generated by the Pacific Northwest National Laboratory (PNNL). One subject was removed due to missing survival outcome. Missing protein expression values were imputed using the Bioconductor package impute under default settings ^[15]. The final dataset consisted of 5162 protein expression values for 83 samples.

Using the CreateOmics function, we first grouped these protein expression values by pathways defined from the June 2018 WikiPathways ^[16] collection for Homo sapiens (http://data.wikipathways.org/20180610/gmt/wikipathways-20180610-gmt-Homo_sapiens.gmt). The AESPCA_pVals function was then used to extract PC1 (the PC that accounts for most variations in data) for each pathway. Next, AESPCA_pVals tested pathway association with overall survival by fitting the Cox proportional hazards model with PC1 as the predictor for each pathway.

The three most significant pathways are the IL-1 signaling pathway, toll-like receptor signaling pathway and Wnt signaling pathway (Supplementary Table 1). Among them, IL-1 signaling pathway is well known for its important roles in tumor angiogenesis, metastasis and chemo-resistance ^[17]. Taken together, these three top pathways strongly suggested that tumor microenvironment and epithelia-stromal interactions promote epithelia-mesenchymal transition (EMT) and suppress immune response in high-grade serous ovarian cancer ^[18].

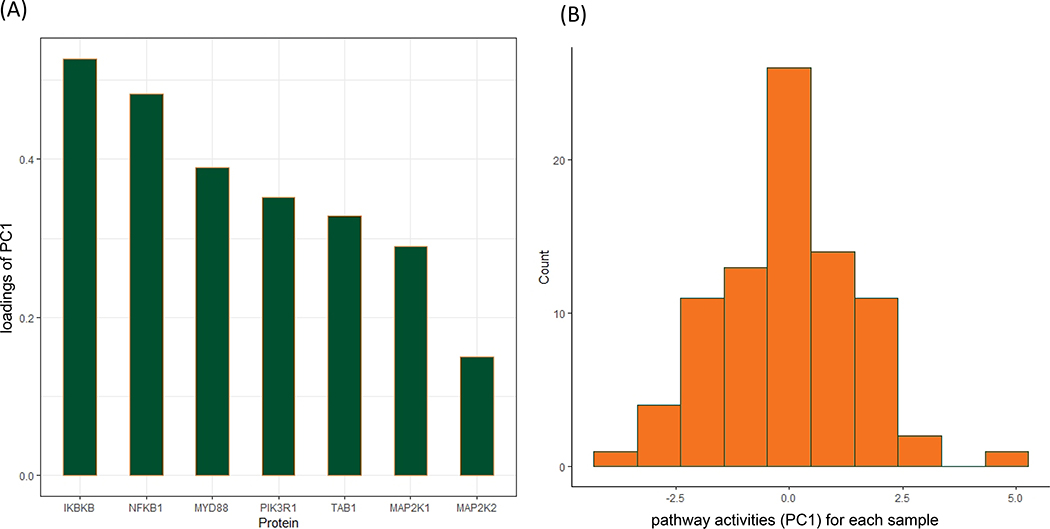
To understand which proteins contributed most to pathway significance, the getPathPCLs function can extract the loadings for PC1 from this pathway (the weights of the proteins in the estimated PC1). Figure 3A provides a visualization for contributions of the relevant genes (IKBKB, NFKB1, MYD88) to PC1 in this pathway. In addition, the getPathPCLs function also returns subject-specific estimates of the first PC. Figure 3B shows there can be considerable heterogeneity in pathway activities between the patients in the IL-1 signaling pathway.

Figure 3.

Protein specific and sample specific estimates for “IL-1 signaling pathway”. (A) Relevant genes selected by AESPCA. Shown are loadings of PC1, which are weights for each gene that contributed to PC1 in AESPCA. (B) Distribution of sample-specific estimate of pathway activities. Shown are estimated PC1 values for each sample in AESPCA.

Users are often also interested in examining the actual dataset used for analysis of the top pathways, especially for the relevant genes within the pathway. The SubsetPathwayData function extracts such a dataset with protein expressions and survival outcomes, matched by each sample for a given pathway. This pathway-specific dataset allows us to further explore the relevant genes in the pathway. For example, we can fit a Cox regression model to individual genes or plot gene-specific Kaplan-Meier curves (Supplementary Figure 1).

3.3. An integrative pathway analysis of gene expression and protein expression data for ovarian cancer

Given the ease in conducting transcriptome-wide studies, and the high sensitivity, broad coverage of genes offered by RNA-seq, RNA has been the focus for many studies. On the other hand, because proteins are more directly involved in biological functions, protein-based studies might provide more direct assessment on functional changes. However, although protein expressions are regulated by changes in mRNA, recent studies showed only moderate concordance between protein and mRNA expression levels^{[19, 20]}. In particular, the estimated correlation between gene expression and protein levels in ovarian tumor samples is about 0.45 ^[20]. This is probably due to post-transcriptional modifications in proteins ^[21].

To effectively leverage information in both protein and gene expression datasets, we performed an integrative analysis using the global test described in Section 2.1, to jointly model gene expression and protein changes within each pathway associated with overall survival times. As our simulation study in Sec 3.1 demonstrated, this joint analysis allows us to effectively combine signals from both proteins and gene expressions.

Briefly, the (IlluminaHiSeq pancan) normalized TCGA ovarian cancer RNA-seq data ^[22] was additionally downloaded from UCSC Xena Functional Genomics Browser (http://xena.ucsc.edu/) ^[23]. The CreateOmics and AESPCA_pvals functions were used to identify RNA-seq pathways significantly associated with survival outcomes. Using samples with matched proteins and RNA-seq expressions, the global test identified 396 significant pathways at nominal significance level of 0.05, of which two pathways (T Cell Receptor Signaling; cell death signaling via NRAGE, NRIF, and NADE) were significant at 10% FDR (Supplementary Table 2), suggesting that adaptive immune response are significantly associated with ovarian cancer prognosis. In contrast, single omics analysis using the same dataset separately resulted in 94 significant RNA-seq pathways and 118 significant protein pathways with nominal p-values less than 0.05. None of the pathways were significant at 10% FDR in single -omics analysis. This example demonstrated that compared to analyzing each dataset separately, the joint analysis improved sensitivity for detecting modest changes within pathways.

3.4. Integrating gene expression data with experimental design information: an analysis of sex-specific pathway gene expression effects on kidney cancer

The pathwayPCA package is capable of analyzing complex studies with multiple experimental factors. For many cancers, there are considerable sex disparities in the prevalence, prognosis, and treatment responses ^[24]. In this case study, we will illustrate using pathwayPCA to test differential association of pathway activities with survival outcomes in male and female subjects.

To understand the underlying biological differences that might contribute to the sex disparities in Cervical Kidney renal papillary cell carcinoma (KIRP), we downloaded the TCGA KIRP gene expression dataset from the Xena Functional Genomics browser ^[23] and tested sex × pathway activity interaction for each WikiPathway. Specifically, we organized the data using the CreateOmics function, estimated pathway activities for each subject using the AESPCA_pVals function, extracted the PCA results with the getPathPCLs function, and then fit the following Cox proportional hazards regression model to each pathway:

$$h(t)=h_0(t)\exp \{{\beta }_1{PC}_1+{\beta }_{2}male+{\beta }_3({PC}_1\times male)\}.$$

In this model, h(t) is expected hazard at time t, h₀(t) is baseline hazard for the reference group, variable male is an indicator variable for male samples, and PC1 is a pathway’s estimated first principal component based on AES-PCA. Supplementary Table 3 shows there are 14 pathways with significant p-values less than 0.05 for the PC1 × male interaction, indicating the association of pathway gene expression (PC1) with survival for these pathways is highly dependent on sex of the subjects.

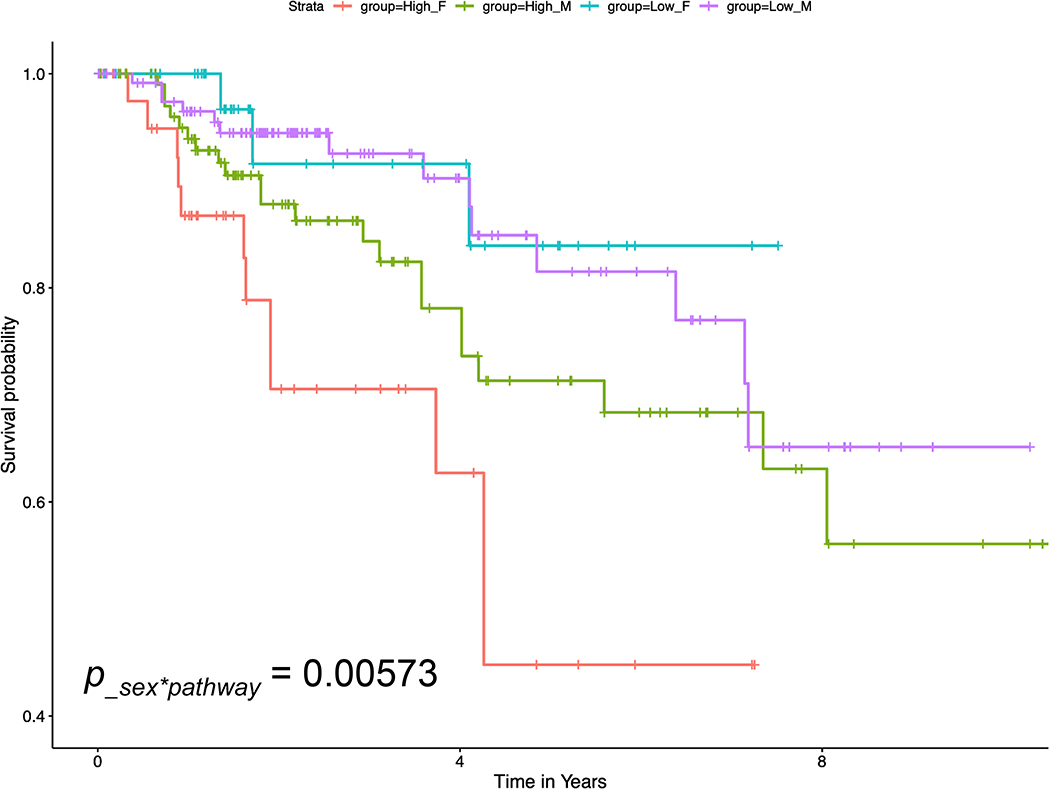
As an example, the pathway with the most significant PC1 × male interaction is the TFs Regulate miRNAs related to cardiac hypertrophy pathway (p-value 0.00573). Cardiac hypertrophy, specifically left ventricular hypertrophy, is highly prevalent in kidney disease patients ^[25]. Gender differences have been observed in cardiac hypertrophy, which may be related to estrogens and testosterone ^[26]. A recent integrative systems biology study showed that the miRNA-mRNA network also plays an important role for gender differences in cardiac hypertrophy ^[27]. The genes with large PC loadings in this identified pathway include PPP3R1, STAT3 and TGFB1, which regulate miRNA hsa-mir-133b, hsa-mir-21 and MIR29A. In Figure 4, we grouped subjects by median PC1 values for each sex. These Kaplan-Meier curves showed that while high or low pathway activities were not significantly associated with survival in male subjects (green and purple curves, respectively), female subjects with high pathway activities (red) had significantly worse survival outcomes than those with low pathway activities (blue).

Figure 4.

The Kaplan-Meier curves showed that while high or low pathway activities in the “TFs Regulate miRNAs related to cardiac hypertrophy” pathway were not associated with survival in male subjects (green and purple curves, respectively), female subjects with high pathway activity (red) had significantly worse survival outcomes than those with low pathway activities (blue). Therefore, the effect of pathway activities on prognosis varied by sex significantly (p = 0.00573).

3.5. A pathway based integrative prediction model for patient prognosis

In this section, we compared accuracy for predicting overall survival using pathway-based elastic-net regression prediction model ^[28] using protein data alone vs. using both protein and RNA-seq data. First, we downloaded level 3 TCGA colon cancer gene expression data and protein data, and MSigDB C2 Canonical Pathways collection^[8]. There are 68 samples with both RNA-seq and protein assays along with clinical info (overall survival time and censoring status) in TCGA data. To assess the accuracy of the prediction models, we randomly split these 68 samples evenly into a training dataset and a testing dataset; this process was repeated 100 times. For each repetition, we followed these analysis steps: (1) Identify predictors using training dataset: we performed pathwayPCA analysis for MSigDB C2 collection of gene sets and selected the 200 most significant gene sets associated overall survival in Cox regression model, using only protein data or using both protein data and RNA-seq data. (2) Estimate predictors using training data: we next estimated subject-specific pathway activities for each sample using getPathPCLs function. (3) Build an elastic-net regression prediction model using training data: we used the function cv.glmnet from R package glmnet ^[29] to train the model with family = “cox” for survival outcome and parameter alpha = 0.5 for the elastic net penalty. The cv.glmnet()function uses cross-validation to identify the value of parameter λ with minimum cross-validation error rate (lambda.min) for the final prediction model. (4) Apply the estimated elastic-net regression model to testing data: PCs for samples in testing data were first estimated by projecting PC loadings estimated from training data. Model with parameters alpha = 0.5, λ = lambda.min was next applied to testing data using these estimated PCs. (5) Measure accuracy on testing dataset: we partitioned survival times and then estimated the time-dependent ROC curves for each partition using the timeROC package ^[30].

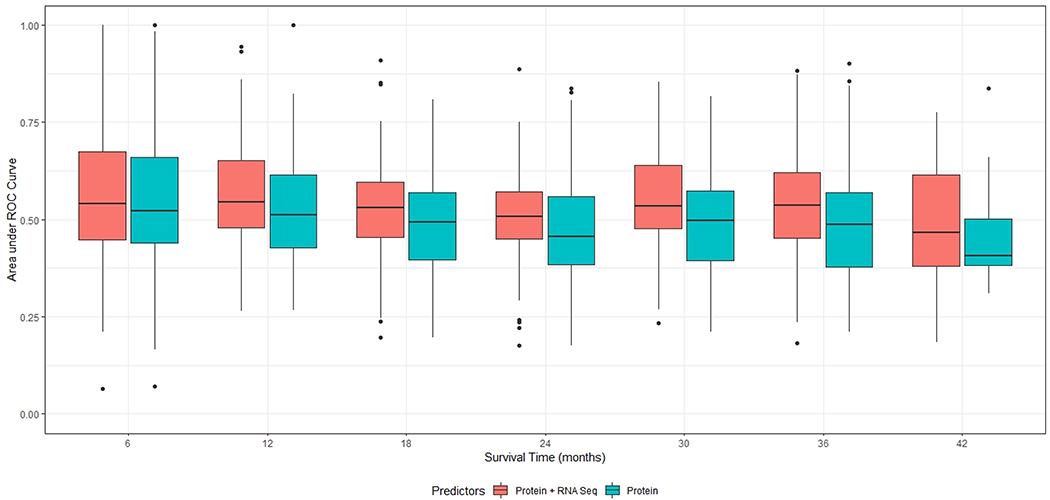
Figure 5 shows the estimated Area under ROC curve (AUC) for the 100 testing datasets over survival time. Elastic-net prediction models were trained with only protein data or with both protein and RNA-seq data using training datasets in each of the 100 random splits. The results showed substantial variability in survival predictions, especially before six months and after three years. Nevertheless, over all time points, incorporating gene expression data with the protein data improved survival prediction accuracy compared with using protein data alone.

Figure 5.

Time-dependent AUCs (area under ROC curve) for pathway-based elastic-net Cox Proportional Hazards prediction models using protein data vs. using both protein and RNA-seq data. The AUC measures the overall discriminative abilities of the prediction model over all thresholds.

4. Discussion

In the illustration of pathwayPCA analysis, we have mainly discussed the workflow using AES-PCA methodology. However, the workflow for the SuperPCA pathway analysis method is the same, except for replacing the AESPCA_pVals function call with a call to the SuperPCA_pVals function instead. In the results using these two approaches, there might be discrepancies in the significant pathways identified and estimated loadings for individual proteins. This is because the gene-selection criteria used by the two methodologies are different. In AES-PCA, the focus is on groups of correlated genes, agnostic to phenotype; while in SuperPCA, the focus is on groups of genes most associated with phenotype. These two techniques in gene selection correspond to different biological hypotheses in how genes within a pathway influence outcomes. While the SuperPCA approach assumes the most significant genes by univariate association within a pathway contribute most to the latent variable that captures pathway activity, users of the AES-PCA approach assume a coherent subset of genes—some of which might not be the most significant genes—contribute most to pathway activities.

In the section “A pathway based integrative prediction model for patient prognosis”, we compared the performance of elastic net prediction model using RNA-seq data and protein data (combination model) vs. the model using protein data alone. To further evaluate the distinct contribution of protein data, we also compared our combination model with the model using gene expression data alone. We found the prediction accuracy of these two models are very similar (Supplementary Figure 2). However, Supplementary Figure 3 shows that in the combination model, a substantial proportion of pathway-specific features estimated from protein expression data were selected by the elastic net models in all simulation datasets, suggesting protein based features provided distinct contributions to survival prediction that could not be provided by gene expression data alone.

In summary, we have presented pathwayPCA, a unique pathway analysis software that utilizes modern statistical methodology including supervised PCA and adaptive, elastic-net PCA for principal component analysis and gene selection. We also proposed an integrative pathway analysis strategy using the global test, which was shown to have superior sensitivity and specificities than alternative approaches for multi-omics data analysis. Moreover, we illustrated building predictions models for patient prognosis using multi-omics data. The strength of pathwayPCA lies in its flexibility and versatility. In particular, it can be used to analyze studies with binary, continuous, or survival outcomes, as well as those with multiple covariates and/or interaction effects. Moreover, under the well-established PCA framework, contributions of individual genes toward pathway significance can be extracted and sample-specific pathway activities can be estimated. Computationally, pathwayPCA is efficient with options for parallel computing on all major operating systems. For most proteomics datasets, testing a few hundred of pathways typically takes only a few minutes. We expect pathwayPCA to be a useful tool for empowering the wider scientific community to analyze and interpret multi-omics data.

Supplementary Material

supp tables

Supp. Table 1. Top 10 most significant WikiPathways associated with overall survival in pathwayPCA analysis of TCGA ovarian cancer protein expression data.

Supp. Table 2. Top 10 most significant MSigDB canonical pathways by integrative analysis of RNAseq and proteomics TCGA ovarian cancer datasets.

Supp. Table 3. Pathways with significant Sex × Pathway interaction in sex-specific pathway analysis of kidney cancer dataset.

Supp. Figure 1 PathwayPCA provides functionality to extract data specific to a particular pathway or gene, which can be used for further in-depth analysis such as (A) Cox regression model (B) Kaplan-Meier survival curves.

Supp. Figure 2 Time-dependent AUCs (area under ROC curve) for pathway-based elastic-net Cox Proportional Hazards prediction models using both protein and RNA-seq data, protein data alone or RNA-seq data alone.

Supp. Figure 3 In elastic net prediction models that used both proteomics and RNA-seq data, a substantial proportion of pathway-based features that were selected as predictive features for patient prognosis were protein-based features. The results are similar when the number of input features (number of pathways considered by model) varied from 200 to 300.

Significance Statement.

New strategies and software for the analysis of multi-omics data are crucial for understanding the complete picture of underlying biological processes involved in diseases. We presented PathwayPCA, a new muti-omics data analysis software package, making modern statistical methodologies freely available to the wider research community. The software can be used to analyze studies with binary, continuous, or survival outcomes, as well as those with multiple covariates and/or interaction effects. Contributions of individual genes toward pathway significance can be estimated and sample-specific pathway activities can be assessed. Computationally, PathwayPCA is efficient with options for parallel computing on all major operating systems.

List of abbreviations

TCGA

Cancer Genome Atlas

CPTAC

Clinical Proteomic Tumor Analysis Consortium

PCA

Principal Component Analysis

PCs

principal components

SuperPCA

supervised PCA approach

AES-PCA

Adaptive, Elastic-net, Sparse PCA

PNNL

Pacific Northwest National Laboratory

PC1

the PC that accounts for most variations in data