Elasticity, Stability, and Quasioscillations of Cell-Cell Junctions in Solid Confluent Epithelia

Abstract

Macroscopic properties and shapes of biological tissues depend on the remodeling of cell-cell junctions at the microscopic scale. We propose a theoretical framework that couples a vertex model of solid confluent tissues with the dynamics describing generation of local force dipoles in the junctional actomyosin. Depending on the myosin turnover rate, junctions either preserve stable length or collapse to initiate cell rearrangements. We find that noise can amplify and sustain transient oscillations to the fixed point, giving rise to quasiperiodic junctional dynamics. We also discover that junctional stability is affected by cell arrangements and junctional rest tensions, which may explain junctional collapse during convergence and extension in embryos.

Significance

Cell deformations and flows are driven by tensions generated in the actomyosin cell cortex. Even though these tensions are dynamic in time and space, the existing theoretical models of morphogenesis often treat them as static. We take a different approach, in which we couple the vertex model of solid tissues with the dynamics of tension generation at the level of the junctional actomyosin. Combining analytical and numerical approaches, we discover various dynamical regimes of junctional movements including junctional collapse and nonperiodic oscillatory contractions. We also discover that junctional stability is affected by whole-tissue effects such as disorder in cell packing. Future generalizations of this model could provide insights into the autonomy of physical processes during morphogenesis across length scales.

Introduction

In confluent tissues, the adjacent cells adhere to one another through narrow joints known as the adherens junctions. These regions are rich with protein complexes, which govern cell-cell adhesion and couple cells’ cytoskeletons (1,2). Forces transmitted along the junctions play a major role in morphogenesis. In particular, contractile tensions generated in the actomyosin (3, 4, 5) drive various types of cell deformations and tissue-scale movements (6,7). For instance, the actomyosin network collapses during cell ingression and oscillates during dorsal closure in Drosophila (8, 9, 10, 11, 12), and directed junctional collapse drives convergence and extension in the early Drosophila embryo (13, 14, 15, 16), whereas junctional fluctuations establish the arrangement of cells in Drosophila pupal notum (17) and fluidize the tissue during vertebrate body axis elongation (18).

Recent measurements of junctional dynamics during tissue remodeling revealed that the rate of junctional collapse often increases with contraction (16,17). This suggests a positive feedback loop between junctional contraction and generation of junctional tension. Apart from driving collapse of the actomyosin, such a feedback loop could establish oscillatory dynamics as previously proposed within a generic theoretical framework of active contractile elements (19).

To explore these dynamics in the context of confluent tissues, we develop a vertex model with a feedback loop between cell-scale junctional contractions and generation of force dipoles at the level of the junctional actomyosin. We find that the nonlinear elastic response of solid tissues to local force dipoles does not satisfy conditions to yield a limit cycle of junctional oscillations. Nevertheless, the variety of dynamical regimes remains rich and includes junctions that can either sustain stable length or collapse. One of our main findings shows that junctional noise establishes quasiperiodic junctional dynamics. We also discover that junctional stability depends on cell arrangements as well as on distribution of junctional rest tensions, which could be relevant for the active junctional remodeling during morphogenesis (13,14).

Materials and methods

The model

The tissue is represented by a planar polygonal network of cell-cell junctions parametrized by the positions of cell vertices r_i = (x_i, y_i) (20, 21, 22). Forces on vertices F_i are assumed conservative such that F_i = $-{\nabla }_{i}W$, where W = $\kappa \sum _k{\left(A_k-A_0\right)}^2+\sum _{ij}{\gamma }_{ij}{l}_{ij}$ is the total potential energy of the system and ${\nabla }_i$ = (∂/∂x_i, ∂/∂y_i). The first sum in the energy goes over all cells and describes cell-area elasticity (A_k and A₀ being the actual and the preferred cell areas, respectively), whereas the second sum goes over all junctions and describes the line energy due to adhesion and cortical tension (l_ij being the junctional length); indices i and j denote head and tail vertices of the junctions. For simplicity, we disregard the usual cell-perimeter-squared energy term (23,24), which is not needed to describe solid tissues studied here. Because of strong friction, the motion of vertices is overdamped:

$$\eta {\dot{\mathit{r}}}_i={\mathit{F}}_i=-2\kappa \sum _k\left(A_k-A_0\right){\nabla }_i{A}_k-\sum _j{\gamma }_{ij}{\nabla }_i{l}_{ij},$$ (1)

where η is the friction coefficient. The tension γ_ij(t) = γ₀ + $∆{\gamma }_{ij}\left(t\right)$, where γ₀ and $∆{\gamma }_{ij}\left(t\right)$ are the average (rest) tension and the time-dependent part, respectively. To ensure stability, γ₀ is assumed positive, which implies that the cortical tension dominates over the adhesion (17,25). From now on, we use dimensionless quantities by choosing $\sqrt{A_0}$, τ₀ = (ηγ₀)⁻¹, and γ₀ as the units of length, time, and tension, respectively, and rescaling the modulus as $\kappa A_0^{3/2}$/γ₀ → κ.

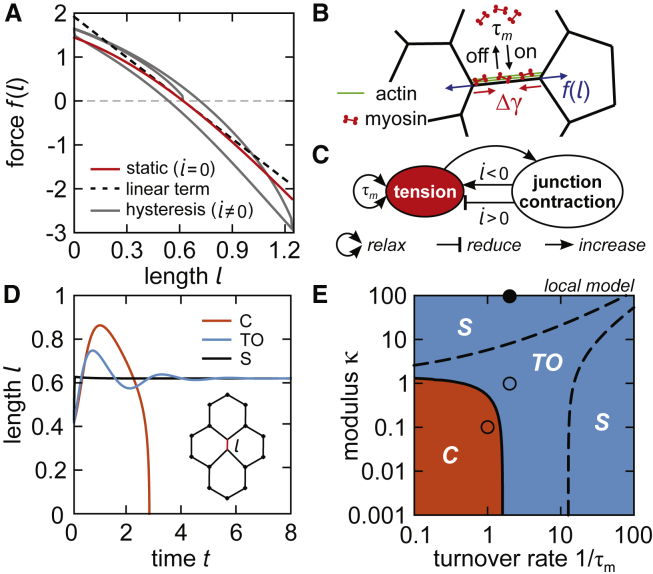
Tissues with constant line tensions (γ_ij = const.) behave as passive elastic materials capable of sustaining shear stresses (23,26). To examine their response to a locally applied force dipole, we assume an excess line tension Δγ on a single junction. This deforms the junction away from its rest length l₀, and the elastic deformation propagates into the bulk (Fig. S1 A). Force balance implies 0 = −2Δγ − f(l), where f(l) is the elastic restoring force, which is well described by f(l) = ${\sum }_{m=1}^3{\alpha }_m{\left(l-l_0\right)}^m$ with α₂/α₁ = 0.33 and α₃/α₁ = −0.10 for a regular honeycomb cell tiling (Figs. 1 A and S1, B and C). The significant contribution of the second-order term yields softening and stiffening behaviors for compression and stretch, respectively (Fig. 1 A). Furthermore, because of friction, f(l) displays hysteresis at nonzero rates of change of junctional length (Fig. 1 A).

Figure 1.

(A) Static force-extension relation (red curve) and hysteresis (gray curve) for a single junction in the honeycomb cell tiling. (B) A schematic of the interplay between the elastic restoring force f(l) and active tension Δγ generated by the junctional myosin is shown. (C) The feedback loop between junctional contraction and tension is shown. (D) Junction length versus time in the local model is given. (E) A phase diagram of the local model exhibits stable (state S), collapse (state C), and stable dynamics with transient oscillations to the fixed point (state TO). Red, blue, and black curves (D) and circles (E) correspond to (1/τ_m, κ) = (1, 0.1), (2, 1), and (2, 100), respectively. To see this figure in color, go online.

Tensions change on timescales associated with the dynamics of the underlying actomyosin (Fig. 1 B). We assume a linear relation between junctional tension and myosin concentration (defined by a number of molecular motors per junction length c_ij(t) = N_ij/l_ij): c_ij(t) = αγ_ij(t), where α is a constant proportionality factor. The total rate of change of the myosin concentration ${\dot{c}}_{ij}={\dot{N}}_{ij}/l_{ij}-N_{ij}{\dot{l}}_{ij}/l_{ij}^2$, where the first and the second term describe changes of the number of motors at a fixed junction length and changes of the junction length at a fixed number of motors, respectively. In particular, the motor-actin binding and unbinding contribute a timescale τ_m and are described by ${\dot{N}}_{ij}$ = (−N_ij + c₀l_ij)/τ_m, where c₀ = αγ₀ is the ambient myosin concentration. In turn, ${\dot{l}}_{ij}$ can be explicitly written in terms of the forces acting at the vertices as ${\dot{l}}_{ij}$ = r_ij ⋅ F_ij/l_ij, where r_ij = r_j − r_i and F_ij = F_j − F_i. Overall, this yields a deterministic dynamic equation for tension fluctuations

$$\dot{\Delta {\gamma }_{ij}}=-\frac{1}{{\tau }_m}\Delta {\gamma }_{ij}-\frac{{\gamma }_{ij}{\mathit{r}}_{ij}\cdot {\mathit{F}}_{ij}}{l_{ij}^2},$$ (2)

where the first term describes tension relaxation due to myosin turnover and the second term describes a coupling between tension dynamics and mechanics of the vertex model. This coupling gives rise to a feedback loop between generation of tension and junctional contractions (Fig. 1 C). In contrast to some previous studies, which describe similar feedback mechanisms using specific chemomechanical models (11,15,27), here the feedback follows directly from the relation between junctional tension and myosin concentration.

Results

Local model

We start by applying the model on a quartet of hexagonal cells (inset to Fig. 1 D). First, we derive the equation of state for the central junction, which reads

$$f\left(l\right)=-3\kappa l_0^3\left(\frac{l}{l_0}-1\right)-2-\frac{4\left(l/l_0-2\right)}{\sqrt{{\left(l/l_0\right)}^2-4l/l_0+7}},$$ (3)

where l₀ = 3^−3/4$\sqrt{2}\approx 0.62$ is the side length of a regular hexagon with unit area. Interestingly, despite its simplicity, the local model exhibits similar elasticity to the full tissue—including softening and stiffening behavior upon junction compression or stretch (Supporting Materials and Methods, Section SI and Fig. S2, A and B). Next, we simulate the dynamics described by Eqs. 1 and 2, starting in a configuration away from the fixed point (l, γ)₀ = (l₀, 1). We find three types of behavior: the junction 1) converges directly back to the fixed point (state S), 2) undergoes damped transient oscillations before reaching the fixed point (state TO), or 3) collapses its length to 0 (state C) (Fig. 1 D). The exact time course of junction length, l(t), depends on the initial conditions.

A linear stability analysis (Supporting Materials and Methods, Section SII) reveals the analytical condition for the Hopf bifurcation:

$${\kappa }^{\text{∗}}=\frac{1}{3l_0^3}-\frac{1}{3l_0^2{\tau }_m}$$ (4)

In particular, the junction is stable for κ > κ^∗ and unstable for κ < κ^∗ (Fig. 1 E). Transient oscillations appear within the stable regime at κ₋ < κ < κ₊, in which ${\kappa }_{\pm }=1/\left(3l_0^3\right)+1/\left(3l_0^2{\tau }_m\right)\pm \left(1/3l_0^2\right)\sqrt{10/\left(l_0{\tau }_m\right)}$ (Fig. 1 E). Importantly, the first Lyapunov coefficient shows that the Hopf bifurcation is always subcritical, meaning that no parameter values yield a stable limit cycle that would describe periodic oscillations like those previously observed in similar dynamical models (11,12,19) (Supporting Materials and Methods, Section SIII).

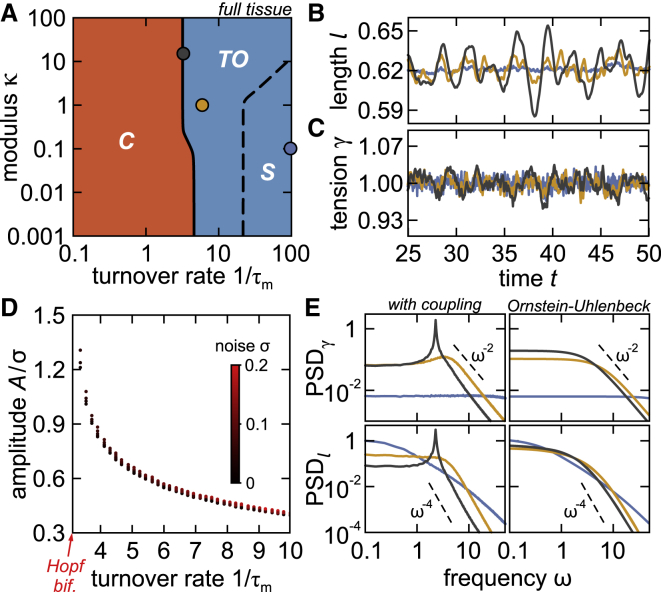
Next, to search for the various types of junctional behaviors in the full-tissue setting, we apply our model to the honeycomb cell tiling and numerically preform the linear stability analysis (Supporting Materials and Methods, Section SIV). We identify the same dynamical regimes as in the local model (Fig. 2 A). However, in contrast to the local model, the collapse regime extends to large κ-values (Fig. 2 A). This is because collective cell deformations in the full-tissue model allow preservation of cell areas even upon junction collapse.

Figure 2.

(A) Phase diagram of the full tissue exhibits stable (S), collapse (C), and transient oscillations to the fixed point (TO). Eigenvalues of the Jacobian were evaluated at (1/τ_m, κ) pairs on an equidistant grid of 100 × 100 points. (B and C) Junctional length (B) and tension (C) versus time are shown for examples with quasioscillations (gray and orange curves) and stochastic fluctuations (blue). (D) Amplitude of length fluctuations versus myosin turnover rate 1/τ_m for σ = 0.01–0.2 (black-to-red color scheme) is given. Raw (noncollapsed) data are shown in Fig. S4. (E) PSDs of length and tension fluctuations are shown. Gray, orange, and blue circles (A) and curves (B–E) correspond to (1/τ_m, κ) = (3.25, 15), (6, 1), and (100, 0.1), respectively, whereas σ = 0.01. To see this figure in color, go online.

Quasioscillations

Binding and unbinding of myosin are stochastic processes, which cause stochastic fluctuations of junctional tensions (17,25,28,29). To explore the role of noise, we add an extra term to the equation for tension, which now reads ${\dot{\gamma }}_{ij}=\Delta {\dot{\gamma }}_{ij}+\sqrt{2{\sigma }^2/{\tau }_m}\times {\xi }_{ij}$. Here, the first term obeys Eq. 2. like before, whereas the second term describes the white noise with long-time variance σ² and $\langle {\xi }_{ij}\left(t\right)\rangle =0$, $\langle {\xi }_{ij}\left(t\right){\xi }_{kl}\left(t^{\prime }\right)\rangle ={\delta }_{ik}{\delta }_{jl}\delta \left(t-t^{\prime }\right)$. Note that in the absence of the coupling term in Eq. 2, our stochastic tension dynamics reduces to the classical Ornstein-Uhlenbeck process, which was previously used to describe stochastic junctional fluctuations (17,25).

We simulate the stochastic dynamics in a honeycomb cell tiling and find that although in the stable (S) regime, length (and tension) fluctuations are noisy (blue curves in Fig. 2, B and C), the movements become more regular in the regime of transient oscillations (state TO) and, in contrast to the deterministic case, manage to sustain a well-defined amplitude (orange and gray curves in Fig. 2, B and C). These movements in fact correspond to the transient oscillations, which eventually die out in the purely deterministic case (Fig. 1 D) but get amplified (Fig. 2 D) and become sustained indefinitely in the presence of the noise. This gives rise to a quasiperiodic trajectory or the so-called quasicycle, which arises in dynamical systems in the presence of the noise when the Jacobian matrix has complex eigenvalues with strictly negative real parts (30, 31, 32). We refer to these junctional movements as quasioscillations.

Next, we examine the observed dynamics in the Fourier space. The quasioscillations give rise to peaks in power spectral densities (PSDs) of tension and length fluctuations, PSD_γ and PSD_l, respectively. These peaks get dominated by the noise when moving away from the bifurcation point (Fig. 2 E and Supporting Materials and Methods, Section SV). In fact, in the limit 1/τ_m → ∞, where the relative contribution of the coupling term in the tension dynamics (Eq. 2) becomes negligible compared to the relaxation term, the PSDs agree with the model in which tensions obey a pure Ornstein-Uhlenbeck process (blue curves in Fig. 2 E).

In confluent tissues, junctions are interconnected and so need to synchronize their quasioscillations. Because three junctions meet at each vertex, junction networks are geometrically frustrated, which can lead to nontrivial spatial patterns of cell deformations (Supporting Materials and Methods, Section SVI).

Inhomogeneous tissues

The stability condition of our local model (Eq. 4) suggests that disorder of cell packing may affect junctional stability. Indeed, it can be recast as l₀ > $l_0^{\text{∗}}$, where the $l_0^{\text{∗}}$ is the critical rest length for collapse. Because the rest lengths are distributed in disordered tissues (inset to Fig. 3 A), there might exist a fraction of junctions that are shorter than $l_0^{\text{∗}}$. These junctions would necessarily collapse and trigger cell rearrangements. To test this possibility, we examine an ensemble of 100 disordered tissues (Supporting Materials and Methods, Section SVII). Starting close to the fixed point (i.e., all junctions at their rest lengths and all tensions equal 1), we simulate the dynamics (Eqs. 1 and 2) at fixed κ = 15 and record the rest lengths of the first 10 collapsing junctions. Here, each junctional collapse initiates a T1 transition, which is performed as soon as the junction length drops below 0.01. The length of the newly created junction is set to 0.001, whereas its tension is reset to γ₀. Unlike in the honeycomb lattice, in which junctions at κ = 15 collapse only for 1/τ_m < 3.2 (Fig. 2 A), in disordered tissues we find short junctions collapsing even at higher 1/τ_m-values (Fig. 3 A). This confirms that the distribution of rest lengths in disordered tissues importantly affects local junctional stability. We note in passing that frequent collapses of short junctions drive partial ordering of disordered tissues (Fig. S6; Videos. S1 and S2).

Figure 3.

(A) Probability distribution function of the rest length of first 10 collapsing junctions for 1/τ_m = 0.01, 1, 3, 5, 7.4, and 10 (black-to-red color scheme). Inset: Distribution of rest lengths in 100 analyzed tissues is shown. (B) Tissue with a supracellular myosin cable of junctions with γ₀ ≥ 1 (red junctions) is shown. The rest tensions on black junctions equal 1. (C) Fraction of high-γ₀ collapsed junctions versus γ₀ is shown. Error bars represent the standard deviation over 100 simulations. To see this figure in color, go online.

Finally, the dimensional form of the stability condition, κ^∗ > γ₀/$\left(3l_0^3\right)-\eta /\left(3l_0^2{\tau }_m\right)$, suggests that the rest junctional tension γ₀ may also affect junctional stability. In particular, junctions with higher γ₀ are expected to have an increased critical rest length $l_0^{\text{∗}}$, possibly resulting in their collapse. We test this prediction by analyzing a tissue that contains a supracellular cable of enriched junctional myosin, which increases the rest tensions on the corresponding junctions compared with other junctions (Fig. 3 B). Without the contraction-tension coupling (Eq. 2), this cable would be stable despite being under higher tension because every vertex within the cable is acted upon by a pair of equal but opposite forces. However, as predicted by the stability condition, the coupling indeed affects the stability of the junctions that are under higher rest tension, making them more susceptible to collapse. To show this, we record the first 10 collapsing junctions and find that the fraction of those with high γ₀ increases with γ₀ (Fig. 3 C).

Discussion

We studied a mechanical model of tissues with a feedback loop between junctional contractions and the dynamics of junctional tensions (Fig. 1). In particular, we used a previously proposed description of force generation at the level of the actomyosin (19) and combined it with the vertex model of solid confluent tissues, which provided a faithful representation of the elasticity underlying the response of solid tissues to local force dipoles at the junctions. Although nonlinearities in this system do not meet the conditions to yield a stable limit cycle of junctional oscillations (Fig. 1 A), we discovered that junctional noise can amplify and sustain quasiperiodic junctional dynamics at biologically relevant myosin turnover rates (Fig. 2; (17)). Importantly, this dynamical regime does not even require nonlinear elasticity and may thus be more common than the limit cycle of periodic junctional oscillations. Another important result of our work highlights the role of cell arrangements and the distribution of rest tensions within the tissue for the junctional stability (Fig. 3). Both effects may be present during convergence and extension in Drosophila embryo, during which the so-called parasegmental boundaries, enriched with the junctional myosin, frequently collapse their junctions (13,14,33).

An interesting future direction would be to employ the area- and perimeter-elasticity vertex model (23,24) and use it to explore tissues that are closer to the solid-fluid transition. These tissues are associated with highly nonlinear elasticity (24,26,34), which could, in contrast to our model, yield a stable limit cycle of junctional oscillations (19). In turn, this could lead to spontaneous organization of junctions into groups of locally synchronized oscillators. Furthermore, the role of correlations between junctions needs to be further investigated. In particular, these correlations can appear because individual junctions are under tension exerted by the actomyosins from two adjacent cells and because cell membranes belonging to the same cell share a common pool of molecular motors. These effects would provide additional sources of coupling between junctions, which could significantly affect their correlated movements. Finally, an alternative model could also assume that junctional tension is proportional to the number of myosin motors rather than to their concentration.

Author Contributions

M.K. designed the research. C.Z. carried out the calculations and analyzed the data. C.Z. and M.K. wrote the manuscript.

Editor: Stanislav Shvartsman.