On Phage Adsorption to Bacterial Chains

Abstract

Bacteria often arrange themselves in various spatial configurations, which changes how they interact with their surroundings. In this work, we investigate how the structure of the bacterial arrangements influences the adsorption of bacteriophages. We quantify how the adsorption rate scales with the number of bacteria in the arrangement and show that the adsorption rates for microcolonies (increasing with exponent ∼1/3) and bacterial chains (increasing with exponent ∼0.5–0.8) are substantially lower than for well-mixed bacteria (increasing with exponent 1). We further show that, after infection, the spatially clustered arrangements reduce the effective burst size by more than 50% and cause substantial superinfections in a very short time interval after phage lysis.

Significance

When bacteria form clusters, they substantially change their exposure to invading phages and other external agents from the well-mixed scenario. Despite this fact, much research has focused on and is focusing on using well-mixed bacteria. Understanding the kinetics of the spatial structures is paramount to developing robust analyses and theories of experimental results. We carefully investigate how the clusters lower the adsorption rate of external phages and how the clustering modifies the hit probabilities for the bacteria.

Introduction

The interaction of predators and prey is a widely studied phenomenon and is observed across all scales of life, from wolves and elk to foxes and rabbits all the way down to phages and bacteria. Across all of these taxa, the prey can utilize a plethora of defensive strategies to increase their odds of survival in the presence of their predator. Many of these strategies have evolved to counter a predator in very specific circumstances, but some strategies are more general.

In this work, we explore the benefits of herding from the perspective of bacteria. Although bacteria do not form herds in the traditional sense of the word, they often form clusters or aggregates. Herding has been shown to be an effective strategy in some ecosystems, in which the localization of prey increases the time it takes for the predator to find the herd of prey (1). There are, however, also strong negative consequences of herding; e.g., if a herd is found, the predator can take down several of the prey at once.

Bacteria and phages constitute an extreme predator-prey system in which the phages, upon killing a bacterium, produce on the order of 100 new phages—sometimes thousands (2). At face value, this amplification of predators should make it difficult for the bacteria to survive, but an ongoing “arms race” between the bacteria and phages has allowed the bacteria to sustain their population. This coevolution is extensively studied, and many intricate bacterial defense mechanisms have been identified, such as restriction-modification systems (3), CRISPR (clustered regularly interspaced short palindromic repeats) (4,5), and abortive infections systems (6).

Bacteria in nature are often found as separated bacteria or as dense arrangements such as microcolonies and biofilms (7, 8, 9, 10, 11, 12). This is often due to external circumstances that dictate how the bacteria can be distributed. For example, bacteria cannot move freely in the soil or other solid media. In liquids, shear forces might prevent the bacteria from forming clusters, but this is not always the case (13). In these environments, the spatial structure has been shown to strongly increase the survival of the bacteria in the presence of phages (14, 15, 16), but there is an important aspect of this structure that has not received a lot of study, namely the delaying of phages reaching the bacteria.

When structured, bacteria can associate into various arrangements ranging from simple pairs (diplococcus and diplobacillus) to continuous chains (streptococcus and streptobacillus) to elaborate clusters (e.g., staphylococcus, palisades, and microcolonies). Although each arrangement might confer some communal benefits via quorum sensing (QS), cross-feeding, etc., we consider only how such arrangements also will act as a phage defense.

Previously, it has been suggested that the bacterial arrangements have a negative effect on bacterial survival because the larger size of the bacterial arrangement means that the phages are adsorbing at higher rates (17). However, this study fails to take into account the increased distance between the arrangements, which leads to net smaller adsorption to bacterial arrangements compared to if the bacteria were unstructured (similar to the study of (1)).

There are several studies that show that the spatial structure of densely packed bacteria might further reduce the ability of phages to attack the bacteria. For example, it is believed that the extracellular matrix of biofilms strongly captures the phages (14,18) and that bacterial microcolonies only expose the surface bacteria to the phages and thereby shield the central bacteria from the phages (15).

Materials and Methods

Simulations

We base our simulations on the code used in (15). Here, the authors simulated individual spherical bacteria and individual phages in three-dimensional space using an agent-based model. In this work, we expand this model to account for elongated bacteria, which requires some modifications. First, we must choose what shape the bacteria will have. Here, we follow the method used in (19) and choose to model the bacteria as cylinders with spherical caps. This shape closely resembles several natural bacteria, e.g., Escherichia coli, and is relatively simple to implement in simulations (19,20). The full details of our model follow, but our simulations essentially consider several elongated bacteria that obey the following constraints:

• 1)The bacteria must keep their shape.
• 2)Two bacteria cannot occupy the same space.
• 3)When we consider chains, two consecutive bacteria must remain connected at the ends.

Each of these constraints is implemented with a corresponding force that controls the interaction.

Mathematically, each of the elongated bacteria are described by the coordinates ${\overline{Q}}_1^i$ = (x₁, y₁, z₁) and ${\overline{Q}}_2^i$ = (x₂, y₂, z₂), and we model the bacteria by the line segment connecting ${\overline{Q}}_1^i$ to ${\overline{Q}}_2^i$. Following (19), we treat this line segment as a spring of length L, meaning that forces on the two ends of the bacterium are described by the potential $V_{\text{int}}^i=\left(1/2\right)k_{\text{int}}{\left(H\left({\overline{Q}}_2^i-{\overline{Q}}_1^i\right)-L\right)}^2$, where $H\left(\overline{v}\right)=\sqrt{\overline{v}{\overline{v}}^T}$ is the length of vector $\overline{v}$ and k_int = 500 N/μm is a stiffness constant. To ensure the bacterial shape is always fixed, we set the parameter k_int to be larger than any other force constants in the simulations.

Each bacterium is assumed to have an extent R around the central line segment, and any bacteria that overlaps with this region will be pushed away. We implement this cell-cell repulsion by use of a piecewise potential. When the cells overlap, we use a spring-like potential, whereas we have zero potential otherwise. If we define the vector ${\overline{w}}_{i,j}$ as the shortest vector between the line segments of two bacteria, the interaction potential takes the form

$$V_{\text{rep}}^{i,j}=\{\begin{array}{cc}\frac{1}{2}{k}_{\text{rep}}{\left(H\left({\overline{w}}_{i,j}\right)-2R\right)}^2,& H\left({\overline{w}}_{i,j}\right)<2R\\ 0,& H\left({\overline{w}}_{i,j}\right)\ge 2R\end{array}.$$

These two potentials are sufficient to describe how elongated bacteria retain their shape and how they interact with their immediate neighbors. For this work, we are interested in modeling chains of bacteria, so we introduce a potential to keep the chain connected:

$$V_{\text{chain}}^{i,j}=\frac{1}{2}{k}_{\text{chain}}\left({\left(H\left({\overline{Q}}_2^j-{\overline{Q}}_1^i\right)-2R\right)}^2{\delta }_{i,j+1}+{\left(H\left({\overline{Q}}_1^j-{\overline{Q}}_2^i\right)-2R\right)}^2{\delta }_{i,j-1}\right),$$

where δ_{i, j} is the Kronecker delta function. This potential defines a spring-like force between the first pole $\left({\overline{Q}}_1\right)$ of bacterium i and the second pole $\left({\overline{Q}}_2\right)$ of bacterium i − 1 and correspondingly between the second pole of bacterium i and the first pole of bacterium i + 1.

In total, the potential felt by cell i is

$$V_i=V_{\text{int}}^i+\sum _{j\ne i}\left(V_{\text{rep}}^{i,j}+V_{\text{chain}}^{i,j}\right).$$

Because we now consider elongated bacteria, we also need to change how the simulations detect collisions of phages and bacteria. In the original code, the phage is considered to have hit a bacterium if its position is less than one cell radii away. In our case, a phage collides with a bacterium if the distance between the phage and the bacterial line segment is less than R.

We generate three types of bacteria arrangements: well mixed, chains, and microcolonies. For the well-mixed bacteria, the position and orientation of each bacterium are uncorrelated, and they are initialized uniformly in the simulation space. In addition, we set the parameter k_chain = 0 N/μm.

We consider an assortment of bacterial chains ranging from chains that appear almost straight to strongly tangled chains. We achieve these configurations by iteratively generating the bacterial chains. Starting with one randomly oriented bacterium, we place a new bacterium at one end such that the angle θ_i between the two consecutive bacteria is less than the parameter Θ (see Fig. 1 B for illustration). We call this parameter the “internal angle,” and it is the main parameter that controls how tightly the bacterial chains are clustered.

Figure 1.

Interaction overview. (A) An illustration of dimensions of the bacteria and the potentials in the simulation is given. (B) An illustration of a chain being generated is given. To see this figure in color, go online.

To be more specific, we, for each consecutive bacterium, draw a random angle azimuthal angle ϕ between [0, 2π] and random inclination angle θ_i between [0, Θ] from a uniform distribution and place the next bacterium a distance 2R from the previous tilted by the angle θ_i in a random (perpendicular) direction. Our chains are thus closely related to the freely rotating chain model from polymer physics, with the exception that our chains will locally repel any overlapping parts.

We note two important aspects of how the internal angle parameter describes the bacterial chains. First, the internal angle is an upper bound on the angle between two bacteria, and therefore, consecutive bacteria have, on average, an angle of Θ/2 between them. Secondly, this upper bound is only imposed when the bacteria are initialized, which means that any overlapping parts of the chains likely will change the angles of the bacteria as the chain relaxes.

The spherical colonies are generated by first generating a chain with L = 0.1 μm and Θ/2π = 0.5 (corresponding to consecutive bacteria on average being at right angles with each other). We then set k_chain = 0 N/μm and expose the bacteria to a force $F_{compress}=k_{compress}\times \left({\overrightarrow{COM}}^i-{\overrightarrow{x}}_c\right)$, which pulls each bacterial center of mass, ${\overrightarrow{COM}}^i$, toward the arrangement center ${\overrightarrow{x}}_c$. We allow the arrangement to compress under this force for a time T_compress(N) (see Table S2 for values) that is chosen so the arrangement has sufficient time to form a tightly packed cluster. After compression, we set the cell lengths to the original value L and let the bacteria relax. This method, although somewhat cumbersome, generates bacterial arrangements that are very spherical. If, for example, the cell length is not set to L = 0.1 μm in the beginning, almost all bacteria in the arrangement align to form a disk of bacteria rather than a sphere.

For each of the bacterial arrangements, there is a reasonable probability that some bacterial pairs overlap, and we therefore let the arrangement relax for some time before adding the phage to the simulation. We have operationally chosen to relax the bacteria in intervals of T = 0.1 h, after which we measure the maximal overlap, d, between any bacterial pairs. If this overlap is more than 1% of R, we repeat relaxation steps until the overlap drops below this value or until the overlap stops decreasing.

In the Supporting Materials and Methods, we show that our bacterial arrangements have very little overlap after relaxation (see Fig. S1 for details).

When adding phages to the system, we must first consider how large of a volume around the bacterial chain we should simulate. For each bacterial chain and spherical colony that we generate, we determine the smallest cube that can encapsulate the bacteria (minimal bounding box) of size ${\ell }_{\text{bb}}\times {\ell }_{\text{bb}}\times {\ell }_{\text{bb}}$. We then construct a test volume that is nine times larger and release test phages inside the volume. We let the phages adsorb for T = 0.1 h or until a fraction of 1 − e⁻¹ phages have been captured to estimate the specific adsorption rate ν. This estimate of ν allows us to construct a simulation volume of size $\ell \times \ell \times \ell$, which is large enough that 90% of the phages remain free at time T = 1 h. For some simulated chains, the bacterial arrangement is very elongated and the estimated length $\ell$ approaches the length of the bounding box ${\ell }_{\text{bb}}$, and we therefore impose that $\ell$ must be larger than $2{\ell }_{\text{bb}}$.

Ideally, we would like the phages to be spatially distributed according to the steady-state distribution. To test how robust our phage distribution is, we have developed an algorithm to equilibrate the phage distribution. The algorithm works by simulating phage diffusion for a time, T_eq, during which, the phages, upon hitting a bacterium, are relocated to a random location in the simulation space. In the Supporting Materials and Methods, we show that our adsorption measurements do not change significantly because we let the phage distribution equilibrate beforehand (see Fig. S9 for details).

Finally, we need to determine what the time step used in the simulations should be. We use a chain of size N = 10, with Θ/2 = 0.3π. Using the algorithm above yields a required box size of $\ell$ ≈ 180 μm, but here we use a conservative size of $\ell$ = 350 μm. In the Supporting Materials and Methods, we test several time steps and find that convergence is achieved around ΔT = 10^−6.5 h, and therefore, we run our simulations with ΔT = 10⁻⁷ h.

We add phages in two ways. For the simulations that measure the adsorption rate and the shielding effects, we uniformly add at least 10⁵ phages to the simulation volume. In the cases in which we must impose a volume of length $2{\ell }_{\text{bb}}$, we scale the number of phages so that the density is conserved. That is, we add ${\left(2{\ell }_{\text{bb}}/\ell \right)}^3$ × 10⁵ phages. When we measure the secondary infections, we remove the selected bacterium from the simulation and introduce 10⁴ phages at its location. These phages are distributed uniformly inside the replaced bacterium and are then free to diffuse in the system.

Data availability

The code and generated data files are available at the online repository located here (21): https://github.com/RasmusSkytte/BacterialChains/tree/v1.1.

Experiment

We use the E. coli strain SP427 (22), which is derived from MC4100 and encoded with a P_A1/O4/O3::gfpmut3b gene cassette (23). This strain was incubated overnight in YT broth (0.8% W/V Bacto tryptone, 0.5% w/v NaCl, 0.5% w/v yeast extract) and subsequently diluted to ∼10³ CFU/mL in a buffer solution (50 mM CaCl₂, 25 mM MgCl₂). 10 μL of the diluted bacteria was then mixed with 0.4 mL of a soft agar consisting of 1% W/V Bacto tryptone, 0.8% w/v NaCl, 0.5% w/v yeast extract, 0.5% w/v Bacto agar, 0.2% w/v glucose, 50 mM CaCl₂, 25 mM MgCl₂, and 10 mM Tris. Note, however, that the mixture in the experiment behaved different from normal conditions and was substantially less viscous than duplicate conditions. The reason for this deviation is unknown, but we hypothesize that the soft agar was not fully melted before the bacteria were added.

The mixture was plated into one well of a six-well plate (P06-1.5H-N) from Cellvis (Mountain View, CA) and incubated for 4 h at 37°C before images were taken. The images capture the green fluorescence signal. For visual clarity, the image has been color inverted and filtered for extra contrast.

Results

In Fig. 2, we show a simple example in which we compare phages adsorbing to two separated bacteria (cocci) with adsorption to two joined bacteria (diplococcus).

Figure 2.

Illustration of two bacterial arrangements. The illustration shows two distinct ways that two bacteria may arrange within a volume V. They can be separate and thus spatially uncorrelated, or they can cluster together and form a single arrangement. To see this figure in color, go online.

Free phages move randomly by diffusion until they encounter a bacterium or they decay. Because their movement is unguided, the time it takes for the phages to reach a bacterial target is well described by diffusion mechanics. Here, we can use a mathematical result derived by Smoluchowski (24), in which he shows that the rate of a small diffusing particle hitting a large relatively stationary target is

$$\eta =4\pi Db,$$

where η is the rate of adsorption, D is the diffusion constant for the particles measured in units of m²/s, and b is the radius of the target (in units of m). Notice that η has units of m³/s⁻¹. If we consider adsorption inside a box of volume V, we can use the specific adsorption rate ν = η/V, which has more familiar units of s⁻¹. Using this rate, we can compare the difference in adsorption rates for two separated bacteria and the adsorption rate for two joined bacteria. When the bacteria are separated, they each occupy a volume of V/2, and we assume they have the same radius of r₀. The phages will then adsorb to either of the bacteria at a rate of

$$\nu =\frac{4\pi D{r}_0}{V/2}=\frac{8\pi D{r}_0}{V}.$$ (1)

Notice that each box has a volume of V/2 and consequently contains N_p/2 phages initially. The free phages inside box 1 and 2 are being adsorbed at the rate of ν, which means that the number of free phages in each box is described by

$$N_P^{\mathrm{1,2}}\left(t\right)=\frac{N_P}{2}\text{exp}\left(-\nu t\right).$$

This also means that the total phage population, N_p = $N_P^1+N_P^2$, is also adsorping at the rate ν:

$$N_P\left(t\right)=N_P^1\left(t\right)+N_P^2\left(t\right)=N_P\text{exp}\left(-\nu t\right).$$

This is the relevant rate because the large burst size makes the finding of subsequent target much faster. If the bacteria are joined together, we will assume they can be treated as a single target of radius r_c. This target is assumed to be spherical and has twice the volume of a single bacterium (V_c = 2V₀). By converting from volume to radius, this means the single target will have radius r_c = 2^1/3r₀. This large target will occupy the full volume V with all the N_p phages. Combined, this means that the phage adsorption rate to the joined target is

$${\nu }^{\prime }=\frac{4\pi D{r}_c}{V}=2^{1/3}\frac{4\pi D{r}_0}{V}.$$ (2)

To fully show the difference in adsorption rates, we take the ratio of the adsorption rate of joined bacteria (Eq. 2) to the separated bacteria (Eq. 1), which, after eliminating the common factor 4πDr₀/V, yields

$$\frac{{\nu }^{\prime }}{\nu }=\frac{2^{1/3}}{2}=2^{-2/3}=0.63.$$

This result shows that conceptually, when the bacteria are joined together, they experience a substantial reduction in the rate of adsorption compared to when they are apart. Note that once a phage adsorbs to one of the bacteria in the cluster, the neighboring bacteria is then almost certainly going to be infected when the first infected bacterium lyses. For this arrangement to have a net benefit, the gain achieved by delaying the initial phage adsorption has to be greater than increased risk to the neighboring bacteria. Furthermore, the assumption that the joined bacterium can be treated as a spherical target is crude, but this approximation improves as the number of bacteria increases.

As we increase the number of bacteria, the bacteria can form microcolonies, e.g., as in soft agar, where they grow to form roughly spherical arrangements (11,12,15,16). Alternatively, the bacteria may arrange themselves in more complicated structures such as biofilms (14,18,25), or the bacteria can stick together to form grape-like clusters (staphylococcus) or elongated chain-like clusters (streptococcus or streptobacillus). In an outlier experiment, we have observed E. coli forming a chain-like structure when the soft agar medium was substantially less viscous than expected (see Fig. 3).

Figure 3.

Chain of E. coli. In some cases, E. coli will grow to form distinct chain-like structures when grown in very soft media. See Materials and Methods for details.

Such chains of bacteria are interesting because they provide another strategy for bacterial formation beyond the well-studied structures such as the microcolony and the biofilm. These chains present a nontrivial geometry that, depending on the angle between consecutive cells, will have widely varying volumetric scaling.

For chains of bacteria, we cannot in general approximate the radius of the bacterial arrangement to be r_c = N^1/3r₀ as we did above for the dense arrangement. Such a chain can either be bunched up, in which case we can approximate with a spherical arrangement, or the chain can be more dispersed, with the most extreme configuration being a straight line.

Using detailed simulations of single bacteria, we construct three types of bacterial arrangements. We test the unstructured arrangement in which the bacteria are widely separated (i.e., well mixed). For structured arrangements, we generate densely packed spherical colonies and elongated chains of bacteria. We generate each arrangement of various sizes N, and for the chains, we use different maximal internal angles Θ, creating chains ranging from (almost) straight lines to small clusters. In Fig. 4, we show three examples of simulated chains, each with different average internal angles, and one example of a spherical colony.

Figure 4.

Examples of simulated arrangements. Our simulation framework lets us construct a wide range of three-dimensional bacterial arrangements. We show here three examples of chains with different degree of clustering (controlled by the internal angles parameter Θ) and one example of a spherical colony. All examples consist of 100 bacteria. To see this figure in color, go online.

For each arrangement we generate, we estimate the required volume to allow for 10% phage adsorption within a 1 h window. Short curled-up chains could be simulated by considering relatively small volumes, whereas long, dispersed chains require a simulation that includes a larger volume for the diffusing phages. We then fill the simulation space with individual phage particles that undergo diffusion until they encounter the bacteria, at which point it is removed from the simulation.

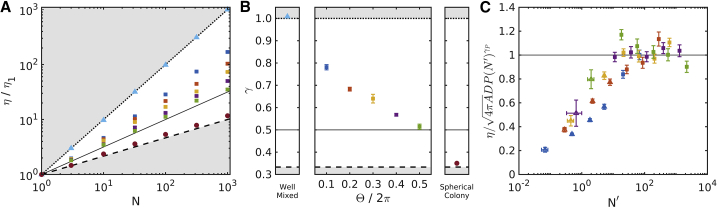
In Fig. 5 A, we show the adsorption rate as a function of the number of bacteria for the various bacterial arrangements. The well-mixed bacteria and the spherical colony effectively constitute the largest and smallest phage targets, respectively, with the bacterial chains having intermediate adsorption rates dependent on the internal angle parameter Θ. We fit each family of curves to the function η(N) = η₀N^γ and find that the exponent γ decreases with the internal angle parameter Θ (see Fig. 5 B).

Figure 5.

Phage adsorption rate. (A) We show how the adsorption rate scales with the number of bacteria, N, in various arrangements. We measure the adsorption rate η in units of the adsorption rate for a single bacterium: η₁ = (1.193 ± 0.003) × 10⁵μm³/h. The adsorption rate is highest for well-mixed bacteria (triangles), intermediate for chains of bacteria (squares), and minimal for spherical colonies (circles). The chains have varying values for Θ/2π: 0.1 (blue), 0.2 (red), 0.3 (yellow), 0.4 (purple), and 0.5 (green). Points are error bars showing standard error (not visible). (B) We fit each family of adsorption rates to η = η₀N^γ, and we show the value of the exponent γ. Error bars indicate standard deviation. For comparison, we show three models of adsorption rate scaling: well-mixed scaling η/η₁ = N (dotted line), random walk scaling η/η₁ = N^0.5 (solid line), and spherical scaling η/η₁ = N^1/3 (dashed line). Gray areas indicate inaccessible areas. (C) A fit to the adsorption rate is shown as a function of N, the persistence length P, and the phage diffusion constant D. Triangles indicate points at which N_i < P_i. Fitted value is γ_P = (0.58 ± 0.001), with a reduced χ² of 4.26. Error bars indicate standard deviation. To see this figure in color, go online.

Another way of describing the family of bacterial chains is by the persistence length, i.e., a measure of the stiffness of the chain. We compute the average persistence length for the data set, P(Θ, N), across 100 replicates and compute the effective length N′ = N/P(Θ, N) of the chains.

The adsorption rate to each family of chains can be modeled by the following equation:

$$\eta \left(N,\Theta \right)={\eta }_0{N}^{\gamma \left(\Theta \right)}.$$

With the measured persistence lengths, we can rescale all the chains by their persistence length to chains that scale with the same exponent γ_P:

$$\eta \left(N,P\right)={\eta }_0\left(P\right){\left(N^{\prime }\right)}^{{\gamma }_P}.$$

This equation considers the chains to consist of fewer but longer links. To approximate the base adsorption rate η₀(P), we use a result derived in (26). Here, the authors provide a useful approximation of the Smoluchowski adsorption rate when the target is nonspherical. Their analysis shows that the surface area A of the bacteria can be used to estimate the adsorption rate: η₀(P) = $\sqrt{4\pi A}DP$ (see Supporting Materials and Methods, Section S4 for details).

In Fig. 5 C, we then plot the adsorption rate as a function of N′ and see that for sufficiently long chains, these collapse onto a scaling of $\sqrt{4\pi A}DP{\left(N^{\prime }\right)}^{{\gamma }_P}$. We can only reliably estimate the persistence length when the length of the chain N is larger than the persistence length, and as a result, we observe deviation from this scaling at small N′.

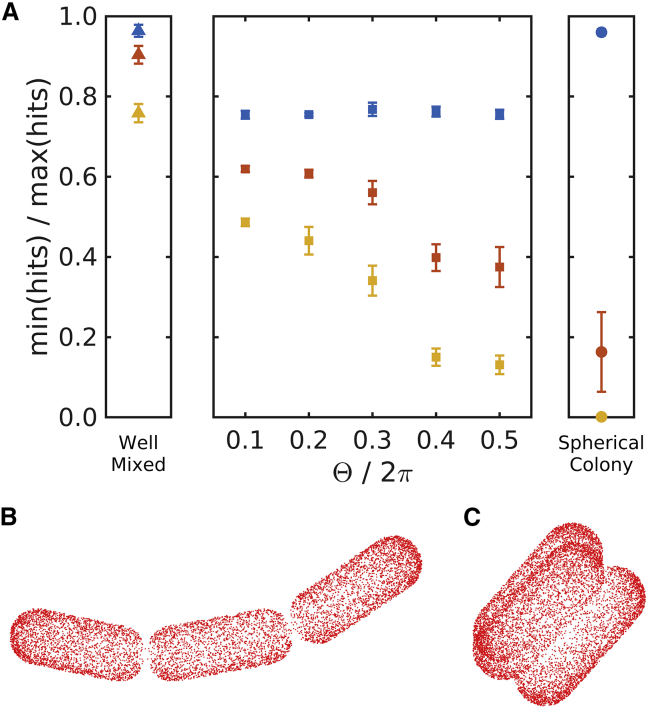
In addition to the reduced adsorption rates of the structured bacterial arrangements, the arrangements nonuniformly expose the bacteria to the surroundings. To quantify this, we track the individual phage collisions and measure the ratio of hits between the most exposed bacterium and the least exposed bacterium. In Fig. 6, we show how this ratio changes for the bacterial arrangements as the number of bacteria increase.

Figure 6.

Shielding effects. (A) The ratio of hits between the most exposed bacterium and the least exposed bacterium is given. The error bars show the measured ratios and standard errors for arrangements of size N = 3 (blue), N = 10 (red), and N = 32 (yellow). The chain arrangements show increasing shielding with increasing size, N, as for the well-mixed bacteria, but also with increasing internal angles Θ when the chains are N ≥ 10. The spherical colony can almost fully shield some bacteria when N ≥ 10 but exhibits almost no shielding at N = 3. (B) Phage hits on a chain of length N = 3 and Θ/2π = 0.1 are shown. (C) Phage hits on a spherical colony of size N = 3 are shown. To see this figure in color, go online.

In general, we observe that the structured arrangements exhibit substantial variability in phage exposure, with some bacteria experiencing relatively few hits and others relatively many. This disparity increases as the arrangements become more tightly clustered.

Note that we observe the ratio of the extremal values, which means that our measurement is sensitive to stochastic noise. For example, notice that the well-mixed bacteria show increasing shielding with increasing N. This is expected because we use a finite number of phages, and stochastic variation will show in these measurements.

The spherical colony is especially efficient in shielding bacteria compared with bacterial chains and well-mixed bacteria. Already for N = 10, some bacteria are almost fully protected against the phage.

Only when the number of bacteria is small, e.g., N = 3, do the chain arrangements have larger variability than the spherical arrangement. This is due to the symmetry of the spherical arrangement whereby all bacteria have equally exposed surface areas, and therefore, the probability of phage adsorption is the same among the bacteria (see Fig. 6 C). This is not so for the chain arrangements. Here, the degree of exposure for the bacteria is substantially more unequal. One reason for this is that the center bacteria has two areas of contact with other bacteria, whereas the end bacteria have only a single area of contact each. Therefore, the center bacterium exposes a smaller surface to outside and consequently is less likely to be hit by the phages (see Fig. 6 B). As the number of bacteria increase, the chains with larger internal angles begin to show more variability than the bacteria with smaller internal angles. The smaller internal angles mean that the bacterial arrangement only gets shielding from the difference in contact areas, whereas the chains with increasing internal angles receive a corresponding increase in shielding as the chains contract and begin to form a spherical colony.

The above results show that 1) the more tightly packed a bacterial arrangement is, the more the phages are delayed from reaching the bacteria and 2) the individual bacteria are not uniformly exposed to the phage attack within the cluster.

Once found by a phage, the colony is most certainly doomed because the progeny phage will be released immediately adjacent to the remaining bacteria. We next investigate these secondary infections.

For each bacterial arrangement, we perform five simulations in which we lyse a bacterium (three simulations when N = 3). These bacteria are chosen equidistantly along the arrangement. The chosen bacteria are removed from the simulation, and 10⁴ phages are spawned in their location. From these phage fates, we bootstrap β-phages 1000 times and quantify the secondary infection by measuring 1) the fraction of the β-phages that remain free 1 h after lysis and 2) the fraction of the β-phages that result in new infected bacteria. These together constitute the effective burst size, which we plot in Fig. 7 A. Each of the chosen bacteria has differing probabilities of being hit by an external phage, so we weighted the effective burst size by these probabilities; e.g., a bacterium at the core of a spherical colony has almost zero chance of being hit and should therefore contribute little to the result.

Figure 7.

Secondary infections. We measure the effects of phage mediated lysis within the bacterial arrangements. (A) The effective burst size β_eff for β = 100 is the number of phages that either cause new infections or remain free to cause future infections (measured 1 h after release). Blue, yellow, and red points indicate N = 10, N = 32, and N = 100, respectively. Error bars indicate standard error. (B–D) Examples of simulated lysis (N = 10, β = 100) are given. Red dots indicate locations of phage encounters. Dark gray indicates the lysed bacterium. (B) Chain with Θ/2π = 0.1 is shown. (C) Chain with Θ/2π = 0.5 is shown. (D) Spherical arrangement is shown. To see this figure in color, go online.

The effective burst size for the structured arrangements is only a fraction of the case when bacteria are well mixed. In Fig. 7, B–D, we show examples of phage collisions from a bootstrapped sample. This highlights how the secondary phages infect the bacterial arrangements nonuniformly.

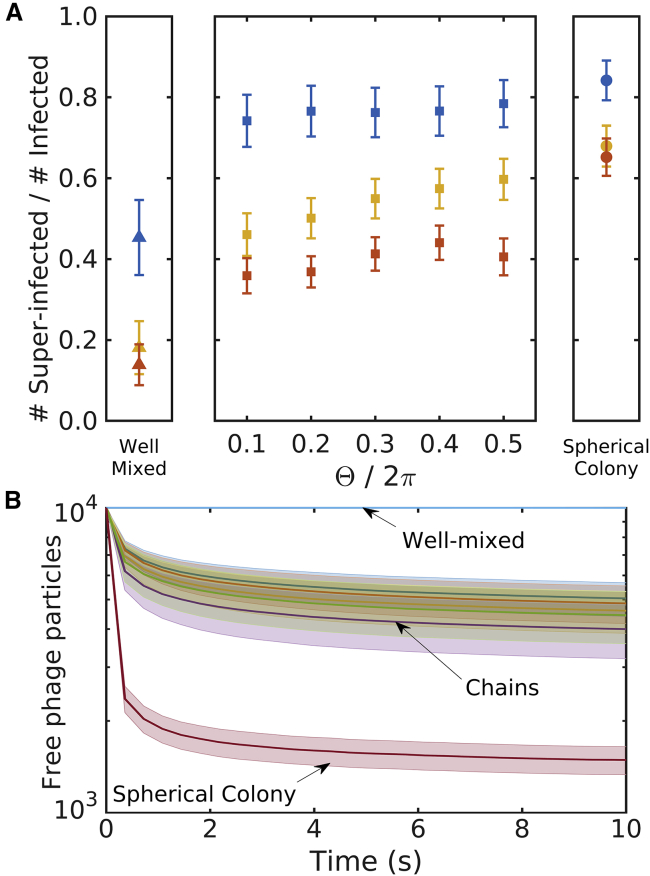
This nonuniformity means that many phages will be superinfecting the nearby bacteria and thus “wasted.” At the same time, it has been known that some temperate and virulent phages behave distinctly different depending on the multiplicity of infection (MOI), and we summarize some concrete examples in the Discussion. Therefore, using the bootstrapped samples from above, we quantify the fraction of infected bacteria that have been superinfected for β = 100 (see Fig. 8 A). Note that this measurement is sensitive to the chosen β-value.

Figure 8.

Superinfections. Neighboring bacteria experience high phage pressure after lysis events. (A) The structured bacterial arrangements exhibit a much higher rate of superinfections than the well-mixed bacteria. Blue, yellow, and red points indicate N = 10, N = 32, and N = 100, respectively. Error bars indicate standard error. (B) Average adsorption curves for N = 10 are given. The structured bacterial arrangements show substantial phage capture within a small time frame. Shaded areas indicate standard error of the weighted mean. To see this figure in color, go online.

In the structured arrangements, the phages are substantially more likely to hit an already infected bacterium than they are to hit an uninfected bacterium. Even when the arrangement contains 100 members, roughly half of the infected bacteria are hit by more than one phage. Furthermore, in these structured arrangements, the progeny phages are released immediately next to susceptible hosts, and when considering the timescale for adsorption (see Fig. 8 B), the phages are adsorbed within a very small time frame.

Discussion

Our investigation shows that the clustering of bacteria substantially changes to their exposure to invading phages. This is a result of several factors: 1) the clustering of bacteria increases the time it takes for the phages to locate the bacteria, 2) the heterogeneous distribution of bacteria within the clusters increase the likelihood of phages superinfecting bacteria, and 3) the phages released by lysis are very likely to superinfect bacteria, causing the effective burst size to decrease substantially.

These changes have profound effects on the virulence of the phage and the effectiveness of bacterial defense systems. For example, for the temperate phage λ, it is known that if the cell is infected with MOI ≥ 2 within a short enough time frame (before the final decision is made), the lysis-lysogeny decision is strongly biased toward lysogeny (27,28). Therefore, the short window of time after lysis during which the bulk of the superinfections occur is likely to cause a high fraction of lysogenic infections, which reduces the virulence of the phage attack. Similarly, some phages, like phage T4, exhibit lysis inhibition, whereby they delay the onset of lysis if the MOI is high (29,30), and such phages are thus much more likely to enter the lysis inhibition state when the bacteria are structured than when they are well mixed. The high fraction of superinfections also modifies the effectiveness of some bacterial defense mechanisms, such as abortive infections systems (6), which in this spatial context can be used to negate the effect of several phages at once. The high local MOI may also protect the bacterial populations by causing “lysis from without” (31,32), whereby the phages themselves cause an aborted infection. Interestingly, these effects are present even at very small clusters, e.g., consisting of three bacteria. It is worth keeping in mind that the increased MOI stemming from the structure of the bacterial cluster comes in addition to the increase in MOI that spatial structure alone brings (16,33).

When bacterial arrangements become large, the bacteria begin to compete internally for resources (12), and this competition may outweigh the benefits of the phage defense described above. This suggests that short- to medium-length chains of bacteria and small bacterial colonies are benefiting from the phage defense properties of their spatial structure without a substantial reduction in available resources. The heterogeneity in resource availability and phage exposure suggests that the bacteria on the edge of the bacterial clusters, because of the higher phage presence, should invest more in bacterial defenses, whereas the bacteria closer to center, because of the reduced nutrient level, should invest more in growth. For the future, it would be interesting to quantify what the tradeoff between phage defense and nutrient limitations is for clustered bacteria.

It has been shown that bacteria may utilize QS to modify their interactions with phages. For example, when (local) cell densities are high, E. coli have been shown to reduce the phage adsorption rate by downregulating the number of surface receptors (34), and Vibrio anguillarum have been shown to reduce the spontaneous induction rate of lysogens (35). We expect QS to have a larger impact on the phage-bacteria interactions when the bacteria are arranged in chains or colonies compared to when the bacteria are well mixed because of the locally higher cell densities in these arrangements. As such, a QS effect may further reduce the adsorption rate for even moderately sized bacterial arrangements. We may even hypothesize that the reduction in lysogen induction rates is a response to the small-scale structure of the bacterial arrangements. If a lysogen undergoes spontaneous induction while in a long chain (e.g., N = 100), the reduced effective burst size may prevent the progeny phages from reaching a new source of hosts. Alternatively, if the lysogens wait until the chain is broken up by other causes, the lysogens in the smaller fragments will have much higher effective burst sizes, and their phages will have a higher chance of escaping the arrangement.

Several other studies have shown that highly structured bacterial arrangements are capable of protecting the bacteria such as when they form a biofilm (14,18) or when they form microcolonies (15,16). Our results show that even small, weakly structured bacterial arrangements can cause substantial changes to the interaction with phages which may help explain why bacterial clustering is so prevalent even in liquid conditions (13). These small-scale structures may be important when interpreting data from bulk measurements. For example, our analysis suggests that small clusters of bacteria may cause an increased rate of lysogeny of λ-like phages because of the increased MOI (27) and, for some ϕH20-like phages, because of the locally high cell densities of the cluster (35). Furthermore, the reduced effective burst size of the phage when invading bacterial clusters suggests that the ratio of free phage particles/number of bacteria will also be smaller for clustered bacteria than well-mixed bacteria.

There are several documented synergistic mechanism for bacteria that may further benefit the bacteria living in clusters; for example, bacteria may utilize QS to modify their local environment when the local population density is high and thus share the burden of resource utilization (36), or the bacteria can evolve additional phage defenses such as abortive infection systems (6). The reduced phage pressure and the benefits of group living from existing as clusters provide the bacteria with a “win-win” scenario and may explain why bacteria have evolved mechanisms to remain clustered even in liquid environments.

Author Contributions

All authors designed the research. R.S.E. carried out all simulations and analyzed the data. All authors wrote the article.

Editor: Alexander Berezhkovskii.