Dye Transport through Bilayers Agrees with Lipid Electropore Molecular Dynamics

Abstract

Although transport of molecules into cells via electroporation is a common biomedical procedure, its protocols are often based on trial and error. Despite a long history of theoretical effort, the underlying mechanisms of cell membrane electroporation are not sufficiently elucidated, in part, because of the number of independent fitting parameters needed to link theory to experiment. Here, we ask if the electroporation behavior of a reduced cell membrane is consistent with time-resolved, atomistic, molecular dynamics (MD) simulations of phospholipid bilayers responding to electric fields. To avoid solvent and tension effects, giant unilamellar vesicles (GUVs) were used, and transport kinetics were measured by the entry of the impermeant fluorescent dye calcein. Because the timescale of electrical pulses needed to restructure bilayers into pores is much shorter than the time resolution of current techniques for membrane transport kinetics measurements, the lifetimes of lipid bilayer electropores were measured using systematic variation of the initial MD simulation conditions, whereas GUV transport kinetics were detected in response to a nanosecond timescale variation in the applied electric pulse lifetimes and interpulse intervals. Molecular transport after GUV permeabilization induced by multiple pulses is additive for interpulse intervals as short as 50 ns but not 5-ns intervals, consistent with the 10–50-ns lifetimes of electropores in MD simulations. Although the results were mostly consistent between GUV and MD simulations, the kinetics of ultrashort, electric-field-induced permeabilization of GUVs were significantly different from published results in cells exposed to ultrashort (6 and 2 ns) electric fields, suggesting that cellular electroporation involves additional structures and processes.

Significance

Electroporation models are based on pore formation in simple, homogeneous, lipidic membranes. Lipid electropores can be directly observed only in molecular simulations in which, in the absence of an electric field, the lifetimes of molecular pores are less than 50 ns. This timescale is inconsistent with the permeabilization kinetics and transport events observed in experiments with bilayers (milliseconds) and cells (minutes). We use ultrashort (6- and 2-ns) pulsed electric fields to facilitate dye transport into lipid vesicles and show that the transport is consistent with molecular simulations of electropore lifetimes and inconsistent with cellular electroporation, suggesting that the responses of biological and lipid membranes differ.

Introduction

Reversible electropermeabilization (electroporation) is widely used in gene and drug delivery, gene editing, and electrofusion, but the structures and mechanisms associated with the electrical disruption of biological membranes have not been established conclusively despite decades of study (1, 2, 3, 4, 5, 6, 7). Early models of pore formation based on the interplay of surface and line tensions around a membrane opening (8,9) were validated using planar lipid bilayer conductance data (3,10,11). In this theoretical framework, transmembrane potential (V_m) lowers the energy (W) required for the formation of a hydrophilic pore of radius r:

$$W=2\pi \gamma r-\pi \sigma r^2-C{V}_m^2{r}^2,$$ (1)

where γ is the line tension, σ is the surface tension, and C is a constant (3,8,9). This formalism was applied to descriptions of electroporation-based transport of molecules into cells and has become the “standard model” of electroporation (12, 13, 14).

The “standard model” of electroporation predicts the formation of populations of hydrophilic pores within a few nanoseconds after the pore formation barrier is overcome, with a concomitant increase in membrane conductance and a drop in transmembrane potential to near zero. The evolution of pore populations during application of a porating electric field is also described by this model as is the annihilation of the pores after the end of the porating electric pulse. Because the various implementations of the standard model are empirical with many fitting parameters, they can fit the results of experiments already performed, but they cannot predict outcomes or reveal underlying molecular mechanisms.

Molecular dynamics (MD) simulations provide physics-anchored reference points for the calculated behavior of electrically stressed lipid bilayers (the simplest biological membranes). MD simulations show how applied electric fields stabilize random incursions of water into the membrane interior and how lipid pores form within nanoseconds as phospholipids reorganize around these water bridges (15, 16, 17, 18). Annihilation of lipid electropores takes 10–100 times longer than pore creation (17).

Cellular electroporation phenomena that are not predicted by standard or molecular models include persistent permeabilization (19, 20, 21, 22), electrosensitization (increased effect with increased delay between pulses) (23), cell size dependence of electropermeabilization (24), complex molecule-specific transport patterns (5,25,26), maintenance or recovery of post-exposure membrane potential (27), and nanosecond bipolar pulse cancellation (the cancellation of the effects of the first electric pulse by a second electric pulse of the opposite polarity) (28,29).

Experiments with purely lipidic systems are essential for understanding how the lipid components of the cell membrane interact with the electric field and therefore for interpreting the role of nonlipid components of the plasma membrane or downstream biological processes, which are critical to the development of predictive models of electroporation. Early work identified key aspects of permeabilizing electrical stress, such as the relation between lipid composition and reversibility of pore formation (2), critical membrane potentials for permeabilization (2,4), pore energies and lifetimes (3,7,10,11), formation of macropores (30), and localization of lipid loss after electric field exposure (31, 32, 33). Experimentally, the existence and lifetime of membrane electropores can be observed only indirectly, for example, in measurements of transport. Experimental validation of the nanosecond-lifetime pore populations observed in MD simulations is constrained by time-resolution limits on data acquisition.

Most reports of nanosecond electric field effects on biomembranes, like those in MD simulations, are based on in vitro or in vivo permeabilization of cells or tissues, which introduces the complexities of cell membranes and cellular physiology (19, 20, 21, 22, 23, 25, 26, 27, 28, 29). A few studies have explored nanosecond-pulsed, electric-field-induced transport across artificial membranes or lipid vesicles (34, 35, 36), but none measured transport kinetics or pore lifetimes after nanosecond pulse permeabilization of lipid membranes (37). Moreover, previous reports of simulated lipid electropore lifetimes (15,16,38,39) have been based on small sample sizes with pores formed under arbitrary conditions and of arbitrary sizes.

Here, we experimentally measure the kinetics of calcein transport into giant unilamellar vesicles (GUVs) exposed to ultrashort electric pulses (2 and 6 ns) and, for the first time, to our knowledge, extract simulated electropore lifetimes using sets of pores systematically stabilized to specific sizes before electric field removal (40). The experimental time-resolution limitation is addressed by using electric pulses separated by only a 50-ns interval, permitting the first, to our knowledge, experimental analysis of electropore lifetime on the nanosecond timescale. Consistent with molecular simulations, a large fraction of the calcein-permeant pores formed under these exposure conditions closed within 50 ns. The time course of calcein transport into GUVs is transient and different from the persistent electropermeabilization seen in cells under the same exposure conditions.

Materials and Methods

GUVs

Pure 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC; Avanti Polar Lipids, Alabaster, Alabama) GUVs containing 200 mM sucrose dissolved in piperazine-N,N′-bis(2-ethanesulfonic acid) (PIPES) (1 mM EDTA, 1 mM N-(2-Hydroxyethyl)ethylenediamine-N,N′,N′-triacetic acid (HEDTA), 10 mM PIPES, and 100 mM KCl (pH 7.4)) were prepared with a gel-assisted protocol (41,42) and stained with 1,1′-dioctadecyl-3,3,3′,3′- tetramethylindodicarbocyanine, 4-chlorobenzenesulfonate salt (DiD) (Invitrogen, Carlsbad, CA) (43). GUVs were pipetted 15 min before the recording into coverglass chambers (Nunc Lab-Tek II; Thermo Fisher Scientific, Waltham, MA) filled with 200 μM calcein (MP Biomedicals, Santa Ana, CA) and 200 mM glucose in PIPES solution in which parallel tungsten-wire electrodes were prepositioned in the chamber well. The calcein concentration was chosen to be below the self-quenching range so that the fluorescence intensity varied linearly with concentration (27).

Microscopy

Images were acquired on a Zeiss LSM 880 confocal microscope (Oberkochen, Germany) using 63×, oil immersion, 1.4 NA objective. The size of the confocal pinhole was set to one Airy disk at 633 nm. Calcein and DiD were excited with 488- and 633-nm lasers, respectively, by alternating every 0.03-ms excitation line scan during raster image formation, and fluorescence was measured (emission bands λ_calcein: 500–561 nm and λ_DiD: 635–735 nm) at a rate of 1 fps using separate acquisitions (tracks) to minimize cross talk.

Image analysis

Images were analyzed with custom MATLAB (The MathWorks, Natick, MA) scripts that track vesicle regions of interest in each frame as described previously (22). The fluorescence intensity change (ΔF) was calculated by subtracting the mean intravesicular intensity before the application of the pulsed electric field exposure from the intravesicular intensity values measured during the experimental time series. A slow, linear, time-dependent, fluorescence change was observed in unexposed vesicles (sham vesicles) characterized in the mean (n = 7), and this linear trend in unexposed vesicle fluorescence was subtracted from all experimental time series. The resulting fluorescence intensity was normalized to extravesicular fluorescence intensity (F_e), and the time series data presented as fractional fluorescence change (ΔF(t)/F_e) with time (t).

Pulsed electric field exposure

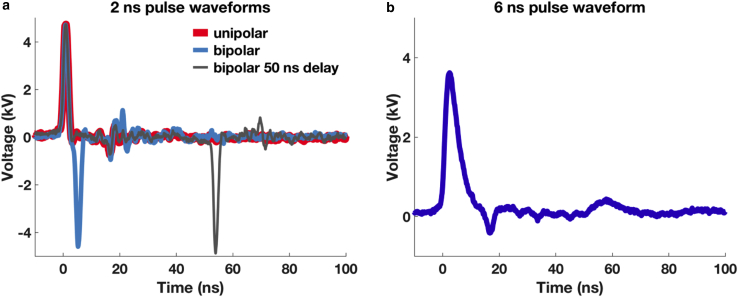
6 or 2 ns—full width at half maximum—electric pulses from FID GmbH pulse generators (6 ns: FPG 10-10NK, 2 ns: FPG 10-1CN6V2; Burbach, Germany) were delivered to lipid vesicles via parallel tungsten-wire electrodes (22,44) 80 μm apart. Pulse exposures were either unipolar or bipolar with equal positive- and negative-phase amplitudes and were monitored and recorded with an oscilloscope. Typical waveforms are shown in Fig. 1. Electric field amplitudes at the vesicles were computed using COMSOL multiphysics (Stockholm, Sweden) are shown in the Supporting Materials and Methods.

Figure 1.

Typical electric pulse waveforms recorded during the experiments. (a) Shown is a 6 ns exposure. (b) Shown are 2 ns exposures: unipolar (red), bipolar without any interphase time interval (blue), and bipolar with 50 ns between the phases (gray). To see this figure in color, go online.

MD simulations

For MD simulations, we used GROMACS 4.6.6 (45,46) on the Old Dominion University High Performance Computing cluster (http://www.odu.edu/hpc) with CHARMM36 lipid topologies and force field parameters (http://mackerell.umaryland.edu/charmm_ff.shtml) (47) and the TIP3P water model (48). The online tool CHARMM-GUI: Membrane Builder was used to create lipid bilayer systems (49). All simulations were carried out under the NPT ensemble with a 2 fs time step. Systems were coupled to a temperature bath at 310 K using the velocity-rescale coupling algorithm (50) and to a pressure bath at 1 bar using the Berendsen algorithm (51) with a relaxation time of 1 ps and compressibility of 4.5 × 10⁻⁵ bar⁻¹ semi-isotropically applied in the normal and in-plane directions relative to the membrane. Bond lengths were constrained using the LINCS algorithm (52) for lipids and SETTLE (53) for water. Short-range electrostatic and Lennard-Jones interactions were cut off at 1.0 nm. Long-range electrostatics were calculated by the PME algorithm (54) with conductive periodic boundary conditions.

Simulation systems and structures

To lipid bilayer systems containing 128 POPC, 64 in each leaflet, and approximately 12,000 water, we added 22 K⁺ and 22 Cl⁻ using the GROMACS function “genion.” Box dimensions are approximately 7 × 7 × 11 nm, and the KCl concentration is ∼125 mM (based on a volume that excludes the membrane interior and interface in which water density is less than 90% of the bulk water density).

The system was equilibrated for 100 ns until a constant area per lipid was achieved (55). A porating electric field of 250 MV/m was applied along the z axis (normal to the bilayer plane) following the method used in (56) to induce formation of an electropore through the lipid bilayer. A procedure similar to the one described in (40) was used to produce stable electropores at different stabilizing field amplitudes: 40, 50, and 60 MV/m. Stabilizing fields are used to generate a range of different pore sizes whose exact dimensions are computed later, as described in the next section. Three independent trials were carried out for each stabilizing field value by randomizing velocities after pore formation (GROMACS MDP file: gen_vel = yes and gen-seed = −1). After 100 ns of stabilization, the electric field was reduced to zero, and the simulations were run for another 100 ns. Periodic boundary conditions can cause artifacts associated with effective electric fields in lipid bilayer systems (39,57), but this should not affect these lifetime measurements, which are carried out on pores after the external electric field is removed.

Pore radius and pore closure time calculations

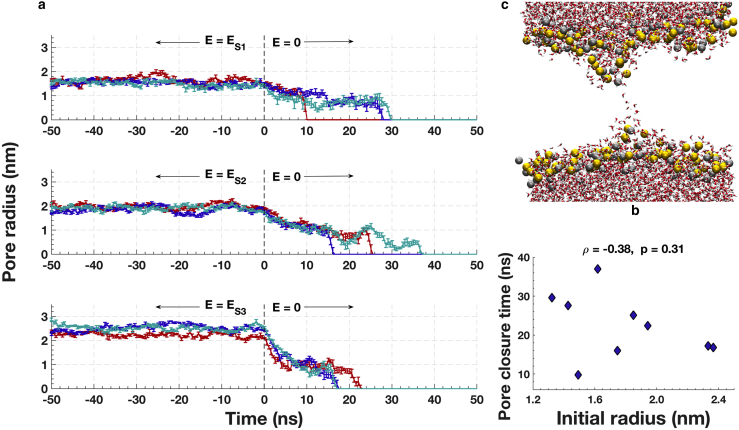
Pore geometry was extracted from GROMACS structure (gro) files generated from the simulations every 100 ps and analyzed with custom MATLAB scripts (The MathWorks). Pores were centered in each frame using POPC density files generated with the GROMACS command “g_density.” The center of the pore was determined as follows: 1) POPC density versus spatial axes plots are smoothed using a Butterworth low-pass filter generated by the native MATLAB function “butter”; 2) the region containing the pore is defined by decreases in POPC density in x, y, and z. The dip defining the pore is chosen as the region in the density profile that is less than 34% of the full range of densities. The pore center, which is in the middle of this dip region, is placed in the center of the simulation box, translating all atoms in the frame accordingly. After centering the pore, the box is divided into 0.2 nm slices in the z-direction. Water molecules in each slice are located, and outliers in the x- and y-directions are eliminated using the native MATLAB function “isoutlier” (The MathWorks), which defines an outlier as a value that is more than three scaled median absolute deviations away from the median. These outliers represent occasional random water intrusions into the lipid bilayer far from the electropore. Next, the center of each z-slice in x and y is determined using the mean of water oxygen locations, and the distance in the x-y plane of each water molecule (oxygen atom) from the slice center is calculated. The water-based radius of each slice is defined as the mean plus two standard deviations of this set of distances. This generates a water-column radius versus z-slice location vector for each frame. The pore radius (r_pore) in a frame is defined to be the mean water-column radius in the 1-nm-long region around the z-center of the pore. Pore radius versus time is plotted in Fig. 4 a using the mean pore radius of every five frames (500 ps). Error bars show the standard deviation of the pore radius value for the same five frames. Pore closure time is defined as the time of the first of three consecutive frames with r_pore = 0; that is, three consecutive frames in which five 0.2-nm-thick z-slices around the box center are water-free.

Figure 4.

(a) Kinetics of pore annihilation for three different pore sizes. Shown are three independent simulations indicated with different colors (red, blue, and cyan) for each pore size, corresponding to each sustaining field (E_S1, E_S2, and E_S3), are shown. Error bars indicate standard deviation of radius (Supporting Materials and Methods). (b) Shown is a snapshot of a typical lipid electropore just before final collapse of the membrane-spanning water column (red and white: water O and H; gold and silver: P and N of lipid headgroups; lipid tails hidden for clarity). The pore is shown 9.5 ns after removal of E_S1 = 40 MV/m sustaining field, 0.5 ns before complete closure (simulation plotted in red in (a), top plot). (c) Shown is a scatter plot showing a lack of correlation between the initial pore radius (mean of the first 1 ns after the electric field removal) and the pore closure time. To see this figure in color, go online.

Results and Discussion

Calcein transport into POPC GUVs after 6 ns electric field exposures

Pure POPC GUVs were prepared using the gel-assisted formation method (41, 42, 43), which has several advantages over the electroformation methods (42) commonly used in experimental studies of GUVs in pulsed electric fields (30,32,33,35,36). Disadvantages of GUVs prepared by electroformation include low yield in physiological buffers, heterogeneity in composition and size, and electric-field-induced oxidation of lipids, which causes increased membrane permeability and altered mechanical properties (42). Polyvinyl alcohol (PVA)-gel-assisted swelling is a facile and rapid method for generating GUVs with a wide range of lipid compositions and ionic strengths. A previous version of this method based on agarose-gel produces vesicles with artifacts that may influence experimental results, mainly by encapsulating agarose inside GUVs and influencing the mechanical properties of the membrane, as elucidated previously (58). These issues, however, do not pose a major problem in the PVA-gel-based method because encapsulating PVA inside GUVs is less likely because of the lower solubility of PVA in water compared with agarose (41). The PVA-gel-assisted swelling method was chosen to ensure high enough yield in an approximately physiological salt concentration.

For fluorescence imaging simultaneous with electrical stimulation, DiD-labeled vesicles were positioned between parallel wire electrodes (22) in the field of view. Membrane permeabilization was monitored with calcein, a small (radial cross section 0.58 nm), impermeant, fluorescent molecule that does not interact with lipids during transport across membranes because of its strongly hydrophilic properties (44,59,60). We have previously shown in simulations and experiments that divalent cation dyes such as YO-PRO-1 (Thermo Fisher Scientific) can significantly interact with lipid membranes (22). Calcein, with a valence −4, has a much higher polar surface area (27,59,60) than YO-PRO-1 (Thermo Fisher Scientific). Previously, calcein did not interact with cell membranes, whereas YO-PRO-1 (Thermo Fisher Scientific) did (22,44).

Confocal fluorescent microscopy of an optical slice through GUVs before electrical stimulation are consistent with a lack of dye in the GUVs interior (Fig. 2 a). GUVs did not change in morphology or size during experiments except for a few instances of GUVs bursting at random times (not correlated with electric pulse delivery), which were excluded from data analysis. Because a systematic investigation of all electroporation parameters was not a goal of this study, the pulse exposure parameters were chosen to provide sufficient calcein transport for detection with this imaging system.

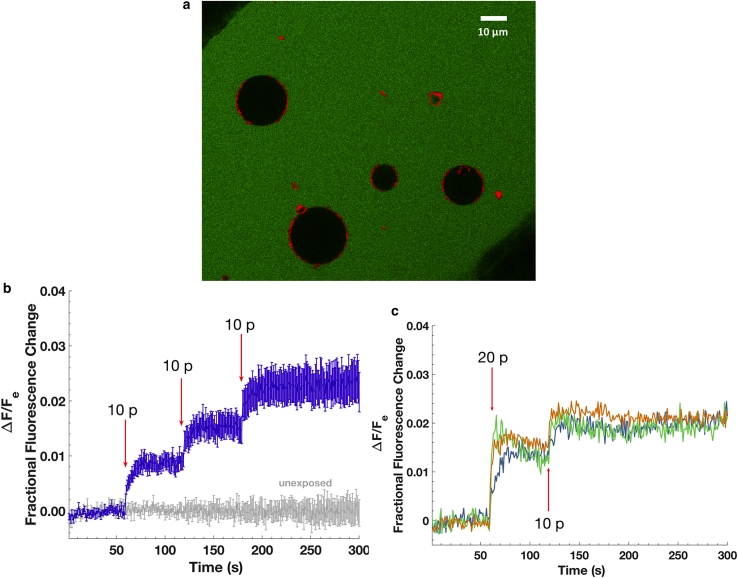
Figure 2.

(a) Confocal image of four POPC GUVs stained with DiD in 200 μM calcein solution at the bottom of a coverglass chamber and between tungsten-wire electrodes before the electric field exposures. Green represents calcein fluorescence, and red represents DiD. (b) Shown is the fractional fluorescence change (ratio of change in intravesicular fluorescence to extravesicular fluorescence) of GUVs exposed to three 1 kHz trains of ten 6 ns electric pulses (at field strengths of 35 MV/m) delivered 1, 2, and 3 minutes into the recording (n = 13) or not exposed to the E-field (n = 7). Arrows indicate the time of each train of pulses. Error bars are standard error of the mean. (c) Shown are the individual traces of the fractional fluorescence change of three GUVs exposed to two initial 1 kHz trains of 10 pulses separated by 500 ms (total of 20 pulses) and, then after 60 s, exposed to one train of 10 pulses (10 p). In both the 20- and 10-pulse trains, each pulse was 6 ns in duration and 35 MV/m in field amplitude. The imaging rate was 1 fps. To see this figure in color, go online.

Exposure of GUVs to a 1kHz train of 10 electrical pulses of a duration of 6 ns and a field strength of 35 MV/m (pulse train delivery ending in 10 ms) resulted in a stepwise increase of intravesicular calcein fluorescence (Fig. 2 b). The increase in fluorescence is approximately proportional to the number of pulses and is additive for successive exposures (Fig. 2 c), consistent with the hypothesis that electric fields induce an opening of lipid pores and calcein transport through the pores, most or all of which close during the 1-ms interpulse interval. The intravesicular calcein concentration is ∼1% of the extracellular concentration for 10 pulses and 2% for 20 pulses—2 and 4 μM, respectively. This degree of entry can be described by simple electrodiffusion through nanometer-size, calcein-permeable pores (Supporting Materials and Methods). Consistent with the membrane charging time constant for GUVs (∼100 ns) being much longer than the duration of these pulses, the correlation between GUVs size and molecular transport is not positive (Fig. S1) in contrast to a positive correlation observed when long pulse durations (100 μs and 5 ms) (32) are used.

Calcein transport into POPC GUVs after 2-ns electric field exposures with polarity reversal

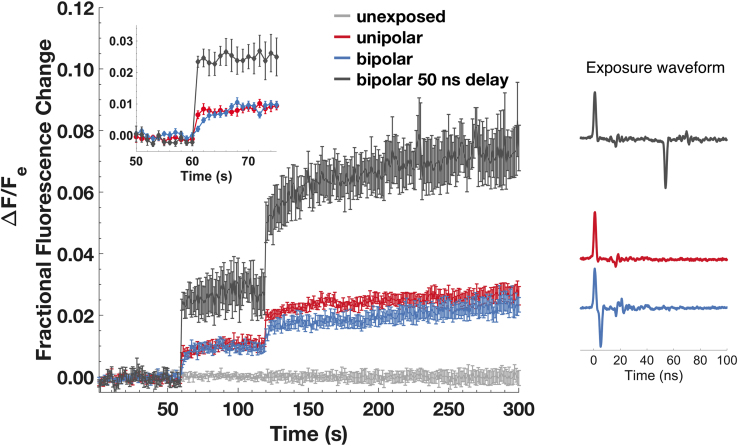
GUV permeabilization was tested for sensitivity to direction and sequence of electric field, i.e., exposure to unipolar and bipolar nanosecond pulses. In cells, the transport of small molecules caused by a unipolar pulse is attenuated or cancelled by a closely following pulse of opposite polarity (28,29,44,61, 62, 63, 64, 65). In other words, a unipolar pulse is more effective in causing small molecule transport into cells than a bipolar pulse of double the duration. For this set of experiments, we delivered 2 ns bidirectional electric pulses to vesicles; these same doses were used in our earlier report on cells (44). The electrical parameters (40 pulses, 45 MV/m field strength, delivered at a 1 kHz repetition rate) were chosen to produce a similar amount of calcein transport as 6 ns pulse trains (Fig. 2 b). 2 ns unipolar and bipolar pulse (2 ns positive and 2 ns negative) exposures, with no interpulse delay (negative pulse immediately follows the positive pulse) result in equal transport of calcein into GUVs, whereas a short delay of 50 ns between the bipolar pulse phases results in at least twice the transport (Fig. 3). That is, for a bipolar pulse with no delay between phases (5 ns interval between the peaks), the negative phase does not significantly affect the calcein permeabilization caused by the preceding positive phase.

Figure 3.

Fractional fluorescence change (ratio of change in intravesicular fluorescence to extravesicular fluorescence of calcein transport as a result of exposure to unipolar (red, n = 9), bipolar with no interpulse delay (blue, n = 10), and bipolar with 50-ns interpulse delay (gray, n = 4)). Trains of 40 pulses (45 MV/m field strength and 2 ns duration) were delivered at a 1-kHz repetition rate 60 and 120 s into the recording. Error bars show standard error of the mean. (Note that the first and second phases of a 2 ns bipolar pulse are each 2 ns in duration.) The inset shows the transition at the first pulse train exposure. Vesicles that are not exposed to the electric field are also shown (n = 7). To see this figure in color, go online.

This absence of bipolar pulse cancellation with GUVs stands in strong contrast to the cancellation effect observed with cells (44), in which bipolar pulses produce severalfold less transport than unipolar pulses. Note, if GUV membrane conductivity does not change during the 2 ns of the first bipolar pulse phase, then the second phase of the bipolar pulse should discharge the membrane, resulting in no transport, similar to the bipolar cancellation effect observed with cells (44).

The data of Fig. 3 can be analyzed within the framework of membrane charging (and discharging) in the standard continuum electroporation models (3,10, 11, 12, 13, 14). We postulate that the positive applied potential of a bipolar pulse induces a high transmembrane potential, which permeabilizes the membrane and increases the membrane conductance. When the negative applied potential arrives without any delay, because of its high conductance, a high transmembrane potential cannot develop across the porated GUV membrane. Thus, the negative phase of the bipolar pulse cannot significantly change the total transport through existing pores and is not predicted (by the standard models) to significantly affect membrane permeabilization-related transport end points. Because the second, undelayed phase of the bipolar pulse causes no significant change in total calcein transport, the GUV membrane must be sufficiently conductive during the second phase of the pulse, and thus, most or all of the conductive electropores are formed within the 2 ns duration of the first phase.

If the second phase of the bipolar pulse is delayed by even 50 ns after the first phase, however, the effect on calcein transport is approximately additive (i.e., the total transport is approximately twice that caused by a unipolar pulse). This is consistent with a membrane that is not significantly conductive after 50 ns when a large fraction of the conductive, calcein-transporting pores due to the first phase closes causes the second, delayed phase to interact with a nonconductive membrane as the first phase did. Note that the total transport ratio for bipolar pulse with 50-ns delay is more than 2 (2.7 and 2.4), which we attribute to the stochastic nature of the measurements that are not resolved because of the limitations in the sample sizes.

MD simulations of electropore lifetime are consistent with GUV permeabilization kinetics

The measurement resolution of GUV membrane permeability after electroporation cannot directly detect molecular fluctuations of lipids or electropores lasting tens of nanoseconds. To model the response of lipid molecules to similar electric fields, MD simulations of constructed electropores were studied to assess their behavior after the removal of an external electric field. Pores were generated and stabilized in molecular simulations of POPC bilayers (128 POPC, ∼12,000 H₂O, and 22 K⁺ and 22 Cl⁻, corresponding to 125 mM KCl, approximating the KCl concentration in the GUV suspensions). Pores are created by a porating field of 250 MV/m and then stabilized with sustaining fields of 40, 50, and 60 MV/m (corresponding to pore radii of 1.3, 2.0, and 2.4 nm, respectively) for 100 ns (40), with three simulations for each condition. The initial porating field facilitates creation of electropores with low computational cost and no effect on their physical properties (40). The lower sustaining fields produce stable pores of three different sizes, allowing relationships between pore size and pore lifetime to be determined. The applied field was then reduced to zero, and pore radius was monitored for another 100 ns. Note, the simulation box size (7 nm × 7 nm × 11 nm) may have had a small effect on electropore properties for the range of sizes examined, but the results here demonstrate that this did not affect the lifetime of the pores significantly.

Fig. 4 a shows the evolution of pore size 50 ns before and after removal of the sustaining electric fields E_S1, E_S2, and E_S3. Pore radius decreases from a value determined by the sustaining field to ∼1 nm and then remains in this metastable state for 10–35 ns before the pore closes (Fig. 4 a). This state terminates when the pore lipid headgroups separate into two groups, leaving behind a quickly collapsing water bridge (17). A typical electropore just before complete annihilation is shown in Fig. 4 b. Snapshots of more frames leading up to the pore collapse can be found in the Supporting Materials and Methods. Pore annihilation time is stochastic and is not correlated with pore size over a range of initial radii of 1.3–2.4 nm (Fig. 4 c).

The behavior of these simulated electropores, resulting in lifetimes in the order of tens of nanoseconds after removal of the electric field, is consistent with the experimental measurements of calcein transport. Experimentally, the second phase of a 2 ns bipolar pulse led to a first phase equivalent or higher transport only if there is sufficient time between the phases (Fig. 3). This time interval agrees with the time needed for molecular bilayers with electropores to return to an unporated state after removal of a permeabilizing electric field. The pore-free, nonconductive state of the membrane makes it possible for induction of a high transmembrane potential, which facilitates pore formation.

Kinetics of fluorescence change and electrodiffusion of calcein

Interestingly, even though the total transport after a train of unipolar pulses is comparable with that after a train of bipolar pulses with no delay between positive and negative phases, the rise time of calcein influx is slower with bipolar pulse exposures (Fig. 3, inset). Additionally, this slower kinetics of the calcein influx is similar to that observed with 6 ns unipolar pulses (Fig. 2 b; Fig. S2), unlike 2 ns unipolar or bipolar exposure with 50 ns delay between phases (Fig. 3, inset). A bipolar pulse with a 2 ns positive and 2 ns negative phase without any interpulse delay induces a transmembrane potential across the membrane for the duration equal to the total of both phases, 4–5 ns, which is comparable with a 6 ns unipolar exposure (Fig. 1; Fig. S2).

The kinetics of calcein influx after the exposure to a train of 6 ns pulses (Fig. 2 b) can be modeled as a fast transition, followed by a slower increase. In the fast process, which has the lifetime characteristics of pores in molecular simulations, there were approximately equal increases in amplitude for each pulse. The slow process amplitude, however, decreases with an increasing time constant with succeeding pulses after the first pulse delivery (Supporting Materials and Methods). We hypothesize that the slower process is due to longer-lasting (seconds) pores, which are more likely to form when the induced membrane potential is sustained for a longer time (i.e., longer pulse durations, 6 and 2 ns bipolar without interpulse interval). This hypothesis also suggests that the increase in the number of longer-lasting (seconds) pores is independent of electric field direction, consistent with the MD simulations, in which field reversal does not affect electropore lifetime. Lipid pores with longer lifetimes are observed experimentally and in simulations when a low membrane potential is present (3,7,40). Moreover, the amplitude of pulse-induced transport after a second bipolar pulse train reaches the level seen after a second unipolar pulse train but more slowly (Fig. 3). This may be an indicator of differences between the persistent pore populations after the two kinds of exposures.

The total amount of calcein transport observed in Fig. 2 b with 6 ns pulse trains or in Fig. 3 with 2 ns unipolar (red trace) or bipolar pulses without interpulse delay (blue trace) can be explained by electrodiffusion through electropores with an ∼50 ns lifetime. These short-lived pores would not be expected to contribute to the slower kinetics observed with 6 ns unipolar (Fig. 2 b) and 2 ns bipolar pulses (Fig. 3, blue trace). A very small number of longer-lived pores could be responsible for this transport. For example, 15 pores with a 1 s lifetime could transport as much as 10⁶ similar size conductive pores with a 50 ns lifetime (Supporting Materials and Methods). Thus, the slower kinetics observed in longer duration pulse conditions is consistent with the hypothesis that a small number of longer-lived pores facilitates diffusive transport long after the pulse exposure ends. Details of the calculations supporting these statements can be found in the Supporting Materials and Methods.

Comparison of GUVs and cells

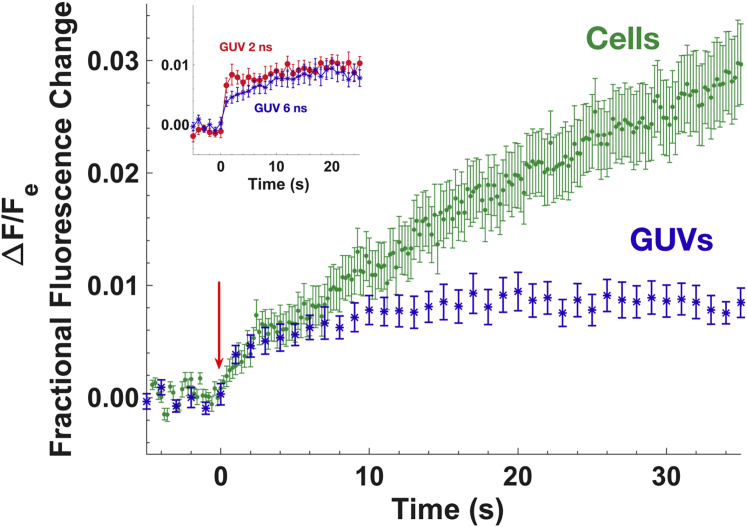
The stepwise intravesicular fluorescence increase after both 2 and 6 ns pulse trains observed with GUVs is not observed with cells after similar exposures (22,27,44). In cells, the intracellular calcein fluorescence increase under similar pulse exposure conditions continues for minutes (27) in contrast with the plateau reached within seconds with GUVs. Fig. 5 compares calcein transport into GUVs and cells during the first 35 s after pulsed electric field exposure. The cell data shown are adapted from earlier experiments with 6 ns pulse trains (27) (10 pulses of 20 MV/m electric field strength delivered at 1 kHz). The inset illustrates the clear plateau after a faster (2 ns pulse exposure) and slower (6 ns pulse exposure) increase in intravesicular calcein fluorescence.

Figure 5.

Intracellular calcein fluorescence increase of U-937 cells (n = 24) exposed to a 1 kHz train of ten 20-MV/m, 6 ns pulses plotted together with the first 30 s after the first exposure of GUVs shown in Fig. 1b (6 ns pulses, 1 kHz train of ten 35 MV/m, n = 13). Fractional fluorescence change is the ratio of intracellular or intravesicular fluorescence change to extracellular or extravesicular fluorescence, respectively. For ease of comparison, the exposure time is translated to 0 s for both recordings. Given are a frame rate of 5 fps for cells and of 1 fps for GUVs. Cell electropermeabilization lasts minutes, whereas GUVs electropermeabilization reaches a plateau in seconds. The inset shows the transition kinetics after exposures of 2 ns unipolar (Fig. 2) and 6 ns unipolar (Fig. 1b) of GUVs. Error bars show standard error of the mean. To see this figure in color, go online.

Differences between cells and GUVs are expected because cells are complex, dynamic machines that actively respond to membrane permeabilization (22,66). The set of transport- and recovery-related structures and processes found in electropermeabilized cells—the electropermeome (22)—may include but is not limited to pores prevented from closing by cytoskeletal constraints (67,68) or obstructions (69), field-induced modifications of membrane proteins (70,71), regions of lipid scrambling (72), and biological responses to disturbance of homeostasis, such as active volume regulation, cell membrane repair, and ATP-dependent pump activity for restoration of ionic imbalance and membrane potential.

Conclusions

The experimental data are consistent with the hypothesis that calcein-permeable lipid electropores in GUVs are created within a few nanoseconds and that most are annihilated within a few tens of nanoseconds, consistent with molecular simulations, but in contrast with the typical persistent electropermeabilization (many seconds to minutes) observed in living cells. Furthermore, the magnitudes of the increases in intravesicular dye concentration are much smaller with nanosecond-pulsed electric fields than those observed in the presence of the pore-forming peptide melittin or exposure to influenza virus at a low pH (43). Nanosecond bipolar pulse cancellation (44), a phenomenon recently described in cells, was not observed in GUVs. The absence of persistent electropermeabilization and nanosecond bipolar cancellation of GUVs suggests that the electropermeabilization of cells involves structures and processes that go beyond transport through lipid pores and that models of electroporation must be modified accordingly.

Author Contributions

E.B.S., S.H., P.T.V., and J.Z. designed the research. S.H. prepared the GUVs. E.B.S. and S.H. performed the GUV experiments. F.C. performed the MD simulations. E.B.S. analyzed the experimental and simulation data and generated the figures. P.S.B. generated the analysis of transport kinetics. E.B.S. and P.S.B. did the analytical calculations. P.T.V. supervised the simulations. P.T.V. and J.Z. supervised the experiments. E.B.S. and P.T.V. wrote the manuscript. P.T.V. and J.Z. supervised the whole work. All authors contributed to writing, editing, and revision of the manuscript.

Editor: Rumiana Dimova.