Abstract
Reference evapotranspiration (ETo) is a basic element for hydrological designing and agricultural water resources management. The FAO56 recommended Penman–Monteith (FAO56-PM) formula recognized worldwide as the robust and standard model for calculating ETo. However, the use of the FAO56-PM model is restricted in some data-scarce regions like Bangladesh. Therefore, it is imperative to find an optimal alternative for estimating ETo against FAO56-PM model. This study comprehensively compared the performance of 13 empirical models (Hargreaves–Samani, HargreavesM1, Hargreaves M2, Berti, WMO, Abtew, Irmak 1, Irmak 2, Makkink, Priestley-Taylor, Jensen–Haise, Tabari and Turc) by using statistical criteria for 38-years dataset from 1980 to 2017 in Bangladesh. The radiation-based model proposed by Abtew (ETo,6) was selected as an optimal alternative in all the sub-regions and whole Bangladesh against FAO56-PM model owing to its high accuracy, reliability in outlining substantial spatiotemporal variations of ETo, with very well linearly correlation with the FAO56-PM and the least errors. The importance degree analysis of 13 models based on the random forest (RF) also depicted that Abtew (ETo,6) is the most reliable and robust model for ETo computation in different sub-regions. Validation of the optimal alternative produced the largest correlation coefficient of 0.989 between ETo,s and ETo,6 and confirmed that Abtew (ETo,6) is the best suitable method for ETo calculation in Bangladesh.
Subject terms: Atmospheric science, Climate change, Hydrology
Introduction
Evapotranspiration (ET) is a physical aerodynamics process in which water moves from liquid to gaseous stage, whereas bringing from the soil to the atmospheric surface1. It denotes to both evaporation from vegetation and soil fields and transpiration from plants. Two distinct processes (evaporation and transpiration) happen concurrently, and there is no alternative way of differentiating one from the other. ET is one of the basic elements of the water cycle, and its estimation is necessary to drought mitigation and management as well as other fields, including agro-meteorology, hydrology, climatology, and environmental studies2–5. For this reason, many drought indices such as Reconnaissance Drought Index (RDI)6, Standardized Precipitation Evapotranspiration Index (SPEI)7, and the Water Surplus Variability Index (WSVI)8 are based on the ET. Besides, two closely associated terms and concepts are potential evapotranspiration (ETp) and reference evapotranspiration (ETo) that estimate the atmospheric evaporation demand. ETp is defined as the rate of water transpired in a specific time by a crop, fully shading the ground, of constant height with adequate soil water setting in the outline9,10. On the other hand, ETo is expressed as the ET rate from a reference crop surface, where the reference crop surface is a theoretical grass or alfalfa with accurate and recognized characteristics1,11. However, the definition of ETo is more precise and specific than the ETp. The application of the terms ETp and ETo have been puzzled for several decades. One ideal example is that Hargreaves and Samani12 used the term “ETp” whereas again Hargreaves and Samani13 applied the term “ETo”. Under the well-known background of global warming in recent decades, the term ETo has been broadly applied in hydrology14–16, agronomy field17–19, irrigation engineering4,20,21 and meteorological field22,23. The application of ETo is also used in the studies of crop water demand. Therefore, knowledge of ETo is of great importance in agricultural water management, hydrological field, climate change, and irrigation practice24,25.
FAO recommended Penman–Monteith (FAO56-PM) method is the sole standard method for estimating ETo1,20,26. The main limitation of the FAO56-PM method is the difficulty in obtaining all necessary input data (air temperature, humidity, solar radiation, and wind speed). In such circumstances, simple equations or alternative methods are often used to estimate ETo27. The major advantages of an optimal empirical method are the simplicity, low cost, ease of application, and easy access to a few climatic input data measured in most of meteorological stations28. Thus, an optimal empirical model is vital for ETo estimation in data-limited regions across the globe, including Bangladesh.
The selection of an optimal empirical model for calculating the ETo is significant for agricultural water resources management, hydrological planning and irrigation designing11,24,29. In recent decades, a large number of empirical models have been developed to estimate the ETo, which have been widely reported in the literature (Table S1). These empirical models can be demarcated into five types mainly based on the data requirement: mass transfer-based30,31, temperature-based11, radiation-based13,32–36, combined-based24,33–35 and the pan evaporation-based models37–39 (Table S1). Earlier studies showed that the performance of various empirical models exhibited spatiotemporal variations, and most of these empirical models might be region-specific that enhanced the uncertainty problem in the identified spatiotemporal patterns. To solve this issue, local adjustment and validation of empirical models are required against the standard FAO56-PM model at various regions with various climatic contexts for accurate estimation of the ETo24. Most of the previous studies revealed that the performance of empirical models for estimating ETo showed significant regional differences40,41. For instance, the calibrated adjusted Hargreaves model performed better than the calibrated Priestley-Taylor model for measuring ETo in Serbia42. Quej et al.43 assessed the performance of the temperature-based ETo models and found that the Hargreaves–Samani model exhibited the best performance in a tropical sub-humid climate. Krishna44 pointed out that the Turc model was an optimal alternative for the estimation of the ETo under a humid subtropical climate, India. Li et al.24 reported that combination-based Valiantzas3 was the best model for estimating ETo in the humid to sub-humid region, China. On the contrary, Pandey and Pandey45 found that the Hargreaves–Samani method had a larger overestimation than the standard FAO56-PM in humid areas of India. These contrasting outcomes can be attributed to variations in regional climate, and geography. However, whether empirical models influence the computation procedure of the ETo against the FAO56-PM model remains uncertain. Therefore, it is crucial to conduct research appraising the performance of the empirical models in Bangladesh to determine an optimal alternative to ETo and their changes shifted overtimes at the regional scale and differ spatially14,15.
Bangladesh, the vast deltaic plain, a low-lying subtropical humid climatic country, is positioned in Southeast Asia, has a total land area of 147,700 square km46 (Supplementary Figure S1). The country has a complex geomorphic setting and complicated hydrologic system which comprises various water bodies, wetlands, floodplain, flood basins, agricultural land, forest, and hilly regions. The elevations of most regions of the country varied from 1 to 60 m above the mean sea level, which forms generally low-lying areas from the east to the west, making a so-called “delta-shaped” landform4. Nevertheless, Bangladesh is not only faced this type of difficulty in obtaining long-term and complete climatic datasets but also this poor country experiences similar phenomena owing to naturals such as a complicated hydro-geographic and climatic setting and humankind e.g., low economic growth, lack of proper knowledge and technological hindering causes. Under this circumstance, for the ETo appraisal of Bangladesh, an alternative empirical model depending on the limited climatic dataset is needed47. Therefore, it is of paramount importance to validate an appropriate alternative model which is easier in calculation procedure with fewer climatic variable requirements and good precision in comparison with the FAO56-PM model in various climatic sub-regions of Bangladesh. To the author's knowledge, so far, a systematic and thorough investigation for choosing an optimal alternative for estimating ETo has not been conducted in Bangladesh till now, particularly at a monthly and regional scale, which in itself is the novelty of this study.
Based on the aforementioned research gaps, in this research, 13 widely employed empirical models selected for performance evaluation, including four temperature-based model (Hargreaves–Samani, Hargreaves M1, Hargreaves M2, and Berti), one mass transfer-based models (WMO) and eight radiation-based models (Makkink, Priestly–Taylor, Jensen–Haise, Abtew, Irmak1, Irmak 2, Turc, and Tabari), based on the extensive literature review of meteorological variables, climatic regional differences, and their universal applicability. Subsequently, this study seeks three hypotheses: first, the various empirical models will generate considerably various outcomes for estimating the ETo at a monthly and regional scale; second, identifying the importance degree of empirical models that can indicate which model is outperformed against the FAO56-PM model at the regional scale and third, the simple linear regression can efficiently validate the 13 models against the FAO56-PM model in different sub-regions and whole Bangladesh. The specific objectives of this study are: (1) to analyze the spatiotemporal changes and the trends of ETo in Bangladesh for the period of 1980–2017 at a monthly scale, (2) to compare the performances of 13 empirical models against the FAO56-PM model for ETo estimation in climatic sub-regions of Bangladesh, (3) to choose an optimal alternative of the FAO56-PM ETo model, which will be easier in ETo quantification and apply few meteorological variables, (4) to identify the most outperformed empirical model against FAO56-PM model using the heuristic random forest method, and (5) to validate 13 empirical models using linear regression to opt an alternative empirical model against FAO56-PM model. The novelty of this research lies in employing 13 empirical models with a heuristic random forest model for the first time in Bangladesh that enables us to find an optimal alternative used for important environmental implication from the most reliable and outperformed equations for ETo computation in different climatic sub-regions of Bangladesh.
Data and methods
Study area description and data sources
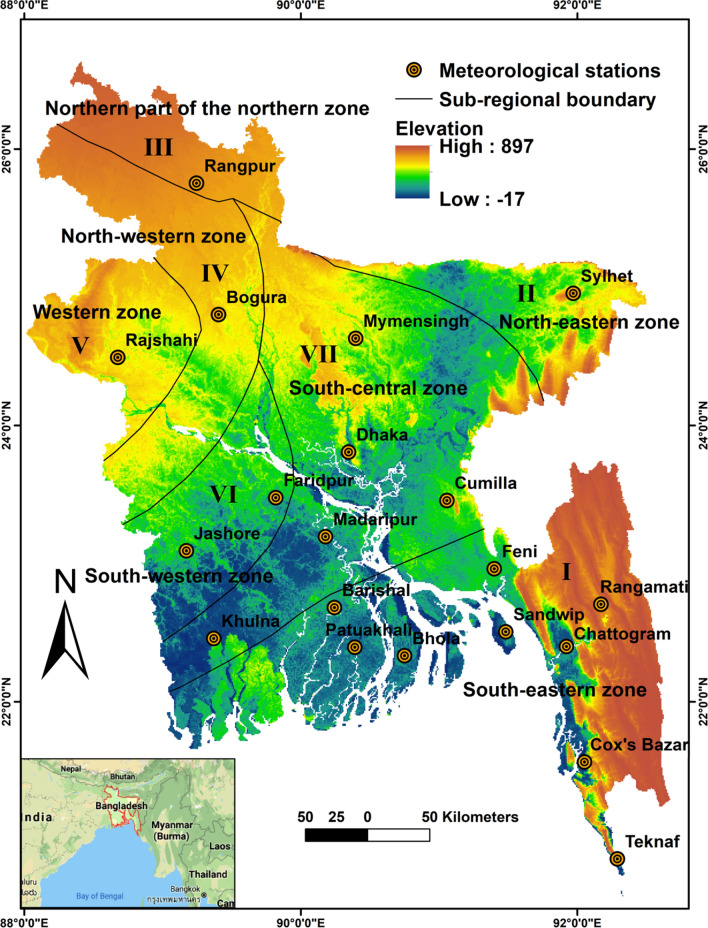
Bangladesh, situated in Southeast Asia, geographically it encompasses between 20° 30′ N and 26° 45′ N latitudes and 88° 0′ E to 92° 45′ E longitudes (Fig. 1). Banglapedia48 divided Bangladesh into seven climatic sub-regions based on climatology and geography as shown in the Supplementary Material of Figure S2. The seven sub-regions are (1) south-eastern zone; (2) north-eastern zone; (3) northern part of the northern zone; (4) north-western zone; (5) western zone; (6) south-western zone and (7) south-central zone. Bangladesh experiences a sub-tropical humid monsoon climate with seasonal differences4.
Figure 1.
Map showing the geographical location of study area, prepared by ArcGis 10.5 (www.esri.com).
Western Bangladesh has usually become drier compared to other regions in Bangladesh49. Here, climatic variability is a regular scenario. Long-term daily average relative humidity, minimum temperature, maximum temperature, wind speed (at 2 m height), net radiation, evapotranspiration across the country are, respectively, 80%, 21.39 °C, 29.94 °C 1.32 ms−1, 10.44 MJm−2day−1, and 3.72 mm day−1.
Bangladesh Meteorological Department (BMD) runs only 43 meteorological stations across the country. The meteorological stations are unevenly distributed all over the country and most of the stations are located in the south-eastern regions. These meteorological stations are available for the climatic dataset, although some of the stations are newly established after the 1990s in Bangladesh and they do not have long-term data records (www.bmd.gov.bd). When more climatic variables are required, the dataset from a smaller number of stations was available. Due to these drawbacks, 20 stations were chosen for ETo estimation over the 38 years from 1980 to 2017. These selected 20 stations embody the seven climatic sub-regions of the country. Daily minimum (Tmin) and maximum temperature (Tmax) (°C), mean relative humidity (Hr) (%), wind speed (Uz) (Knots) and sunshine hour (h day−1) datasets of 20 stations were sourced from the BMD. Net radiation (Rn) and wind speed at 2 m height (U2) cannot directly be measured by weather stations. Daily Rn and U2 were estimated using the procedures recommended by Allen et al.1 with the available meteorological datasets. A brief geographical and meteorological description of the selected stations is found in the Supplementary Material of Table S2. However, missing data in almost all the 20 stations was found. After the initial screening test, missing data of the 20 stations were less than 5% for the period of 1980–2017. Missing data for each station were filled by the existing records for the respective days from the adjacent neighbor stations. It is worthy to note that sunshine hour dataset in this study is continuous with no missing data. More details about the fill-up of missing meteorological datasets is given in the Supplementary Material (Table S3). The BMD follows the guideline of World Meteorological Organization (WMO) for weather dataset collection and record archiving. However, quality control of the dataset was primarily undertaken thoroughly by checking namely, positive values of parameters, for example, Tmin is lower than Tmax, and humidity is less than 100%. The homogeneity tests of the dataset were conducted to exhibit any anomaly in the dataset50. All of the datasets were passed through the quality control by the staff of the BMD.
FAO56 Penman–Monteith model (FAO56-PM model)
The FAO56-PM equation is used for estimating daily ETo of this study. This model is well-known as the standard model for estimating ETo across the whole world, which was proposed by Allen et al.1 The original form of FAO56-PM model is expressed by the following Eq. (1):
| 1 |
where, ETo is the reference evapotranspiration (mm day−1), isthe net radiation atcrop surface (MJm−2 day−1), Gis the soil heat flux density (MJ m−2 day−1), T is the average daily air temperature at 2 m height (°C), is the wind speed at 2 m height (ms−1), is the saturation vapour pressure (kPa), is the actual vapour pressure (kPa), is the saturation vapour pressure deficit (kPa), is the slope of vapour pressure curve (kPa °C−1), γ is the psychrometric constant (kPa °C−1). Allen et al.1 recommended G = 0. The detailed procedures of ETo estimation is found in FAO 56 paper1.
Rn is calculated by the Eqs. (2–11):
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| 10 |
| 11 |
U2 is calculated from the following Eq. (12) recommended by Allen et al.1,
| 12 |
where, Rns is the net solar or shortwave radiation (MJ m−2 day−1), Rnl is the net outgoing longwave radiation (MJ m−2 day−1), Rs is the global solar or shortwave radiation (MJ m−2 day−1), N and n are, respectively, the maximum and actual possible sunshine duration, Ra is the extraterrestrial radiation (MJ m−2 d−1), Gsc is the solar constant (0.0820 MJ m−2 min−1), dr is the inverse relative distance Earth-Sun, ωs is the sunset hour angle (rad), φ is latitude (rad), δ is solar declination (rad), J is the number of the day in the year between 1 (1 January) and 365 or 366 (31 December), σ is the Stefan-Boltzmann constant (4.903 × 10−9 MJ K−4 m−2 day−1), α is albedo (α = 0.23), Tmaxk and Tmink are, respectively, the maximum and minimum absolute temperatures during 24-h, and Rso is the clear sky solar radiation (MJ m−2 day−1). Allen et al.1 recommended 0.25 for as and 0.50 for bs. Uz is measured wind speed at Zm above ground surface (ms−2) and z is respective station elevation above sea level (m).
According to Allen et al.1, Saturation Vapour Pressure (es), Actual Vapour Pressure (ea), Slope Vapour Pressure Curve (∆) and Psychrometric Constant (γ) are calculated by the following Eqs. (13–19), respectively:
| 13 |
| 14 |
| 15 |
| 16 |
| 17 |
| 18 |
| 19 |
where, es is the mean saturation vapour pressure (kPa), are the saturation vapor pressure at maximum and minimum temperature, respectively. ea is the actual vapour pressure function (kPa) and Hr is the mean relative humidity. Tave, Tmax and Tmin are the mean, maximum and minimum air temperature, respectively, in °C and exp [·] is 2.7183 (base of natural logarithm) raised to the power [··]. P is the atmospheric pressure (kPa), λ is the latent heat of vaporization (2.45 MJ kg−1), Cp is the specific heat at constant pressure (1.013 × 10–3 MJ kg−1 °C−1), ε is the ratio molecular weight of water vapour/dry air (0.622).
Empirical models
A primary survey of literature clearly showed that the 13 ETo empirical model performed usually well in various sub-regions worldwide. Abtew51, Jensen and Haise52, Irmak53, Makkink54, Priestley-Taylor55, Hargreaves-Samani13, Berti56, WMO30, Tabari40, and Turc57 models were chosen to compare to the FAO56-PM model. The 13 empirical models were chosen based on the available input meteorological variables, universal acceptance and their applicability worldwide (Table S1). The Hargreaves–Samani (HS), Hargreaves M1 (HM1), Hargreaves M2 (HM2) and Berti models used in this study, as the HS, HM1 and HM2 models require only the temperature and extraterrestrial radiation datasets and Berti model requires only temperature data, making these models less complex. Therefore, the 13 empirical models used in the present study can be classified into the three classes: four temperature-based model (Hargreaves–Samani, Hargreaves M1, Hargreaves M2, and Berti), one mass transfer-based models (WMO), eight radiation-based models (Makkink, Priestly–Taylor, Jensen–Haise, Abtew, Irmak1, Irmak2, Tabari, and Turc). The performances and application of these models had never been validated in Bangladesh so far. The studied models, input parameters, computed equations with references are outlined in Table 1.
Table 1.
The original form of the 13 empirical models associated with the input parameters.
| Sl. no. | Models | Models input | Equations | Proposed by |
|---|---|---|---|---|
| Temperature-based | ||||
| ETo,1 | Hargreaves–Samani | Ra, Tave, Tmax, Tmin | ET0,1 = [0.0023 × Ra (Tave + 17.8) (Tmax − Tmin)0.5]/λ | Hargreaves and Samani13 |
| ETo,2 | Hargreaves M1 | Ra, Tave, Tmax, Tmin | ET0,2 = [0.408 × 0.0030 × (Tave + 20) (Tmax − Tmin)0.4 × Ra | Hargreaves and Samani13 |
| ETo,3 | Hargreaves M2 | Ra, Tave, Tmax, Tmin | ETo,3 = | Hargreaves and Samani13 |
| ETo,4 | Berti | Ra, Tave, Tmax, Tmin | ET0,3 = /λ | Bertiet al.56 |
| Mass transfer-based | ||||
| ETo,5 | WMO | U2, es − ea | ET0,4 = (0.1298 + 0.0934U2)(es − ea) | WMO30 |
| Radiation-based | ||||
| ETo,6 | Abtew | Rs, Tmax | ET0,5 = | Abtew51 |
| ETo,7 | Irmak1 | Rs, Tave | ET0,6 = | Irmak et al.53 |
| ETo,8 | Irmak2 | Rn, Tave | ETo,7 = 0.489 + 0.289 Rn + 0.023 Tave | Irmak et al.53 |
| ETo,9 | Makkink | Rs, Tave | ET0,8 = | Makkink54 |
| ETo,10 | Priestley-Taylor | Rn, Tave | ET0,9 = | Priestley and Taylor55 |
| ETo,11 | Jensen–Haise | Rs, Tave | ET0,10 = | Jensen and Haise52 |
| ETo,12 | Tabari | Rs, Tmin, Tmax | ET0,11 = 0.156Rs—0.0112Tmax + 0.0733Tmin—0.478 | Tabari et al.40 |
| ETo,13 | Turc | Rs, Tave | ETo,13 = 0.013 | Turc57 |
Tave, Tmax, and Tmin are the mean (average), maximum, and minimum temperature (°C), respectively and λ is the latent heat of vaporization (2.45 MJ kg−1), and (after Peng et al.11).
Performance evaluation of 13 empirical models
Performance evaluation of 13 empirical models, based on the accuracy of each model for estimating ETo, was undertaken by six statistical criteria. The six statistical criteria were the mean bias error (MBE)58; mean absolute error (MAE), correlation of determination (R2), root mean square error (RMSE)43; relative error (RE), Nash–Sutcliffe efficacy coefficient (NSE)59 expressed by the following Eqs. (20–25):
| 20 |
| 21 |
| 22 |
| 23 |
| 24 |
| 25 |
where, , and n are the observed ETo (estimated by FAO56-PM), estimated ETo (estimated by empirical models) and total observations, respectively.
Modified Mann–Kendall test
Modified Mann–Kendall (MMK) test is a non-parametric test which was applied for detecting the increasing and decreasing trend of ETo,s in Bangladesh during 1980–201760. To carry out this MKK test, it is imperative to confirm the serial autocorrelation of the time series dataset. Hence, the serial autocorrelation should be excluded before employing the MMK test. To exclude the serial autocorrelation, the trend free pre-whitening approach proposed by Yue and Wang61 has been utilized. The original form of MK test62,63 statistics (S) is as followed:
| 26 |
| 27 |
Direction of increasing or decreasing trend is indicated by S. The variance64 of S is followed by the Eq. (29):
| 28 |
V*(S), is the modified variance61 given by following Eq. (30):
| 29 |
n/n* is termed as correction factor and denoted65 by following Eq. (31):
| 30 |
Test statistic Z is calculated by following Eq. (32):
| 31 |
Positive Z statistic indicates increasing trend of ETo,s and negative Z statistic indicates decreasing trend of ETo,s in Bangladesh.
Sen’s slope of estimator
Sen’s slope of estimator66 was applied for calculating the change of ETo,s in Bangladesh per decade and the statistics is as followed:
| 32 |
Q is denoted as the slope between xj and xk.
The spatial distributions of the monthly ETo and its trends are mapped.
Spatial distributions of the monthly meteorological variables; ETo,s, ETo,i, trends and the other examined variables are mapped by the inverse distance weighted interpolation model in ArcGIS 10.5 software.
Random forest (RF) model
The RF is a heuristic decision tree-based supervised machine learning model67 that is appropriate for addressing the existence of the over-fitting problem to the decision trees, and other machine learning algorithm68. The RF is most robust, can handle numerous heterogeneous covariates, and has been effectively employed into the hydrological field69, genetic engineering field70 and hydro-meteorological field71. The RF model has been benefited from the two more powerful algorithms e.g., bagging and random binary trees, which are called the powerhouse of this model. For developing the RF model, the number of trees and features in each split is essential. RF is a classifier which comprises of an assortment of classifier trees for m = 1, …, M which relies on the parameters and every single tree casts a unit vote for input x71. Each tree generates an individual class which then combined and the majority vote predicts the final results. Present study optimized its accuracy with 100 trees, 1 execution slot, 5 seeds and with maximum depth 1. As a tree-based ensemble learning model, this model has extensively used to evaluate the importance degree of any climatic dataset in various regions25,72. To the best of author’s knowledge, the RF model has not yet been employed to explore the importance degree of 13 empirical models against the FAO56-PM model in Bangladesh. The RF model is used to know which model is most reliable and dominant for estimating ETo. More detailed about the RF model can be found elsewhere46,71.
Results
Spatial distribution of meteorological variables
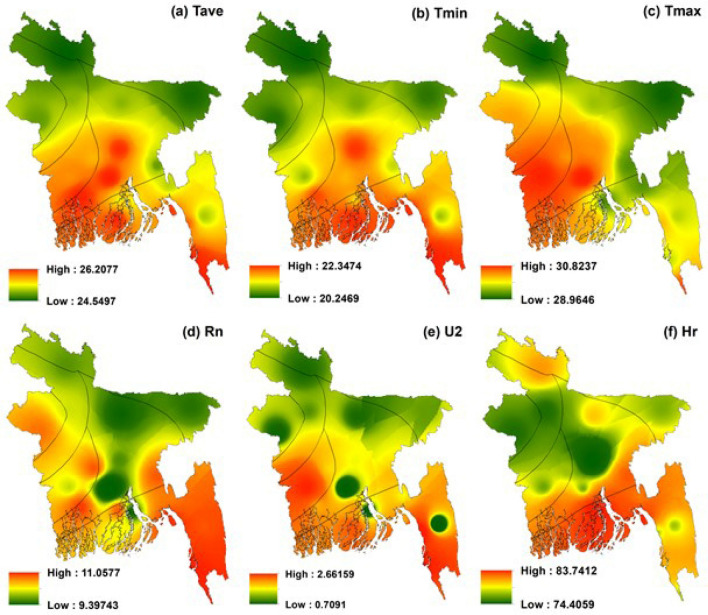
Figure 2 represents the distribution of multi-year mean meteorological variables of Tave, Tmin, Tmax, Rn, U2, and Hr from 1980 to 2017. Distribution of Tave (Fig. 2a), Tmin (Fig. 2b) and Tmax (Fig. 2c) showed almost similar results. Sub-region VI showed the higher values of historical temperature, while sub-regions II and III entirely showed the lowest temperature. Sub-region V showed the lowest temperature for the distribution of Tave and Tmin and moderate temperature for Tmax. Sub-regions I, IV and VII showed the moderate values. The higher rate of net radiation was observed in the sub-region I and lower rate of net radiation was found in the sub-regions II and III (Fig. 2d). Average values of Rn were seen in the sub-regions IV, V, VI, and VII. The highest wind speed was found in the sub-region of VI and the lowest in the sub-regions II, III and V (Fig. 2e). Sub-region I experienced a comparatively higher rate of Hr as it located near the Bay of Bengal from where this region took available moisture and sub-region V experienced the lower rate of Hr (Fig. 2f).
Figure 2.
Spatial distribution of multi-year mean meteorological variables in Bangladesh, prepared by ArcGis 10.5 (www.esri.com).
Spatial and temporal patterns of ETo,s and ETo,i
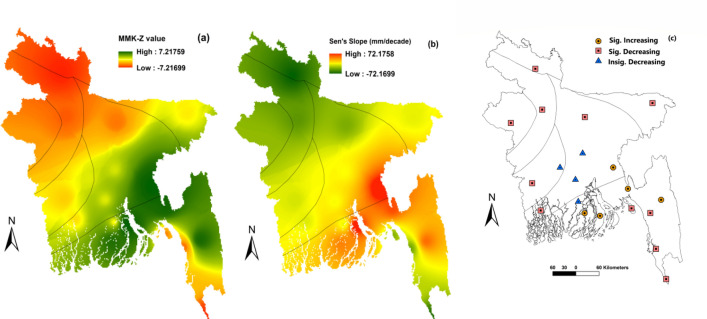
Figure 3 represents the long-term multi-year mean monthly trends of ETo,s (FAO56-PM). Most parts of sub-regions I and VII showed the higher values of MMK-Z statistic and the sub-regions III, IV and V showed the lowest values of MMK-Z statistic (Fig. 3a). Moderate values are shown in the sub-regions II and VI. In general, the rates between increasing and decreasing of ETo,s was from 72.18 to − 72.17 mm per decade (Fig. 3b). Figure 3c shows the nature of the trend whether it was significant or insignificant. The significant increasing trend of ETo,s was detected in Bhola, Cumilla, Feni (); Rangamati, and Patuakhali () in the sub-regions I and VII.
Figure 3.
Representation of the multi-year mean monthly ETo,s trends of (a) MMK-Z values (mm); (b) Sen’s slope estimation and (c) station wise increasing or decreasing trends of Bangladesh, prepared by ArcGis 10.5 (www.esri.com).
All the weather stations of sub-regions II (); III, IV () and V () showed a significant decreasing trend of ETo,s. Faridpur, Madaripur, Dhaka and Barishal of sub-regions I and VII showed an insignificant decreasing trend of ETo,s. Cox’s Bazar (); Teknaf, Sandwip and Chattogram () of sub-region I; Jashore () of sub-region VI and Mymensingh () and Khulna () of sub-region VII showed a significant decreasing trend of ETo,s.
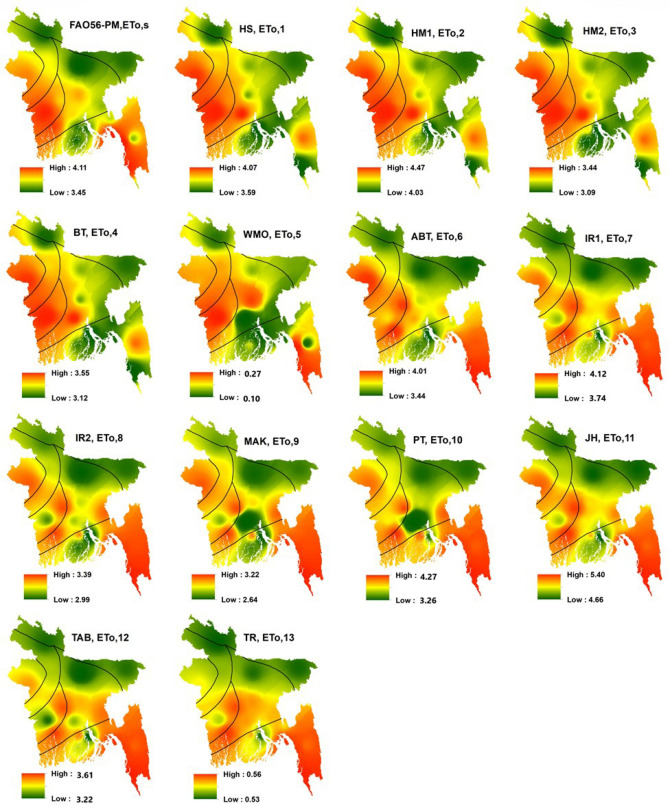
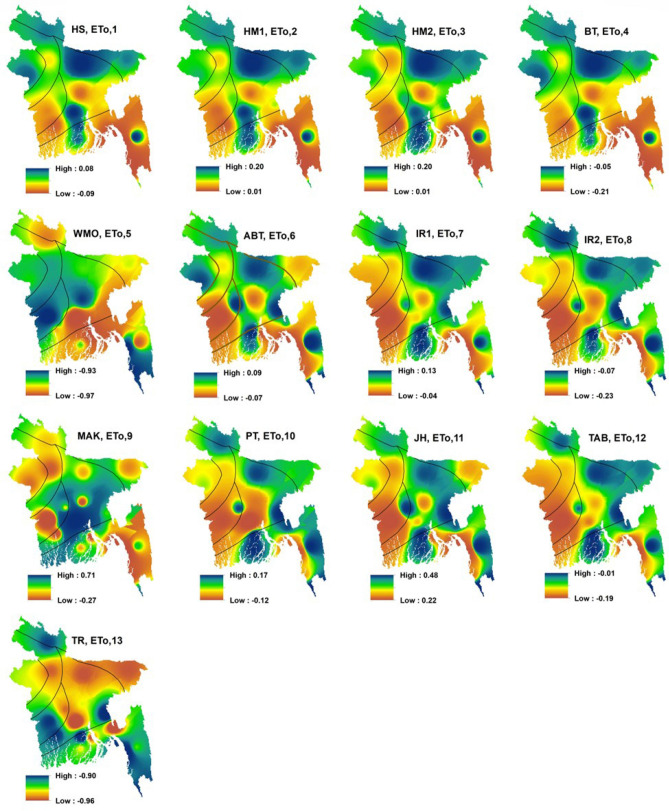
Spatial distribution of multi-year mean monthly ETo,s and ETo,i from 1980 to 2017 is presented in Fig. 4. The higher value (4.12 mm) of ETo,s seen in the sub-regions V, VI and some parts of region I. The lower value (3.46 mm) of ETo,s seen in the sub-regions II, III and some part of the sub-regions I, IV and VII. The distribution of ETo,i showed the homogeneous distribution of ETo,s. The high-low values of spatial distribution of ETo,1 (temperature-based); ETo,6; ETo,7; ETo,10 (radiation-based) models were analogous with that of ETo,s. ETo,5 (mass transfer-based) and ETo,13 (radiation-based) models showed the most heterogeneity with ETo,s. Sub-regions V and VI showed the highest value of ETo (computed by most of the empirical models and FAO56-PM) and all the models found that the sub-regions II and III experienced a lower rate of ETo. All the models revealed that moderate ETo was experienced by the sub-regions I, IV and VII. Approximately, similar zonation (based on the highest and lowest values) was observed between ETo,s and ETo,6.
Figure 4.
Spatial distribution of multi-year mean monthly ETo,s and ETo,i in Bangladesh, prepared by ArcGis 10.5 (www.esri.com).
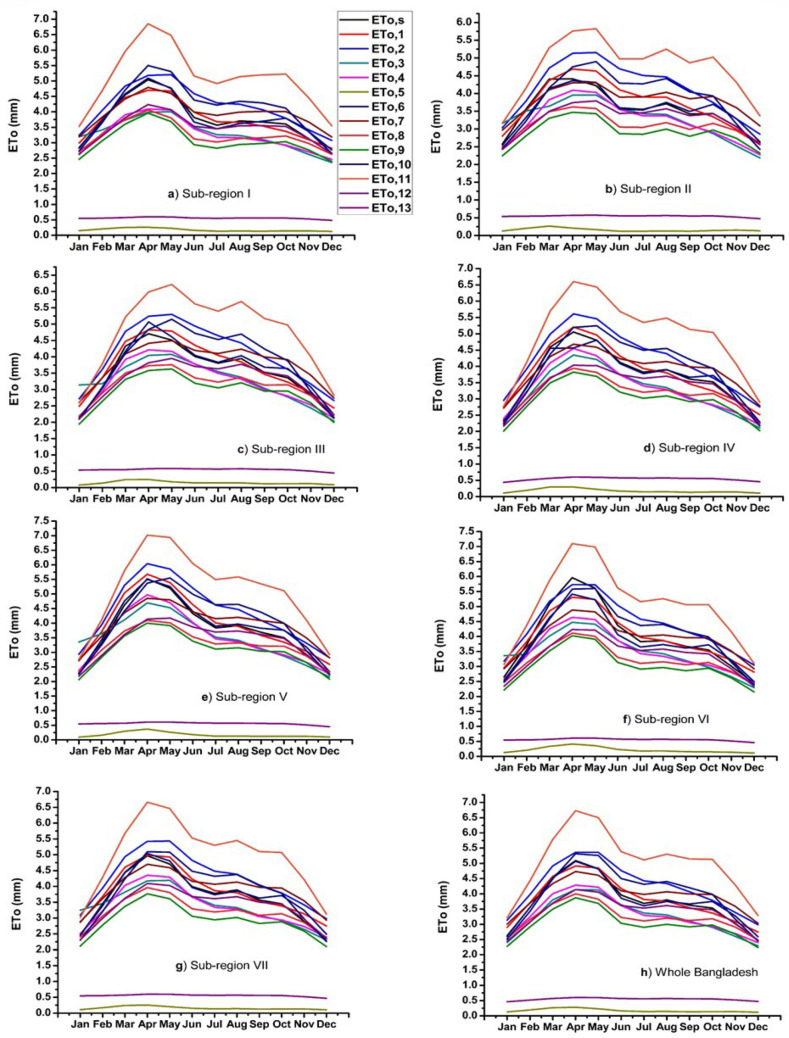
Temporal distribution of long-term monthly ETo,s, and ETo,i in different sub-regions, as well as whole Bangladesh for the period of 1980–2017, is shown in Fig. 5. The highest rate of reference evapotranspiration (ETo,s and ETo,i) occurred in April in all the regions of Bangladesh. The lowest ETo (both ETo,s and ETo,i) found in January and December. Except for sub-regions II and III, the range of the rate of ETo,s, and ETo,i was the same in all the sub-regions. Among the 13 empirical models, ETo,5; ETo13 (elevated the lowest values than ETo,s) and ETo,11 (elevated the highest values than ETo,s) models showed the most deficit values of ETo,i compared to ETo,s identifying least suitable method for estimating ETo. Conversely, the values estimated by ETo,6 showed the closest values to ETo,s demonstrating as the most preferable model for estimating ETo. ETo,1 and ETo,7 also estimated values with the smallest difference with ETo,s in all the regions, confirmed as the preferable method for estimating ETo. Moderate values estimated by ETo,2; ETo,4; ETo,8; ETo,9; ETo,10 and ETo,12 models compared to ETo,s.
Figure 5.
Temporal distribution of multi-year mean monthly ETo,s and ETo,i in different sub-regions and whole Bangladesh.
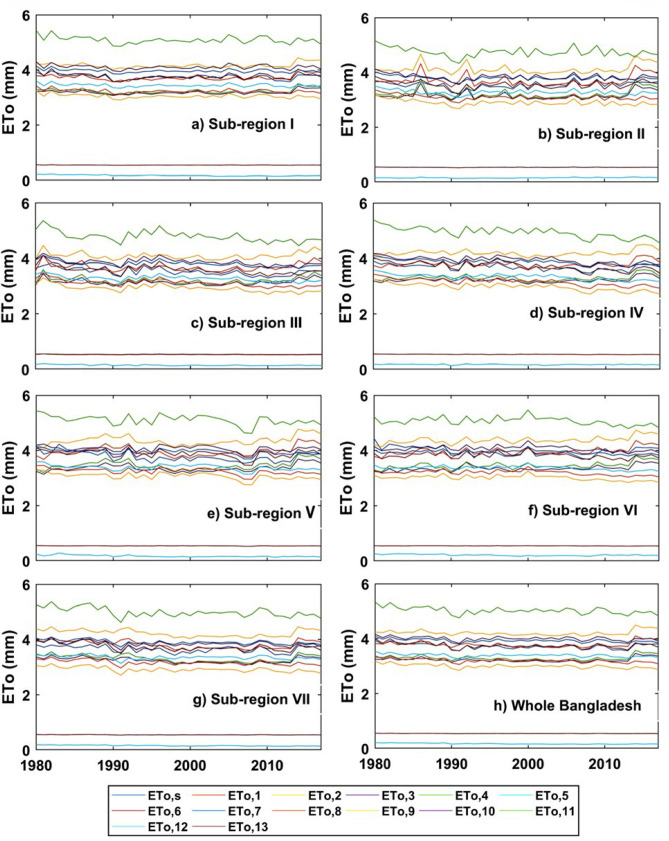
Long term inter-annual variation of ETo,s, and ETo,i from 1980 to 2017 are represented by Fig. 6. It also demonstrates similar results as shown in Fig. 5. The largest deviation from the ETo,s values occurred by estimating ETo,i (values lower than 1) by both ETo,5 and ETo,13 models. The Fig. 6 shows that the rate of ETo in each sub-region along with whole Bangladesh, estimated by both ETo,s and ETo,i models, declined gradually. Unlike the multi-year monthly distribution, the range (from 0 to 5.5 mm) of ETo values was nearly similar in every sub-regions and Bangladesh. Like the multi-year monthly distribution, ETo,6; ETo,1; ETo,7 and ETo,10 showed the very closest values to ETo,s in each sub-region. Values larger than that of ETo,s found by ETo,11. Based on the spatiotemporal distribution of ETo,i estimated by 13 empirical models in each sub-region and whole Bangladesh, the empirical models can be ranked in ascending order based on the closest values to ETo,s as ETo,6 > ETo,1 > ETo,7 > ETo,10 > ETo,3 > ETo,2 > ETo,12 > ETo,4 > ETo,8 > ETo,9 > ETo,11 > ETo,13 > ETo,5.
Figure 6.
The inter-annual variations of ETo,s and ETo,i in different sub-regions and whole Bangladesh.
Performance appraisal of 13 empirical models for estimating ETo
Figure 7 shows the long term monthly RE of ETo,i by spatial distribution for the period of 1980–2017. RE of the maximum ETo,i covered mutually positive and negative values. The lowest RE was observed in ETo,i calculated by ETo,6. Furthermore, ETo,1; ETo,7; ETo,10 and ETo,12 models also produced lower RE, respectively. The worst performance with the high RE belongs to the ETo,5 and ETo,13 models. The relative error in different sub-regions varied with the variation of different empirical models. The ETo,11, ETo,9, ETo,8, ETo,2, ETo,3 and ETo,4 models also recognized as the worst models, respectively, producing high RE.
Figure 7.
Spatial distribution of relative error values for multi-year mean monthly ETo,i in Bangladesh, prepared by ArcGis 10.5 (www.esri.com).
Table 2 shows the long term mean monthly and annual RMSE for 13 selected ETo,i models for whole Bangladesh. The higher RMSE was produced by the ETo,5; ETo,13 and ETo,11 models, respectively. The ETo,6, ETo,3, ETo,7 and ETo,1 models generated the least RMSE for calculating ETo. The descending order of the other models based on performance was ETo,2 > ETo,9 > ETo,4 > ETo,10 > ETo,8 > ETo,12.
Table 2.
Root Mean Square Error (RMSE) values of the 13 empirical models for calculating ETo,i at the monthly and annual timescales for Bangladesh. The bold values indicate the optimal model among other models.
| ETo,i | ET0,1 | ET0,2 | ET0,3 | ET0,4 | ET0,5 | ET0,6 | ET0,7 | ET0,8 | ET0,9 | ET0,10 | ET0,11 | ET0,12 | ET0,13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Month/year | |||||||||||||
| Jan | 0.8428 | 0.6065 | 0.2472 | 1.2001 | 3.6024 | 0.6445 | 0.7391 | 1.2053 | 1.4635 | 1.2277 | 0.5630 | 1.2919 | 2.1696 |
| Feb | 0.1778 | 0.2978 | 0.5039 | 0.5073 | 3.5384 | 0.1224 | 0.1562 | 0.5903 | 0.8282 | 0.3469 | 0.7474 | 0.6696 | 3.0446 |
| Mar | 0.8772 | 1.2064 | 0.7722 | 0.3474 | 3.4644 | 0.5213 | 0.6215 | 0.1384 | 0.2671 | 0.7748 | 2.0732 | 0.1221 | 3.9983 |
| Apr | 1.2023 | 1.6439 | 0.9778 | 0.5885 | 3.4517 | 0.1097 | 1.0133 | 0.3032 | 0.2066 | 1.5978 | 3.0151 | 0.4335 | 4.4995 |
| May | 1.1439 | 1.6483 | 0.7211 | 0.5334 | 3.4982 | 0.2788 | 0.9108 | 0.2805 | 0.2841 | 1.5718 | 2.8234 | 0.3941 | 4.2382 |
| Jun | 0.5031 | 1.0590 | 0.3541 | 0.2434 | 3.5659 | 0.2386 | 0.4159 | 0.5439 | 0.7337 | 0.8229 | 1.7057 | 0.3194 | 3.3993 |
| Jul | 0.3903 | 0.7151 | 0.3648 | 0.4633 | 3.5911 | 0.2045 | 0.3112 | 0.6522 | 0.8568 | 0.6409 | 1.4344 | 0.2689 | 3.1328 |
| Aug | 0.3050 | 0.6421 | 0.5209 | 0.5180 | 3.5873 | 0.2181 | 0.3912 | 0.5703 | 0.7650 | 0.7311 | 1.6220 | 0.2223 | 3.2419 |
| Sep | 0.2573 | 0.3774 | 0.5441 | 0.6840 | 3.5962 | 0.2237 | 0.2989 | 0.6237 | 0.8279 | 0.5066 | 1.4465 | 0.2449 | 3.0685 |
| Oct | 0.4074 | 0.1889 | 0.6452 | 0.8218 | 3.5926 | 0.2847 | 0.3048 | 0.5850 | 0.7819 | 0.3394 | 1.4457 | 0.2989 | 2.9804 |
| Nov | 0.6533 | 0.3651 | 0.4289 | 1.0397 | 3.5916 | 0.1981 | 0.2054 | 0.8368 | 1.0631 | 0.5793 | 0.6273 | 0.7131 | 2.5004 |
| Dec | 0.9907 | 0.7483 | 0.2197 | 1.3340 | 3.6142 | 0.1554 | 0.7190 | 1.2593 | 1.5035 | 1.2897 | 0.5162 | 1.2602 | 2.0195 |
| Year | 0.1045 | 0.4872 | 0.5062 | 0.4441 | 3.5580 | 0.0484 | 0.2064 | 0.5317 | 0.7337 | 0.2805 | 1.3012 | 0.3444 | 3.1848 |
Table 3 represents the long term mean monthly and annual MAE values of 13 empirical models used for estimating ETo,i. Lower values of MAE indicates higher accuracy. Respectively, ETo,6 and ETo,1 models produced the smallest MAE values for both the monthly and annual ETo,i values in Bangladesh. Higher MAE values produced by the models (respectively) of ETo,5, ETo,13, ETo,11, ETo,9 and ETo,8 in calculating both the monthly and annual ETo,i.
Table 3.
Mean Absolute Error (MAE) values of 13 empirical models for calculating ETo,i at the monthly and annual timescales for Bangladesh. The bold values indicate the optimal model among other models.
| ETo,i | ET0,1 | ET0,2 | ET0,3 | ET0,4 | ET0,5 | ET0,6 | ET0,7 | ET0,8 | ET0,9 | ET0,10 | ET0,11 | ET0,12 | ET0,13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Month/year | |||||||||||||
| Jan | 0.398 | 0.562 | 0.222 | 0.273 | 2.497 | 0.260 | 0.425 | 0.251 | 0.384 | 0.256 | 0.613 | 0.264 | 2.163 |
| Feb | 0.369 | 0.716 | 0.489 | 0.387 | 3.363 | 0.293 | 0.306 | 0.416 | 0.643 | 0.309 | 0.879 | 0.491 | 3.039 |
| Mar | 0.361 | 0.471 | 0.760 | 0.601 | 4.296 | 0.320 | 0.336 | 0.884 | 1.063 | 0.389 | 1.232 | 0.866 | 3.992 |
| Apr | 0.443 | 0.470 | 0.952 | 0.831 | 4.814 | 0.330 | 0.411 | 1.095 | 1.222 | 0.488 | 1.640 | 0.954 | 4.491 |
| May | 0.374 | 0.605 | 0.694 | 0.646 | 4.591 | 0.315 | 0.314 | 1.000 | 1.137 | 0.575 | 1.681 | 0.770 | 4.227 |
| Jun | 0.350 | 0.810 | 0.318 | 0.415 | 3.794 | 0.231 | 0.244 | 0.736 | 0.930 | 0.593 | 1.428 | 0.366 | 3.391 |
| Jul | 0.305 | 0.742 | 0.320 | 0.457 | 3.546 | 0.187 | 0.309 | 0.578 | 0.786 | 0.651 | 1.430 | 0.200 | 3.125 |
| Aug | 0.285 | 0.557 | 0.493 | 0.575 | 3.657 | 0.190 | 0.297 | 0.600 | 0.800 | 0.644 | 1.503 | 0.220 | 3.235 |
| Sep | 0.287 | 0.473 | 0.521 | 0.581 | 3.490 | 0.174 | 0.381 | 0.503 | 0.707 | 0.599 | 1.524 | 0.164 | 3.063 |
| Oct | 0.283 | 0.340 | 0.631 | 0.615 | 3.394 | 0.296 | 0.468 | 0.359 | 0.555 | 0.505 | 1.600 | 0.167 | 2.974 |
| Nov | 0.280 | 0.436 | 0.413 | 0.365 | 2.880 | 0.336 | 0.584 | 0.213 | 0.356 | 0.288 | 1.281 | 0.204 | 2.496 |
| Dec | 0.366 | 0.538 | 0.196 | 0.244 | 2.370 | 0.262 | 0.565 | 0.232 | 0.296 | 0.232 | 0.819 | 0.221 | 2.013 |
| Year | 0.226 | 0.500 | 0.500 | 0.448 | 3.557 | 0.178 | 0.244 | 0.528 | 0.731 | 0.343 | 1.299 | 0.341 | 3.183 |
Table 4 shows the NSE coefficient of empirical models used for calculating ETo,i at the annual and monthly time scale in Bangladesh. Approximately, all the models gave negative NSE value indicating the least correlated method with ETo,s. In both monthly and annual timescales, ETo,6 outperformed as it gave positive NSE value, except for the month of October and November. The performance accuracy of ETo,1 was comparatively higher than that of other models except for ETo,6, ETo,13, ETo,5 and ETo,11 models. In annual timescale, the order of the performance of the models was ETo,6 > ETo,7 > ETo,1 > ETo,10 > ETo,12 > ETo,4 > ETo,2 > ETo,8 > ETo,9 > ETo,3 > ETo,11 > ETo,5 > ETo,13.
Table 4.
Nash–Sutcliffe efficiency (NSE) coefficients of the 13 empirical models for calculating ETo,i at the monthly and annual timescales for Bangladesh. The bold values indicate the optimal model among other models.
| ETo,i | ET0,1 | ET0,2 | ET0,3 | ET0,4 | ET0,5 | ET0,6 | ET0,7 | ET0,8 | ET0,9 | ET0,10 | ET0,11 | ET0,12 | ET0,13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Month/year | |||||||||||||
| Jan | − 0.274 | − 1.258 | − 1.033 | 0.123 | − 35.578 | 0.255 | − 0.39 | 0.354 | − 0.302 | 0.336 | − 1.958 | 0.258 | − 155.576 |
| Feb | − 0.103 | − 2.353 | − 5.205 | − 0.426 | − 58.766 | 0.238 | 0.312 | − 0.449 | − 1.77 | 0.166 | − 3.821 | − 0.828 | − 225.502 |
| Mar | − 0.093 | − 0.559 | − 9.619 | − 1.523 | − 89.31 | 0.142 | 0.003 | − 3.595 | − 5.338 | − 0.23 | − 7.404 | − 3.525 | − 283.656 |
| Apr | − 0.065 | − 0.089 | − 10.441 | − 1.993 | − 74.489 | 0.362 | − 0.061 | − 3.579 | − 4.554 | − 0.105 | − 8.519 | − 2.672 | − 241.254 |
| May | 0.187 | − 0.754 | − 4.042 | − 1.022 | − 72.584 | 0.354 | 0.338 | − 3.021 | − 4.07 | − 0.452 | − 9.741 | − 1.603 | − 173.139 |
| Jun | − 0.127 | − 3.507 | − 1.077 | − 0.462 | − 81.971 | 0.38 | 0.467 | − 2.519 | − 4.436 | − 1.483 | − 11.67 | − 0.159 | − 190.445 |
| Jul | − 0.495 | − 5.005 | − 1.591 | − 1.531 | − 109.474 | 0.436 | − 0.093 | − 2.268 | − 4.824 | − 3.206 | − 17.811 | 0.422 | − 190.097 |
| Aug | − 0.233 | − 2.778 | − 4.285 | − 2.871 | − 121.219 | 0.351 | − 0.03 | − 2.678 | − 5.35 | − 3.301 | − 20.738 | 0.263 | − 203.639 |
| Sep | − 0.415 | − 2.248 | − 7.579 | − 3.418 | − 124.944 | 0.419 | − 0.781 | − 1.972 | − 4.612 | − 3.229 | − 23.887 | 0.48 | − 271.754 |
| Oct | − 0.481 | − 0.762 | − 9.322 | − 3.902 | − 119.488 | − 0.355 | − 1.729 | − 0.846 | − 2.843 | − 2.18 | − 26.957 | 0.439 | − 219.231 |
| Nov | − 0.309 | − 1.496 | − 7.088 | − 1.192 | − 82.924 | − 0.672 | − 2.958 | 0.103 | − 0.97 | − 0.236 | − 16.758 | 0.266 | − 273.802 |
| Dec | − 0.371 | − 1.721 | − 0.683 | 0.106 | − 42.958 | 0.047 | − 1.95 | 0.255 | − 0.226 | 0.281 | − 5.249 | 0.311 | − 141.118 |
| Year | − 0.477 | − 4.116 | − 25.07 | − 3.474 | − 211.012 | 0.176 | − 0.341 | − 4.411 | − 8.788 | − 1.498 | − 28.244 | − 1.667 | − 1030.942 |
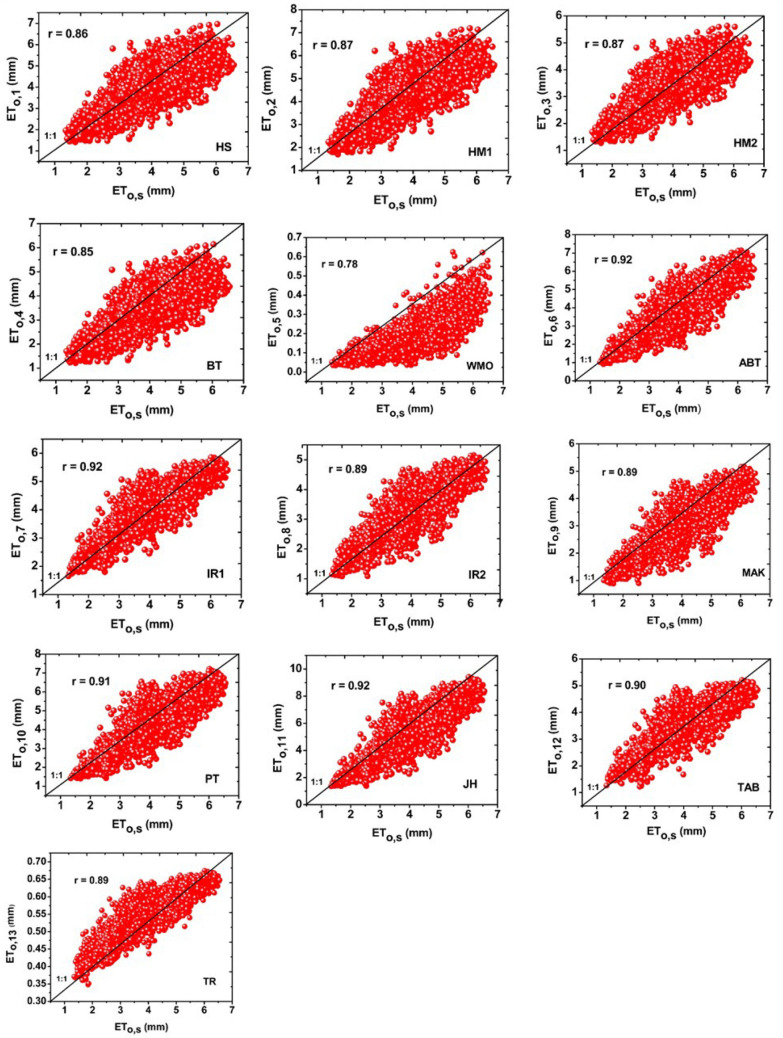
MBE at both long term annual and monthly time scale in calculating ETo,i in Bangladesh is shown in Table 5. ETo,6 and ETo,1 showed higher performance accuracy, producing lower MBE values. Again, ETo,5; ETo,13 and ETo,11 models showed the least performance accuracy for calculating ETo,i. Other models showed moderate performance accuracy in estimating ETo,i. From the above discussions of performance accuracy, ETo,6 revealed as the suitable alternative model for estimating ETo in Bangladesh. Whereas, ETo,5; ETo,13 and ETo,11models explored as the worst performed empirical models inappropriate for estimating ETo in Bangladesh. Figure 8 shows the scatter plots of daily ETo,s vs. ETo,i of Bangladesh during 1980–2017. The ETo,6; ETo,7 and ETo,11 models outperformed among 13 empirical models with higher r-value (0.92). ETo,10 (r-value 0.91) and ETo,12 (r-value 0.90) performed well, respectively, which produced r-values ≥ 0.90.
Table 5.
Mean Bias Error (MBE) values of the 13 empirical models for calculating ETo,i at the monthly and annual timescales for Bangladesh. The bold values indicate the optimal model among other models.
| ETo,i | ET0,1 | ET0,2 | ET0,3 | ET0,4 | ET0,5 | ET0,6 | ET0,7 | ET0,8 | ET0,9 | ET0,10 | ET0,11 | ET0,12 | ET0,13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Month/year | |||||||||||||
| Jan | 0.271 | 0.509 | − 0.222 | − 0.090 | − 2.497 | − 0.025 | 0.380 | − 0.091 | − 352 | − 0.118 | 0.591 | − 0.181 | − 2.163 |
| Feb | 0.153 | 0.654 | − 0.489 | − 0.307 | − 3.363 | 0.002 | 0.138 | − 0.398 | − 0.640 | − 0.129 | 0.871 | − 0.482 | − 3.039 |
| Mar | 0.011 | 0.354 | 0.787 | − 0.561 | − 4.296 | − 0.043 | − 0.225 | − 0.883 | − 1.063 | − 0.073 | 1.225 | − 0.865 | − 3.995 |
| Apr | − 0.179 | 0.269 | 0.945 | − 0.806 | − 4.814 | − 0.024 | − 0.360 | − 1.094 | − 1.222 | 0.224 | 1.636 | − 0.952 | − 4.498 |
| May | 0.025 | 0.540 | 0.690 | − 0.603 | − 4.591 | − 0.009 | − 0.213 | − 0.999 | − 1.137 | 0.438 | 1.679 | − 0.767 | − 4.230 |
| Jun | 0.215 | 0.805 | 0.315 | − 0.346 | − 3.794 | − 0.101 | 0.137 | − 0.731 | − 0.927 | 0.542 | 1.427 | − 0.343 | − 3.397 |
| Jul | 0.129 | 0.740 | 0.311 | − 0.392 | − 3.546 | − 0.08 | 0.294 | − 0.578 | − 0.786 | 0.628 | 1.430 | − 0.153 | − 3.120 |
| Aug | − 0.043 | 0.541 | 0.482 | − 0.555 | − 3.657 | − 0.050 | 0.268 | − 0.600 | − 0.800 | 0.604 | 1.503 | − 0.187 | − 3.230 |
| Sep | − 0.081 | 0.442 | 0.531 | − 0.559 | − 3.490 | 0.043 | 0.370 | − 0.500 | − 0.707 | 0.574 | 1.524 | − 0.100 | − 3.055 |
| Oct | − 0.161 | 0.254 | 0.625 | − 0.605 | − 3.394 | 0.218 | 0.444 | − 0.351 | − 0.554 | 0.454 | 1.600 | − 0.051 | − 2.956 |
| Nov | 0.074 | 0.371 | 0.421 | − 0.320 | − 2.880 | 0.261 | 0.572 | − 0.109 | − 0.338 | 0.154 | 1.280 | 0.013 | − 2.356 |
| Dec | 0.258 | 0.502 | 0.187 | − 0.087 | − 2.370 | 0.107 | 0.546 | − 0.002 | − 0.249 | − 0.038 | 0.804 | − 0.006 | − 2.113 |
| Year | 0.056 | 0.480 | − 0.500 | − 0.436 | − 3.557 | 0.025 | 0.198 | − 0.528 | − 0.731 | 0.274 | 1.299 | − 0.338 | − 3.283 |
Figure 8.
Scatter plots showing the comparisons of daily ETo,i and ETo,s in Bangladesh.
All the scatter plots produced r values with significant p-value (< 0.05) indicating a strong correlation between ETo,s and ETo,i. Among 13 empirical models, ETo,5 recognized as the worst model with a lower accuracy and reliability than other models as this model produced the r-value of 0.78 which is less than 0.80. From the comparisons of 13 empirical models by RE, RMSE, MAE, NSE, MBE and scatter plots, ETo,6 model found as the best suitable alternative model against the ETo,s model for calculating ETo for all the sub-regions and whole Bangladesh.
Exploring the most suitable model for ETo computation using the RF algorithm
The importance degree analysis of the empirical models was calculated by the RF method at different sub-regions of Bangladesh. The RF model depicted a suitable significant model followed by other analyses against the FAO56-PM model for all of the sub-regions (Table 6). The best performed model is highlighted by bold face and the least performed model is marked by italic face (Table 6) for estimating ETo. As can be seen from Table 6, the ETo,6 outperformed for ETo estimation in all the sub-regions of Bangladesh as it produced a comparatively higher importance degree. Whereas, ETo,5 found as the worst model producing the lowest importance degree among all the models.
Table 6.
Importance degree of 13 empirical models against FAO56-PM model in seven sub-regions in Bangladesh using RF model.
| Models | I | II | III | IV | V | VI | VII |
|---|---|---|---|---|---|---|---|
| ETo,1 | 4.27 | 6.27 | 9.03 | 2.22 | 2.46 | 5.10 | 5.07 |
| ETo,2 | 3.99 | 6.16 | 4.34 | 2.34 | 5.81 | 5.81 | 4.87 |
| ETo,3 | 9.02 | 7.27 | 5.61 | 2.51 | 5.15 | 5.15 | 4.87 |
| ETo,4 | 7.46 | 6.57 | 7.53 | 5.00 | 9.47 | 2.71 | 4.45 |
| ETo,5 | 3.78 | 2.69 | 3.57 | 2.12 | 2.71 | 2.46 | 4.14 |
| ETo,6 | 16.00 | 24.65 | 26.70 | 23.57 | 28.23 | 28.23 | 19.61 |
| ETo,7 | 8.70 | 8.14 | 7.01 | 7.68 | 5.10 | 9.47 | 8.65 |
| ETo,8 | 9.38 | 7.99 | 7.48 | 9.98 | 9.55 | 9.55 | 8.91 |
| ETo,9 | 8.37 | 8.43 | 5.40 | 8.51 | 6.00 | 6.00 | 6.11 |
| ETo,10 | 8.36 | 8.74 | 7.95 | 8.30 | 7.78 | 7.78 | 6.96 |
| ETo,11 | 8.81 | 6.48 | 7.05 | 11.05 | 8.98 | 8.98 | 8.89 |
| ETo,12 | 7.90 | 3.85 | 4.84 | 10.30 | 2.91 | 2.91 | 10.90 |
| ETo,13 | 3.97 | 2.76 | 3.46 | 6.44 | 5.85 | 5.85 | 6.58 |
Bold face indicates the highest importance degree while italic face denotes the least importance degree.
Validation of the best alternative model for ETo,s
Validation is very important for determining the most suitable model from several potential models. All the applied empirical models need to validate to ensure whether the pre-analyses gave the accurate results or not and to find the best suitable alternative empirical model against the FAO56-PM. Validation was undertaken by utilizing the linear correlation method. Following Peng et al.11, the linear correlation was calculated by the below Eq. (33):
| 33 |
where, a and b denoted as fitted coefficients.
Table 7 shows the fitted a, b and R2 values of correlation between ETo,s and ETo,i in seven sub-regions and whole Bangladesh. A strong correlation between ETo,s and ETo,i was found in all sub-regions and whole Bangladesh. Values of R2 is greater than 0.8 in every sub-regions and in whole Bangladesh for all the 13 empirical models indicating a strong correlation between ETo,s and ETo,i. The model which is highly correlated with the ETo,s is highlighted with light pink color. Among 13 models ETo,6 performed best, producing greater R2 values than the other models. ETo,6 model is simple among all the models used in this study as this model utilized only Tmax and Rs. Rs is calculated from Tmax and Tmin. Tmax and Tmin are available everywhere in each region and can estimate easily. So, it can be affirmed that the ETo,6 is the best suitable, preferred, accurate, simple and reliable model, highly consisted with the results of pre-analyses (spatial and temporal distribution, performance evaluation and importance degree analysis), for ETo estimation in all the sub-regions and whole Bangladesh.
Table 7.
Fitted a, b and R2 values of correlation between ETo,s and ETo,i in seven sub-regions and whole Bangladesh.
| Sub-region | Parameter | ET0,1 | ET0,2 | ET0,3 | ET0,4 | ET0,5 | ET0,6 | ET0,7 | ET0,8 | ET0,9 | ET0,10 | ET0,11 | ET0,12 | ET0,13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | A | 0.738 | 0.761 | 0.435 | 0.645 | 0.058 | 1.089 | 0.712 | 0.697 | 0.760 | 1.151 | 1.479 | 0.683 | 0.089 |
| B | 0.954 | 1.229 | 1.559 | 0.815 | 0.045 | − 0.312 | 1.292 | 0.619 | 0.196 | 0.215 | − 0.458 | 0.879 | 0.078 | |
| R2 | 0.901 | 0.919 | 0.911 | 0.978 | 0.917 | 0.989 | 0.988 | 0.986 | 0.984 | 0.986 | 0.984 | 0.988 | 0.921 | |
| II | A | 0.781 | 0.794 | 0.787 | 0.688 | 0.055 | 1.076 | 0.694 | 0.702 | 0.754 | 1.038 | 1.393 | 0.641 | 0.078 |
| B | 0.934 | 1.310 | 1.222 | 0.782 | 0.040 | − 0.259 | 1.335 | 0.608 | 0.225 | 0.155 | − 0.188 | 1.003 | 0.045 | |
| R2 | 0.958 | 0.96 | 0.942 | 0.956 | 0.86 | 0.982 | 0.98 | 0.982 | 0.98 | 0.974 | 0.978 | 0.98 | 0.88 | |
| III | A | 0.744 | 0.782 | 0.752 | 0.651 | 0.054 | 1.032 | 0.695 | 0.667 | 0.716 | 1.051 | 1.38 | 0.656 | 0.067 |
| B | 1.061 | 1.333 | 1.342 | 0.908 | 0.045 | − 0.049 | 1.351 | 0.760 | 0.395 | 0.163 | − 0.070 | 0.956 | 0.055 | |
| R2 | 0.956 | 0.96 | 0.961 | 0.955 | 0.848 | 0.988 | 0.976 | 0.987 | 0.974 | 0.974 | 0.974 | 0.974 | 0.854 | |
| IV | A | 0.713 | 0.747 | 0.735 | 0.624 | 0.060 | 1.051 | 0.694 | 0.675 | 0.727 | 1.051 | 1.401 | 0.660 | 0.079 |
| B | 1.154 | 1.435 | 1.255 | 0.990 | 0.050 | − 0.162 | 1.306 | 0.660 | 0.279 | 0.062 | − 0.236 | 0.894 | 0.058 | |
| R2 | 0.943 | 0.951 | 0.964 | 0.941 | 0.856 | 0.984 | 0.978 | 0.978 | 0.978 | 0.976 | 0.976 | 0.978 | 0.861 | |
| V | A | 0.782 | 0.805 | 0.741 | 0.687 | 0.071 | 1.000 | 0.631 | 0.591 | 0.644 | 0.953 | 1.302 | 0.582 | 0.085 |
| B | 1.006 | 1.315 | 1.233 | 0.856 | 0.097 | 0.099 | 1.564 | 1.012 | 0.628 | 0.457 | 0.179 | 1.179 | 0.099 | |
| R2 | 0.956 | 0.962 | 0.967 | 0.955 | 0.803 | 0.974 | 0.972 | 0.970 | 0.970 | 0.970 | 0.972 | 0.968 | 0.812 | |
| VI | A | 0.619 | 0.643 | 0.687 | 0.543 | 0.083 | 0.817 | 0.520 | 0.493 | 0.538 | 0.813 | 1.084 | 0.488 | 0.098 |
| B | 1.504 | 1.819 | 1.612 | 1.295 | 0.115 | 0.566 | 1.868 | 1.233 | 0.866 | 0.833 | 0.751 | 1.424 | 0.122 | |
| R2 | 0.955 | 0.956 | 0.954 | 0.952 | 0.866 | 0.978 | 0.964 | 0.966 | 0.966 | 0.968 | 0.970 | 0.964 | 0.871 | |
| VII | A | 0.744 | 0.799 | 0.778 | 0.649 | 0.052 | 0.995 | 0.67 | 0.626 | 0.663 | 1.023 | 1.363 | 0.646 | 0.056 |
| B | 1.091 | 1.306 | 1.124 | 0.943 | 0.033 | 0.097 | 1.455 | 0.882 | 0.493 | 0.107 | 0.009 | 0.994 | 0.043 | |
| R2 | 0.968 | 0.972 | 0.952 | 0.966 | 0.914 | 0.979 | 0.98 | 0.976 | 0.974 | 0.976 | 0.974 | 0.98 | 0.911 | |
| Whole BD | A | 0.796 | 0.846 | 0.784 | 0.696 | 0.061 | 1.046 | 0.654 | 0.691 | 0.706 | 1.098 | 1.418 | 0.660 | 0.071 |
| B | 0.818 | 1.054 | 1.102 | 0.699 | 0.056 | − 0.151 | 0.763 | 1.348 | 0.363 | − 0.091 | − 0.258 | 0.929 | 0.057 | |
| R2 | 0.743 | 0.766 | 0.787 | 0.736 | 0.615 | 0.856 | 0.803 | 0.849 | 0.811 | 0.843 | 0.851 | 0.825 | 0.601 |
Discussions
Increasing and decreasing as well as significant and non-significant trends were found across the country from 1980 to 2017. The rates between increasing and decreasing of ETo,s was 72.18 to − 72.17 mm per decade in this study. For example, Bhola, Cumilla, Feni, Rangamati and Patuakhali showed a significant increasing trend of ETo,s and non-significant decreasing trend of ETo,s found in Faridpur, Madaripur, Dhaka and Barishal of sub-regions I and VII (southeastern and south-central regions). The significant decreasing trend of ETo,s showed by the sub-regions of II, III, IV and V. Cox’s Bazar, Teknaf, Sandwip, Chattogram, Jashore, Mymensingh and Khulna showed a significant decreasing trend of ETo,s. From the above results, it is evident that the trend of ETo,s was decreasing gradually in Bangladesh from 1980 to 2017. Rahman et al.15 found that most of the area of Bangladesh showed decreasing trends and some parts of the study area showed an increasing trend of ETo,s which is analogous to the results of this study. Decreasing the trend of ETo,s may be the results of worldwide climate change impacts. Spatial distribution of the long-term mean monthly between ETo,s and ETo,6 (Abtew) in Bangladesh shown a homogenous pattern. By contrary, ETo,5 (WMO) and ETo,13 (Turc) models produced the least close values to ETo,s in terms of spatial distribution. Temporal distribution of long-term monthly ETo,s, and ETo,i in Bangladesh found that the highest and lowest rate of ETo occurred in April and January–December, respectively. Peng et al.11 and Li et al.24 showed that the highest and lowest rate of ETo,s occurred in China in July (dissimilar to this study) and January–December which is similar to this study. Long term inter-annual variation of ETo,s, and ETo,i in Bangladesh revealed that ETo,5 and ETo,13 models produced very lower values, identifying the least performed method for calculating ETo. Previous studies5,11,24,29 along with this study revealed that ETo values obtained by both ETo,s and ETo,i models were very closer to each other in the month of January–December (cold season) and highest discrepancy occurred among them in the hot summer season.
Long term monthly RE (relative error) of ETo,i revealed that the WMO and Turc models were the least suitable with greater RE values and Abtew model was an optimal alternative with lower RE values against the FAO56-PM for calculating ETo in Bangladesh. The values of RMSE, MAE, NSE, and MBE had the strong concurrence with the RE exploring the same results as Abtew (ETo,6) was the best alternative and WMO (ETo,5); Turc (ETo,13) were the least suitable model for estimating ETo in Bangladesh. Gabriela and Irmak73 evaluated the impact of the meteorological variables on the estimates of 13 empirical models in various regions and found that the Doorenbos and Pruitt (ETo,12) ranked top in the three regions of Iran under sub-humid to sub-arid climate conditions which are in disagreement with the results of this study. Identification of the best suitable model against ETo,s varies from region to region and country to country. It might be due to the variation of geographical and meteorological variations from one country to another country and input model combinations. Correlation between long term daily ETo,s and ETo,i in Bangladesh was explored that a very strong correlation aligns with no one line (1:1) existed between ETo,s and ETo,6 (Abtew) with the r values of 0.92. Li et al.24 also found a strong correlation (R2 was 0.972) between daily ETo,s and ETo,13 (Valiantzas 3) in China. Xystrakis and Matzarakis35 found a strong correlation (r-value 0.993) between monthly ETo,s, and ETo,i (Turc) in Greece. There also existed a strong correlation (r-value 0.996) between ETo,s, and ETo,i (Blaney–Criddle) explored by Tabari et al.40 in Iran. Peng et al.11 found the largest correlation between monthly ETo,s, and ETo,653 in China. Present study found the Abtew (ETo,6) model as the most reliable model for estimating ETo, compared to the other empirical models in all the sub-regions of Bangladesh, as this model produced a higher importance degree.
Evaluation of the performance of different empirical models for estimating the ETo,s was finally validated by Eq. (33). This study explored that Abtew (ETo,6) model outperformed other models with R2 values ranged from 0.856 to 0.989 at all the sub-regions of Bangladesh. This is in good agreement with the earlier performance appraisal results in which RMSE, MAE, MBE, and NSE are the lowest in ETo,6 model. The main reason is that this model has high precision, easy, consistent; requiring less climatic datasets and strong association with FAO56-PM. This model provides satisfactory outcomes and generally uses simple computable parameters and has easy model forms. Djaman et al.33 also found a similar result as this study that the Abtew was the best alternative model against the FAO56-PM in New Mexico, USA. Li et al.24 found Valiantzas 3 as the outperformed model among 13 empirical models for estimating ETo with R2 values ranged from 0.882 to 0.993. Peng et al.11 explored ETo,656 as the best-performed model at all the sub-regions and EMC among ten empirical models for calculating ETo with R2 values ranged from 0.87 to 0.99. Shiri5 showed Priestley–Taylor outweighed the other 6 empirical models for estimating ETo with R2 values ranged from 0.636 to 0.792. Mohawesh38 found Penman as the best-performed model in different regions of Jordan for estimating ETo,s with R2 values ranged from 0.66 to 0.7874. Similarly, the mass-transfer-based model was the optimal model in computing ETo compared to the other models in humid regions in Iran40 and forest regions in Greece32. Based on the accuracy, reliability, simplicity and higher correlation with ETo,s, the most suitable method for ETo calculation in Bangladesh is ETo,6 model.
Conclusions
In this study, daily meteorological datasets from 20 weather stations from seven sub-regions in Bangladesh for the period of 1980–2017 were used. A widespread comparison between ETo,s (calculated by FAO56-PM) and ETo,i (calculated by HS, HM1, HM2, BT, WMO, ABT, IR1, IR2, MAK, PT, JH, TAB, TR, respectively) has been carried out. The possible roles of these 13 empirical models against the FAO56-PM were also explored in this study. Out of 20 stations, 5 stations showed an increasing trend of ETo,s; 11 stations showed a decreasing trend and 4 stations showed no trend of ETo,s. Spatiotemporal distribution of ETo,s, and ETo,i revealed that the model proposed by Abtew model showing the closest distribution of ETo,i to ETo,s. RE, RMSE, MAE, MBE, and NSE were employed for evaluating the empirical models which were identified ETo,6 as the outperformed model with the lowest errors for calculating ETo in different sub-regions and whole Bangladesh. By contrast, ETo,5 (WMO) and ETo,13 (Turc) models selected as the poorer alternative models with the higher statistical errors. RF model also confirmed the Abtew as the outperformed model. The linear regression model showed that a strong linear correlation was found between FAO56-PM and Abtew model. Validation by using Eq. (33) explored the similar outcomes that the ETo,6 model outperformed than the other models. This study recommends the model proposed by the Abtew (ETo,6) as the best alternative model with high accuracy, reliability and lowest errors for all the sub-regions and whole Bangladesh for calculating ETo when full climatic datasets for FAO56-PM model are unavailable. Future study should be focused on the evaluation of machine learning ensemble models for estimating daily ETo in Bangladesh. This research is a vital scientific contribution to ETo quantification and influential empirical models in Bangladesh where the large set of meteorological datasets could not be acquired. This study provides an important guidance for agricultural water practices, hydrological processes and irrigation management in Bangladesh, also useful as well as the similar subtropical climate region elsewhere in the world.
Supplementary information
Acknowledgements
The authors are grateful to the authority of the Department of Disaster Management, Begum Rokeya University (BRUR), and Bangladesh Meteorological Department (BMD), Dhaka, Bangladesh for providing data facilities and others logistic support during the research period.
Author contributions
R.S., A.R.M.T.I., and Q.B.P. designed, organized and wrote the paper. Q.B.P., M.D., and N.T.T.L. assisted in analyzing and processing the data. Q.B.P., M.D, N.T.T.L. and N.A. help to investigate the results. Q.B.P.: supervision. All authors revised the manuscript cautiously.
Data availability
The datasets investigated in the present research are easily reached from the corresponding author on request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
is available for this paper at 10.1038/s41598-020-77183-y.
References
- 1.Allen, R. G., Pereira, L. S., Raes, D. & Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements, FAO Irrigation and Drainge Paper, 56, FAO, pp. 1–326 (1998).
- 2.McMahon TA, Peel MC, Lowe L, Srikanthan R, McVicar TR. Estimating actual, potential, reference crop and pan evaporation using standard meteorological data: A pragmatic synthesis. Hydrol. Earth Syst. Sci. 2013;17(4):1331–1363. doi: 10.5194/hess-17-1331-2013. [DOI] [Google Scholar]
- 3.Liu X, Xu C, Zhong X, Li Y, Yuan X, Cao J. Comparison of 16 models for reference crop evapotranspiration against weighing lysimeter measurement. Agric. Water Manag. 2017;184:145–155. doi: 10.1016/j.agwat.2017.01.017. [DOI] [Google Scholar]
- 4.Islam AT, Shen S, Yang S, Hu Z, Chu R. Assessing recent impacts of climate change on design water requirement of Boro rice season in Bangladesh. Theor. Appl. Climatol. 2019 doi: 10.1007/s00704-019-02818-8. [DOI] [Google Scholar]
- 5.Shiri J. Modeling reference evapotranspiration in island environments: Assessing the practical implications. J. Hydrol. 2019;570:265–280. doi: 10.1016/j.jhydrol.2018.12.068. [DOI] [Google Scholar]
- 6.Vangelis H, Spiliotis M, Tsakiris G. Drought severity assessment based on bivariate probability analysis. Water ResourManag. 2010;25:357–371. [Google Scholar]
- 7.Vicente-Serrano SM, Beguería S, López-Moreno JI. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010;23(7):1696–1718. doi: 10.1175/2009JCLI2909.1. [DOI] [Google Scholar]
- 8.Gocic M, Trajkovic S. Drought characterisation based on water surplus variability index. Water Resour. Manage. 2014;28:3179–3191. doi: 10.1007/s11269-014-0665-4. [DOI] [Google Scholar]
- 9.Penman HL. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. Series Math. Phys. Sci. 1948;193(1032):120–145. doi: 10.1098/rspa.1948.0037. [DOI] [PubMed] [Google Scholar]
- 10.Xiang K, Li Y, Horton R, Feng H. Similarity and difference of potential evapotranspiration and reference crop evapotranspiration—A review. Agric. Water Manag. 2020;232:106043. doi: 10.1016/j.agwat.2020.106043. [DOI] [Google Scholar]
- 11.Peng L, Li Y, Feng H. The best alternative for estimating reference crop evapotranspiration inifferent sub-regions of mainland China. Sci. Rep. 2017;7(1):5458. doi: 10.1038/s41598-017-05660-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hargreaves GH, Samani ZA. Estimating potential evapotranspiration. J. Irrig. Drainage Division. 1982;108(3):225–230. [Google Scholar]
- 13.Hargreaves GH, Samani ZA. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985;1(2):96–99. doi: 10.13031/2013.26773. [DOI] [Google Scholar]
- 14.Mojid MA, Rannu RP, Karim NN. Climate change impacts on reference crop evapotranspiration in North-West hydrological region of Bangladesh. Int. J. Climatol. 2015;35(13):4041–4046. doi: 10.1002/joc.4260. [DOI] [Google Scholar]
- 15.Rahman MA, Yunsheng L, Sultana N, Ongoma V. Analysis of reference evapotranspiration (ETo) trends under climate change in Bangladesh using observed and CMIP5 data sets. Meteorol. Atmos. Phys. 2019;131(3):639–655. doi: 10.1007/s00703-018-0596-3. [DOI] [Google Scholar]
- 16.Pham MT, Vernieuwe H, De Baets B, Verhoest N. A coupled stochastic rainfall-evapotranspiration model for hydrological impact analysis. Hydrol. Earth Syst. Sci. 2018;22(2):1263–1283. doi: 10.5194/hess-22-1263-2018. [DOI] [Google Scholar]
- 17.Ismail SM, El-Nakhlawy FS. Measuring crop water requirement and crop coefficient for blue panic crop under arid conditions using draining lysimeters. Irrig. Drainage. 2018;67(3):454–460. doi: 10.1002/ird.2230. [DOI] [Google Scholar]
- 18.Samuel A, Girma A, Zenebe A, Ghebreyohannes T. Spatio-temporal variability of evapotranspiration and crop water requirement from space. J. Hydrol. 2018;567:732–742. doi: 10.1016/j.jhydrol.2018.01.058. [DOI] [Google Scholar]
- 19.Wu D, Fang S, Li X, He D, Zhu Y, Yang Z, et al. Spatial-temporal variation in irrigation water requirement for the winter wheat-summer maize rotation system since the 1980s on the North China Plain. Agric. Water Manag. 2019;214:78–86. doi: 10.1016/j.agwat.2019.01.004. [DOI] [Google Scholar]
- 20.Islam ARMT, Shen S, Yang S. Predicting design water requirementofwinterpaddyunderclimatechangeconditionusingfrequency analysis in Bangladesh. Agric. Water Manag. 2018;195:58–70. doi: 10.1016/j.agwat.2017.10.003037. [DOI] [Google Scholar]
- 21.Srivastava RK, Panda RK, Chakraborty A, Halder D. Comparison of actual evapotranspiration of irrigated maize in a sub-humid region using four different canopy resistance based approaches. Agric. Water Manag. 2018;202:156–165. doi: 10.1016/j.agwat.2018.02.021. [DOI] [Google Scholar]
- 22.Lin P, He Z, Du J, Chen L, Zhu X, Li J. Impacts of climate change on reference evapotranspiration in the Qilian Mountains of China: Historical trends and projected changes. Int. J. Climatol. 2018;38(7):2980–2993. doi: 10.1002/joc.5477. [DOI] [Google Scholar]
- 23.Paredes P, Pereira LS. Computing FAO56 reference grass evapotranspiration PM-ETo from temperature with focus on solar radiation. Agric. Water Manag. 2019;215:86–102. doi: 10.1016/j.agwat.2018.12.014. [DOI] [Google Scholar]
- 24.Li M, Chu R, Islam ARM, Shen S. Reference evapotranspiration variation analysis and its approaches evaluation of 13 empirical models in sub-humid and humid regions: A case study of the Huai river basin, eastern China. Water. 2018;10(4):493. doi: 10.3390/w10040493. [DOI] [Google Scholar]
- 25.Salam R, Islam ARMT. Potential of RT, Bagging and RS ensemble learning algorithms for reference evapotranspiration prediction using climatic data-limited humid region in Bangladesh. J. Hydrol. 2020 doi: 10.1016/j.jhydrol.2020.125241. [DOI] [Google Scholar]
- 26.Pereira LS, Allen RG, Smith M, Raes D. Crop evapotranspiration estimation with FAO56: Past and future. Agric. Water Manag. 2015;147:4–20. doi: 10.1016/j.agwat.2014.07.031. [DOI] [Google Scholar]
- 27.Droogers P, Allen RG. Estimating reference evapotranspiration under inaccurate data conditions. Irrig. Drain. Syst. 2002;16:33–45. doi: 10.1023/A:1015508322413. [DOI] [Google Scholar]
- 28.Mendicino G, Senatore A. Regionalization of the Hargreaves coefficient for the assessment of distributed reference evapotranspiration in southern Italy. J. Irrig. Drain. 2013;139(5):349–362. doi: 10.1061/(ASCE)IR.1943-4774.0000547. [DOI] [Google Scholar]
- 29.Farzanpour H, Shiri J, Sadraddini AA, Trajkovic S. Global comparison of 20 reference evapotranspiration equations in a semi-arid region of Iran. Hydrol. Res. 2019;50(1):282–300. doi: 10.2166/nh.2018.174. [DOI] [Google Scholar]
- 30.World Meteorological Organization (WMO) Measurement and Estimation of Evaporation and Evapotranspiration; Technical Paper (CIMO-Rep) Geneva: WMO; 1966. [Google Scholar]
- 31.Yeh, H.F. Comparison of evapotranspiration methods under limited data, current perspective to predict actual evapotranspiration, Daniel Bucur, IntechOpen. 10.5772/intechopen.68495(2017).
- 32.Bourletsikas A, Argyrokastritis I, Proutsos N. Comparative evaluation of 24 reference evapotranspiration equations applied on an evergreen-broadleaved forest. Hydrol. Res. 2018;49(4):1028–1041. doi: 10.2166/nh.2017.232. [DOI] [Google Scholar]
- 33.Djaman K, O’Neill M, Diop L, Bodian A, Allen S, Koudahe K, Lombard K. Evaluation of the Penman-Monteith and other 34 reference evapotranspiration equations under limited data in a semiarid dry climate. Theoret. Appl. Climatol. 2019;137(1–2):729–743. doi: 10.1007/s00704-018-2624-0. [DOI] [Google Scholar]
- 34.Muhammad MKI, Nashwan MS, Shahid S, Ismail TB, Song YH, Chung ES. Evaluation of empirical reference evapotranspiration models using compromise programming: A case study of Peninsular Malaysia. Sustainability. 2019;11(16):4267. doi: 10.3390/su11164267. [DOI] [Google Scholar]
- 35.Xystrakis F, Matzarakis A. Evaluation of 13 empirical reference potential evapotranspiration equations on the island of Crete in southern Greece. J. Irrig. Drainage Eng. 2011;137(4):211–222. doi: 10.1061/(ASCE)IR.1943-4774.0000283. [DOI] [Google Scholar]
- 36.Chu R, Li M, Shen S, Islam ARM, Cao W, Tao S, Gao P. Changes in reference evapotranspiration and its contributing factors in Jiangsu, a major economic and agricultural province of eastern China. Water. 2017;9(7):486. doi: 10.3390/w9070486. [DOI] [Google Scholar]
- 37.Trajkovic S, Kolakovic S. Comparison of simplified pan-based equations for estimating reference evapotranspiration. J. Irrig. Drain Eng. 2010;136(2):137–140. doi: 10.1061/(ASCE)IR.1943-4774.0000133. [DOI] [Google Scholar]
- 38.Mohawesh OE. Evaluation of evapotranspiration models for estimating daily reference evapotranspiration in arid and semiarid environments. Plant Soil Environ. 2011;57(4):145–152. doi: 10.17221/240/2010-PSE. [DOI] [Google Scholar]
- 39.Yao T, Lu H, Feng W, Yu Q. Evaporation abrupt changes in the Qinghai-Tibet plateau during the last half-century. Sci. Rep. 2019;9:20181. doi: 10.1038/s41598-019-56464-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tabari H, Grismer ME, Trajkovic S. Comparative analysis of 31 reference evapotranspiration methods under humid conditions. Irrig. Sci. 2013;31(2):107–117. doi: 10.1007/s00271-011-0295-z. [DOI] [Google Scholar]
- 41.Almorox J, Quej VH, Martí P. Global performance ranking of temperature-based approaches for evapotranspiration estimation considering Köppen climate classes. J. Hydrol. 2015;528:514–522. doi: 10.1016/j.jhydrol.2015.06.057. [DOI] [Google Scholar]
- 42.Shamshirband S, Amirmojahedi M, Gocić M, Akib S, Petković D, Piri J, Trajkovic S. Estimation of reference evapotranspiration using neural networks and cuckoo search algorithm. J. Irrig. Drain Eng. 2016 doi: 10.1061/(asce)ir.1943-4774.0000949. [DOI] [Google Scholar]
- 43.Quej VH, Almorox J, Arnaldo JA, Moratiel R. Evaluation of temperature-based methods for the estimation of reference evapotranspiration in the Yucatán peninsula, Mexico. J. Hydrol. Eng. 2019;24(2):05018029. doi: 10.1061/(ASCE)HE.1943-5584.0001747. [DOI] [Google Scholar]
- 44.Krishna AP. Selection of the Best Method of ET o Estimation Other Than Penman-Monteith and Their Application for the Humid Subtropical Region. Agricultural Research. 2015;4(2):215–219. doi: 10.1007/s40003-015-0153-y. [DOI] [Google Scholar]
- 45.Pandey P, Pandey V. Evaluation of temperature-based Penman-Monteith (TPM) model under the humid environment. Model. Earth Syst. Environ. 2016;2(3):152. doi: 10.1007/s40808-016-0204-9. [DOI] [Google Scholar]
- 46.Rahman MS, Islam ARMT. Are precipitation concentration and intensity changing in Bangladesh overtimes? Analysis of the possible causes of changes in precipitation systems. Sci. Total Environ. 2019;690:370–387. doi: 10.1016/j.scitotenv.2019.06.529. [DOI] [PubMed] [Google Scholar]
- 47.Kisi, O.&Alizamir, M. Modelling reference evapotranspiration using a new wavelet conjunction heuristic method: wavelet extreme learning machine vs wavelet neural networks. Agric. For. Meteorol., 263, 41–48. 10.1016/j.agrformet. 2018.08.007 (2018).
- 48.Banglapedia. National Encyclopedia of Bangladesh. Asiatic Society of Bangladesh, Dhaka(2014).
- 49.Islam, A. R. M., Shen, S., Hu, Z., & Rahman, M. A. Drought hazard evaluation in boro paddy cultivated areas of western Bangladesh at current and future climate change conditions. Advances in Meteorology. 10.1155/2017/3514381(2017).
- 50.Islam ARMT, Rahman MS, Khatun R, Hu Z. Spatiotemporal trends in the frequency of daily rainfall in Bangladesh during 1975–2017. Theoret. Appl. Climatol. 2020 doi: 10.1007/s00704-020-03244-x. [DOI] [Google Scholar]
- 51.Abtew W. Evapotranspiration measurements and modeling for three wetland systems in South Florida 1. JAWRA Journal of the American Water Resources Association. 1996;32(3):465–473. doi: 10.1111/j.1752-1688.1996.tb04044.x. [DOI] [Google Scholar]
- 52.Jensen, M. E., &Haise, H. R. Estimating evapotranspiration from solar radiation. Proceedings of the American Society of Civil Engineers, Journal of the Irrigation and Drainage Division, 89, 15–41(1963).
- 53.Irmak S, Irmak A, Allen RG, Jones JW. Solar and net radiation-based equations to estimate reference evapotranspiration in humid climates. Journal of irrigation and drainage engineering. 2003;129(5):336–347. doi: 10.1061/(ASCE)0733-9437(2003)129:5(336). [DOI] [Google Scholar]
- 54.Makkink GF. Testing the Penman formula by means of lysimeters. Journal of the Institution of Water Engineerrs. 1957;11:277–288. [Google Scholar]
- 55.Priestley CHB, Taylor RJ. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972;100(2):81–92. doi: 10.1175/1520-0493(1972)100<0081:OTAOSH>2.3.CO;2. [DOI] [Google Scholar]
- 56.Berti, A., Tardivo, G., Chiaudani, A., Rech, F., &Borin, M. Assessing reference evapotranspiration by the Hargreaves method in north-eastern Italy. Agricultural Water Management, 140, 20–25. 10.1016/j.agwat.2014.03.015(2014).
- 57.Turc, L. Estimation of irrigation water requirements, potential evapotranspiration: a simple climatic formula evolved up to date.Annals of Agronomy, 12,13–49 (1961).
- 58.Kato, T. Prediction of photovoltaic power generation output and network operation. In Integration of Distributed Energy Resources in Power Systems. Academic Press, 77–108 (2016).
- 59.Nash JE, Sutcliffe JV. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970;10(3):282–290. doi: 10.1016/0022-1694(70)90255-6. [DOI] [Google Scholar]
- 60.Praveen B, Talukdar S, Shahfahad MS, Mondal J, Sharma P, Islam ARMT, Rahman A. Analyzing trend and forecasting of rainfall changes in India using non-parametrical and machine learning approaches. Sci. Rep. 2020;10:10342. doi: 10.1038/s41598-020-67228-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Yue S, Wang C. The Mann–Kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resour. Manage. 2004;18(3):201–218. doi: 10.1023/B:WARM.0000043140.61082.60. [DOI] [Google Scholar]
- 62.Mann HB. Nonparametric tests against trend. Econometr. J. Econ. Soc. 1945 doi: 10.2307/1907187. [DOI] [Google Scholar]
- 63.Kendall MG. Rank Correlation Methods. 2. New York: Hafner Publishing Co; 1955. [Google Scholar]
- 64.Rahman MA, Yunsheng L, Sultana N. Analysis and prediction of rainfall trends over Bangladesh using Mann–Kendall, Spearman’s rho tests and ARIMA model. Meteorol. Atmos. Phys. 2016 doi: 10.1007/s00703-016-0479-4. [DOI] [Google Scholar]
- 65.Bayley GV, Hammersley JM. The "effective" number of independent observations in an autocorrelated time series. Suppl. J. R. Stat. Soc. 1946;8(2):184–197. doi: 10.2307/2983560. [DOI] [Google Scholar]
- 66.Sen P. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968;63:1379–1389. doi: 10.1080/01621459.1968.10480934. [DOI] [Google Scholar]
- 67.Breiman L. Random forests. Mach. Learn. 2001;45(1):5–32. doi: 10.1023/A:1010933404324. [DOI] [Google Scholar]
- 68.Strobl C, Boulesteix AL, Zeileis A, Hothorn T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007;8(1):25. doi: 10.1186/1471-2105-8-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Wang Z, Lai C, Chen X, Yang B, Zhao S, Bai X. Flood hazard risk assessment model based on random forest. J. Hydrol. 2015;527:1130–1141. doi: 10.1016/j.jhydrol.2015.06.008. [DOI] [Google Scholar]
- 70.Díaz-Uriarte R, De Andres SA. Gene selection and classification of microarray data using random forest. BMC Bioinform. 2006;7(1):3. doi: 10.1186/1471-2105-7-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Zheng Y, He Y, Chen X. Spatiotemporal pattern of precipitation concentration and its possible causes in the Pearl River basin, China. J. Cleaner Prod. 2017;161:1020–1031. doi: 10.1016/j.jclepro.2017.06.156. [DOI] [Google Scholar]
- 72.Wang S, Lian J, Peng Y, Hu B, Chen H. Generalized reference evapotranspiration models with limited climatic data based on random forest and gene expression programming in Guangxi, China. Agric. Water Manag. 2019;221:220–230. doi: 10.1016/j.agwat.2019.03.027. [DOI] [Google Scholar]
- 73.Arellano MG, Irmak S. Reference (potential) evapotranspiration. I: Comparison of temperature, radiation, and combination-based energy balance equations in humid, subhumid, arid, semiarid, and Mediterranean-type climates. J. Irrig. Drainage Eng. 2016;142(4):04015065. doi: 10.1061/(ASCE)IR.1943-4774.0000978. [DOI] [Google Scholar]
- 74.Jensen DT, Hargreaves GH, Temesgen B, Allen RG. Computation of ETo under nonideal conditions. J. Irrig. Drain. Eng. 1997;123(5):394–400. doi: 10.1061/(ASCE)0733-9437(1997)123:5(394). [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets investigated in the present research are easily reached from the corresponding author on request.