Abstract
In this paper, a modified form of the Proportional Integral Derivative (PID) controller known as the Integral- Proportional Derivative (I-PD) controller is developed for Automatic Generation Control (AGC) of the two-area multi-source Interconnected Power System (IPS). Fitness Dependent Optimizer (FDO) algorithm is employed for the optimization of proposed controller with various performance criteria including Integral of Absolute Error (IAE), Integral of Time multiplied Absolute Error (ITAE), Integral of Time multiplied Square Error (ITSE), and Integral Square Error (ISE). The effectiveness of the proposed approach has been assessed on a two-area network with individual source including gas, hydro and reheat thermal unit and then collectively with all three sources. Further, to validate the efficacy of the proposed FDO based PID and I-PD controllers, comprehensive comparative performance is carried and compared with other controllers including Differential Evolution based PID (DE-PID) controller and Teaching Learning Based Optimization (TLBO) hybridized with Local Unimodal Sampling (LUS-PID) controller. The comparison of outcomes reveal that the proposed FDO based I-PD (FDO-I-PD) controller provides a significant improvement in respect of Overshoot (Osh), Settling time (Ts), and Undershoot (Ush). The robustness of an I-PD controller is also verified by varying parameter of the system and load variation.
1 Introduction
The electrical power system consist of highly complex structures having various network of varied loads are interconnected. The basic purpose of AGC is to provide desired amount of power within satisfactory quality to entire users. The system will be stable when there is an equilibrium between generated power and consumers load. Since, the consumers load normally changes, the active power drawn from the generator increases which reduce the speed of generator or turbine due to variation in frequency. The modern power system comprises of numerous network areas which are connected to transmission lines via tie-lines. AGC plays a key role to sustain the exchange of power between the control regions via tie-lines and retain the frequency at predetermined value [1, 2].
Automatic Generation Control (AGC) performs a significant contribution in maintaining the stability of the power system. In this regards, substantial consideration has been paid by researches to deal with the Load Frequency Control (LFC). However, initially, most of the work has been performed in the single area network. For instance, the authors in [3, 4] considered a single area network of hydro power generation and reheat thermal power respectively. On the other hand some of the authors worked in single source generation of multi- area IPS and utilized different control techniques. For example Satheeshkumar and Shivakumar in [5] used Ant Lion Optimization (ALO) method for the tuning of Proportional Integral (PI) controller of three area IPS. The authors consider single source of thermal generation units for area-1, hydro units for area-2 and Photo-voltaic (PV) for area-3. The outcomes yielded from the proposed method are compared with Genetic Algorithm (GA), Bat Inspired Algorithm (BIA) and PSO. Similarly, the works related to the single source multi-area are presented in reference [6–10].
In past few decades, numerous control techniques have been employed for the AGC of single as well as multi-area with multi-source IPS. Mohanty et al. [11] have deliberate LFC of single area with multi-source including hydro, gas and thermal units by employing I/PI/PID controllers. The DE optimization algorithm is considered in order to tune the proposed controller gains. The authors also extended the research work to two-area diverse power generation systems. The authors in [12] used TLBO with PD-PID controller for two- area network with multi-source system considering hydro, gas and thermal generation units. Patel et al. in [13] suggested a Fractional Order (FO) fuzzy PID controller for two area IPS considering three generation units in one area and three sources in other area. The gain of the controllers are optimized with Ant Lion Optimization (ALO) method.
The literature survey reveals that the nature-inspired meta-heuristic optimization algorithms have received tremendous attention from researchers due to their strengths and capabilities to solve numerous complex optimization problems in engineering. These techniques have also been successfully employed for the tuning of controller parameters. For instance, a Grouped Grey Wolf Optimizer (GGWO) [14] algorithm was used for the optimization of PI controller parameters on Doubly Fed Induction Generator (DFIG) based on wind turbines. In work [15], a Democratic Joint Operator Algorithm (DJOA) was applied for the tuning of PID controller gains of Permanent Magnetic Synchronous Generator (PMSG) considering wind energy conversion system. Authors in [16] considered photo-voltaic inverters based on solar energy harvesting by employing Ying Yang Pair Optimization (YYPO) algorithm to optimize the parameters of perturbation observer based fractional order PID controller. Similarly, Yang et al. [17] proposed a robust fractional order PID controller tuned with Interactive Teaching-Learning Optimizer (ITLO) for solving super capacitor energy storage system. Various researchers have attempt to solve the AGC problem by employing different meta-heuristic optimization algorithms. Of these methods, authors have utilized Genetic Algorithm (GA) [18], (PSO) [19], (DE) [20], Improved-Ant Colony Optimization (I-ACO) [21], Firefly Algorithms (FA) [22], Improved Grey Wolf Optimization (IGWO) [23], Teaching Learning Base Optimization (TLBO) [24], Symbiotic Organisms Search Algorithm (SOSA) [25], Salp Swarm Algorithm (SSA) [26], Imperialist Competitive Algorithm (ICA) [27], Sine Cosine Algorithm (SCA) [28] and Backtracking Search Algorithm (BSA) [29]. While some of the authors have also applied hybrid techniques like TLBO hybridized with Local Unimodal Sampling (TLBO-LUS) [30], Improved Firefly with Pattern Search (IF-PS) [31], PSO hybrid with Gravitational Search Algorithm (PSO-GSA) [32], PSO hybridized with Chemical Reaction Optimization (HPSO-CRO) [33], and Hybrid PSO with Levy Flight algorithm (HPSO-LF) [34].
So far it remains a very challenging and critical task, due to the omnipresent problems of high dimensionality, non-differentiability and multimodality, to effectively and efficiently achieve the global optimum of engineering problems. Recently, a meta-heuristic algorithm called as Fitness Dependent Optimizer (FDO) has been developed to explore the swarming behavior of the bees. In short there are different types of bees: queen bees (responsible for making decision and produce offspring), worker bees (works under the command of queen bees) and scout bees (responsible for exploring environment and exploit the desirable targets) [35]. FDO algorithm has the advantages of fast convergence, simple to implement and adjust due to few parameters, higher efficiency and probability to find the global optimum and efficient exploration and exploitation. In this regards, FDO algorithm has been applied for the AGC problem to optimize the parameters of the proposed controller.
Initially, for the AGC problem integral controller has been widely used to control the load frequency of the system. But due to its slower response, the researchers have preferred to use PI controller which has the advantages of simple structure, low cost, fast response and easy to implementation [36]. The poor dynamic response of the PI controller has been improved by designing PID controller which has been widely used in industries due to its better performance, easy to design and stability [37, 38]. Similarly, the performance of PID controller has been improved by modifying the structure of PID controller without changing the system parameters. The modified form of PID controller known as I-PD controller has been successfully employed for the problem of magnetic levitation system [39], time delayed unstable process [40], and speed control of DC motor [41]. However, the literature reveals that modified form of PID controller has not been explored for the AGC problem. Therefore, in this paper the modified form of PID controller has been successfully applied.
In this paper, a novel modified form of PID controller known as I-PD controller is develop for AGC of multi-source IPS. In the proposed control model each area contains three different generation sources including hydro, reheat thermal and gas. Further, the parameters of the proposed controller is optimized with a more recent meta-heuristic algorithm known as Fitness Dependent Optimize (FDO). Moreover, the effectiveness of proposed approach has been assessed on two area network with four different scenarios i.e. reheat thermal, hydro, gas and multi-source power system. To quantify efficacy of the proposed controller’s detailed comparative performance is made with the results obtained by DE-PID, TLBO-PID, LUS-PID, LUS-TLBO-PID, FA-PID, FA-I-PD, PSO-PID, PSO-I-PD and TLBO-I-PD. Further, various performance criteria including IAE, ITAE, ITSE, and ISE have been used to check the performance of the system. Finally, the robustness of I-PD controller has been verified by varying the system parameters within a range of ± 50%.
The respite of the research work is structured as follows: Section 2 represents the material and methods followed by controller structure and optimization technique, While in section 3 implementation and results are demonstrated. The presented research work is concluded with future direction in section 4.
2 Materials and methods
2.1 Controller structure
In early AGC method, the integral controller had been used to control the system frequency and tie-lines power. However, due to its slower time response, the researchers used Proportional Integral (PI) controller which have the advantages of its low cost, simple structure and faster time response. The poor dynamic performance of PI controller has been improved by PID controller and their modified form I-PD controller which are nowadays very commonly used in practical [42, 43]. In I-PD controller, the proportional parameter and the derivative parameter are put in feedback form while, integrator parameter are put in feed forward direction, as depicted in Fig 1, while in PID controller all the parameters are put in feed forward direction which are depicted in Fig 2.
Fig 1. Structure of I-PD controller.

Fig 2. Structure of PID controller.

The input of PID /I-PD controller for area 1 and 2 is specified by Area Control Error (ACE).
| (1a) |
| (1b) |
where β1 and β2 represents biased parameters of frequency for area-1 and 2 respectively. ΔF1 and ΔF2 represents the frequency variation for area-1 and 2 respectively. Similarly, ΔPtie12 shows the tie line variation from area-1 to area- 2 and ΔPtie12 represent the tie line variation from area-2 to area-1.
To optimize the parameters of a controller, one of the essential steps is to determine the objective function. In this paper four different performance criteria, i.e., ITSE, ISE, ITAE and IAE are applied to verify the system performance and are given in below equations.
| (2a) |
| (2b) |
| (2c) |
| (2d) |
2.2 Fitness dependent optimizer
Several optimization methods are introduced by researchers in the field of power system to optimize the gains of the controllers by determination of fitness function. A nature-inspired meta-heuristic computational technique known as Fitness Dependent Optimizer (FDO) is deployed in this work to tune the various gains of the proposed controller. FDO starts from the initialization population of scout randomly in search space Km; m = 1, 2, 3, ……, n. The number of the scout bees were equal to population size and each scout contains three parameters known as Kp, Ki and Kd denote the gains of PID/I-PD Controller. Each scout bee denotes a new exposed hive (solution). Scouts bee are randomly searching more position to find best solutions. A previously discovered hive is ignored when new search space is find out. So each time the algorithm finds a better new solution the previous one is discarded. Moreover, if the scout bee does not find the best solutions by moving forward, then it comes back to its previous direction hoping for optimal solutions. However, if the prior solution is unable to provide a better new solution then the existing solution will be considered as the best solution that has been discovered yet. During random movement of the scout bees, each time adding pace to the present position, the scout hopes to determine the best solution. The results are compared with global best and hence it is repeated until the optimal solution not achieved or generation is stopped The movement of scouts is represented as below:
| (3) |
where m denotes current search agent, t denotes current iteration, K indicate scout bees and pace p is the movement rate and direction. Generally, pace p depends on Fitness Weight wf and can be articulated as follows:
| (4) |
where represents the value of the best global solution, km,t,f is the value of current solution and α is a weight factor which is used for the controlling of wf and its value is either 1 or 0. If the value of α is 1 then, it represent high level of convergence while if the value is 0 then there is no effect on Eq (4) but often it provides more stable search. The value of wf should be in the range of [1, 0]. But in some cases it may be equal to 1, for instance, when the current and global best solution are equal. The value of wf will be equal to 0 when is equal to 0. Finally, the case km,t,f = 0 should be ignored. Hence, the rules given below must be considered:
| (5a) |
| (5b) |
where R is the random number in the range of [1, −1]. The elementary steps of the FDO are shown in the algorithm 1.
Algorithm 1: Fitness Dependent Optimizer
Cost function J(.);
Generate scout bee population km,t; m = 1, 2, ⋯, n
While Boundary not reached do
for all For each scout bee km,t do
R ← r ∈ [−1 1] %random walk
if km,t,f == 0 then
wf = 0
else
end if
if wf == 0ORwf == 1 then
p ← R km,t
else
if R ≥ 0
else
end if
end if
Km,t+1 ← Km,t + p
If Km,t+1,f < km,t,f then
Save km,t+1,f
Save p
else
Km,t+1 ← Km,t + p
if Km,t+1,f < Km,t,f then
Save km,t+1,f
Save p
else keep current position
endIf
endIf
end for
end while
3 Implementation and results
In this section FDO-I-PD and FDO-PID controllers are considered and employed for a two-area IPS with three different generation units to assess their performance. Further, to evaluate the performance of these controllers, a two-area IPS with a single generation unit including hydro, reheat thermal and gas is considered and then the same two-area network with all three sources is investigated via simulations with 1% step load perturbation (SLP). In prvious work, four various performance criteria are used ITSE, ISE, ITAE, and IAE. However, ITSE [19, 32, 36], ISE [25, 26] and ITAE [11, 13] are mostly used for AGC. For the comparison among various performance criteria Eq (2a)–(2d) are executed in Matlab and identified that ITSE provides minimum error as compared to others criteria which are show in Table 1. Hence, ITSE criteria is preferred as an objective function to tune the gains of controller. Further, for the sake of comparison three other methods such as PSO, TLBO and FA are used for tuning of I-PD/ PID controller. The convergence rate for different methods using ITSE criteria is depicted in Fig 3. The time response performance is evaluated by comparing with DE-PID, LUS-PID, LUS-TLBO-PID fuzzy based LUS-TLBO-PID controllers. The parameters of FDO is chosen from Table 2. For simulation a population of 30 and generation of 60 numbers are considered. The optimization was performed by 30 times for each algorithm and the best optimal gains are picked during optimization which are specified in the Tables 3–6 for reheat thermal unit, hydro, gas and multi-source unit respectively.
Table 1. Comparative performance for different indices criteria.
| Controller with Techniques | Performance Indices | |||
|---|---|---|---|---|
| ITSE | ITAE | ISE | IAE | |
| FDO-PID | 0.000056 | 0.000093 | 0.00067 | 0.0147 |
| FDO-I-PD | 0.000026 | 0.000019 | 0.00056 | 0.0036 |
| PSO-PID | 0.000130 | 0.000210 | 0.00230 | 0.0096 |
| PSO-I-PD | 0.000190 | 0.000560 | 0.00980 | 0.0663 |
| FA-PID | 0.000350 | 0.000100 | 0.00450 | 0.0023 |
| FA-I-PD | 0.000040 | 0.000080 | 0.00470 | 0.0196 |
| TLBO-PID | 0.000055 | 0.000023 | 0.00230 | 0.0210 |
| TLBO-I-PD | 0.000070 | 0.000090 | 0.00120 | 0.0020 |
Fig 3. Rate of convergence for different algorithms.

Table 2. Values of Fitness Dependent Optimizer parameters.
| Parameters | Values | Parameters | Values | Parameters | Values |
|---|---|---|---|---|---|
| Number of Population NP | 30 | Number of generation Ng | 60 | Lower bound Lb | -2 |
| Upper bound Ub | 2 | Number of dimensions Nd | 9 | Weight Factor γ | 0.0 |
| random number α | [-1, 1] | - | - | - |
Table 3. Optimum gains of PID /I-PD controllers optimized with different methods for reheat thermal unit.
| Controller with Techniques | Reheat Thermal Power | ||
|---|---|---|---|
| Kp | Ki | Kd | |
| FDO-PID | 0.260 | 1.903 | -1.680 |
| FDO-I-PD | 0.340 | 1.000 | -0.670 |
| PSO-PID | 1.023 | 1.010 | -0.223 |
| PSO-I-PD | 1.305 | 0.011 | -0.435 |
| FA-PID | 0.350 | 0.001 | 0.450 |
| FA-I-PD | -0.030 | 0.600 | 2.800 |
| TLBO-PID | 0.450 | 1.230 | -0.080 |
| TLBO-I-PD | 1.700 | 0.900 | -0.203 |
Table 6. Optimum values of I-PD/ PID controllers tuned with various techniques for power system.
| Controller with Techniques | Reheat Thermal Power | Hydro Power System | Gas Power System | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Kp | Ki | Kd | Kp | Ki | Kd | Kp | Ki | Kd | |
| FDO-PID | 0.36 | 0.23 | -0.67 | 0.47 | 0.23 | -0.32 | 1.36 | 0.23 | 0.67 |
| FDO-I-PD | 0.56 | 0.09 | -0.56 | 1.03 | 0.90 | 0.01 | 1.56 | 0.90 | 0.56 |
| PSO-PID | 0.23 | 1.00 | -0.03 | 1.96 | 1.10 | 0.01 | 0.23 | 1.00 | 0.23 |
| PSO-I-PD | 1.19 | 1.56 | 0.23 | 1.63 | 0.90 | 0.01 | 1.19 | 0.56 | -0.23 |
| FA-PID | 0.35 | 0.01 | -0.45 | 1.10 | 2.00 | 1.00 | 0.35 | 0.01 | 0.45 |
| FA-I-PD | 0.60 | 1.80 | 0.45 | 1.16 | 1.96 | -0.03 | 0.60 | -1.80 | 0.45 |
| TLBO-PID | 0.45 | 0.23 | 0.89 | 1.07 | 1.90 | 0.10 | 0.45 | 0.23 | -0.23 |
| TLBO-I-PD | 0.70 | 1.90 | 0.49 | 2.00 | 0.90 | 0.10 | 0.70 | 1.90 | -0.23 |
Table 4. Optimum gains of PID /I-PD controllers optimized with different methods for hydro power unit.
| Controller with Techniques | Hydro Power system | ||
|---|---|---|---|
| Kp | Ki | Kd | |
| FDO-PID | 1.163 | 1.962 | -0.003 |
| FDO-I-PD | 1.200 | 1.012 | 1.001 |
| PSO-PID | 0.962 | 0.003 | 0.002 |
| PSO-I-PD | 1.012 | 1.001 | 1.012 |
| FA-PID | 1.002 | 1.002 | 0.001 |
| FA-I-PD | 1.013 | 1.012 | 0.080 |
| TLBO-PID | 0.450 | 0.093 | -0.080 |
| TLBO-I-PD | 0.700 | 0.010 | -0.230 |
Table 5. Optimum gains of PID /I-PD controllers optimized with different methods for gas generation unit.
| Controller with Techniques | Gas Power system | ||
|---|---|---|---|
| Kp | Ki | Kd | |
| FDO-PID | 0.723 | 0.112 | -1.012 |
| FDO-I-PD | 0.305 | 0.811 | 0.029 |
| PSO-PID | 0.962 | 0.003 | 0.002 |
| PSO-I-PD | 1.060 | 0.723 | 0.687 |
| FA-PID | 1.002 | 1.002 | 0.001 |
| FA-I-PD | 0.062 | 1.100 | 0.458 |
| TLBO-PID | 1.072 | 1.007 | -0.238 |
| TLBO-I-PD | 0.723 | 0.112 | -1.012 |
3.0.1 Two-area reheat thermal power system
The Transfer Function (TF) model of thermal reheat power with a two-area interconnected system is provided in Fig 4. Rth1 and Rth2 denote the droop constant of area 1 and area 2 respectively, whereas ΔPD indicates the change in load perturbation and Kt represent thermal constant. Similarly, ΔF1 and ΔF2 represent the change of frequency in area 1 and area 2 respectively. The transfer function of the governor, reheat, and turbine for area 1 and area 2 are represented in below equations respectively.
| (6) |
| (7) |
| (8) |
So, the overall transfer function for reheat thermal power system for area-1 and area-2 is given in Eq (9).
| (9) |
Fig 4. Two-area model with reheat thermal power system.

The TF diagram for two-area reheat thermal IPS are developed in Matlab/Simulink using the values of the gains from Table 7. The system is evaluated with I-PD/ PID controllers with 1% SLP at t = 0s. Figs (5–10) depicts the responses of load frequency in each area and tie-line power. In pursuance to examine the effectiveness of the FDO-PID and FDO-I-PD control strategies, the output responses are compared with several other algorithms based PID and I-PD controllers including PSO-PID, PSO-I-PD, FA-PID, FA-I-PD, TLBO-PID, and TLBO-I-PD. The comparison of transient response specifications are quantified and presented in Table 8.
Table 7. Parameter setting for two-area interconnected power system [13].
| Parameters | Values | Parameters | Values | Parameters | Values |
|---|---|---|---|---|---|
| β1, β2 | 0.431 MW/Hz | Rth1, Rth2, Rhy1, Rhy2, Rg1, Rg2 | 2.40 Hz/p.u | Tgh | 0.080 s |
| Tt | 0.30 s | K1 | 0.30 | Tr | 10 s |
| KP | 68.95 | Tp | 11.490 s | T12 | 0.0430 |
| a12 | -1 | Tw, yc | 1 s | Trs | 5 s |
| Trh | 28.70 s | Tgh, Tcd, TDC | 0.20 s | xc | 0.60 s |
| Kg | 0.1304 | KDC, xg | 1 | bg | 0.050 s |
| Kt | 0.5434 | Tcr | 0.010 s | TF | 0.230 s |
| Kh | 0.3268 | - | - | - | - |
Fig 5. Results for reheat thermal unit in area 1 with PID controller.

Fig 10. Results for reheat thermal unit of tie-line power with I-PD controller.

Table 8. Comparative performance between different algorithms for reheat thermal with two-area power system.
| Controller with Techniques | Settling Time Ts s | Overshoot Osh | Undershoot Ush | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ΔF1 | ΔF2 | ΔPtie | ΔF1 | ΔF2 | ΔPtie | ΔF1 | ΔF2 | ΔPtie | |
| FDO-PID | 2.9 | 9.2 | 10.3 | 0.00000 | 0.00250 | 0.00021 | -0.00400 | -0.00200 | -0.00200 |
| FDO-I-PD | 1.9 | 10.1 | 4.9 | 0.00000 | 0.00012 | 0.00000 | -0.00050 | -0.00090 | -0.00620 |
| PSO-PID | 6.5 | 9.1 | 8.4 | 0.00180 | 0.01630 | 0.00160 | -0.01000 | -0.00690 | -0.01010 |
| PSO-I-PD | 8.2 | 14.2 | 6.2 | 0.00150 | 0.00030 | 0.00930 | -0.00680 | -0.00130 | -0.00910 |
| FA-PID | 6.3 | 10.4 | 8.7 | 0.01200 | 0.00280 | 0.00081 | -0.08400 | -0.01700 | -0.00500 |
| FA-I-PD | 10.9 | 16.5 | 9.3 | 0.00072 | 0.00025 | 0.00710 | -0.00480 | -0.00110 | -0.00180 |
| TLBO-PID | 6.4 | 10.2 | 11.6 | 0.01300 | 0.00270 | 0.00091 | -0.06300 | -0.01800 | -0.00160 |
| TLBO-I-PD | 3.8 | 14.3 | 8.3 | 0.00020 | 0.00310 | 0.00000 | -0.00460 | -0.00070 | -0.01100 |
The comparison of results from Fig 5 and Table 8 reveal that FDO-PID controller completely eliminates overshoot Osh as compared to PSO, FA and TLBO based PID controller which is dire need of a controller for the system stability. Further, settling time (Ts) and undershoot (Ush) yielded by FDO-PID are better than PSO/FA/TLBO based PID controller. The results shown in Fig 6 further reveal that FDO-PID controller provides less Osh than PSO-PID however, at the cost of slight increase in Ts, but better than FA-PID and TLBO-PID.
Fig 6. Results for reheat thermal unit in area 2 with PID controller.

The results given in Figs 7 and 8 further shows that FDO-I-PD controller for both area 1 and area 2 outperform in terms of Ts, Osh and Ush which is less than PSO/FA/TLBO base tuned PID controllers. The results shown in Fig 9 reveals that FDO-PID has lesser Osh as compared to other controllers at the cost of increase in settling time for PSO-PID and FA-PID but still better than TLBO-PID. The outcome given in Fig 10 express the overall superiority of FDO-I-PD than other controllers in all aspects i.e less Ts, Osh and Ush. The overall comparison of the results for area 1 and 2 for reheat thermal power system is quantified and presented in Table 8.
Fig 7. Results for reheat thermal unit in area 1 with I-PD controller.

Fig 8. Results for reheat thermal unit in area 2 with I-PD controller.

Fig 9. Results for reheat thermal unit of tie-line power with PID controller.

3.1 Two area hydro power system
The transfer function (TF) diagram for the hydro power system with two areas are shown in Fig 11. Where Kh represent the hydro constant of the system and Rh1 and Rh2 shows droop constant of the hydro unit for area 1 and 2 respectively. The transfer function of the governor, pen stock turbine, and transient droop compensation for area 1 and area 2 are represented in below equations respectively.
| (10) |
| (11) |
| (12) |
Hence, the overall transfer function for hydro power system for area-1 and area-2 is given in Eq (13).
| (13) |
Fig 11. Two-area model with hydro power unit.

The TF model of two-area hydro power system have been assessed with FDO-PID and FDO-I-PD. The results are compared with PID and I-PD with other tuning techniques i.e.PSO, TLBO and FA. The results obtained from two-area hydro power system with PID and I-PD controllers are given in Figs (12–17).
Fig 12. Results for hydro power unit in area 1 with PID controller.

Fig 17. Results for hydro power unit of tie-line power with I-PD controller.

The results obtained from interconnected hydro power system with PID controller are given in Fig 12 which shows the better performance of FDO-PID controller as compared to TLBO/FA/PSO based PID controller. The results in Fig 13 reflect that FDO-PID provides output response with zero overshoot (Osh = 0.0000) as compared to PSO-PID (Osh = 0.0029), FA-PID (Osh = 0.0019) and TLBO-PID (Osh = 0.0006) controllers. Similarly, the results also express that FDO-PID yields lesser Ush and Ts as compared to PID controller with other tuning techniques. The results depicted in Fig 14 indicate that FDO-I-PD controller provides excellent results with zero Osh in load frequency of area 1, less settling time and undershoot as associated with other techniques like PSO, FA and TLBO with same controllers. The results illustrated in Fig 15 express that FDO base tuned PID controller have less settling time, undershoot and overshoot than PSO, TLBO and FA base tuned PID controller. However, a minor change of 0.001 in overshoot can be clearly seen than PID based controller optimized with FDO algorithm. From Fig 16 it can be seen that FDO base tuned algorithm have less settling time nonetheless of minor increased in overshoot which is completely eliminated by FDO based tuned I-PD controller which is indicated in Fig 17 but still better than other used techniques in terms of Ts, Osh and Ush. A comprehensive comparison results for two-area hydro power system and change in tie-lines in terms of Ts, Osh and Ush are given in Table 9. The representation of bold values indicates the best results.
Fig 13. Results for hydro power unit in area 2 with PID controller.

Fig 14. Results for hydro power unit in area 1 with I-PD controller.

Fig 15. Results for hydro power unit in area 2 with I-PD controller.

Fig 16. Results for hydro power unit of tie-line power with PID controller.

Table 9. Comparative performance between different algorithms for two-area hydro power system.
| Controller with Techniques | Settling Time Ts | Overshoot Osh | Undershoot Ush | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ΔF1 | ΔF2 | ΔPtie | ΔF1 | ΔF2 | ΔPtie | ΔF1 | ΔF2 | ΔPtie | |
| FDO-PID | 2.83 | 2.30 | 3.20 | 0.00000 | 0.00000 | 0.00020 | -0.00760 | -0.00430 | -0.00023 |
| FDO-I-PD | 2.90 | 5.30 | 4.00 | 0.00000 | 0.00100 | 0.00000 | -0.00410 | -0.00190 | -0.00100 |
| PSO-PID | 7.30 | 6.40 | 10.10 | 0.00290 | 0.00190 | 0.00600 | -0.06400 | -0.00520 | -0.01300 |
| PSO-I-PD | 6.70 | 9.80 | 8.70 | 0.00600 | 0.00500 | 0.00730 | -0.00420 | -0.00130 | -0.00460 |
| FA-PID | 4.30 | 5.60 | 10.20 | 0.00190 | 0.00060 | 0.00420 | -0.04300 | -0.00700 | -0.00600 |
| FA-I-PD | 5.40 | 10.1 | 6.80 | 0.00800 | 0.00700 | 0.00490 | -0.00930 | -0.00150 | -0.00430 |
| TLBO-PID | 2.40 | 4.20 | 4.60 | 0.00060 | 0.00056 | 0.00100 | -0.06200 | -0.00560 | -0.00500 |
| TLBO-I-PD | 3.10 | 6.20 | 4.40 | 0.00210 | 0.00300 | 0.00000 | -0.00420 | -0.00170 | -0.00900 |
3.2 Two-area gas power system
The Transfer Function (TF) diagram of two area gas power generation is show in Fig 18. Where Rg1 and Rg2 represents droop constant of the gas unit for area 1 and 2 respectively and Kg represent the gas constant. The transfer function of the valve position, speed governor, compressor discharge and fuel with combustion reaction for area 1 and area 2 are represented in below equations respectively.
| (14) |
| (15) |
| (16) |
| (17) |
Hence, the overall transfer function for gas power system for area-1 and area-2 is given in Eq (18).
| (18) |
The TF model of two-area gas power system are established in Matlab/Simulink using Table 7. The system is assessed with FDO base optimized PID/I-PD controllers to evaluate the achievement of the proposed techniques and their outcomes are compared with some recent optimization algorithms like TLBO, FA and PSO. The results obtained from two-area gas power system for area 1 and 2 with PID and I-PD controllers are given in Figs (19–24).
Fig 18. Two-area model with gas power system.

Fig 19. Results for gas unit in area 1 with PID controller.

Fig 24. Results for gas unit of tie-line power with I-PD controller.

In Fig 19 the results reveal that FDO base PID controller completely eliminate the overshoot (osh = 0.000), less settling time (Ts = 2.1) and undershoot (Ush = −0.0048) as compared to PSO (Osh = 0.0036, Ts = 5.9s, Ush = −0.0072), FA (Osh = 0.021, Ts = 3.9s, Ush = −0.0083), and TLBO (Osh = 0.019, Ts = 5.2s, Ush = −0.0049) base PID controller. The results depicted in Fig 20 express that FDO base tuned PID controller have similar settling time and overshoot but less undershoot than TLBO base tuned PID controller, nonetheless better than remaining techniques i.e. FA and PSO.
Fig 20. Results for gas unit in area 2 with PID controller.

The results given in Figs 21 and 22 indicates that FDO base tuned I-PD controller for change in frequency with area 1 and area 2 have good performance in terms of Ts, Osh and Ush which is less than PSO/FA/TLBO base tuned PID controllers. In inclusive comparison of the results for area 1 and 2 of gas power system in settling time, overshoot, undershoot and different performance indices are given in Table 10. The outcome shown in Fig 23 articulates that FDO base tuned PID controller for change in tie- line power have better results in all aspects i.e TS, Osh and Ush from other applied techniques with same controller. From Fig 24 it can observed that FDO base optimized I-PD controller have better result than same controller tuned with PSO/FA/TLBO in terms of lesser Osh, TS and USh. The best results are indicated with bold formats.
Fig 21. Results for gas unit in area 1 with I-PD controller.

Fig 22. Results for gas unit in area 2 with I-PD controller.

Table 10. Comparative performance between different algorithms for two-area gas power system.
| Controller with Techniques | Settling Time Ts | Overshoot Osh | Undershoot Ush | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ΔF1 | ΔF2 | ΔPtie | ΔF1 | ΔF2 | ΔPtie | ΔF1 | ΔF2 | ΔPtie | |
| FDO-PID | 2.1 | 10.2 | 3.1 | 0.00000 | 0.00013 | 0.00003 | 0.00730 | -0.00720 | -0.00059 |
| FDO-I-PD | 4.0 | 3.9 | 5.2 | 0.00000 | 0.00000 | 0.00000 | -0.00100 | -0.00084 | -0.00047 |
| PSO-PID | 5.9 | 12.4 | 10.4 | 0.03600 | 0.00390 | 0.00040 | -0.00480 | -0.00160 | -0.00110 |
| PSO-I-PD | 8.7 | 9.6 | 5.9 | 0.00730 | 0.00201 | 0.00930 | -0.00460 | -0.00019 | -0.00054 |
| FA-PID | 3.9 | 12.3 | 7.9 | 0.00210 | 0.00320 | 0.00016 | -0.00490 | -0.00170 | -0.00064 |
| FA-I-PD | 6.8 | 9.2 | 6.3 | 0.00490 | 0.00000 | 0.00021 | -0.00430 | -0.00082 | -0.00052 |
| TLBO-PID | 5.2 | 10.2 | 6.8 | 0.01000 | 0.00013 | 0.00017 | -0.00830 | -0.00080 | -0.00061 |
| TLBO-I-PD | 4.4 | 5.9 | 10.1 | 0.00000 | 0.00000 | 0.00000 | -0.00900 | -0.00089 | -0.00096 |
Fig 23. Results for gas unit of tie-line power with PID controller.

3.3 Two-area multi-source interconnected power system
The Transfer Function (TF) diagram for multi-source with two-area IPS is depicted in Fig 25. In each control area the system is equipped with reheat thermal, gas power and hydro power unit which makes the system more complicated as compared to generation unit which are individually applied in two area power system. Two-area multi-source interconnected power system have been developed in Matlab Simulink and the values have been used from Table 7. The system is assessed with FDO base tuned I-PD/ PID controllers and the superiority of the proposed techniques are compared with other techniques i.e LUS-PID, LUS-TLBO-PID, FA-PID, TLBO-PID, PSO-PID and DE-PID. The results are depicted in Figs (26)–(31).
Fig 25. Two-area with multi-source power system.

Fig 26. Results for multi-source in area 1 with PID controller.

Fig 31. Results for multi-source of tie-line power with I-PD controller.

The results shown in Fig 26 for multi-source interconnected power system of area 1 reveals that PID controller with FDO base algorithm have no overshoot, less settling time and undershoot as associated with other techniques like PSO, TLBO and FA. The results depicted in Fig 27 express that FDO base tuned PID controller have less overshoot and settling time than TLBO and FA base tuned PID controller however at the cost of 0.001 increase in undershoot, but shows better improvement than PSO base tuned PID controller.
Fig 27. Results for multi-source in area 2 with PID controller.
The results shown in Fig 28 express that FDO-PID has less settling time Ts, undershoot Us h and overshoot Os h than PSO-PID, TLBO-PID and FA-PID. However, a minor change of 0.001 in Os h can be clearly seen than FDO-PID. The results given in Fig 29 indicates that FDO-I-PD technique for change in frequency of area 2 has no overshoot, less settling time and undershoot as compared with other techniques like PSO-I-PD, FA-I-PD and TLBO-I-PD. The results given in Figs 30 and 31 reflect that FDO-I-PD for change in tie line power have good performance in terms of Ts, Osh and Ush which is less than PSO/FA/TLBO base optimized PID/I-PD controllers. A comprehensive comparison results for two-area multi- source power system and tie lines in terms of Ts, Osh and Ush are given in Table 11. The representation of bold values indicates the best results. the percentage improving comparing with different techniques is shown in bar chart of Fig 32.
Fig 28. Results for multi-source in area 1 with I-PD controller.

Fig 29. Results for multi-source in area 2 with I-PD controller.

Fig 30. Results for multi-source of tie-line power with PID controller.

Table 11. Comparative performance between different algorithms for two-area multi-source power system.
| Controller with Techniques | Settling Time Ts | Overshoot Osh | Undershoot Ush | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ΔF1 | ΔF2 | ΔPtie | ΔF1 | ΔF2 | ΔPtie | ΔF1 | ΔF2 | ΔPtie | |
| FDO-PID | 5.20 | 12.70 | 4.30 | 0.00000 | 0.00021 | 0.00020 | -0.00047 | -0.00130 | -0.00056 |
| FDO-I-PD | 2.30 | 1.65 | 2.10 | 0.00000 | 0.00000 | 0.00000 | -0.00450 | -0.00500 | -0.00058 |
| PSO-PID | 5.90 | 13.40 | 9.30 | 0.00930 | 0.00250 | 0.00630 | -0.00054 | -0.00016 | -0.00580 |
| PSO-I-PD | 2.90 | 9.20 | 6.80 | 0.00400 | 0.00400 | 0.00080 | -0.00720 | -0.05500 | -0.00910 |
| FA-PID | 6.30 | 13.10 | 7.10 | 0.00021 | 0.00036 | 0.00610 | -0.00052 | -0.00110 | -0.00510 |
| FA-I-PD | 4.30 | 4.10 | 5.90 | 0.00000 | 0.00000 | 0.00043 | -0.00490 | -0.00900 | -0.00640 |
| TLBO-PID [30] | 9.37 | 3.76 | 4.76 | 0.00172 | 0.00043 | 0.00017 | -0.01972 | -0.01279 | -0.00307 |
| TLBO-I-PD | 2.20 | 2.20 | 2.20 | 0.00000 | 0.00000 | 0.00011 | -0.00530 | -0.00500 | -0.00130 |
| LUS-TLBO Fuzzy-PID [30] | 5.26 | 2.96 | 2.36 | 0.00055 | 0.00021 | 0.00008 | -0.00895 | -0.00301 | -0.00096 |
| DE Fuzzy-PID [30] | 5.30 | 2.90 | 2.60 | 0.00073 | 0.00024 | 0.00009 | -0.01297 | -0.00589 | -0.00160 |
| LUS-TLBO-PID [30] | 9.22 | 3.34 | 4.98 | 0.00167 | 0.00042 | 0.00015 | -0.01689 | -0.01133 | -0.00289 |
| LUS-PID [30] | 9.29 | 4.62 | 6.36 | 0.00185 | 0.00046 | 0.00015 | -0.02105 | -0.01517 | -0.00358 |
| DE-PID [11] | 13.84 | 8.35 | 9.35 | 0.00203 | 0.00077 | 0.00019 | -0.02657 | -0.02214 | -0.00475 |
Fig 32. Comparison in sense of improvement% with reference DE-PID [11].

3.4 Sensitivity analysis
The robustness of an I-PD controller is verified by varying the system parameters of two areas multi-generation system within a range of ± 50% with a step of ± 25%. Fitness dependent algorithm (FDO) is employed to check the performance of the proposed controller by varying some parameters of the system from their nominal values such as turbine constant (Tt), droop constant R and governor constant (Tg). The results yielded from sensitivity analysis for ΔF1, ΔF2, and ΔPtie with variation in Tt, R and Tg is depicted in Figs 33–41. It can be observed from results that our proposed controller provides robustness by changing system parameters Tt, R and Tg for ΔF1, ΔF2, and ΔPtie respectively within a range of ± 50%. Further, it can also be observed from Figs 33–41 that the system response plotted with variation in various parameters are very close to the nominal values and hence, the controller gains need not be re-tuned for a change of system parameters and load conditions within a range of ± 50%.
Fig 33. Results for variation in R with ΔF1.

Fig 41. Results for variation in Tt with ΔPtie.
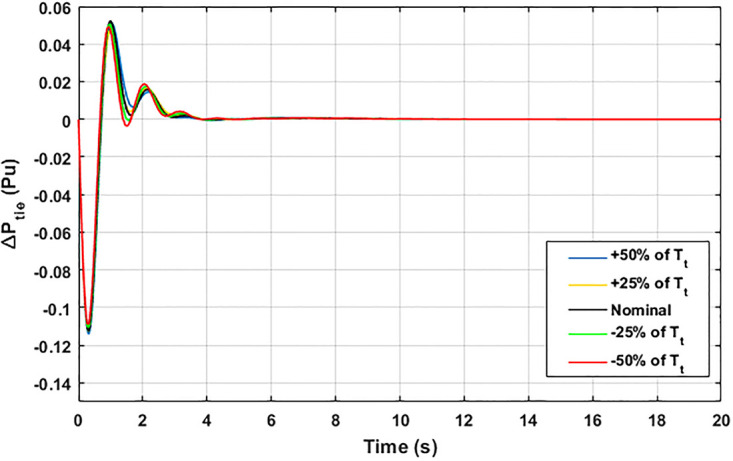
Fig 34. Results for variation in R with ΔF2.

Fig 35. Results for variation in R with ΔPtie.

Fig 36. Results for variation in Tg with ΔF1.

Fig 37. Results for variation in Tg with ΔF2.

Fig 38. Results for variation in Tg with ΔPtie.

Fig 39. Results for variation in Tt with ΔF1.

Fig 40. Results for variation in Tt with ΔF2.

4 Conclusion
In this paper, PID and I-PD controllers have been designed and successfully implemented to handle Automatic Generation Control (AGC) of multi-source with multi-area Interconnected Power System (IPS). Fitness Dependent Optimizer (FDO) algorithm has been used to attain the gains of these controllers. The effectiveness of FDO based controllers i.e. FDO-PID and FDO-I-PD are evaluated on two-area with reheat thermal, gas and hydro power system individually and then collectively with all three generation units present in the system. The transient response performance achieved by the designed controllers with 1% step load perturbation are presented and quantified in detail via simulations and compared with several other controller techniques. The comparison of results evidently shows that FDO-PID and FDO-I-PD controllers provide superior results in respect of Settling time (Ts), overshoot (Osh), and undershoot (Ush) for thermal reheat, gas, hydro and multi-source power generation. It is observed th at FDO-I-PD as compared to DE-PID completely eliminates Osh in load frequency of both areas and in tie-line power, while 83.38%, 80.24%, and 77.54% improvement in Ts in area-1 and area-2 load frequency, and tie-line power are achieved respectively. Similarly, FDO-I-PD also provides an improvement of 83.1%, 77.4%, and 87.8% in Ush as compared DE-PID. The results further show that FDO- I-PD as compared to LUS-PID provides significant improvement of 75.24%, 64.28% and 66.98% in Ts of load frequency forΔF1, ΔF2, and ΔPtie respectively, while an improvement in Ush of 63.23%, 49.43% and 57.58% are achieved for load frequency of ΔF1, ΔF2, and ΔPtie respectively. The supremacy of FDO based PID and I-PD controllers proposed in this work clearly demonstrate the capability of these controllers to tackle the automatic generation control problem effectively with oscillation-free and quick response. In future studies, the performance of the same power system can be improved by employing robust FOPID controller and powerful meta-heuristic algorithms. The same power system may be extended by incorporating with other renewable energy sources.
Supporting information
(PDF)
Data Availability
All relevant data are within the manuscript and its Supporting information files.
Funding Statement
There is no specific grant for this Article.
References
- 1. Arya Y. A novel CFFOPI-FOPID controller for AGC performance enhancement of single and multi-area electric power systems. ISA Trans. 2020, 100:126–135. 10.1016/j.isatra.2019.11.025 [DOI] [PubMed] [Google Scholar]
- 2. Alhelou HH, Hamedani-Golshan ME, Zamani R, Heydarian-Forushani E, Siano P. Challenges and Opportunities of Load Frequency Control in Conventional, Modern and Future Smart Power Systems: A Comprehensive Review. Energies. 2018, 11 10.3390/en11102497 [DOI] [Google Scholar]
- 3. Sutterfieldand J, Caprez G, Hanelineand J, Bergman A. Automatic generation control for hydro System. IEEE Trans Energy Convers. 1988. [Google Scholar]
- 4. Nanda J, Mangla A, Suri S. Some new findings on automatic generation control of an interconnected hydrothermal system with conventional controllers. IEEE Transactions on Energy Conversion. 2006, 21:187–194. 10.1109/TEC.2005.853757 [DOI] [Google Scholar]
- 5. Satheeshkumar R, Shivakumar R. Ant Lion Optimization Approach for Load Frequency Control of Multi-Area Interconnected Power Systems. Circuits and Systems. 2006, 7:2357–2383. 10.4236/cs.2016.79206 [DOI] [Google Scholar]
- 6. Kusic GL, Sutterfield JA, Caprez AR, Haneline JL, and Bergman BR. Automatic generation control for hydro systems. IEEE Trans Energy Convers. 1988, 3(1):33–39. 10.1109/60.4196 [DOI] [Google Scholar]
- 7. Chen C, Zhang K, Yuan K, Teng X. Tie-Line Bias Control Applicability to Load Frequency Control for Multi-Area Interconnected Power Systems of Complex Topology. Energies. 2017, 10. [Google Scholar]
- 8. Gozde H, Taplamacioglu MC. Automatic generation control application with craziness based particle swarm optimization in a thermal power system. Int J Electr Power Energy Syst. 2011, 33:8–16. 10.1016/j.ijepes.2010.08.010 [DOI] [Google Scholar]
- 9. Rani P, Jaswal R. Automatic load frequency control of multi—area power system using ANN controller and Genetic algorithm. International Journal of Engineering Trends and Technology (IJETT). 2016, 4. [Google Scholar]
- 10. Singh SP, Prakash T, Singh VP. Analytic hierarchy process based automatic generation control of multi-area interconnected power system using Jaya algorithm. Eng Appl Artif Intell. 2017, 60:35–44. 10.1016/j.engappai.2017.01.008 [DOI] [Google Scholar]
- 11. Mohanty B, Panda S, and Hota P. Controller parameters tuning of differential evolution algorithm and its application to load frequency control of multi-source power system. International Journal of Electrical Power Energy Systems. 2014, 54:77–85. 10.1016/j.ijepes.2013.06.029 [DOI] [Google Scholar]
- 12.Debnat MK, Patel NC, Mallick RK. Optimal base PD-PID controller for automatic generation control of multi-source tuned by teaching learning base optimization algorithm. IEEE conference. 2016, 77–85.
- 13. Patel NC, Sahu BK, Bagarty DP, Das P, Debnath MK. A novel application of ALO-based fractional order fuzzy PID controller for AGC of power system with diverse sources of generation. International Journal of Electrical Engineering Education. February 2019. 10.1177/0020720919829710 [DOI] [Google Scholar]
- 14. Yang B, Zhang X, Yu T, Shu H, Zeng F. Grouped grey wolf optimizer for maximum power point tracking of doubly-fed induction generator based wind turbine. Energy Conversion and Management. 2017, 133:427–443. 10.1016/j.enconman.2016.10.062 [DOI] [Google Scholar]
- 15. Yang B, Yu T, Shu H, Zhang X, QU K, Jiang L. Democratic joint operations algorithm for optimal power extraction of PMSG based wind energy conversion system. Energy Conversion and Management. 2018, 159:312–3226. 10.1016/j.enconman.2017.12.090 [DOI] [Google Scholar]
- 16. Yang B, Yu T, Shu H, Zhu D, Zeng F, Sang Y, et al. Perturbation observer based fractional-orderPID control of photovoltaics inverters for solar energy harvesting via Yin-Yang-Pair optimization. Energy Convers. Manag. 2018, 171:170–187. 10.1016/j.enconman.2018.05.097 [DOI] [Google Scholar]
- 17. Yang B, Wang J, Wang J, Shu H, Li S, He T, et al. Robust Fractional-order PID Control of Supercapacitor Energy Storage Systems for Distribution Network Applications: A Perturbation Compensation based Approach. Journal of Cleaner Production. 2020, 279 10.1016/j.jclepro.2020.123362. [DOI] [Google Scholar]
- 18. Daneshfar F, Bevrani H. Multiobjective design of load frequency control using genetic algorithms. Int J Elect Power Energy System. 2012, 54:257–263. 10.1016/j.ijepes.2012.04.024 [DOI] [Google Scholar]
- 19. Morsali J, Zare K, Hagh MT. Performance comparison of TCSC with TCPS and SSSC controllers in AGC of realistic interconnected multi-source power system. Ain Shams Engineering Journal. 2016, 7:143–158. 10.1016/j.asej.2015.11.012 [DOI] [Google Scholar]
- 20. Panigrahi TK, Behera A, Sahoo AK. Novel approach to Automatic Generation Control with various Non-linearities using 2-degree-of-freedom PID controller. Energy Procedia. 2017, 138:464–469. 10.1016/j.egypro.2017.10.182 [DOI] [Google Scholar]
- 21. Chen G, Li Z, Zhang Z, Li S. An Improved ACO Algorithm Optimized Fuzzy PID Controller for Load Frequency Control in Multi Area Interconnected Power Systems. IEEE Access. 2020, 8:6429–6447. 10.1109/ACCESS.2019.2960380 [DOI] [Google Scholar]
- 22. Sufyan M, Abd Rahim N, Tan C, Muhammad MA, Sheikh Raihan SR (2019) Optimal sizing and energy scheduling of isolated microgrid considering the battery lifetime degradation. PLoS ONE 14(2): e0211642 10.1371/journal.pone.0211642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Sahu PC, Prusty RC, Panda S. Improved‑GWO designed FO based type‑II fuzzy controller for frequency awareness of an AC micro grid under plug in electric vehicle. Journal of Ambient Int and Humanized Computing. March 2020. 10.1007/s12652-020-02260-z [DOI] [Google Scholar]
- 24. Sahu RK, Panda S, Rout UK, Sahoo DK. Teaching learning based optimization algorithm for automatic generation control of power system using 2-DOF PID controller. International Journal of Electrical Power and Energy Systems. 2016, 77:287–301. 10.1016/j.ijepes.2015.11.082 [DOI] [Google Scholar]
- 25. Guha D, Roy PK, Banerjee S. Symbiotic organism search algorithm applied to load frequency control of multi-area power system. Energy Systems. 2018, 9:439–468. 10.1007/s12667-017-0232-1 [DOI] [Google Scholar]
- 26. Hasanien HM, Fergany EL. Salp swarm algorithm-based optimal load frequency control of hybrid renewable power systems with communication delay and excitation cross-coupling effect. Electr Power Syst Res. 2019, 176 10.1016/j.epsr.2019.105938 [DOI] [Google Scholar]
- 27. Arya y. Improvement in automatic generation control of two-area electric power systems via a new fuzzy aided optimal PIDN-FOI controller. ISA Transactions. 2018, 80:475–490. 10.1016/j.isatra.2018.07.028 [DOI] [PubMed] [Google Scholar]
- 28. Tasnin W, Saikia LC. Maiden application of an sine-cosine algorithm optimized FO cascade controller in automatic generation control of multi-area thermal system incorporating dish-stirling solar and geothermal power plants, IET Renewable Power Generation. 2018, 12(5):585–97. [Google Scholar]
- 29. Guha D, Roy PK, Banerjee S. Application of backtracking search algorithm in load frequency control of multi-area interconnected power system. Ain Shams Engineering Journal. 2018, 9:257–276. 10.1016/j.asej.2016.01.004 [DOI] [Google Scholar]
- 30. Sahu Bk, Pati Tk, Nayak JR, Panda S, and Kumar S. A novel hybrid LUS–TLBO optimized fuzzy PID controller for load frequency control of multi-source power system. Electrical power and Energy System. 2016, 1:58–69. 10.1016/j.ijepes.2015.07.020 [DOI] [Google Scholar]
- 31. Rajesh KS, Dash SS, Rajagopal R. Hybrid improved firefly -pattern search optimized fuzzy aided PID controller for automatic generation control of power systems with multi-type generations. Swarm Evol Comput. 2019, 44:200–211. 10.1016/j.swevo.2018.03.005 [DOI] [Google Scholar]
- 32. Veerasamy v et al. , A Hankel Matrix Based Reduced Order Model for Stability Analysis of Hybrid Power System Using PSO-GSA Optimized Cascade PI-PD Controller for Automatic Load Frequency Control. IEEE Access. 2020, 8:71422–71446. 10.1109/ACCESS.2020.2987387 [DOI] [Google Scholar]
- 33. Mohanty B, Hota P. A hybrid chemical reaction-particle swarm optimisation technique for automatic generation control. Journal of Electrical Systems and Information Technology. 2018, 5:229–244. 10.1016/j.jesit.2017.04.001 [DOI] [Google Scholar]
- 34. Barisal AK, Panigrahi TK, Mishra S. A Hybrid PSO-LEVY Flight Algorithm Based Fuzzy PID Controller for Automatic Generation Control of Multi Area Power Systems: Fuzzy Based Hybrid PSO for Automatic Generation Control. Int J Energy Optim Eng. 2017, 6:42–63. [Google Scholar]
- 35. Abdullah JM, Ahmed T. Fitness dependent optimizer: Inspired by the bee swarming reproductive process. IEEE Access. 2019, 7:43473–43486. 10.1109/ACCESS.2019.2907012 [DOI] [Google Scholar]
- 36. Naidu K, Mokhlis H, Abakar AH, Terzija V. Application of Firefly Algorithm With Online Wavelet Filter in Automatic Generation Control of an Interconnected Reheat Thermal Power System. International Journal of Electrical Power Energy Systems. 2014, 63:401–413. 10.1016/j.ijepes.2014.05.055 [DOI] [Google Scholar]
- 37. Pradhan PC, Sahu RK, Panda S. Firefly algorithm optimized fuzzy PID controller for AGC of multi-area multi-source power systems with UPFC and SMES. Engineering Science and Technology, an International Journal. 2016, 19:338–354. 10.1016/j.jestch.2015.08.007 [DOI] [Google Scholar]
- 38. Shankar R, Kumar A, Raj U, Chatterjee K. Fruit fly algorithm-based automatic generation control of multi-area interconnected power system with FACTS and AC/DC links in deregulated power environment. Int Trans Electrical Energy Syst. 2019, 29:1–25. [Google Scholar]
- 39. Sain D, Swain SK, Mishra SK. Real Time Implementation of Optimized I-PD Controller for the Magnetic Levitation System using Jaya Algorithm. IFAC-PapersOnLine. 2018, 51(1):106–111. 10.1016/j.ifacol.2018.05.018 [DOI] [Google Scholar]
- 40. Chakraborty S, Ghosh S, Naskar AK. I–PD controller for integrating plus time-delay processes. IET Control Theory Applications. 2017, 11(17):3137–3145. 10.1049/iet-cta.2017.0112 [DOI] [Google Scholar]
- 41. Ketthong T, Tunyasirut S, Puang D. Design and implementation of i-pd controller for dc motor speed control system by adaptive tabu search. International Journal of Intelligent Systems and Applications. 2017, 9(9):69 10.5815/ijisa.2017.09.08 [DOI] [Google Scholar]
- 42. Rajinikanth V, Latha K. I-PD Controller Tuning for Unstable System Using Bacterial Foraging Algorithm: A Study Based on Various Error Criterion. Applied Computational Intelligence and Soft Computing. 2012, 10:1–10. 10.1155/2012/329389 [DOI] [Google Scholar]
- 43. Odili JB, Mohmad Kahar MN, Noraziah A (2017) Parameters-tuning of PID controller for automatic voltage regulators using the African buffalo optimization. PLoS ONE 12(4): e0175901 10.1371/journal.pone.0175901. [DOI] [PMC free article] [PubMed] [Google Scholar]



