Some thoughts on counts in sequencing studies

Abstract

Measurements in sequencing studies are mostly based on counts. There is a lack of theoretical developments for the analysis and modelling of this type of data. Some thoughts in this direction are presented, which might serve as a seed. The main issues addressed are the compositional character of multinomial probabilities and the corresponding representation in orthogonal (isometric) coordinates, and modelling distributions for sequencing data taking into account possible effects of amplification techniques.

INTRODUCTION

Experimental measurements in omics sciences are frequently counts of events, sequences or taxa, here generically called features. These counts are usually spread out over a large number of features, which can range from tens to thousands. Although the number of counts from one sample is commonly large, say some thousands, the number of features not observed is large as well, producing many zero counts. These zero counts can be >50% or even 80%, as occurs systematically in microbiome studies (1). Moreover, the total number of counts in an individual sample is normally irrelevant (2,3). The crucial problem is that the probabilities of one count of a feature poorly describe the possible interrelationships between them; that is, the abundances of features are not enough for a suitable description of the behaviour of the whole community, which in turn is the main goal in most omics studies.

Generally, observations are modelled as random events, and their joint distribution is the main tool for the interpretation of experimental facts. For instance, if some observed counts are assumed to be multinomial, the goal of the analysis is to estimate the multinomial probabilities, which are the parameters of the distribution. Unfortunately, the covariance structure of the multinomial distribution is determined by the multinomial probabilities, thus producing a very rigid model (4). In order to solve this problem, several generalizations have been proposed. The most immediate is to assume that the parameters of the multinomial distribution are random as well. This option matches very well the Bayesian approaches, in which the joint distribution (posterior distribution) of the multinomial probabilities is the target of the estimation (5).

In this context, assuming that the joint distribution of the multinomial probabilities (parameters) is a Dirichlet distribution—the Bayesian conjugate of the multinomial—is a commonplace. The resulting distribution is called multinomial–Dirichlet distribution (6). Disappointingly, this posterior distribution—or the corresponding predictive distribution for observations—is not able to fully describe overdispersion in counts, as is frequently observed in omics sciences (7).

There are alternatives based on univariate count distributions (geometric, negative binomial, Poisson). In these cases, the need of modelling joint distributions drives us to assume that the univariate parameters are random (Bayesian approach) and have a joint distribution. Alternatively, the univariate parameters can be linked in a model with new parameters. One of the first approaches was the Poisson-lognormal distribution (8). The review by Inouye et al. (9) is an excellent reference for the multivariate generalizations of the Poisson distribution. The negative binomial distribution is used extensively in ecology and microbiology (10–12). Recently, some attention has been paid to the multinomial-logistic normal distribution (13,14), which is a reference distribution in this contribution.

Mentioned approaches, based on mixtures of multinomials, have been successful in modelling the inflated presence of zeros, even better than zero-inflated distributions. However, their weakness is that they can be considered as being overparametrized in high or even moderate dimensional cases, as the size of the involved covariance matrix (or other dependence parameters) to be estimated grows with the square of the number of features involved. This is especially problematic if the number of features in the dataset exceeds the sample size.

The goal of this contribution is 2-fold. The first goal is to discuss the compositional character of count data and of the parameters describing distributions of abundances and how they can be represented in orthogonal (isometric) coordinates; additionally, a simplification of the multinomial-logistic normal distribution is presented. It is based on the asymptotic distribution of the multinomial parameters. The second goal is modelling distributions for sequencing data taking into account possible effects of amplification techniques.

The next section is a discussion on the compositional characteristics of count data. The third section addresses standard modelling of counts with the multinomial distribution. The fourth section deals with the distribution of log-ratio coordinates obtained from multinomial counts or, more specifically, with the asymptotic distribution of multinomial counts. The fifth section studies the asymptotic distribution of multinomial parameters and the consequences of the amplification of sequencing data. Some final conclusions are also provided.

ARE COUNTS COMPOSITIONAL?

Sequencing data, despite being obtained from counts, are frequently described by relative abundances and, then, the latter are considered compositional data (2,3,13,15). All these references, among others, intuitively explain the compositional character of count data in the context of omics sciences. However, these explanations do not focus on the sample space approach for compositional data (16,17), which provide further insight into the nature of the problem we are referring to.

Any experiment provides output observations, commonly called data. The first step in modelling data is to determine to which set the possible outputs belong. This set is called sample space. However, data analysis frequently requires further structure like the scale, addition and/or distance between observations. In many situations, this important step of modelling is skipped since, implicitly, quantitative observations are assumed embedded in the real space (positive and negative values, absolute scale, addition is the ordinary sum, distance is the ordinary Euclidean distance). However, there are many instances in which these assumptions can be considered inadequate. This is the case of compositional data. The need of a formal definition of a sample space is especially important if observations are assumed to be random, since assumptions on the sample space affect very elementary statistical descriptors like the mean and the variance (18).

In general, count observations are assumed random, and their sample space can be the non-negative integer numbers 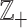, including the zero. If several features, say D, are counted simultaneously, the resulting array of counts is an element of the set 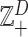, the set of vectors of D non-negative integers. Further structure can be introduced in this set in different ways in order to support the operations required to analyse these count data. For instance, one can assume that the scale of the counts on the ith feature is absolute; that is, the increment from n_i to n_i + 1 is always the same independently of the value of n_i. Using this absolute scale, the differences between 0 and 1, 4 and 5, and 1000 and 1001 are the same. This scale may be inappropriate in many instances where counts of the order of thousands and zero, one or small counts appear in the same sample. In this case, a relative scale (also known as ratio scale or multiplicative scale) may be more adequate. For instance, from 4 to 5 the increment can be described as (multiplicative) increment, whereas the (multiplicative) increment from 1000 to 1001 is . Commonly, relative scales are transformed into absolute scales by taking logarithms. However, the presence of zeros precludes this simple technique, since the log transformation places the log(0) at −∞. In fact, a zero count is not relative to anything. Moreover, additive group operations (addition) are generally required, for instance, to compute an average of vectors of counts. The standard addition has some shortcomings; for instance, the opposite operation (subtraction) is not closed in 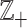since the result can be negative, which is outside 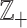. In some cases, the problem with the zeros can be circumvented by assuming that counts can be fractions, and zero may be viewed as a small fraction or pseudo-count (19).

The conclusion is that the analysis of sample counts is not the main goal for several reasons. Two reasons for this deserve to be mentioned: (i) the amount of counts strongly depends on the experimental conditions (2) and (ii) at present, we do not know how to model the sample space for random counts in order to reasonably answer current research questions, the interdependence of different features and their relationship with other variables external to count observations.

As mentioned in the first section, most of the time, interest is centred on theoretical relative frequencies, that is, on probabilities of one count for a given feature. If there are D features, let 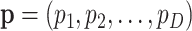denote the probabilities of occurrence of each feature. The interpretation of these probabilities depends on the probability distribution of the observed counts. In a multinomial sampling, 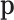is readily identified with the parameters of the multinomial distribution and, consequently, as unknown but fixed values. In a Bayesian context, the probabilities 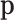are considered random and their interpretation depends on their posterior distribution (20,21). In mixture models, like the multinomial-logistic normal, 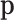is not a parameter of the distribution of observed counts, as it is considered a dummy parameter and is consequently marginalized. However, many research questions are referred to 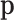, whether representing fixed or random parameters. In this situation, it is necessary to determine an adequate sample space for  when it is considered random or fixed.

In many instances, a set of probabilities like can be considered a composition obeying the Aitchison geometry of the simplex (18,22,23), which is a particular Euclidean type of geometry. In fact, probabilities are scale invariant: they can be expressed as proportions as well as percentages without loss of information. As a consequence, information is in the ratios between probabilities (17). The addition in the Aitchison geometry is called perturbation (4). It consists of a component-wise multiplication of the composition by positive coefficients. This change is a shift of the composition, sometimes interpreted as biasing (24). If , are compositions, then the perturbation of 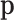by is

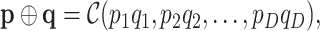where 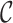is an optional normalization of the result to add to 1 and 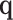may or may not be normalized to unit sum. Also, compositional perturbation is readily interpreted as the application of the discrete Bayes formula (4,17), and taking subcompositions is a conditional probability. Therefore, 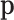can be considered as compositional.

Considering 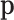as compositional has an important consequence: it can be advantageously represented using orthogonal (Cartesian) coordinates, as corresponds to a Euclidean geometry (18,25). These coordinates are obtained using an isometric log-ratio transformation (ilr) also known as the orthogonal log-ratio transformation. Examples of the use of ilr in microbiome analysis can be found in (13,26). Note that orthogonal coordinates refer to coordinates defined with respect to an orthonormal basis of the simplex.

Summarizing, count data contain compositional information, but the extraction requires a modelling step: assuming a distribution in which the probabilities 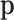are parameters that can be estimated from the count data. These probabilities can conveniently be considered compositional. In practice, in the absence of zero counts, the estimation of p_i is commonly the relative frequency n_i/N of the ith feature. This obvious estimation may be misleading in the presence of zero or small counts, since most research questions are on 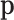and not on their estimators, the relative frequencies.

FIRST STEPS IN MODELLING COUNT DATA

The dominant practice in metagenomics and particularly in microbiome analysis is directed to three kinds of simple statistical analysis: explorations of relative frequencies and their representation and display, differential expression of genes in different populations and discrimination of such populations. For the three mentioned goals, probabilistic and statistical modelling can be reduced to a minimum. Exploratory analysis requires the rudiments of the sample space; differential expression is commonly afforded using univariate statistics over the relative abundances of features (or some normalization of them) and then combined using multiple testing techniques. Discrimination between populations is more demanding theoretically speaking, but simplified models allow obtaining some results. The consequence of this situation is that only a little effort has been made to study the adequate probabilistic and statistical models for sequencing count data.

In the decade 2010–2019, the compositional character of most omics data has become clear. Slowly but increasingly, the log-ratio approach for analysing omics data has turned into an important tool in the field. This approach, based on log-transformed relative frequencies, is confronted with the omnipresence of zeros in almost all datasets. This fact requires further modelling of the sample space for proportions, abundances and frequencies, and also establishing adequate probability distributions of the observed relative frequencies, which are needed for dealing with the zeros.

One of the first broadly used elementary models for count data is the multinomial distribution. Denote the counts for D features by 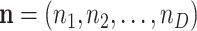and assume they are random. The sum of these counts is the number of trials N. Denoting , ∑_ip_i = 1, the probabilities of one read for the corresponding features, the probability distribution (pd, for short) of the multinomial distribution is

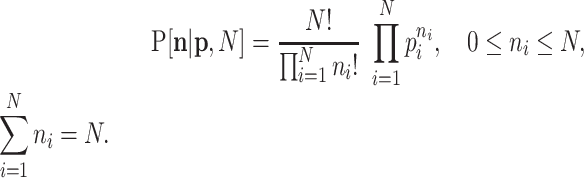(1)

Remarkably, this pd admits zeros in the counts n_i in a natural way.

Immediately, researchers realize that many research questions ask for the estimation of the probability parameters in , which are clearly the theoretical relative abundances of each feature. As a consequence, the first problem is the estimation of from the observed counts and possibly from other observed variables. Usually, the first trial is to estimate p_i using the relative abundance n_i/N, which is the maximum likelihood estimator for the parameters of the multinomial distribution. This estimation works well for moderate to large abundances but fails dramatically for low counts and, particularly, for zero counts. Remember that the valuable properties of maximum likelihood estimators are asymptotic; that is, they hold for large samples, thus avoiding zero or low counts. Therefore, they fail for zero counts. It is a well-known fact that observing zero times a given feature does not imply that the feature is not there, especially if there are more features than cases. With these facts in mind, Bayesian estimation methods appear as an alternative: the multinomial parameters are assumed random and a prior distribution for them is established; let 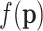be such a prior distribution. Then, the Bayes theorem provides the posterior distribution of the multinomial parameters

(2)

where 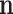are now the observed counts and 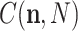is a normalizing constant that depends on the observations. Once a prior distribution 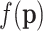is selected and after the observations  have been observed, this distribution of the multinomial probabilities provides central values and variability characteristics of . This model is very popular (20,21), mainly because the Dirichlet distribution is well known as the Bayesian conjugate of the multinomial, being enough for exploratory analysis, treatment of zeros (26,27), and for differential expression analysis.

Alternatively to the Dirichlet distribution as a prior distribution, the normal on the simplex (16,18,28), also known as logistic normal distribution (4,29), could be selected as a natural and flexible prior.

Although the Bayesian estimation of the multinomial probabilities has been proven competitive in exploratory analysis of count data with many zeros, it has some drawbacks (21). The most important one is that there is no guarantee that count data coming from sequencing follow a multinomial distribution. Furthermore, there are cases in which counts in a single feature are incompatible with a binomial counting scheme. They can exhibit zero inflation, overdispersion and multimodality. Overdispersion can be approximately modelled using the multinomial with parameters distributed Dirichlet or normal in the simplex although this strategy involves some computational problems (30,31), but this is not the case with zero inflation and multimodality.

THE COMPOSITIONAL CHALLENGE

Up to now, the fact that count data contain compositional information did not appear in the discussion above. The only reference to this matter was that the vector of multinomial probabilities, one of the targets of any analysis, is compositional. However, compositional data analysis (CoDA) offers important tools, both for exploratory analysis of relative frequencies and for the study of random compositions. The incorporation of these tools into the omics world and the analysis of sequencing data are a challenge that the researchers in the field are starting to face.

When starting a statistical analysis of compositional data, probability distributions are necessary. Before introducing CoDA, the Dirichlet distribution was almost the only available one for compositional data, albeit based on the Euclidean geometry induced in the simplex from real space, that is, considering the mean and covariance of probabilities as if they were real random quantities. In the 1980s, Aitchison (4,29) showed the limitations of the Dirichlet distribution and proposed the logistic normal distribution as a solid candidate to be the reference in CoDA. The recognition of the particular algebraic–geometric structure of the sample space of CoDA, and the reformulation of CoDA in terms of orthogonal coordinates ilr (18,28,32), provides a more consistent use and parametrization of the logistic normal distribution, now called normal on the simplex (18,28).

In the decade 2000–2010, it became clear that relative abundances from a -multinomial sampling should be asymptotically logistic normal, with being the centre (compositional mean) of such distribution. This made the hypothesis of logistic normality a natural one. However, there was no description of the covariance structure of this asymptotic distribution.

After CoDaWork 2015 (33), it was shown that the asymptotic distribution of -multinomial observations converges in law to a normal distribution on the simplex with a particular covariance matrix when the number of counts is large enough. For D features and the multinomial distribution in Equation (1), the random composition can be represented in ilr coordinates using a (D, D − 1)-contrast matrix 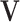that represents a given orthonormal basis of the D-part simplex. 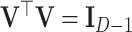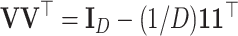The contrast matrix satisfies and , where denotes the identity matrix of size k, 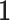is a D-vector of ones and (·)^⊤ denotes transposition. The ilr coordinates are [see details in (18)]. For a large N, the asymptotic distribution of the converges in law to a multivariate normal distribution with mean and covariance

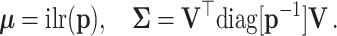Asymptotic conditions are attained for a large number of trials, but this number depends on the 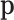to be estimated. Appendix C reproduces the derivation of this asymptotic distribution.

However, this normal on the simplex distribution inherits the shortcomings of the multinomial distribution, namely the fact that its covariance structure is completely determined by the multinomial parameters, thus lacking flexibility. However, at the same time, this is an example of a normal distribution on the simplex with a reduced number of parameters.

A STRATEGY FOR MULTIVARIATE MODELLING OF COUNTS

Many experimental procedures in molecular biology use polymerase chain reaction (PCR) to replicate DNA segments (34,35). In each PCR cycle, specific sequences are ideally duplicated. These procedures of high-throughput sequencing start collecting sequences. In order to classify the produced segments and measure their abundance in a sample, an amplification of the sample is required. After a large number of PCR cycles, one can assume that each sequence, or class of them known as operational taxonomic unit (OTU), grows approximately exponentially at the same rate. In this ideal PCR process, the relative frequencies of OTUs are preserved as long as the replication rates are approximately equal. In fact, assuming that the abundances of the OTUs in the initial sampling were and that along the PCR amplification the abundances evolve exponentially with rates 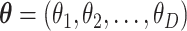in time, the abundance after a time t would be

If the initial relative abundance is , M = ∑_im_i, the relative abundance at time t is

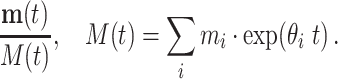If all θ_i are equal, the relative frequencies 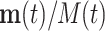are constant along the replication process. In case that the θ_i values are not equal, a compositional perturbation of the initial (unobserved) relative abundances is produced; that is, the relative frequency is multiplied by the term exp(θ_it), thus modifying the final (observed) frequencies into 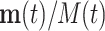. Fortunately, compositional perturbation modifies the compositional mean with the same perturbation, but the theoretical compositional variability remains unaltered. When the equality of the θ_i values can be approximately assumed, the PCR procedure is acceptable for quantifying relative abundances in the initial sample. Unfortunately, this is true for observed abundances, but unobserved OTUs in the first sampling remain unobserved after PCR. This process resembles the genetic drift or bottleneck, which is able to modify relative frequencies and completely suppress some alleles (36).

The multinomial bottleneck

Although simplistic, the distribution of counts corresponding to a multinomial sampling—followed by a homogeneous exponential amplification and, finally, by a new multinomial sampling—is relevant to show that some characteristics of microbial samples of OTUs are reproduced by the multinomial–multinomial distribution (MMD) of counts.

Consider a multinomial probability density (pd) of counts in D classes, , with probability parameters , ∑_ip_i = 1, and total number of counts M = ∑_im_i. The multinomial pd is

(3)

This pd may be identified with the sampling of taxa from a microbiome population before replication or amplification. In this sampling, D and M can be similar in order of magnitude. This sampling will likely produce a large number of zero counts in many features, many of them corresponding to features with relatively small p_i, but also some of the zero counts can correspond to not so small probabilities.

Assuming homogeneous amplification after replication, the relative frequencies of the observed features are approximately maintained. Then, the amplified population is multinomially resampled. Let the probabilities of this resampling be 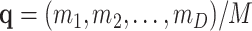; then, the pd is

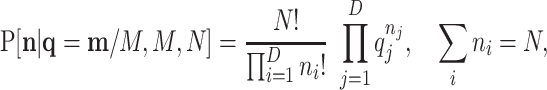(4)

where N is the number of multinomial trials. Note that the original D features have been reduced due to the fact that some m_i turned out to be zero in the first sampling. The effective number of factors in the products of Equation (4) is equal to the number of non-null counts in 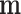that can be substantially less than D.

As 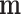is not observed, it can be marginalized from the joint pd of 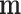and in the standard way, shown in Appendix B. The value of M is also unobservable and could also be marginalized following the technique described in Appendix A. It can also be left as a parameter in the pd of the observations 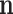. After marginalization of , the MMD (pd) of the observations is

(5)

where 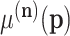are the ordinary moments of a multinomial with probabilities 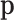. The orders of the moments are in 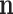. Figure 1 is a scheme of the MMD generation.

Figure 1.

Scheme of MMD double sampling and multinomial bottleneck. From top to bottom: 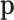contains the true relative frequencies in the sample and is the estimation target. Features are sampled with a multinomial distribution 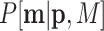. Counts in 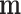are not observed. A replication process is applied, e.g. PCR, thus producing an exponential growth of features whose m_i ≠ 0. A new multinomial sampling is carried out with probabilities 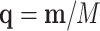, only if equal rates of replication are assumed. Features that were not previously sampled, m_i = 0, are not resampled in this second multinomial sampling. The counts obtained in this second sampling are observed and constitute the data. The procedure ends estimating using some estimator .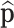

The simulation of the MMD in (5) is easily carried out (see Appendix D). However, this pd is in its present stage not practical because the computation of the multinomial ordinary moments is very time consuming. This could change if more efficient algorithms are developed. Additionally, the pd is based on two strictly multinomial samplings and homogeneous amplification, which are not credible in experimental conditions of sequencing and PCR.

The microbiome samples, for instance, at the level of genus, have some relevant characteristics: (i) many features (genera) are seldom observed across the sample; (ii) a given feature, in samples with a moderate to large number of trials, may present a large number of zeros and simultaneously large counts can appear across samples; and (iii) a histogram of counts for a given feature can present several modes, one at the zero, and others at different numbers of counts. These characteristics are reproduced in an MMD simulation, thus suggesting that something similar occurs in practice. Figure B1 in Appendix B shows some of these characteristics.

This multinomial bottleneck puts a doubt on the characteristics of the zero counts observed in sequencing data after a PCR or amplification. The zeros produced in the second multinomial sampling are likely produced in features whose multinomial probability is relatively small. However, the second sampling reproduces the zeros from the first sampling, which can correspond to relatively medium, or even large, probabilities. The arising question is now whether the observed zero counts should be considered missing values better than zero due to small abundances. These considerations suggest that substitution of zero counts could be severely flawed in the scenario of PCR or amplified counts. It seems that conceiving the zero problem as an estimation of the probabilities better than a mere substitution can be a suitable strategy. Distributions like MMD (Equation 4) allows such estimation without any substitution.

As mentioned previously, the MMD (Equation 4) might not be useful in practice. A way of simplifying MMD is to assume that the second multinomial sampling after amplification is carried out in asymptotic conditions. This leads to substitute the second multinomial distribution by the asymptotic distribution of the multinomial distribution presented in the fourth section and Appendix C. This new distribution is named multinomial–asymptotic normal distribution (MAND). As in the case of MMD, MAND is easily simulated (see Appendix D). Both distributions reasonably reproduce the zero pattern in microbiome samples. However, an efficient procedure of computing the likelihood of both distributions is still needed, thus avoiding substitution of zeros and allowing the estimation of parameters by maximum likelihood or by Bayesian procedures.

CONCLUSION

There are many open questions and ways to explore in relation to count data. Only a few thoughts have been presented here, which are by no means exhaustive of those present in the literature. However, it seems that there is no complete and generally accepted theoretical framework available in which to embed new developments. Particularly interesting is the conception of amplification techniques (e.g. PCR) as a double sampling, which may explain the zero patterns frequently observed in sequencing data. The double sampling, here modelled with the MMD and MAND, may question the conception of zeros as due to a low frequency of the corresponding feature. This is an open field of research that is calling for new ideas and procedures.

APPENDIX A: MULTINOMIAL WITH A RANDOM NUMBER OF TRIALS

The multinomial distribution depends on the number of trials considered. Frequently, the number of trials (sometimes called library size, particularly in microbiome analysis) changes from sample to sample. This circumstance has motivated rarefaction techniques (37,38), which try to homogenize the number of trials along samples. In order to avoid this wasting of information in rarefaction, the multinomial distribution seems to be useful when the number of trials is random, or it is, at least, illustrative. This appendix presents this family of distributions of counts.

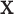Let be a random vector of multinomial counts, given the probabilities of D categories (features) , with ∑_ip_i = 1, and the number of trials N. The probability function of is

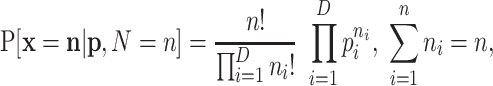(A1)

where 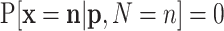whenever .

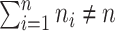Consider the number of trials N is a random variable with probability function f(n|θ), n = 0, 1, 2, …, or for a subset of these integers denoted by 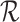; θ denotes one or more parameters for the probability function f. Obvious examples for f are Poisson, negative binomial (including the geometric distribution) or even a shifted binomial. The goal is to find 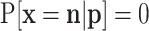without the condition on N. The standard procedure is first to consider the joint probability function of and N, and then to marginalize, i.e. remove N from the expression. The joint probability is

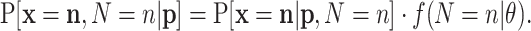(A2)

Marginalization is carried out by summing Equation (A2) over the support of N. The terms in Equation (A2) are null except in the case that n = ∑_ix_i. Then, the sum is restricted to the only value such that n = ∑_in_i. As a consequence, the desired probability function is

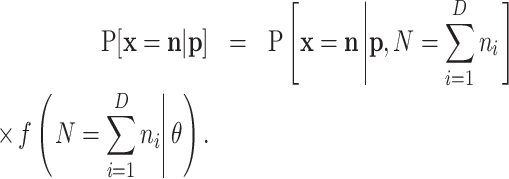(A3)

This probability function is easily computable, as the two factors can be computed from standard numerical functions.

Figure A1 shows the effect of considering the number of trials in a binomial (multinomial of two categories) as random and Poisson distributed (green crosses) with mean equal to 50. The blue (red) curves correspond to a probability of the binomial equal to 0.1 (0.4). The circled points are the probabilities when the number of binomial trials is 50 and the plus sign points are probabilities with the random number of trials. It is clear that the randomized number of trials flattens the probability functions, i.e. increases variability, but in a moderate way. The overdispersion observed in sequencing data cannot be explained with the variability of the number of trials in the sample.

Figure A1.

Probability functions. Green (crossed): Poisson probabilities, mean equal to 50, for the number of binomial trials. Circled: binomial probabilities with p = 0.1 in blue and with p = 0.4 in red. Plus signs: mixture of binomials with number of trials distributed Poisson, mean equal to 50; binomials with p = 0.1 in blue and with p = 0.4 in red.

Note that, in order to obtain the pd in Figure A1, the pd in Equation (A3) needs to be marginalized again to obtain the distribution of a single category. This consists of an integration over a discrete simplex. In the case of a binomial, it is a sum on the complementary category.

APPENDIX B: A GENERAL MIXTURE OF DISCRETE PROBABILITY DISTRIBUTIONS OF COUNTS

Consider a probability function (pd) of counts, , in D classes with probability parameters , and total number of counts M = ∑_im_i. A multinomial random sampling corresponds to this type of pd written as 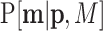. If this probability function is a multinomial, it is

(B1)

This pd may be identified with the sampling of taxa from a microbiome population before replication or amplification and where D and M are similar in order of magnitude. After replication, taxa are resampled with probability 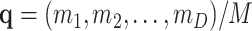following a pd 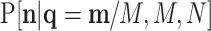, where N is the total number of counts in this second sampling. In the case in which this second sampling is also multinomial, it is

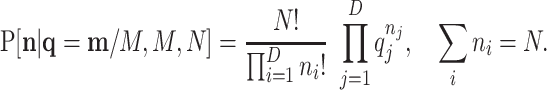(B2)

As 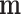is not observed, it can be marginalized from the joint pd of 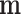and 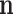in the standard way:

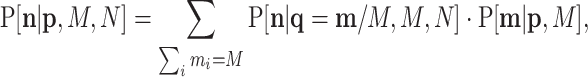(B3)

which in the case of a multinomial is

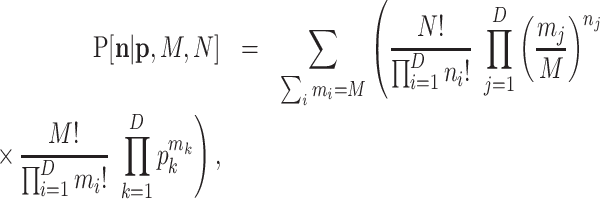(B4)

where ∑_in_i = N. The 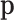is the parameter of interest as it represents the true relative abundances; N is an observed parameter and M can be taken as another parameter that indirectly controls the proportion of zeros in the observed sample. Remarkably, if M is not very large compared to D, the expected number of zero counts may be large, and the corresponding taxa can or cannot appear in the second sampling. When the value of M is not of interest, it can also be marginalized as in Appendix A.

Equation (B4) can be rearranged for a better visualization as

The term within the sum is the -ordinary moment of a multinomial with parameter 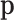. The moment generating function of 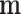is

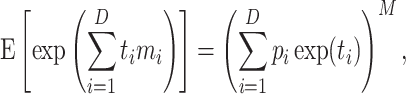from which the -ordinary moment can be computed. However, the easy analytical expression corresponds to the factorial moments, and ordinary moments are complicated combinations of those (6,39). The multinomial–multinomial pd can be written in a compact form denoting the 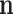-ordinary moments of as ,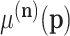

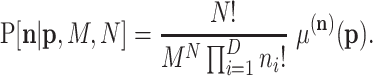(B5)

This explicit expression of MMD contrasts other mixtures of multinomials in which the marginalization requires a tedious computing. However, obtaining the values of also involves difficulties.

Difficulties for the formal calculus of MMD are compensated by the easy simulation of samples. An illustration has been computed for 300 features whose probabilities are a 300-term sequence from 100 to 1 over 300, thus spanning two orders of magnitude probabilities. In the first multinomial sampling, M = 250 trials were drawn so that, at least, 50 features counted m_i = 0. Then, the second multinomial sampling (sample size 50) with probabilities q_i = m_i/M was carried out, thus obtaining a zero-inflated and dispersed sample of counts. Figure B1 shows histograms of the 50 samples for four features whose probabilities were 0.0066 (red), 0.0044 (orange), 0.0023 (green) and 0.0002 (blue), respectively. The first characteristic is that the zero count is the most frequent count in the four histograms. The second feature of the histograms is that they are multimodal and highly dispersed. This figure shows that MMD is able to reproduce the features observed in sequencing data after PCR like overdispersion and zero inflation, but also reveals multimodality. This should be the case when the replication process is uniform for all features present in the first sampling.

Figure B1.

Histograms of four features simulated from an MMD. Red, orange, green and blue histograms correspond to true relative frequencies (probabilities) of 0.0066, 0.0044, 0.0023 and 0.0002, whose expected number of counts is marked by vertical lines. The width of bins is 1 count.

APPENDIX C: THE ASYMPTOTIC DISTRIBUTION OF ILR COORDINATES

We briefly rederive an earlier theoretical result concerning the asymptotic distribution of the ilr coordinates under a multinomial sampling. This was first obtained for D = 3 (40) and later extended for general D (33). Consider a multinomial sampling scenario in which n multinomial observations are given, and the observed relative frequencies are in . As is the maximum likelihood estimator of the multinomial probabilities 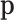, in asymptotic conditions, the distribution of 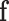approaches (weak convergence in distribution or law) the multivariate normal distribution

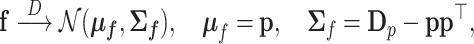with . The present goal is to look for the asymptotic distribution of the ilr coordinates of 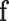, denoted by 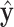, associated with a given contrast matrix 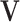. For a regular transformation of parameters , according to the multivariate delta method (41,42), the asymptotic centred distribution of the maximum likelihood estimator is

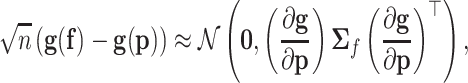(C1)

where 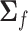is the covariance matrix of 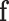. When applied to the maximum likelihood estimator of the multinomial probabilities 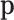, transformed into 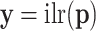, the transformation is identified as 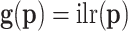. The computation of derivatives in Equation (C1) can be carried out as

The covariance matrix 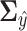becomes

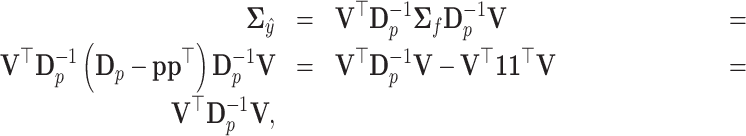since 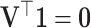. Note that the covariance matrix 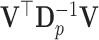is, in general, not diagonal and, therefore, the ilr coordinates of 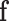will be correlated. These correlations have a structure that only depends on and the chosen contrast matrix . The matrix 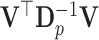is diagonal only for equal multinomial probabilities, which correspond to 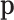equal to the neutral element of the simplex. Substituting the values of derivatives and the covariance matrix in Equation (C1), the asymptotic distribution of satisfies

where 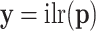; the D over the limit arrow denotes convergence in distribution or in law. This statement can be alternatively written as

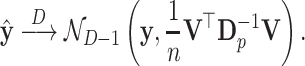(C2)

In many situations, n = 1, as the likelihood of , given a N trial multinomial independent sample of size n, is proportional to the likelihood of given a single multinomial observation with nN trials.

APPENDIX D: SIMULATION OF MMD AND MAND SAMPLES

The MMD is easily simulated once some parameters are given. These parameters are as follows (notation in ‘The multinomial bottleneck’ section): D, the number of features to be considered; M, the number of trials in the first multinomial sampling; , the true probabilities of counting each feature in the first sampling; and N, the number of multinomial trials in the second sampling. Similarly, the MAND can also be simulated.

An interesting point is how to roughly estimate the mentioned parameters to proceed to a simulation of MMD and MAND mimicking a given sequencing sample.

We selected a sample of oral microbiota (16S rRNA) classified into 229 bacterial genera from the HMQCP v35 dataset downloaded on 22 October 2015 from http://hmpdacc.org/HMQCP/ (43). This dataset was also used in (26). Only 180 observations on the buccal mucosa from different human individuals have been used for this example.

In the reference sample, the number of bacterial genera (features) reported is 229, but only 103 contain >4 non-null counts. The removed genera may be practically nonexistent or they were not counted in the first multinomial sampling. Thus, we can reasonably assume that the number of genera that play a role in the first multinomial sampling is D = 103. A bizarre assumption is that the number of multinomial trials is the same for each individual or case. According to that, the number of trials in the first sampling is, at least, the number of genera that were counted once or more times; this lower bound is 52 in the reference sample. The maximum number of counted genera across the sample is an underestimation of M (number of trials in the first multinomial sampling). In our case, we take M = 100. If we assume that the replication rates in the PCR process are equal for all the genera, then the probabilities 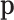are approximately proportional to the observed counts in the reference sample. Finally, the average total number of counts per individual or case may be an estimation of N. This was N = 5693 and the corresponding variance exceeded largely the mean (∼14 × 10⁶), thus making the Poisson approximation of N unrealistic. We preferred to assume that N has a triangular distribution whose mode, minimum and maximum are 5500, 800 and 20000, respectively, inspired on the reference oral microbiome sample whose characteristics were 5693, 748 and 28549 for mean, minimum and maximum, respectively. To obtain some reasonable values for 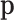, a monotonic sequence of 103 probability values was taken from 1 to 1000 divided by their sum.

The following R function rMMD produces a simulation of sample counts with the corresponding zero pattern. The R function rMAN allows the simulation of sequencing data following the distribution MAND. However, this simulation does not give counts but relative frequencies with the corresponding zero pattern. Except for this difference of output format, the zero pattern produced by the two functions is very similar for large N in rMMD, like those suggested above. The reader can check these facts using calls to the functions rMMD and rMAN which can be downloaded from https://github.com/EgozcueJuanjo/SimulationMMD. An example of use of the functions and their output are also downloadable.

FUNDING

Ministry of Science, Innovation and Universities and European Regional Development Fund [RTI2018-095518-B-C21 (C22) (MCIU/AEI/FEDER)].

Conflict of interest statement. None declared.