Abstract
This study aimed to explore the currently competing and new semimechanistic clearance models for monoclonal antibodies and the impact of clearance model misspecification on exposure metrics under different study designs exemplified for cetuximab. Six clearance models were investigated under four different study designs (sampling density and single/multiple‐dose levels) using a rich data set from two cetuximab clinical trials (226 patients with metastatic colorectal cancer) and using the nonlinear mixed‐effects modeling approach. A two‐compartment model with parallel Michaelis–Menten and time‐decreasing linear clearance adequately described the data, the latter being related to post‐treatment response. With respect to bias in exposure metrics, the simplified time‐varying linear clearance (CL) model was the best alternative. Time‐variance of the linear CL component should be considered for biotherapeutics if response impacts pharmacokinetics. Rich sampling at steady‐state was crucial for unbiased estimation of Michaelis–Menten elimination in case of the reference (parallel Michaelis–Menten and time‐varying linear CL) model.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
☑ Characterization of complex clinical pharmacokinetics (PK) of monoclonal antibodies (mAbs) is hindered by limited availability of informative PK data over a wide dose range.
WHAT QUESTION DID THIS STUDY ADDRESS?
☑ This study explored semi‐mechanistic clearance (CL) models for mAbs and implications of study design differences on identifiability of the CL models.
WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?
☑ This analysis provides a population PK model incorporating both time‐varying CL, related to treatment response, and target‐mediated drug disposition (TMDD) component, and stresses the importance of informing the population models with rich data.
HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?
☑ Time‐variance of CL in addition to TMDD should be considered for biotherapeutics if response impacts PK. Informing PK analyses with rich data (i.e., through pooling data from multiple clinical trials at later stages of drug development) is crucial for reliable metrics derivation for exposure‐response relationships.
The emergence of new biologic therapies has led to dramatic improvement in the survival of patients with cancer. 1 However, a fully mechanistic understanding of the behavior of monoclonal antibodies (mAbs) is still lacking, as their distribution and elimination are subject to complex pharmacokinetics (PKs) that may change over time 2 due to their protein nature with high affinity to their pharmacological target. Therefore, a quantitative description of their PK profile, especially clearance (CL), is a challenging task. The elimination of mAbs is expected to comprise target‐mediated drug disposition (TMDD; saturated at higher exposure and nonlinear/linear at lower concentrations) and nonspecific CL, which may be linear, nonlinear, and/or time‐dependent, so both linear and nonlinear clearance are physiologically possible. However, quantification of each of these components in a model is highly dependent on the data (i.e., the sampling scheme and dose range investigated), potentially leading to identification of different models for the same drug.
The mAbs targeting the epidermal growth factor receptor (EGFR) are among the most successful targeted therapies for patients with rat sarcoma proto‐oncogene (RAS) wild‐type metastatic colorectal cancer (mCRC), one of the most common causes of cancer death worldwide. 3 Availability of rich PK data sets for cetuximab (Erbitux; Merck KGaA, Darmstadt, Germany) approved in mCRC offered us the opportunity to reconciliate the different published population PK models for this mAb, which differ in the elimination model of the compound. The first published model considered only Michaelis–Menten elimination 4 ; then, Azzopardi et al. proposed a parallel linear and zero‐order elimination, 5 and others found a simple linear elimination. 6
To explore different semimechanistic CL models for mAbs and investigate implications of study design differences on identifiability of the CL models, we conducted a population PK analysis on a pooled data set, using cetuximab as a case study. The objectives of this study were to: (1) refine the population PK models of cetuximab in patients with mCRC taking into account the TMDD of the biologic therapy; while also (2) comparing mechanistically plausible CL implementations (including linear, nonlinear, and time‐varying CL) and test how response may or may not interfere with PK; and (3) investigate implications of study designs typical for various phases of drug development on the model performance and parameter identifiability.
METHODS
Clinical trial design and population
The data for this analysis originate from two multicenter clinical trials in patients with advanced mCRC (a phase I (PhI) trial 7 and EVEREST 8 ). The PhI trial was a phase I, open‐label, multicenter trial designed to evaluate the PK and pharmacodynamics (PD) of cetuximab. The EVEREST trial was a phase I/II, open‐label, randomized, controlled, multicenter trial aiming to evaluate PK and PD of cetuximab dose escalation as well as pharmacogenomic and pharmacogenetic aspects. Full study descriptions are reported elsewhere. 7 , 8
Treatment administration
In the PhI trial, patients received intravenous cetuximab monotherapy for the first 6 weeks, followed by cetuximab‐FOLFIRI (folinic acid, 5‐fluorouracil, and irinotecan) co‐therapy (Figure 1a ). The patients were assigned to the following treatment groups:
Initial 400 mg/m2 cetuximab infusion, followed by weekly dose of 250 mg/m2 (approved dosing regimen (ADR)) (arm A);
Cetuximab dose of 400 mg/m2 every 2 weeks (q2w),
Cetuximab dose of 500 mg/m2 q2w,
Cetuximab dose of 600 mg/m2 q2w, and
Cetuximab dose of 700 mg/m2 q2w (arm B)
Figure 1.
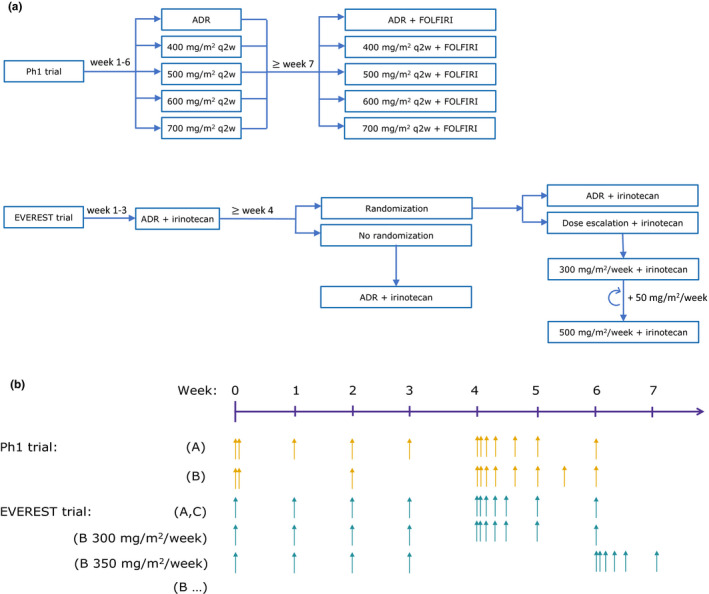
Overview of the analyzed clinical trials: a phase I (PhI) trial 7 and EVEREST trial. 8 (a) Dosing algorithm; (b) pharmacokinetic sampling schedule. The PhI trial comprised two arms. In arm A, the patients received the approved dosing regimen (ADR). In arm B, after the initial 2‐hour infusion of 400 mg/m2, the patients received 2‐hour 400 mg/m2, 2.5‐hour 500 mg/m2, 3‐hour 600 mg/m2, or 3.5‐hour 700 mg/m2 infusions q2w. In the EVEREST trial, all patients initially received cetuximab ADR in combination with irinotecan; after 3 weeks of treatment the patients eligible for randomization either continued receiving ADR (group A) or underwent dose escalation (group B), whereas the patients not eligible for randomization continued the treatment with ADR (group C). In group B, with each dose increase of 50 mg/m2 the dense sampling interval was shifted, denoted as “(B…)” for EVEREST in the figure. For all arms/groups the sampling continued until the patients dropped out of the study or until the study end. ADR, approved dosing regimen for cetuximab (2‐hour 400 mg/m2, 1‐hour 250 mg/m2 once weekly); FOLFIRI, co‐medication with irinotecan (30–90 minutes of 180 mg/m2) + 5‐fluorouracil (180 mg/m2 bolus and 2400 mg/m2 as infusion over 46 hours) + folic acid (2‐hour 400 mg/m2); q2w, every 2 weeks.
Starting from week 7, in addition to cetuximab, all patients started FOLFIRI treatment, which comprises irinotecan (180 mg/m2), 5‐fluorouracil (180 mg/m2 bolus and 46‐hour 2400 mg/m2 infusion), and folic acid (2‐hour 400 mg/m2 infusion). The treatment was continued until disease progression or an unacceptable adverse event.
In the EVEREST trial (Figure 1a ), all patients received cetuximab ADR‐irinotecan co‐therapy for the first 3 weeks. On the fourth week, patients who had not required irinotecan discontinuation and had not experienced skin reaction of grade > 1 or any other cetuximab‐related toxicity of grade > 2 were randomized to continue the ADR (group A) or undergo cetuximab dose escalation (group B). The dose escalation comprised increasing the cetuximab dose by 50 mg/m2/week up to the maximum dose of 500 mg/m2/week. Patients not eligible for randomization continued the cetuximab ADR‐irinotecan treatment (group C). The treatment was continued until disease progression or an unacceptable adverse event.
PK assay and sampling
For the PK analysis, the serum cetuximab concentration was measured by an enzyme‐linked immunosorbent assay. 7 Figure 1b illustrates the sampling schedules in the two studies.
In the PhI trial, PK samples were taken before and at the end of the first cetuximab infusion, as well as at minimum cetuximab concentrations (C min) until day 29. For the dosing interval starting on day 29, dense sampling (Figure 1b ) was performed as follows: patients receiving ADR (arm A) were sampled at the end of infusion and at 4, 24, 48, 96, and 168 hours after the start of infusion, whereas patients in other treatment groups (arm B) were sampled at the end of infusion and at 4, 24, 48, 96, 168, 240, and 336 hours after the start of infusion. After the dense sampling interval, blood samples were collected at C min until the end of the study in both arms.
In the EVEREST trial, PK samples were taken before the first dose and at C min until week 29. In patients on ADR (groups A and C), dense sampling (at the end of infusion and 6, 24, 48, 72, and 168 hours after the start of infusion) was performed over the dosing interval starting on day 29. The patients undergoing dose escalation (group B) were sampled in such a way that five patients from each dose level were intensively sampled for one dosing interval, starting on the second dose of the dose level. After the dense sampling interval, C min samples were collected from all patients until the end of the study.
Population PK analysis
A population PK model was developed using the nonlinear mixed‐effects modeling approach. The data were analyzed using the Stochastic Approximation Expectation Maximization estimation method in NONMEM (version 7.3.0), PsN (version 4.4.8), and Pirana (version 2.9.2), whereas R (version 3.3.2) and RStudio (version 1.1.456) were used for preprocessing and postprocessing of data. The “log‐transform both sides” approach was used.
Confirmed by graphical analysis, we used the previously published two‐compartment model. 4 , 5 We investigated six elimination models from the central compartment: linear clearance (LCL), 6 linear clearance with exponential change over time (TVARCL), 9 , 10 Michaelis–Menten clearance (MMCL), 4 linear clearance and Michaelis‐Menten (MMCL + LCL), linear clearance with exponential change over time and Michaelis–Menten (MMCL + TVARCL), and linear clearance and zero‐order (LCL + 0.EL) 5 clearance (Figure 2a ). The differential equations for the change of drug amount in the central compartment (parameters part of elimination process marked in bold) were as follows:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where A 1 denotes drug amount in central compartment; A 2, drug amount in peripheral compartment; C 1, the concentration in central compartment; Q, intercompartmental exchange rate; CL, linear clearance from central compartment; I max, maximum change in time‐varying linear clearance; η Imax, between‐patient variability in I max; t 50, time at which clearance is halved; γ, curve shape factor; V max, maximal rate of saturable elimination; K m, concentration at half V max; and k 0, zero‐order rate constant of elimination from central compartment.
Figure 2.
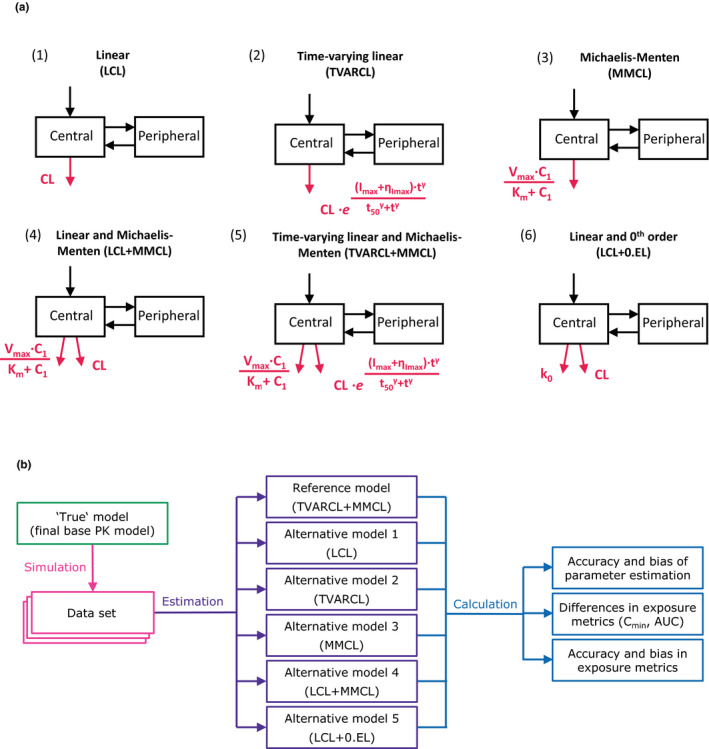
Overview of the analysis workflow. (a) Graphical representation of the investigated base pharmacokinetic (PK) models for cetuximab. (b) Flowchart illustrating the stochastic simulation and estimation (SSE) analysis per study design scenario. The final PK base (reference, “true”) model was used to simulate 200 data sets in the stochastic simulation step. The reference and five alternative models were subsequently fit to the simulated datasets. Thus, altogether 6 × 200 = 1,200 model fits were performed. For each model accuracy and bias of parameter estimates, exposure metrics (AUC and C min after the second dose and in steady state), and their bias and accuracy were calculated and compared. The process was repeated for four study designs in total differing in sampling density and number of dose levels. C1 denotes drug concentration in central compartment; C 2, drug concentration in peripheral compartment; CL, linear clearance from central compartment; I max, maximum change in time‐varying linear clearance; K m, concentration at half V max; k 0, zero‐order rate constant of elimination from central compartment; ηI max, between‐patient variability in I max; Q, intercompartmental exchange rate; t 50, time at which clearance is halved; V max, maximal rate of saturable elimination; γ, curve shape factor. Parts of the model related to clearance are shown in red.
The distribution of individual parameter values was assumed to follow a log‐normal distribution. For covariate model development, a full fixed‐effects modeling approach was used, as proposed by Gastonguay, 11 whereby preselected covariates were simultaneously included in the final base model. The criteria for inclusion/exclusion of a covariate comprised statistical relevance (null value not covered by confidence interval) and clinical relevance (difference in baseline linear CL greater than ± 25% relative to typical CL value), impact on between‐subject variability reduction, and extent of covariate effect on model parameters. Model discrimination was based on plausibility and precision of parameter estimates, the Akaike information criterion (AIC), 12 goodness‐of‐fit plots, and visual predictive checks.
Study design investigations
In the second part of this analysis, implications of study designs, on the model performance and parameter identifiability were assessed. Using the final base PK model (MMCL + TVARCL) as a reference model, 200 data sets were simulated, each comprising 100 patients, making a total of 20,000 virtual patients. The six investigated models were fit to the simulated data sets under four study‐design scenarios, using the stochastic simulation and estimation (SSE) PsN feature, 13 amounting to a total of 4,800 model fits (Figure 2b ).
The body surface area (BSA) of the virtual population of 100 patients was sampled to correspond to the distribution of the clinical database (Table 1 ) and assumed to be constant over time. In all study designs, all virtual patients received the same initial cetuximab induction dose of 400 mg/m2 with infusion rate of 5 mg/min. The infusion rate for subsequent doses was 10 mg/min. The 100 virtual patients were relegated to four study designs (A–D), which differed in sampling density (dense vs. sparse) and dose levels (single vs. multiple‐dose levels) and were chosen to correspond to typical trial designs in the initial phases of drug development (A and B) and later (e.g., phase III trials (C and D)). The investigated study designs were as follows:
Study design A, the virtual patients were stratified in order to ensure that all dose levels were present across the whole range of BSA. The patients were first stratified in four groups corresponding to the BSA quartiles in order to avoid having only low or only high doses in one BSA quartile. To achieve further randomization of the dose distribution, within each group the patients were further randomly stratified to receive 200, 250, 300, 350, 400, 450, or 500 mg/m2 every week starting from the second dose. In addition to the C min sampling described below, additional samples were taken after the fifth dose, at the end of infusion, and 4, 24, 48, 72, and 96 hours after infusion start, corresponding to the clinical trials;
Study design B, the virtual patients were treated according to the approved dosing regimen of cetuximab (250 mg/m2 every week; i.e., single dose level). The sampling was performed in the same manner as in study design A;
Study design C, the virtual patients were treated in the same manner as in study design A, and only C min samples were taken;
Study design D, the virtual patients were treated according to the approved dosing regimen of cetuximab (single dose level) and only C min samples were taken.
Table 1.
Summary of baseline patient characteristics (n patients = 226; n pharmacokinetic samples = 3,821)
| Continuous | Median (min–max) |
|---|---|
| Age, years | 61 (26–81) |
| Duration of cetuximab therapy, months | 5.8 (0.25–27.3) |
| Weight, kg | 72 (41–132) |
| Body surface area, m2 | 1.85 (1.37–2.70) |
| Amphiregulin concentration, pg/mL | 226 (8.50–5080) |
| Epidermal growth factor concentration, pg/mL | 12.7 (0.61–633) |
| Interleukin 8 concentration, pg/mL | 42.0 (1.76–5650) |
| Transforming growth factor‐α concentration, pg/mL | 2.52 (0.404–131) |
| Vascular endothelial growth factor concentration, pg/mL | 278 (46.7–1720) |
| Creatinine clearance, mL/min | 95.5 (31.0–218) |
| Categorical | n (%) |
|---|---|
| Female | 82 (36) |
| RAS mutation present | 81 (36) |
| ECOG performance status | |
| 0 | 154 (68) |
| 1 | 69 (31) |
| 2 | 3 (1) |
| RECIST response achieved | 63 (28) |
ECOG, Eastern Cooperative Oncology Group; RAS, rat sarcoma proto‐oncogene; RECIST, Response Evaluation Criteria in Solid Tumors.
Under each study design, all virtual patients were sampled at C min after each dose for 12 weeks. At week 12, the patients were separated into 5 groups of 20 patients. Each group was sampled once a month for 3 months, until a study duration of 18 months (Figure S1 ).
To assess the performance across the models, for each investigated study design, clinically relevant exposure metrics (C min and area under the curve (AUC)) as well as their bias and accuracy were calculated (Supplementary Material), in addition to the standard set of parameters provided by the PsN output (including parameter estimates and their bias and accuracy; Figure 2b ). The PK metrics after the second dose and at steady‐state (i.e., at the approximate time when 90% of maximal CL decrease has occurred per the reference model (week 60)), were considered. The bias (i.e., mean error) was calculated according to the following equation:
where N denotes number of simulated trials repetitions (200); n, the number of patients (number of patients in a trial ∙ number of simulated trial repetitions; i.e., 200∙100 = 20,000); refi, the parameter/exposure metric values of an individual i for the reference PK (MMCL + TVARCL) model; and esti, the respective values for the alternative models (C min: individual prediction value at defined timepoints), and AUC: integral of central compartment.
RESULTS
PK model comparison
In total, 3,821 PK samples from 226 patients (PhI (N = 62) and EVEREST (N = 164)) were analyzed. The relevant patient characteristics are given in Table 1 . Based on AIC computed using Stochastic Approximation Expectation Maximization‐importance sampling algorithm, the two‐compartment model with parallel Michaelis–Menten and linear clearance that changes exponentially over time (MMCL + TVARCL) outperformed the second best model by 334 points for predicting the serum cetuximab concentration‐time profiles in the analyzed population (Table 2 ). By decreasing the value of AIC, we found TVARCL, MMCL + LCL, MMCL, and LCL models, whereas the worst model was the one assuming elimination as first‐order and zero‐order mixed processes.
Table 2.
Comparison of all investigated base models
| LCL | TVARCL | MMCL | MMCL + LCL | MMCL + TVARCL | LCL + 0.EL | |
|---|---|---|---|---|---|---|
| LCL, L/h (RSE%) | 0.0222 (3) | 0.0262 (3) | ‐ | 0.0153 (4) | 0.0174 (5) | 0.0206 (‐) |
| V 1, L (RSE%) | 3.84 (3) | 3.67 (3) | 3.75 (3) | 3.71 (2) | 3.65 (3) | 3.82 (‐) |
| Q, L/h (RSE%) | 0.0188 (17) | 0.0282 (12) | 0.0332 (19) | 0.0323 (4) | 0.0368 (5) | 0.0216 (‐) |
| V 2, L (RSE%) | 3.38 (12) | 1.65 (11) | 2.67 (8) | 3.25 (6) | 2.65 (4) | 3.31 (‐) |
| K M, mg/L (RSE%) | ‐ | ‐ | 283 (26) | 9.81 (5) | 13.3 (21) | ‐ |
| V max, mg/h (RSE%) | ‐ | ‐ | 9.48 (17) | 0.882 (5) | 0.861 (5) | ‐ |
| I max, % (RSE%) | ‐ | –19.6 (16) | ‐ | ‐ | –23.1 (20) | ‐ |
| T 50, weeks (RSE%) | ‐ | 7.26 (15) | ‐ | ‐ | 20.5 (29) | ‐ |
| γ (RSE%) | ‐ | 2.54 (24) | ‐ | ‐ | 1 FIX | ‐ |
| K0, mg/h (RSE%) | ‐ | ‐ | ‐ | ‐ | ‐ | 0.0472 (‐) |
|
η LCL, CV% (RSE%) [Shr%] |
38.3 (6) [6] |
36.6 (6) [6] |
‐ |
37.9 (8) [19] |
36.1 (23) [23] |
39.4 (‐) [8] |
|
η V1, CV% (RSE%) [Shr%] |
26.8 (11) [31] |
27.3 (10) [31] |
26.4 (15) [32] |
25.9 (11) [32] |
26.2 (10) [32] |
27.4 (‐) [32] |
|
η V2, CV% (RSE%) [Shr%] |
103.9 (13) [27] |
84.1 (9) [39] |
83.4 (17) [29] |
61.2 (9) [27] |
61.3 (14) [32] |
104.4 (‐) [29] |
|
η Vmax, CV% (RSE%) [Shr%] |
‐ | ‐ |
30.5 (9) [6] |
43.6 (10) [34] |
48.8 (12) [12] |
‐ |
|
η Tmax, CV% (RSE%) [Shr%] |
‐ |
25.2 (11) [29] |
‐ | ‐ |
51.5 (18) [35] |
‐ |
|
η K0, CV% (RSE%) [Shr%] |
‐ | ‐ | ‐ | ‐ | ‐ |
150.3 (‐) [57] |
| Additive RUV, mg/L (RSE%) | 9.44 (11) | 7.79 (12) | 8.14 (13) | 5.85 (12) | 4.85 (22) | 8.65 (‐) |
| Proportional RUV, CV% (RSE%) | 23.1 (5) | 22.8 (4) | 23.4 (5) | 24.0 (4) | 23.5 (4) | 22.9 (‐) |
| AIC (SAEM‐IMP) | –6132 | –6990 | –6534 | –6947 | –7324 | –5990 |
0.EL, zero‐order elimination; AIC, Akaike information criterion; I max, maximum change in time‐varying clearance; K 0, zero‐order rate constant of elimination from central compartment; K M, Michaelis‐Menten rate constant; LCL, linear clearance; MMCL, Michaelis‐Menten clearance; η, between‐patient variability; Q, intercompartmental exchange rate; RSE, relative standard error; RUV, residual unexplained variability; Shr, shrinkage; T 50, time at which clearance is halved; TVARCL, time‐varying linear clearance; V 1, central volume of distribution; V 2, peripheral volume of distribution; V max, maximum rate of saturable elimination; γ, curve shape factor.
The model exhibiting the best performance comprised parallel Michaelis–Menten and time‐varying linear clearance (MMCL + TVARCL).
Parameter estimates for the investigated models are presented in Table 2 . All fixed‐effect parameters of the MMCL + TVARCL model showed excellent precision with relative standard error below 30%. Between‐patient variability in baseline linear CL, V1, V2, Vmax, and Imax was ≤ 61.3 coefficient of variation with satisfactory shrinkage. As indicated by goodness‐of‐fit plots (Figure S3 ), the model describes the clinical data well.
Covariate model
As body size is known to impact the PKs of mAbs, 14 baseline BSA was investigated for influence on baseline CL and volumes of distribution. The most appropriate implementation of baseline BSA was via power function with exponent fixed to 0.75 for CL and 1 for volumes of distribution. 15 The inclusion of BSA decreased objective function value for ~ 60 points, and slightly decreased between‐patient variability in baseline CL, V 1, and V 2 by 8.6%–11.8% (up to 5.4 percentage points, respectively), as well as additive residual unexplained variability (4.85–4.68 µg/mL).
Based on biological and clinical relevance, the following covariates were preselected for full fixed‐effect covariate modeling: patient‐related factors (age, sex, RAS mutation status, and creatinine clearance), therapy‐related factors (dose group and co‐medication with irinotecan or 5‐fluorouracil/folic acid), and EGFR ligand and other disease‐related measurements (serum concentration of amphiregulin, epidermal growth factor, interleukin‐8, transforming growth factor‐α, vascular endothelial growth factor, and Eastern Cooperative Oncology Group performance status). None of the investigated covariates were statistically or clinically relevant (Figure S2 ), thus the final model comprised only the effect of BSA described above.
Study design investigations
Parameter estimates of the reference model and their bias indicate that across study designs the reference model parameter estimates were the least biased (Table S2 ). However, bias of many parameters increased substantially in case of sparse sampling compared with rich sampling. The highest change is observed for Michaelis–Menten CL parameters, where changing to either single‐dose level or sparse sampling resulted in substantial increase in the parameter bias. Median objective function value across model fit repetitions was lowest for the true (MMCL + TVARCL) model, suggesting that this model, in fact, resulted in the best fit from all investigated models, under all study designs. This was further confirmed by the highest percentage of cases. The reference (TVARCL + MMCL) model was chosen as the best based on the AIC value under all study designs; only a slight variation existed among different study designs, which followed the expected pattern: 93% in the case of the most informative study design (multiple dose levels and rich sampling) and 80% for the least informative study design (one dose level and sparse sampling).
As a reference “background” bias comparison, bias in C min and AUC from the reference model was calculated using simulated datasets as reference (horizontal lines in Figure 3 and Figure 4 ); as anticipated, this bias was of very low extent. Comparing the five alternatives to the reference MMCL + TVARCL) model, bias in C min at steady‐state was consistently lower than bias for C min after the second dose for all models and across all investigated study designs (Figure 3 ). All alternative models, except for the MMCL model, resulted in a negligible bias in C min at steady‐state. With respect to bias in C min after the second dose, the TVARCL model exhibited the smallest bias.
Figure 3.
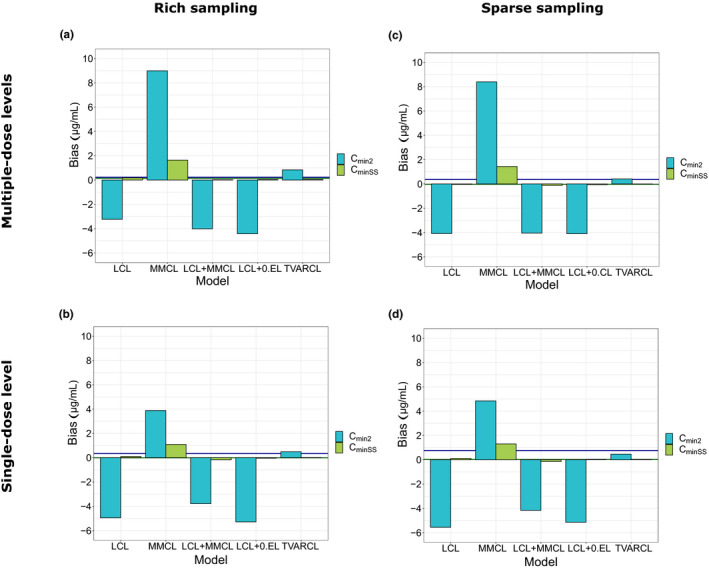
Bias in minimum concentration after the second (C min2) dose and C min in steady–state (C minSS) compared with reference MMCL + TVARCL model. (a) Study design A: multiple‐dose levels and rich sampling. (b) Study design B: single‐dose level and rich sampling. (c) Study design C: multiple‐dose levels and sparse sampling. (d) Study design D: single‐dose level and sparse sampling. Horizontal lines represent “background” bias for the reference model compared with the simulated observations. 0.EL, zero‐order clearance; LCL, linear clearance; MMCL, Michaelis‐Menten clearance; TVARCL, time‐varying linear clearance
Figure 4.
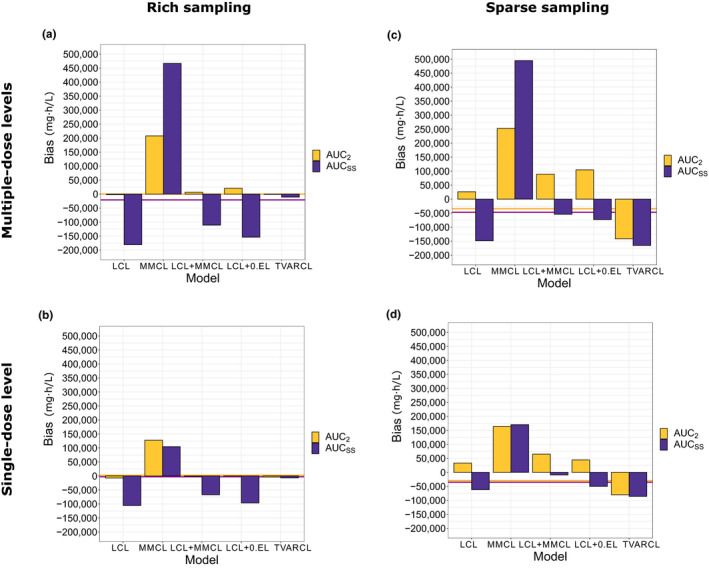
Bias in AUC after the second dose and AUC in steady‐state compared with reference MMCL + TVARCL model. (a) Study design A: multiple‐dose levels and rich sampling. (b) Study design B: single‐dose level and rich sampling. (c) Study design C: multiple‐dose levels and sparse sampling. (d) Study design D: single‐dose level and sparse sampling. Horizontal lines represent “background” bias for the reference model compared to the individual predictions from the original, reference model, used for simulations. AUC, area under the curve; AUCss, area under the curve in steady‐state; 0.EL, zero‐order clearance; LCL, linear clearance; MMCL, Michaelis‐Menten clearance; TVARCL, time‐varying linear clearance.
In study designs with rich sampling (A and B), bias in AUC after the second dose was consistently lower than bias in AUC at steady‐state for all models (Figure 4 ). The TVARCL model resulted in the lowest bias for both exposure metrics. Compared with rich sampling, sparse sampling (study designs C and D) overall resulted in higher bias, especially in AUC after the second dose. Across all study designs and for both AUC metrics, the bias was the highest for the MMCL model. Overall, the impact of study design was more pronounced for bias in AUC than C min (Figure S7 ).
Altogether, changes in study design altered accuracy of the PK metrics to a lesser extent than bias (Figure S5 and Figure S6 ). Differences in inaccuracy of C min across study designs were minimal (< 1.5 µg/mL) and can be considered negligible (Figure S5 ). Study designs with a single‐dose level (B and D) resulted in higher accuracy (lower root mean squared error) compared with multiple‐dose level designs, regardless of the sampling density.
DISCUSSION
This study revealed that cetuximab CL is best described by parallel nonlinear and linear clearance that changes exponentially over time. Rich sampling at steady‐state was crucial for unbiased estimation of Michaelis–Menten elimination in case of the true (MMCL + TVARCL) model (Table S2 ).
New consolidated PK model of cetuximab
Due to the dataset combining rich and sparse data with multiple dose levels collected over more than 2 years, we have been able to identify, to the best of our knowledge for the first time, a complex approximated TMDD model of cetuximab with time varying clearance (MMCL + TVARCL). Cetuximab clearance was best described by a combination of Michaelis–Menten and linear CL components, thus demonstrating both exposure‐dependency and time‐dependency of cetuximab PK, respectively. The nonlinear CL of a maximum rate of 0.861 mg/h was identified, with 50% of maximum value reached at a drug concentration of 13.3 mg/L. Nonlinear CL at very low cetuximab concentrations (C<<Km) was approximately four times higher than baseline linear CL (0.0647 vs. 0.0174 L/h, respectively). In parallel, the linear CL component decreased exponentially with mean maximal decrease of ~ 18% (155% coefficient of variation), reaching 50% of the maximal decrease after ~ 5 months of therapy.
Two previous analyses identified simpler population PK models for cetuximab, 4 , 5 likely due to less informative data (i.e., lower number of patients and only one dose level). Azzopardi et al. 5 investigated cetuximab PK in patients with colorectal cancer and found that clearance was best described by the LCL + 0.EL model. Dirks et al. 4 found that the Michaelis–Menten elimination was most appropriate to describe cetuximab clearance in patients with squamous cell carcinoma of the head and neck. They also investigated a potential time change in CL and found that cetuximab elimination was not time‐dependent. The disagreement of our findings with the study by Dirks et al. might be due to differences in the investigated populations. The median duration of cetuximab treatment was significantly shorter in the study by Dirks et al. (6 weeks) compared with our population (~ 23 weeks), which might have resulted in insufficient informativeness of the data with respect to potential time change in CL.
We further found that disregarding either of the two CL components (i.e., considering only the time‐varying linear CL or TMDD component) resulted in significantly inferior model performance compared with the model with both clearance components (as identified in the final PK model). For the final (MMCL + TVARCL) model, relative relevance of the different identified clearance components is illustrated in Figure S4 . The linear pathway contributed to a larger extent to the total cetuximab clearance than the nonlinear one; neglecting the change of clearance over time resulted in minor differences in the cetuximab concentration‐time profile of a typical patient. For a typical individual after the first dose under ADR, the nonlinear CL at C max (197 µg/mL) was 0.00409, and at C min (48.3 µg/mL) 0.0139 L/h. Furthermore, the change of mAb CL over time has previously been related to disease status in patients with cancer, 9 , 16 which is in accordance with our findings as explained below. Thus, the ability to identify the change of CL over time is dependent on disease status change (e.g., initial disease burden and magnitude of change) in the investigated time frame and population (i.e., if an investigated population exhibits no relevant change in disease status, no change in CL over time is expected).
Study design investigations
The capacity to identify a more or less complex model is highly sensitive to the study design. Impact of study design on how well the data informs each model parameter can be assessed by comparing bias in parameter estimates of the reference model across the study designs. 17 Our results (Table S2 ) suggest that, in study designs with single‐dose levels and/or sparse sampling, the bias in parameters of Michaelis–Menten CL increases the most. This implies that data with only one dose level are less informative for nonlinear CL, which is expected because this CL component is relevant only for the lower exposure range, and might not be captured with only single level dosing. On the other hand, our findings suggest that sparse sampling does not provide enough information to estimate all the parameters, even if multiple‐dose level data are available (Table S2 ).
Both rich and sparse sampling designs were investigated to assess bias and accuracy of parameter estimates and derived exposure metrics. The sampling density was found to be a more influential factor than number of dose levels. Our results indicate that the effect of study design depends on the PK metric considered. For instance, having sparse instead of dense sampling in the TVARCL model resulted in similar (or even slightly decreased) bias in C min, whereas the bias in AUC increased substantially. This is because the investigated sparse sampling study designs consisted of only C min samples and thus did not inform the earlier part of the PK curve (especially C max) essential for AUC calculation. Additional sampling at C max in addition to C min samples should reduce the bias in AUC. On the other hand, bias in AUC was lower for all investigated models in single‐dose level designs compared with multidose level designs, and a similar trend is observed for bias in C min.
Altogether, our findings imply that the TVARCL model is the best overall approximation to the true (MMCL + TVARCL) model. In study design A, in which the AUC calculation is well informed due to rich sampling and the role of nonlinear CL is expected due to low dose levels, the TVARCL model resulted in overprediction of C min after the second dose. This behavior is mechanistically expected, as the contribution of Michaelis–Menten CL, which is not accounted for in this model, is more important for C min than the AUC calculation, and it is expected to be more pronounced in the earlier phase of therapy (i.e., after the second dose) before the decrease of linear CL becomes significant and when the accumulation of the drug is not pronounced.
Mechanisms of clearance change
The role of nonlinear CL in disposition of mAbs has been well‐established and is mechanistically explained by the presence of TMDD. 2 , 18 , 19 On the other hand, time dependence of PK of mAbs has only recently come into focus and the understanding of its origin remains hypothetical. Time‐dependent elimination has previously been described for mAbs indicated in oncology. 9 , 10 , 16 , 20
To investigate potential reasons for the CL change, the time‐varying CL component in responders and nonresponders to cetuximab therapy was compared. The response was defined as per Response Evaluation Criteria in Solid Tumors (RECIST). 21 Patients with complete or partial response were classified as responders, whereas patients with stable or progressive disease were classified as nonresponders. The average magnitude of decrease in CL was higher in responders than in nonresponders (Figure 5 ), implying that CL change is related to post‐treatment disease status in these patients, in accordance with previously reported findings. 9 , 16 , 22 Mechanistically, the effect of disease status might comprise changes in TMDD (lower target abundance in responders) and/or cancer‐related cachexia (lower protein turnover in responders). 20 Due to inflammation, the protein turnover rate in patients with cancer is increased compared with that in healthy individuals, as indicated by measures such as decreased albumin concentration. 2 Decrease over time in disease (and thus inflammatory) status will be reflected in normalization of protein turnover rate, that would, in turn, lead to decrease in nonspecific (linear) elimination of therapeutic proteins, including cetuximab. We identified an initial decrease in cetuximab CL in both groups of patients, although it is of a lower extent in nonresponders than responders (Figure 5 ). Krippendorff et al. 23 demonstrated that upon administration of an anti‐EGFR drug, there is a steep initial decrease in receptor activation due to blockage by the drug, followed by a gradual increase as drug exposure decreases. At high drug doses, a complete and long‐lasting saturation of the target can be accomplished. Regardless of the outcome of the treatment (i.e., whether a patient is a responder or nonresponder), this initial effect is expected to be observed. In responders, further decline in CL over time is expected due to mechanisms elaborated above. However, in nonresponders, the increase in disease burden would over time prevail, resulting in a net increase in CL.
Figure 5.
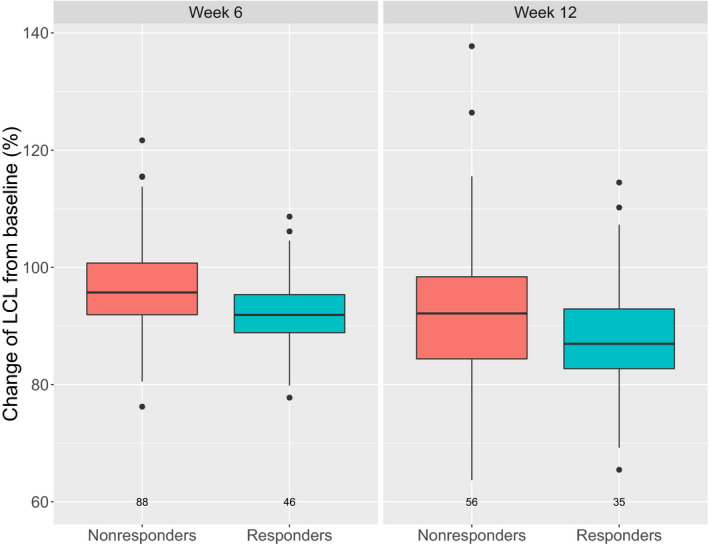
Change of linear clearance (LCL) from baseline at week 6 and week 12 of therapy, stratified by post‐treatment response.
Exposure‐response and therapeutic drug monitoring
The findings of time‐dependent change of cetuximab elimination in this study underline the bidirectional PK‐PD relationship, which is intuitively anticipated for mAbs. The bidirectional interaction between PK and PD has important implications on assumption of exposure‐response causality and thus exposure‐response analyses. In traditional exposure‐response analyses, a unidirectional exposure‐response relationship is assumed (i.e., exposure is considered the independent variable). However, in the presence of the time‐dependent changes in elimination that are related to the patient response, this assumption fails to hold true, as response impacts exposure. As a consequence, in this case, the exposure‐response relationship is overestimated compared with the true underlying relationship. 2 , 22 Thus, in the case of drugs with time‐varying elimination, assumptions underlying therapeutic drug monitoring might be shattered. In addition, identifying and accounting for baseline biomarkers for disease status (e.g., cachexia 24 ) would help to overcome these limitations.
In conclusion, a two‐compartment model with parallel Michaelis–Menten and linear CL that changes exponentially over time best characterized the PK of cetuximab. The magnitude of decrease in clearance over time is higher for responders than nonresponders, calling for better understanding of exposure‐response analyses and therapeutic drug monitoring in the presence of time‐varying clearance. Furthermore, the importance of informing the population models with rich data is stressed, supporting analysis of pooled data from multiple trials at later stages of drug development instead of using only sparse data (e.g., in the case of phase III clinical trials).
Funding
The clinical trials were funded by Merck KGaA, Darmstadt, Germany.
Conflict of Interest
A.M.G., A.K., and M.B. are employees of Merck KGaA, Darmstadt, Germany. M.B. reports shares. W.H. reports grants from an industry consortium (AbbVie Deutschland GmbH & Co. KG, Boehringer Ingelheim Pharma GmbH & Co. KG, Grünenthal GmbH, F. Hoffmann‐La Roche Ltd, Merck KGaA, and Sanofi) for the PharMetrX PhD program. P.G. is an employee of Merck Serono S.A., Lausanne, Switzerland, an affiliate of Merck KGaA, Darmstadt, Germany. C.K. reports grants from an industry consortium (AbbVie Deutschland GmbH & Co. KG, Boehringer Ingelheim Pharma GmbH & Co. KG, Grünenthal GmbH, F. Hoffmann‐La Roche Ltd, Merck KGaA, and Sanofi) for the PharMetrX PhD program, Diurnal Ltd., and grants from the Innovative Medicines Initiative‐Joint Undertaking (“DDMoRe”).
Author Contributions
A.M.G. wrote the manuscript. A.M.G., A.K., W.H., P.G., and C.K. designed the research A.M.G. and A.K. performed the research. All authors analyzed the data. All authors contributed to review and approval of the manuscript.
Supporting information
Supplementary Material
Tables S1‐S2
Acknowledgments
The authors would like to acknowledge Anne Drescher for the preparation of the base dataset and preliminary analysis, as well as colleagues from Merck who were involved in the clinical trials and analyses. Medical writing assistance was provided by ClinicalThinking, Inc., Hamilton, NJ, USA, and funded by Merck KGaA, Darmstadt, Germany.
References
- 1. Martini, G. et al Present and future of metastatic colorectal cancer treatment: a review of new candidate targets. World J. Gastroenterol. 23, 4675–4688 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Ryman, J.T. & Meibohm, B. Pharmacokinetics of monoclonal antibodies. CPT Pharmacometrics Syst. Pharmacol. 6, 576–588 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. World Health Organization: Latest global cancer data. <https://www.who.int/cancer/PRGlobocanFinal.pdf> (2018). Accessed November 7, 2019.
- 4. Dirks, N.L. , Nolting, A. , Kovar, A. & Meibohm, B. Population pharmacokinetics of cetuximab in patients with squamous cell carcinoma of the head and neck. J. Clin. Pharmacol. 48, 267–278 (2008). [DOI] [PubMed] [Google Scholar]
- 5. Azzopardi, N. et al Cetuximab pharmacokinetics influences progression‐free survival of metastatic colorectal cancer patients. Clin. Cancer Res. 17, 6329–6337 (2011). [DOI] [PubMed] [Google Scholar]
- 6. Girard, P. , Kovar, A. , Brockhaus, B. , Zuehlsdorf, M. , Schlichting, M. & Munafo, A. Tumor size model and survival analysis of cetuximab and various cytotoxics in patients treated for metastatic colorectal cancer. The 22nd of the Population Approach Group in Europe; 11–14 June, 2013; Glasgow, Scotland. Abstract 2902. [Google Scholar].
- 7. Tabernero, J. et al Cetuximab administered once every second week to patients with metastatic colorectal cancer: a two‐part pharmacokinetic/pharmacodynamic phase I dose‐escalation study. Ann. Oncol. 21, 1537–1545 (2010). [DOI] [PubMed] [Google Scholar]
- 8. Van Cutsem, E. et al Intrapatient cetuximab escalation in metastatic colorectal cancer according to the grade of early skin reactions: the randomized EVEREST study. J. Clin. Oncol. 23, 2861–2868 (2012). [DOI] [PubMed] [Google Scholar]
- 9. Liu, C. et al Association of time‐varying clearance of nivolumab with disease dynamics and its implications on exposure response analysis. Clin. Pharmacol. Ther. 101, 657–666 (2017). [DOI] [PubMed] [Google Scholar]
- 10. Wilkins, J. et al Population pharmacokinetic analysis of avelumab in different cancer types. In Abstracts for American conference on pharmacometrics 2017 (ACoP8). J. Pharmacokinet. Pharmacodyn. 44(suppl. 1), 11–143 (2017). [DOI] [PubMed] [Google Scholar]
- 11. Gastonguay, M. Full covariate models as an alternative to methods relying on statistical significance for inferences about covariate effects: a review of methodology and 42 case studies. Poster presented at PAGE 2011, Athens, Greece. Abstract 2229.
- 12. Mould, D.R. & Upton, R.N. Basic concepts in population modeling, simulation, and model‐based drug development – Part 2: introduction to pharmacokinetic modeling methods. CPT Pharmacometrics Syst. Pharmacol. 2, e38 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Lindbom, L. , Ribbing, J. & Jonsson, E.N. Perl‐speaks‐NONMEM (PsN)—a Perl module for NONMEM related programming. Comput. Method Programs Biomed. 75, 85–94 (2004). [DOI] [PubMed] [Google Scholar]
- 14. Dirks, N.L. & Meibohm, B. Population pharmacokinetics of therapeutic monoclonal antibodies. Clin. Pharmacokinet. 49, 633–659 (2010). [DOI] [PubMed] [Google Scholar]
- 15. Lobo, E.D. et al Antibody pharmacokinetics and pharmacodynamics. J. Pharm. Sci. 93, 2645–2668 (2004). [DOI] [PubMed] [Google Scholar]
- 16. Baverel, P.G. et al Population pharmacokinetics of durvalumab in cancer patients and association with longitudinal biomarkers of disease status. Clin. Pharmacol. Ther. 103, 631–642 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Walther, B.A. & Moore, J.L. The concepts of bias, precision and accuracy, and their use in testing the performance of species richness estimators, with a literature review of estimator performance. Ecography 28, 815–829 (2005). [Google Scholar]
- 18. Kloft, C. et al Population pharmacokinetics of sibrotuzumab, a novel therapeutic monoclonal antibody, in cancer patients. Invest. New Drugs 22, 39–52 (2004). [DOI] [PubMed] [Google Scholar]
- 19. Kuester, K. , Kovar, A. , Lüpfert, C. , Brockhaus, B. & Kloft, C. Refinement of the population pharmacokinetic model for the monoclonal antibody matuzumab: external model evaluation and simulations. Clin. Pharmacokinet. 48, 477–487 (2009). [DOI] [PubMed] [Google Scholar]
- 20. Bajaj, G. , Wang, X. , Agrawal, S. , Gupta, M. , Roy, A. & Feng, Y. Model‐based population pharmacokinetic analysis of nivolumab in patients with solid tumors. CPT Pharmacometrics Syst. Pharmacol. 6, 58–66 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Tsuchida, Y. & Therasse, P. Response evaluation criteria in solid tumors (RECIST): new guidelines. Med. Pediatr. Oncol. 37, 1–3 (2001). [DOI] [PubMed] [Google Scholar]
- 22. Wang, Y. , Booth, B. , Rahman, A. , Kim, G. , Huang, S.M. & Zineh, I. Toward greater insight on pharmacokinetics and exposure‐response relationship for therapeutic biologics in oncology drug development. Clin. Pharmacol. Ther. 101, 582–584 (2017). [DOI] [PubMed] [Google Scholar]
- 23. Krippendorff, B.F. , Oyarzun, D.A. & Huisinga, W. Predicting the F(ab)‐mediated effect of monoclonal antibodies in vivo by combining cell‐level kinetic and pharmacokinetic modelling. J. Pharmacokinet. Pharmacodyn. 39, 125–139 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Lobato, G. C. et al Associations between baseline serum biomarker levels and cachexia/precachexia in pretreated non‐small cell lung cancer (NSCLC) patients. J. Clin. Oncol. 37(15_suppl), 3054 (2019). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Material
Tables S1‐S2


