Dynamic polaronic screening for anomalous exciton spin relaxation in two-dimensional lead halide perovskites

Anomalous exciton spin dynamics in 2D perovskites indicates screened coulombic interaction for exciton polaron.

Abstract

Two-dimensional lead halide perovskites with confined excitons have shown exciting potentials in optoelectronic applications. It is intriguing but unclear how the soft and polar lattice redefines excitons in layered perovskites. Here, we reveal the intrinsic exciton properties by investigating exciton spin dynamics, which provides a sensitive probe to exciton coulomb interactions. Compared to transition metal dichalcogenides with comparable exciton binding energy, we observe orders of magnitude smaller exciton-exciton interaction and, counterintuitively, longer exciton spin lifetime at higher temperature. The anomalous spin dynamics implies that excitons exist as exciton polarons with substantially weakened inter- and intra-excitonic interactions by dynamic polaronic screening. The combination of strong light matter interaction from reduced dielectric screening and weakened inter-/intra-exciton interaction from dynamic polaronic screening explains their exceptional performance and provides new rules for quantum-confined optoelectronic and spintronic systems.

INTRODUCTION

Two-dimensional (2D) lead halide perovskites, which consist of lead halide octahedra sheets sandwiched between insulating organic cations, have attracted intense research interests as an exciting family of optoelectronic materials for light-emitting devices, photodetectors, and photovoltaic applications (1, 2). Compared to their 3D counterpart, 2D perovskites shows layer-tunable electronic properties, strong light absorption, and superior environmental stability. Among many interesting topics on 2D lead halide perovskites, the property of excitons is especially fascinating. Because of quantum confinement and reduced dielectric screening from the 2D layered structure, electrons and holes in 2D perovskites inherently form strongly confined excitons with binding energy as large as 0.5 eV (3, 4).

On the other hand, in contrast to conventional inorganic semiconductors, the crystal lattice of lead halide perovskites is soft and polar and exhibits large anharmonicity and dynamic disorder, leading to strong electron-phonon coupling (5). As a result, both experimental and theoretical studies have implied that charge carriers in 3D perovskites are dressed by surrounding lattice deformation, forming large polarons (6–10). The polaronic effect has been considered as one key factor to the exceptional photophysical properties of 3D perovskites, including slow electron-hole bimolecular recombination (6–10) and hot carrier thermalization (11). From both a fundamental and a technical point of view, a critical question emerges about the interplay of polaronic and excitonic effects on exciton properties in 2D perovskites. Recent 2D electronic spectroscopy study on lead iodide monolayer has shown unusual spectral structure and exciton-induced dephasing and attributed to exciton polaron in 2D perovskites (12, 13). These studies suggest the complex exciton nature and dynamics in 2D layered perovskites, which are yet to be revealed.

In this study, we seek to unravel the intrinsic exciton properties, especially how excitons are redefined by coupled electronic and structural dynamics in 2D perovskites, by investigating exciton spin dynamics. Unlike exciton population dynamics, which can be obscured by other effects (e.g., defects), the exciton spin dynamics in 2D layered materials with a strong excitonic effect is governed by exchange interaction, which is proportional to the electron-hole binding energy (14, 15). Therefore, exciton spin dynamics provides a facile and sensitive probe to target exciton dynamic properties and inter-/intra-exciton interactions in 2D perovskites. With circular-polarized transient absorption (TA) measurements on 2D CsPbBr₃ nanoplates (NPs), we observe anomalous exciton spin dynamics including (i) more than one order of magnitude smaller exciton-exciton interaction-induced spin flip constant and (ii) unusual slower intra-exciton spin flip with temperature. These results strongly imply that excitons in 2D perovskites exist as exciton polarons dressed by thermally activated lattice distortion. The dynamic polaronic screening leads to substantially weakened inter- and intra-exciton interaction in 2D perovskites, despite reduced static dielectric screening and large steady-state binding energy. The dynamic polaronic screening of exciton polaron in 2D perovskites has strong implications for their optoelectronic applications and the origin of slow electron-hole recombination in 3D perovskites.

RESULTS AND DISCUSSION

We synthesized three-layer (3L) CsPbBr₃ NPs using a previously reported solution approach with slight modifications (see details in Materials and Methods) (16). The NPs are capped with oleylammonium ligands and can be well dispersed in nonpolar solvents or deposited into films using drop cast or spin coating. The obtained NPs have a lateral size of 15 ± 2 nm and a thickness of <2 nm (see fig. S1), which indicates a strong quantum confinement only along the vertical direction as a true 2D system. As shown in Fig. 1, CsPbBr₃ NPs exhibit a sharp exciton absorption peak at 2.71 eV and a redshifted (by ~38 meV) photoluminescence (PL) with a high quantum yield of ~90%. The absorption peak corresponds to 3L (1.8 nm) corner-shared octahedral inorganic lattice (Fig. 1B, inset) (16, 17). The sharp exciton peak and the absence of PL from other thickness or layer edge states (18) indicate uniform and high-quality 3L NPs. The exciton PL decay is shown in Fig. 1B with a lifetime of ~5.4 ns by single exponential fitting.

Fig. 1. Optical spectral and exciton lifetime in 3L CsPbBr₃ NPs.

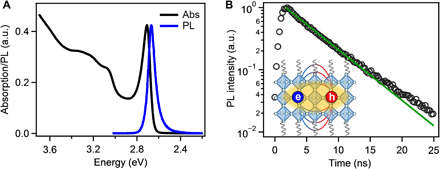
(A) Absorption and PL spectra of 3L CsPbBr₃ PLs in toluene solution. (B) PL decay kinetics of 3L CsPbBr₃ NPs in solution and the single exponential fitting with a lifetime of ~5.4 ns. Note the y axis in logarithm scale. Inset: Scheme of 3L CsPbBr₃ structure and exciton interaction. a.u., arbitrary units.

Because of quantum/dielectric confinement effect and reduced dielectric screening, electrons and holes in 2D perovskites are strongly confined to form excitons. Excitonic features dominate the optical absorption spectra of 2D perovskites, from which the steady-state exciton binding energy (E_b) can be extracted (3, 17). E_b in 3L CsPbBr₃ has been determined to be ~180 meV (3, 17), which is ~7 kT at room temperature. Because electron and hole in 2D materials interact mainly through surrounding medium, E_b remains similar at 4 K and room temperature (3, 17). We estimated the exciton versus free carrier ratio in 3L CsPbBr₃ NPs using the Saha-Langmuir equation (see note S1). As shown in fig. S2, exciton is the dominant species (>95%) at room temperature and exciton thermal dissociation, in principle, is negligible. However, as we will show later, the large E_b extracted from steady-state optical absorption spectra does not reflect photoexcited exciton properties in 2D perovskites.

To assess the exciton properties after photoexcitation in 2D perovskites, we performed spin- and energy-resolved femtosecond TA spectroscopy study on exciton spin dynamics in CsPbBr₃ NPs. For materials with large spin-orbital coupling, their spins can be optically orientated by circularly polarized light (19–21). As shown in Fig. 2A, the conduction band minimum and valance band maximum in lead halide perovskites have s and p symmetry with S = 1/2 and J = 1/2, respectively (19). Because of spin-related optical transition rule, right (left) circularly polarized light σ⁺ (σ⁻) can selectively excite electron from valance band m_S = −1/2 (1/2) to the conduction band m_J = 1/2 (−1/2) state, creating exciton with angular momentum J_M = 1 (−1) (20, 21). In spin-resolved TA measurement, we excite CsPbBr₃ NPs with circularly polarized pump pulse and, after a certain delay time, measured the relative transmittance change (ΔT/T) using a circularly polarized supercontinuum probe pulse with the same or opposite polarization configurations (SPC or OPC) (see Materials and Methods for details). The pump-probe cross-correlation was determined to be <100 fs.

Fig. 2. Spin-resolved TA measurement on 3L CsPbBr₃ NPs under resonant excitation.

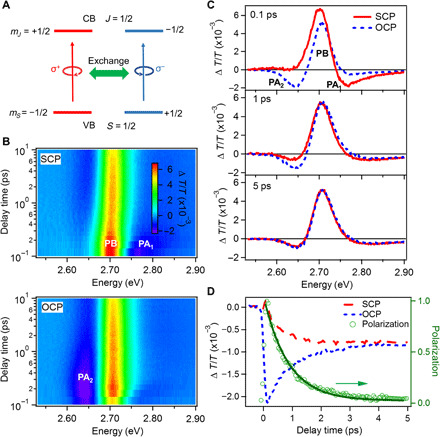
(A) Scheme showing spin-dependent optical transitions in CsPbBr₃ under resonance condition in single electron picture. Right (left) circular polarized light σ⁺ (σ⁻) couples to the transition of electron from valance band m_S = −1/2 (1/2) to the conduction band m_J = 1/2 (−1/2) state, creating an exciton with J_M = 1 (−1). (B) 2D color plot of TA spectra for same (top) and opposite (bottom) pump-probe circular polarization configurations, respectively. (C) Spectral evolution for same and opposite pump-probe configuration at different pump-probe time delay (0.1, 1, and 5 ps). The spectra features associated with PB, PA₁, and PA₂ are indicated. (D) TA dynamics for same and opposite pump-probe configurations at the PA₂ low energy side. Calculated valley depolarization kinetics and its single exponential fit are also plotted.

Spin-resolved TA spectra and dynamics of CsPbBr₃ NPs by 2.73 eV resonant excitation to ensure unity initial spin orientation are shown in Fig. 2. The pump fluence was kept very low such that the exciton Auger recombination is negligible. Figure 2B shows the 2D color plot of TA results for the SPC (top) and OPC (bottom), respectively. A few representative TA spectral comparison at indicated delay times is displayed in Fig. 2C for better view. While both configurations exhibit the same spectral features at a later time (~5 ps), including a positive bleach at exciton resonance and negative induced absorptions adjacent to that, substantial spectral evolution can be observed in the first 5 ps. Right after photoexcitation (0.1 ps), TA spectra of SPC exhibit a photoinduced bleach (PB) at exciton absorption position (~2.7 eV) and a photoinduced absorption (PA) feature at the blue side (~2.77 eV), while those of OPC show a PB at exciton absorption position and a PA feature at the red side (~2.64 eV). A similar TA spectral shape has been observed in 2D (C₆H₅C₂H₄NH₃)₂PbI₄ perovskite film (21). We label these TA features as PB, PA₁, and PA₂, as shown in Fig. 2 (B and C).

Generally speaking, TA spectra at the exciton transition region originate mainly from two mechanisms: (i) conventional band filling due to occupation of photoexcited excitons/carriers and (ii) coulombic effect. The coulombic effect is substantially enhanced in low-dimensional system and contains multiple forms, including band renormalization, biexciton effect, and exciton screening (21, 22). While the effect of band filling is the decrease of transition strength, the coulombic effect usually manifests as both intensity reduction and peak shifting. The effects from all these mechanisms are usually entangled together. Fortunately, some of these effects are spin dependent, including phase space filling and biexciton effect, which provides a facial approach for the exciton spin dynamics analysis (22, 23).

Right after resonant photoexcitation (0.1 ps) by σ⁺ pump pulse, the presence of J_M = +1 exciton leads to the PB for both SPC (σ⁺ probe) and OPC (σ⁻ probe) by spin-independent exciton screening effect and additional PB for SPC by spin-dependent phase space filling. Therefore, PB of exciton resonance appears in both SPC and OPC configurations but is larger in the former. On the other hand, the presence of J_M = +1 exciton at band edge shifts probed excitonic transitions through the biexciton effect. The biexciton effect is repulsion for excitons with same spins due to the Pauli exclusion principle and attraction with opposite spins (21, 23). Therefore, the biexcitonic effect generates opposite PA position for different configurations, that is, PA under SPC (OPC) appears on the blue (red) side of exciton transition. This is exactly shown by PA₁ (PA₂) on 0.1 ps TA spectra (Fig. 2C). The difference on TA spectra at 0.1 ps between SPC and OPC indicates the creation of spin polarization, which vanishes in ~5 ps (Fig. 2C).

In principle, the coalescence process of either PA or PB signal between SPC and OPC provides the spin depolarization process. Without resorting to complicated spectral modeling/decomposition, which might introduce artifacts, here, we rely on low-energy side PA₂ to extract the exciton spin dynamics. Unlike PB and PA₁, the low-energy side of PA₂ contains only the spin-dependent biexcitonic effect without spin-independent contributions. This can be seen by the presence of TA signal only in OPC but not in the other right after photoexcitation (Fig. 2C, 0.1 ps). The TA kinetics of the low-energy side of PA₂ under SPC (ΔT/T_SPC) and OPC (ΔT/T_OPC) are plotted in Fig. 2D, which show the conversion and equilibration between excitons with different spins. The spin relaxation kinetics P(t) can be calculated by

$$P(t)=\frac{\mathrm{\Delta }T/T_{\text{SPC}}-\mathrm{\Delta }T/T_{\text{OPC}}}{\mathrm{\Delta }T/T_{\text{SPC}}+\mathrm{\Delta }T/T_{\text{OPC}}}$$ (1)

The spin relaxation kinetics under resonant excitation are shown in Fig. 2D. It starts from unity and decays in a single exponential form with a lifetime τ_s (rate k_s) of ~0.86 ps (1.16 ps⁻¹). The exciton spin relaxation lifetime is three orders of magnitude shorter than population lifetime, representing the pure spin depolarization process.

As a comparison, we also measured the spin depolarization process in 3D CsPbBr₃ bulk film in the same way, and the results are shown in fig. S3. The spin lifetime in 3D film is determined to be 3.2 ± 0.1 ps at room temperature, which is about four times longer than that in 3L NPs. This is expected because electron-hole binding energy and exchange interaction are markedly enhanced in 2D NPs over bulk (3, 4). The electron-hole exchange interaction acts as a fluctuating effective magnetic field and facilitates spin precession and relaxation, as described by the Maialle-Silva-Sham (MSS) mechanism (14). This mechanism has been shown to govern the exciton spin relaxation process in different excitonic systems such as III-V group semiconductor quantum wells (QWs) (14, 24) and 2D transition metal dichalcogenides (TMDCs) (15, 25–27). Here, we do not need to consider another traditional exchange mechanism between a conduction band electron and heavily doped valence band holes described by the Bir-Aronov-Pikus (BAP) mechanism because perovskites NPs are not intentionally doped.

To emphasize the importance of resonant excitation on spin polarization study, we first examine how the excitation energy (E_ex) affects exciton spin polarization. Following the above method but changing E_ex, the spin depolarization kinetics P(t) at different E_ex are shown in Fig. 3A. We also show in Fig. 3B the initial maximum polarization as a function of excess energy (energy difference between excitation energy and 2.71 eV exciton resonance). As shown in Fig. 3, the exciton spin polarization for all excitation energies exhibits a similar decay process in ~5 ps but with different initial polarization value. When E_ex is progressively tuned away from exciton resonance, the initial exciton polarization for band edge exciton decreases monotonically, from 1 for 2.73 eV to 0.12 for 3.45 eV.

Fig. 3. Effect of excitation energy on spin relaxation.

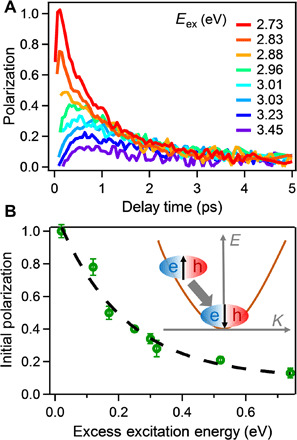
(A) Spin relaxation kinetics at different excitation energies (from 2.73 to 3.45 eV). (B) Initial spin polarization amplitude as a function of excess excitation energy relative to exciton transition of 3L CsPbBr₃ NPs (E₀ = 2.71 eV). The dashed line is a guide to the eye. Inset: Scheme showing the exciton spin relaxation during the cooling process in energy-momentum space.

The decreasing of initial polarization with E_ex can be understood by electron-hole exchange or MSS mechanism. The magnitude of magnetic field Ω(K) from the electron-hole exchange interaction is proportional to the exciton center-of-mass momentum K, which increases with excess excitation energy (see note S2). Hence, excitons created by higher-energy photon undergo faster spin flip. Under resonant circular polarization excitation, unity spin polarized excitons are directly created at band edge with K ≈ 0. With increasing E_ex, excitons are initially created at high energy with large K and then cool to band edge by phonon emission. During the exciton cooling process, a fraction of photo-orientated exciton spins has undergone a fast flipping process (scheme in Fig. 3B), which explains smaller initial spin polarization for band edge exciton with increasing E_ex. Similar feature has also been observed in other excitonic systems including III-V group QWs (14, 24) and TMDCs (26, 28).

Insights about exciton properties in 2D perovskite NPs come from investigating the effects of excitation density and lattice temperature on spin relaxation dynamics. Under resonant excitation, we increase the average exciton number (⟨N⟩) per NP or exciton density ρ by increasing pump fluences. ⟨N⟩ was determined by TA signal saturation curve, and ρ was calculated by ⟨N⟩/a², where a is the later size of NPs (see note S3). Figure 4A shows the exciton spin relaxation dynamics for ⟨N⟩ ranging from 0.2 to 4.8 or ρ from 8 × 10¹⁰ to 1.9 × 10¹² cm⁻². With increasing ⟨N⟩ or ρ, exciton spin polarization decays marginally faster. The exciton spin relaxation rate k_s as a function ⟨N⟩ or ρ is plotted in Fig. 4B, exhibiting a linear relationship. This linear dependence has also been observed in III-V group QWs (23, 29) and TMDCs (30), which has been attributed to the inter-exciton exchange interaction. The classical MSS mechanism considers the exciton spin relaxation by the electron-hole exchange interaction within an exciton (intra-exciton). With increasing ⟨N⟩ or ρ, the exchange interactions between excitons (inter-exciton), which include both electron-electron and hole-hole terms, become strong and add into spin depolarization (scheme in Fig. 4B) (23, 29, 30).

Fig. 4. Effect of exciton density on spin relaxation.

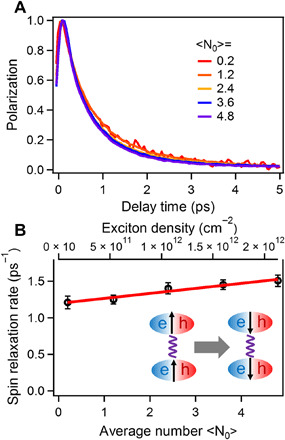
(A) Spin relaxation kinetics at different exciton densities. ⟨N⟩ is average exciton number per NP. (B) Spin relaxation rate as a function of injected exciton density (black circles) and the linear fit (red line). Inset: Scheme of exciton spin depolarization process by inter-exciton exchange interaction.

A linear fit (Fig. 4B) on k_s as a function of ρ yields a slope β_{ex − ex} of 0.06 ± 0.01 cm² s⁻¹. β_{ex − ex} is a phenomenological constant reflecting exciton-exciton exchange interaction strength (30). As a comparison, β_{ex − ex} of monolayer MoSe₂ has been determined to be 3.49 cm² s⁻¹ (30). The ~60 times smaller β_{ex − ex} in 3L CsPbBr₃ NPs indicates the substantially screened exciton-exciton interaction compared to TMDC monolayer. This is unexpected given that the steady-state E_b of monolayer TMDC on the insulating substrate is ~0.3 eV (31, 32), comparable to that of 3L CsPbBr₃ NPs. We note that despite the different forms and environments for colloidal CsPbBr₃ NP and TMDCs, the same 2D exciton nature with similar E_b still allows a direct and meaningful comparison on exciton interactions and properties. An unusually weak inter-exciton interaction in 2D perovskites has also been inferred from order(s) of magnitude smaller exciton-exciton annihilation rate (33) and exciton-induced dephasing constant (12) compared to TMDCs with similar E_b. As we will show, this is due to the strong dynamic lattice screening at excited-state equilibrium lattice configuration of lead halide perovskites, which cannot be captured by E_b from steady-state absorption measurement at ground-state equilibrium configuration.

To reveal the screening mechanism and the nature of excitons in 2D perovskites, we performed temperature (T)–dependent spin depolarization measurements. The exciton spin relaxation kinetics at T ranging from 80 to 340 K are shown in Fig. 5A. We obtained the spin relaxation rate k_s by single exponential fitting (Fig. 5A) and plotted k_s as function of T in Fig. 5B. Exciton spin depolarization in 2D CsPbBr₃ NPs shows a generally slower trend by almost an order of magnitude with increasing temperature, with k_s (τ_s) of ~4.4 ps⁻¹ (0.23 ps) at 80 K to ~0.6 ps⁻¹ (1.67 ps) at 340 K. This finding is both unexpected and notable as most 3D semiconductors and 2D QWs including TMDCs exhibit faster carrier/exciton spin depolarization at higher T (19, 25, 30). As a comparison, spin depolarization in 3D CsPbBr₃ film shows a normal behavior, i.e., longer lifetime with decreasing T (see fig. S5). Here, we focus on the exciton properties in 2D perovskites by contrasting the 3L sample here to 3D polycrystalline perovskite film, where exciton is the relevant dominant species in the former and free carriers in the latter for the picosecond spin depolarization process at room temperature. A careful study on 2D perovskites with different layers would be interesting but beyond the scope of the current study (34). We note that the exciton fine structure in perovskite cannot explain this unusual temperature dependence, as the fine structure splitting energy in CsPbBr₃ NPs is about 0.5 to 2 meV (35) and a thermal equilibrium can always be assumed in the investigated temperature range (77 to 340 K).

Fig. 5. Effect of temperature on spin relaxation and dynamic screening in exciton polaron.

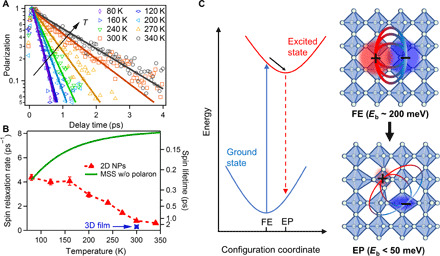
(A) Exciton spin relaxation kinetics (open symbols) at different temperatures from 80 to 340 K and their single exponential fits (sold lines). Note the y axis in logarithm scale. (B) Exciton spin relaxation rate as a function of T for 3L CsPbBr₃ NPs (red triangles). The spin relaxation rate in 3D CsPbBr₃ film at room T (blue crossing) is also shown for comparison. The green line is the trend from the MSS mechanism without considering the polaronic effect, showing the increase in spin relaxation rate with T. The green line has been scaled at low 80 K to match the experimental point. (C) Configuration space representation of potentials of ground state and excited state with different equilibrium positions under harmonic approximation. The equilibrium position of the ground state is denoted as FE, and that of the excited state is denoted as EP. Scheme of transformation from free exciton with large columbic interaction to exciton polaron with lattice distortion and substantially screened columbic interaction by the dynamic polaronic effect.

According to the MSS mechanism, which governs exciton spin dynamics in excitonic system, k_s can be given by (14)

$$k_s\approx \langle {\mathrm{\Omega }}_K^2\rangle {\mathrm{\tau }}_p$$ (2)

where $\langle {\mathrm{\Omega }}_K^2\rangle$ is the square of magnetic field averaged over exciton states and τ_p is exciton scattering time. The magnetic field Ω_K is proportional to K and electron-hole exchange strength J. J has been assumed to be T independent, and the thermal distribution of K yields T dependence in the conventional MSS model (14, 15). At low temperature where exciton distribution in K space is governed by collisional broadening rather than thermal broadening, $\langle {\mathrm{\Omega }}_K^2\rangle$ is inversely proportional to τ_p, and hence, k_s depends on T weakly. As T increases, exciton thermal distribution dominates and averaging over thermal distribution yields a linear dependence of $\langle {\mathrm{\Omega }}_K^2\rangle$ on T, i.e., $\langle {\mathrm{\Omega }}_K^2\rangle \propto T$ (15, 24, 30). Another factor, τ_p, depends on T through thermally activated phonon scattering, which is nontrivial to determine directly. Here, we estimated the temperature effect on τ_p on the basis of PL linewidth (Γ) by τ_p ∝ 1/Γ (27). The extracted Γ increases with T due to phonon scattering (fig. S6). We modeled Γ with the following phenomenological equation: Γ(T) = Γ₀ + A/[ exp (E_ph/k_BT) − 1], where the first term is the T-independent contribution and the second term is phonon scattering contribution with an effective phonon energy E_ph and a constant A (fig. S6) (36, 37). In 2D perovskites, both in-plane polar optical phonons and out-of-plane homopolar (nonpolar) optical phonons can contribute to the exciton-phonon scattering at high temperature (36). Here, we do not differentiate specific phonon modes but just capture the temperature effect on linewidth using this phenomenological model. With the knowledge of T effect on both $\langle {\mathrm{\Omega }}_K^2\rangle$ and τ_p, we can model the dependence of k_s on T by Eq. 2. The modeled trend by the classical MSS mechanism is plotted in Fig. 5B (green line), with amplitude scaled to experimental results at 80 K.

Because of exciton thermal distribution, the MSS model yields a faster spin relaxation with increasing T, which has been generally observed for exciton spin relaxation in TMDCs (25, 30, 38). As shown in Fig. 5B, the slower k_s with T in 2D CsPbBr₃ NPs is opposite to the trend given by the MSS model. None of the conventional spin relaxation pathways including Elliott-Yafet (EY) and D’yakonov-Perel’ (DP) mechanisms would yield slower spin relaxation at higher temperature (see note S4). To the best of our knowledge, the increase of spin lifetime with T has only been observed in two reports on inorganic QWs at the temperature region where excitons are thermally dissociated into free carriers such that the electron-hole exchange interaction is suppressed with temperature (39, 40). This scenario cannot apply here because steady-state E_b in 2D CsPbBr₃ NPs is about one order of magnitude larger than kT and conventional exciton thermal dissociation is impossible (see note S1).

We now seek to understand the anomalous exciton spin relaxation in 2D CsPbBr₃ NPs. The slower spin depolarization with T in 2D perovskites suggests a weaker J or electron-hole coulomb interaction at higher T. As introduced in the beginning, compared to conventional inorganic semiconductors, the crystal lattice of lead halide perovskites is soft and polar with large anharmonicity, leading to strong electron-phonon coupling (5, 8, 37, 41). As a result, charges in perovskites are dressed by surrounding lattice deformation as large polarons and protected from impurity scattering and electron-hole recombination (6, 8–10). The polaronic effects in lead halide perovskites are further hybridized with dynamic disorder and ferroelectric-like response, forming dynamic ferroelectric large polarons with enhanced coulomb screening (42).

Following the success of large polaron in 3D perovskites, we propose the exciton polaron picture as shown in Fig. 5C: After free exciton absorption transition at ground-state equilibrium lattice configuration (denoted as FE), excitons at the excited state in 2D perovskites relax and localize as exciton polarons with equilibrium configuration (denoted as EP) different from that in the ground state, contributing to band edge properties (e.g., PL emission). In exciton polarons, the electrons and holes with distinct lattice deformation are mutually separated in real space because of opposite structural displacements (i.e., bond compression by hole and elongation by electron for lead halide sublattice) but still bound by coulomb interaction due to reduced dimensionality (7–9). As a result, compared to free 2D excitons with overlapping electron and hole and strong coulomb interaction, the electron-hole spatial localization and separation in exciton polaron lead to a much weaker intra- and inter-excitonic interaction. In contrast to steady-state dielectric screening as determined by absorption measurement, we denote it as dynamic polaronic screening because it only takes place at the excited state with dynamically correlated electronic and structural change. The screened inter-excitonic interaction well explains order(s) of magnitude smaller β_{ex − ex}, exciton-exciton annihilation rate (33), and exciton-induced dephasing constant (12) in 2D perovskites compared to TMDCs, despite comparable steady-state E_b.

The dynamic polaronic screening of the intra-excitonic interaction in exciton polaron also explains the anomalous T-dependent exciton spin depolarization in 2D CsPbBr₃ NPs. The polaron formation is induced by electron coupling to the thermal vibration of lead halide lattice (8, 37). In the Fröhlich polaron model, polaron coupling constant α and polaron localization energy are proportional to dielectric response factor $1/\overline{\mathrm{\epsilon }}=1/{\mathrm{\epsilon }}_{\infty }-1/{\mathrm{\epsilon }}_0$, where ε_∞ and ε₀ are optical and static dielectric constants of the material, respectively. $1/\overline{\mathrm{\epsilon }}$, which reflects pure dielectric response of lattice, is especially large and T dependent in lead halide perovskites because of its structural dynamics (37). In CsPbBr₃, ε₀ has been shown to be close to ε_∞ at low T (<60 K) due to frozen lattice motion but increases quickly above that due to thermally activated lattice vibration and large anharmonicity (37). The increase in ε₀ with T leads to a monotonic increase in the α polaronic effect (see note S5 and fig. S7). In addition, the coulomb interaction between optical phonon and a perfectly correlated exciton with large E_b (>E_ph) should be weak, due to the cancellation effect from electron and hole. Because of the thermal dynamic disorder in CsPbBr₃ crystal lattice, the fluctuating electrostatic potential at high T can induce dynamic charge transfer (or dipolar) character in 2D excitons, which facilitates exciton-phonon coupling and exciton polaron formation (9, 10). The strong polaronic effect at higher T provides faster and larger dynamic screening on the electron-hole intra-exciton interaction, slowing down the exciton spin flip process. This mechanism shares similar feature with exciton thermal dissociation in conventional QWs, but the underlying physics are fundamentally different.

Because of dynamic polaronic screening, the large E_b on exciton dynamic in 2D perovskites can only be manifested by low T measurement. As ε_∞ is close to ε₀ and crystal lattice is largely frozen at 80 K (37), we can assume that the dynamic polaronic screening is negligible and E_b for relaxed exciton is the same (~180 meV) as the steady-state E_b. At 80 K, k_s of 3L 2D NPs is about two orders of magnitude faster than that in 3D film, revealing the truly dominant electron-hole exchange interaction on the exciton spin depolarization process. With increasing T, the difference is getting smaller because of the opposite T dependence on k_s in 2D and 3D CsPbBr₃.

Comparing 80 and 300 K (room temperature) results in 2D NPs (Fig. 5B) allows estimation of the redefined exciton binding energy in exciton polaron. The measured exciton spin lifetime is ~6.5 times longer at 300 K, while the conventional MSS model assuming T-independent J predicts ~2 times shorter. As k_s is proportional to J², this indicates that J in exciton polaron is about four times weaker at 300 K compared to 80 K. This value should be considered as a lower boundary, as exciton spin depolarization at 300 K (compared to 80 K) contains more contributions from other mechanisms (e.g., EY and DP). As J is proportional to E_b, this implies that E_b in exciton polaron is less than 50 meV at room temperature. This value is comparable to the steady-state E_b in 3D CsPbBr₃ film (41), highlighting the strong dynamic polaronic effect. On the basis of the Wannier exciton model, reduced exciton binding energy implies a larger exciton radius, but a quantitative estimate cannot be made because both dielectric constant and effective mass are temperature dependent for exciton polaron.

The dynamic polaronic screening in 2D perovskites has profound implications for their optoelectronic applications, especially their light to electricity conversion process. On the one hand, the exciton radiative and Auger lifetime, which is governed by intra- and inter- exciton interactions, should be substantially prolonged at room temperature by dynamic polaronic screening. We observed longer exciton PL lifetime with increasing T for 3L CsPbBr₃ NPs (see fig. S8), and Deng et al. (33) reported more than one order of magnitude exciton Auger annihilation rate compared to TMDCs, confirming a weakened excitonic interaction in 2D perovskites. On the other hand, while the large steady-state excitonic effect endows 2D perovskites with strong light-harvesting property, unscreened 2D excitons tend to recombine fast before their dissociation to free carrier. Fortunately, the dynamic polaronic screening substantially reduces the exciton binding energy at the excited state, which facilitates exciton dissociation and carrier collection. The combined strong light harvesting, long exciton lifetime, and facial carrier generation from exciton polaron in 2D perovskites are crucial for their exceptional photovoltaic applications (1, 2). Recent studies on 2D perovskites have also shown the presence of the low-energy edge state for exciton dissociation into longer-lived free carriers (1). However, unlike the intrinsic dynamic polaronic effect, these edge states are likely extrinsically formed by partially merged adjacent layers (18) and also require exciton diffusion from bulk region to edge.

This result also sheds light on photophysical properties in 3D perovskites. The long carrier lifetime and slow electron-hole recombination in 3D perovskites have been generally ascribed to two origins: the polaronic effect and the Rashba effect. In materials with large spin-orbit coupling and inversion symmetry breaking, the Rashba effect induces spin-polarized band splitting and shifting in k space, generating indirect bandgap character (43, 44). While the CsPbBr₃ crystal structure is centrosymmetric, local thermal fluctuation can create dynamic symmetry breaking and Rashba effect (5, 43). The Rashba effect has also been invoked in discussing the spin depolarization process in perovskites (34, 45). In principle, both the polaronic effect and the Rashba effect can retard electron-hole recombination, but differentiating their relative contribution has been a longstanding challenge. Fortunately, the polaronic effect and the Rashba effect have the opposite T effect on exciton spin relaxation. Symmetry breaking and Rashba effect from thermal lattice fluctuation (46) create larger effective magnetic field at higher T, which facilitates the spin depolarization process (see note S4). On the basis of the experimental results, we speculate that polaronic effect might be the dominant mechanism for slow electron-hole recombination in 3D perovskites.

In conclusion, to reveal the exciton properties in 2D perovskite, we investigated the exciton spin dynamics that is sensitive to the inter- and intra-exciton exchange interactions. By performing exciton density and temperature-dependent measurements, we observed anomalous exciton spin flip behaviors including (i) orders of magnitude smaller inter-excitonic interaction compared to TMDC with comparable steady-state binding energy and (ii) longer exciton spin lifetime by almost an order of magnitude or smaller intra-excitonic interaction with temperature increasing from 80 to 340 K. These unusually exciton spin dynamics can be well explained by exciton polaron in 2D perovskites. Because of soft and polar lattice with large anharmonicity and dynamic disorder, the correlated motion of electronic and structure degrees of freedom leads to spatially localized and bound electron-hole wave function accompanied with opposite lattice deformation. Despite large steady-state binding energy, the inter- and intra-excitonic interactions are substantially weakened by the dynamic polaronic screening in 2D perovskites. This has strong implications to the exceptional performance of 2D perovskite optoelectronic devices and sheds light on the origin of slow electron-hole recombination in 3D perovskites. The dynamic polaronic effect also provides exciting opportunities to design low-dimensional quantum-confined systems for optoelectronic and spintronic applications.

MATERIALS AND METHODS

Sample synthesis

3L CsPbBr₃ perovskite NPs were synthesized by a previous reported solution approach with slight modifications (16). To prepare precursor solution, 367 mg of PbBr₂ and 212 mg of CsBr were dissolved in 2 ml of dimethyl sulfoxide and 1 ml of 40 weight % HBr, respectively. PbBr₂ precursor (0.1 ml) and CsBr precursor (0.1 ml) were added successively under continuous stirring to a mixture of toluene (5 ml), 1-octadecene (0.5 ml), oleic acid (0.5 ml), and oleylamine (0.5 ml). About 20 s later, the solution turned turbid white. At this time, 0.5 ml of butanol was added rapidly to quench the reaction. After 1-min stirring, the NPs were collected by holding the supernatant after centrifugation at 8000 rpm. The supernatant was further annealed in oven at 80°C for 2.5 min. After the supernatant was cooled down and turned turbid blue, it was centrifuged again at 10,000 rpm for 10 min to collect the precipitation. The precipitation was dispersed and stored in 2 ml of toluene for further characterization.

TA measurement

For femtosecond TA spectroscopy, the fundamental output from Yb:KGW laser (1030 nm, 100 kHz; Light Conversion Ltd.) was separated to multiple light beams. One was introduced to a noncollinear optical parametric amplifier and a second-harmonic generation crystal β-barium borate (BBO) to generate a certain wavelength for pump beam. The other was focused onto a BBO crystal to generate 515-nm pulses and then focused onto a YAG crystal to generate continuum blue light as probe beam. The temporal delay between them is controlled via a motorized delay stage. The pump and probe pulses overlapped spatially in the sample, and the transmitted probe light was collected by a linear array detector (TA-100, Time-Tech Spectra, LLC). We use colloidal solution samples for all room temperature measurement because of their high-quality and drop-cast thin films from colloidal solution for temperature-dependent measurements to avoid solvent coagulation.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/47/eabb7132/DC1