Long-range remote focusing by image-plane aberration correction

Abstract

Laser scanning plays an important role in a broad range of applications. Toward 3D aberration-free scanning, a remote focusing technique has been developed for high-speed imaging applications. However, the implementation of remote focusing often suffers from a limited axial scan range as a result of unknown aberration. Through simple analysis, we show that the sample-to-image path length conservation is crucially important to the remote focusing performance. To enhance the axial scan range, we propose and demonstrate an image-plane aberration correction method. Using a static correction, we can effectively improve the focus quality over a large defocusing range. Experimentally, we achieved ∼three times greater defocusing range than that of conventional methods. This technique can broadly benefit the implementations of high-speed large-volume 3D imaging.

1. Introduction

Laser scanning has been employed in many key technologies. In manufacturing [1], laser scanning based cutting has been routinely used to achieve high spatial precision. In 3D printing [2], laser scanning based methods are employed for printing metal structures. In hospitals, laser scanning has been applied to vision correction [3] and novel endoscopes [4]. In biomedical sciences, a variety of 3D imaging technologies are based on laser scanning [5–10]. In remote sensing, laser scanning enables LIDAR technology [11]. Therefore, the advances of laser scanning techniques are crucially important to many disciplines.

The commonly employed laser scanners such as galvo, MEMS mirror, and polygon scanners can only implement fast 2D transverse scanning [12]. The axial scanning can be implemented by sample translation, lens translation, or mechanical lens focus adjustment, which are rather slow compared to the transverse scanning. For fast 3D scanning applications, a variety of novel solutions have been developed, which include liquid lenses [13,14], ultrasonic lenses [15,16], wavefront control [17–19], remote focusing [20,21], etc. Liquid lenses are simple and of low cost. The working principle is based on the lens surface deformation, which allows a scanning rate of ∼100 Hz. For high-resolution and high-quality imaging, the perfect defocusing wavefront is defined by ndcosθ where n is the refraction index, d is the defocusing distance and θ is the angle of incidence [20]. As the objective lenses are designed and manufactured to meet the Abbe sine condition (distance to optical axis proportional to sinθ on pupil plane), the pupil-plane spatial profile of the defocusing wavefront is uniquely defined for a given maximum half cone angle. As a result, the liquid lenses induced defocusing will contain aberration (deviation from the ideal defocusing wavefront) and lead to reduced Strehl ratio and spatial resolution. Ultrasonic lenses are based on the ultrasound pressure wave driven refractive index change, which is rather fast (e.g. 100 kHz – 1 MHz). Similar to liquid lenses, ultrasonic lenses also suffer from aberration [15]. To achieve aberration free defocusing, holographic wavefront control has been employed [18,19,22–24]. In addition to producing the perfect defocusing wavefront, wavefront control can also correct the existing system aberration and yield near diffraction limited focus [17,25–28]. The defocusing range is often limited by the wavefront control device. For long-range defocusing, spatial light modulators (SLM) are often employed for their large number of pixels [29,30]. For applications involving femtosecond pulses, the inherent temporal coherence of the laser pulses sets an additional limit on the defocusing range as the SLM based wavefront control involves phase wrapping [31,32]. The state-of-the-art SLM offers a ∼200 Hz update rate, which allows quick stepwise defocus adjustment. For continuous axial scanning, the SLM needs to update wavefront many times along the scan path and therefore the scanning rate is low. Towards high-speed aberration-free continuous axial scanning, remote focusing has been developed [21]. The idea is to image the pupil of the proximal objective lens to the pupil of the distal objective with the same maximum half cone angle and thus the same defocusing wavefront profile. A galvo driven miniature mirror can be positioned near the focal plane of the proximal objective to achieve rapid (up to ∼kHz) focusing control [20,21]. Ideally, remote focusing can achieve aberration-free defocusing until the defocusing wavefront starts to challenge the field-of-view (FOV) supported by the objective lenses. However, the experimentally measured aberration-free defocusing range is often much smaller. In this work, we analyze the source of aberration and provide a simple solution to increase the axial scan range.

2. Methods

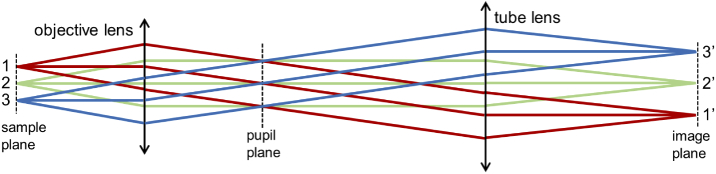
The essence of remote focusing is about the perfect relay imaging of defocusing wavefront. A key question to ask is whether the common commercially available objective lenses are actually designed for such a task. For microscopy applications, the goal is to image the point emission on the sample plane to the final image plane. Geometrically, all the paths between an emission point (e.g. point 1 in Fig. 1) to its image point (point 1’) need to have identical optical path lengths. Otherwise, the focus will contain aberration. Is this path length a constant for all points within the FOV of the objective lens? For example, are the path lengths 1-1’, 2-2’, and 3-3’ all identical? For most microscopy applications (e.g. bright-field imaging, wide-field fluorescence imaging, confocal microscopy, and two-photon laser scanning microscopy), there is no need to achieve such sample-to-image path length conservation, which is also not considered in most lens designs. However, the path length conservation is precisely what we need to achieve aberration-free remote focusing.

Fig. 1.

Sample-to-image path length conservation is the key to aberration free remote focusing.

For simplicity, let’s consider a telecentric imaging system (Fig. 1). For a plane wave propagating along the optical axis (the central rays of points 1, 2, 3), it will be focused by the objective lens into a single point on the pupil plane. Given the telecentricity of the tube lens, this focus will be collimated by the tube lens into a plane way on the final image plane. In this way, a plane wave is relay imaged to a plane wave. Therefore the sample-to-image path lengths are conserved. In other words, the path lengths 1-1’, 2-2’, and 3-3’ are all identical for this perfect telecentric imaging system. In a remote focusing system, the defocusing wavefront on the sample plane is first imaged to the intermediate image plane and then to the sample plane of the second objective lens. For a sample-to-image path length conserved system, the defocusing wavefront is relay imaged with only an additional phase constant (the sample-to-image optical path length) and is therefore aberration free. However, for non-telecentric imaging systems, the sample-to-image path may have spatial dependence (e.g. 1-1’≠ 2-2’≠ 3-3’), which adds an additional phase profile to the relayed defocusing wavefront and causes aberration. The amount of aberration depends on the defocusing distance. For zero defocusing, the optical beam only occupies a diffraction limited spot (e.g. only point 2 in Fig. 1) on the sample plane and therefore experiences no sample-to-image path length variation. With increased defocusing, the optical beam occupies a larger area on the sample plane and therefore encounters more of the path length variation.

One way to quantify the sample-to-image path length variation and to assist the optimal alignment of a remote focusing system is to send in a plane wave to the sample plane of the objective lens and to measure the optical wavefront at the image plane of the tube lens. The tube lens position should be adjusted so that the wavefront on the image plane is collimated. The residual deviation from a plane wave becomes the source of aberration (the aforementioned sample-to-image path length variation) in remote focusing. We propose to position a wavefront corrector at the image plane to compensate for the sample-to-image path length variation and improve the range of aberration free remote focusing.

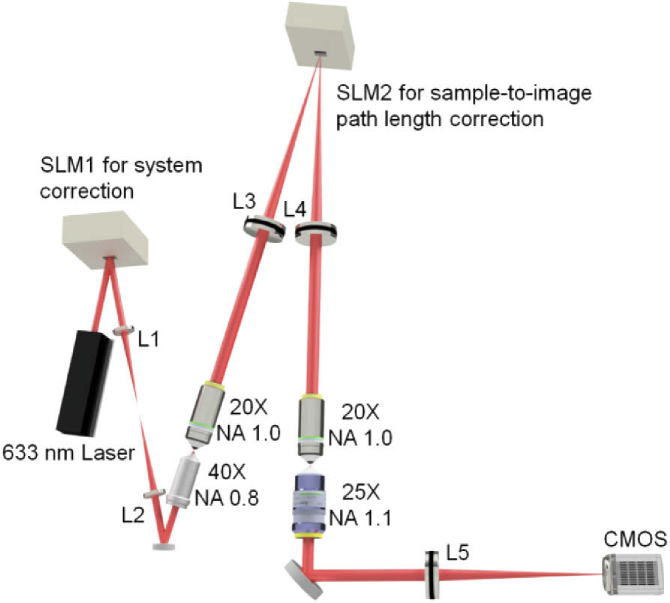
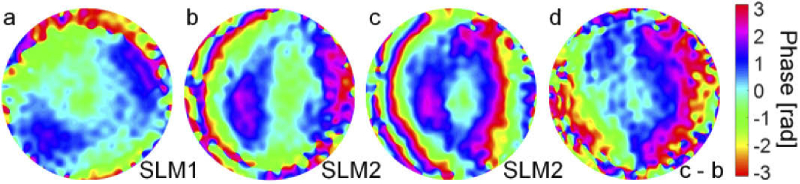
Experimentally we implemented a remote focusing system with an input NA of 0.8 (Fig. 2). We used a pair of identical objective lenses of NA 1.0 to relay the focus. For detection, we used a NA 1.1 objective lens. The laser wavelength was 633 nm. We used SLM1 to measure and correct the overall system aberration (Fig. 3(a)) only at zero defocusing. The wavefront measurement was based on the parallel phase modulation technique developed by our lab [28,33–35]. Basically, we kept half of the pixels on the SLM stable while simultaneously modulating the other half of the pixels, each pixel at a unique frequency, and then retrieved the phase information through the Fourier transform of the focus intensity modulation data. The second SLM was positioned on the common imaging plane (SLM2 in Fig. 2) for sample-to-image path length correction. We performed wavefront measurement only at +280 and −280 μm defocusing (+ means moving the 40x away from the 20x). At either position, the wavefront (Figs. 3(b) and 3(c)) occupied ∼420 μm FOV on the sample plane and 11.7 mm on SLM2 (active area 12 × 16 mm²).

Fig. 2.

Optical configuration for the image-plane correction based long-range remote focusing. L1-L5, telecentric lenses of focal length 100, 100, 250, 250, 200 mm, respectively; SLM 1 and 2, phase only spatial light modulators (Hamamatsu). All objectives are water dipping lenses (40x and 25x from Nikon, 20x from Olympus).

Fig. 3.

(a) System correction wavefront measured by SLM1. (b, c) Image-plane correction wavefront measured by SLM2 at −280 and 280 μm defocusing, respectively. (d) The phase difference between b and c.

3. Results

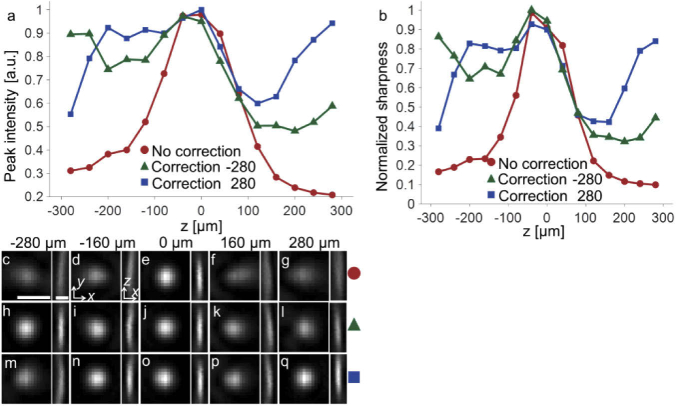
With the system correction (Fig. 3(a)) applied, the measured focus size (x = 0.434, y = 0.472, z = 2.64 μm) at 0 defocusing was very close to the diffraction limited value (x = 0.443, y = 0.475, z = 2.16 μm) which was based on the rigorous vector computation [36] for linearly polarized incident light and a pupil filling factor of 1 for NA 0.8 (matching the intensity profile measured at the pupil of the 25x objective lens). Using either correction (Figs. 3(b) and 3(c)), we could achieve a greater high-peak-intensity defocusing range (Fig. 4(a)). For example, the defocusing range for achieving above ∼70% peak intensity (with respect to the zero defocusing value) was 153 μm without the sample-to-image path length correction. The range was extended to 423 and 338 μm with the correction measured at 280 and −280 μm defocusing applied, respectively. Similarly, the range for achieving above ∼80% peak intensity was only 123 μm without correction. The range was extended to 359 and 215 μm with the correction measured at 280 and −280 μm defocusing applied, respectively.

Fig. 4.

(a) Focus peak intensity as a function of defocusing. (b) Image sharpness (the summation of pixel intensity square divided by the square of pixel intensity summation) as a function of defocusing. (c-g) Transverse and axial focus profiles measured without path length correction at −280, −160, 0, 160, and 280 μm defocusing, respectively. Scale bar: 1 μm. (h-l) Focus profile with the path length correction measured at −280 μm defocusing applied. (m-q) Focus profile with the path length correction measured at 280 μm defocusing applied.

4. Discussion

The results show that the sample-to-image path length correction was indeed effective in extending the range of remote focusing system. Specifically, the range for high-quality focusing was increased by ∼300%. We noticed that the focus intensity plot (Fig. 4(a)) was not entirely flat and the correction measured at one side of the defocusing range was not fully effective on the other side. This was likely due to the imperfect optical performance or alignment of the two 20x objectives and the relay lenses (L3 and L4 in Fig. 2). Nevertheless, the achieved axial scan range was already substantial for many imaging applications [37,38].

One concern for high power laser applications is that the wavefront corrector was positioned on the image plane. For zero defocusing, it means that the laser focus will dwell on the device surface. One solution is to fabricate a freeform reflective metal surface using high-precision diamond milling to serve as the wavefront corrector. Without phase wrapping, it will also offer better achromatic performance than SLM for broadband emission sources. A similar idea is to leverage the advance of freeform glass fabrication [39] to make a transparent wavefront corrector. Both the metal reflector and the glass corrector will greatly enhance the power handling capability.

The defocusing range was measured at 633 nm wavelength in this work. For applications that utilize longer wavelength (e.g. ∼930 nm in two-photon laser scanning microscopy), the range will be even longer because the Strehl ratio has approximately a negative exponential dependence on the square of the optical frequency [40]. The lower refractive index and longer wavelength can inherently tolerate more imperfection.

5. Conclusion

In this work, we analyzed the requirement to achieve perfect remote focusing. The sample-to-image path length conservation is crucial to avoid aberration for relaying defocused wavefront, which can be satisfied by a perfect telecentric relay system. To compensate for the sample-to-image path length variation, we propose to position a wavefront corrector at the common image plane of the remote focusing system. Experimentally, we increased the defocusing range by ∼300% using such a method for high-quality focusing. As high-speed 3D scanning is becoming widely adopted in many disciplines, we expect that the proposed method will find a broad range of applications and inspire innovations.

Funding

National Institutes of Health10.13039/100000002 (RF1MH120005, U01NS094341, U01NS107689).

Disclosures

The authors declare no conflicts of interest.