Lagrangian modeling of inactivation of airborne microorganisms by in-duct ultraviolet lamps

Abstract

There has been increasing interest in modeling the UV inactivation on airborne microorganisms via the Lagrangian approach as a result of its outstanding features in calculating UV dose with particle trajectory. In this study, we applied the Lagrangian method to model the disinfection performance of in-duct UV lamps on three bacteria: Pseudomonas alcaligenes, Salmonella enterica and Escherichia coli, respectively. For modeling, the airborne bacteria's inactivation was determined by critical survival fraction probability (CSFP) and maximal bearable UV dose (MBUD) methods, respectively. The results indicated that Lagrangian modeling utilizing the MBUD method needs to appropriately evaluate the maximal UV dose (D_mb), which is bearable for airborne microorganisms. The disinfection efficacy obtained by using the CSFP method agreed well with experimental measurements. Within the Lagrangian framework, the recommended empirical value for critical survival fraction (F_sc) was 0.4 for modeling the disinfection efficacy of in-duct UV lamps. Besides, the disinfection efficacies of in-duct UV lamps with full luminous length on P. alcaligenes and E. coli were 100% with Re within the range of 4.11 × 10⁴ to 8.22 × 10⁴. Moreover, the present numerical model was also applied for further validation with inactivation measurements of in-duct UV lamps performed by the U.S. Environmental Protection Agency (EPA). Based on the results, the UV disinfection efficacies obtained by the present modeling method had a closed agreement with EPA experimental results. It deserved to pay more investigations on the optimal value of F_sc in further for accurately applying Lagrangian modeling on air UV disinfection.

1. Introduction

Over the past two decades, the prevalence of respiratory diseases has extremely threatened public health security and negatively impacted society and economic development. Among these diseases are influenza, tuberculosis (TB), severe acute respiratory syndrome (SARS) in 2003, middle east respiratory syndrome (MERS) in 2012 and novel coronavirus disease (COVID-19) pandemic [[1], [2], [3], [4]]. Recently, the World Health Organization (WHO) reported that COVID-19 has caused more than 770,866 deaths worldwide until 18 Aug 2020 [5]. However, there is no effective treatment for this emerging virus so far [6]. It has been demonstrated that respiratory illness virus transmitted through aerosol transmission and mainly infected people via close-contact, respiratory droplet, saliva and droplet nuclei [1,2,[7], [8], [9]]. Active preventive measures are necessary to cut off the aerosol transmission of respiratory illness virus. Individual protection such as facemask is usefully suggested to cut off airborne pathogen transmission between an infected person and healthy person [10], whereas sterilization technologies are also necessary to reduce the risk of infection.

Recently, different disinfection approaches, have been investigated such as ultraviolet germicidal (UVGI) lamp, negative ionizer and cold plasma, for inactivating airborne pathogens in heating, ventilation, and air conditioning (HVAC) systems [[11], [12], [13], [14]]. Although an HVAC system delivers comfortable humidity and air temperature in the indoor environment, it may also become airborne pathogens source by a poor corresponding maintenance [15,16]. Based on previous works, it was found that the UV lamp installed in the HVAC system significantly results in fewer work-related symptoms among office people [17,18]. Recent studies indicated that installing UVGI lamp in ventilation duct (in-duct) is an energy-saving and efficient way to avoid airborne bacteria transmit from the HVAC system to the indoor environment [[19], [20], [21], [22]].

The computational fluid dynamics (CFD) technique is one of the most convenient ways to assess the performance of UVGI. CFD method is beneficial in obtaining airborne bacteria local movement characteristics under complicated airflow pattern by numerically solving air fluid and airborne bacteria conservation equations. Eulerian and Lagrangian methods are both common CFD methods in modeling airborne bacteria movement [[23], [24], [25]]. In the former, airborne bacteria are treated as the continuous phase and airborne bacteria movement is described by the scalar transport equation. The Eulerian method has been successfully utilized to simulate the inactivation of in-duct UVGI and upper-room UVGI [19,[26], [27], [28], [29]].

The Lagrangian method is another CFD option for modeling airborne bacteria movement in an indoor environment. Airborne bacteria are considered as the discrete particles and each particle's movement is tracked by incorporating its force balance equation along the trajectory. Lagrangian simulations have been extensively utilized to model the movement characteristic of discrete contaminant source pollution, coughing, and sneezing [[30], [31], [32], [33]]. Studies indicated that both Eulerian and Lagrangian methods could simulate particle deposition and dispersion well in ventilated rooms, however, the results indicated that the Lagrangian method is much more efficient than the Eulerian method in modeling unsteady source of the particle [31]. Zhang and Chen (2007) [31] studied coughing cases in a ventilated airliner cabin utilizing the Eulerian and Lagrangian methods. They found that the Eulerian method needs sufficiently small time step and hundreds of iterations per step to solve particle concentration equation together with momentum and energy equations, however, the Lagrangian method did not take more extra computing time for particle tracking in comparison to the steady cases.

The Lagrangian approach has been applied successfully in simulating the UV/H₂O water disinfection system [[34], [35], [36]]. In water advanced oxidation processes, hydroxyl radicals are generated by UV irradiance combined with chemical species to degrade organic compounds [35]. Nevertheless, the knowledge of UV water disinfection cannot be applied directly to air disinfection. UVC light can be refracted and reflected in water, and irradiance is attenuated more quickly than in air. Hence, air disinfection requires a lower UV dose than water disinfection for achieving the same disinfection efficacy [37]. In recent years, the increasing interest in the application of in-duct UV disinfection to prevent airborne pathogen transmission in HVAC systems has intensified the need for the Lagrangian method to numerically study the UV irradiation's disinfection performance.

Different from the Eulerian method for modeling the UV disinfection efficacy, within the Lagrangian method, UV dose received by airborne bacteria is integrated along with airborne bacteria trajectory. In the particle force balance equation, UV inactivation cannot be considered as an additional item since it is not a vector force. The effect of UV inactivation is determined by the viability of airborne microorganisms. When UV irradiance damages the airborne bacteria's deoxyribonucleic acid (DNA), the airborne microorganisms cannot replicate by itself and it is regarded as inviable status. Then, the inviable bacteria will be deleted from the tracked list. Hence, in Lagrangian modeling, the criterion for airborne microorganisms losing viability must be predetermined. Previous studies employed critical survival fraction probability (CSFP) and maximal bearable UV dose (MBUD) methods. In the latter method, the bacteria are considered with lost viability when receiving a higher UV dose than maximal bearable UV dose recommended by previous works. However, the former method utilized airborne microorganisms' survival exponential function to judge the viability of bacteria. If the statistics of survival fraction of airborne microorganisms were lower than critical survival fraction (F _sc) in simulation, bacteria were considered with lost viability. Alani et al. (2001) used Lagrangian modeling UV disinfection on tuberculosis (TB) bacteria in a ventilated isolation room. In their studies, viable TB would become inactive when receiving 500 μJcm⁻² or higher UV doses [38]. Their maximal bearable UV dose refers to the results that 50% test bacteria have been inactivated in 500 μJcm⁻² UV dose in the experiment [39]. In the literature, using the CSFP method seems more popular than the MBUD method in determining the bacteria viability for Lagrangian modeling. For instance, Xu et al. (2013) and Pichurov et al. (2015) studied numerically upper-room ultraviolet germicidal on Mycobacterium parafortuitum and Bacillus atrophaeus in a ventilated room using the CSFP method [40,41]. Pichurov et al. (2015) found Lagrangian modeling was more accurate than Eulerian modeling [41]. Capetillo et al. (2015) investigated the performance of multi UV lamps in the ventilation duct using the CSFP method based on the Environmental Protection Agency (EPA) UVGI experiment [42]. In the above three numerical works, bacteria viability was all determined via bacteria survival fraction probability. Nevertheless, the optimal value of critical survival fraction was not given and the effect of critical survival fraction on UV disinfection was never investigated. The Lagrangian method is advantageous in calculating of UV dose since the calculation accumulation was along a particle moving trajectory. Though, its accuracy was closely dependent on the application of CSFP and MBUD methods in the right way. However, no studies have been performed to compare the accuracy of CSFP and MBUD methods.

In this work, we applied the Lagrangian method to assess the inactivation of the in-duct UVGI lamp on Escherichia coli (ATCC 10536), Pseudomonas alcaligenes (ATCC 14909), and Salmonella enterica (ATCC 53648). The differences between the above two bacteria viability judgment methods were numerically investigated and compared with the experimental findings. The UV dose was calculated in the simulations with the exposure time and spatial irradiance. The spatial irradiance is the sum of emissive and diffusive irradiance, which were predicted by a mathematical model. To further validate the present CSFP method, EPA's in-duct UV inactivation experiment was also studied. The average UV dose and disinfection efficacy were compared in detail. The findings will provide multi perspectives to comprehend the in-duct UV inactivation performance.

2. Simulation methods

The Eulerian-Lagrangian method was used in our simulation to model the air and airborne microorganisms. The air phase was regarded as the continuous carrier fluid and simulated by the Eulerian method, however, airborne microorganisms’ dispersion in the air was modeled by the Lagrangian method. It was presumed that airborne microorganisms follow airflow without disturbing the airflow structure. The turbulent airflow in the ventilation duct was treated by the realizable k - ε model. Through the discrete random walk (DRW) model, the dispersion of airborne microorganisms was described to consider particle instantaneous fluctuating turbulent velocity utilizing stochastic methods. The instantaneous fluctuating turbulent velocity obeyed the Gaussian probability distribution assumption which was defined as

$$\overrightarrow{v`}=\varsigma \sqrt{\frac{2k}{3}}$$ (1)

where $\overrightarrow{v`}$ is air instantaneous fluctuating velocity vector, ζ represents normally distributed random number, and k denotes turbulent kinetic energy.

2.1. Lagrangian model

By integrating the force balance on airborne microorganisms, the trajectory of airborne microorganisms was described and the force balance equation was expressed as [43]:

$$\frac{d{\overrightarrow{v}}_b}{dt}=F_d\left(\overrightarrow{v}-{\overrightarrow{v}}_b\right)+\frac{\overrightarrow{g}\left({\rho }_b-\rho \right)}{{\rho }_b}+{\delta }_i\sqrt{\frac{\pi S_0}{\Delta t}}+\frac{5.188{\nu }^{1/2}\rho d_{ij}}{{\rho }_b{d}_b{\left(d_{lk}{d}_{kl}\right)}^{1/4}}\left(\overrightarrow{v}-{\overrightarrow{v}}_b\right)$$ (2)

The terms in the right part of Eq. (2) represent the Stokes' drag force, gravity, Brownian force and Saffman's lift force, respectively. $\overrightarrow{v}$ is air velocity, ${\overrightarrow{v}}_b$ represents the airborne microorganism velocity and F _d is written as

$$F_d=\frac{18\mu }{{\rho }_b{d}_b^2{C}_c}$$ (3)

where μ is the molecular viscosity of air, ρ denotes the air density, ρ _b is airborne microorganism density, ρ _b = 1000 kgm⁻³, d _b represents airborne microorganisms diameter, d _b = 1.0 μm, C _c is the Cunningham correction:

$$C_c=1+\frac{2\lambda }{d_b}\left(1.257+0.4e^{-\left(1.1d_b/2\lambda \right)}\right)$$ (4)

where λ represents the molecular mean free path, λ = 66 × 10⁻⁹ m, $\overrightarrow{g}$ is the gravity vector, δ _i denotes Gaussian random numbers, Δt is time step and

$$S_0=\frac{216\nu k_{B}T}{{\pi }^2\rho d_b^5{\left(\frac{{\rho }_b}{\rho }\right)}^2{C}_c}$$ (5)

T is the absolute air temperature, ν represents the kinematic viscosity, k _B denotes the Boltzmann constant, k _B = 1.38 × 10⁻²³ m²kgs⁻²K⁻¹ and d _ij is the deformation tensor.

The boundary condition of Eq. (2) was adjusted with “escaped” for ventilation duct inlet and outlet, and it was “trapped” for ventilation duct wall and UVGI lamp wall, respectively.

2.2. The UV dose was given as

$$D=\underset{t_i}{\overset{t_p}{\int }}{I}_r\left(x,y,z\right)dt$$ (6)

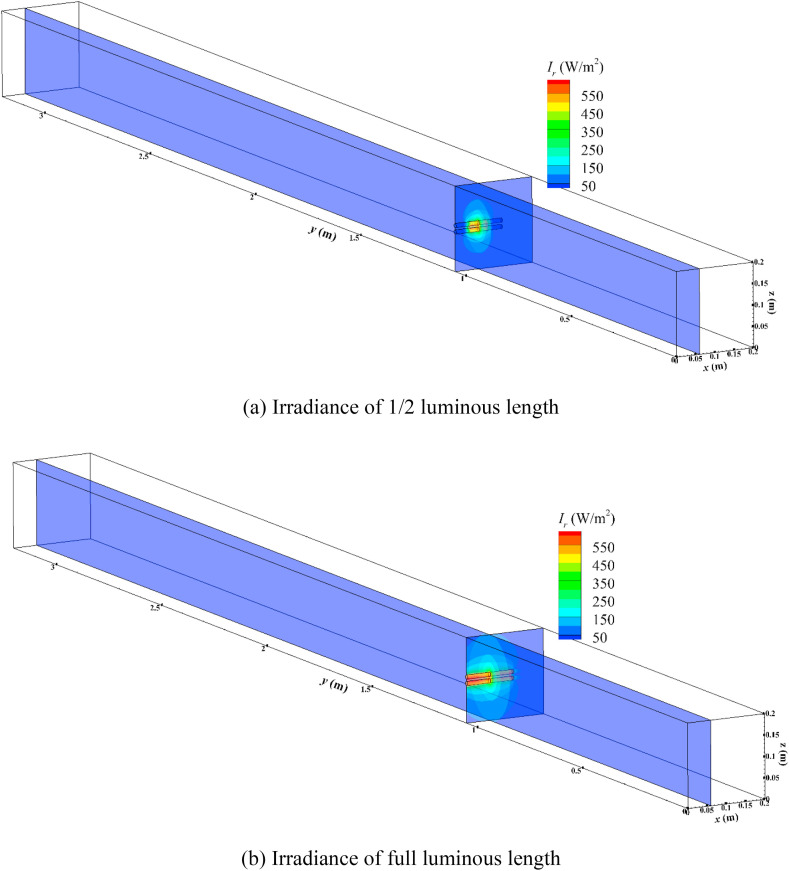
where D represents the UV dose received by airborne microorganisms, Jm⁻², t _i, and t _p are time in which airborne microorganisms enter the ventilation duct and arrive present location, respectively. I _r(x, y, z) is the spatial irradiance at spatial location (x, y, z) and I _r(x, y, z) is predicted through a mathematical model introduced in our previous works [44]. Fig. 1 represents the predicted spatial irradiance of half and full luminous length of in-duct UVGI lamp. Spatial irradiance (I _r(x, y, z)) includes emissive irradiance from UVGI lamp and diffuse irradiance reflected from the duct wall. It should be noted that the predicted spatial irradiance can be also regarded as equivalent to fluence rate that is defined to evaluate the UV power per unit area at a specific point from all directions incoming UVC rays [[45], [46], [47]]. The prediction was already validated in our previous works [44]. During the simulation process, Eq. (6) was numerically solved along the trajectory of airborne microorganisms.

Fig. 1.

The irradiance contour of in-duct UVGI lamp.

When airborne microorganisms expose to irradiance, the survival fraction (F _s) is an exponential function [19,29] and it is written as

$$F_s=e^{-Z\cdot D}$$ (7)

where Z represents the susceptibility of airborne microorganisms and is also termed Z value, m²/J. F _s is also the ratio of the number of airborne microorganisms gathered in the sample plane under in-duct UV lamp-on and lamp-off conditions.

The disinfection efficacy (η) of in-duct UVGI is evaluated with UVGI lamp off and on experiments [19,48]. Based on this method, the disinfection efficacy (η) can be calculated as,

$$\eta =\left(1-\frac{\sum _t{\left(n_{on,sampling}\right)}_t}{\sum _t{\left(n_{off,sampling}\right)}_t}\right)\times 100\%$$ (8)

where $\sum _t{\left(n_{on,sampling}\right)}_t$,$\sum _t{\left(n_{off,sampling}\right)}_t$are airborne microorganisms collected in sample plane (y = 1.4 m) for in-duct UVGI lamp on and off circumstances, respectively. When airborne microorganisms receive higher UV doses, the calculated F _s of microorganisms will be lower. If the UV dose received by microorganisms is lower than the critical survival fraction (F _sc), then the airborne microorganisms will be regarded as inactivation. At last, fewer airborne microorganisms will be counted in downstream and the disinfection efficacy will be higher.

To better understand the fate of airborne microorganisms in the duct, the percentages of airborne microorganisms dealt with various mechanisms were also determined. The percentage of airborne microorganisms inactivated by UV irradiation is defined as

$$P_{uv}=\frac{\sum _{t=0}^{\tau }{\left(n_{in}-n_{trap}-n_e\right)}_t-n_s}{\sum _{t=0}^{\tau }{n}_{in,t}}\times 100\%$$ (9)

where τ is the total computational time, n _in,t represents the number of airborne microorganisms injected from inlet boundary surface at time t, n _trap denotes the number of airborne microorganisms trapped by the duct wall surface at time t, n _e represents the number of airborne microorganisms escaped from ventilation duct outlet at time t, n _s is the number of airborne microorganisms suspended in the air at last. The numerator indicates the total number of irradiance-inactivated airborne microorganisms during the computational time.

The percentage of airborne microorganisms eliminated by other mechanisms was defined as

$$P_j=\frac{\sum _{t=0}^T{\left({\varphi }_k\right)}_t}{\sum _{t=0}^T{n}_{in,t}}\times 100\%$$ (10)

where P _j is the percentage of airborne microorganisms dealt with different mechanisms, ϕ _k represents the expression of various mechanisms, the expressions of P _j and ϕ _k are provided in Table 1 .

Table 1.

Expressions of P_j and ϕ_k.

Pj	Pe	Ptrap	Ps
ϕk	ne	ntrap	ns

Subscript e, trap and s represent airborne microorganisms which escape from outlet, are trapped by wall and suspend in air, respectively.

2.3. Numerical procedure

Experiments were performed to assess the disinfection of 1/2 and full luminous length of in-duct UVGI on P. alcaligenes, E. coli and S. enterica with 9 m × 0.2 m × 0.2 m galvanized steel ventilation duct system for Re from 4.11 × 10⁴ to 9.58 × 10⁴ (velocity 3–7 m/s) in our previous work before [19,44]. The susceptibility constants of test bacteria and disinfection efficacy were investigated within experiments. Harvest bacteria solution was continually nebulized with clean compressed air in duct upstream during the experiment. One UVC lamp (Philips PL-S TUV 9W) luminous tubes were inserted into the duct from the side while leaving accessories outside of the duct. The irradiance was measured with a radiometer (ILT1400, International Light Technologies) downstream of the UVC lamp. The sample was collected at the UVC lamp downstream 0.35 m plane. More details of the experiment were provided in our previous works [19,44].

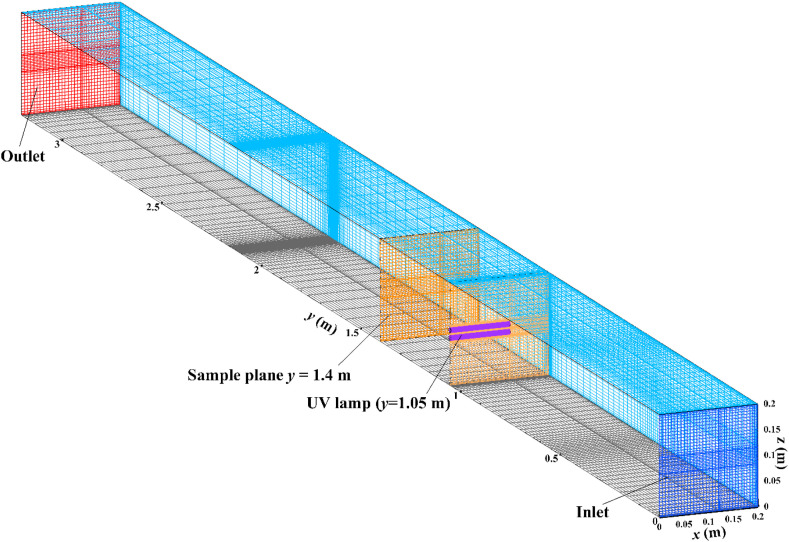
In this study, simulation cases were set based on the experiments. In the numerical physical model, the length of the ventilation duct was 3.2 m and one UVGI lamp was installed at the location y = 1.05 m from the inlet. It was assumed that the airflow pattern has been fully developed at the inlet. Fig. 2 represents the computational grid style where 267,106 non-uniform structure grid cells were used in the simulation. The bare luminous tubes were inserted from the left wall of the duct. For 1/2 luminous length lamp, luminous tubes were covered with black tape from two sides and maintained only half luminous length tubes in the center. Airborne microorganisms were assumed to be spherical with 1000 kg/m³ density and 1.0 μm diameter. At first, by solving continuity, momentum, and turbulence equations, the airflow field was obtained. The air velocity was monitored at the center of the duct in the process and by the steady value, the modeling will stop. Then, irradiance was calculated with a mathematical model coded into ANSYS Fluent solver with user-defined functions. The predicted spatial irradiance was maintained in each numerical grid cell. The trajectory of airborne microorganisms was obtained by integrating the Lagrangian force balance equations (Eq. (2)) based on the computational airflow field and predicted irradiance. Survival fraction (F _s) and UV dose (D) were calculated with the predicted irradiance saved in computational grid cells by existing the tracked airborne microorganisms. Airborne microorganisms were injected from the duct inlet surface at the beginning of each time-step. The injected numbers of airborne microorganisms may affect computational time and numerical accuracy. To minimize the impact of injected particle numbers, the disinfection efficacy of half luminous length in-duct UVGI lamp on E. coli was modeled at Re = 8.22 × 10⁴ (v = 6 m/s) for injected numbers of 3404, 5106, 10212 and 49358, respectively. The disinfection efficacies are presented in Table 2 . The results indicated that η obtained by three different injected numbers was within the range of 48.6%–48.9%, however, the disinfection efficacy of another injected number was 49.1%. The disinfection efficacies were difficult to distinguish for different injected numbers. Ultimately, 5106 particle numbers were used to save computational resources and time.

Fig. 2.

The grid style of the simulation cases.

Table 2.

Disinfection efficacy (η) of 1/2 luminous length of in-duct UVGI lamp on E. coli for different injected airborne microorganisms with F_sc = 0.4 and Re = 8.22 × 10⁴ (v = 6 m/s).

Particle number	Disinfection efficacy η
3404	48.6%
5106	48.8%
10212	49.1%
49358	48.9%

To couple with the pressure and velocity, the SIMPLE algorithm was used. Using the second Order Upwind scheme, the convection terms were discretized except the QUICK scheme for the airborne bioaerosol transport equation. Then, Green-Gauss Cell-Based theorem was used to calculate the gradient. The transient term was discretized with the First Order Implicit scheme. The airborne microorganisms’ motion equations were solved with the implicit and Runge-Kutta scheme. The equations were numerically solved in unsteady-state with the time step of 0.1 s. During the numerical simulation, the highest residual value was less than 10⁻⁵s and a high residual value was always found in the dissipation rate (ε) equation.

3. Results and discussion

3.1. Effects of critical survival fraction (F_sc)

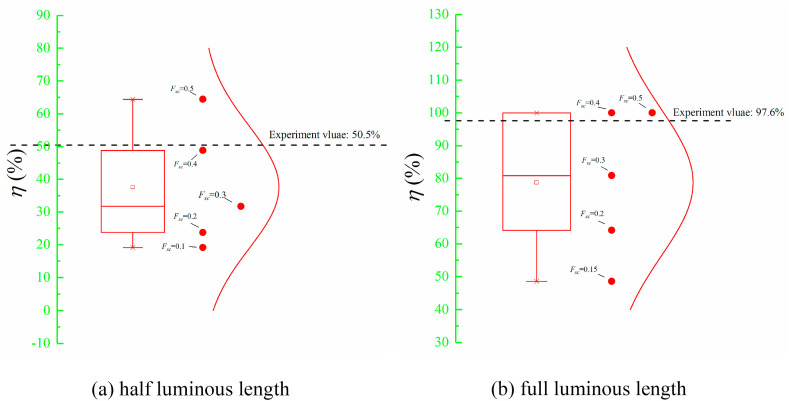
The effects of critical survival fraction (F _sc) were assessed for modeling the disinfection efficacy of an in-duct UV lamp with two luminous lengths on E. coli at Re = 8.22 × 10⁴ (v = 6 m/s). The discrete data points in Fig. 3 were the disinfection efficacy (η) of the in-duct UV lamp obtained by the corresponding label F _sc case. The range of the box chart was determined by the 25th and 75th percentiles of the disinfection efficacies’ data. The upper and lower lines in the box chart represent the maximum and minimum values, respectively. The results indicated that there is a monotonous relationship between disinfection efficacy (η) and F _sc. The reason is if F _sc was higher, airborne microorganisms were easily regarded as inactivated microorganisms and they had a higher probability to be eliminated from the particle trajected list. Ultimately, fewer airborne microorganisms can pass through the UV irradiance field to arrive at the sample plane, hence, the higher disinfection efficacy will be resultant. Because the spatial irradiance was much higher for UV lamp with full luminous length compared to the half luminous length, the disinfection efficacy (η) of UV lamp with half luminous length was lower than the full luminous case at the same F _sc. The disinfection efficacy (η)was over 100% with F _sc = 0.4 for full luminous length case (Fig. 3 (b)) and η there is no significant difference after following a higher F _sc case. It can be observed that the numerical results of η are very close to the experiment values by adjusting F _sc as 0.4 for both luminous length cases. Hence, F _sc = 0.4 was recommended for modeling the disinfection efficacy through Lagrangian methods.

Fig. 3.

Disinfection efficacy (η) of in-duct UVGI lamp on E. coli for different F_sc with Re = 8.22 × 10⁴ (v = 6 m/s).

3.2. Comparing two bacteria viability judgment methods

MBUD and CSFP judgment methods were used to study the disinfection of half luminous length in-duct UV lamp on E. coli at Re = 4.11 × 10⁴–9.58 × 10⁴ (velocity 3–7 m/s), respectively. In the simulation, the maximal UV dose (D _mb) was kept at 500 μJcm⁻² based on the disinfection tests on Serratia marcescens and Mycobacterium bovis BCG [38].

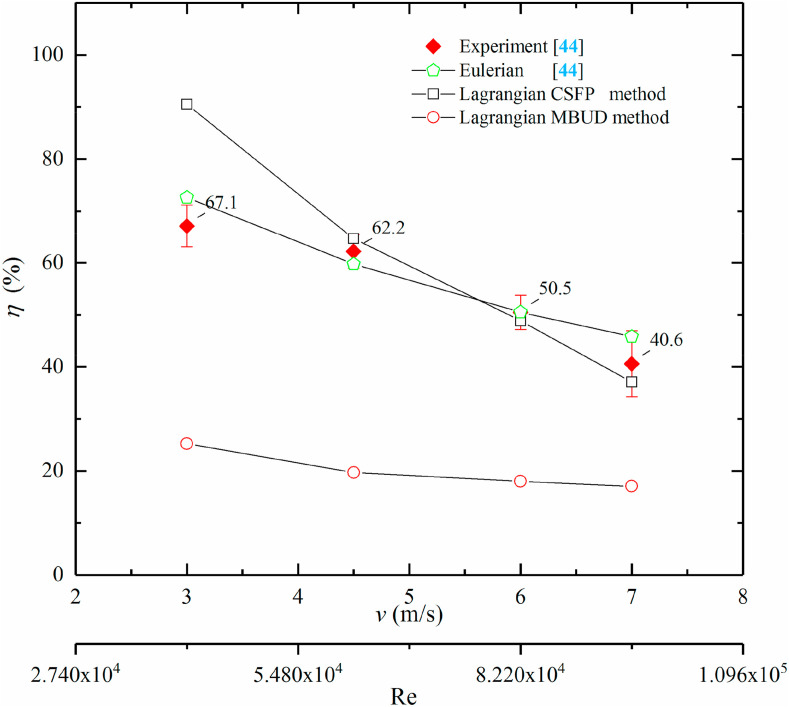
In Fig. 4 , the results obtained with CSFP and MBUD methods are presented and compared with experiment and Eulerian modeling results which were reported in our previous works [44]. It was indicated that the disinfection efficacies (η) obtained by MBUD approaches were much lower than others. However, the disinfection efficacies gained by the CSFP method were well consistent with experiment value except at Re = 4.11 × 10⁴ (v = 3 m/s) and they were slightly better than the results from Eulerian modeling. Since the effects of Z-value and UV dose (Eq. (7)) were both considered for the calculation of F _s in the CSFP method, there was a good agreement between the results from the CSFP method and the experimental values. The results also suggested that utilizing the MBUD method in the Lagrangian modeling needs to further consider the individual discrepancy of airborne microorganisms for predicting the disinfection efficacy of UV lamps. Namely, if Lagrangian modeling was used along with the MBUD method, optimal value of D _mb should be evaluated for the test airborne microorganisms at first. It is worth noting that Eq. (7) is also one of the best ways to calculate D _mb. If the D _mb in the MBUD method is calculated by Eq. (7) using the Z value of tested airborne microorganisms and the corresponding F _sc, then the results of the MBUD method will be equivalent to that of the CSFP method.

Fig. 4.

Disinfection efficacy (η) of half luminous length of in-duct UVGI lamp on E. coli for different methods with Re = 4.11 × 10⁴–9.58 × 10⁴ (velocity 3–7 m/s).

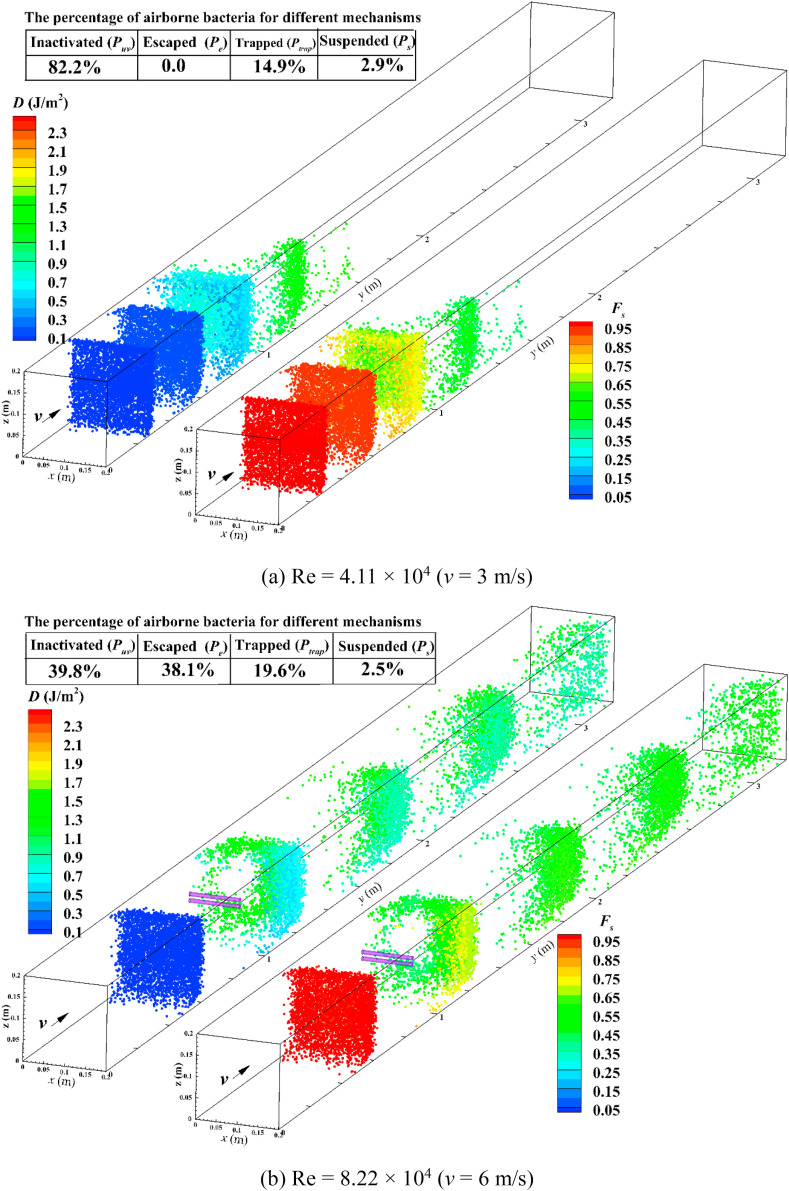
Fig. 5 displays UV dose (D) and survival fraction (F _s) of E. coli for in-duct UV lamp with half luminous length at F _sc = 0.4 and various Re utilizing CSFP method. The values of D and F _s were illustrated by different colors with survival airborne microorganisms in the last time step. Since airborne microorganisms spent a longer time in the duct, they have more chances for irradiance exposure. Therefore, the values of D incremented along the airborne microorganism's trajectory. Considering an inverse trend of the variation of F _s, the airborne microorganisms received more UV dose and lower survival fraction, ultimately. Under higher velocity of airflow, airborne microorganisms will travel more quickly through the duct and they will receive a lower UV dose. Therefore, more airborne microorganisms survived in Re = 8.22 × 10⁴ than in Re = 4.11 × 10⁴. This is also in line with the decrement tendency of disinfection efficacy in Fig. 4. The figure also represents the percentage of airborne microorganisms that dealt with other mechanisms. A reduction was observed in the percentage of airborne microorganisms inactivated by irradiance (P _uv) from 82.2% to 39.8% by increasing Re from Re = 4.11 × 10⁴ to Re = 8.22 × 10⁴. However, the percentage of particles escaped from the outlet (P _e) changed from 0% to 38.1%. The reason is the airborne microorganisms survived from irradiance inactivation, which has a higher chance of elimination by ventilation air.

Fig. 5.

UV dose (D) and survival fraction (F_s) of E. coli for half luminous length of in-duct UV lamp with F_sc = 0.4 and different Re.

3.3. Disinfection by in-duct UV lamp on airborne microorganisms

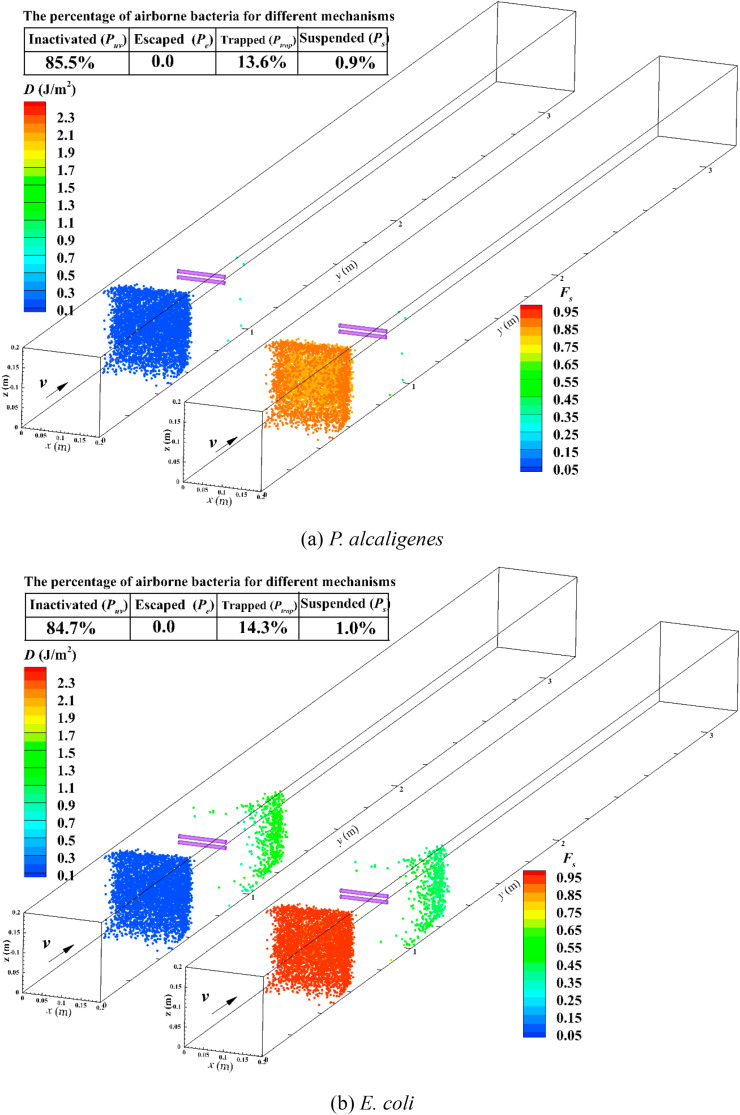
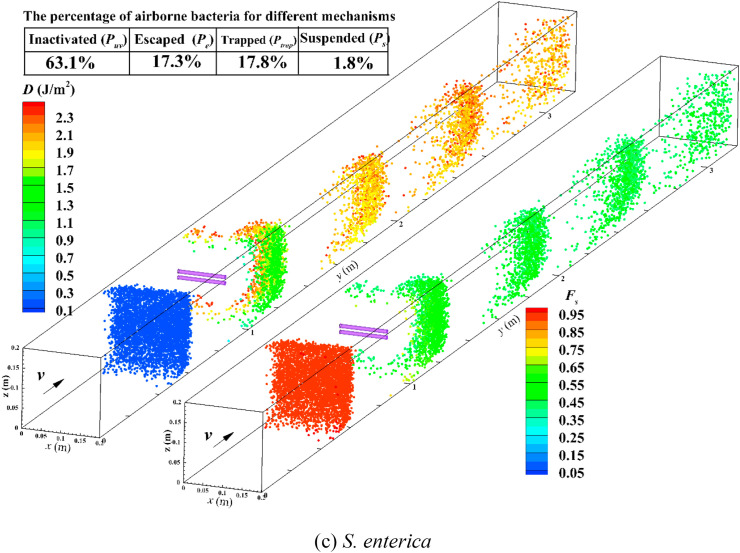
The disinfection of in-duct UV lamps with full luminous length on P. alcaligenes, E. coli and S. enterica were assessed with F _sc = 0.4 for various Re, respectively. Fig. 6 shows the UV dose (D) and survival fraction (F _s) with F _sc = 0.4 and Re = 8.22 × 10⁴. The results showed that P _uv was 85.5%, 84.7% and 63.1% for P. alcaligenes, E. coli and S. enterica accordingly. Moreover, their Z-values reported in our previous work [19] also reduced in the following order: 1.0 m²/J, 0.6 m²/J, and 0.39 m²/J. It can be stated that bacteria with higher Z-value was more sensitive to irradiance. The percentage of S. enterica suspended in air (P _s) was 1.8%, which was the highest value among the three test bacteria. Few airborne microorganisms suspended in the duct were caused by the fact that airflow in the duct was a single-pass pattern without further disturbance. Moreover, airborne microorganisms cannot stay for a long time in high airflow rate cases, and for low airflow rates, they would easily receive enough UV dose for inactivation. The disinfection efficacies of three test bacteria with different Re are shown in Fig. 7, Fig. 8, Fig. 9 . The disinfection efficacies of P. alcaligenes and E. coli were nearly 100% for Re from 4.11 × 10⁴ to 8.22 × 10⁴, however, η was lower for S. enterica and it reduced from 100% to 71.6%. This also can be directly perceived from the nonexistence of P. alcaligenes and E. coli at downstream of the sampling surface (y = 1.4 m) in Fig. 6. Besides, the modeling accuracies of results of the Lagrangian-CSFP method and Eulerian method were compared by using one-way analysis of variance (ANOVA) compared to the experimental results. The probability values (P-values) of Lagrangian-CSFP and Eulerian methods are 0.70 and 0.81 for half luminous length cases (Figs. 4), 0.99 and 0.51 for full luminous length cases (Fig. 7, Fig. 8, Fig. 9), respectively. The results indicated that the Lagrangian CSFP method is relatively better than the Eulerian method for full luminous length cases (larger P-value for Lagrangian than that for Eulerian), whereas it is just the reverse for half luminous length cases. This may be due to the difference in UV dose estimations among these two methods. The Lagrangian method integrates the UV dose along the movement trajectories of airborne microorganisms and the microorganisms’ trajectories can be highly affected by the turbulent vortex. For half luminous length cases, airborne microorganisms receive less UV dose than in full luminous length cases. Airborne microorganisms will have a chance to arrive nearby the nonluminous part of the UV lamp and the integration may be affected by turbulent eddy more obviously in this area. While the Eulerian method considers the inactivation of UV irradiance as the sink term in microorganism transport equations. This sink term is the product of Z value, spatial irradiance, and spatial concentration of airborne microorganisms. Thus, the calculation of UV dose in the Eulerian method is not directly affected by the flow pattern compared to the Lagrangian method.

Fig. 6.

UV dose (D) and survival fraction (F_s) of different airborne microorganisms for in-duct UV lamp with full luminous length at F_sc = 0.4 and Re = 8.22 × 10⁴ (v = 6 m/s).

Fig. 7.

Disinfection efficacy (η) of full luminous length of in-duct UV lamp on P. alcaligenes for different methods with F_sc = 0.4.

Fig. 8.

Disinfection efficacy (η) of full luminous length of in-duct UV lamp on E. coli for different methods with F_sc = 0.4.

Fig. 9.

Disinfection efficacy (η) of full luminous length of in-duct UV lamp on S. enterica for different methods with F_sc = 0.4.

Fig. 10 represents the average UV dose (D _avg) calculated on the y = 1.4 m sample plane for various luminous length of in-duct UV lamp and air supply velocity without considering UV inactivation. Average UV dose (D _avg) was the arithmetic mean of UV dose of airborne microorganisms sampled in-plane (y = 1.4 m) expressed as [42]:

$$D_{avg}=\frac{\sum _{i=1}^n{D}_i}{n}$$ (11)

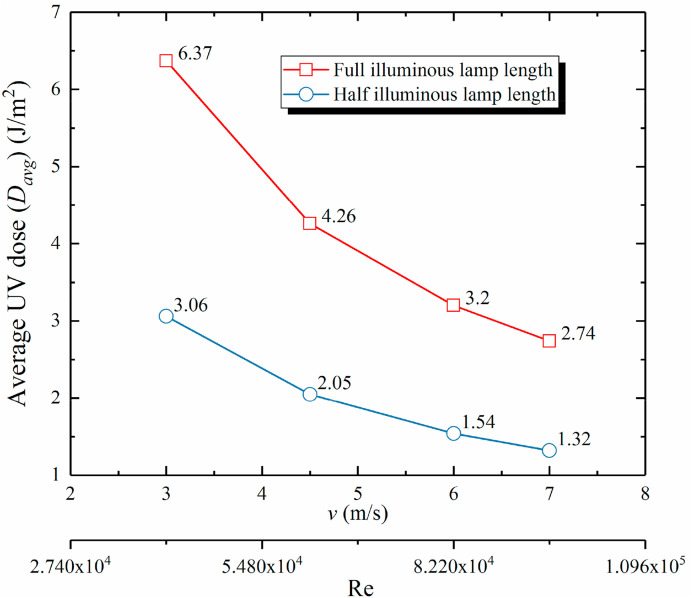
where n is the total number of particles sampled in-plane and D _i represents the UV dose of particle i. To calculate the average UV dose, it was supposed that airborne microorganisms were immune to ultraviolet disinfection. The bacteria can travel through the duct without considering ultraviolet inactivation and regardless of UV dose received by the bacteria. Therefore, the average UV dose can represent the maximal strength of ultraviolet irradiance which they have passed through based on the corresponding exposure time. However, airborne microorganisms have diversities and higher Z-value airborne microorganisms were more vulnerable to ultraviolet in real, they may be killed before arriving sample plane. Moreover, if the average UV dose was estimated with high Z-value airborne microorganisms, the inactivation may be ultimately underestimated. As shown in Fig. 10, by increasing the air velocity, UV dose linearly declined since airborne microorganisms spent less time in-duct with higher air velocity. By reducing the luminous length of the UV lamp by half, the average UV dose was almost one half of the full luminous length case.

Fig. 10.

Average UV dose (D_avg) of different luminous length of in-duct UV lamp on y = 1.4 m sample plane with different air supply velocity.

3.4. Study of U.S. Environmental Protection Agency (EPA) experiment cases

Although within the CSFP method, our experiment cases were well modeled with F _sc = 0.4, there was still incompletely interpreting the reason for the optimal value of F _sc, 0.4 by biological theory. To further validate the method, the present model was applied to assess the experiment cases of the U.S. Environmental Protection Agency's (EPA's) National Homeland Security Research Center (NHSRC). The inactivation efficiency of an in-duct ultraviolet light system was evaluated by NHSRC against airborne microorganisms [49]. Four UV lamps were inserted the duct from side and perpendicular to airflow direction in the test, however, the ballast box was left outside of the duct. Three microorganisms, Serratia marcescens, MS2 bacteriophage and Bacillus atrophaeus were selected to examine. The other test conditions are provided in Table 3 and more details of the experiment can be found in the literature [49].

Table 3.

Conditions of EPA experiment case [49].

Condition	600/R-06/051
Number of UVC lamps	4
Total UVC power per lamp	8.5 W
Diameter of the lamp (T6)	19 mm
Length of the lamp	538.2 mm
Dimension of duct	610 mm × 610 mm
Air flow rate	0.93 m3/s
Air temperature	23 °C

In the modeling, the physical duct model was built with 610 mm × 610 mm × 1830 mm dimensions based on the literature [42,50]. The duct was then meshed with 348, 400 non-uniform structure computational grid cells. UV irradiance was predicted by our mathematical model [44]. The emissive irradiance from UV lamp and reflection from the duct wall were considered in the prediction. By achieving a steady flow field, 5600 particles were injected from the inlet surface at the beginning of each time step. The average UV dose and disinfection efficiency were calculated with airborne microorganisms in the outlet surface. Table 4 represents the comparison of present modeling and EPA experiment measurement. Based on the table, the numerical results of literature [42,50] are also indicated. It was different from Section 3.3 that D _avg in Table 3 has been considered UV disinfection. Due to the very low of Z-value of B. atrophaeus, D _avg calculated with B. atrophaeus was similar to non-considering the UV disinfection. The EPA's D _avg was obtained from the linear deformation of Eq. (7) and the expression was written as

$$D_{avg}=-\frac{\ln F_s}{Z}$$ (12)

Table 4.

Comparison of Lagrangian modeling and EPA experiment (600/R-06/051) measurement.

Microorganisms	Z value (m−2·J)	Average UV dose Davg (J·m−2)				Disinfection efficacy η (%)
		EPA [49]	Ref. [50]	Ref. [42]	Present	EPA [49]	Ref. [42]	Present
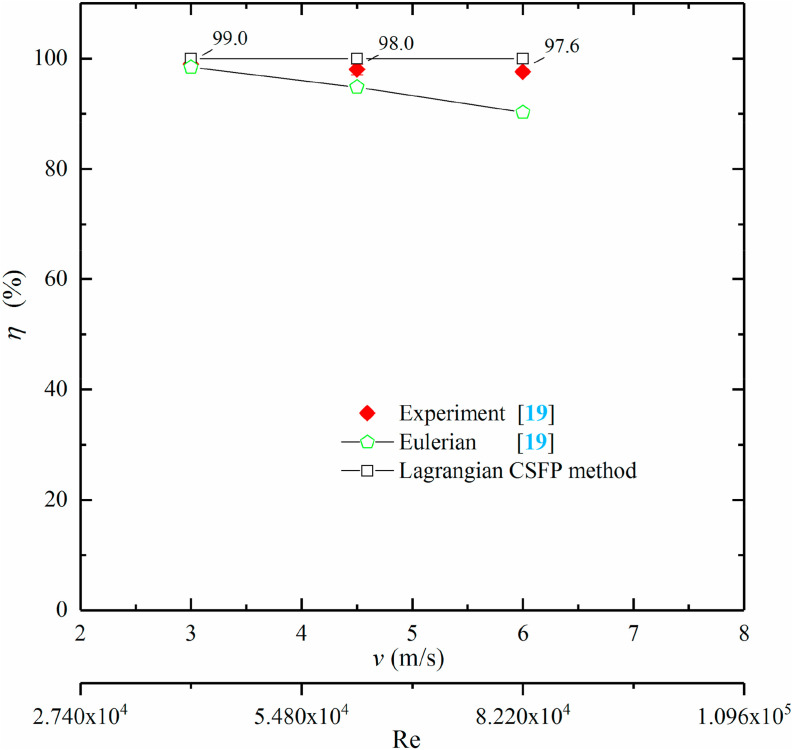
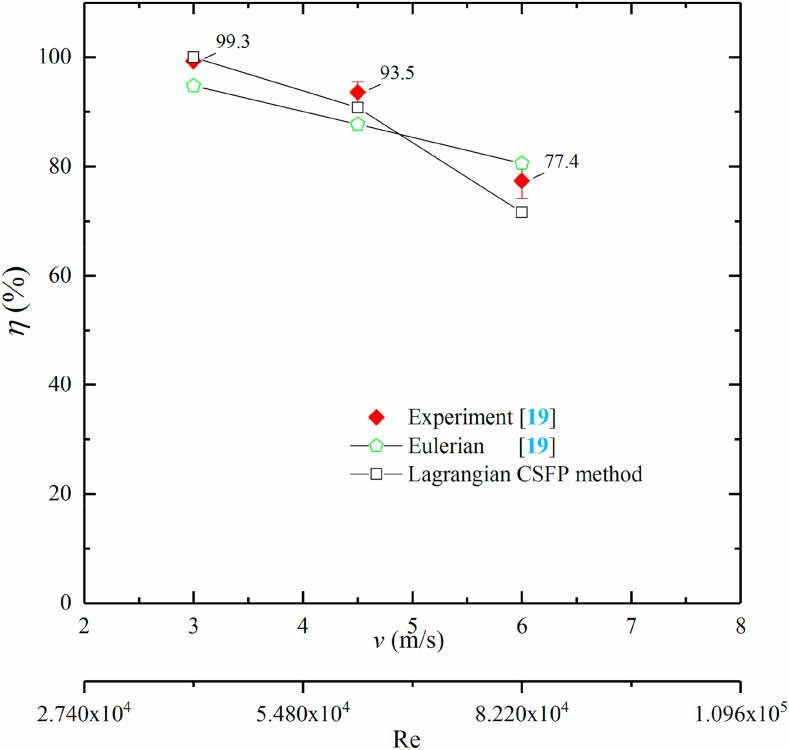
S. marcescens	0.92	–	18b	–	–	99.8	99.99	100
MS2 bacteriophage	0.038–0.048	–	18b	15.82c	16.63c	46	49.35	54.43
B. atrophaeus	0.016	2.95a	18b	15.82c	20.36c	0	13.68	0.00

^aCalculated by D_avg = lnF_s/Z, where D_avg was average UV dose, F_s was the survival fraction of airborne microorganisms, Z was Z value of airborne microorganisms.

^bCalculated by D_avg = I_ravg·t_f, where I_ravg was average spatial irradiance of whole duct, t_f was the time particle pass through duct, t_f = V/Q, where V was the volume of duct, Q was air flow rate.

^cCalculated by D_avg=(D₁+D₂+ … +D_i)/n, where n was the total number of particles sampled in outlet plane, D_i was the UV dose of particle i.

EPA calculated D _avg through B. atrophaeus's data with Z = 0.016 m²/J in their cases. In the present modeling, Z values are also utilized which were recommended by EPA and Capetillo et al. (2015) [42,49]. Capetillo et al. (2015) [42] also used the arithmetic mean of UV dose of all particles sampled in the outlet (Eq. (11)) to calculate their average UV dose, however, Kowalski (2009) [50] calculated the average UV dose of EPA's experiment cases with the average airflow time and irradiance. The expression was written as

$$D_{avg}=I_{ravg}\cdot t_f$$ (13)

where I _ravg is the average spatial irradiance of duct, t _f represents the time particle pass through the duct, t _f = V/Q, V is the volume of duct, Q denotes the airflow rate. The average spatial irradiance (I _ravg) was calculated by a computer model that was developed to predict the emissive irradiance and reflection of the duct wall. He also found that the reflection was important for calculating the UV dose.

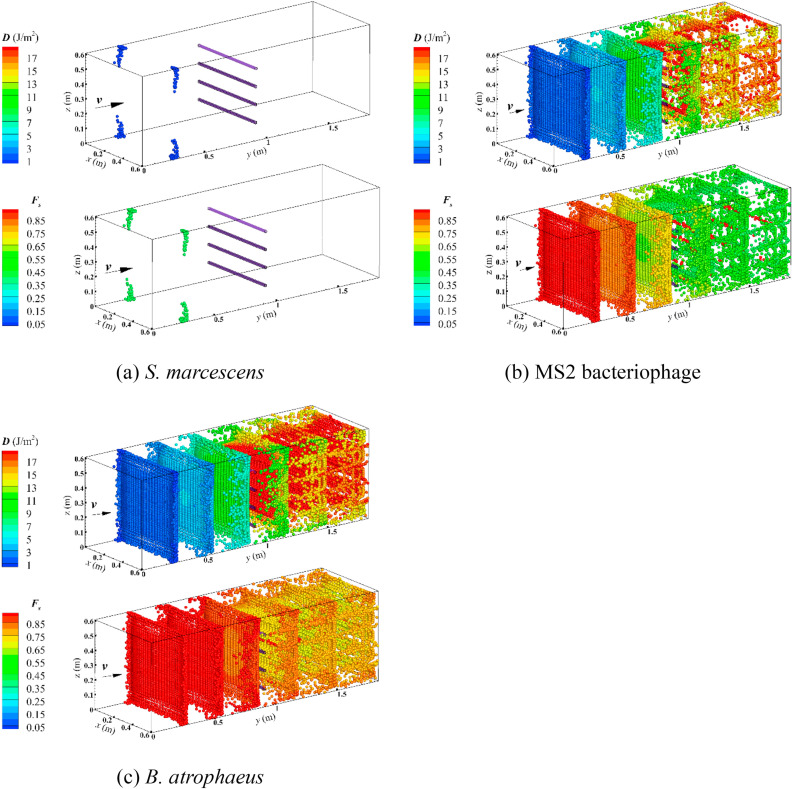
Eqs. (11), (12), (13)) were different and applied on the basis of various input conditions. For comparing their results, it is essential to keep the calculation conditions consistent. For EPA's calculation (Eq. (12)), the survival fraction of airborne microorganisms was closely dependent on the sampling location. If the sample location was nearer the airborne nebulizer, the sampled airborne microorganisms would receive a lower UV dose compared to sampling in a farther downstream location. Of course, F _s was higher for those microorganisms with a lower UV dose at the end. In the experiment of EPA, the length of ventilation duct and the coordinates of their sample location were not given, hence, the parameters of numerical cases cannot be exactly equivalent to the experiment and there was a significant difference between the average UV dose calculated by CFD method (Eq. (11)) and EPA (Eq. (12)). Although Capetillo et al. (2015) [42] used an identical physical model, they did not state that their calculation was performed on the basis of which airborne microorganisms. Table 4 indicates that the average UV dose obtained by the present method with MS2 bacteriophage was very closed to the value of Capetillo et al. (2015) [42]. The average UV dose was none with S. marcescens for both simulations in Table 4. Because D _avg was the arithmetic mean (Eq. (11)) of UV dose at the sample plane in downstream of UV lamp in these works and the value of D _avg was saved with the survival particle during simulation, if airborne microorganisms were very sensitive to irradiance, they failed to pass through UV lamp and ultimately cannot be sampled in downstream of the UV lamp. For instance, Fig. 11 (a) represents that none of S. marcescens was sampled at downstream of the UV lamp and we cannot obtain the average UV dose from survival particle. The disinfection efficacies obtained with the present work were in line with the results of the EPA experiment well. Fig. 11 also represents the numerical results of UV dose (D) and survival fraction (F _s) of three test microorganisms for the EPA experiment case. It is indicated that the survival fraction of S. marcescens was the fewest, however, the value of B. atrophaeus was the highest. Although airborne microorganisms were uniformly injected from the inlet surface, the UV dose obtained by each airborne microorganism was much different and depended on the distribution of irradiance and the exposure time.

Fig. 11.

UV dose (D) and survival fraction (F_s) of three test microorganisms for EPA experiment case (600/R-06/051) at F_sc = 0.4 and Re = 1.04 × 10⁵.

It should be emphasized that although the CSFP method was validated well with modeling the above experiment cases, its optimal value F _sc = 0.4 was empirical and cannot be directly interpreted well with biotechnology. Unlike the MBUD methods, it is impossible for biological experiment tests to quantificationally discover the optimal critical survival fraction to regard the airborne microorganisms as inviable. Further studies are required since the Lagrangian method was an optimal CFD method for modeling the UV disinfection process.

4. Conclusion

The accurate prediction of the disinfection efficiency of UV lamps on airborne microorganisms by CFD simulations is crucial and very helpful to develop its engineering application. In this study, the Lagrangian method was used to assess the disinfection efficacy of an in-duct UV lamp with half and full luminous length on P. alcaligenes, E. coli and S. enterica with Re from 4.11 × 10⁴ to 9.58 × 10⁴ (velocity 3–7 m/s). The distribution of spatial UV irradiance in the ventilation duct was predicted by a mathematical model based on the view factor method, as explained in previous work. The results of disinfection efficacy predicted by simulations were compared with the experimental measurements of our former works. Critical survival fraction probability and maximal bearable UV dose were used as the bacteria viability judgment approaches and their accuracy was studied in detail.

The results indicated that microorganisms’ individual differences to UV irradiation should be further considered for modeling the performance of in-duct UV lamps using the MBUD method. Besides, the results obtained with the CSFP method were well matched with experiment data. It was indicated that the optimal value of the survival fraction of airborne microorganisms (F _s) was recommended as 0.4 based on our experiment data. Moreover, the percentage of airborne microorganisms inactivated by UV irradiance reduced with Re. The disinfection efficacy of in-duct UV lamp with full luminous length on P. alcaligenes and E. coli were almost 100% with Re from 4.11 × 10⁴ to 8.22 × 10⁴. There was a good consistency between the results obtained from Lagrangian modeling and experiment data and they were relatively better compared to Eulerian modeling.

CSFP method was also used to study EPA experiment cases with optimal empirical value F _sc = 0.4. The average UV dose and disinfection efficacy obtained by the present method were compared with the results of experiment measurement and previous CFD simulation works. The results indicated that there was a slight difference between the average UV dose owing to the difference in their calculation way and conditions. The disinfection efficacies obtained by the present method were well-matched with the experiments. It is worth noting that the optimal value of critical survival fraction probability requires further future investigations.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary data to this article: