Computational design of mixed chirality peptide macrocycles with internal symmetry

Abstract

Cyclic symmetry is frequent in protein and peptide homo‐oligomers, but extremely rare within a single chain, as it is not compatible with free N‐ and C‐termini. Here we describe the computational design of mixed‐chirality peptide macrocycles with rigid structures that feature internal cyclic symmetries or improper rotational symmetries inaccessible to natural proteins. Crystal structures of three C2‐ and C3‐symmetric macrocycles, and of six diverse S2‐symmetric macrocycles, match the computationally‐designed models with backbone heavy‐atom RMSD values of 1 Å or better. Crystal structures of an S4‐symmetric macrocycle (consisting of a sequence and structure segment mirrored at each of three successive repeats) designed to bind zinc reveal a large‐scale zinc‐driven conformational change from an S4‐symmetric apo‐state to a nearly inverted S4‐symmetric holo‐state almost identical to the design model. These symmetric structures provide promising starting points for applications ranging from design of cyclic peptide based metal organic frameworks to creation of high affinity binders of symmetric protein homo‐oligomers. More generally, this work demonstrates the power of computational design for exploring symmetries and structures not found in nature, and for creating synthetic switchable systems.

Short abstract

PDB Code(s): 6UFU, 6UG2, 6UG3, 6UG6, 6UGB, 6UGC, 6UCX, 6UD9, 6UDR, 6UDW, 6UDZ, 6UF4, 6UF7, 6UF8, 6UFA and 6UF9;

1. INTRODUCTION

Symmetric protein quaternary structures, which are built from many identical copies of a single protein chain, play key functional and structural roles in biology and have advantages as building blocks for nanomaterials since a small number of repeated interfaces can generate large and complex assemblies. ¹ , ² , ³ , ⁴ , ⁵ Such structures have also proved useful for engineering high‐avidity binders to symmetry‐matched targets of therapeutic interest. ⁶ Macromolecules with internal symmetry in their sequences and tertiary structures would be particularly advantageous for both nanomaterial and therapeutic development, since the complexity of dealing with multiple chains can be avoided. Metal–organic frameworks (MOFs), for example, are often built from internally‐symmetric small‐molecule chelators. ⁷ , ⁸ , ⁹ While there are many small molecules with internal symmetry, natural proteins and peptides with internal symmetry are extremely rare, at least in part because true internal symmetry requires that the chain be circular, with no free N‐or C‐terminus. Perhaps the best‐studied natural example of an internally‐symmetric peptide macrocycle is gramicidin S, a 10‐residue antimicrobial agent with C2 symmetry. ¹⁰ , ¹¹ Small synthetic peptide macrocycles with simple, patterned repeating sequences have been found to give rise to C2 or C3 structural symmetries, ¹² , ¹³ , ¹⁴ but to our knowledge there has been no systematic effort to explore the space spanned by such structures. We and other groups have designed asymmetric linear and macrocyclic foldamers, ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ , ¹⁹ but the peptide design field currently lacks general computational methods for designing symmetric molecules.

We set out to develop general methods for computationally designing internally‐symmetric peptide macrocycles with conformational rigidity imparted by large energy gaps between a symmetric ground state and all alternative conformations. To this end, we incorporated methods for sampling and designing with internal cyclic or improper rotational symmetries into the Rosetta heteropolymer design software. ¹⁸ , ¹⁹ , ²⁰ , ²¹ , ²² Our sampling methods use robotics‐inspired kinematic closure methods ¹⁸ , ²³ , ²⁴ to provide analytical solutions for dihedral values yielding closed macrocycle conformations. Dihedral angles in all asymmetric units of the macrocycle (henceforth referred to as “lobes”) are required to match those in the first “reference” lobe to within a certain tolerance in the cyclic symmetric case, and after inversion in the case of improper rotational symmetries. Subsequent symmetric sequence design algorithms ensure that residue identities and conformations in neighboring lobes match (for cyclic symmetry) or match with chirality inversion and inversion of dihedral values (for improper rotational symmetry). We apply the methods to the design of peptide macrocycles with cyclic symmetries (C2 or C3) and improper S2 and S4 rotational symmetries that are inaccessible to homochiral proteins, but which can be accessed by heterochiral peptides.

2. RESULTS

2.1. Structures of designed peptide macrocycles with C2 and C3 symmetry

We developed a computational pipeline, summarized in the methods and in Figure S1, for designing internally‐symmetric peptide macrocycles. This pipeline involved steps of symmetric backbone conformational sampling, clustering, symmetric sequence design, filtration to discard designs with undesirable features, and final computational validation by large‐scale conformational sampling. We first applied this pipeline to create macrocycles with C2 and C3 symmetry, with asymmetric units ranging from 3 to 5 residues. To assess the completeness of our sampling of cyclic peptide conformational space, we defined four backbone dihedral bins (A, B, X, and Y), with A and B representing right‐handed helical and strand regions of Ramachandran space, respectively, and X and Y representing the mirror image bins (see Data S1). We compared the number of bin sequences (AABAYYXY, for example) sampled to the total number of unique bin patterns possible for each peptide size and symmetry type designed, with the latter determined analytically using Burnside's lemma ²⁵ (see Section 2.1.3 of Data S1). Where possible, we also assessed whether the solution space for designs was fully sampled by examining the set of low‐energy structures obtained to determine whether both members of mirror‐related bin strings were represented, since the occurrence of just one member of such isoenergetic pairs indicates incomplete sampling of the solution space. We were able to sample with many‐fold redundancy over all bin patterns possible for peptides up to 24 residues in length, and found only a small subset for each length that were compatible with chain closure for each symmetry (Table 1). The mirror test suggested that the identified conformations completely cover the space of possibilities for C2‐symmetric macrocycles with up to eight residues, and C3‐symmetric macrocycles up to 18 residues. For higher‐order symmetries, such as C5, complete sampling by the mirror test was possible up to 30 residues (Table S1).

TABLE 1.

Summary of peptide macrocycle backbone conformations found for symmetries explored

Symmetry type a	Size (residues)	Max. bin strings possible	Bin strings observed	Conformational clusters observed b
C2	6	24	8	3
	8	70	13	6
	10	208	57	25
	12	700	15	16
	14	2,344	108	96
	16	8,230	1,122	898
	18	29,144	2,171	1,770
	20	104,968	2,585	2,108
C3	6	10	1	1
	9	24	4	2
	12	70	3	3
	15	208	4	4
	18	700	3	3
	21	2,344	14	11
	24	8,230	20	19
S2	6	12	1	1
	8	32	2	1
	10	104	9	6
	12	344	4	4
	14	1,172	173	85
	16	4,096	294	162
	18	14,572	469	303
	20	52,432	707	464
S4	8	4	2	1
	12	12	1	1
	16	32	7	7
	20	104	22	19
	24	344	18	17
	28	1,172	27	22
	32	4,096	13	12

^a Only symmetry types that were synthesized are listed here. For full analysis of other symmetry types (e.g., C4, C5), please see Data S1.

^b Results of clustering with a radius of 1.5 Å are reported. For full clustering analysis, please refer to Data S1.

We carried out large‐scale conformational sampling on each of the designed sequences, and selected for chemical synthesis peptide macrocycles with large energy gaps between the designed conformation and all alternative states. We began by synthesizing one C2‐symmetric and five C3‐symmetric peptide macrocycles and their mirror‐image enantiomorphs to facilitate the crystallization of the synthesized molecules from racemic mixtures. ²⁶ With this approach we succeeded in crystallizing the C2‐symmetric peptide and three of the five C3‐symmetric peptides (Figure 1). The observed conformation of the C2 symmetric peptide (designated C2‐1) matched its designed conformation within a backbone heavy‐atom RMSD of 1 Å, but with notable deviation in the ψ dihedral angle of residue dSER1 and the ϕ dihedral angles of residues dGLU2 and AIB8, which inverted the dSER1‐dGLU2 amide bond, allowing it to form a new hydrogen bond with dGLU7. Despite this local structural change, the overall fold of the peptide was largely preserved. This is the first computationally‐designed macrocycle of which we are aware that uses 2‐aminoisobutyric acid (AIB), a non‐canonical, conformationally‐constrained amino acid, instead of proline to ensure conformational rigidity. Only one enantiomer was observed in this crystal structure, but an alternative crystal form was identified that incorporates both enantiomers, albeit with a distorted conformation (see Figure S2). Table S2 shows sequences, crystallization conditions, space groups, and backbone heavy‐atom RMSD values for all peptides.

FIGURE 1.

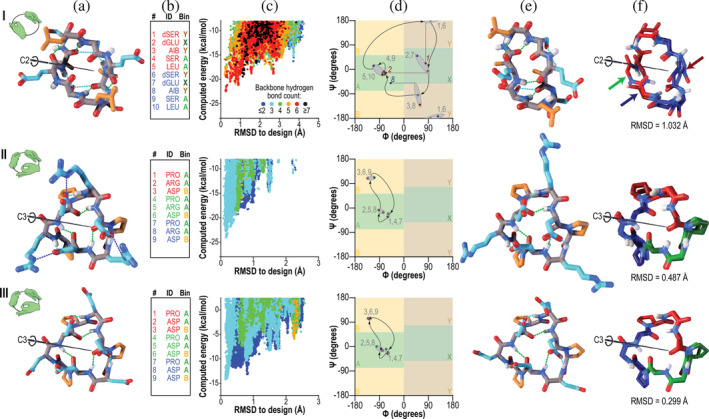
Designed peptides with cyclic (C2 or C3) symmetries. Columns: (a) Computer models produced by Rosetta design. Backbone‐backbone, backbone‐sidechain, and sidechain‐sidechain hydrogen bonds are shown as green, cyan, and blue dashed lines, respectively. Backbone atoms are shown in grey, polar side‐chains in cyan, and apolar side‐chains in orange. The C2 or C3 symmetry axis is shown as a black rod. Hand icons depict the symmetry. (b) Designed amino acid sequences and Ramachandran bin strings. Amino acids are coloured red and blue (C2 symmetry) or red, green, and blue (C3 symmetry) to indicate different repeating units. (c) Computed energy landscape of design, in which each point represents a structure prediction trajectory, with computed energy plotted against RMSD to the designed structure. Colors represent the number of backbone hydrogen bonds. (d) Ramachandran map representation of the designed structures (grey points) compared to the experimentally‐determined structures (points colored by symmetry lobe, as in column b). Grey numbers indicate sequence positions, and curved arrows show the progression through the sequence. Grey ovals group the designed and observed backbone angles, as a guide to the eye. In the case of peptide C2‐1, three residues, indicated with red and blue numbers, showed considerable deviation in φ (horizontal dashed lines) or ψ (vertical dashed line). (e) Structures determined by X‐ray crystallography. Colors are as in column a. (f) Overlay of the designed model (lighter colors) with the X‐ray crystal structure (darker colors). Symmetric lobes are shown in colors matching sequences in column b. Side‐chains other than those of proline are omitted for clarity. Rows: (I) Peptide C2‐1. The backbone heavy‐atom RMSD between crystal structure and design was 1 Å, mainly due to shifts in ψ of residue 1 and φ of residue 2 (red dashed lines in column d and blue and green arrows in column f) which together rotated the amide bond between residues 1 and 2 by 180°, and in φ of residue 8, which reoriented a backbone carbonyl (red arrow) in the absence of the hydrogen bond that would have been donated to it by the rotated amide proton. Despite these changes, much of the structure overlaid well on the design. (II and III) Peptides C3‐2 and C3‐3, which shared a common backbone configuration. Crystal contacts resulted in somewhat different conformations of polar side‐chains, but the backbone heavy‐atom RMSDs to the designs were 0.5 and 0.3 Å, respectively, yielding near‐perfect alignment in both cases (column e)

Two of the three C3‐symmetric peptides that we succeeded in crystallizing closely matched the design models (Figure 1). Design C3‐1 adopted a conformation different from the design (Figure S3) likely due to three buried polar hydrogen atoms that form hydrogen bonds with carbonyl oxygens in adjacent peptide molecules. ²⁷ , ²⁸ Recognizing this to be an undesirable structural feature that was poorly penalized by our automated scoring function, from this point forward we filtered designs, selecting only those designs lacking unsatisfied buried polar groups. Crystal structures of peptides C3‐2 and C3‐3, which lack buried unsatisfied polar atoms, closely matched their designs, with backbone heavy‐atom RMSD values of 0.5 Å and 0.3 Å, respectively. The two have a common fold stabilized by three proline residues and three backbone hydrogen bonds.

2.2. Structures of designed peptide macrocycles with S2 symmetry

We next explored symmetries inaccessible to natural proteins. Unlike proteins built only from L‐amino acids, peptides built from mixtures of D‐ and L‐amino acids can access symmetries involving mirror operations, such as improper rotational symmetries. Using the same symmetric sampling, clustering, and sequence optimization strategy, we designed and synthesized a panel of 6 peptide macrocycles with S2 symmetry, ranging in size from 8 to 12 amino acids (designs S2‐1 through S2‐6). These peptides have a sequence that repeats twice, with the chirality of residues in the second lobe inverted relative to the first, yielding a second lobe with a conformation mirroring that of the first. Six designs were selected for synthesis representing a diverse range of backbone conformations and hydrogen bonding patterns. We were able to crystallize all six of these peptides, and to determine their structures by direct phasing methods.

In all cases the observed conformation closely matched the design (overlays in Figure 2, column f), with a maximum backbone heavy‐atom RMSD of 0.6 Å (peptide S2‐3) and a minimum of 0.4 Å (peptide S2‐1). The folds of these peptides are all stabilized by d‐ and l‐proline residues and backbone hydrogen bonds (Figure 2). The designed conformation of peptide S2‐6, a 12‐residue peptide with sequence aNkhPeAnKHpE (where lowercase and uppercase letters represent d‐ and l‐amino acid residues, respectively), has a crimped conformation remarkably forming eight backbone hydrogen bonds, of which six were preserved in the crystal structure. The remaining two were lost to a slight rotation of the amide bond between dASN8 and LYS9, which positioned the donor and acceptor groups where they could instead make hydrogen bonds to water. The crystal structure deviated from the design by a backbone heavy‐atom RMSD of only 0.4 Å. In all other cases, the designed backbone hydrogen bonding patterns were preserved, with two exceptions: a subtle relaxation of the backbones of peptides S2‐4 and S2‐5 replaced two direct backbone‐backbone hydrogen bonds in the designs with bridging water molecules (Figure 2d,e).

FIGURE 2.

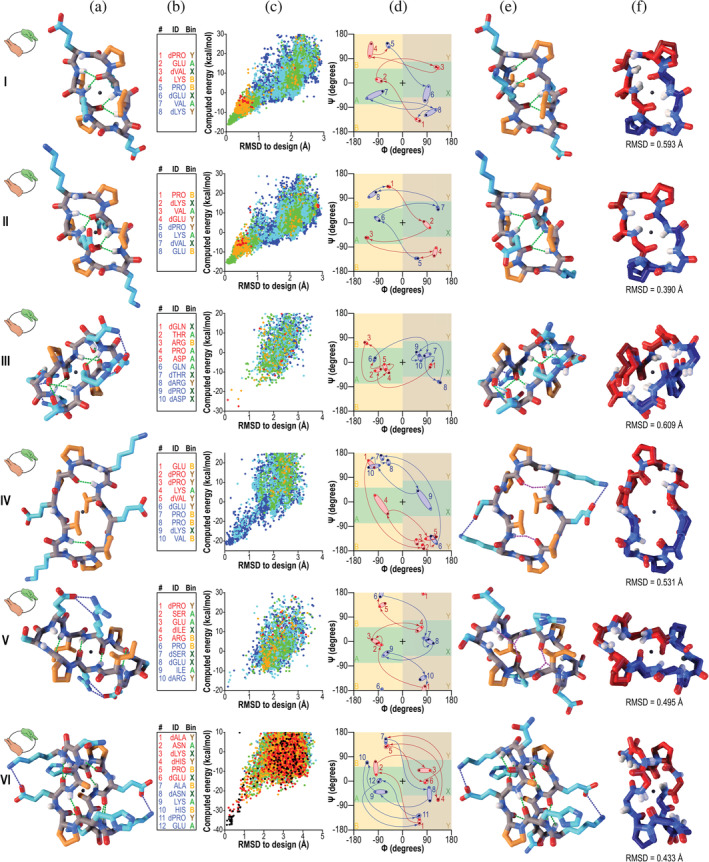
Designed peptides with S2 improper rotational symmetry. Unless noted otherwise, columns and colors are as in Figure 1. The symmetry is illustrated with left and right hands, shown in green and orange respectively, in icons in column a. Centers of inversion are shown as black spheres in columns a and e. In column d, pink and light blue ovals indicate the first and second symmetry lobes, respectively, which are related to one another by mirroring (a 180° rotation about the origin in Ramachandran space). Bright red and bright blue points represent the design, and dark red and dark blue points represent the crystal structure. (I–VI) Peptides S2‐1–S2‐6. In each of peptides S2‐4 and S2‐5, two designed backbone‐backbone hydrogen bonds were observed to be replaced with a bridging water molecule in the crystal structure (dashed purple lines in column e)

2.3. Metal‐induced conformational switching in a designed S4‐symmetric polypeptide macrocycle

We next explored the possibility of using the new design methods to create conformational switches. We sampled S4‐symmetric polypeptide conformations with four repeats in which alternating lobes had opposite chirality, and developed a computational strategy to select backbones that could present metal‐binding side‐chains for tetrahedral coordination of a central metal ion (see Data S1). We designed sequences with l‐ and d‐histidine residues positioned to chelate the metal ion, AIB and other residues to stabilize the fold, and apolar side‐chains on the surface to stabilize an alternative, inside‐out conformation in the absence of metal. The sequences of these designs repeat four times, with residues in the second and fourth lobes possessing chirality and conformations inverted relative to equivalent residues in the first and third lobes. We carried out large‐scale conformational sampling to select designs with low‐energy designed conformations with the histidine side‐chains positioned to bind zinc. In several designs, we noted that large‐scale conformational sampling predicted a second energy minimum corresponding to an inside‐out fold with the apolar side‐chains in the core and the histidines exposed. We selected a single design for synthesis, S4‐1, which has sequence KLqeXHklQEXhKLqeXHklQEXh, in which X represents AIB (Figure 3).

FIGURE 3.

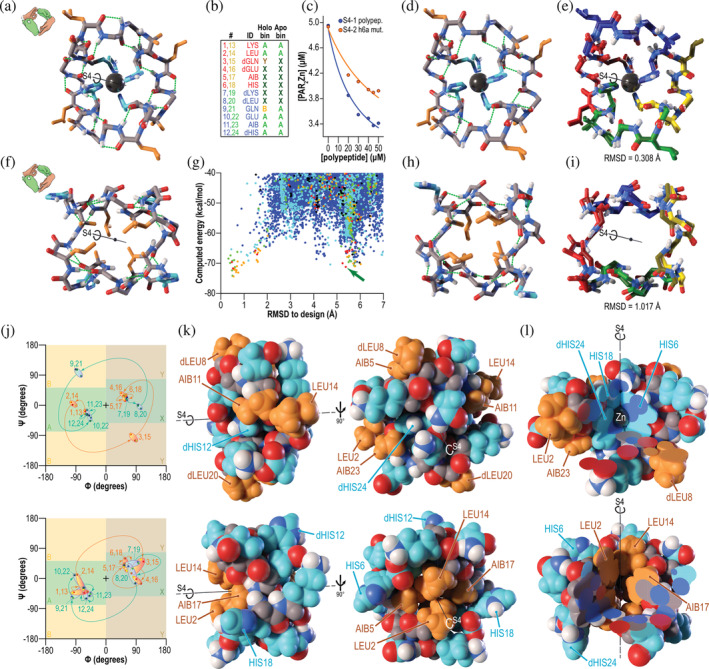
A designed biconformational metal‐binding polypeptide with S4 improper rotational symmetry. (a) Design model of S4‐1 polypeptide. Backbone hydrogen bonds are shown as dashed green lines, the central bound zinc atom, as a dark grey sphere, polar side‐chains as cyan sticks, apolar side‐chains as orange sticks, and backbone atoms as grey sticks. Solvent‐exposed glutamate, glutamine, and lysine side‐chains are omitted for clarity. In this and subsequent panels, the S4 symmetry axis is shown as a black line. The icon adjacent to each letter illustrates the symmetry, with left and right hands colored as in Figure 2. (b) Sequence and expected Ramachandran bins for each residue in the metal‐bound (“Holo bin”) and metal‐free (“Apo bin”) states. Colors in the first two columns correspond to colors of symmetric lobes in panels e and i. Bin colors correspond to the shaded regions in the plots in panel j. (c) Polypeptide S4‐1 titration into PAR₂Zn solution to measure metal affinity by competition. Based on the known affinity of PAR for zinc, the measured affinity of the S4‐1 polypeptide for zinc was 0.32 nM (curve of best fit). (d) X‐ray crystal structure of zinc‐bound S4‐1 polypeptide. The (i + 3 → i) 3₁₀ helix hydrogen bond pattern that was designed was observed. (e) Overlay of S4‐1 design and crystal structure (with symmetric lobes colored as in panel b). The backbone heavy‐atom RMSD was 0.3 Å, and metal‐binding histidine side‐chains and surface‐exposed leucine side‐chains showed excellent agreement to the design. (f) S4‐symmetric lowest‐energy predicted alternative structure with RMSD greater than 2 Å from the design (green arrow in panel g) in the absence of zinc. Although only one glutamine residue per lobe undergoes a major conformational change, this allows inversion of the structure, so that apolar side‐chains are now buried. (g) Computationally predicted energy as a function of RMSD to the designed conformation. Colors indicate number of backbone hydrogen bonds: ≤15 (blue), 16 (cyan), 17 (green), 18 (orange), 19 (red), or ≥20 (black). The identified alternative fold is marked with a green arrow. (h) X‐ray crystal structure of zinc‐free S4‐1 polypeptide. The observed hydrogen bond pattern more closely resembled the (i + 3 → i) 3₁₀ helix pattern observed in the original design than the pattern predicted in the alternative state. Nevertheless, the major shift, burying apolar side‐chains, was observed. (i) Overlay of prediction and crystal structure for alternative apo state of S4‐1 polypeptide. For clarity, only the backbone is shown. The RMSD between predicted alternative apo state and observed state in the crystal structure was 1 Å. (j) Ramachandran plots for the zinc‐bound (top) and zinc‐free (bottom) conformations. Curved arrows and numbers indicate progression through the sequence. Two‐toned red/yellow (lobes 1 and 3) and blue/green (lobes 2 and 4) ovals serve as guides to the eye to link designed and observed dihedral values at each position. Top panel: S4‐symmetric designed zinc‐bound conformation (two‐toned points) and the observed zinc‐bound conformation (solid colors matching panel B). All backbone dihedral values observed were very close to those designed. Bottom panel: predicted S4‐symmetric alternative, zinc‐free conformation (solid colors matching panel B) and the observed symmetric structure (two‐toned points). Although there was more deviation between the prediction and the observed structure, all points fell in the predicted Ramachandran bins. (k) Space‐filling sphere models showing the major conformational change between zinc‐bound (top) and zinc‐free (bottom) states. Colors are as in panel a. Apolar side‐chains that are solvent‐exposed in the zinc‐bound state (orange) are buried in the apo‐state, while metal‐binding histidine residues that are buried in the zinc‐bound state are exposed in the apo‐state, yielding a fully polar surface (cyan). (l) Cutaway views of zinc‐bound (top) and zinc‐free (bottom) S4‐1 crystal structures. The zinc‐bound state has a well‐packed polar core consisting mainly of zinc‐binding histidine side‐chains (cyan side‐chains, top), with the central zinc atom lying on the symmetry axis and mirror plane. The apo‐state has a well‐packed apolar core more like that of a conventional protein (orange side‐chains, bottom)

The 24‐amino acid polypeptide S4‐1 crystallized in space group $P\overline{1}$. The backbone conformation in the crystal structure (which contained a single copy of the peptide in the asymmetric unit), matched the design with a backbone heavy‐atom RMSD of 0.3 Å, with a central metal ion (believed to be zinc) very close to that in the design model. The central metal‐coordinating l‐ and d‐histidine side‐chains matched the design with a side‐chain heavy‐atom RMSD of 0.1 Å. The zinc affinity of S4‐1 was 0.32 nM, as measured by competition with the colorimetric chelator 4‐(2‐pyridylazo)resorcinol (PAR) (Figure 3c and Data S1).

The central metal ion plays an important structural role in holo‐S4‐1, stabilizing a conformation that presents four apolar d‐ and l‐leucine side‐chains to aqueous solvent (Figure 3a,d,e,k,l), and as noted above large‐scale conformational sampling runs predicted an alternative conformation with these groups buried in the absence of the metal ion (Figure 3f,g). To explore this possibility, we solved the structure of the apo‐polypeptide. Without zinc, the polypeptide crystallized in space group P2₁2₁2, and did indeed adopt a very different conformation from the holo‐structure, packing apolar d‐ and l‐leucine side‐chains against AIB residues in the core, and projecting the d‐ and l‐histidine side‐chains that previously coordinated zinc outward (Figure 3h,k,l). The observed apo‐state conformation matches the predicted alternative state to a backbone heavy‐atom RMSD of 1 Å (Figure 3i).

3. DISCUSSION

The 10 new peptide and polypeptide macrocycles presented here have diverse, rigid backbone folds closely matching the design models, in nearly all cases with sub‐Ångstrom accuracy. The structures were designed in four different symmetry classes (C2, C3, S2, and S4), the latter two of which are inaccessible to proteins or other natural macromolecules built from building‐blocks of only one handedness. Likely because of their symmetry, the success rate of the designs was quite high, both in terms of crystallization of the designed peptides (11 of 13) and their close match to predicted structures (10 of 11).

3.1. Expanding the set of usable chemical building‐blocks for computational design

Past design efforts aimed at producing folding macrocycles focused on peptides built from canonical L‐amino acids and their mirror‐image D‐amino acid counterparts. ¹⁸ , ¹⁹ Although large proteins are stabilized primarily by the formation of a core of well‐packed apolar side‐chains, smaller peptides lack large buried volumes, and tend to be stabilized by intrinsic conformational preferences of amino acid residues. Proline is the most conformationally‐constrained canonical amino acid, and has been essential to the success of past designs; however, proline cannot be used in all contexts. Since the proline side‐chain connects to the backbone nitrogen, eliminating the backbone amide hydrogen, proline cannot serve as a backbone hydrogen bond donor. Moreover, the proline delta carbon alters the conformational preferences of the preceding residue. And of course there are configurations in which the proline side‐chain can clash with other side‐chains. It is therefore convenient to have additional conformationally‐constrained amino acids from which to choose when designing. By adding support for designing with AIB, we were able to include an achiral yet conformationally‐constrained residue with narrow preferences for the regions of Ramachandran space favored by both l‐ and d‐proline, but which is nonetheless able to form backbone hydrogen bonds. This permitted the AIB residues in peptide C2‐1 to donate hydrogen bonds to serine side‐chains, as well as the incorporation of AIB in the holo‐S4‐1 design in the midst of a 3₁₀ helix, a secondary structure that would have been disrupted by proline. In the apo state, the AIB side‐chains were able to pack closely with nearby leucine side‐chains, an arrangement that would have resulted in side‐chain clashes had proline been substituted. We anticipate that the ability to expand the set of conformationally‐constrained amino acids for computational design will open new opportunities for stabilizing structures that cannot be stabilized by canonical amino acids or their mirror images alone.

3.2. Near‐exhaustive exploration of conformational space for larger molecules

The design of rigidly‐folded heteropolymers requires efficient means of sampling backbone conformations, both to identify conformational states compatible with a given function that can be stabilized by a suitable choice of sequence, and to validate designed sequences by exploring possible alternative low‐energy conformational states. This is particularly challenging when designing with non‐canonical amino acid residues, requiring unbiased sampling methods that are not reliant on known structures. Because N‐fold symmetric molecules have far fewer (1/N) conformational degrees of freedom than similarly sized asymmetric molecules, the new methods make comprehensive sampling tractable for much larger systems. By focusing on internally‐symmetric macrocycles, we were able to achieve exhaustive or near‐exhaustive coverage of the conformation spaces for peptides with up to 30 amino acids for the highest‐order symmetries (Table S1)—a size range well beyond that which can be sampled exhaustively for asymmetric macrocycles. Since many applications of designed, well‐folded heteropolymers require molecules that are able to present large binding interfaces (e.g., for nanomaterial self‐assembly or therapeutic target binding), or molecules large enough to possess internal binding pockets (e.g., for small‐molecule binding or catalysis), we anticipate that our computational methods for designing larger symmetric structures with non‐canonical building blocks will have broad applicability.

3.3. Design of metal‐dependent peptide conformational dynamics

Our most complex design, the 24‐residue S4‐1 polypeptide, binds zinc with sub‐nanomolar affinity, and undergoes a major conformational change in the presence of zinc. Both the apo and holo states are well‐structured, with the former burying apolar side‐chains and the latter exposing them (Figure 3). Engineered switching behavior could ultimately be used to create cell‐permeable molecules that could serve as drugs. Similar conformational switching behavior is observed in the natural peptide macrocycle cyclosporine A, and is thought to underlie this drug's cell permeability: in the lipid bilayer, cyclosporine is able to adopt a conformation in which all hydrogen bond donors and acceptors are internally satisfied, and apolar groups are lipid‐exposed, promoting its lipid‐solubility, while in an aqueous environment, the molecule changes conformation to expose its polar groups to water, promoting water‐solubility. ²⁹ , ³⁰ The ability to control this switching behavior with a metal ion like zinc could also provide a means of ensuring that the permeation is unidirectional: while extracellular free zinc concentrations are in the nanomolar to micromolar range, ³¹ high‐affinity zinc binding within the cell lowers the free zinc concentration to picomolar levels. ³² Achieving cellular permeability would likely require further design to ensure that the apolar‐exposed state internally satisfies all hydrogen bond donors and acceptors. A future extension of our approach would be to engineer a symmetric macrocycle drug able to undergo a conformational change to pass through a membrane and to present a large, symmetric surface to bind with high affinity and specificity to a symmetric interface on a homooligomeric intracellular target protein.

3.4. Concluding remarks

We have presented general methods for computational design and validation of symmetric, well‐folded polypeptide macrocycles, including those incorporating metals as structural elements, and have demonstrated robust ability to control structure with sub‐Ångstrom accuracy in laboratory experiments, culminating in an engineered, metal‐dependent conformational switch. The ability to design symmetric, well‐folded polypeptide macrocycles opens up new avenues for both therapeutic design and for bounded and unbounded nanomaterial design, and shows that methods originally developed for protein design can now be used to robustly design molecules quite unlike those that exist in nature.

4. MATERIALS AND METHODS

4.1. Modifications to the Rosetta software suite

Extensive modifications to the Rosetta software suite enabled the design of internally‐symmetric peptide macrocycles, including those able to coordinate a central metal ion. New Rosetta modules were implemented to be compatible with both the PyRosetta and RosettaScripts scripting languages, ³³ , ³⁴ allowing their use in the development of future, application‐specific design protocols. Rosetta source code and compiled executables are provided free of charge to academic, government, and not‐for‐profit users through http://www.rosettacommons.org, and the software is licenced to commercial users for a fee. Computational developments are summarized here and described in detail in Data S1.

The Rosetta symmetry code ³⁵ was refactored to add support for mirror operations and improper rotational symmetries, and to correctly interconvert between mirrored amino acid types. Rosetta's simple_cycpep_predict and energy_based_clustering applications, both described previously, ¹⁸ , ¹⁹ were enhanced to allow sampling and clustering of quasi‐symmetric backbones with a given symmetry (where a quasi‐symmetric backbone is one that is nearly symmetric, but in which small deviations from perfect symmetry are allowed). A Rosetta module (“mover”) for converting quasi‐symmetric structures to fully symmetric structures, called the SymmetricCycpepAlignMover, was added. The interface and internal handling of non‐canonical amino acids during design was greatly reworked, with the user‐controlled PackerPalette introduced to control the set of chemical building‐blocks used for a given design task, permitting deprecation of many problematic idiosyncrasies present in the previous interface to streamline the design process.

To enable the design of metal‐binding peptides, Rosetta's CrosslinkerMover was enhanced with support for a range of metal coordination geometries, with support for asymmetric structures or for the symmetry classes compatible with a given coordination geometry. For example, this mover allows the design of a tetrahedrally‐coordinated zinc in an asymmetric structure or in a C2‐ or S4‐symmetric structure, with suitable repetition of conformations and amino acid identities of the liganding residues.

4.2. Computational design protocol

To design symmetric peptides, we first sampled quasi‐symmetric mainchain conformations using the simple_cycpep_predict application, and enumerated conformations with the energy_based_clustering application. In the case of the S4‐1 polypeptide, this step was modified to sample only those backbone conformations capable of coordinating a central metal ion. Next, with scripts written in the RosettaScripts scripting language, we converted quasi‐symmetric cluster centers to fully symmetric structures, and carried out sequence design with Rosetta's symmetric design algorithms. Finally, we validated each designed sequence by large‐scale conformational sampling, again using the simple_cycpep_predict application, to identify those designed sequences that uniquely favored the designed conformation. Computations were carried out on the University of Washington Hyak cluster, the Argonne National Laboratory Mira and Theta supercomputers, and the Simons Foundation Gordon and Iron clusters. Additionally, some validations were carried out using the Rosetta@Home distributed computing platform, which uses volunteer computers, cellular telephones, and mobile devices through the Berkeley Open Infrastructure for Network Computing (BOINC). ³⁶ Full details of each step, sample command‐lines, and representative RosettaScripts scripts are provided in Data S1.

4.3. Solid‐phase peptide synthesis and purification

Peptides were synthesized using standard Fmoc solid‐phase peptide synthesis techniques using a CEM Liberty Blue peptide synthesizer with microwave‐heated coupling and deprotection steps. Peptides with 12 amino acids or fewer that contained l‐aspartate or l‐glutamate were synthesized tethered by the acidic side‐chain to preloaded Fmoc‐l‐Asp(Wang resin LL)‐ODmab or Fmoc‐l‐Glu(Wang resin LL)‐ODmab resin, and were cyclized on‐bead by a coupling reaction following deprotection of the C‐terminus with 2% (vol./vol.) hydrazine monohydrate treatment in dimethylformamide (DMF). Larger peptides were synthesized with the C‐terminus coupled to Cl‐TCP(Cl) resin from CEM, cleaved from the resin with 1% (vol./vol.) TFA treatment in dicholoromethane (DCM), and cyclized by a solution‐phase coupling reaction prior to final deprotection. Peptides were purified by reverse‐phase HPLC with a water‐acetonitrile gradient, lyophilized, and redissolved in buffer suitable for subsequent experiments (typically 100 mM HEPES, pH 7.5). Masses and purities were assessed by electrospray ionization mass spectrometry with a Thermo Scientific TSQ Quantum Access mass spectrometer. Full synthetic and purification protocols are described in Data S1.

4.4. X‐ray crystallography

Peptides were crystallized by hanging droplet vapour diffusion, with pH, buffer, ionic strength, and precipitants all optimized for each peptide. Growth conditions for the crystals of each peptide are described in Data S1. Diffraction data were collected at the Argonne National Laboratory Advanced Photon Source (APS) beamlines 24‐ID‐C and 24‐ID‐E.

4.5. Metal‐binding assays

To confirm zinc content of the S4‐1 and S4‐2 peptides, and to measure zinc affinity, we used a variant of the 4‐(2‐pyridylazo)resorcinol (PAR) assay described previously. ³⁷ , ³⁸ , ³⁹ We carried this assay out in 96‐well plates (200 μL total solution volume per well). To confirm metal content, 10 μM polypeptide was denatured in 6 M guanidinium hydrochloride (Sigma‐Aldrich, St. Louis, MO), 100 mM HEPES, pH 7.5, and 200 μM PAR, and the change in absorbance at 490 nm was monitored using a SpectraMAX M5e plate reader (Molecular Devices, San Jose, CA). Standard curves were prepared with ZnCl₂ to convert absorbance changes to zinc concentrations. The metal affinity of the S4‐1 and S4‐2 polypeptides was measured by competition with PAR, given the known dissociation constants of the PAR₂‐Zn complex. Full protocols and mathematical details for both assays are provided in Data S1.

AUTHOR CONTRIBUTIONS

Christine Kang: Data curation; formal analysis; investigation; methodology; writing‐original draft; writing‐review and editing. Michael R. Sawaya: Data curation; formal analysis; methodology; validation; visualization; writing‐original draft; writing‐review and editing. Stephen Rettie: Formal analysis; methodology; resources; validation; writing‐original draft; writing‐review and editing. Xinting Li: Formal analysis; methodology; resources; validation; writing‐review and editing. Inna Antselovich: Formal analysis; methodology; validation; writing‐review and editing. Timothy Craven: Software; writing‐review and editing. Andrew Watkins: Methodology; software; writing‐review and editing. Jason Labonte: Software; writing‐review and editing. Frank DiMaio: Methodology; software; writing‐review and editing. Todd Yeates: Conceptualization; formal analysis; funding acquisition; methodology; project administration; resources; supervision; validation; writing‐original draft; writing‐review and editing. VK Mulligan: Conceptualization; Data curation; Software; Formal analysis; Investigation; Methodology; Validation; Visualization; Writing‐original draft; Writing‐review and editing. D. Bakar: Conceptualization; Methodology; Funding acquisition; Project administration; Resources; Supervision; Writing‐original draft; Writing‐review and editing.

CONFLICT OF INTEREST

V. K. M. is a co‐founder of Menten AI, in which he holds equity. The other authors report no conflicts of interest.

Supporting information

Data S1 Complete description of computational and experimental methods, including software development and architecture, computational peptide design protocols, synthetic and structural methods, supplementary figures (8), supplementary data tables (2), and supplementary references.

Mulligan VK, Kang CS, Sawaya MR, et al. Computational design of mixed chirality peptide macrocycles with internal symmetry. Protein Science. 2020;29:2433–2445. 10.1002/pro.3974