Identification of Normal Pressure Hydrocephalus by Disease-Specific Patterns of Brain Stiffness and Damping Ratio

Abstract

Objectives:

To perform a whole-brain analysis of alterations in brain mechanical properties due to normal pressure hydrocephalus (NPH).

Materials and Methods:

Magnetic resonance elastography (MRE) exams were performed on 85 participants including 44 cognitively unimpaired controls, 33 with NPH, and 8 who were amyloid-positive with Alzheimer clinical syndrome (A+ AlzCS). A custom neural network inversion was used to estimate stiffness and damping ratio from patches of displacement data, accounting for edges by training the network to estimate the mechanical properties in the presence of missing data. This learned inversion was first compared to a standard analytical approach in simulation experiments, and then applied to the in vivo MRE measurements. The effect of NPH on the mechanical properties was then assessed by voxel-wise modeling of the stiffness and damping ratio maps. Finally, a pattern analysis was performed on each individual’s mechanical property maps by computing the correlation between each person’s maps with the expected NPH effect. These features were used to fit a classifier and assess diagnostic accuracy.

Results:

The voxel-wise analysis of the in vivo mechanical property maps revealed a unique pattern in participants with NPH, including a concentric pattern of stiffening near the dural surface and softening near the ventricles, as well as decreased damping ratio predominantly in superior regions of the white matter (family-wise error corrected P<0.05 at cluster level). The pattern of stiffness changes in each participant predicted NPH status in this cohort, separating participants with NPH from control and A+ AlzCS groups with areas under the receiver operating characteristic curve of 0.999 and 1, respectively.

Conclusions:

This study provides motivation for further development of the neural network inversion framework, and demonstrates the potential of MRE as a novel tool to diagnose NPH and provide a window into its pathogenesis.

Introduction

Differentiating normal pressure hydrocephalus (NPH) from other forms of dementia such as Alzheimer’s disease (AD), frontotemporal dementia, and Lewy body dementia is important for selecting treatment, as NPH may be effectively treated with shunt placement (1–3). NPH is clinically characterized by cognitive impairment, gait abnormality, and urinary incontinence. However, clinical presentation is variable and clinical features often overlap with other conditions. Improvement in clinical symptoms, particularly gait, following a large volume lumbar puncture has been used at our institution and others to assist in making the diagnosis as well as predicting response to shunt placement (4, 5). This is an invasive procedure and difficult to apply widely to the aging population. Establishing non-invasive biomarkers to distinguish NPH from other neurodegenerative diseases and identifying patients with NPH who are more likely to be shunt responsive has the potential to improve patient care and outcomes.

MRI has been playing a greater role in the diagnosis of NPH over the past few decades via structural features such as ventriculomegaly out of proportion to the degree of cortical volume loss and crowding of the sulci at the vertex (6–8), segmentation-based algorithms (9–11), and flow studies showing increased flow through the cerebral aqueduct (12–15). These metrics remain imperfect in differentiating dementias. Given the hypothesized role of tissue biomechanics in the pathogenesis of NPH (16–21), magnetic resonance elastography (MRE) may have unique value not only for the diagnosis of NPH, but to provide insight into its development. However, initial MRE studies in NPH have been contradictory, with some showing a global decrease in stiffness and viscosity (22, 23), and others from our group indicating increased stiffness in parietal and occipital lobes with a trend toward decreased stiffness in the frontal lobes. The discrepancies between the studies may be due to differences in processing techniques, regions of analysis, and partial volume effects.

Therefore, the purpose of this work is to explore changes in brain viscoelasticity due to NPH across the entire brain. Such an analysis, however, presents the challenge of making a fair comparison between groups with significantly different brain morphologies, knowing that traditional MRE inversion algorithms (used to estimate mechanical properties from the measured displacement field) are biased near edges (26). To address this technical challenge, we will use the recently developed neural network inversion (NNI) framework (27), but modify the training data so that some of the measurements in each patch are excluded. Then, when this NNI is applied in vivo, measured displacements from outside the brain parenchyma can be removed prior to inversion to ensure the mechanical property estimates are derived only from measurements within the brain. The NNI is also modified to provide a viscoelastic description of the material by estimating both stiffness and damping ratio. This modified NNI will be evaluated in simulation experiments and compared to a standard, direct inversion method (28). We will then use this NNI to investigate the changes in mechanical properties due to NPH with a voxel-wise analysis, and assess the predictive power of the MRE results to distinguish participants with NPH from control participants and patients with Alzheimer clinical syndrome.

Materials and Methods

Participant recruitment

A total of 85 participants were included in this IRB-approved study after obtaining informed written consent. Thirty-three patients with NPH were recruited with inclusion criteria of: (1) the classic triad of clinical symptoms, (2) findings on anatomical MRI, and (3) improvement in symptoms following large-volume lumbar puncture. Findings on anatomical MRI included enlarged ventricles, typically out of proportion to the size of the sulci, often with increased T2 signal in the periventricular white matter resulting from transependymal cerebrospinal fluid (CSF) leakage (1, 29). Data from 44 cognitively unimpaired (CU) participants were taken from a previous study (30). These participants were recruited from the Mayo Clinic Study of Aging (31), in which they underwent an amyloid PET exam to ensure they did not have a significant level of this pathology. Data from 8 amyloid-positive patients with Alzheimer clinical syndrome (A+ AlzCS) were also included from a previous study (32). Demographic information is included in Table 1.

Table 1.

Demographic information by group.

	CU	NPH	A+ AlzCS
Number	44	33	8
Sex (% female)	47.8	36.4	25
Age (mean ± std dev)	74.5 ± 9.3	73.3 ± 6.8	84.2 ± 3.6

Data acquisition

MRE data were acquired on 3T MR scanners using a flow-compensated, spin-echo, EPI pulse sequence. Fourteen NPH participants were scanned on Discovery MR750 systems (GE, Waukesha, WI) with all others scanned on an HDxt system (GE, Waukesha, WI). MRE data were collected on the HDxt system with the following parameters: 60-Hz vibration; TR/TE = 3600/62 ms; FOV = 24 cm; 72×72 imaging matrix interpolated to 80×80; 48 contiguous 3-mm thick axis slices; one 18.2-ms, 4-G/cm, motion-encoding gradient (MEG) on each side of the refocusing pulse; x, y, and z motion-encoding directions; and 8 phase offsets spaced evenly over one period of 60-Hz motion. For the scans performed on the MR750 systems, 5-G/cm, 16.7-ms duration MEGs were used to reduce the TE to 57 ms while maintaining the same motion sensitivity as the HDxt acquisitions. A 3D T1-weighted image was also collected to segment the brain and guide the transformation of an atlas to the space of the MRE data. On the HDxt scanner, this image was acquired with an IR-SPGR pulse sequence with the following parameters: sagittal orientation, superior-inferior frequency-encoding direction, TR/TE = 7.0/2.8 ms, 11° flip angle, TI = 400 ms, FOV = 27 cm, 256×256 imaging matrix, BW = ±31.25 kHz, 1.75x ASSET acceleration, and 200 slice locations with 1.2-mm spacing. On the MR750 scanners, this image was acquired with an MP-RAGE pulse sequence with the following parameters: sagittal orientation, superior-inferior frequency-encoding direction, TR/TE = 7.4/3.0 ms, 8° flip angle, TI = 900 ms, FOV = 26 cm, 256×256 imaging matrix, BW = ±31.25 kHz, and 170 slice locations with 1.2-mm spacing.

Neural network inversion training

Brain masks and a lobar atlas were computed and transformed into MRE space to facilitate training and subsequent application of the NNI. Brain masks were computed by segmentation of the T1-weighted images to produce probabilistic maps of gray matter, white matter and cerebral spinal fluid using SPM5 with a custom template and priors (33, 34). Tissue probability maps along with a lobar atlas were then registered and resampled to the MRE magnitude image using the T1-weighted image as the reference image, as previously described (26). Voxels where the probabilities of gray matter plus white matter were greater than CSF were included in the brain mask. The masks were also segmented into 5 subregions, which were chosen to avoid inversion of data across major dural folds (that act as wave sources) and the lateral sulcus (where CSF separates anatomically distinct regions and expands due to atrophy). These subregions were the cerebellum; the union of the frontal lobes, deep gray matter and white matter, parietal lobe and corpus callosum (left and right hemispheres); and the union of the occipital and temporal lobes (left and right hemispheres).

As in the initial description of NNI (27), synthetic patches of displacement data were used to train a neural network, which is then applied to in vivo data to estimate the mechanical properties. For each training example, stiffness (defined as the product of density and the square of wave speed) was first randomly assigned in the range of 0.5 to 5 kPa with a uniform distribution, corresponding to a particular wave number, k. After selecting stiffness, a material attenuation, α, was randomly chosen as a fraction of the wave number. This fraction was randomly assigned in the range of 0 to 0.5. Damping ratio can then be computed from the wave number and attenuation coefficient according to the equation, $\zeta =\frac{k\alpha }{k^2-{\alpha }^2}$, under the assumptions of an isotropic and homogeneous material. Training patches were 7 voxels in each dimension with an isotropic voxel size of 3 mm to match the in vivo images. Total displacements were simulated as the superposition of displacements from a randomly selected number of point sources (1–5 sources per example chosen from a uniform distribution), where the location of each source was also chosen randomly within a sphere of radius equal to 5 times the wavelength of the stiffest possible material. Source locations were assigned by random selection of a radius, as well as polar and azimuthal angles with respect to the center of the patch. If the source fell within the simulated displacement patch, it was shifted to the nearest location outside the patch. The simulated displacements from each source were then computed according to the equation, $u\left(r,t\right)=\frac{1}{r}\text{exp}\left(-\alpha r\right)\text{sin}\left(kr-\omega t\right)$, where u is the displacement, r is the distance from the source, t is time, α is the material attenuation, k is the wave number, and ω is the vibrational frequency. This equation reflects the damped harmonic motion of a wave in a homogeneous material (35), with the 1/r term accounting for 3D geometrical spreading to maintain conservation of energy (36). The displacements from each point source were normalized by the mean amplitude in the patch, and then rescaled by a randomly chosen factor in the range of 0 to 1 taken from a uniform distribution. In this way, point sources that are close to the displacement patch do not dominate the total displacement field due the relative lack of geometrical spreading of the wave front. Zero-mean Gaussian noise was then added to the displacements, scaled such that the mean signal-to-noise ratio (SNR) over the patch was randomly assigned in the range of 1 to 20 selected from a uniform distribution. Finally a mask patch was randomly selected from the in vivo brain masks, and applied to the displacement patch. From these simulated patches, three inputs were used to train the NNIs including the real and imaginary parts of the first temporal harmonic of the displacements, and the mask. The phase of the displacement field was shifted so phase was 0 at the central voxel, and displacements were scaled from −1 to 1 as previously described (27).

Separate NNIs were fit to predict stiffness and damping ratio using the Keras API (37) with a TensorFlow backend (38). We used Inception-like network architecture (39) to allow different filter shapes. The full architecture is shown in Supplemental Figure 1. NNIs were fit to minimize mean squared error (MSE) using an Adam optimizer (40) with a mini-batch size of 100 examples and 1000 mini-batches per epoch. To help avoid overfitting, mini-batches of training data were generated in real time until the stopping criterion was reached, so training examples were never reused. Network fitting was performed at 3 learning rates (0.001, 0.0003, and 0.0001), each time stopping when the MSE over the epoch was not improved in 3 consecutive epochs. Since examples with the most missing data were the most difficult to learn, weights were applied to the training examples to linearly increase the penalty with increasing number of missing voxels.

Evaluation of NNI in test set

NNI performance was then evaluated in a test set of 100,000 examples, and compared to our standard implementation of direct inversion (DI) (28). To put DI on a more equal footing, we tested different degrees of pre-smoothing with a quartic kernel (to stabilize Laplacian estimation) (41), as well as median filtering within the mask after mechanical property estimation (to suppress outliers), while constraining the DI footprint to the same 7×7×7 patch as NNI. We used the combination of filtering that gave the best correlation between DI results and the true mechanical properties, which was pre-smoothing with a 3×3×3 quartic kernel, followed by DI, followed by a 3×3×3 median filter. We then fit the relationship between the true mechanical properties and each of the DI- and NNI-based estimates using a restricted cubic spline regression (5 knots placed at the 5^th, 27.5^th, 50^th, 72.5^th, and 95^th percentiles of the data). Since DI can produce large outliers that obscure these relationships, examples where stiffness was estimated at more than 10 kPa or the absolute value of the damping ratio was greater than 1 were excluded from this analysis.

Application of NNI to in vivo data

The processing steps for in vivo data analysis are summarized in Supplemental Figure 2. Mechanical property estimation was performed separately in the 5 subregions (defined above), and final maps were computed by union of those subregion estimates. To remove longitudinal waves, the curl of the displacement field was computed within each subregion of the brain (intersection of brain mask and region assignment) using previously described edge-aware methods (26). The trained NNIs (one each for stiffness and damping ratio) were then evaluated at each voxel for each of the 3 components of the curl, after the phase adjustment and scaling as described above. Estimates from the 3 components of the curl were combined with amplitude squared weighting. Since the corpus callosum is included in 2 subregions, the mean of those two estimates was used in the final mechanical property maps.

Simulation experiment

To compare mechanical property maps estimated by NNI and DI in brain-shaped objects, we performed a set of simulation experiments where the geometry was defined from the in vivo data from the 44 CU participants. For each participant, a total intracranial volume mask was first computed by thresholding the sum of the gray matter, white matter, and CSF probability maps (in MRE space) at 0.5, followed by a morphological dilation. Wave sources were then placed in all the voxels immediately surrounding this volume, with displacements from each source computed according to the previously defined wave equation, and the total displacement field taken as the superposition. The brain mask was then applied to create a realistic pattern of missing data. An example of one of these images is shown in Supplemental Figure 3. Note that the arrangement of point sources in this way produces a converging wave field, unlike the training examples, and so provides some insight into the generalizability of the NNIs to different wave geometries. Next, zero-mean Gaussian noise was added such that the median SNR of each simulated data set was equal to 10. This procedure was completed 9 times for each participant, including each combination of stiffness equal to 2, 3 and 4 kPa, and damping ratio equal to 0.15, 0.30, and 0.45. Stiffness and damping ratio maps were then computed using both NNI and DI. NNI was applied as in vivo, except that the curl was not required. DI was applied as in the test set with 3×3×3 quartic pre-smoothing and 3×3×3 within-mask median post-filtering.

This simulation experiment sought to observe any consistent biases in the mechanical property estimates across participants, and so the estimated maps from each participant were normalized to a custom in-house template designed for older participants including those with neurodegeneration (34), and the mean mechanical property map was computed for each combination of stiffness, damping ratio, and inversion technique. Normalization was performed by, first, estimating the rigid-body transformation to move the MRE magnitude image to the T1-weighted image, and then applying this deformation together with the previously computed deformation field that normalizes the T1-weighted image to the template. Nearest neighbor interpolation was used to resample the mechanical property maps to avoid the introduction of underestimates at the edges. Each map was smoothed by an edge-aware Gaussian kernel (FWHM = 5 mm). This step was applied to (1) reduce the effect of any anatomical misalignment remaining after normalization for the in vivo data, and (2) effectively dilate the stiffness maps to fill in sulci thus reducing missing data for subsequent voxel-wise modeling. Next, a smoothed brain mask was computed by morphological closing of the brain mask in template space and applied to the smoothed mechanical property maps. Finally, the model was fit at each voxel, which in the case of this simulation experiment was simply the mean across participants.

Voxel-wise modeling of mechanical property maps

In vivo mechanical property maps for all 85 participants were normalized to template space, smoothed, and masked as described above. To test for significant group-wise differences while controlling for nuisance variables, a linear model was then fit to the data at each voxel with predictors including age, sex, scanner system, and group. Since there is not perfect alignment between the participants’ maps even with normalization, participants with data missing at a particular voxel were excluded from model fitting on a voxel-by-voxel basis. Model fitting was performed in voxels where at least half of the participants in each group had valid data.

Significance testing was performed with an approximate permutation test to detect differences in mechanical properties in the NPH group as compared to each of the CU and A+ AlzCS groups. Overall, four different contrasts were tested (NPH>CU and NPH>A+ AlzCS for each of stiffness and damping ratio). The overall cluster-level family-wise error (FWE) rate was controlled at 5% by considering P<0.025 significant for each mechanical property. More specifically, for a given mechanical property and contrast of interest, an uncorrected cluster map was computed where the p-value of an F-test on group was less than 0.01 and the p-value on a T-test on the specific pair-wise group comparison was also less than 0.01. The spatial extent of a FWE-corrected significant cluster was then estimated by randomly shuffling the data labels 1,000 times. Each time, the linear model was fit, the two uncorrected cluster maps were computed, and the maximum cluster size (using 18-voxel connectivity) found in either of the two contrasts was recorded. The 97.5^th percentile of this distribution was then set as the minimum cluster size of statistical significance.

To observe the magnitude of effects that could be expected simply due to different brain shapes, we performed a simulation experiment similar to the one described above but including all 85 participants. In this simulation experiment, every participant was prescribed the same stiffness (2.33 kPa) and damping ratio (0.22), equal to the global means of the constant terms estimated in vivo. These simulated data where then inverted either by NNI or DI, and modeled as in the in vivo data. Unthresholded maps of the effects are presented and summarized in the Supplemental Digital Content.

Individual pattern analysis for differentiating clinical groups

After observing a unique pattern of mechanical properties in the NPH group, we aimed to assess how well these patterns could be used to discriminate participants with NPH from the other two groups. This analysis was performed in two steps, each using leave-one-out cross validation. First, we computed the spatial correlation of each participant’s mechanical property maps with the maps of expected changes due to NPH computed from the remaining participants. To perform this calculation for a given participant, first that participant’s maps were held aside and the remaining 84 participants were used for voxel-wise modeling. Since we aim to diagnose NPH, the model here was simplified to include age, sex, scanner system, and NPH status, akin to a one-versus-all classifier while controlling for nuisance effects. The mechanical property maps for that individual were then corrected for age, sex, scanner system, and mean mechanical property using the result from the other 84 participants. Then we computed the correlation coefficient between the corrected map and the estimated difference due to NPH from the other 84 participants. The correlation was computed only over voxels with non-zero data in both maps (37,495 ± 1,542 voxels included in calculation, mean ± standard deviation), and converted to a z-score by the Fisher r-to-z transformation. This calculation was performed for both stiffness and damping ratio maps for each participant. Second, we used support vector machine classifiers (again fitting a separate model for each participant not using that participant’s data) to estimate an NPH score for each participant (the signed distance to the decision boundary) given his or her correlation coefficients. These classifiers were fit in MATLAB 2017b (MathWorks, Natick, MA) with a linear kernel and box constraint, C=1. This model was chosen instead of a simpler logistic regression because a maximum likelihood estimate was not possible in some samples that had complete separation between groups. Using these scores, we finally computed the area under a receiver operating characteristic (ROC) curve to assess the degree to which these spatial patterns could discriminate NPH participants from the other two groups.

Results

NNI is more accurate than DI for estimating both stiffness and damping ratio in the test set.

Test set results are summarized in Figure 1. NNI-based estimates are more accurate than analogous DI-based estimates. The spline regression line also shows less bias in the NNI-based estimates, though bias in the NNI estimates can be seen at the top (for both stiffness and damping ratio) and bottom (for damping ratio) of the training range. Also note that the DI-based estimates are systematically biased by increasing amounts of missing data in the patch, while the effect of missing data on the NNI-based estimates manifests more as increased variance than as a bias (except near the edges of the training range). The same data are plotted in Supplemental Figure 4 but with the color-coding altered to show the effect of SNR. Those plots show that the NNI-based estimates are more accurate at high SNR as expected, but the effect of SNR on the DI-based estimates appears random. Since DI is negatively biased by noise (26, 27), this result suggests that the effect of missing data is substantially larger than the effect of noise. This inference is further supported by modeling the squared errors in a test set, where the partial correlation between DI-based errors and the number of non-zero voxels controlling for SNR was computed as −0.41, while the converse correlation with SNR controlling for missing voxels was −0.01. The effects of missing data and SNR on the NNI-based errors were more similar in magnitude with both partial correlations estimated as approximately −0.15.

Figure 1.

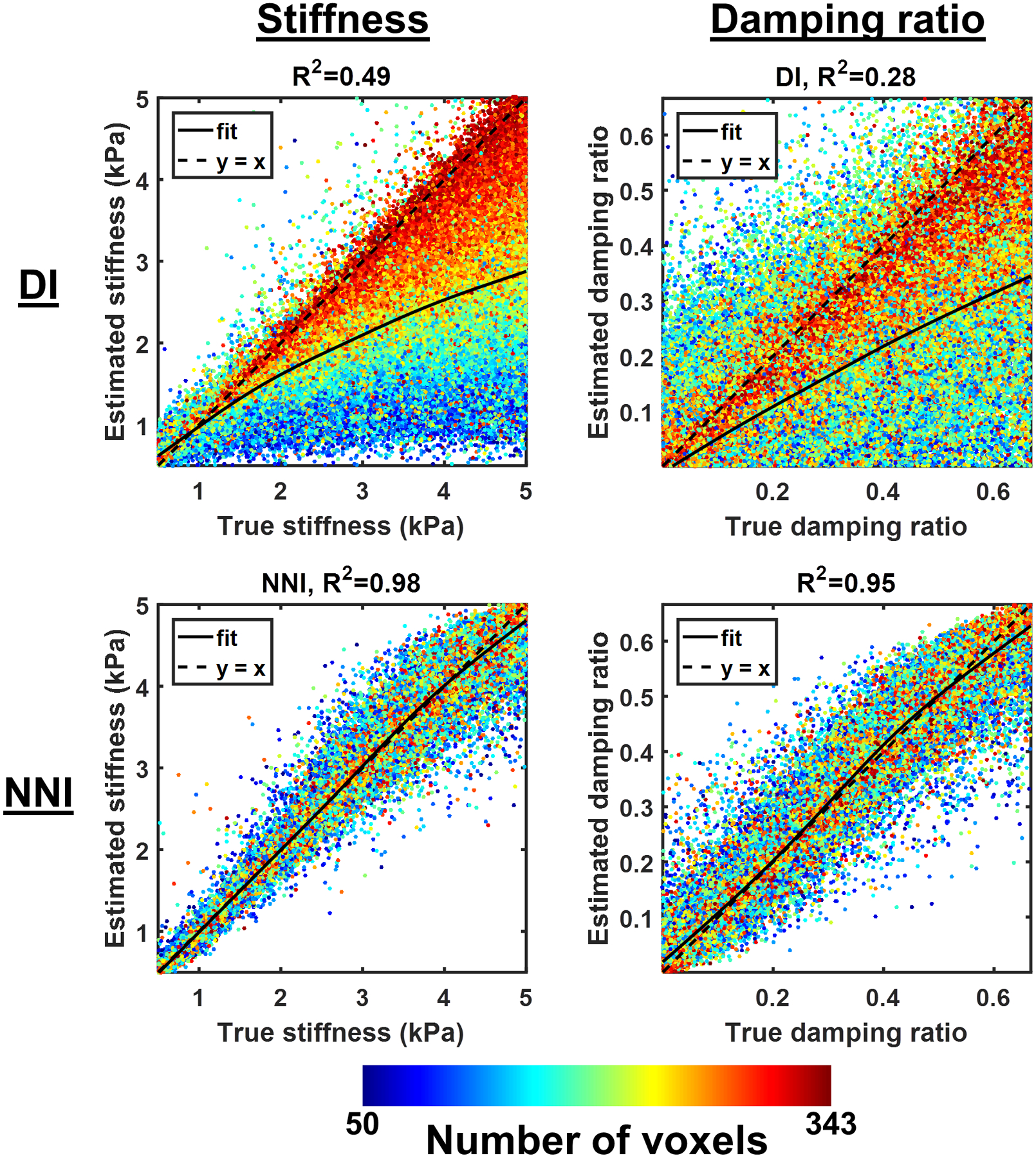
Summary test set results. Each plot shows the correlation between the estimated stiffness (left column) or damping ratio (right column), either by direct inversion (DI, top row) or neural network inversion (NNI, bottom row), and the true stiffness in a test set of 100,000 examples. The color of each point in the scatter plot indicates the number of non-zero voxels in the mask patch for that example.

NNI-based mechanical property estimates are less susceptible to partial volume effects than DI in simulated data.

Figure 2 shows a slice of the mean stiffness maps computed in the simulated data using DI and NNI for each combination of stiffness and damping ratio. Consistent with previous simulation results (26), the DI-based stiffness maps are underestimated at the edge for all stiffness values. The NNI stiffness maps are observably flatter (consistent with the homogeneous assigned stiffness), though do show some consistent errors (e.g., at the location of the genu of the corpus callosum). The analogous results for damping ratio are shown in Figure 3. Here with DI, we observe negative damping ratios at the outer edges of the simulated data and overestimates at inner edges. These biases are again reduced by NNI. Notably, neither inversion method exhibits an obvious interaction between stiffness and damping ratio estimates, meaning that the stiffness estimates for a given prescribed stiffness were mostly unaffected by varying damping ratio, and vice versa.

Figure 2.

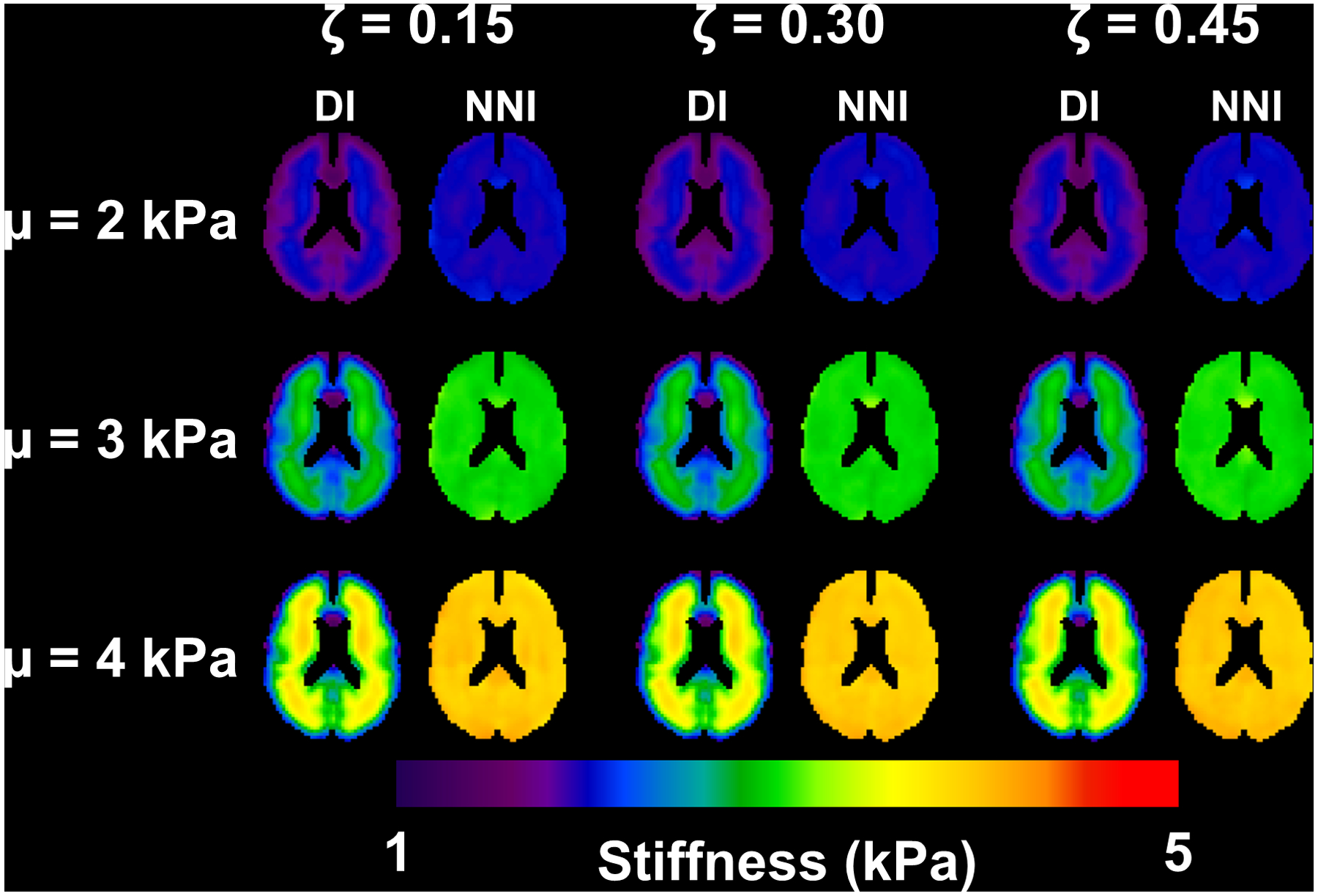
Mean stiffness maps from simulation experiment. Each panel includes the direct inversion (DI) and neural network inversion (NNI) result for a particular combination of stiffness and damping ratio.

Figure 3.

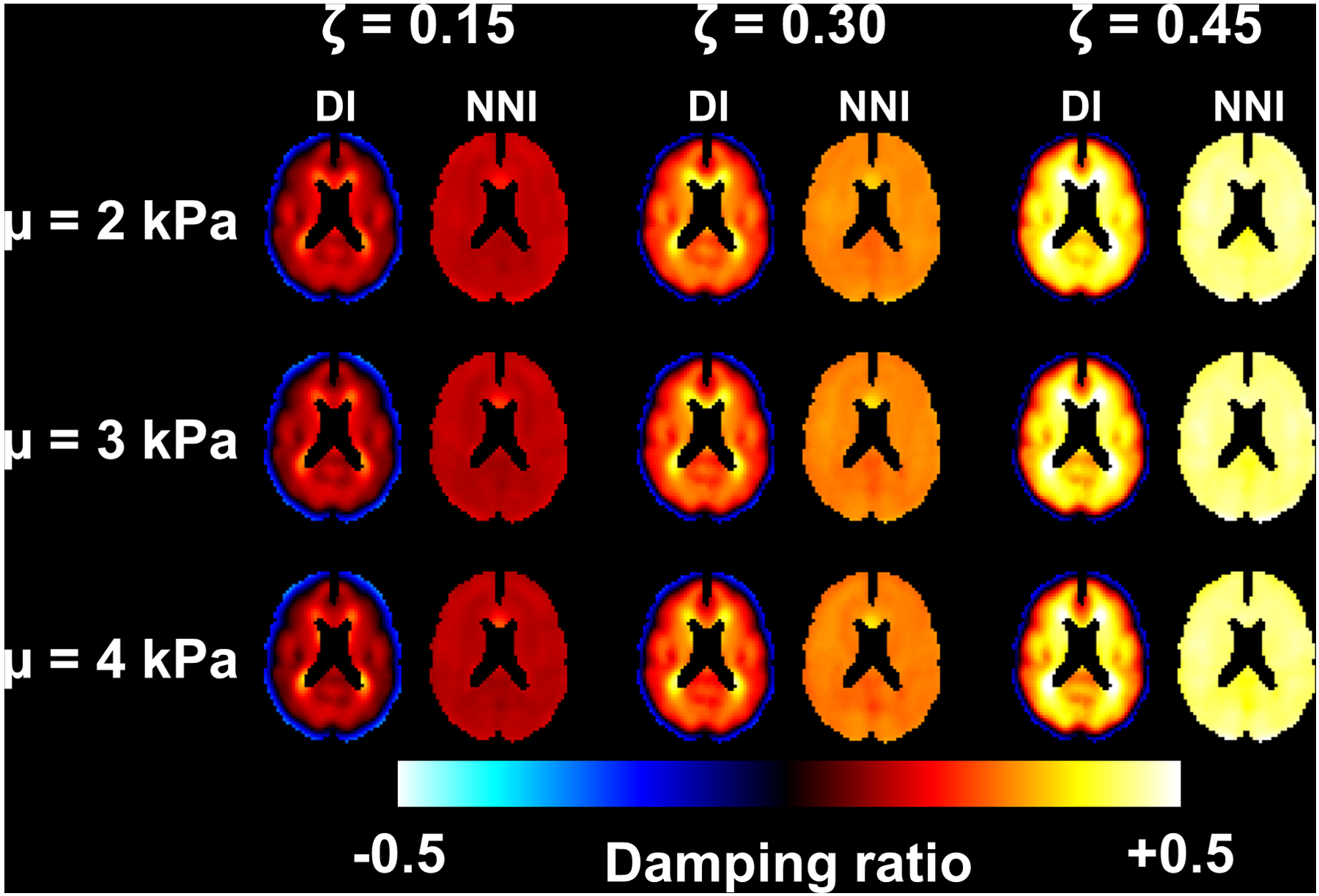
Mean damping maps from simulation experiment. Each panel includes the direct inversion (DI) and neural network inversion (NNI) result for a particular combination of stiffness and damping ratio.

Stiffness and damping ratio are both modified by NPH in a disease-specific pattern.

Mean stiffness maps in each of the three groups (corrected for age, sex, and scanner system), along with maps of the differences in stiffness due to NPH are shown in Figure 4. To more completely display the observed patterns of stiffness changes, the transparency of the difference maps is modulated by the uncorrected P-value computed by T-test. FWE-corrected maps showing only statistically significant clusters are included in Supplemental Figure 5. The difference maps show a concentric pattern of stiffness changes with periventricular softening and stiffening near the dural surfaces, though the softening is less pronounced when comparing the NPH and A+ AlzCS groups since AD also causes decreased stiffness. Mean damping ratio maps for each group with the corresponding transparency-modulated difference maps are shown in Figure 5, while the FWE-corrected difference maps are shown in Supplemental Figure 6. The difference maps indicate that NPH predominantly causes decreased damping ratio, with these differences particularly prominent at the level of the lateral ventricles and superior.

Figure 4.

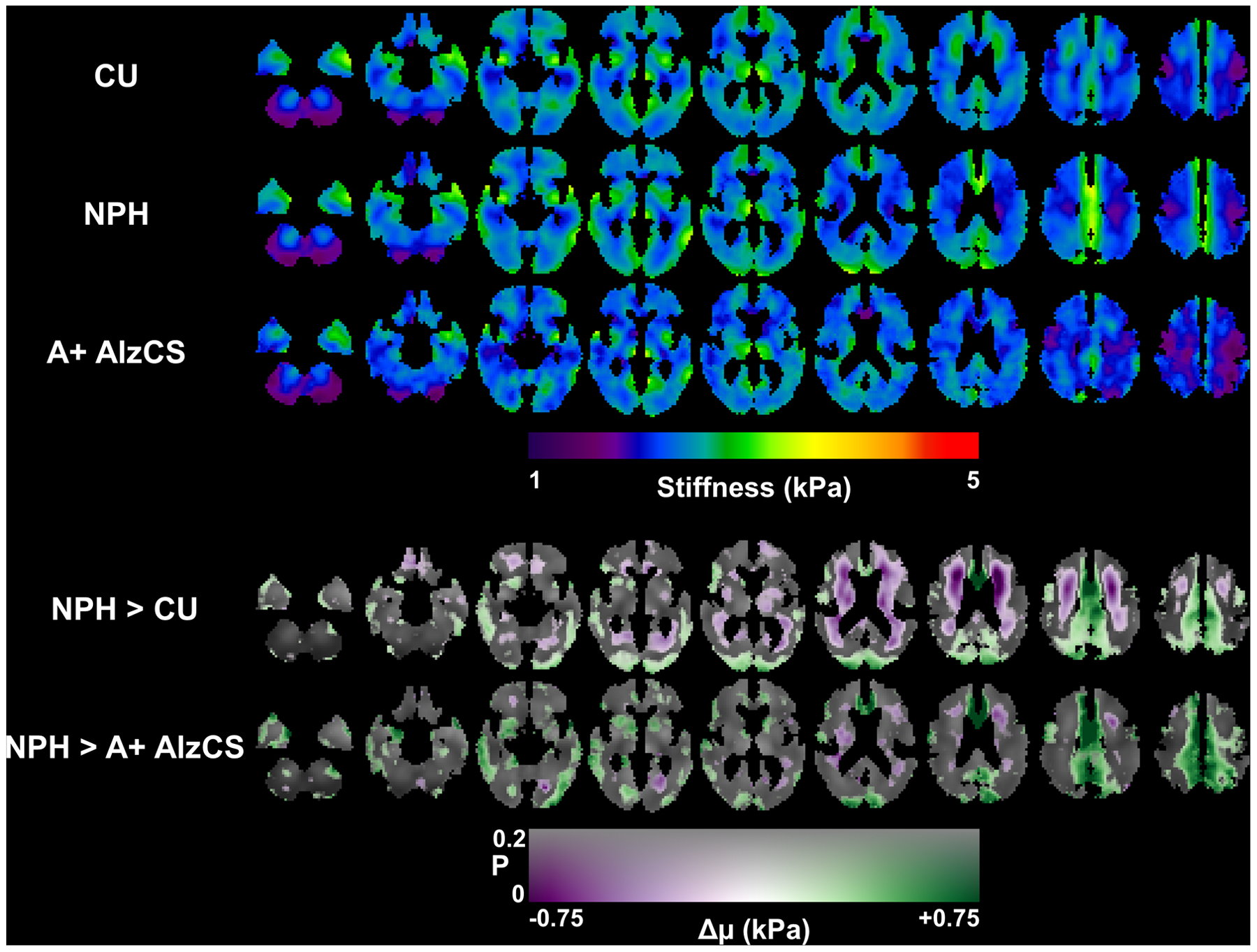
Top panel: Mean stiffness maps for each of the 3 groups after correction for age and sex. Each column shows a different slice location, arranged from inferior to superior positions. Bottom panel: Maps of the estimated change in stiffness (Δμ) due to NPH with respect to both the CU and AD groups. The difference map is overlaid on the mean CU stiffness map, with color representing the magnitude of the stiffness change and transparency encoding the uncorrected P-value estimated from a T-test on the relevant model coefficient.

Figure 5.

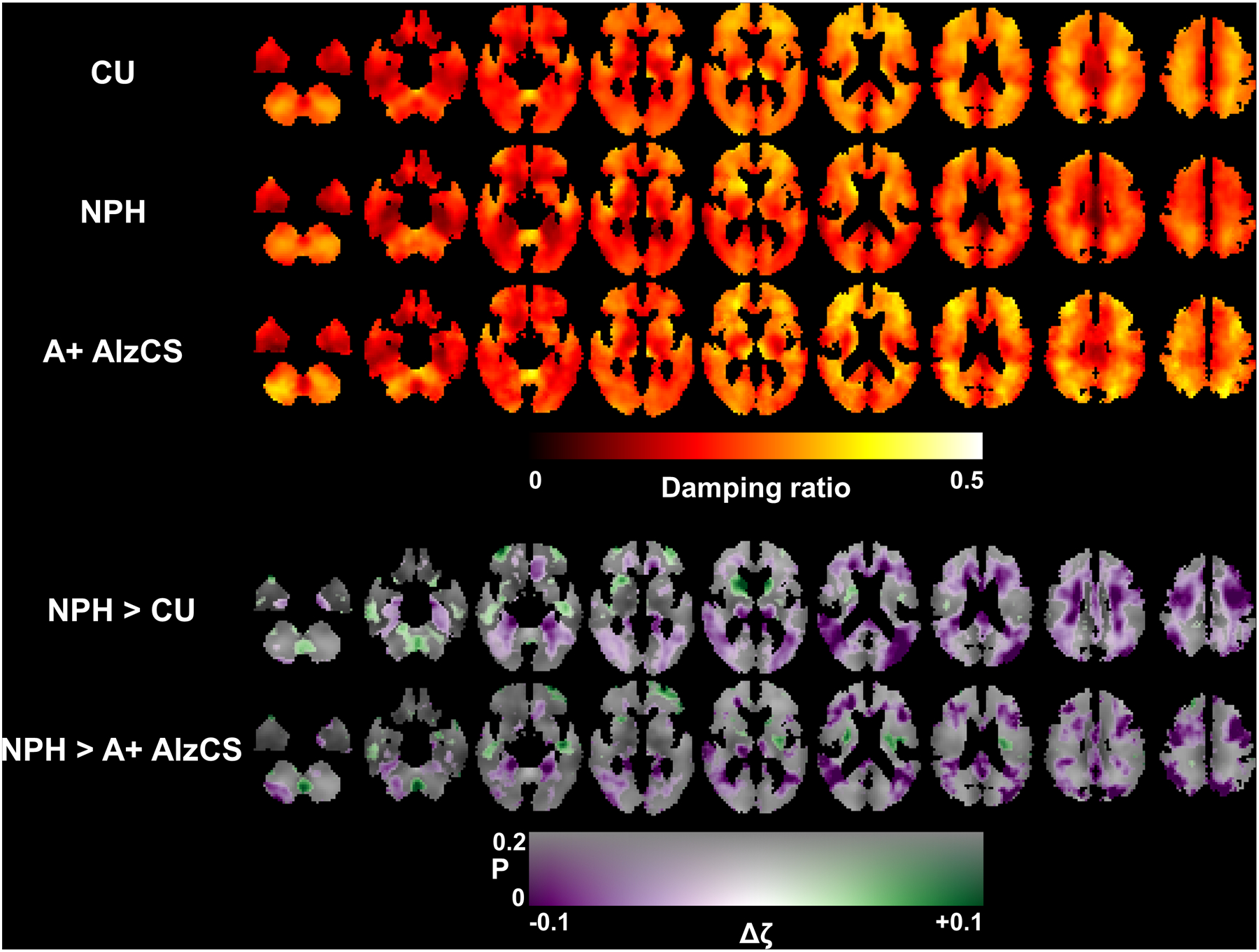
Top panel: Mean damping ratio maps for each of the 3 groups after correction for age and sex. Each column shows a different slice location, arranged from inferior to superior positions. Bottom panel: Maps of the estimated change in damping ratio (Δζ) due to NPH with respect to both the CU and A+ AlzCS groups. The difference map is overlaid on the mean CU stiffness map, with color representing the magnitude of the stiffness change and transparency encoding the uncorrected P-value estimated from a T-test on the relevant model coefficient.

Results from the second simulation experiment, which aims to observe the potential confounding effect of group-wise differences in brain morphology (mediated through edge-related bias from inversion), are summarized in Supplemental Figures 7–11. Briefly, when using DI to investigate group-wise differences in mechanical properties, effects can be observed both in stiffness (Supp. Fig. 7) and damping ratio (Supp. Fig. 8). These effects are reduced by NNI (Supp. Figs. 9 and 10). The voxel-wise distributions of the estimated group-wise effects for each mechanical property and contrast of interest are summarized in a set of histograms in Supplemental Figure 11. Ideally, these maps would be equal to 0 at all voxels. Using DI, we can see that the simulations based on NPH participants (with large proportions of CSF to total intracranial volume) are biased toward low stiffness and low damping ratios, particularly evident in the NPH>CU contrast. The magnitude of this bias is reduced when comparing groups with more similar morphologies (NPH>A+ AlzCS). Using NNI, both bias and variance are reduced.

Individual patterns in mechanical properties predict NPH diagnosis.

A scatter plot of the correlations between each individual’s corrected mechanical property maps with the expected NPH effect is shown in Figure 6. The plot shows that participants with NPH are clustered away from the CU and A+ AlzCS participants. Using these two features to estimate an NPH score for each participant, we computed areas under the ROC curve of 0.999 and 1 for separating the NPH group from the CU and A+ AlzCS groups, respectively. There is a positive correlation indicating that the stiffness and damping ratio patterns are predictive of one another, even in the CU and A+ AlzCS participants.

Figure 6.

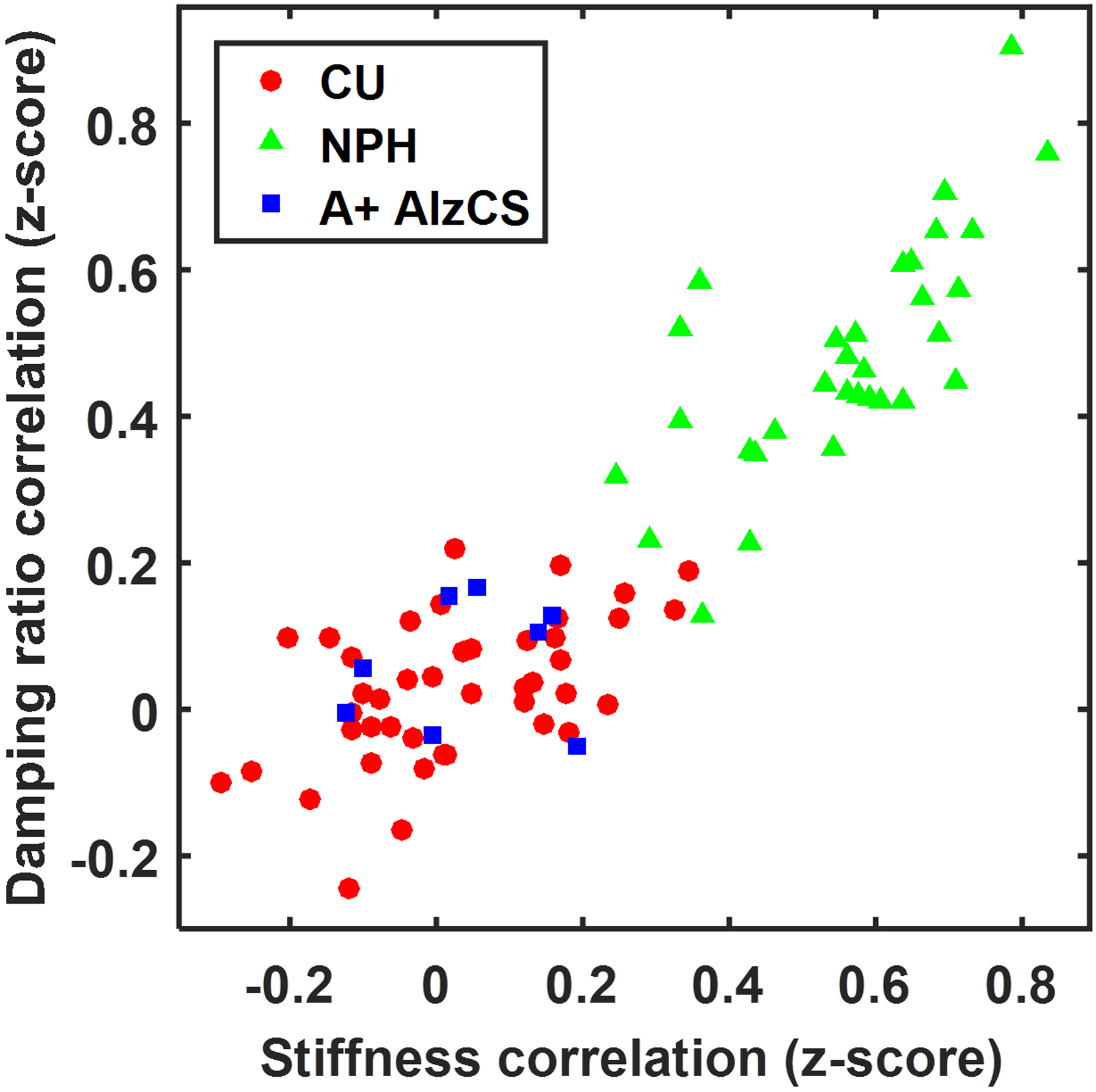
Scatter plot showing the spatial correlation between each participant’s age- and sex-corrected mechanical property maps and the estimated NPH effect.

Discussion

This study can be summarized in two parts. First, we used the NNI framework to develop a custom MRE inversion for the brain that provides accurate stiffness and damping ratio estimates in the presence of missing data. This behavior can be leveraged to provide more accurate stiffness estimates near edges in vivo by masking out displacement measurements from outside the brain prior to inversion. This technique is widely applicable to brain MRE studies of either normal physiology or diffuse disease. Second, the application of this inversion in a cohort of control, NPH and A+ AlzCS participants demonstrated a unique pattern of viscoelastic alterations due to NPH. Further, the agreement between an individual’s mechanical property maps and the expected NPH changes is highly predictive of that person’s clinical classification.

With respect to NNI development, three major modifications were made relative to previously described methods (27). First, we applied mask patches taken from in vivo data to the training examples so the NNI would learn to make accurate property estimates in the presence of missing data. In simulation, this method was shown to substantially reduce bias at edges. Previously when we wanted to compare stiffness estimates between two groups with different morphologies, we relied on erosion of the regions of interest until, based on simulation results, only voxels free of this edge-related bias were included (26). This approach coupled with the use of DI, which has larger noise-induced variance than NNI, limited our analyses to large, lobar ROIs. With these edge-effects significantly reduced, we can use the NNI-based estimates to evaluate changes in tissue mechanics closer to the edge of the brain in a voxel-wise manner. Second, whereas the previous NNI method used a simple, fully-connected neural network architecture, here we have implemented a convolutional neural network to better leverage the spatial information within our training patches. In our experience developing this NNI, we found that increased model complexity in general, and convolutional architecture more specifically, substantially improved performance in the presence of missing data. Third, while the previous NNI assumed no attenuation, the one used in this study was trained to estimate material attenuation while also accounting for geometrical spreading of the wave front. In the simulation experiments, the NNI provided accurate damping ratio estimates even when the geometry of the wave field was substantially altered from the training data. Qualitatively, the in vivo damping ratio maps computed here appear to agree with previous reports, including relatively small damping ratios in the corpus callosum with larger values found in the corona radiata (42). We also found increasing damping ratio moving from posterior to anterior portions of the corpus callosum as reported in (42), as well as relatively lower damping ratios in deep gray nuclei relative to the rest of the cerebrum (43).

Furthermore, these findings help explain the seeming discrepancies in previous MRE studies of NPH, as it appears all of those previous findings agree with the results shown here when accounting for the ROI selection. Streitberger et al. and Freimann et al. reported decreased global stiffness in 1 to 3 slices centered on the lateral ventricles (22, 23). Focusing on the stiffness changes at the level of the lateral ventricles in Figure 4, we can see that at this location most of the stiffness changes are negative. Further in agreement with previous studies, we would expect the softening effect to be larger when considering a periventricular ROI, as previously reported. On the other hand, the lobar analysis of Fattahi et al. reported increased stiffness in the parietal and occipital lobes (24), which again is consistent with Figure 4 of this study, since those lobes contain the stiffening effect near the dural surface with less of the softening effect. The ratio of the number of voxels with NPH-driven stiffening to softening was 2.3 in the parietal lobes and 2.15 in the occipital lobes. The frontal lobes, which showed a trend toward softening in (24), contain areas of both significant increases and decreases in stiffness, though extent of decreased stiffness is larger in volume within this region (ratio of softening to stiffening was 1.3). With respect to NPH-driven changes in viscosity, Streitberger et al. and Freimann et al. reported a decrease in the α parameter of the springpot model (22, 23), which is consistent with our finding of predominantly decreased damping ratio. Fattahi et al. and Perry et al. did not consider damping ratio.

Resolution of prior discrepancies in MRE evaluation of NPH and the ability to differentiate those with NPH from CU and A+ AlzCS participants supports a role for MRE in diagnosis of NPH. However, further investigation is necessary to establish the utility of MRE for this purpose including a prospective replication study, particularly for assessing the ability to discriminate NPH from A+ AlzCS where our sample was limited, as well as an analysis of the predictive value added by MRE when accounting for standard clinical imaging. Regarding NPH pathogenesis, the finding of softening in the periventricular white matter suggests degeneration of these white matter tracts. The subsequent dysfunction of these white matter projections may explain the symptomology of NPH including gait disturbances (white matter tracts from the mesial precentral gyrus) and incontinence (white matter projections from the mesial frontal and cingulate gyrus) (44, 45).

The limitations of this study will be the subject of future investigations. The incorporation of missing data into the NNI training examples provided accurate estimates at edges in simulation, while the edge-related artifacts that challenge traditional algorithms were not apparent in vivo. Nonetheless, it is important to note that this approach only accounts for the numerical challenge of missing measurements at edges, but since it still assumes a smooth underlying displacement field, it does not account for any alterations in wave propagation at the boundary. We have also included voxels with up to 50 percent cerebrospinal fluid in the brain mask, which assumes that the displacements in the fluid largely follow the displacement of the adjacent tissue. The impact of these assumptions will require further investigation. Another limitation of the inversion is that the spatial footprint was expanded to 7 voxels in order to more accurately estimate the mechanical properties close to edges, where more than half the data may be missing. Given that the training examples in this work assume homogeneous material properties, this expanded footprint will blur the resulting mechanical property maps. This limitation may be overcome by replacing the simple analytical wave simulations with a finite difference or finite element model. Finally, we would note that when interpreting the results and reproducibility of the study, one must consider how the diagnosis of NPH is made at their institution, as variability exists in diagnostic criteria which may alter population and findings.

In conclusion, this work shows that NNIs can be trained to obtain accurate estimates of both stiffness and damping ratio in the presence of missing data in simulation, demonstrating the flexibility of the NNI framework to deal with inversion challenges in the MRE field. Applying these NNIs in vivo, we found that NPH causes a unique spatial pattern of mechanical property alterations, and that pattern analysis in individuals is highly predictive of clinical status. Taken together, the results warrant further investigation into the use of NNIs to estimate mechanical properties from MRE data, and the use of MRE to diagnose, understand, and predict outcomes in NPH.