Significance
There exists a curious lacuna in our understanding of the development and evolution of cortical areas in the brain. Whereas massive research effort has focused on the development of primary sensory and motor areas, few such studies of higher cortical areas have been done, particularly at the earliest stages of development. In parallel, there exists intense interest in the interpretation of higher cortical areas across species, in how new areas of larger brains emerge. Using a network model of the developing cortex, we show here that new cortical areas may be the natural outcome of regularly scaling brains, arising as necessary products of an activity-driven developmental program conserved in the evolution of the cortex.
Keywords: development, evolution, network neuroscience, cortical areas, topographic maps
Abstract
While the mechanisms generating the topographic organization of primary sensory areas in the neocortex are well studied, what generates secondary cortical areas is virtually unknown. Using physical parameters representing primary and secondary visual areas as they vary from monkey to mouse, we derived a network growth model to explore if characteristic features of secondary areas could be produced from correlated activity patterns arising from V1 alone. We found that V1 seeded variable numbers of secondary areas based on activity-driven wiring and wiring-density limits within the cortical surface. These secondary areas exhibited the typical mirror-reversal of map topography on cortical area boundaries and progressive reduction of the area and spatial resolution of each new map on the caudorostral axis. Activity-based map formation may be the basic mechanism that establishes the matrix of topographically organized cortical areas available for later computational specialization.
In 1909, Brodmann divided the entire expanse of the human cerebral cortex into 52 “areas,” an analysis that organized research on the cortex for the following century (1). Brodmann systematically described cortical areas, from the coronal apex down, anterior to posterior. The histological evidence available to him included the presence and quantity of neurons and fiber layers, details of staining, characterization of cell body types and process elaborations of neurons in each area, and the numbers of nonneuronal cells, together called “cytoarchitectonics.”
Subsequent work, in the description of connectivity and topographic representation (2–4), pharmacological and immunohistochemical characterization of neuronal types (5), electrophysiological characterization of single neuron properties, neuroimaging (6), and gene expression (7) largely have reified Brodmann’s divisions, although subdividing and elaborating his choices. Progressively, over more than a century, cortical areas became to be defined by a conjunction of interrelated properties. The features of connectivity, response properties of single neurons, and topological organization now dominate the definition of a “cortical area.” Each cytoarchitectonic area of cortex differs from its immediate neighbors in the particular thalamic nuclei, subcortical regions, or intracortical areas it connects with. Each defined area could be further associated with a particular collection of electrophysiologically defined receptive field types, ranging over Hubel and Wiesel’s edge detectors in the primary visual cortex, “Area 17” (8), to a hierarchy of abstract decision properties in frontal cortex (9). The particular feature most central to the present study is that a cortical area typically presents a topologically organized representation of a sensory or motor surface like the retina or cochlea, secondary computed representations like intermodal egocentric space, or computed dimensions like “decision abstraction” (10).
By this progressive confluence of dimensions, cortical areas retained their unique status of the central unit of cortical organization, but the computational role of an area was subject to continuous revision. At first, by analogy to the electronics of the research era, each area was usually imagined as an input–output device that performed a particular transformation in accord with its unique within-area circuitry, passing on its results to other areas to be integrated with other inputs in a rough hierarchy first described by Felleman and Van Essen (11), often named according to their apparently dominant function.
Any typology defined by a loose aggregation of properties generates controversies. From the start, the uncertain relationship of neurological symptoms to the proposed function of areas (for example, the language and other functions of “Broca’s area”; ref. 12) caused controversy on the computational centrality of the cortical area. Adjacent areas might have only unimpressive differences in the ratios of electrophysiological classes of neurons, contrasted with the distinct functional names assigned to them (e.g., “Color” vs. “Motion”; ref. 13). Neuroimaging expands the controversy, where varying methods of analysis can alternately distinguish unique functions associated with each area (e.g., “Fusiform Face Area”; ref. 14) or a near unlimited depth of distinct sensory, motor, or integrative functions reaching across specific areas (reviewed in refs. 15 and 16). Influential network analyses, which typically define cortical areas as network “nodes,” can demonstrate new functional groupings over the classical typologies (17), but if metric distance as well as node “identity” linked to area is considered, different organizational principles emerge (18, 19). Comparing cortical organization in different species, where larger cortices usually present more and more “areas,” the question arises whether the new areas are add-ons, duplications, subdivisions, or complete reorganizations of larger defined zones (20–22).
A distinct developmental duality in the mechanisms by which cortical areas are positioned in the cortical surface and innervated has the potential to point to what mechanisms might generate nonprimary cortical areas. Primary sensory and motor areas are distinct from all other areas by being recognizable at the earliest developmental stages, genomically, neuroanatomically, and physiologically (7). Primary sensory areas uniquely attract and recognize, trophically require, and topographically organize input from their respective primary sensory thalamic nuclei with extreme specificity (21, 23–25) earlier than secondary cortical areas receive thalamic input (26). These primary cortical areas, positioned on the overall cortical surface by diffusible gradients emanating from the rostral and caudal poles of the cortical plate (28), are often said to “organize” the cortical map. A curious absence in cortical research becomes evident at this point. Although literally thousands of studies have been performed on the development of the topology, connectivity, and single-unit response properties of primary sensory and motor areas (for example, refs. 27 and 28), few to no such studies of “secondary” or “association” areas, particularly at the earliest stages of development, now well-known for primary visual or somatosensory cortex, have been done.
Decades of work characterizing the topography of the visual-field representations in the occipital and parietal cortex (6, 29), coupled with a similar depth of work uncovering the multiple mechanisms of topographic-map formation in the brain (30, 31), offer a way in to understand how nonprimary cortical fields might develop (Fig. 1A). Primary visual cortex, V1, is the largest in surface area of the visual representations and has a point-to-point representation of the retinal surface at high resolution. Secondary visual cortex, smaller in area, is topographically continuous with V1, mirror-reversing the V1 center-to-periphery retinotopic map at its anterior border while retaining its up–down polarity. “V3” is narrower still, again reversing polarity; further maps begin to fractionate. Overall, the anatomical and physiological topographic “resolution” of these maps decreases with distance from V1 (32).
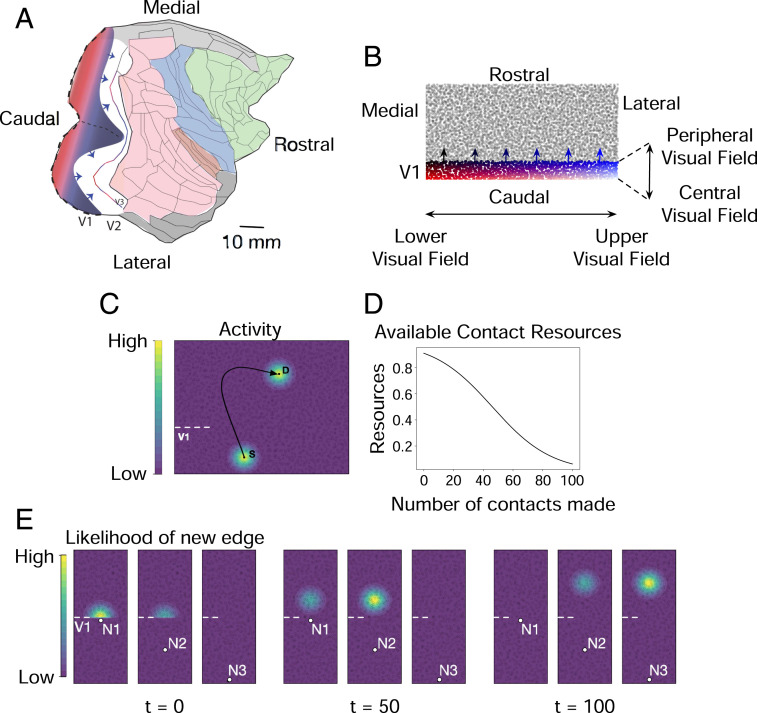
Fig. 1.
(A) Flattened representation of the right cortical hemisphere of a macaque monkey. The dotted line is where V1 is cut down the horizontal meridian to flatten it. Arrows show advancing axons exiting V1 into V2. The colored regions are frontal (green), limbic (gray), somatosensory (blue), and extended occipital–interparietal cortex (pink). Reprinted from ref. 48. Copyright (2015), with permission from Elsevier. (B) The initial state of the network model. Individual nodes represent a neural population under a 1 mm 1 mm piece of cortex. The network grows in sequential steps by forming new directed edges from nodes in V1 to nodes in the rest of the cortical sheet. (C) Contour plot illustrating spread of neural activity in a representative piece of the model. Activity of V1 node S generates correlated activity in its immediate spatial neighborhood. This activity falls off as a Gaussian outward from S. Activity in S also generates correlated activity on a distant node D to which S projects an edge to. Activity of D spreads to its neighborhood and falls off as a Gaussian outward from D. At each growth step, new edges preferentially form between nodes that have high activity correlations. (D) As new edges are added to a node, its available contact (synaptic) resources decreases as a sigmoidal function. New edges preferentially form between nodes that have a larger number of available contact resources. (E) Contour plot in a representative piece of the model, illustrating the likelihood (probability) of a new edge emanating from one of three nodes (S1, S2, S3) in V1 and terminating in any of the nodes outside of V1. The distribution of probabilities are shown at three different time points. In the network’s initial state (time t = 0, when no edges have yet formed), new edges are more likely to form between node S1 and nodes outside of V1 that are in immediate spatial proximity to S1. Subsequently at time t = 50 (followed by t = 100), new edges are more likely to form between node S2 (followed by S3) and nodes outside of V1 further along the caudorostral axis.
Secondary cortical areas could be generated directly by the early, topographically organized, and active axon innervation from primary cortical areas, using activity-driven mechanisms so amply demonstrated in the organization of binocular receptive fields, orientation selectivity, and so forth in primary visual cortex but largely missing the molecular axon/substrate recognition systems critical for the early emergence of V1 topography. We have found that such a generative process, operating within a network model of the developing visual cortex, gives rise to known properties of secondary visual areas, including mirror symmetry and progressive change in map size and resolution along the caudorostral axis of the cortex. Our results suggest that this developmental program has been conserved in the evolution of the neocortex and has formed the basis on which new cortical areas have emerged in regularly scaling brains.
Results
Growth Model.
We used the relative dimensions of the areas and border lengths of primary and secondary visual cortical regions of the rhesus macaque (Fig. 1A) to initialize a network model whose nodes are localized populations of neurons and whose edges are representative axons. Spatial parameters of the model approximately correspond to the actual two-dimensional surface view of the visual cortex, taken from ref. 19, which in turn were derived from refs. 18 and 33. Surface area lies atop an entire hierarchy of factors, from volume to neuron and synaptic densities, all worth investigation after the first-order effects are established.
The model comprises 5,000 nodes, each representing the neural population under a 1 mm 1 mm piece of cortex. The nodes are distributed across a 100 mm 50 mm model cortical sheet. Specifically, the sheet is divided into 5,000 equally sized units and a node is placed at a location chosen uniformly at random within each unit.
We represent the primary visual cortex (V1) in a 100 mm 10 mm region of the model cortical sheet and potential secondary areas in the remaining region. The initial state of the model is shown in Fig. 1B, where the location of nodes within V1 are color-coded. In the macaque cortex, the horizontally extended blue-to-black edge represents the peripheral visual field on an unrolled cortex, and the white-to-red edge represents the central visual field. V1 nodes along the caudorostral axis (white-to-blue, red-to-black) span 90° center-to-periphery of the visual field. The blue-to-black boundary is located at the anterior-most aspect of V1 and is curved. The representation used for this model employs the approximate ratio of the length of the peripheral border to the length of the peripheral-to-vertical meridian: essentially, the horizontal meridian is “split” and laid on the abscissa, the white-to-red axis, and spans 180° up-to-down of the central visual field.
We model cortical development by means of a developmental program that adds new directed edges to the network, originating at nodes in the primary visual cortex and terminating at nodes in potential secondary visual areas. The program unfolds over sequential growth steps, and a constant number of edges are added to the network at each step. The source and destination nodes of a new edge are drawn from a probability distribution that is a function of two variables: 1) pairwise activity correlations between nodes in the network and 2) available number of contact resources at each node. Pairwise activity correlations arise from spontaneous excitation of V1 nodes at every growth step, which in the cortex arises from multiple sources (34–36). Excitation of a V1 node generates correlated excitation in nodes in its immediate spatial neighborhood as well as in the neighborhood of nodes where it projects edges to (Fig. 1C), corresponding to a spread of neural activity outwards from excited nodes. New edges preferentially form between nodes whose activities are more correlated. As these new edges are added, the number of contact resources of the connecting nodes decline (Fig. 1D), corresponding to a depletion of synaptic contact points in the respective neural populations. Model equations are provided in Materials and Methods.
Thus, during the growth of the network, a new edge is more likely to form between two nodes that have higher activity correlations and more contact resources compared with other node pairs in the network. Addition of these edges alter pairwise activity correlations in the network and the available contact resources of the connecting nodes, thereby altering the probability distribution from which subsequent edges are drawn (Fig. 1E).
Topographically Organized Mirror-Reversing Maps.
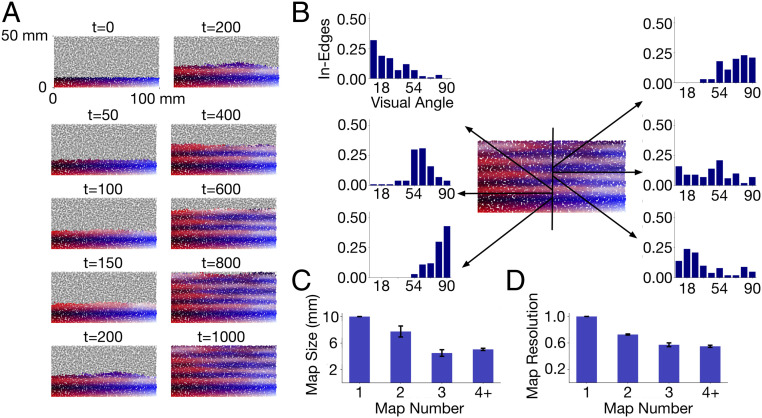
The generation of maps in secondary visual areas from the “seed” map of V1 is demonstrated in Fig. 2. The figure depicts the progressive formation of new topographically organized areas at 10 time points. The initial state of the network is shown at time t = 0. The location of nodes in V1 are color-coded with the red-to-black and the white-to-blue progressions representing locations center-to-periphery of the visual field and the white-to-red and the blue-to-black progressions representing locations up-to-down. As the developmental program progresses in time, the visual-field locations that nodes outside of V1 come to represent are also depicted by color. Specifically, each (red–green–blue) color component of a node outside of V1 is determined by averaging the corresponding color component of its incoming edges, where each edge is assigned the color of its source node (residing in V1).
Fig. 2.
(A) Sequential steps of network growth from the initial state at time t = 0 to the final state at time t = 1,000. At each growth step, new edges are added from nodes in V1 to nodes outside of V1. The location of the center-to-periphery visual field represented by each node is color-coded. The gradual change in color along the caudorostral axis depicts the progression of the topographical representation within a map and the mirror-reversals across successive maps. (B) Receptive fields of six nodes along the caudorostral axis. The bar graphs depict the visual field represented at each of the nodes. Each bar shows the number of incoming edges (normalized count) from V1 nodes that represent particular center-to-periphery locations (shown as visual angles) of the visual field. (C) Size of successive maps, averaged across multiple 1 mm × 50 mm slices along the caudorostral axis. Error bars depict SD. (D) Center-to-periphery receptive field resolution in successive maps. Resolution of a node is measured as , where is the SD of the center-to-periphery visual-field angles represented in the incoming edges of the node. Nodes have higher resolution when their incoming edges represent more similar points of the visual field. Values are averaged across all nodes in the maps.
The first nodes to establish synaptic contacts in “V2” are those close to V1 nodes representing peripheral locations up-to-down, because of correlated activity arising from their immediate spatial propinquity. As new edges are added, the next to establish contacts are those representing positions less peripheral, as contact resources of the most peripheral nodes decline. The mirror-reversal of the horizontal axis of the visual field proceeds in this fashion forward, and by t = 200, the first representation of the visual field is complete, “V2,” and the next mirror-reversal emerges, this time of the vertical meridian of the central visual field, initiating “V3.” Eight mirror-reversing representations of the visual field are established by t = 1,000. The distribution of incoming edges at six indicated nodes at this time is shown in Fig. 2B.
Map Size and Resolution.
Each of the successive maps arising from the growth of the network represents the full central-to-peripheral extent of the visual field. Consistent with approximate size ratios measured in the macaque, successive maps from V1 to V3 compress in size along the caudorostral axis. This is shown in Fig. 2C, where, on average, V2 and V3 are around 80 and the size of V1, respectively. In tandem with this successive size compression, the resolution of the maps, as measured by the distribution of incoming edges in their nodes, successively falls (Fig. 2D).
The successive reduction in map resolution and size arises as proximal V1 nodes with correlated activity tend to project edges to the same V2 node. Thus, each V2 node comes to represent a larger area of the visual field and have a coarser resolution compared with the point-to-point retinotopic mapping in V1; consequently, the overall V2 map is compressed relative to V1. In contrast to the high-resolution V1 nodes at the V1–V2 boundary, lower-resolution V2 nodes at the V2–V3 boundary initiate a coarse V3 map that undergoes a further reduction in resolution and size as compared with V1 and V2.
Spatial Spread of Correlation Envelope.
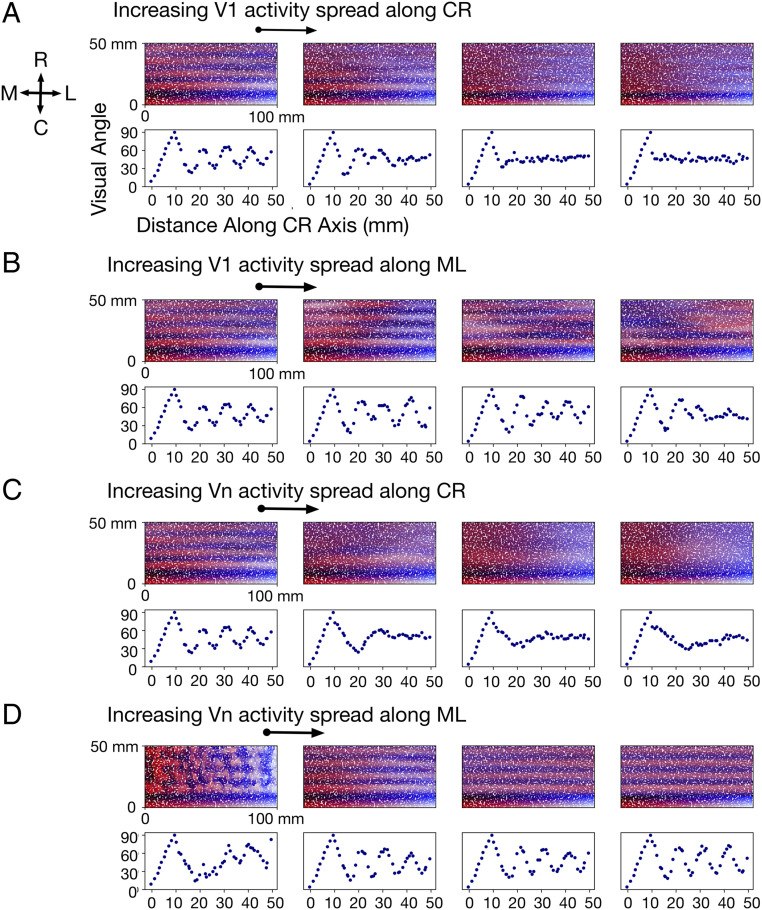
Excitation of a V1 node in the network model is accompanied by correlated excitation in nodes of its immediate neighborhood (Fig. 1C), the extent of which is defined by a two-dimensional Gaussian function parameterized by a spread along the mediolateral axis () and a spread along the caudorostral axis () (Materials and Methods). The spatial extent of these spreads affect the degree of activity correlations between nodes, with a broader spread generating higher activity correlations. Excitation of a V1 node also generates correlated excitation on nodes in secondary visual areas to which it projects edges to (Fig. 1C). This excitation spreads to the neighborhood of the receiving node, the extent of the neighborhood being defined by a second Gaussian parameterized by spreads along each of the two axes. Below, we investigate map properties as the activity spreads in V1 and the secondary visual areas are systematically varied.
The effect of increasing activity spread in V1 while the activity spread in the secondary areas is kept constant is shown in Fig. 3A (increase along caudorostral axis) and Fig. 3B (increase along mediolateral axis). Note particularly the sensitivity to activity spread along the caudorostral axis in Fig. 3A. The left-most map uses a Gaussian function with SD and , corresponding to a spread that falls off to of its peak value within 0.5 mm along either axes. Here, eight topographic maps form from the initial V1 seed, corresponding to eight mirror-reversals. Note the periodic change in represented visual angle along the propagating axis.
Fig. 3.
(A) Effect of increasing the activity spread in V1 along the caudorostral (CR) axis. From left to right, this spread ( in Eq. 1) is set to 0.5 mm (leftmost), 1.0 , 1.5, and 2.0 mm (rightmost), respectively. In all four sets of graphs, activity spread in V1 along the mediolateral (ML) axis is held constant at 0.5 mm, and activity spread in secondary visual areas along the CR and ML axes are held constant at 0.5 and 5.0 mm, respectively. Visual angles represented in a 1 mm × 50 mm slice along the CR axis are shown below each map. The visual angle represented in a node is measured as the mean of the visual angles represented in its incoming edges. (B) Effect of increasing the activity spread in V1 along the ML axis. In the four sets of graphs, from left to right, this spread ( in Eq. 1) is set to 0.5, 2.5, 5.0, and 7.5 mm, respectively. In all four sets of graphs, the spread in V1 along the CR axis is held constant at 0.5 mm, and that in secondary visual areas along the CR and ML axes are held constant at 0.5 and 5.0 mm, respectively. (C) Effect of increasing the activity spread in secondary visual areas (Vn) along the CR axis. In the four sets of graphs, from left to right, this spread is set to 0.5, 1.0, 2.5, and 5.0 mm, respectively. In all four sets of graphs, the spread in Vn along the ML axis is held constant at 5.0 mm, and that in V1 along the CR and ML axes are both held constant at 0.5 mm. (D) Effect of increasing the activity spread in Vn along the ML axis. In the four sets of graphs, from left to right, this spread is set to 0.5, 5.0, 12.5, and 25.0 mm, respectively. In all four sets of graphs, the spread in Vn along the CR axis is held constant at 0.5 mm, and that in V1 along the CR and ML axes are both held constant at 0.5 mm.
The second map from the left in Fig. 3A shows the effects of increasing the spread of to 1.0. This corresponds to a Gaussian that falls off to of its peak within 1 mm along the caudorostral axis. In this case, resolution of the visual map has declined, and topographic organization beyond the fifth map has essentially disappeared. A larger spread along the caudorostral axis increases activity correlations between nodes in V1 along this axis, resulting in V1 nodes within a spatially extended region to project to common targets. Consequently, the resolution of visual-field representations in secondary areas is reduced. When the spread increases further (fourth column in Fig. 3A), notice that while the caudorostral periodicity of the maps virtually disappears, mediolateral alignment of the maps remain for a few iterations.
The effect of increasing activity spread in the secondary areas while the activity spread in V1 is kept fixed is shown in Fig. 3C (increase along caudorostral axis) and Fig. 3D (increase along mediolateral axis). Note particularly the effects of mediolateral spread in Fig. 3D. A small spread of the Gaussian (leftmost column; and ) induces local clusters of correlations and generates disorderly maps. When the spread along this axis is increased (second from the left column; ), orderly maps emerge. This is a consequence of higher activity correlations along the mediolateral axis that establishes continuity of a particular center-to-periphery visual-field location represented along this axis. Interestingly, the initial distribution of growing axons is somewhat anisotropic over the embryonic cortex (38), a potential source of these anisotropic correlations. As the spread is increased further along the mediolateral axis, map order and periodicity stay intact; thus, the activity spread along the other axis and the activity spread in V1 is the dominating influence in this parameter regime.
Scaling Cortex Size.
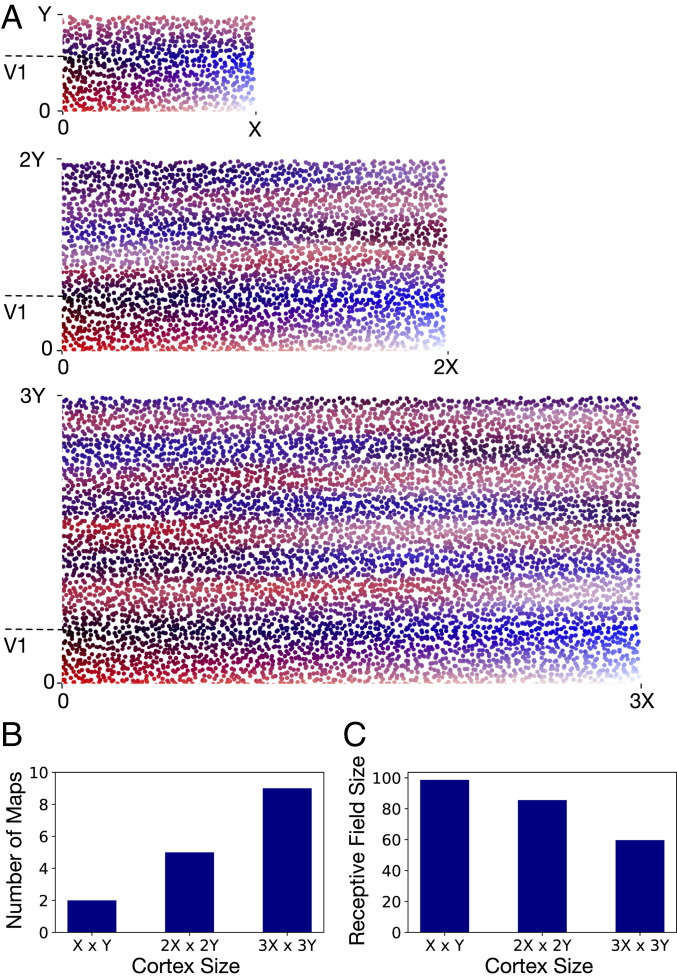
As the cortex increases in size from mouse to macaque, V1 axons extend to an expanded area of the cortical surface whose parameters are described in ref. 19. We investigate the effects of this expansion on the properties of the maps generated by our model (Fig. 4). As before, we are using surface area as is normally measured in both these species, uncorrected for neuronal density and other significant species differences, to investigate first-order effects on map formation.
Fig. 4.
(A) As the size of the model cortex is increased, the developmental program generates systematic variations in cortical organization. Most notably, a larger number of topographically organized secondary visual areas emerge as the total surface area of the cortex is increased. The largest cortex shown is threefold larger along each dimension compared with the smallest cortex. The number of nodes per unit surface area is the same in all three cortices. The largest cortex has 7,200 nodes in total, and the two smaller cortices have 3,200 nodes and 800 nodes, respectively. The length of V1 along the propagating axis is held constant (at ) for all three cortices. (B and C) The number of maps and the average size of V2 receptive fields in the cortices shown in A. The receptive field size of a V2 node is measured as the SD of up-to-down visual-field angles represented in its incoming edges.
We find that, as the cortical surface area increases, a larger number of topographically organized secondary visual areas are generated (Fig. 4 A and B). The expanded area available for V1 axonal outgrowth results in repeated mirror flips of the V1 topographic map arising from the iterative mechanisms of map propagation in the developmental program. Furthermore, the increase in cortical surface area along the mediolateral axis results in reduced activity correlations between V1 nodes representing distinct up-to-down locations of the visual field. As a consequence, the likelihood of these nodes projecting to common targets is reduced, resulting in finer resolution of visual-field representations in secondary visual areas of the larger cortex (Fig. 4C).
Discussion
Principal Findings and Empirical Support.
The investigations presented here show that iterated topographic maps of a “seed” map can be generated from minimal information sources. The critical information source parametrically explored here is the activity correlation between neuronal populations that arise due to the formation of synaptic contacts between them.
Map development is conceptualized as extending from the seed region in successive steps. The first map of the secondary visual areas mirror-reverses at the border of V1 and is smaller in overall spatial dimensions than V1. Multiple mirror-reversals and maps are formed by this process, with each one smaller in spatial dimension than the prior map in the first couple of iterations and with lesser spatial resolution at each of its nodes overall. Progressive flattening of the V1 activity spread eventually disrupted map propagation, except for some “passive” alignment of similar receptive field areas on the mediolateral axis (x axis in Fig. 3A, rightmost column).
This developmental program did not specify any preference of edges for any particular part of the substrate (often called “axon–target interaction”) other than preferences arising from activity correlations, any recognition process between edges (often called “axon-axon recognition”) (30), nor the size of the “cortical areas” to be formed, except by the limits of the overall area of the propagating region. Receptive fields were composed only from the convergence of the most-correlated edges.
The overall spatial parameters of the maps explored were chosen to represent the spatial parameters of the actual visual cortex in two-dimensional form but with no attempt to relate neuron numbers to node numbers. These parameters included 1) the area of the seed region, 2) the area of the region for propagation, 3) the initial spatial extent of extending axons implied by Gaussian envelopes of correlations, and 4) the large asymmetry in the length of the border over which maps propagate, compared with the shorter dimension on the propagating axis. The border of V1 with secondary visual areas corresponds to the upper-to-lower limit of the visual field on its first mirror-reversal and the vertical meridian of the visual field on the second mirror-reversal. The other axis, the “propagating” axis, at its midpoint is the horizontal meridian of the visual field, which is “cut” to lay out the map on one continuous axis on the graph, as in Fig. 1B, exactly analogous to the procedure used to lay out the curved cortical surface in Fig. 1A.
The particular connectional geometry of visual areas seen in the cortex is interesting, considering the immense number of possible arrangements of array-to-array maps: the ovoid hemisphere of V1 is “linearized” to a strip with its long axes representing the lateral periphery and the cut the horizontal meridian. A benefit to this arrangement is evident in Fig. 1B: a large part of the propagating map and the secondary region is lined up “passively” on its longest axis in the network’s initial state, while topographic order must be established by additional cellular mechanisms on the mirror-propagating axis. Interestingly, the somatosensory- and possibly auditory-propagating regions have similar shapes in their initial and iterating maps.
The propagation of the V1 map is iterative and proceeded along the caudorostral axis from the nodes closest to V1 to nodes most distant. This propagation was driven by activity correlations between neighboring nodes and wiring limits within nodes that had established connections. These two minimal features, activity-based attachment and wiring density limits, were essential to establish map polarity, initially forming edges between highly correlated nodes located at the V1–V2 border and subsequently between nodes further away from the border, as contact resources of nodes at the border declined. This process propagated and ordered the rest of the V2 map and its mirror-reversing iterations. It is worth underlining that multiple additional mechanisms might contribute to map organization: a major lesson learned from multiple investigations of retinotectal map formation in multiple vertebrates, following Sperry’s initial work (39), was the demonstration that virtually all possible sources of order were exploited in map formation, including spatial and temporal maturational asymmetries, neuron/location-recognition systems, and activity-dependent ordering (31).
Since this model generates a sequentially appearing map without positing any maturational gradients or sequential axon spread, empirical information on the question of how such maps actually arise would be a useful test of the model, but to our knowledge, no such fine-grained information of the early progression of map formation exists. This process takes place within several early gradients in the cortex and should be distinguished from them. The entire cortex has a rostral-to-caudal progression of neuron generation followed immediately by axon extension and establishment of intracortical and callosal connectivity, much of that prior to thalamic input (26). Superimposed on the rostral-to-caudal neurogenesis gradient is the gradient of thalamocortical innervation of the cortex. The primary sensory thalamocortical regions are generated early, by a large margin, and establish effective connections early (26). There is evidence for maturation of function proceeding out from primary sensory areas into the hierarchy of whole areas (37) but no evidence yet of sequential map formation arising from the generation of a cortical area.
One surprising observation of studies of both developing (38) and mature intracortical axon extent is how very large the area of overall cortex is that may be reached from a “point” origin in the cortex (18, 19) (if recovered from identified single axons, the covered area becomes patchier but not larger in its outside perimeter). In the mouse, the range of projections from a point injection can reach 80 to 90% of the cortical surface; in the rhesus monkey, whose surface area is 200 greater than the mouse’s, the range is about 50%. The terminations of the axons from this point have an “exponential distance falloff” in which most terminations (50 to 90%) are close to the origin, and the remaining small fraction reach further (19). Looking in a developing rodent, the hamster, which is born early enough so that the cortex may be injected when the final supragranular cortical neurons, the main source of intracortical projections, have only just migrated into position (26), the full range of axon extent (as a percentage of cortical surface area, which is quite small at this point) is established almost immediately (37). There is no “front” of axon outgrowth, so the spatial correlations of activity by which the maps are found must be found within the whole axon outgrowth complement. Interestingly, the overall pattern of axon outgrowth is set up when the cortical surface is only about 20% of its adult area (26), so like most of the brain, axon stretch rather than axon extension will characterize most axon growth (40), a fact hypothesized to be of material importance in the establishment of gyri and sulci (41).
The sources of topographically organized activation of the cortex are multiple, including the endogenous correlations of any of the contributing structures, “retinal waves,” and eventually the sensory periphery. Each have separate time courses and different degrees of spatiotemporal correlations (34), and a further complication is that their influences must be first organized in the transitory subplate (42). The cortex becomes unresponsive to retinal waves before eye opening (35), at which time, the cortical areal extent has approximately doubled (26).
The emergence of the retinotopic map in V1 has been extensively studied in several species from the earliest accessible times, typically postnatal and post-eye opening. The initially surprising, but now well-accepted, result that the V1 retinotopic map is close to or at its adult specificity at its very first emergence was quickly established (as contrasted with the stabilization of ocular-dominance columns or midbrain visuotopic maps that stabilize later). The primary sensory and sensorimotor nuclei of the thalamus and their corresponding cortical projection regions appear both temporally and informationally privileged (23, 36, 43). These thalamic nuclei are generated before all other thalamic nuclei and establish their cortical connections first as well (26). The neurons that will become somatosensory (or somatomotor), auditory, and visual cortices are not generated prematurely but rather are positioned at their typical relative locations within the cortical plate by rostral and caudal polarizers (44). Once positioned, genomic studies demonstrate that the early primary sensory regions are different from all other cortical areas, replete with gene expression for surface proteins and receptors implicated in axon–target interaction and topographic-map polarization and organization (7). Both molecular and activity-dependent processes are thought to contribute to the early stabilization of the geniculocortical map.
Overall, therefore, the premise that primary cortex, V1, is a retinotopically organized source of correlated activity, with axons in place across the cortical surface with the potential to organize secondary cortical areas, has strong support in multiple species. At this point, the enormous lacuna in understanding cortical development in nonprimary areas presents itself. Massive research efforts focused on the precise mechanisms of pre- and postexperience retinotopic organization of V1 have existed in parallel with intense interest in what the “nature” of cortical areas are. However, there seem to be no studies whatsoever of the early development of topographic order in extrastriate areas, and only a few demonstrating the simple presence of any secondary visual areas (45). Notably, an early neurophysiological study, inspired by the demonstration of “face” and “hand” recognition cells in monkey inferotemporal cortex, looked for the same in infant monkeys and found instead virtually no cells activated by visual input (46). This null finding finds support in the very late emergence of face-responsive areas anywhere in the cortex in human children in an extensive series of studies using functional MRI (47).
Much of the lateral convexity of the cortex is multimodal, with visual, auditory (spatial, not tonotopic), and somatomotor maps in rough spatial register. In fact, the lateral convexity of the somatomotor cortex may be conceived as a single, mainly contralateral egocentric representation, with lower visual field, sounds, and lower limbs represented dorsally and medially and upper somatomotor regions represented near the Sylvian fissure or its equivalent (48). As it is known that the somatosensory and visual maps are fixed early in development, some fundamental intermodal topographic scaffolding may well be established before extrauterine life. Thereafter, while the spatial and temporal correlations between different modalities may not be as strong as those of localized neurons within a modality, seeding the model presented here with a second modality could be imagined as simply incorporating a second seed region with some pattern of correlated activity with the first. Topographically aligned nodes in the two seed regions will preferentially form edges onto common targets if their activities are sufficiently correlated. In this case, the question would be how little correlation might be necessary to give some spatial registration to the maps, and the optimum timing of multimodal input with respect to a more dominant map, to be matched to a yet nonexistent empirical database.
“Evolution” of Cortical Areas and Organization in Cortices of Varying Size.
In general, the number of cortical areas increases with overall cortical area. In the first 20 to 30 y of cortical-mapping studies, enough different species studied with rough and roughly similar techniques could be found to estimate that the rate of increase of number of cortical areas to overall cortical area was approximately linear over the range of brain sizes represented by small rodents and shrews to carnivores and small monkeys (49, 50). Interestingly, peripheral visual acuity interacted with this function, appearing to result in more areas. Better technical expertise, completeness, and complexity in the study of a few select species have now made newer studies incomparable with older ones, so that such comparisons are no longer possible. While systematic quantitative comparisons across species are not possible, qualitative descriptions certainly are.
The interpretation of extrastriate regions in mice.
From the outset, there has been substantial disagreement about the region of the brain surrounding primary visual cortex laterally and medially in mice (and other rodents) responsive to visual stimulation. One camp held that a number of cortical areas could be found, corresponding to the range of secondary visual areas in primates (51), while a second camp found a single V2 much like monkey, although topographically disorderly (52). Representatives of these positions may be found to this day (specialized regions; ref. 53), with a new entrant, dividing the circumstriate belt into two, with its mostly medial and mostly lateral regions corresponding respectively to the dorsal and ventral streams described in primates (45). For the purposes of this paper, the only necessary features of mouse extrastriate cortex are a small region of visually responsive cortex abutting the V1 border, of uncertain topographic organization.
Characteristic changes in organization in larger brains.
The pattern of change in organization of areas in larger brains is drawn mostly from the comparison of rhesus macaques, humans, and several New World (South American) monkeys (4, 32, 54). The number of cortical areas increases, and generally each area contains a representation of the entire visual field (with a few debated cases). For the first several areas, a clear mirror-symmetric replication is observed (V1, center to periphery; V2, periphery to center; V3, center to periphery), each map smaller in surface area than the preceding one. Thereafter, the topographic ordering may have become so degenerate (for example, in some lateral parietal areas, every receptive field may represent the center of gaze) that mirroring may not be possible to detect. Nevertheless, cortical areas may be organized in rough hierarchy by virtue of their pattern of feedback versus feedforward circuitry, and corresponding architectonics, showing that decrease in overall size continues to an asymptote. How are we to understand this addition of cortical areas?
Conserved Rules of Development Inform the Interpretation of New Cortical Areas.
The model described here constrains the interpretation of what a “new” area means. Empirical proof is required: it will be essential to demonstrate iterative development of secondary cortical areas in an animal with a large enough brain to produce several orderly retinotopic maps and show that it is correlated activity, and not molecular prespecification of connectivity (as seen in V1), that produces them. New cortical areas would thus be the outcome of the changing geometry of regularly scaling brains. In a small extrastriate area, only one orderly map can be supported, mirror-flipped, V2; in a slightly larger one, two maps, V2 and V3, and so forth. The question of homology of areas across species can be at least partially resolved. In a larger brain with an additional visual cortical area, it cannot be said that a “new cortical area” has been specified. Rather, a larger extrastriate region has been produced, by allometrically predictable enlargement of the cortex, and that region has been subdivided by activity-dependent self-organization into three, rather than two, retinotopic maps, or five instead of three, and so forth. The most distal map from V1 is not the “new” area, as all areas have undergone reorganization, it is simply the most distal division of the whole reorganized region. Nevertheless, it is not hard to see how such an underlying process, in the context of overall hierarchical organization of the cortex, might serve as a mechanism by which a new regularity in the pattern of sensory input to the whole organism, or a particular pattern of experience could produce new computational possibilities.
Materials and Methods
Physical Composition of the Model.
The visual cortex of the rhesus macaque is modeled as a network comprising 5,000 nodes, each representing localized neural populations in a 1 mm 1 mm piece of cortex. The nodes are distributed across a 100 mm 50 mm model cortical sheet. Specifically, the sheet is divided into 5,000 equally sized units and a node is placed at a location chosen uniformly at random within each unit.
The primary visual cortex is represented in a 100 mm 10 mm region of the model cortical sheet. The network is programmed to grow in sequential steps by adding new directed edges from nodes in the primary visual cortex to nodes within the rest of the cortical sheet. This represents the formation of new synaptic contact points between neurons in the respective populations as the cortex develops. The relative dimensions of primary and secondary cortical regions and their borders conform approximately to those observed for the rhesus macaque cortex (Fig. 1 A and B).
Parameters Determining Activity Correlation.
At every growth step, each of the nodes of the model V1 spontaneously generate a unit level of excitation (equal to 1), corresponding to spontaneous neural activity during development. These unit excitations are generated one node at a time, and their specific order is random. Unit excitation in one V1 node is accompanied by correlated excitation in neighboring V1 nodes (Fig. 1C). Specifically, correlated excitation on V1 node arising from a unit level of excitation in V1 node is determined by a two-dimensional Gaussian function:
| [1] |
Here, and are the respective positions of nodes and along the mediolateral axis of the cortical sheet, and are their respective positions along the caudorostral axis, and and are parameters that determine the spread of the Gaussian along each of the axes.
Excitation of V1 nodes also generate correlated excitation in nodes within the rest of the model cortical sheet. Specifically, unit excitation of a V1 node generates excitation on node that it projects edges to (Fig. 1C) in proportion to the number of projected edges. These edges also induce excitation on nodes residing in the neighborhood of , based on a Gaussian function of distance from . This function takes the same form as the right-hand side of Eq. 1 but is parameterized independently. It represents a spread of excitation outward from node .
Thus, unit excitation of a V1 node results in pairwise activity correlations between all nodes in the network. Given unit excitation of a V1 node, the activity correlation between two nodes and is computed as , where and are resulting excitation levels of node and node , respectively. In a given growth step, the net activity correlation between nodes and equals the sum of their activity correlations as unit excitations are generated in each of the V1 nodes, one at a time.
Network Growth.
Based on these activity correlations, the network generates new edges emanating from nodes within V1 and terminating on nodes that reside outside of V1. New edges are drawn from a probability distribution that evolves as the network grows. Specifically, at each growth step, the probability of a new edge from node to node equals
| [2] |
where is the net activity correlation between node and node , is a measure of the available contact (synaptic) resources in the two nodes, and is a normalization constant. Thus, new edges preferentially form between nodes that have higher activity correlation and more available contact resources.
The measure of available contact resources between nodes and in Eq. 1 is defined as , where is a measure of available axonal contact resources in node and is a measure of available dendritic contact resources in node . Both these terms follow a logistic decay as edges are added to nodes and (Fig. 1D). Specifically,
| [3] |
where is the number of outgoing edges of node , is the number of outgoing edges of V1 nodes on average (which increases as the network grows), and is a constant set to 0.1. Similarly,
| [4] |
where is the number of incoming edges of node , and is a constant set to 0.05.
The network is initialized without edges and grows in sequential growth steps, with a constant number of edges added in each step. The source and destination nodes of each of these edges are independently drawn from the probability distribution of Eq. 2. The probability distribution evolves as the network grows (Fig. 1E), as new edges alter pairwise activity correlations and the available contact resources in the network.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission. L.A.K. is a guest editor invited by the Editorial Board.
Data Availability.
Software code of the model is freely available from the ModelDB public archive (http://modeldb.yale.edu/266800).
References
- 1.Brodmann K., Vergleichende Lokalisationslehre der Grosshirnrinde in ihren Prinzipien dargestellt auf Grund des Zellenbaues (Barth, 1909). [Google Scholar]
- 2.Kaas J. H., “Cortical areas and patterns of cortico-cortical connections” in Cortical Areas: Unity and Diversity, Schüz A., Miller R., Eds. (CRC Press, 2002), pp. 191–204. [Google Scholar]
- 3.Kaas J. H., Neocortex in early mammals and its subsequent variations. Ann. N. Y. Acad. Sci. 1225, 28–36 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Markov N. T., et al. , A weighted and directed interareal connectivity matrix for macaque cerebral cortex. Cerebr. Cortex 24, 17–36 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Miller D. J., Bhaduri A., Sestan N., Kriegstein A., Shared and derived features of cellular diversity in the human cerebral cortex. Curr. Opin. Neurobiol. 56, 117–124 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Coalson T. S., Van Essen D. C., Glasser M. F., The impact of traditional neuroimaging methods on the spatial localization of cortical areas. Proc. Natl. Acad. Sci. U.S.A. 115, E6356–E6365 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bakken T. E., et al. , A comprehensive transcriptional map of primate brain development. Nature 535, 367–375 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hubel D. H., Wiesel T. N., Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J. Physiol. 160, 106–154 (1962). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Badre D., Nee D. E., Frontal cortex and the hierarchical control of behavior. Trends Cognit. Sci. 22, 170–188 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kaas J. H., Topographic maps are fundamental to sensory processing. Brain Res. Bull. 44, 107–112 (1997). [DOI] [PubMed] [Google Scholar]
- 11.Felleman D. J., Van Essen D. C., Distributed hierarchical processing in the primate cerebral cortex. Cerebr. Cortex 1, 1–47 (1991). [DOI] [PubMed] [Google Scholar]
- 12.Bates E., et al. , Voxel-based lesion–symptom mapping. Nat. Neurosci. 6, 448–450 (2003). [DOI] [PubMed] [Google Scholar]
- 13.Schiller P. H., On the specificity of neurons and visual areas. Behav. Brain Res. 76, 21–35 (1996). [DOI] [PubMed] [Google Scholar]
- 14.Kanwisher N., McDermott J., Chun M. M., The fusiform face area: A module in human extrastriate cortex specialized for face perception. J. Neurosci. 17, 4302–4311 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Poldrack R. A., Halchenko Y. O., Hanson S. J., Decoding the large-scale structure of brain function by classifying mental states across individuals. Psychol. Sci. 20, 1364–1372 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Anderson M. L., Kinnison J., Pessoa L., Describing functional diversity of brain regions and brain networks. Neuroimage 73, 50–58 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bullmore E., Sporns O., Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198 (2009). [DOI] [PubMed] [Google Scholar]
- 18.Ercsey-Ravasz M., et al. , A predictive network model of cerebral cortical connectivity based on a distance rule. Neuron 80, 184–197 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Finlay B. L., Principles of network architecture emerging from comparisons of the cerebral cortex in large and small brains. PLoS Biol. 14, e1002556 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kaas J. H., Evolution of columns, modules, and domains in the neocortex of primates. Proc. Natl. Acad. Sci. U.S.A. 109, 10655–10660 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Rakic P., Evolution of the neocortex: A perspective from developmental biology. Nat. Rev. Neurosci. 10, 724–735 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Krubitzer L. A., Seelke A. M., Cortical evolution in mammals: The bane and beauty of phenotypic variability. Proc. Natl. Acad. Sci. U.S.A. 109, 10647–10654 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cunningham R. J., Haun F., Chantler P. D., Diffusible proteins prolong survival of dorsal lateral geniculate neurons following occipital cortex lesions in newborn rats. Dev. Brain Res. 37, 133–141 (1987). [DOI] [PubMed] [Google Scholar]
- 24.Pallas S. L., “Cross-modal plasticity as a tool for understanding the ontogeny and phylogeny of cerebral cortex” in Cortical Areas: Unity and Diversity, Shuez A., Miller R., Eds. (CRC Press, 2002), pp. 245–272. [Google Scholar]
- 25.O’Leary D. D., Sahara S., Genetic regulation of arealization of the neocortex. Curr. Opin. Neurobiol. 18, 90–100 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Workman A. D., Charvet C. J., Clancy B., Darlington R. B., Finlay B. L., Modeling transformations of neurodevelopmental sequences across mammalian species. J. Neurosci. 33, 7368–7383 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Espinosa J. S., Stryker M. P., Development and plasticity of the primary visual cortex. Neuron 75, 230–249 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.O’Leary D. D., Schlaggar B. L., Tuttle R., Specification of neocortical areas and thalamocortical connections. Annu. Rev. Neurosci. 17, 419–439 (1994). [DOI] [PubMed] [Google Scholar]
- 29.Van Essen D. C., Glasser M. F., Dierker D. L., Harwell J., Cortical parcellations of the macaque monkey analyzed on surface-based atlases. Cereb. Cortex 22, 2227–2240 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Udin S. B., Fawcett J. W., Formation of topographic maps. Annu. Rev. Neurosci. 11, 289–327 (1988). [DOI] [PubMed] [Google Scholar]
- 31.Cang J., Feldheim D. A., Developmental mechanisms of topographic map formation and alignment. Annu. Rev. Neurosci. 36, 51–77 (2013). [DOI] [PubMed] [Google Scholar]
- 32.Dumoulin S. O., Wandell B. A., Population receptive field estimates in human visual cortex. Neuroimage 39, 647–660 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Horvat S., et al. , Spatial embedding and wiring cost constrain the functional layout of the cortical network of rodents and primates. PLoS Biol. 14, e1002512 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wong R. O., Retinal waves and visual system development. Annu. Rev. Neurosci. 22, 29–47 (1999). [DOI] [PubMed] [Google Scholar]
- 35.Gribizis A., et al. , Visual cortex gains independence from peripheral drive before eye opening. Neuron 104, 711–723 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Naegele J. R., Jhaveri S., Schneider G. E., Sharpening of topographical projections and maturation of geniculocortical axon arbors in the hamster. J. Comp. Neurol. 277, 593–607 (1988). [DOI] [PubMed] [Google Scholar]
- 37.Fulcher B. D., Murray J. D., Zerbi V., Wang X. J., Multimodal gradients across mouse cortex. Proc. Natl. Acad. Sci. U.S.A. 116, 4689–4695 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Cahalane D. J., et al. , Network structure implied by initial axon outgrowth in rodent cortex: Empirical measurement and models. PloS One 6, e16113 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sperry R. W., Chemoaffinity in the orderly growth of nerve fibre patterns and connections. Proc. Natl. Acad. Sci. U.S.A. 50, 703–710 (1963). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Smith D. H., Stretch growth of integrated axon tracts: Extremes and exploitations. Prog. Neurobiol. 89, 231–239 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Van Essen D. C., A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature 385, 313–318 (1997). [DOI] [PubMed] [Google Scholar]
- 42.Herrmann K., Antonini A., Shatz C. J., Ultrastructural evidence for synaptic interactions between thalamocortical axons and subplate neurons. Eur. J. Neurosci. 6, 1729–1742 (1994). [DOI] [PubMed] [Google Scholar]
- 43.Khalil R., Levitt J. B., Zinc histochemistry reveals circuit refinement and distinguishes visual areas in the developing ferret cerebral cortex. Brain Struct. Funct. 218, 1293–1306 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ragsdale C. W., Grove E. A., Patterning the mammalian cerebral cortex. Curr. Opin. Neurobiol. 11, 50–58 (2001). [DOI] [PubMed] [Google Scholar]
- 45.Kourtzi Z., Augath M., Logothetis N. K., Movshon J. A., Kiorpes L., Development of visually evoked cortical activity in infant macaque monkeys studied longitudinally with fMRI. Magn. Reson. Imag. 24, 359–366 (2006). [DOI] [PubMed] [Google Scholar]
- 46.Rodman H. R., Scalaidhe S. P., Gross C. G., Response properties of neurons in temporal cortical visual areas of infant monkeys. J. Neurophysiol. 70, 1115–1136 (1993). [DOI] [PubMed] [Google Scholar]
- 47.Cohen Kadosh K., Cohen Kadosh R., Dick F., Johnson M. H., Developmental changes in effective connectivity in the emerging core face network. Cereb. Cortex 21, 1389–1394 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Finlay B. L., Uchiyama R., Developmental mechanisms channeling cortical evolution. Trends Neurosci. 38, 69–76 (2015). [DOI] [PubMed] [Google Scholar]
- 49.Finlay B. L., Cheung D., Darlington R. B., “Developmental constraints on or developmental structure in brain evolution” in Processes of Change in Brain and Cognitive Development, Munakata Y., Johnson M., Eds. (Oxford University Press, Oxford, UK, 2005), pp. 131–162. [Google Scholar]
- 50.Finlay B. L., Brodsky P., “Cortical evolution as the expression of a program for disproportionate growth and the proliferation of areas” in Evolution of Nervous Systems, Kaas J. H., Ed. (Academic Press, Oxford, UK, 2006), pp. 73–96. [Google Scholar]
- 51.Olavarria J., Mignano L. R., Van Sluyters R. C., Pattern of extrastriate visual areas connecting reciprocally with striate cortex in the mouse. Exp. Neurol. 78, 775–779 (1982). [DOI] [PubMed] [Google Scholar]
- 52.Caviness V. S., Jr, Frost D. O., Tangential organization of thalamic projections to the neocortex in the mouse. J. Comp. Neurol. 194, 335–367 (1980). [DOI] [PubMed] [Google Scholar]
- 53.Marshel J. H., Garrett M. E., Nauhaus I., Callaway E. M., Functional specialization of seven mouse visual cortical areas. Neuron 72, 1040–1054 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Rosa M. G., Tweedale R., Brain maps, great and small: Lessons from comparative studies of primate visual cortical organization. Phil. Trans. Biol. Sci. 360, 665–691 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Software code of the model is freely available from the ModelDB public archive (http://modeldb.yale.edu/266800).