Predicting an epidemic trajectory is difficult

Predicting the trajectory of a novel emerging pathogen is like waking in the middle of the night and finding yourself in motion—but not knowing where you are headed, how fast you are traveling, how far you have come, or even what manner of vehicle conveys you into the darkness. A few scattered anomalies resolve into defined clusters. Cases accumulate. You assemble information about temporal sequences, identify a causative agent, piece together a few transmission histories, try to estimate mortality rates. A few weeks pass. Everyone wants to know how far the disease is going to spread, how fast that is going to happen, and what the final toll will be. They want predictive models. However, predictive models are difficult to develop and subject to wide uncertainties. In PNAS, Castro et al. (1) demonstrate one reason why. They show that based on early data it is nearly impossible to determine precisely whether interventions will be sufficient to quell an epidemic or whether the epidemic will continue to grow unabated. At best, we can predict the likelihoods of these opposing scenarios—scenarios that describe completely different worlds. In one a disaster has been narrowly averted, but in the other millions of people become infected and the global economy is upended.

The fundamental problem in predicting epidemic trajectories is the way in which uncertainties compound. To begin with, epidemics are stochastic processes. Luck matters—–particularly when superspreading is important—and happenstance shapes patterns of geographic spread (2). Early on, little is known about the parameters describing the spread of infection. What is the generation interval, how long is the infectious window, and what is the basic reproductive number in any particular setting? How is the disease transmitted, how long does it remain in the environment, and what are the effects of seasonality?

Without answers to these questions, it is hard to predict the impact of infection control and social distancing measures (3). Suppose an outbreak grows from 4 cases on day zero to 16 cases on day 6 to 64 cases on day 12. If social distancing cuts the basic reproduction number $R_0$ by two-thirds, will that be sufficient to stop the spread of disease? Based on the case counts alone, we cannot tell. If $R_0$ is 2 and transmission occurs after 3 days, the intervention would succeed. If instead $R_0$ is 4 and transmission occurs after 6 days, it would fail.

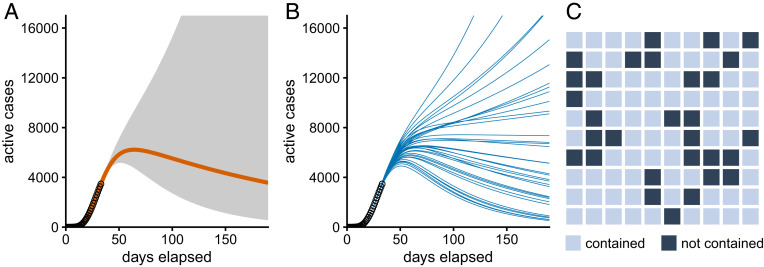
Castro et al. (1) demonstrate that the very nature of epidemic spread precludes effective prediction based on early data. They show that even if an epidemic proceeds according to simple deterministic mathematical dynamics it will be extremely difficult to make long-range predictions based on observed case numbers from the initial phase of the outbreak. This is a direct mathematical consequence of the exponential nature of early transmission dynamics. Even minor inaccuracies in the estimated parameters rapidly compound, so that precise predictions can be made only a few weeks into the future. Forecasting further out, the uncertainties become so large that we cannot hope to predict the actual number of active cases that will likely be reached (Fig. 1).

Fig. 1.

Visualizing uncertainty in predicting epidemic outcomes. All three panels display the same scenario, an epidemic that has been developing for 33 days. In this particular example, given the observed caseloads for the initial 33 days, there is a 70% chance that the epidemic is contained, and thus a 30% chance of unbounded growth. (A) Median outcome (solid orange line) with uncertainty cone indicating the range of outcomes that have 95% probability. (B) Sample of 35 independent, equally likely individual outcomes. (C) Frequency framing. Each square indicates one possible outcome. Light squares represent epidemics that are contained, and dark squares represent epidemics that are not contained. Simulation data courtesy of Mario Castro.

What we can do is estimate is the probability with which a specific outcome may occur. We can calculate—and with care, visualize (4)—the fraction of predicted trajectories that exceed a certain number of cases by a certain date, or that reach their maximum below a certain value, or in which the epidemic is successfully contained. We can aspire to well-calibrated forecasts, even if there are constraints on the sharpness with which we can predict the future.

Castro et al. (1) draw attention to an additional source of uncertainty. They demonstrate that epidemic predictions are sensitive to the exact amount of data available for fitting. We would normally expect that having more data is better, and that prediction uncertainty systematically declines with every additional data point that is incorporated into the model fit. Instead, however, uncertainty can increase with added data points, in particular near the mitigation–inhibition threshold where the epidemic is just barely contained. Castro et al. demonstrate this effect convincingly in movie S1 of ref. 1, where they show how prediction accuracy changes as new daily cases are added.

These results underscore the importance of a fundamental question in science communication: How can we accurately convey predictions that are probabilistic in nature? This question is well-studied in the context of weather forecasts. Even though forecasts have become increasingly accurate (5), they have a reputation for being misleading and unreliable. The crux of the problem is that most people expect a hard binary prediction—will it rain tomorrow, or not?—when the weather forecast inherently can only provide a probabilistic estimate—there is a 30% chance of rain tomorrow. What happens in our minds is that we hear the probabilistic prediction and turn it into a deterministic one. “A 30% chance of rain” becomes “it’s going to be sunny.” We are deeply disappointed when, about 30% of the time, the opposite transpires. This mistake of interpreting a probabilistic statement as deterministic has been dubbed “deterministic construal error” (6), and most static visualizations facilitate, if not outright encourage, it.

Most commonly, probabilistic predictions of time courses are shown as a median outcome surrounded by a cone of uncertainty (Fig. 1A). This type of visualization appears natural but draws excessive attention to the most likely outcomes. Looking at Fig. 1A, readers may assume that the epidemic will necessarily be brought under control because this is what happens on the orange line representing the median outcome. The effect is exacerbated when the cone of uncertainty omits considerable probability mass, as with hurricane forecasts where the cone of uncertainty includes the path of the hurricane’s center in only about two-thirds of the cases (7).

Alternatively, we sometimes see multiple outcomes overlaid on one another as individual traces (Fig. 1B). Such diagrams do a better job of highlighting the variability in possible outcomes, but it remains difficult to intuit the relative likelihood of various outcomes. Instead, we could show only one trace at a time but switch the display every half second or so to reveal a new trajectory. Movie S1 provides an example. Such animated plots, termed “hypothetical outcome plots,” may be more easily interpreted by viewers (8). Of course, animations require a dynamic medium such as a web browser, which can be a serious drawback. For print, it may be helpful simply to visualize the relative frequencies of different outcomes (e.g., the epidemic is contained or not) by drawing a checkerboard pattern of differently colored squares in the appropriate proportions (Fig. 1C). This type of visualization is called “frequency framing,” and it helps viewers obtain an intuitive understanding of the relative likelihood of different events. For example, an event with a 30% probability is sufficiently likely that its occurrence should not be discounted. Most readers will understand this intuitively from looking at a figure such as Fig. 1C.

Because data visualizations presented in research papers are often extracted for use on social media, in news broadcasts, or in press conferences, they should be sufficiently self-contained as to make sense when lifted out of the manuscripts in which they originally appeared. For example, when diagrams indicate uncertainty ranges, readers tend to assume that these ranges include the full scope of feasible outcomes. This was not the case for the original Institute for Health Metrics and Evaluation (IHME) COVID model (9). That model attempted to predict the trajectory of the pandemic in the United States, empirically fitting case counts to a distribution anchored on data from China, Italy, and Spain. As such, the IHME model only encompassed scenarios in which lockdown measures were sufficient to bring the US pandemic under control. The cones of uncertainty depicted on the model and in frequent White House press briefings during April did not represent the full span from best case to worst case. Rather, they represented the range of trajectories we might expect to see in a best-case situation where the epidemic was brought under control and eradicated by midsummer. This visualization gaffe may have contributed to undue optimism that the pandemic would be gone by autumn of 2020. The reverse cone of uncertainty in these model projections—the cone narrowed to zero deaths by August 2020—exacerbated the potential for misinterpretation.

Although not the focus of the paper by Castro et al. (1), changing social factors pose a further and formidable obstacle to predicting epidemic trajectories. Castro et al. consider a SIR (susceptible–infected–recovered) model with an additional compartment representing confinement: individuals that have been removed from the susceptible pool by entering some form of isolation. In their model, the rates with which individuals enter or leave this confinement state are fixed once some sort of intervention has been implemented. In practice the government policies and individual attitudes that affect these rates are anything but static. They evolve unpredictably, both in response to extrinsic political factors and to the epidemic dynamics themselves.

Individual behavior coevolves with the epidemic trajectory. Much as changes in economic policy alter optimal individual decisions in ways that undermine macroeconomic models—this is known as the Lucas critique (10)—epidemic control measures change individual incentives to avoid transmission risk and thus alter the dynamics by which disease spreads. For example, in the absence of effective controls, people may take greater precautions as case numbers are rising. As case numbers start to decline, we see the reverse. This behavior generates a feedback cycle that can sustain an epidemic for a long time, as preventative measures lapse just when the epidemic is about to be brought under control. The epidemic curve of COVID-19 in the United States may illustrate a dynamic of this kind. Where predictive models make it into the popular consciousness they play into the feedback cycle as well—sometimes in ways that undermine their own predictions. When models predict catastrophe, politicians and citizens alike react in ways that help control disease. When models suggest that an epidemic is certain to resolve in short order, onerous control measures feel like overkill, people relax, and the epidemic persists.

When using mathematical models to guide policy decisions or interventions, we need to remember that epidemic forecasting models do not give us exact predictions. Rather, they suggest ranges of possible outcomes. We cannot afford to hope for the best possible outcome and plan accordingly. If predictions have large uncertainties, prudent policy errs on the side of caution. This seems obvious yet has been frequently ignored with COVID-19, at dreadful cost.