The evolution of altruism and the serial rediscovery of the role of relatedness

Significance

The canonical explanation for the evolution of altruism (“kin selection”)—which was mathematically derived in the 1960s by W. D. Hamilton—emphasizes the importance of genetic relatedness. Over the past three decades, numerous authors claim to have discovered alternative explanations. We systematically analyze the models substantiating these claims and reveal that in every model the interacting individuals are genetically related and that the authors have therefore unwittingly rediscovered Hamilton’s insight.

Abstract

The genetic evolution of altruism (i.e., a behavior resulting in a net reduction of the survival and/or reproduction of an actor to benefit a recipient) once perplexed biologists because it seemed paradoxical in a Darwinian world. More than half a century ago, W. D. Hamilton explained that when interacting individuals are genetically related, alleles for altruism can be favored by selection because they are carried by individuals more likely to interact with other individuals carrying the alleles for altruism than random individuals in the population (“kin selection”). In recent decades, a substantial number of supposedly alternative pathways to altruism have been published, leading to controversies surrounding explanations for the evolution of altruism. Here, we systematically review the 200 most impactful papers published on the evolution of altruism and identify 43 evolutionary models in which altruism evolves and where the authors attribute the evolution of altruism to a pathway other than kin selection and/or deny the role of relatedness. An analysis of these models reveals that in every case the life cycle assumptions entail local reproduction and local interactions, thereby leading to interacting individuals being genetically related. Thus, contrary to the authors’ claims, Hamilton’s relatedness drives the evolution to altruism in their models. The fact that several decades of investigating the evolution to altruism have resulted in the systematic and unwitting rediscovery of the same mechanism is testament to the fundamental importance of positive relatedness between actor and recipient for explaining the evolution of altruism.

Academic discoveries are often made simultaneously and independently by multiple scientists (1–3). In the 17th century, Newton and Leibniz independently developed calculus. The theory of evolution by natural selection was discovered independently by Charles Darwin (1858) and Alfred Wallace (1858). There are also instances of the same discovery being made many years apart. The heliocentric solar system was first discovered by the Ancient Greek astronomer Aristarchos of Samos ($\sim$310 to 230 BC), but received little attention until it was independently rediscovered 18 centuries later by the Renaissance mathematician Nicolaus Copernicus. Such asynchronous rediscoveries have become rare in a globalized world of communication between distant regions and accessible online information. However, over the past few decades a striking exception has unfolded in the evolutionary sciences, where many researchers have repeatedly rediscovered that interactions between relatives favor the evolution of altruistic traits, despite this mechanism having been uncovered and mathematically described more than half a century ago by W. D. Hamilton (4–6). What is more, unlike previous cases, this rediscovery does not seem to have resulted from ignorance of the existence of previous work, but from a failure to recognize the equivalence between the processes underlying the models.

The question of the genetic evolution of altruism—defined here as a behavior decreasing the expected survival and/or reproduction (fitness) of the actor while increasing the fitness of the recipient—rose to prominence because altruism seemed paradoxical in a Darwinian world. In 1963, Hamilton showed that to understand the genetic evolution of altruism, and more generally of any trait, it is crucial to consider the average fitness of all individuals bearing a given allele responsible for producing a change in that trait. In particular, in a population of homogeneous individuals, an altruism-inducing allele will increase in frequency when $rb-c>0$, where $-c$ is the average effect of the altruism-inducing allele on the fitness of its bearer, $b$ is the average effect on the fitness of recipients, and $r$ is the genetic relatedness between the actor and the recipients (7).

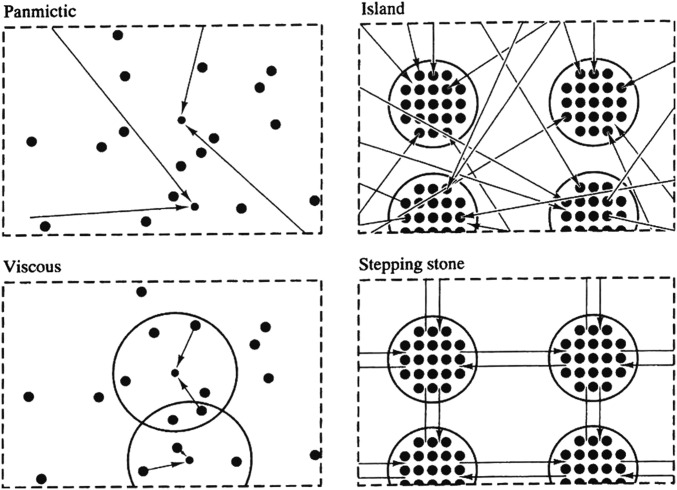
Relatedness $r$ is a regression coefficient measuring how the alleles in a particular individual covary in frequency with those of individuals with whom the individual interacts (8, 9). Relatedness is thus a measure of the extent to which the recipient of altruism is more likely than a random individual in the population to carry the altruism-inducing allele present in the actor. Usually, such assortment results from actor and recipient having inherited identical alleles from a recent common ancestor (i.e., alleles in actor and recipient are identical by descent; see Box 1 for more complex situations). For example, family structure results in particular relatedness patterns: In diploid species where mating occurs randomly in the population, siblings have a relatedness of 1/2 (i.e., they have a 50% chance of having inherited the same allele from their parents at any given locus) and the relatedness between aunt and nephew is 1/4. Because the best-known cases of altruism occur between highly related individuals, John Maynard Smith coined the term kin selection to describe the operation of natural selection in a context where interactions occur among genetically related individuals (10, 11). Unfortunately, this has sometimes given the incorrect impression that kin selection operates only within structured families. In reality, kin selection operates as soon as there is limited genetic mixing and interacting group size is not infinite, as in the “viscous,” “island,” and “stepping-stone” models of spatial population structure described in Fig. 1. In these models, dispersal is limited and locally interacting individuals are likely to sharealleles from a common ancestor who lived in the same spatial neighborhood in previous generations. Under limited dispersal, the genetic components of evolving traits expressed by an actor therefore affect the reproduction and survival of others who share alleles identical by descent with the actor at the loci determining the trait. This is the defining condition for kin selection to operate (12, 13). Since most if not all populations are likely to exhibit some form of limited genetic mixing (14), hence most if not all social traits are likely to be shaped by kin selection to at least some extent (15). Importantly, limited genetic mixing also implies that interactions occur locally and hence that related individuals are more likely to compete against each other than are individuals sampled at random from the population. This leads to the occurrence of “kin competition.” Under certain situations, kin competition can cancel out the indirect benefits of altruism and prevent the evolution of phenotypes increasing the survival and reproduction of neighbors (13, 16). Yet, even in this context, phenotypic evolution is shaped by kin selection.

Box 1: Relatedness and Green Beard Models.

Relatedness is a measure of assortment of alleles between actor and recipient, where assortment means that actor and recipient share more alleles that are identical by state than the population average. And assortment, whereby individuals bearing altruistic alleles preferentially benefit from the altruism of other individuals bearing altruistic alleles, is a necessary condition for genetic altruism to be favored by kin selection (4, 12, 17). As explained in the main text, in family-structured populations and under limited dispersal, assortment results from actor and recipient sharing identical-by-state alleles that are identical by descent, so that interacting individuals are positively related. While identity by descent is the main mechanism generating assortment, identical-by-state assortment can also occur without identity by descent. One such scenario is where the same altruistic allele arises frequently through mutation and recognizes replicate copies in other individuals. This is the “green beard effect” (42, 43), a mechanism for the evolution of altruism discussed (but not investigated formally) by Hamilton (6) and Dawkins (42). While the green beard mechanism it is an intriguing thought experiment, it is unlikely that it could drive the genetic evolution of altruism independent of kin selection. First, its requirements are very stringent: A single Mendelian element must encode a signal, the ability to discriminate among others on the basis of that signal, and an altruistic phenotype. Second, if these requirements are met, modeling shows that the process is generally unstable (44). Finally, even when green beard models entail interactions among relatives, where one would expect them to be more stable, without a near perfect association between signal and altruistic phenotype, the evolutionary dynamics tend to remain unstable (45).

Fig. 1.

Population structure and relatedness, reproduced from Hamilton (17), who discussed how limited dispersal induced by various population structures influences patterns of relatedness and thereby affects the evolution of social behavior. In the panmictic and viscous models, smaller dots indicate younger individuals, and arrows indicate parenthood. In the island and stepping-stone models, younger individuals are not shown because reproduction occurs within groups. Arrows indicate dispersal between groups. For the viscous, island, and stepping-stone models, locally interacting individuals are positively related under limited dispersal, and the local relatedness structure has been explored in the field of population genetics (13, 18–21). The viscous model with continuous space is the most challenging to analyze and remains the least explored, yet it is probably the most realistic model for plant populations. Most of the papers rediscovering kin selection use either the island model (using groups of size $>$1 and with interactions occurring within groups) or the stepping-stone model (using “groups” composed of a single individual, represented as the node of a lattice structure; since migration links nodes, the population becomes a network with interactions occurring between neighboring nodes). Reprinted with permission from ref. 17.

Despite the fact that kin selection is known to operate under limited dispersal, mathematical and simulation models employing the population structures described in Fig. 1 often claim to have found new mechanisms to account for the evolution of altruism. A number of previous studies have taken particular such models and mathematically proved that relatedness is positive among interacting individuals and that altruism would not evolve without it (22–27). However, these efforts have enjoyed little success in curbing false claims about the novelty of the mechanism driving the evolution of altruism. And, while a core of evolutionary biologists working on altruism remain confident about the central role of relatedness, the larger circle of evolutionists and laypeople who follow this literature now believe that the issue remains unsolved. Here we therefore take a different approach. We broadly survey the literature to identify papers claiming alternative mechanisms and then analyze the life cycle assumptions of these models (i.e., the demographic, behavioral, and genetic assumptions underlying all events faced by organisms in an evolving population) to investigate whether they allow the evolution of altruism without positive relatedness between interacting individuals (i.e., whether altruism can evolve without kin selection).

Results and Discussion

The claims of novel mechanisms to account for the evolution of altruism are too numerous to review comprehensively. Therefore, we identified the most prominent examples by selecting the top 100 Google Scholar search results for each of “evolution of cooperation” and “evolution of altruism” (SI Appendix, Tables S1 and S2; total = 195 papers; 5 appeared under both). Seventy-six of these papers do not present formal evolutionary models. We scrutinized the life cycles of the remaining 119 papers, which do present formal evolutionary models. These models investigate the dynamics of either genetic variants (alleles) or cultural variants (memes) with most considering only two competing variants (one “altruistic” and one “selfish”). In many of the models, whether the expression of a particular allele (or meme) results in altruism (i.e., $c>0$ and $b>0$) or merely cooperation—defined as a behavior increasing the fitness of both actor and recipient (i.e., $c<0$ and $b>0$)—depends on the parameter values determining the life cycle. This parameter dependence arises because the costs and benefits are defined operationally as the lifetime fitness effects of an actor on recipients and are therefore complex functions of all life cycle features. In particular, since costs and benefits are affected by kin competition, they depend on parameters defining the spatial structure of the evolving population (equation 7.13 in ref. 13, equations 5–7 in ref. 24, and figures 1 and 2 in ref. 28), and since they are affected by the type of interaction and the likelihood of repeated interaction, they depend on parameters defining the behavioral interactions between individuals (equation 5 in ref. 29 and equations 8 and 9 in ref. 26). These (lifetime) fitness costs $c$ and benefits $b$ are therefore nontrivial to calculate and essentially never correspond directly to the proximate costs and benefits of the prisoner’s dilemma stage game matrix to which they may be naively equated (the exception being a panmictic population with one-shot interactions). Further, for a given situation, the cost $c$ may change sign, from altruism (positive) to cooperation (negative), as a function of the model’s parameter values, such as dispersal rate and group size (see figures 1 and 2 in ref. 28 for illustrative examples). Since quantitatively calculating $c$ and $b$ can be very demanding for a given model, we here qualitatively infer whether $c$ is expected to be positive or negative as this can often be done on examination of the life cycle assumptions. Overall, altruism evolved under some parameter values in models presented in 89 of these papers. Among the remaining 30 papers, cooperation evolved in 28 cases, and we were unable to assess whether altruism or cooperation evolved in the remaining 2 cases (marked as “insufficient information” in SI Appendix, Tables S1 and S2).

Among the 89 altruism models, 46 adopted Hamilton’s conceptual framework, attributing the evolution of altruism to positive relatedness. The remaining 43 all claimed alternative mechanisms. To evaluate the veracity of their claims, we first subdivided these 43 papers into those where the role of relatedness was denied (17 cases; SI Appendix, Table S3), and those which made little or no mention of relatedness (26 cases; SI Appendix, Table S4).

Among the 17 papers where the presence/role of relatedness was denied (SI Appendix, Table S3), our analysis of the life cycles of the models showed that the proposed scenario led to positive relatedness between interacting agents in every case. Moreover, in most of these models, agents reproduced clonally (e.g., “parents pass on their type to their offspring”) with interactions occurring among nearest neighbors, as in the stepping-stone model of Fig. 1, with only one individual per node/group. This represents the tritest instance of kin selection. Relatedness coefficients equal 1 between parent and offspring and between siblings, and dispersal is limited to neighboring nodes so parents place offspring therein and subsequently interact with them. While many of these models are framed in terms of the transmission of cultural variants (or memes) and are often called “strategies” (with strategies with higher payoffs being more frequently “imitated”), from a conceptual evolutionary dynamics perspective these models are indistinguishable from genetic models, since they both investigate the differential proliferation of different variants in a population. Different modes of cultural transmission (e.g., payoff-biased learning, vertical transmission, one to many transmission such as following a leader) (30) will affect the level of relatedness between interacting individuals as well as the amount of (cultural) kin competition between them, and this can result in higher or lower selection pressure on altruism than under genetic transmission (31). However, no other mechanism has been discovered, since selection still acts on the social trait according to relatedness (and competition) because traits are inherited and subject to differential proliferation. Thus, altruism spreads via cultural transmission when altruistic actors preferentially help individuals to whom they are positively culturally related. Hence, these models represent an advance only insofar as Hamilton never applied his framework to cultural evolution [this was pioneered in the 1990s (32) and has been applied concretely to the calculation of cultural relatedness in the “island model” of Fig. 1 (31) and reviewed (33)]. The inconsistency between the novelty claims of these publications and their content is difficult to explain. One likely contributing factor is the nonbiological framing of the models; terms such as “site update” and “strategy invasion” replace birth and death, and “players” and “neighbors” replace organisms, siblings, and offspring. This semantic divergence obfuscates the relation between these models and the established theory.

The 26 papers which make little or no mention of relatedness attribute the evolution of altruism to diverse alternative mechanisms including “social diversity,” “social viscosity,” “topological heterogeneity,” “network heterogeneity,” “network reciprocity,” “spatial reciprocity,” “spatial structure,” and “multiplex structure” (SI Appendix, Table S4). Analysis of these models revealed that in every case interacting individuals are related, relatives benefit from each other’s altruism, and kin selection therefore operates. This occurs through limited dispersal (or limited cultural mixing) and local interaction as in the island and stepping-stone models of Fig. 1. Again, the framing of these models obscures the underlying role of relatedness. For example, Szolnoki et al. (ref. 34, p. 2) write, “First, a randomly selected player $x$ acquires its payoff $p_x$ by playing the game with its nearest neighbors. Next, one randomly chosen neighbor denoted by $y$ also acquires its payoff $p_y$ by playing the game with its four neighbors. Lastly, player $x$ tries to enforce its strategy $s_x$ on player $y$ in accordance with the probability, $W\left(s_x\hspace{0.17em}\to \hspace{0.17em}{s}_y\right)=w_x/\left(1+exp\left[\left(p_y-p_x\right)/K\right]\right)$, where $K$ denotes the amplitude of noise.” For a biologist, this translates as follows: Individuals are randomly killed and tend to be replaced by the clonal offspring of their most fecund neighbors. In this situation, individuals will interact preferentially with clonal relatives, and interactions are likely to occur between parents and offspring and siblings owing to the stepping-stone structure (Fig. 1) of the model. Altruistic alleles (or memes) therefore spread through genetic (or cultural) kin selection.

The most commonly cited alternative mechanism to kin selection is “spatial selection.” This mechanism was pioneered by Martin Nowak, who has been uniquely vocal in attempting to differentiate it from kin selection [e.g., “it is clear that kin selection is different from group selection and different from spatial selection” (ref. 35, p. 26)] despite his claims being repeatedly and formally dismissed (22–27). Using Google Scholar we therefore identified his 10 most impactful spatial selection papers (SI Appendix, Table S5). All of these papers use models where individuals interact with relatives and where kin selection affects the evolution of altruism. Three of these Nowak papers already feature in SI Appendix, Table S3 [Traulsen and Nowak (36) and Nowak et al. (37)] and SI Appendix, Table S4 [Ohtsuki et al. (38)]. The remaining seven constitute SI Appendix, Table S6. The models are of various types but all use lattice or graph population structures, which are akin to the stepping-stone model of Fig. 1. The occurrence of such clear-cut rediscovery is easier to understand when considering the chronological development of the separate literatures. While Nowak’s earlier models adopted rather different assumptions from those of the more biologically oriented concurrent/earlier kin selection literature, they converged to them over time (Box 2).

Box 2: Evolution of Theoretical Evolution Models.

We here briefly explore the “rediscovery” history of the spatial selection literature. This is useful as through understanding this history, one can better understand how such large-scale rediscovery could have occurred. The broad assumptions of Martin Nowak and colleagues’ models differed from those of “typical” kin selection models initially [in the 1990s; reviewed in 2004 (13)] and converged to them only over time. Unlike typical kin selection models, the simulations of Nowak and May (46, 47) do not allow for any chance effects in reproduction (i.e., genetic drift). The models are therefore fully deterministic, meaning that altruism can never spread when rare, since a single altruistic mutant will be immediately eliminated as it would be surrounded on all sides by nonaltruists receiving higher payoffs. This means that relatedness can never build up. But, when the simulations are initiated with multiple altruists so that interacting individuals experience identical-by-state assortment, then altruism can be maintained but undergoes chaotic temporal dynamics [e.g., Nowak and May (47)]. While the initial altruists are identical by state, and not related, their offspring are identical by descent (related) and likely to interact, since there is limited genetic mixing. Kin selection therefore plays a role in the evolutionary dynamics of altruism [as acknowledged by Nowak and May (ref. 47, p. 76)]. In the simulations of Nowak et al. (48, 49) chance effects in reproduction are allowed, meaning that local genetic drift allows relatedness to build up and altruistic alleles increase in frequency when rare, so that kin selection can operate at all allele frequencies. Finally, Ohtsuki et al. (38) provide mathematical solutions to the spread of altruism in stepping-stone–like models under weak selection. This paper makes the same assumptions as previous kin selection models and analyzing the model with Hamilton’s rule yields identical results (22, 24). Over time, the spatial selection models thus became more biologically realistic as they converged to typical previous kin selection models.

The claims that spatial structure affects the evolution of altruism are not incorrect per se. As Hamilton himself emphasized (17), limited dispersal and local interaction lead to positive relatedness among interacting individuals, which may promote altruism under certain biological scenarios, as long as kin competition is not too strong. Hence, the finding that spatial selection favors altruism is not novel, and the emphasis on space can be misleading; space is merely a proxy for relatedness patterns and in itself not sufficient to explain altruism. Space providesno detailed information about the fitness cost $c$ and benefit $b$, depending on which the same spatial arrangement may favor altruism and/or intensify kin competition. Moreover, to focus on such a proxy is unhelpful as it is difficult to intuit how the evolution of altruism will respond to different biological assumptions. Consider mating systems. It is clear that polyandry (where females mate with multiple males) will result in decreased relatedness among interacting individuals relative to monoandry (where females mate with only one male) (39); relatedness also decreases with migration, group size, and environmental disturbance, while it tends to increase with survival and variance in reproductive success (13). In other words, how life cycle factors affect relatedness has been extensively worked out and is often intuitively clear, allowing empiricists to make and test predictions across diverse biological systems (40). It is unclear, however, how different biological assumptions (e.g., a change in the mating system or group composition) would interact with spatial selection. Consequently, these models do not provide testable predictions for biological scenarios beyond their authors’ many and highly specific assumptions.

While it remains surprising that so many specific models not tightly connected to the preceding literature are published, we envisage at least three reasons for the serial rediscovery of the role of relatedness. First, these models are often presented by people with strong formal training, but who are not evolutionary biologists (e.g., physicists, economists, mathematicians), and who have a limited understanding of genetics. Hamilton’s rule is a population genetics theory result, and population genetics itself is an application of dynamical system and stochastic process theories. Yet, while these latter theories are well known to formally trained scientists, nonbiologists tend to approach the problem of the evolution of altruism from a textbook dynamical systems perspective, thereby narrowly focusing on the iconic replicator equation while eschewing well-established and important population genetic results. Second, Hamilton’s rule seems so intuitively clear to evolutionary biologists that they often do not engage with it as a formal population genetic theory and are not always rigorous in providing hard proofs to substantiate models of the evolution of social traits. This is exemplified by the fact that it took four decades to formally integrate Hamilton’s rule into the wider context of evolutionary game theory and adaptive dynamics. The basis of a conceptually transparent and wide-ranging kin selection theory was obtained only at the turn of the 20th century (41), while it was treated as such long before. Finally, some authors simply do not engage at all with the extensive kin selection theory literature, aware that doing so would cost considerable time and effort and could limit the boldness of the originality claims that they felt able to make “in good faith.” This has proved particularly true for some evolutionists from nonbiological backgrounds who have been highly successful in publishing studies dramatically overselling the novelty of their findings.

Conclusion

The field of evolutionary science has become replete with claims of novel mechanisms for the evolution of altruism. Previous papers have reanalyzed specific “novel” models to show their exact equivalence to results from preceding kin selection models (22–27) and thus their redundancy with established knowledge. Here, we have conducted a broader-scale analysis of these claims to reveal how and why these authors have unconsciously constructed situations in which kin selection operates. While we examined only the most prominent papers, we are not aware of any other paper that provides a biologically relevant explanation for the evolution of altruism by a mechanism other than positive relatedness between actor and recipient, as originally outlined by Hamilton (4–6, 17). The fact that researchers from diverse fields across the social and natural sciences have systematically reached similar conclusions is testament to the stricture of Hamilton’s ideas.

Materials and Methods

To systematically evaluate the claims that altruism could evolve by mechanisms other than kin selection, we selected the first 100 Google Scholar search results for each of evolution of altruism (SI Appendix, Table S1) and evolution of cooperation (SI Appendix, Table S2). In Google Scholar, papers are ranked according to their relevance to the search terms as well as the number of citations, meaning that our results will feature the most relevant and impactful papers, with a bias toward older papers. For each search result, we proceeded as follows:

• 1)We assessed whether a formal evolutionary model was presented. The search results come from fields as diverse as law, economics, physics, and biology and range in substance from theoretical research to empirical research, to reviews, books, and philosophical treatises.
• 2)For papers which presented a formal evolutionary model, we qualitatively evaluated whether altruism or cooperation increases in frequency under selection in the models presented in the paper; that is, whether $b>0$ and $c>0$. All models have $b>0$ because all consider a situation where individuals increase the survival or reproduction of others (i.e., helping behavior). Whether $c>0$ depends on the models’ assumptions and population state. For instance, when interactions are modeled as a one-shot prisoner’s dilemma game under panmixia, the action “defect” always results in a higher payoff than the action “cooperate,” and $c>0$. But, for various more complicated scenarios (e.g., other types of game, repeated interaction, small interactive group sizes), actors may derive direct benefits from their action, in which case the sign of $c$ depends on specific parameter settings (13, 24, 26, 28, 29), as well as on the frequency of traits, alleles, or memes in the population. We therefore classified these papers according to whether the evolved trait is “altruism,” “cooperation,” or “parameter dependent” (SI Appendix, Tables S1, S2, and S5).
• 3)If altruism could evolve in at least one model presented in a given paper, we next identified the mechanism to which the authors attributed the evolution of altruism and subdivided the papers which attribute the evolution of altruism to an evolutionary process other than kin selection into two categories: those which deny the role of relatedness in their models (SI Appendix, Table S3, where quotes denying relatedness are provided) and those which make no mention of relatedness (SI Appendix, Table S4, where the proposed alternative mechanism is identified). For both of these categories we examined the life cycle assumptions model, in particular the modes of reproduction (e.g., the dispersal kernel) and interactions (e.g., the group size within which individuals interact), to evaluate whether the model is expected to lead to positive relatedness between interacting individuals. If relatedness is expected to be nonzero on the basis of this qualitative analysis, we then stated that kin selection operates.

In addition to these analyses, we focused on the most frequently cited alternative mechanism to kin selection: spatial selection, pioneered by Martin Nowak. We used the search term “Nowak cooperation” to identify his 10 most impactful spatial selection papers (SI Appendix, Table S5). We categorized all search results according to the scheme described above and then, again, analyzed the life cycle assumptions of these models to identify the modes of interaction and reproduction. Based on these, we indicated whether or not kin selection will operate (SI Appendix, Table S6).

Data Availability.

All study data are included in this article and SI Appendix.