Analysis of deep learning neural network combined with experiments to develop predictive models for a propane vertical jet fire

Abstract

Fires are important responsible factors to cause catastrophic events in the process industries, whose consequences usually initiate domino effects. The artificial neural network has been shown to be one of the rapid methods to simulate processes in the risk analysis field. In the present work, experimental data points on jet fire shape ratios, defined by the 800 K isotherm, have been applied for ANN development. The mass flow rates and the nozzle diameters of these jet flames have been considered as input dataset; while, the jet flame lengths and widths have been collected as output dataset by the ANN models. A Bayesian Regularization algorithm has been chosen as the three-layer backpropagation training from Multi-layer perceptron algorithm. Then it has been compared with a Radial based functions algorithm, based on single hidden layer. The optimized number of neurons in the first and second hidden layers of the MLP algorithm, and in the single hidden layer of the RBF algorithm has been found to be twenty and fifteen, respectively. The best MSE validation performance of MLP and RBF networks has been found to be 0.00286 and 0.00426 at 100 and 20 epochs, respectively.

Chemical engineering; Energy; Petroleum engineering; Safety engineering; Thermodynamics; Computational mathematics; Artificial neural networks; Environmental hazard; Jet fire; Propane; Simulation; ANN; MLP; RBF.

1. Introduction

Fires are one of the main causes of accidental events in the oil and gas industries. The jet fire scenario is one of the basic root causes of these accidents, due to the domino effect, in the petroleum industries (Gomez-Mares et al., 2008; Casal, 2017). Other fire accidents are usually caused by jet flames heat fluxes and flame impingement, due to the proximity of jet fires to structures of process and equipment (Casal, 2017). Jet fires can lead to catastrophic events such as the Piper Alpha accident, caused by heat fluxes generated by a continuous jet fire (Chamberlain, 2002). Jet fires can also cause other accidents, through domino effects, such as releases of toxic gases and explosions (Sonju and Hustad, 1984; Cowley et al., 1990; Davenport, 1994; Delvosalle, 1996; Chamberlain, 2002; Gomez-Mares et al., 2008; Palacios et al., 2009; Assael and Kakosimos, 2010; Reniers, 2010; Lilley, 2013). The study of the behavior and shape of a jet flame can provide an in-depth look in the risk analysis in the chemical industries. Thus, the simulation and prediction of jet fire geometry, via jet flame length and width, can be a great help in the assessment of accurate quantitative industrial risk analysis.

Several authors have investigated the jet flame shape; some of these studies have been focused on the thermal factor of jet flames (Brzustowski et al., 1975; Becker et al., 1981; Pfenning, 1985; McCaffrey, 1989; Santos and Costa, 2005; Palacios and Casal, 2011; Mashhadimoslem et al., 2020a, Mashhadimoslem et al., 2020b). The jet flame shape has also been found to depend on the mass flow rates and the exit nozzle diameters. For example, some authors have provided equations correlating the jet flame shape with the mass flow rates and exit nozzles (Hawthorne et al., 1948; Baron, 1954; Steward, 1970; Suris et al., 1977; Kalghatgi, 1983; Sonju and Hustad, 1984; Hustad and Sonju, 1986; Chamberlain, 1987; Bagster and Schubach, 1996; Wen and Huang, 2000; Schefer et al., 2004, 2007; Cumber and Spearpoint, 2006; Smith et al., 2006; Brennan et al., 2009; Palacios and Casal, 2011; Palacios et al., 2012, 2016; Zhang et al., 2014; Schmidt et al., 2015; Zhou et al., 2016; Gopalaswami et al., 2016; Laboureur et al., 2016; Liu and Hu, 2019; Palacios and Rengel, 2020). Concerning the jet flame thermal boundary, (Palacios and Casal, 2011) determined the propane jet flame boundary, by visible and infrared images, to correspond to a temperature of 800 K. The jet flame shape has also been predicted through models, based on experimental studies and computational fluid dynamic (CFD) approaches (Mashhadimoslem et al., 2020a, Mashhadimoslem et al., 2020b). Nowadays various methods, such as CFD simulation methods and commercial software, are also used to predict jet fire's behavior. The experimental models need open field and/or laboratories with instrumental facilities, and the CFD studies require the processor system and computational time, depending on the size of the analyzed physical geometry. Machine learning has been shown to be one promising tool to develop a predictive approach (Franke et al., 2017; Sun et al., 2019; Lattimer et al., 2020). Machine learning can be used to predict jet flame's shape and behavior. The artificial neural networks (ANN), called ‘deep learning’, can be applied to predict a jet fire in the process safety field. Rapid computational, saving computational time and high accuracy are the hallmarks of neural networks for predicting processes. The experimental and CFD methods require more computational time and cost impact than neural networks. There are few studies that have applied ANN to predict and model jet fires scenarios. Some of them have reviewed risk assessment in process industries and developed numerical computational studies. Shultz and Fischbeck (1999) prepared the risk assessment of accidents, occurred in offshore platforms during 1986 and 1995, using ANN models. Sun et al. (2019) developed an ANN approach to accurate predict the thermal radiation consequences of jet fire and pool fire scenarios occurred in process industries. Lattimer et al. (2020) compared accidental fire scenarios predictions using ANN and CFD studies. These studies showed ANN could provide full-field predictions of 2–3 orders of magnitude faster than the CFD simulations. Sarbayev et al. (2019) proposed an ANN method to analyse a system failure in the Tesoro Anacortes Refinery accident. Raeihagh et al. (2020) proposed an ANN model to give a higher level of accuracy and reliability, in terms of pipe risk assessment, in a gas refinery. Mashhadimoslem et al., 2020a, Mashhadimoslem et al., 2020b compared hydrogen and propane jet fires radiation using CFD studies. The results were used to develop a fire consequence model for risk assessment in process industries. Some scholars have successfully applied ANN to predict combustion factors under many conditions. For example, Emami and Fard (2012) applied ANN to predict the steady laminar flamelet model for a turbulent jet. They coupled ANN results in a CFD code to reduce computational time, compared with the employed time in the numerical integration for CFD calculations, obtaining good accuracy. Franke et al. (2017) utilized ANN to tabulate a combustion chemical mechanism and simulate a combustion model, providing significant savings in computational time. Sinaei and Tabejamaat (2017) introduced a large eddy simulation model for methane jet flames, using an ANN approach. They showed the potential savings of the ANN method in computational costs in comparison with other methods. Pereira and De Bortoli (2018) developed a new combustion mechanism for an ethanol jet flame, using ANN approach. Owoyele's et al. (2020) suggested method used an ANN approach to improve CFD code computational time for combustion simulations. Seltz et al. (2019) developed stoichiometric predictions for turbulent premixed jet flames of methane and air, based on ANN approach. Si et al. (2020) optimized a methane combustion chemical mechanism using an ANN approach for the CFD simulations. In the present study, the experimental geometrical data (i.e. flame shape) of vertical jet fires of propane have been used as input and output data for the development of the learning of a network. Table 1 shows a summary of several experimental and numerical studies on jet fires of various fuels.

Table 1.

Summary of experimental and numerical works on jet fires.

References	Nozzle diameter (mm)	Fuel	Jet Orientation	Remark
Hawthorne et al. (1948)	3–8	Propane, acetylene, carbon monoxide, city gas, hydrogen, mixtures of CO2-city gas and H2-propane	Vertical	Jet flame length correlated with mole fraction.
Suris et al. (1977)	1.5–11	Methane, propane and hydrogen	Horizontal, Vertical	Jet flame length correlated with Froude number.
Sonju and Hustad (1984)	2–80	Propane and methane	Vertical	Subsonic jet flame lengths analysis.
Bagster and Schubach (1996)	25, 50	Propane	Vertical	Jet flame length correlations, based on molecular weight and temperature.
Wen and Huang (2000)	380, 620	Propane	Vertical	CFD simulation based on Magnussen's soot model.
Santos and Costa (2005)	5–8	Propane and ethylene	Vertical	Jet flame length correlations, based on Froude Number.
Smith et al. (2006)	1	Propane	Horizontal	Jet flame length correlations, based on buoyancy effects.
Cumber and Spearpoint (2006)	10, 20	Propane	Horizontal	Jet flame length simulated by a CFD approach.
Schmidt et al. (2015)	2.2	LPG	Vertical	Jet flame length correlation, based on Froude Number.
Palacios et al. (2009, 2011, 2012)	10–43	Propane	Vertical	Jet flame shape suggested by a cylindrical shape.
Zhang et al. (2014)	19	Propane	Vertical	Jet flame shape proposed by cylindrical and elliptical shapes.
Zhou et al. (2016)	19	Propane	Horizontal	Jet flame shape proposed by a line source model.
Gopalaswami et al. (2016)	19	LPG	Horizontal	Jet flame shape correlated with Froude Number.
Laboureur et al. (2016)	19	LPG	Horizontal	Jet flame shape investigated by an image processing approach.
Palacios et al. (2016)	1–51	Propane and methane	Vertical	Jet flame shape correlated with mole concentrations.
Liu and Hu (2019)	3–6	Propane	Vertical	Jet flame shape correlated with Froude number.
Palacios and Rengel (2020)	1.63–3.67	Propane	Vertical, Horizontal	Jet flame geometry simulated by a CFD approach.
Mashhadimoslem et al. (2020a)	12.75	Propane	Vertical	Jet flame shape simulated by a CFD approach.
Mashhadimoslem et al. (2020b)	12.75	Propane and hydrogen	Vertical	Jet flame length and radiation simulated by a CFD approach.
Sun et al. (2019)	-	35 flammable chemicals	-	Jet flame radiation distance predicted by an ANN approach.

2. Experimental set-up

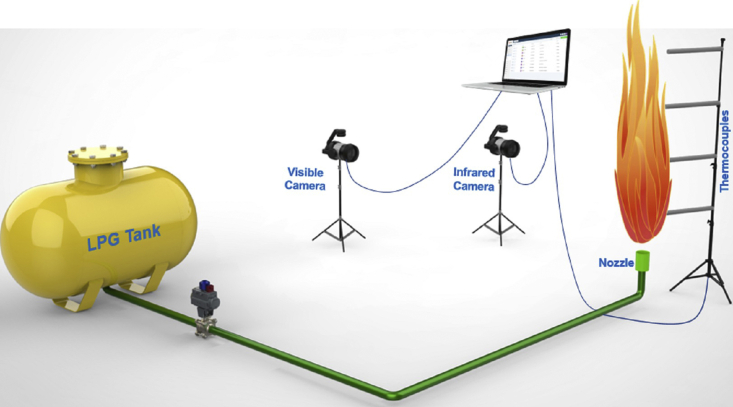
The jet flame shape boundary experiments concern vertical jet fires, obtained with circular nozzles ranging between 12.75 mm and 43.1 mm, under subsonic and sonic velocities in the open field. Propane was used as a fuel and the experiments were recorder by visible and infrared cameras. Further details of the experimental set-up and results data can be found in (Palacios and Casal, 2011). The jet flame boundary was defined by the 800 K isothermal, obtaining jet flame lengths (L) and jet flame diameters as “equivalent diameters” (D_eq). For all the data, D_eq was calculated as the ratio of the jet flame area (A) to the radiant jet flame length (L):

$$D_{eq}=\frac{A}{L}$$ (1)

The mass flow rates, jet flame lengths and jet flame diameters ranged between 0.01 kg/s to 0.54 kg/s, 0.8 m–10.14 m, and 0.24 m–1.44 m, respectively. The above-mentioned variables were applied as input (i.e. mass flow rates and nozzle diameters) and target data (i.e. jet flame lengths and equivalent diameters), respectively, to study the jet flame shape ratio. The schema of the experimental set-up is shown in Figure 1.

Figure 1.

A schematic view of the experimental set-up.

3. Mathematical methodology

3.1. Artificial neural network (ANN) theory

The neural network method follows the structure of the human brain and nerves, and it is perhaps the most popular method among network classifiers, over the past two decades (Dixon and Candade, 2008). An ANN (or neural network) is a mathematical or computational model that simulates the structural or functional aspects of biological neural networks. In the past, ANNs have been very attractive to computer scientists. In fact, studies on the network began in the early 1940s. The structure of ANNs was used to analyze and classify data for various subjects in the 1940s (Hebb, 1949). Due to the impossibility of overcoming theoretical obstacles, neural networks were forgotten between the 1960s and 1980s. In the 1980s, Hopfield, Rumelhart, Grossberg and Widrow developed again this method (Hopfield, 1982; Rumelhart et al., 1986; Widrow et al., 1987; Grossberg, 2012). Today, these theoretical obstacles have been removed, and neural networks are one of the most widely used tools to achieve many different goals (Debar et al., 1992). One of the benefits of the neural network is less computational time to solve complex problems. If there is no relationship between the data, artificial neural networks are used to find the connection between them, based on the patterned from human neural networks. Neural network's features include parallel processing (high speed), generalizability, nonlinear calculations, communication of input and output data, adaptability, response to noise data, fault tolerance and learning (Siddique and Adeli, 2013). The smallest unit of processing data is a neuron. A neuron is a computational unit, whose input and output are numbers. A number of signals enter into a cell and collect them. In neural networks, the target is to obtain the appropriate values of weights (w) for given (f) functions. At first, each input (x_i) is multiplied by the corresponding weight (w), then all the values are added together, and the threshold or bios value (b) is added to the sum of the values. A summary of this process is shown for inputs data in Eq. (2):

$$net=(\sum _{i=1}^n{w}_i{x}_i)+b$$ (2)

At the end of this step, the results are entered into a transfer function (f) and the output values (y) are obtained through Eq. (3):

$$y=f\left(net\right)$$ (3)

The transfer form functions are usually ramp, linear and step or sigmoid (S shape). The neuron cells connect together and form a layer of neurons. One or more neurons layers structure the network. Two different types of neural networks can be obtained, depending on the connection and configuration of the neurons. Figure 2 shows the feedforward neural network, one type of the ANN, with X₁, X₂… and X_n as the model input variables, n the number of input nodes, w_ij the weight factor of the neuron and input node, b the threshold value of a neuron i, and Y_i as the output of a neuron i.

Figure 2.

A feedforward neural network.

3.1.1. Multi-layer perceptron (MLP)

Learning in neural networks finds algorithms to determine the communication in the weights of neurons. The most common of these algorithms is the multi-layer perceptron (MLP) method. The function of this method is shown in Eq. (4):

$$g=f(w{x}_i^k+\theta )$$ (4)

where g is an output vector, θ represents the threshold limit, w represents the weighted vector of coefficients, and x_k represents an input vector (Richards and Richards, 1999). A multilayer perceptron usually consists of an input layer, one or more latent layers, and an output layer that receives, processes, and displays information.

The structure of the MLP neural network consists of an input layer, hidden multilayers, and an output layer, as shown in Figure 3. The purpose of the training algorithm in this network is to try to reduce the average squares of the general error, which has two parts: (i) Forward pass, and (ii) Backward pass. In forward pass, the input vector is applied to the network, and the network output is calculated. In backward pass, the error is calculated as the difference between the network output and the desired output, and according to the criterion function, an appropriate signal to the error is generated. Then, this signal moves backward from layer to layer, and then modifies the weights from the input layer. The modified weights minimized the average of the total square of the errors. Finally, the purpose of the training algorithm in the network is to reduce the average squares of the general error. In this work, the Bayesian training method is used to solve the network. It has been applied to train the neural network feedforward propagation algorithm. This method, as in the statistical approach, firstly assumes that the values of weights and biases are related to a function of distribution with an unknown variance (Siddique and Adeli, 2013; Foresee and Hagan, 1997; Nguyen, 1998). The MLP neural network output can be developed as follows:

$${\gamma }_{jk}=F_k(\sum _{i=1}^{N_{k-1}}{w}_{ijk}{\gamma }_{i(k-1)}+{\beta }_{jk})$$ (5)

where ${\gamma }_{jk}$ and ${\beta }_{jk}$ are the neuron j's outputs from the k's layer and bias weight for a neuron j in a layer k, respectively. In the beginning of the network training process, w_ijk are the link weights that were selected randomly, and F_k are the nonlinear activation transfer functions. These functions may be considered in many different forms, such as an identity function, a binary step function, a binary sigmoid, a bipolar sigmoid, a Gaussian, and a linear function (Fausett, 2006).

Figure 3.

A neural network, using a feedforward MLP method with backpropagation to describe the jet fire shape defined by the 800 K isotherm.

3.1.2. Radial basis function network

The Radial Based Function (RBF) network is a type of feedforward networks with a single hidden layer, firstly introduced by (Broomhead and Lowe, 1988). The optimization of the neurons in the single hidden layer, involves very strong networks to simulate any continuous function with an acceptable degree of accuracy. The methodology used by the RBF algorithm network is similar to the MLP algorithm, but the characteristics of the hidden layer neurons being fully different. The hidden layer collects the data from the input layers and transfers them to the Gaussian transfer function to convert the data into nonlinear functions. The performance responses are linearly integrated to generate the output layer data. In the RBF neural network algorithm, the transfer functions between the input layer and the hidden layer are nonlinear functions; while the transfer functions between the hidden layer and the output layer are linear functions. The hidden neurons in the RBF networks actually take the distance (geometric size or Euclidean size) between the input vector and the weights. In order to achieve this goal, experimental data on jet flame shape were obtained from (Palacios and Casal, 2011). The RBF output layer, based on linear combiners, is given by Eq. (6):

$$f\left(x\right)=\sum _{i=1}^N{w}_{ij}G(\Vert x-c_i\Vert \ast b)$$ (6)

where N is the number of data set for training, w_ij is the weight related to each hidden neuron, x is the input variable, C_i is the center points, and b is the bias. The centralized response from the hidden point using a Gaussian function is obtained through Eq. (7):

$$G(\Vert x-c_i\Vert \ast b)=\exp \left((-\frac{1}{2{\sigma }_i^2}{(\Vert x-c_i\Vert \ast b)}^2\right)$$ (7)

where σ_i is the spread of Gaussian function. It represents the range of ||x−ci || into the input space where the RBF neuron should respond. In Eq. (7), the $1/2{\sigma }_i^2$ coefficient in the RBF activation function controls the width of the bell curve and optimizes the fit between the activation function and data. The structure of the RBF neural network, consisting of an input layer, a single hidden layer, and an output layer, is shown in Figure 4.

Figure 4.

A neural network, using a RBF method, to describe the jet fire shape defined by the 800 K isotherm.

3.2. Work cycle for model design

The work cycle for the integrated artificial neural network model design process includes five main steps, as shown in Figure 5. The first step involves data gathering. Then the jet flame data, including mass flow rates, nozzle diameters, jet flame lengths and equivalent diameters, is defined. The input data involves the mass flow rates and nozzle diameters; while the output data (target) involves the jet flame lengths and equivalent diameters. The third step is the polarization of the data to the network, like machine language. In the next stage, the network architecture is created with the selection of learning algorithms. The ANN model training process is applied along with a network training validation. It includes network input and output adjustments to match the data and select the training. At this stage, the model is taught to optimize the performance of the model, by using a set of training data to set network parameters, such as weight, bias and/or thresholds. During the training process, the network validation data is improved using a set of data, and then the network testing process is performed by the tested data. The training of the network stops when generalizations improved. The performance of the trained model is evaluated by statistical criteria, involving the square of the coefficient of multiple correlation (R²) and the mean square error (MSE), to compare the model outputs with the data set. In the final step, the best network pattern is selected and the model is developed. During the development of the MLP and RBF models, several configurations are evaluated and the network performance is optimized, by changing the number of hidden layers, the number of neurons in the hidden layers, and the network training algorithm, in order to obtain the best network to predict the output parameters. Finally, when the optimized error from the tested trained inputs is obtained, the training algorithm ends.

Figure 5.

A schematic view of an ANN work cycle model design.

4. Results and discussion

4.1. Backpropagation training algorithm

Three different Learning algorithms of MLP back-propagation (BP) algorithms (i.e., Levenberg – Marquardt (LM) (Hagan and Menhaj, 1994)), Bayesian Regularization (BR) (MacKay, 1992; Ticknor, 2013), and Scaled Conjugate Gradient (SGG) (Møller, 1990), were applied to find the best algorithm for the ANN. To achieve the desired architecture, various steps were followed, according to the work cycle diagram shown in Figure 5. After the preparation of the experimental data, the mass flow rates and outlet nozzles of jet flames were set as input data; while the jet flame length and width were set as output. The experimental data from the jet flame shape were divided into three distinguished sets, including training, validation, and test dataset. In the next step, all the main input data was randomly selected. The 70% of the total data points were used as the network training (50 dataset); 15% of the total data points were used as the network validation for the data; and 15% of the total data points were tested with the resulting network, to provide an independent measure of the network performance during and after training. Before implementing the algorithms, a normalization operation was performed to examine the various ranges to prevent that any data could not be greater than others. The input and output dataset variables range between -1 and 1, and were normalized by Eq. (8):

$$X_{norm}=\frac{(X-X_{\min })}{(X_{\max }-X_{\min })}$$ (8)

where, X_norm is the normalized data, X is a raw input variable and X_max and X_min are the maximum and minimum of the data in the dataset, respectively.

If the range of data variables is very wide, it is prefer that the input and output data variables be normalized for neural network modeling. For the definition of number of neurons in each hidden layer, the selection of activation functions of network is very important in ANN modeling development. This is determined by trial and error, through the comparison of the architectural performance with the different networks, after the training step. During the network training, in order to find the appropriate values of the network parameters, the predicted network error shall be kept to a minimum value for each step of the mean square error (MSE) in each iteration. The MSE and the square of the correlation coefficient (R²) were used as evaluation criteria to compare the model outputs with the evaluation dataset. MSE and R² were calculated as follows (Piñeiro et al., 2008; Kobayashi and Salam, 2000):

$$MSE=\frac{1}{n}\sum _{i=1}^n{\left(Y_{predicted}-Y_{actual}\right)}^2$$ (9)

$$R^2=\frac{\sum _{i=1}^n{\left(Y_{predicted}-Y_{actual}\right)}^2}{\sum _{i=1}^n{\left(Y_{predicted}-Y_{mean}\right)}^2}$$ (10)

where, Y_actual and Y_predicted are the experimental and the predicted values by the artificial neural network output development, respectively.

4.2. Optimization of the number of neurons using MLP and RBF models to predict a jet fire

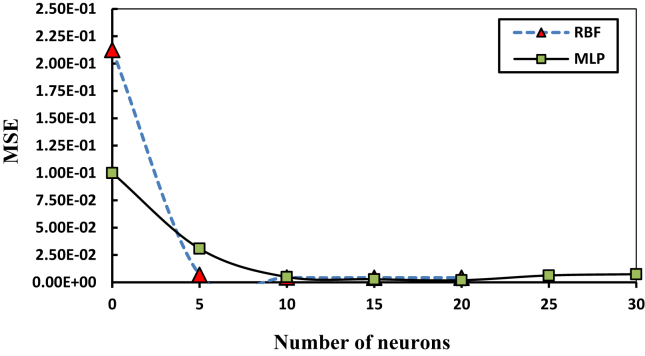
In the present work, various neuron activation functions were applied. Sigmoid and pureline transfer functions for hidden and output layers were selected, respectively. The optimum number of neurons was selected based on the minimum value of MSE, during the training process of the algorithm, and the maximum value of R². Figure 6 shows the number of neurons in MLP, varying from 1 to 30. It was found that the Bayesian Regularization backpropagation algorithm have the lowest MSE value for the vertical jet fire parameters (Table 2). The above-mentioned algorithm with fifteen neurons was found to be and selected as the best MLP model. Figure 6 also shows the optimal number of neurons for the RBF model, with a Gaussian function, be 20 neurons with a single layer. The best MSE validation performance of MLP and RBF networks models were 0.00286 and 0.00426 at 100 and 200 epochs, respectively (Figure 7).

Figure 6.

Optimization of the number of neurons, using MLP and RBF structures, to predict the shape of a vertical jet fire of propane.

Table 2.

Backpropagation MLP training algorithms for the prediction of the shape of a vertical jet fire of propane.

Backpropagation algorithms	Function	Testing mean square error (MSE)	Regression R2 value	Epoch	Run Time (min)
Levenberg-Marquardt	trainlm	0.0037361	0.99244	15	0.35
Bayesian Regularization	trainbr	0.0028691	0.99315	100	0.52
Scaled Conjugate Gradient	trainscg	0.0064836	0.98842	62	0.23

Figure 7.

MSE values for the (a) MLP and (b) RBF models, during the validation performance.

4.3. ANN setup for prediction of jet fire shape

A general picture of MLP and RBF structure methods have been depicted in Figure 8. The MLP and RBF networks were structured with two hidden layers of 15 and 5 neurons and single hidden layer of 20 neurons, respectively. In the MLP structure, the multilayer feed forward network consisted of four layers. The first one was the input layer, through which the experimental data of vertical jet fires (i.e. the mass flow rates and the nozzle diameters, as input parameters data), were imported into the network; then two hidden layers were used. The last layer concerns the target data, which was calculated through the output data (i.e. the jet flame heights and the jet flame diameters). Between these two mentioned layers, there were other hidden layers. The number of hidden layers depends on the accuracy that is required for a particular problem. In this research, the number of hidden layers was set to two, providing reasonable accuracy. According to the neurons optimization process in the MLP structure, the number of neurons at the second hidden layer was set to be five. The transfer function applied in this layer was a tangent sigmoid transfer function; while in the output layer, the number of neurons had to be two, with a purelin (linear) transfer function.

Figure 8.

An artificial neural network using (a) MLP and (b) RBF structures to predict the shape of a vertical jet fire of propane.

The designed network regression R² values for the MLP model in all the figures shown in Figure 9 (i.e. training step, validation step, test step, and all the data) were close to one (R² = 0.99315). Figure 9 also shows a close accurate correlation between the MLP model of ANN outputs and the target values from the prepared propane jet flame dataset. The 3-D curves of the MLP and RBF model algorithms are shown in Figure 10. They have been obtained to understand the interaction between the effects of the jet flames variables (i.e. mass flow rates and nozzles diameters), and to determine the jet flame variables of propane jet flames, through the drawn surfaces. The spectrum color in the plots and the response surfaces represent the interaction between the propane mass flow rates and the nozzle diameters. Figure 10 (a₁, a₂) and (b₁, b₂) also identify the vertical propane jet flame length and jet flame diameter, using two variables factors, such as the mass flow rate and nozzle diameter. Thus, the slope curved in the 3-D response surfaces in Figure 10 (a₁, a₂) and (b₁, b₂), show the jet flame length and the jet flame diameter, depending on the mass flow rates. The 3-D surface curves evaluate the effect of the two above-mentioned parameters (i.e. mass flow rates and nozzle diameters), by considering a third parameter being a constant, such as the jet flame length and jet flame diameter parameters. The predicted and experimental normalized data of the MLP and RBF models was fitted in Figure 11 for propane jet fire shapes. As shown in Figure 11 (a₁, a₂) and (b₁, b₂), the agreement between the simulated results and the experimental parameters was found to be better using the MLP model (R² = 0.993) than the RBF model (R² = 0.991). These results have also shown the predicted models to match accurately to the experimental data.

Figure 9.

Predicted propane jet flame shapes data with a MLP model, during (a) the training step; (b) the validation step; (c) the test step and (d) all the data.

Figure 10.

Response surfaces plots, obtained with artificial neural networks, using MLP (a₁, a₂) and RBF (b₁, b₂) models to predict propane jet flame shapes, defined by the 800 K isotherm.

Figure 11.

Experimental data on propane jet flame lengths (L) and flame diameters (D_eq), defined by the 800 K isotherm, and predicted by (a₁, a₂) MLP and (b₁, b₂) RBF normalized models.

The optimized ANN weights matrix of propane jet fire shapes, defined by the 800 K isotherm, have been predicted by the MLP model and summarized in Table 3.

Table 3.

Characteristic parameters of the ANN-MLP model.

Neuron		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
First hidden layer	wi	-3.8348	5.4522	3.1679	5.1276	5.2126	4.8174	4.6505	5.0408	-3.4404	4.1241	-4.8222	3.1232	-3.7465	-3.0789	-5.3698
		-3.836	0.4011	4.3925	-1.7458	1.4754	2.451	2.7845	-1.9087	4.1949	3.5267	2.6375	-4.4152	3.9108	-4.275	0.1695
	b	5.4206	-4.5941	-3.8842	-3.0974	-2.3501	-1.5808	-0.691	0.1109	-0.7868	1.4991	-2.1142	3.1335	-3.8843	-4.7929	-5.4768
Second hidden layer	wi	0.082	0.3507	-0.1512	-0.0253	0.4294	-	-	-	-	-	-	-	-	-	-
		-0.5066	-0.4941	0.5051	0.1918	-0.0081	-	-	-	-	-	-	-	-	-	-
		0.6262	0.2748	0.7067	-0.0442	-0.4482	-	-	-	-	-	-	-	-	-	-
		-0.0889	-0.0442	0.0758	0.909	0.1287	-	-	-	-	-	-	-	-	-	-
		-0.0669	0.6242	-0.3838	0.5546	0.8486	-	-	-	-	-	-	-	-	-	-
		0.2699	-0.3457	-0.0041	-0.3334	0.6843	-	-	-	-	-	-	-	-	-	-
		-0.1206	-0.4081	0.6197	0.2019	-0.2584	-	-	-	-	-	-	-	-	-	-
		-0.4705	-0.0118	-0.5744	-0.2166	0.2288	-	-	-	-	-	-	-	-	-	-
		-0.3597	-0.3911	0.4739	0.4825	-0.197	-	-	-	-	-	-	-	-	-	-
		0.5149	0.0294	-0.4244	0.437	0.2985	-	-	-	-	-	-	-	-	-	-
		0.4447	0.302	0.4126	0.3153	-0.5391	-	-	-	-	-	-	-	-	-	-
		-0.2374	-0.6688	-0.1229	0.075	-0.4292	-	-	-	-	-	-	-	-	-	-
		-0.0538	-0.3377	-0.2207	0.3147	0.6927	-	-	-	-	-	-	-	-	-	-
		0.5354	0.1026	-0.0822	0.4257	-0.1948	-	-	-	-	-	-	-	-	-	-
		0.654	0.4846	-0.538	0.6364	-0.1201	-	-	-	-	-	-	-	-	-	-
	b	-1.6171	-0.9369	0.0292	0.4807	1.4711	-	-	-	-	-	-	-	-	-	-
Output layer	wl	0.1342	-0.4171	-	-	-	-	-	-	-	-	-	-	-	-	-
		-0.5398	-0.2115	-	-	-	-	-	-	-	-	-	-	-	-	-
		0.2912	0.3019	-	-	-	-	-	-	-	-	-	-	-	-	-
		0.0618	-0.0008	-	-	-	-	-	-	-	-	-	-	-	-	-
		0.6243	0.849	-	-	-	-	-	-	-	-	-	-	-	-	-
	b	-0.1918	-0.6996	-	-	-	-	-	-	-	-	-	-	-	-	-

w_i: weights between input and hidden layers.

w_l: weights between hidden and output layers.

5. Conclusions

In this research, propane vertical jet fire shapes have been used for the development of artificial neural networks. This research analyses a database on vertical propane jet fire shapes, defined by the 800 K isothermal temperature, involving 70 data sets and predicting the jet fire shapes through ANN. The ANN results have shown good agreement with the experimental propane jet flame shapes, when the jet flame length and the jet flame diameter are considered as output data, and the dimensionless mass flow rates and nozzle diameters are considered as input data of the network. In the present study, the MLP model, using three functions with backpropagation algorithms, and the RBF model, using the Gaussian function, have been developed to predict the output parameters (i.e. jet flame lengths and jet flame diameters). The minimum square error (MSE) and the coefficient of determination (R²), as statistics values, have been calculated for the two above-mentioned models to choose the best model and assess the fitting performance. The Bayesian Regularization backpropagation algorithm, with a tangent sigmoid transfer function (trainbr) in hidden layers and a linear transfer function (purelin) in the output layer, has given the best performance among other MLP models. The best validation performance of the MLP and RBF models, with an optimized number of neurons, has given an overall R² value of 0.993, MSE = 0.00286 at 100 epochs; and an overall R² value of 0.991, MSE = 0.00426 at 20 epochs, respectively. The optimal number of neurons for the MLP and RBF models has found to be 20 for the two hidden layers in the MLP model, and single layer for the RBF model. A comparison between two networks has shown negligible discrepancies between the results of the RBF and MLP models (with 20 neurons). The contribution of the present work has been to simultaneously simulate and accurately predict, through two ANN performed algorithms, the jet fire shape with significantly reduced computational times. The CFD computational time for a simulated propane jet fire, defined by the 800 K isotherm, has been 1100 min per run (Mashhadimoslem et al., 2020a, Mashhadimoslem et al., 2020b); while in the present study, the propane jet flame geometry, defined by the 800 K isotherm, has been determined in 2115 s, a reduced time, compared with previous CFD works. This work has presented a robust and efficient hybrid approach, to simulate the jet fire shape and optimize the training of feedforward MLP and RBF neural network algorithms. The ANN weights matrix, developed in the present work, could be easily incorporated into another related software for a bigger ANN related project. This work has also offered reliability on the ANN architectures, as prediction deep learning using experimental data, to provide more accurate predictions for jet fire accidents in the process industries. The current obtained models could be improved by adding more training datasets, to cover more jet fire scenarios in different operational conditions. The ANN development, based on various hydrocarbon fuels with extended different conditions (i.e. nozzle diameters and mass flow rates), could be relevant in future studies, to attempt to improve safety, specifically in the safety and risk engineering domain.

Declarations

Author contribution statement

H. Mashhadimoslem and A. Ghaemi: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

A. Palacios: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

Data will be made available on request.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.