The costs and benefits of estimating T ₁ of tissue alongside cerebral blood flow and arterial transit time in pseudo‐continuous arterial spin labeling

Abstract

Multi‐post‐labeling‐delay pseudo‐continuous arterial spin labeling (multi‐PLD PCASL) allows for absolute quantification of the cerebral blood flow (CBF) as well as the arterial transit time (ATT). Estimating these perfusion parameters from multi‐PLD PCASL data is a non‐linear inverse problem, which is commonly tackled by fitting the single‐compartment model (SCM) for PCASL, with CBF and ATT as free parameters. The longitudinal relaxation time of tissue T _1t is an important parameter in this model, as it governs the decay of the perfusion signal entirely upon entry in the imaging voxel. Conventionally, T _1t is fixed to a population average. This approach can cause CBF quantification errors, as T _1t can vary significantly inter‐ and intra‐subject. This study compares the impact on CBF quantification, in terms of accuracy and precision, of either fixing T _1t, the conventional approach, or estimating it alongside CBF and ATT. It is shown that the conventional approach can cause a significant bias in CBF. Indeed, simulation experiments reveal that if T _1t is fixed to a value that is 10% off its true value, this may already result in a bias of 15% in CBF. On the other hand, as is shown by both simulation and real data experiments, estimating T _1t along with CBF and ATT results in a loss of CBF precision of the same order, even if the experiment design is optimized for the latter estimation problem. Simulation experiments suggest that an optimal balance between accuracy and precision of CBF estimation from multi‐PLD PCASL data can be expected when using the two‐parameter estimator with a fixed T _1t value between population averages of T _1t and the longitudinal relaxation time of blood T _1b.

List of abbreviations

ASL

arterial spin labeling

ATT

arterial transit time

CBF

cerebral blood flow

CRLB

Cramér‐Rao lower bound

FIM

Fisher information matrix

GM

gray matter

GRASE

gradient‐echo and spin‐echo

HR

high resolution

KW

Kruskal‐Wallis

LR

low resolution

MLE

maximum likelihood estimator

NLE

non‐linear least‐squares estimator

PASL

pulsed arterial spin labeling

PCASL

pseudo‐continuous arterial spin labeling

PCC

Pearson correlation coefficient

PLD

post‐labeling delay

PDF

probability density function

PVE

partial volume effect

SAR

specific absorption rate

SCM

single‐compartment model

SNR

signal‐to‐noise ratio

WM

white matter.

1. INTRODUCTION

Pseudo‐continuous arterial spin labeling (PCASL) is a non‐invasive magnetic resonance imaging (MRI) method to quantify brain perfusion. ¹ , ² , ³ In PCASL, a train of very short radiofrequency pulses and gradient pulses inverts the longitudinal magnetization of hydrogen nuclei in arterial blood as they pass through a plane perpendicular to the blood flow in the carotid region. ⁴ Labeled blood water, serving as an endogenous tracer, travels through the arterial vascular tree to the brain tissue, where it exchanges with tissue water. After a certain post‐labeling delay (PLD), when (part of) the labeled bolus has perfused into the brain tissue, a ‘labeled image’ is acquired. ⁵ The difference between a labeled image and an image obtained without prior labeling provides a relative measure of perfusion. ⁵ Cerebral blood flow (CBF) can be absolutely quantified by fitting a perfusion model to such difference image data. The accuracy and precision of CBF quantification from PCASL data depend on the ASL acquisition strategy and the quantification model.

Choosing an acquisition strategy in which the perfusion signal is sampled at multiple PLDs has two distinct advantages. Firstly, it allows for the quantification of the arterial transit time (ATT), which is the time it takes for blood to flow from the labeling plane to the imaging voxel, alongside the CBF. Secondly, CBF quantification from multi‐PLD PCASL data is more accurate than from conventional single‐PLD PCASL, ¹ , ⁶ , ⁷ which is vulnerable to under‐ or overestimation of CBF, especially when the ATT varies over a large range in a subject or in the studied population. ⁶ , ⁷

The single‐compartment model (SCM), introduced by Buxton et al., ⁸ is the most widely used quantification model in multi‐PLD PCASL experiments. The SCM takes local variability in the ATT into account and assumes that relaxation of the labeled spins is governed entirely by the longitudinal relaxation time of brain tissue T _1t upon arrival in the imaging voxel. ⁸ While it is known that the SCM overestimates the time the label resides in tissue, ⁹ this has no impact on the importance of T _1t as a possible confounder when quantifying with the SCM. In most cases, T _1t is fixed to a certain population average for white matter (WM) and gray matter (GM). This can compromise the accuracy of CBF quantification for multiple reasons. Firstly, there is no consensus on average population values for T _1t. ¹⁰ Furthermore, it has been shown that T _1t varies across patients, differs spatially within one tissue and changes in brain lesions with perfusion disorders, such as stroke, ¹¹ neurodegenerative diseases, ¹² or tumors. ¹³ , ¹⁴ Finally, ASL images are typically acquired at low spatial resolution, resulting in partial volume effects, which may influence the effective T _1t. In order to avoid a possible estimation bias caused by fixing T _1t to a certain value, it can be estimated locally alongside the perfusion parameters, CBF and ATT. However, adding a parameter to be estimated reduces the estimation precision, which can be problematic in a low‐SNR imaging modality such as ASL.

The effect of T _1t on quantification has been studied in previous work. In ¹⁵ , the impact of different T _1t values on CBF quantification was shown for single‐PLD continuous ASL. Qin et al ¹⁶ used information criteria to conclude that estimating the CBF, the ATT and T _1t is feasible, yet for a very low spatial resolution (7mm isotropic). In this work, we compare the impact on CBF quantification accuracy and precision of either choosing a fixed T _1t value or estimating it alongside CBF and ATT when fitting the SCM to multi‐PLD PCASL data, acquired at a recommended ¹ spatial resolution of 4mm in‐plane and 5mm through‐plane. Furthermore, in order to maximally compensate for the expected reduced precision when estimating CBF, ATT, and T _1t together, the design of the multi‐PLD PCASL experiment is optimized for this three‐parameter estimator. ASL MRI acquisition settings have often been optimized for pulsed ASL (PASL). ¹⁷ , ¹⁸ , ¹⁹ Besides the difference in the kinetic model between PASL and PCASL, experiment design of PCASL has more parameters to be optimized. Indeed, the optimization of the PASL experiment design is limited to searching optimal inversion times, while the design of the PCASL experiment can be optimized with respect to both the acquisition time points and the labeling duration, as will be done in this work. Optimizing the acquisition time points and the labeling duration for a three‐parameter estimator contrasts this study from recent work of Woods et al., ²⁰ in which the PLDs of a multi‐PLD PCASL experiment were optimized for two‐parameter (i.e., CBF and ATT) estimation.

The statistical quality assessment of the two‐ and three‐parameter estimator is performed by means of test‐retest simulation and real data experiments. Both options to solve the inverse problem at hand are at opposite sides of the accuracy‐precision trade‐off. It is our goal to provide insight in which option balances accuracy and precision of CBF quantification best for the recommended spatial resolution ¹ in ASL.

2. THEORY

This section consists of two major parts. Firstly, a two‐ and a three‐parameter estimator for parameter quantification from multi‐PLD PCASL data are defined in sections 2.1 and 2.2. Secondly, an optimal experiment design method for maximizing the precision of perfusion parameter estimation with the three‐parameter estimator is proposed in section 2.3.

2.1. Single‐compartment quantification model for PCASL data

The intensity and dynamic evolution of the PCASL difference signal ΔM in a certain voxel depend on the acquisition settings and on the global or local characteristics of the brain and its vasculatory system. When assuming that labeled water enters the tissue instantaneously upon arrival in the imaged voxel and that the concentration of labeled water is constant throughout the label bolus, PCASL difference data can be described by Buxton's SCM ⁸ :

$$g(t)=\left\{\begin{array}{ll}0& 0<t<\Delta t\\ 2\alpha M_{0b}f{T}_{1t}^{\prime }{e}^{-\Delta t/T_{1b}}\left(1-e^{-\frac{t-\Delta t}{T_{1t}^{\prime }}}\right)& \Delta t<t<\tau +\Delta t\\ 2\alpha M_{0b}f{T}_{1t}^{\prime }{e}^{-\Delta t/T_{1b}}{e}^{-\frac{t-\tau -\Delta t}{T_{1t}^{\prime }}}\left(1-e^{-\tau /T_{1t}^{\prime }}\right)& t>\tau +\Delta t\end{array}\right.$$ (1)

with f the CBF, Δt the ATT, α the labeling efficiency, M _0b the signal of a voxel filled with fully relaxed blood, T _1b the longitudinal relaxation time of blood, and $T_{1t}^{\prime }=T_{1t}\lambda /(\lambda +f{T}_{1t})$ the apparent longitudinal relaxation time, with λ the equilibrium blood/tissue partition coefficient of water. ⁸ The time point t=0 is defined as the beginning of labeling.

In the model described by Equation (1), the labeling duration τ is assumed to be constant. PCASL data is acquired at a certain acquisition time t _i=τ+PLD_i. In a standard PCASL sequence, it is not possible to acquire data during labeling. Therefore, for a fixed τ, data can only be acquired at acquisition times t>τ. Hence, unless Δt>τ, a significant part of the dynamic increase of the difference signal, described by the second regime in Equation (1), is not accessible for sampling, while it might contain valuable information. A way to nevertheless acquire data at acquisition times t<τ is to choose a shorter labeling duration τ _s<τ and sample the signal at t=τ _s+PLD_s, with PLD_s a post‐labeling delay that is shorter than the minimal Δt. This short PLD is crucial to allow sampling of the PCASL signal during the second regime. It has been shown by Buxton et al. ⁸ that the entire dynamic increase of the difference signal for a labeling duration τ _s<τ equals the initial part of this regime for a labeling duration τ. ⁸ Therefore, the entire evolution of the difference signal for a constant labeling duration τ, described by Equation (1), can be sampled at each time point t by using the sampling procedure described above. Throughout this work, a multi‐time‐point PCASL acquisition scheme can therefore be defined by a single constant τ and a set of acquisition time points $\mathrm{t}={\{t_i\}}_{i=1}^N$, knowing that for each t _i<τ the real data acquisition needs to be performed with a unique τ _s<τ in combination with a very short PLD_s.

2.2. Maximum likelihood estimation

Parameter estimation in this work is performed with the maximum likelihood estimator (MLE), which takes the probability distribution of the data into account. PCASL difference data result from the voxel‐wise subtraction of two magnitude images, the control and label image. Typically, the intensity of magnitude images, reconstructed from data acquired with multiple coils, follows a Rician or non‐central chi‐distribution, depending on the reconstruction method. ²¹ However, knowing that these images are typically acquired at a low spatial resolution, which guarantees a reasonably high SNR, it can be assumed that the intensities in control and label images follow a Gaussian distribution. ²² , ²³ In that case, the resulting difference data will also be adequately described by a Gaussian distribution. Therefore, the joint probability density function (PDF) of PCASL difference data is well approximated by a multi‐variate Gaussian distribution. For independent Gaussian distributed data, having a constant (noise induced) variance in each data point, the MLE is equivalent to the unweighted non‐linear least‐squares estimator (NLE) ²⁴ :

$$\widehat{\mathit{\theta }}=\arg \underset{\mathit{\theta }}{\max }L\left(\mathit{\theta }\right|\mathbf{\Delta M})=\arg \underset{\mathit{\theta }}{\min }\sum _{i=1}^N{\left(\Delta M_i-g(t_i;\mathit{\theta })\right)}^2,$$ (2)

with θ the parameter vector, $\widehat{\mathit{\theta }}$ the MLE, $\mathbf{\Delta M}={\left\{\Delta M_i\right\}}_{i=1}^N$ a set of PCASL difference data points acquired at acquisition times $\mathit{t}={\{t_i\}}_{i=1}^N$ and L(θ|ΔM) the likelihood function. Two options for the parameter vector, θ ₁={f,Δt} and ${\mathit{\theta }}_2=\{f,\Delta t,T_{1t}^{\text{'}}\}$, give rise to a two‐parameter NLE (NLE2) and a three‐parameter NLE (NLE3), respectively.

2.3. Optimization of multi‐PLD PCASL acquisition settings for NLE3

The precision of NLE3 will be lower than that of NLE2 due to the larger amount of unknown parameters to be estimated. However, the precision of NLE3 can be maximized by optimizing the experimental design. Cramér‐Rao lower bound (CRLB) theory is the tool of choice to build such an optimization framework. The relation between the CRLB and the variance of any unbiased estimator $\widehat{\mathit{\theta }}$ of θ is summarized by the Cramér‐Rao inequality ²⁵ :

$$\text{cov}\left(\widehat{\mathit{\theta }}\right)\ge {\mathit{I}}^{-1}\left(\mathit{\theta }\right),$$ (3)

with $\text{cov}\left(\widehat{\mathit{\theta }}\right)$ the covariance matrix of $\widehat{\mathit{\theta }}$ and I ⁻¹(θ) the inverse of the Fisher information matrix (FIM). The inverse of the FIM is often referred to as the CRLB matrix. The diagonal elements of the CRLB matrix are the Cramér‐Rao lower bounds on the variances of unbiased estimators of the elements of θ. ²⁴

The FIM I(θ) of a set of data points depends on the joint PDF of these data points and its dependence on the unknown parameter vector θ. The latter dependence is captured by the parametric perfusion model g(θ) that describes the expected values of the data points. Since this model depends on the acquisition settings of the multi‐PLD PCASL experiment, so does the FIM and the CRLB matrix. This last dependency can be exploited for experiment design. Starting from the CRLB matrix, different optimization criteria can be chosen by transforming it to a scalar function ²⁶ :

$$q_h\left(\mathit{\theta }\right)=\frac{\partial h\left(\mathit{\theta }\right)}{\partial {\mathit{\theta }}^T}\mathit{I}{\left(\mathit{\theta }\right)}^{-1}\frac{\partial h\left(\mathit{\theta }\right)}{\partial \mathit{\theta }},$$ (4)

with h(θ) a scalar function and ∂h(θ)/∂ θ ^T a row vector. In this work, the choice was made to focus on maximizing the precision of CBF estimation as this is the main parameter of interest. The CRLB of f can be isolated by choosing h(θ)=f in Equation (4).

For a certain choice of τ, the CRLB of f can be minimized with respect to t. The CRLB also depends on the underlying parameter vector θ, which varies spatially within the brain as well as between different subjects. Therefore, optimization of the acquisition settings should be performed for a representative prior distribution p(θ) of θ in the target population. For a continuous prior distribution, the optimal acquisition times t, for a given value of τ, are found by minimizing a weighted integral:

$$\widehat{\mathit{t}}={\left.\arg \underset{\mathit{t}}{\min }\underset{\mathit{\theta }}{\int }{q}_h(\mathit{\theta },\mathit{t})p\left(\mathit{\theta }\right)d\mathit{\theta }\right|}_{h\left(\mathit{\theta }\right)=f}.$$ (5)

Note that Equation (5) represents a general framework for optimization of PCASL settings. Indeed, the scalar function h(θ) provides flexibility with respect to which parameters are chosen for optimization of the acquisition settings. For example, the trace of I ⁻¹(θ) could be minimized with $h\left(\mathit{\theta }\right)=f+\Delta t+T_{1t}^{\text{'}}$.

The integral in Equation (5) can be approximated by evaluating q _h(θ,t) at a large number M of randomly selected samples of p(θ). The optimization in Equation (5) can therefore be approximated by

$$\widehat{\mathit{t}}={\left.\arg \underset{\mathit{t}}{\min }\frac{1}{M}\sum _{j=1}^M{q}_h({\mathit{\theta }}_j,\mathit{t})\right|}_{h\left(\mathit{\theta }\right)=f},$$ (6)

with θ _j a randomly selected sample from p(θ).

Besides t, the labeling duration τ and the number of PCASL label‐control image pairs N are also optimizable. Therefore, the optimization in Equation (6) was repeated for multiple values of τ and N:

$$\{\tilde{\mathit{t}},\tilde{\tau },Ñ\}=\arg \underset{\{\tau ;N\}}{\min }\left\{{\left.\underset{\mathit{t}}{\min }\sum _{j=1}^M{q}_h({\mathit{\theta }}_j,\mathit{t},\tau )\right|}_{h\left(\mathit{\theta }\right)=f}\right\}.$$ (7)

Note that acquisition schemes are optimized for different values of τ and N instead of optimizing them alongside t, which would be impractical. Indeed, optimizing N alongside t would change the dimensionality of the optimization space within the optimization, which is not possible in most optimization algorithms. Furthermore, for each labeling duration, there will be a different set of optimal acquisition time points t. Therefore, optimizing τ together with t will increase the number of local minima in the optimization space, and thereby increase the risk of ending up in a local minimum. On top of that, this multi‐step approach allows to study how the minimized criterion changes as a function of τ and N.

In order to guarantee clinically feasible results, the optimization is performed under a fixed total acquisition time constraint. The total time needed to obtain a PCASL label or control image is determined by the acquisition time t _i, the read‐out time and the additional waiting period for MR specific absorption rate (SAR) limit restrictions. Only t _i is independent of the read‐out approach and the subject. As it is not our goal to optimize for a specific readout strategy or a single subject, a total acquisition time constraint T was imposed only on the read‐out‐ and subject‐independent acquisition time of N PCASL label‐control image pairs:

$$\{\tilde{\mathit{t}},\tilde{\tau },Ñ\}=\arg \underset{\{\tau ;N\}}{\min }\left\{{\left.\underset{\mathit{t}}{\min }\sum _{j=1}^M{q}_h({\mathit{\theta }}_j,\mathit{t},\tau )\right|}_{h\left(\mathit{\theta }\right)=f,{\sum }_{i=1}^{N}2t_i\le T}\right\},$$ (8)

The optimization problem Equation (8) was solved using the MATLAB function patternsearch, ²⁷ , ²⁸ thereby imposing t _i<t _i+1 (without loss of generality) and using a large number of randomly generated starting points t ₀.

3. METHODS

In order to analyze the accuracy and precision of the estimators, four distinct experiments were performed. As a first indication of the identifiability of the parameters of NLE2 and NLE3, the condition number of both inverse problems is determined in section 3.1. In section 3.2, details of the optimization experiment are specified starting from the optimization framework for NLE3 introduced in section 2.3. The performance of NLE2 and NLE3 are compared in a simulation and a real data experiment. Details of these experiments are described in section 3.3 and 3.4, respectively. Throughout all experiments, α=0.85 ⁴ and T _1b=1.65 s. ²⁹ The equilibrium magnetization of blood M _0b was set to one for the optimization and in the simulation experiment. In the real data experiment, it was approximated using a proton density‐weighted image M _0t, according to recommendations, ¹ and subsequently given as a fixed value to the estimator.

3.1. Parameter identifiability analysis

The identifiability of the parameters in a parameter estimation problem can be quantified by the condition number of the associated FIM. The larger this condition number, the more ill‐conditioned (and hence noise sensitive) the estimation problem. The extreme case of an infinite condition number corresponds with a singular FIM, reflecting that the parameter estimation problem is ill‐posed. This means that the CRLB does not exist and the model parameters are unidentifiable. ²⁴ In a more moderate case, a high FIM condition number indicates an ill‐conditioned inverse problem symptomized by a low precision, high correlations between parameters and poor identifiability. ³⁰ , ³¹ , ³² , ³³ The condition number κ of the FIM I(θ,t,τ) is calculated for NLE2 and NLE3 as ³³ :

$$\kappa \left(I\right(\mathit{\theta },\mathit{t},\tau \left)\right)=\left|\right|I{(\mathit{\theta },\mathit{t},\tau )}^{-1}\left|{|}_2\right|\left|I\right(\mathit{\theta },\mathit{t},\tau \left)\right|{|}_2=\frac{{\sigma }_{\min }\left(I\right(\mathit{\theta },\mathit{t},\tau \left)\right)}{{\sigma }_{\max }\left(I\right(\mathit{\theta },\mathit{t},\tau \left)\right)},$$ (9)

with ||·||₂ the Euclidean norm, and σ _min(·) and σ _max(·) the maximal and minimal singular value of the FIM, respectively. To compare the identifiability of the parameters of the two‐ and three‐parameter model employed by NLE2 and NLE3, respectively, the condition number of the corresponding FIMs were calculated for multiple randomly selected parameter vectors θ from the prior distribution p(θ) of WM and GM, defined in section 3.2, and assuming an N=24 equidistant sampling scheme.

3.2. Experiment design optimization

When performing the optimization for NLE3 defined in Equation (8), a prior distribution p(θ) needs to be chosen that reflects the target population. In this work, it is our goal to test the overall feasibility of NLE3, which is not specific to a certain pathology. To that end, p(θ) was approximated by a Gaussian distribution based on reported distributions in the literature for both WM and GM in the general population, ¹⁰ , ³⁴ , ³⁵ , ³⁶ , ³⁷ , ³⁸ as shown in Table 1. From the prior distribution of each parameter, for WM and GM, 10000 samples were randomly selected and combined to parameter vectors θ _j. Therefore, the resulting optimization criterion consists of a sum of M=20000 CRLBs.

TABLE 1.

Mean and standard deviation of Gaussian prior distributions p(θ) representative of the distribution of the respective parameters in the general population. The prior distribution for T _1t is compatible with reported literature values for a 3T field strength ¹⁰

	White matter	Gray matter
f [mL/100g/min]	23.0±5.0 34 , 35 , 36	53.9±11.0 37
Δt [s]	1.15±0.30 38	0.95±0.30 38
T 1t [s]	0.89±0.06 10	1.45±0.14 10

The set of evaluated labeling durations ranged from 0.8 to 1.8 s with increments of 0.1 s, while N ranged from 18 to 30 image pairs. As τ is set to lower durations, the PCASL signal decreases, yet a higher amount of images N can be acquired within the time constraint T. Conversely, the PCASL signal increases with longer label durations, at a cost of a lower amount of images though. The chosen ranges for τ and N were set wide enough to explore both extremes and find the optimum in between.

The time constraint T was set to 2 minutes. The resulting total acquisition time depends on the read‐out approach and the SAR requirements. In this work, real data acquisition was performed using a 3D gradient‐echo and spin‐echo (GRASE) readout scheme ³⁹ , ⁴⁰ with a readout time of 330 ms per image. For whole brain coverage, two segments would be needed, doubling the total number of images. Assuming a waiting period after each readout between 500 and 1500 ms to meet SAR requirements, the total acquisition time related to these optimized acquisition schemes was 5 to 8 minutes.

3.3. Simulation experiments

Simulation data were generated using the following three‐step procedure. Firstly, starting from ground truth high resolution (HR) brain perfusion parameter maps and using a five‐parameter two‐compartment perfusion model, ¹⁶ , ⁴³ HR PCASL data was created at N=24 conventional equidistant and N=24 optimized acquisition times. The details of both acquisition schemes, which have an identical total acquisition time, are described in Table 3. Note that Table 3 contains the optimized acquisition scheme, of which the details are more thoroughly described in section 4.2. The ground truth parameter maps for each of the five parameters were created by assigning random values from their respective prior distributions (see Tables 1 and 2) to a 1×1×1 mm³ HR brain tissue segmentation map derived from images of BrainWeb. ⁴⁴ For the Δt map, the selection was performed pseudo‐randomly to guarantee limited differences in Δt values between neighbouring voxels, as they are expected to be supplied by the same artery. Secondly, as PCASL data is usually acquired at a low resolution due to the low SNR, the HR data was downsampled to a resolution of 4×4×5 mm³ by averaging the signals of the 80 corresponding 1×1×1 mm³ HR voxels. Finally, zero‐mean Gaussian distributed noise with a fixed standard deviation σ was added voxel‐wise to the LR data. Let the SNR in a voxel be defined as the difference signal intensity, averaged over the entire dynamic perfusion signal range, divided by σ. Then, simulation experiments were run with average SNRs of 10, 15, 20, and 25 in GM voxels.

TABLE 3.

(a) Equidistant and (b) optimal acquisition settings. The labeling duration τ equals 1800ms and 1100ms for the equidistant and optimized scheme, respectively. For acquisition times t<τ, a shorter labeling duration τ _real<τ was used for real data acquisition, as described in section 2.1. For t−τ<100ms, τ _real was also shortened to comply with a lower bound in scanner software of 100ms on the PLD. In all other cases, τ _real=τ

τ real [ms]	PLD [ms]	t [ms]	τ real [ms]	PLD [ms]	t [ms]
400	100	500	1033	100	1133
574	100	674	1100	243	1343
748	100	848	1100	337	1437
922	100	1022	1100	607	1707
1096	100	1196	1100	694	1794
1270	100	1370	1100	792	1892
1444	100	1544	1100	897	1997
1617	100	1717	1100	988	2088
1791	100	1891	1100	1050	2150
1800	265	2065	1100	1100	2200
1800	439	2239	1100	1181	2281
1800	613	2413	1100	1221	2321
1800	787	2587	1100	1261	2361
1800	961	2761	1100	1314	2414
1800	1135	2935	1100	1395	2495
1800	1309	3109	1100	1496	2596
1800	1483	3283	1100	1568	2668
1800	1657	3457	1100	1665	2765
1800	1830	3630	1100	2597	3697
1800	2004	3804	1100	2611	3711
1800	2178	3978	1100	2622	3722
1800	2352	4152	1100	2624	3724
1800	2526	4326	1100	2648	3748
1800	2700	4500	1100	2659	3759
	(a)			(b)

TABLE 2.

Mean and standard deviation of Gaussian prior distributions of k _w, the blood‐to‐water exchange rate of water accounting for a finite permeability of the capillary wall, and δ _a, the intra‐voxel travel time accounting for an extended travel time through non‐permeable vasculature, in the five‐parameter PCASL model defined in ¹⁶

	White matter	Gray matter
k w [s−1]	2.10±0.30 41	1.83±0.30 41
δ a [s]	0.573±0.062 42	0.573±0.062 42

Parameter estimation was performed with maximum likelihood estimators NLE2 and NLE3, as defined in section 2.2. For NLE2, $T_{1t}^{\prime }$ was fixed to a tissue‐specific value. Knowing that in a real data experiment the average T _1t in WM and GM is not accurately known, three versions of NLE2 were implemented. The $\{T_{1,\text{WM}}^{\prime },T_{1,\text{GM}}^{\prime }\}$‐couple was set to {0.8 s,1.3 s},{0.9 s,1.45 s} and {1.0 s,1.6 s}, respectively. Note that the second $\{T_{1,\text{WM}}^{\prime },T_{1,\text{GM}}^{\prime }\}$‐couple contains the true average simulation values. Estimation with NLE3 was studied on equidistant and optimal data. NLE2 was only evaluated using the equidistant data, as the optimization was performed specifically for NLE3.

The process of creating noisy data and re‐estimating the perfusion parameters was repeated K=50 times for each SNR. The performance of both estimators was assessed in terms of accuracy and precision. To this end, estimates of the bias and standard deviation of the estimators NLE2 and NLE3 of a given parameter of interest were obtained from the sample of K realisations by calculating the sample mean of the difference between the ground truth value of this parameter and its estimates, and the sample standard deviation of the estimates, respectively. To calculate the bias estimates, the ground truth LR parameter maps were obtained by downsampling the original ground truth HR parameter maps. Furthermore, an LR tissue segmentation map was obtained by labeling an LR voxel as a certain tissue type if more than 90% of the corresponding HR voxels were labeled as that specific tissue type. All remaining voxels were considered voxels with partial volume effects (PVE). The LR tissue segmentation map was used for two purposes. Firstly, in assigning a GM or WM T _1t value for quantification with NLE2. In the case of PVE voxels, the GM or WM T _1t value was chosen dependent on the predominant tissue type. Secondly, the tissue segmentation map allowed to analyze the simulation results per tissue type, when needed.

3.4. Real data experiments

Whole‐brain multi‐PLD PCASL data were obtained from three healthy volunteers (22 year‐old male, 30 year‐old female, 38 year‐old male) using the 3D GRASE sequence (spatial resolution = 4×4×5 mm³, readout time per shot = 330 ms, segments for whole brain coverage = 2, TE = 18ms, FOV_read = 256mm, FOV_phase = 192mm, FOV_slice = 120mm), acquired on a Siemens 3.0T MR scanner with a 32‐channel head coil. The repetition time for each label‐control pair was set to the sum of the labeling duration, PLD, readout time and an additional waiting period to comply with SAR requirements, depending on the subject. The labeling plane was positioned based on a 40s angiogram, adhering to recommendations. ¹ The acquired data consisted of multiple sets of N=24 label‐control image pairs, obtained alternating between the equidistant and optimized acquisition scheme (see Table 3). The total acquisition time of each set of 24 label‐control pairs was 5 to 8 minutes, depending on individual SAR requirements. Including an HR anatomical image (sequence: MPRAGE, spatial resolution = 1×1×1 mm³, TR = 2250ms, TE = 4ms, TI = 900ms, FOV_read = 256mm, FOV_phase = 256mm, FOV_slice = 176mm) for tissue segmentation and an equilibrium magnetization image (M _0t) (sequence: 3D GRASE, spatial resolution = 4×4×5 mm³, segments for whole brain coverage = 2, TR = 6000ms, TE = 18ms, FOV_read = 256mm, FOV_phase = 192mm, FOV_slice = 120mm) for absolute quantification, data acquisition was within one hour for each subject. With this acquisition time limit, the number of sets of N=24 label‐control image pairs acquired at equidistant and optimal sampling schemes was K=3 for one subject and K=4 for two subjects. For each subject, the control images, label images, and M _0t image were scaled with a single global scaling map, kept static for the duration of data acquisition, for bias field correction. The label images, control images, and M _0t image per subject were mutually aligned using mutual information motion correction. ⁴⁵ After registration, PCASL difference images were created by pairwise subtraction of label images from control images.

Perfusion parameters were estimated from the different sets of N=24 difference images with the same estimators as in the simulation experiment described in section 3.3. For absolute quantification, M _0b was approximated by M _0t/λ with λ=0.9. ¹ As NLE2 estimation and analysis of the results requires WM and GM tissue segmentation in the LR difference images, an LR WM and GM mask was calculated in a multi‐step approach. First, from the HR anatomical image, an HR WM and GM mask was obtained by means of multilevel image thresholding. ⁴⁶ From the HR tissue segmentation map, an HR GM and WM mask were isolated. Second, a geometrical transformation matrix was obtained from a multi‐modal intensity‐based registration between the HR anatomical image and the LR M0t image. Third, the geometrical transformation was applied to the HR GM and WM masks. Finally, as geometrically transforming an HR mask removes its binary character, voxels in the map resulting from the geometrical transformation of an HR mask were set to zero or one with 0.5 as a threshold to obtain an LR WM and GM mask.

Assuming underlying perfusion parameters remain constant within a single scan session, the repeated acquisition of the equidistant and optimized datasets allowed for a performance assessment of the different estimators. As there is no ground truth information, the accuracy of the estimators can only be judged relative to each other by comparing their sample means for a certain parameter. The precision of the estimators for f in GM was evaluated using a voxel‐wise and a slice‐based metric. As a voxel‐wise metric, the relative sample standard deviation $s(\widehat{f})$ was defined as the sample standard deviation divided by the sample mean. As a slice‐based metric, the Pearson correlation coefficient (PCC) between the estimates of f of two different runs within an axial slice of the brain can be determined. ⁴⁷ If there are K runs of the experiment, ${\sum }_{m=1}^{K-1}m$ PCCs can be determined for a single axial slice. This procedure was performed in ten axial slices.

4. RESULTS

The optimal acquisition settings for NLE3 are presented and analyzed in section 4.2. The accuracy and precision of NLE2 and NLE3 are compared by examining the results of the simulation and real data experiment in section 4.3 and 4.4, respectively.

4.1. Parameter identifiability analysis

The FIM condition numbers associated with NLE2 and NLE3 are summarized in Figure 1. These results clearly show that the NLE3 inverse problem is more ill‐conditioned. It is an indication that NLE3 will be more vulnerable to poor identifiability of parameters and low estimation precision compared to NLE2. Extracting maximal information in a certain total acquisition time by means of optimal experiment design can improve the conditionedness of the estimation problem of NLE3.

FIGURE 1.

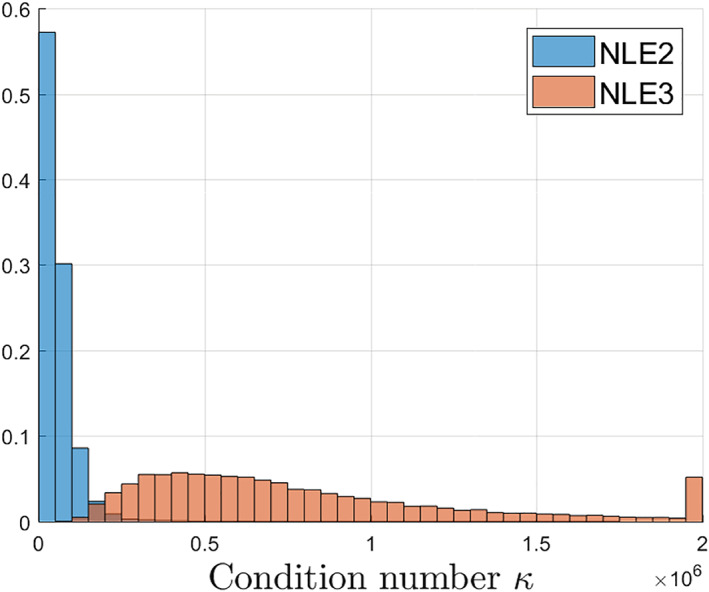
Distribution of the condition numbers κ(I(θ,t,τ)) of NLE2 and NLE3 for multiple parameter vectors θ randomly selected from the prior distribution p(θ), defined in Table 1, and assuming an N=24 equidistant acquisition scheme

4.2. Experiment design optimization

The optimization criterion value after optimization for different τ and N is shown in Figure 2. For a fixed labeling duration, increasing the amount of images adds information up to the point where optimizing acquisition times has to be balanced with the total acquisition time constraint. The minimum of this set of values is the final result of the optimization defined in Equation (8) for NLE3, which is reached for $Ñ=24$, $\tilde{\tau }=1.1$ s and a certain set of acquisition times $\tilde{\mathit{t}}$. These optimal acquisition settings are shown in Table 3, alongside the equidistant sampling scheme with τ=1.8 s used throughout this work. Note that the settings in Table 3 are described for real data acquisition, in accordance with the explanation in the final paragraph of section 2.1. More specifically, t _i is shorter than τ=1.8s for the first 8 acquisition times in the equidistant scheme. Therefore, images were acquired with adjusted labeling durations τ _s for these acquisition times. Furthermore, as scanner software imposed a lower limit of 100ms on the PLD in real data acquisition, the ninth acquisition time in the equidistant scheme and the first acquisition time in the optimized scheme were also acquired with a slightly shortened labeling duration (see Table 3). An example in a single voxel of data acquired with both acquisition schemes, accompanied by a fit of the perfusion model with the parameters estimated with NLE3, is shown in Figure 3.

FIGURE 2.

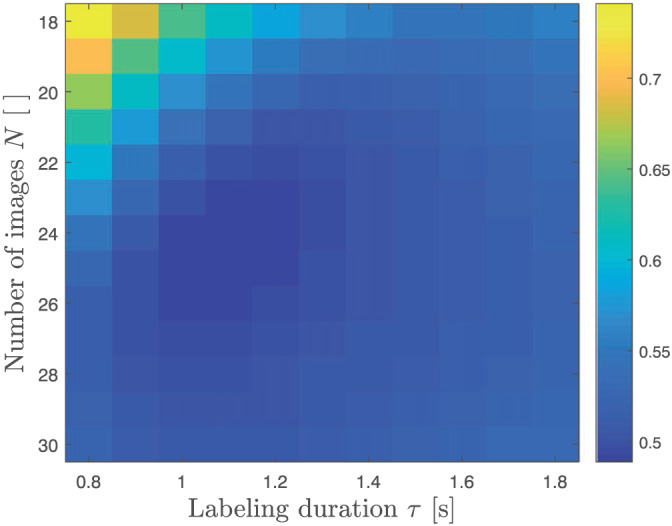
Minimal optimization criterion value associated with the optimal acquisition times $\tilde{\mathit{t}}$, for different combinations of τ and N. The minimum is located at $Ñ=24$ and $\tilde{\tau }=1.1$ s and corresponds with the optimal settings defined by Equation (8)

FIGURE 3.

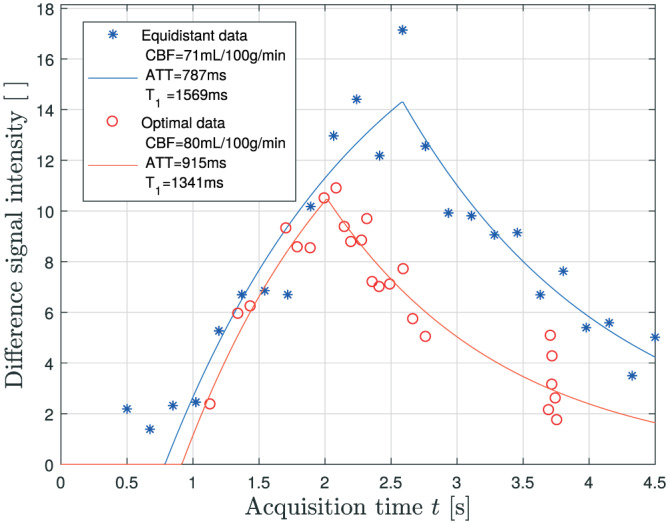
An example of PCASL difference data, acquired with the equidistant (blue asterisks) and optimal acquisition settings (red circles) described in Table 3, in a gray matter voxel of one of the subjects. The blue and red curve represent the NLE3 fit to the equidistant and optimal data, respectively

The distribution of the optimal acquisition times can be explained by examining the contribution of each possible acquisition time point to the Fisher information. The Fisher information for a single parameter ${\theta }_j^k$ at a single time point t _i, assuming Gaussian distributed data, is closely related to the FIM and is defined as ${\left(\partial g\right(t_i;{\mathit{\theta }}_j)/\partial {\theta }_j^k)}^2(1/{\sigma }^2)$. ²⁴ For f, Δt and $T_{1t}^{\prime }$, the Fisher information was calculated for each of the M=20000 parameter vectors θ _j at acquisition time points starting at 0 s and up to 6 s with increments of 1 ms. For each of the three parameter, the M Fisher information values were summed at each time point. Subsequently, for each parameter, the set of summed Fisher information values between 0 and 6 s were normalized to the maximum value. Assuming τ=1.1 s, the normalized summed Fisher information for f, Δt and $T_{1t}^{\prime }$ at each acquisition time point is shown in Figure 4. The optimal acquisition times are grouped into two distinct parts: a set distributed between 1 and 3 s and repeated measurements around 3.7 s. The distributed set coincides with the peaks of the Fisher information of the three parameters of NLE3 (Figure 4). The repeated measurements around t=3.7 s can be attributed to the local maximum in the Fisher information for $T_{1t}^{\prime }$. This shows that, despite of optimizing the acquisition settings for estimating f, the resulting optimal settings also include acquisition times that are of high importance for precisely estimating Δt and $T_{1t}^{\prime }$.

FIGURE 4.

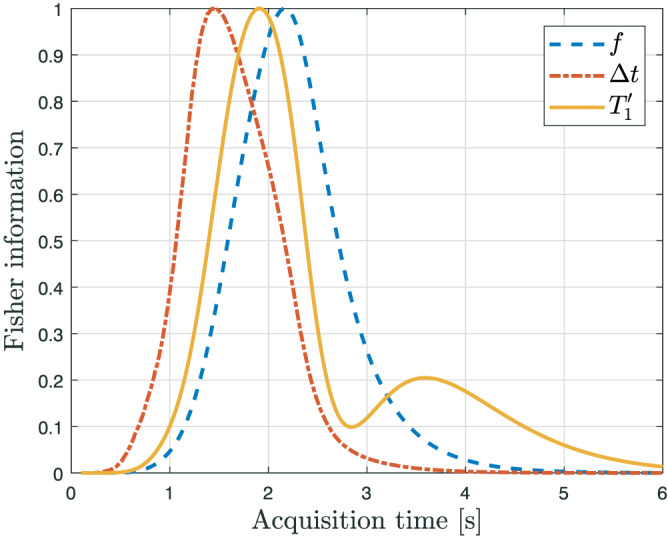
For each parameter of NLE3, the normalized summed Fisher information at each acquisition time point t _i, as defined in section 3.2, is shown. The Fisher information for a parameter θ _j of a single time point t _i, assuming Gaussian distributed data, is defined as (∂ g(t _i;θ)/∂ θ _j)²(1/σ ²). Maxima in the Fisher information correspond to acquisition times that contribute maximally to the estimation precision for that specific parameter

4.3. Simulation experiments

The results for the simulation experiment performed with an average SNR of 10 in GM, which is to be expected in background‐suppressed 3D GRASE real data, ⁴⁸ are summarized in Figure 5. The bias and standard deviation estimates of f for NLE2 and NLE3 in a slice of the simulated brain are shown in the first two rows of Figure 5.

FIGURE 5.

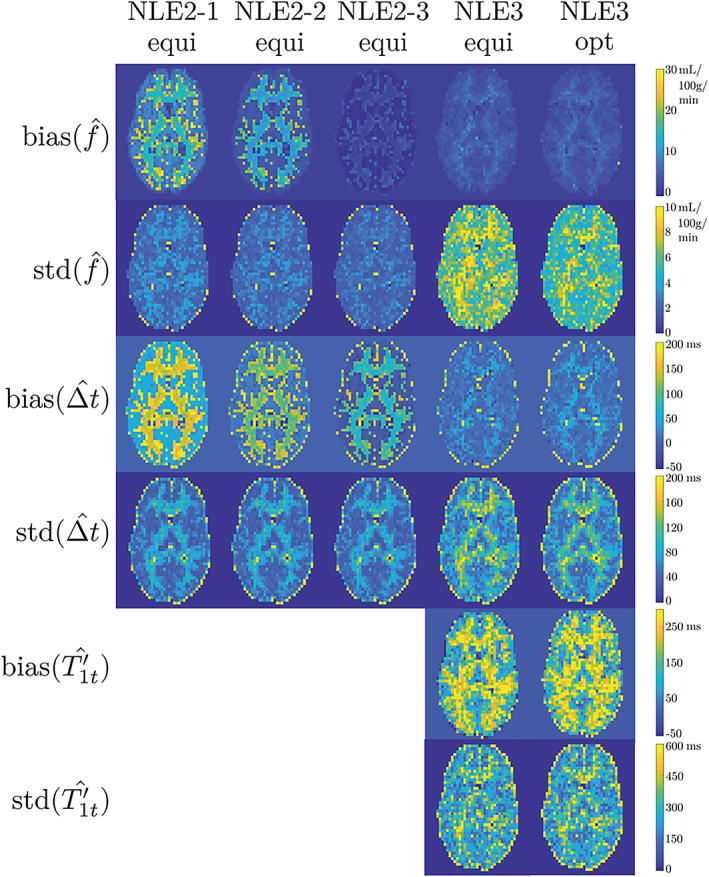
The first and second row show one and the same slice of, respectively, the estimated bias and standard deviation maps for the CBF obtained from simulation experiments for an average SNR of 10 in GM, as described in section 3.3. NLE2‐1, NLE2‐2 and NLE2‐3 refer to the different versions of NLE2 with $T_{1,\text{GM}}^{\prime }$ fixed at 1300, 1450 and 1600 ms, respectively. The ‘equi’ and ‘opt’ labels refer to whether the estimator was examined using the equidistant or optimal datasets. The third and fourth row, on the one hand, and the fifth and sixth row, on the other hand, show the estimated bias and standard deviation maps for the ATT and $T_{1t}^{\prime }$, respectively. Note that $T_{1t}^{\prime }$ is only estimated with NLE3

The bias of NLE2 depends strongly on the choice of fixed T _1t value. In WM and GM, the spatial mean value of f increases by 15% when the T _1t value is reduced by approximately 10%. Regardless of the T _1t choice, the bias of NLE2 is highest in voxels with PVEs on the edges between WM and GM. NLE3 is showing a bias in the estimation of f that is hardly substantial, even in voxels affected by PVE. In such PVE voxels, NLE3 finds $T_{1t}^{\prime }$ values between the $T_{1t}^{\prime }$ values it would find for voxels containing only WM and only GM. While the $T_{1t}^{\prime }$ value in such voxels has no physiological meaning, it allows NLE3 to accurately estimate f. Note that among the NLE2 estimators, NLE2‐3 with $\{T_{1,\text{WM}}^{\prime }=1.0\mathrm{s},T_{1,\text{GM}}^{\prime }=1.6\mathrm{s}\}$ has the lowest bias, while the underlying average values of T _1t are lower. This can be attributed to the creation of simulation data with a more accurate, more complex two‐compartment perfusion model with a prolonged stay of the labeled bolus in the blood compartment. Compared to the SCM, relaxation towards equilibrium of the labeled spins is governed for a larger percentage by T _1b in the two‐compartment model. Furthermore, the bias of NLE2‐3 is slightly lower than the bias of NLE3, except in voxels with partial volume effects. This is remarkable, because it is not possible for NLE2 to have a better goodness of fit than NLE3, knowing that both estimators use the same model, with NLE3 having a higher degree of freedom. It can be explained by the fact that the data was simulated with a more complex model than the estimation model. This makes it possible for NLE2‐3 to have a lower CBF estimation bias than NLE3, even though NLE3 provides a better model fit.

The standard deviation estimates of f show the expected superior precision of NLE2 compared to NLE3. The average gain in precision when estimating with NLE3 using optimally acquired data instead of equidistant data is 20%. Despite this improvement, the precision of NLE3 can still not compete with that of NLE2. Indeed, NLE2 and the optimized NLE3 have an average relative sample standard deviation of 9% and 19%, respectively.

The results for Δt and $T_{1t}^{\prime }$ are shown in the remaining four rows of Figure 5. Estimation of Δt follows the same overall trends as estimation of f, except for the fact that the average standard deviation for estimation of Δt with NLE3 is approximately equal when using equidistant or optimally acquired data. This is to be expected as the acquisition settings were optimized for the CBF parameter only. The bias maps for $T_{1t}^{\prime }$ show that NLE3 overestimates $T_{1t}^{\prime }$, which is compatible with the observation that NLE2 has the lowest bias for $T_{1t}^{\prime }$ values between the underlying $T_{1t}^{\prime }$ and T _1b. Furthermore, compared to f and Δt, the standard deviation for estimation of $T_{1t}^{\prime }$, relative to its underlying value, is significantly higher.

Besides for an SNR of 10 in GM, the simulation experiment was also repeated for an SNR of 15, 20 and 25 to assess how estimation accuracy and precision of NLE2 and NLE3 change as a function of SNR. The average relative estimation bias and average relative standard deviation for GM for the considered SNRs are shown in Figure 6. In terms of estimation accuracy, there were no significant differences between the different SNRs (Figure 6a). In terms of precision, an SNR of 20‐25 is necessary for the NLE3 in optimized conditions to match the average standard deviation of NLE2 at an SNR of 10 (Figure 6b). Assuming that doubling the total acquisition time to acquire another repetition of the data set increases the SNR of the data set with a factor $\sqrt{2}$, the acquisition time would need to be increased with a factor of 4 to 6.25 in order for estimation with NLE3 to be as precise as estimation with NLE2, considering their precisions are equal for an SNR of 10 and 20‐25, respectively.

FIGURE 6.

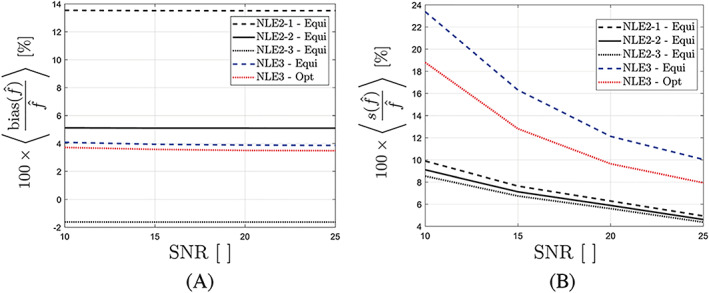
The average relative bias (a) and average relative standard deviation (b) for CBF estimation in GM as a function of the average SNR obtained from simulation experiments described in section 3.3. Results are shown for NLE2 using equidistant data, and NLE3 using equidistant and optimal data

4.4. Real data experiments

The estimates of f for the different runs, for one subject, are shown in Figure 7. Two important features can already be observed qualitatively. Firstly, similar to the observation in the simulation experiment, estimation values of f increase as T _1t is fixed to a smaller value. Secondly, NLE3 produces more physiologically unrealistic results, especially in white matter. All voxels with f>120 mL/100g/min were filtered out, resulting in f maps that are more sparsely filled. The SNR in white matter is too low to estimate f with reasonable precision from 24 multi‐PLD difference signals with NLE3.

FIGURE 7.

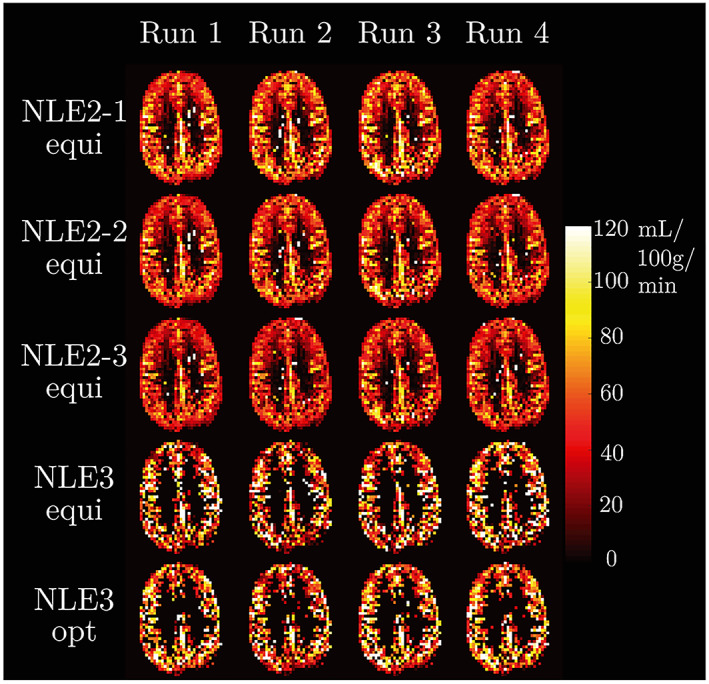
For one subject, f maps are shown resulting from applying NLE3 and three versions of NLE2 to the equidistant data subsets and NLE3 to the optimal data subsets. Only voxels with an f<120 mL/100g/min were retained. For NLE2, WM and GM voxels were differentiated using a segmentation map created from an acquired HR anatomical image

For all subjects and every estimator, the spatial mean and standard deviation are shown for the different perfusion parameters in GM (Table 4). For each subject, an increase of 150 ms in NLE2‐T _1,GM value causes a decrease of 7% to 10% in spatial mean estimate of f (first three rows of Table 4a). These results confirm the dependence of NLE2 on the choice of a fixed T _1t value for estimation of f. A similar decrease is seen for Δt, however limited to 1% to 3% (first three rows of Table 4b). The spatial mean estimates of f and Δt obtained with NLE3 from equidistant and optimal data (final two rows of Table 4a and 4b) lie within the range of the results of the different versions of NLE2. Furthermore, for f, the difference in spatial mean estimate value, obtained from using NLE3 on equidistant and optimal data, respectively, is limited. However, the mean $T_{1,\text{GM}}^{\prime }$ results for NLE3 (Table 4c) are high compared to most literature values of T _1,GM, ¹⁰ knowing that the difference between $T_{1t}^{\prime }$ and T _1t should only be about 1%. ⁸ Note that this overestimation of $T_{1t}^{\prime }$ can be partly due to a prolonged stay of labeled spins in the blood compartment, which is not correctly accounted for in the SCM. ⁹ , ¹⁶ Also, the spatial standard deviation for $T_{1,\text{GM}}^{\prime }$ is very large, indicating NLE3 is not reliable for $T_{1t}^{\prime }$ estimation. It is noteworthy that all these results are in agreement with the trends observed in the simulation experiments in section 4.3.

TABLE 4.

For each subject, the spatial mean and standard deviation of the parameters in GM are shown per estimator

	S1	S2	S3
NLE2‐1‐equi	51.7±19.4	52.1±19.2	50.4±18.2
NLE2‐2‐equi	47.6±18.1	48.2±17.9	46.6±17.1
NLE2‐3‐equi	44.1±17.0	44.7±16.7	43.4±16.1
NLE3‐equi	47.7±21.6	49.7±20.1	48.4±20.4
NLE3‐opt	48.4±21.2	50.6±19.9	47.1±20.5
	(a) $\widehat{f}$ in GM [mL/100g/min]
NLE2‐1‐equi	708±360	847±457	1230±575
NLE2‐2‐equi	686±358	827±460	1203±575
NLE2‐3‐equi	664±354	811±458	1181±577
NLE3‐equi	631±266	830±390	1145±453
NLE3‐opt	709±241	855±435	1205±387
	(b) $\widehat{\Delta t}$ in GM [ms]
NLE3‐equi	1687±732	1855±926	1873±914
NLE3‐opt	1529±619	1901±927	2025±1078
	(c) $\widehat{T_{1t}^{\prime }}$ in GM [ms]

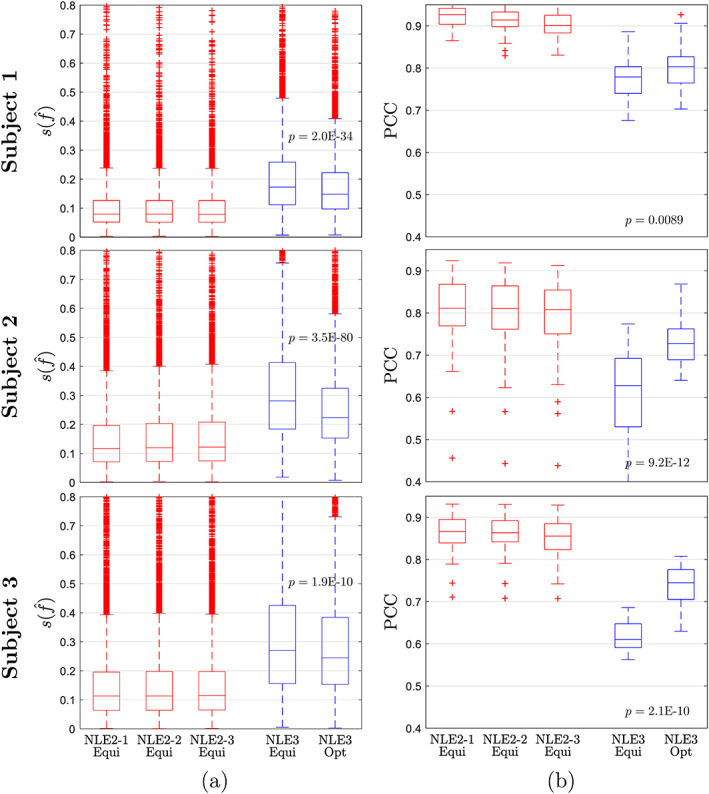
The distribution of $s(\widehat{f})$ within GM for every estimator and every subject is shown in Figure 8a. Similarly, for each subject and each estimator, the PCCs for f are grouped and compared in Figure 8b. The relative sample standard deviation and PCC metric show compatible results. Firstly, NLE3 performs at a significantly higher precision when applied to optimal data compared to equidistant data. Non‐parametric Kruskal‐Wallis (KW) tests comparing the sets of $s(\widehat{f})$ for both data types show a significantly lower median $s(\widehat{f})$ in the optimized experiment for all three subjects. Similarly, KW tests demonstrate a significantly higher correlation between test‐retest results in the optimized experiment. Secondly, not surprisingly, both metrics show that NLE2 operates at a precision unattainable for NLE3, even in optimized conditions.

FIGURE 8.

Boxplots of (a) the relative sample standard deviations $s(\widehat{f})$ in all GM voxels and (b) the per‐slice PCCs for f. Each boxplot shows the results for a certain estimator applied to data of a certain subject. A non‐parametric KW test comparing the results of NLE3 for equidistant and optimal data was performed. The p‐values related to the KW test are shown between the respective boxplots

Note that NLE2 achieves an median relative precision between 7 and 12% for f estimation (first three boxplots for each subject in Figure 8a), while for NLE3 in optimized conditions it ranges from 15 to 25% (last boxplot for each subject in Figure 8a). Contrary to the slice‐based metric, the relative sample standard deviation provides quantitative results on the precision of an estimator. To the best of our knowledge, no such results have been previously reported on CBF estimation in multi‐PLD PCASL.

5. DISCUSSION AND CONCLUSIONS

In this paper, the accuracy and precision with which perfusion parameters can be estimated from multi‐PLD PCASL data, using a single‐compartment model, were studied. A two‐ (NLE2) and three‐parameter (NLE3) estimator were compared, where the only difference between both estimators was whether $T_{1t}^{\prime }$ was fixed at a certain value or estimated alongside the perfusion parameters, respectively. As the total acquisition time for each multi‐PLD PCASL imaging sequence was 5 to 8 minutes and recommendations regarding spatial resolution were respected, the reported statistical quantitative measures are representative for a clinically feasible multi‐PLD PCASL experiment.

A major part of this work consisted of optimizing the acquisition settings of NLE3 in order to maximally compensate for the expected drop in precision caused by the addition of an extra parameter compared to NLE2. In PCASL, acquisition times can be optimized for a certain labeling duration or they can be optimized simultaneously. Furthermore, a choice can be made to either allow acquisition times t _i ≤ τ or conversely only allow t _i ≥ τ, which de facto becomes an optimization of the PLDs only. ⁴⁹ In the present work, optimal acquisition times t were searched for different labeling durations τ, while allowing t _i ≤ τ. Compared to only optimizing the PLDs, this optimization approach pushes the boundaries of the multi‐PLD PCASL experiment to higher levels of estimation precision. Simulation and real data experiments showed an increase of 10 to 20% in precision for NLE3 in optimized conditions compared to conventional equidistant acquisition settings. In terms of precision, however, NLE3 in combination with an optimal acquisition scheme is still no match for NLE2. More importantly, the median relative CBF precision for the optimized NLE3 was still as high as 15‐25% in real data experiments. This level of reproducibility is unacceptable in a clinical setting.

The NLE2 had a higher precision with a median sample standard deviations in the real data experiment between 7 and 12%. However, the simulation and real data experiments clearly showed a dependence of CBF estimation on the choice of fixed $T_{1t}^{\prime }$ value. A reduction of approximately 10% in $T_{1t}^{\prime }$ value for GM resulted in an average CBF value increase of 15% in the simulation experiment and 7‐10% in the real data experiment. Note that these results are relative, comparing versions of NLE2 with different fixed $T_{1t}^{\prime }$ values. The simulation experiment showed that the largest inaccuracies are to be expected at the edges between two tissue types. Inaccuracies related to PVE will be present for any NLE2 estimator, independent of the fixed $T_{1t}^{\prime }$ choice. Therefore, NLE2 in combination with a fixed $T_{1t}^{\prime }$ value is inherently inaccurate. However, the simulation experiment showed that CBF estimation bias in NLE2 is lowest for a fixed $T_{1t}^{\prime }$ value in between the true underlying $T_{1t}^{\prime }$ and T _1b value, reflecting the prolonged stay of the labeled bolus in the blood compartment in the more accurate two‐compartment model.

The optimization of PCASL acquisition settings described in sections 2.3 and 3.2 for NLE3 was also repeated for NLE2. The theoretical gain in precision compared to estimating with NLE2 using equidistant settings was found to be of the same order as for NLE3 using the optimized settings compared to the equidistant acquisition strategy, in simulations as well as in real data experiments. These results were not included in this work as they have no impact on which estimator performs better. It was shown in simulations that NLE2 and NLE3 perform approximately equally well in terms of bias when an appropriate fixed T1t value is chosen for NLE2. In terms of precision, NLE3 in optimized conditions still had a significantly lower precision than NLE2 using equidistant data. As the performance balance in terms of accuracy and precision is already tipped in favor of NLE2, further increasing the precision of NLE2 by means of experiment design is not vital for the comparison between NLE2 and NLE3.

It is important to note that, next to $T_{1t}^{\prime }$, other parameters in the SCM (i.e., T _1b, M _0b and α) can also cause inaccuracies due to a difference between the fixed or determined value and the true underlying value. It should however be stressed that T _1b, M _0b and α are not good candidates to estimate voxel‐wise alongside the CBF and ATT, contrary to $T_{1t}^{\prime }$. The CBF, T _1b, M _0b and α are not independently identifiable in the SCM (see Equation 1). An alternative would be to estimate α and T _1b from data obtained in separate MRI experiments, ⁵⁰ , ⁵¹ similarly to how M _0b is estimated from a proton density image. Which one of these parameters has the highest possible impact on CBF quantification accuracy deserves further study. On top of that, the SCM is inherently biased as it is an approximation of the underlying physical perfusion process. Therefore, even with exact knowledge of all fixed parameters, CBF and ATT estimation will remain biased to a certain degree.

Replacing the SCM by a more complex (i.e., more accurate) model could be a viable option. Multiple studies have improved upon single‐compartment models in terms of a more accurate representation of the evolution of the ASL signal. Accounting for a finite permeability of the capillary wall to water diffusion in a two‐compartment model, ⁹ , ⁴³ incorporating a prolonged stay of labeled water in arterial microvasculature after arriving in the imaged voxel, ⁵ , ⁵² allowing a change of concentration of labeled water as a function of time ⁴³ and correcting for dispersion of the labeled bolus ⁵³ are the most notable developments. Unfortunately, extra parameters are introduced in these models. This work has made clear that it is not a feasible option to estimate extra parameters alongside the CBF and the ATT within the boundaries of data acquisition at the recommended spatial resolution and a limited total acquisition time. Hence, extra parameters need to be fixed to certain literature values, which again introduces inaccuracies, or have to be obtained from other experiments, which prolongs the total acquisition time. The only case in which another model might improve upon the SCM in terms of estimation accuracy and precision, is if estimation of only the CBF and the ATT with this model is less susceptible to fixing certain parameters in the model. Future work will focus on finding and testing suitable candidate models. The simplified solution to the two‐compartment model neglecting backflow, as proposed by Parkes et al, ⁹ could be such a candidate.

In conclusion, it is shown that T _1t plays a central role in quantification of CBF from multi‐PLD PCASL with the single‐compartment model. Fixing $T_{1t}^{\prime }$ to a certain value may cause a significant bias when estimating the CBF and the ATT with NLE2. Estimating $T_{1t}^{\prime }$ alongside the CBF and the ATT with NLE3 is too detrimental to the precision, even with optimized acquisition settings. One may raise the question: is it at all possible to estimate the CBF with sufficient accuracy and precision while using the single‐compartment model? Regarding precision, the experiments presented in this paper clearly indicate that NLE2 is the only viable option within the limits of a reasonable total acquisition time and a recommended spatial resolution. ¹ Despite the dependence of NLE2 CBF estimation on the $T_{1t}^{\prime }$ choice, simulation experiments suggest that fixing $T_{1t}^{\prime }$ in between the population average of T _1t for either WM or GM and the population average of T _1b minimizes the risk of a systematic bias in CBF estimation. Therefore, CBF estimation from multi‐PLD PCASL data acquired at the recommended ¹ spatial resolution with NLE2 using such prolonged fixed $T_{1t}^{\prime }$ values provides the optimal balance between accuracy and precision.

Bladt P, den Dekker AJ, Clement P, Achten E, Sijbers J. The costs and benefits of estimating T ₁ of tissue alongside cerebral blood flow and arterial transit time in pseudo‐continuous arterial spin labeling. NMR in Biomedicine. 2020;33:e4182 10.1002/nbm.4182