Abstract
Natural disasters may have catastrophic and long‐lasting impacts on communities' physical, economic, and social infrastructure. Slow recovery of educational services following such events is likely to cause traumatic stress in children, lead families to out‐migrate, and affect the community's overall social stability. Methods for quantifying and assessing the restoration process of educational systems and their dependencies on other supporting infrastructure have not received adequate attention. This study introduces, for the first time, a new framework to evaluate the functionality, recovery, and resilience of a school system following severe earthquake events. The framework considers both the quantity and quality of education services provided, school enrollment, and staff employment, as well as the interaction between various agents such as staff, students, parents, administration, and community. A virtual testbed community, Centerville, is utilized to highlight the application of this framework. The impact of school reopening policies on the number of students enrolled as well as the potential for homeschooling is also considered. The availability of various enrollment alternatives for students, backup classroom space and functioning utility systems, and facilitation of staff and supplies transfer between schools substantially increase the resilience of the education service.
Keywords: community resilience, earthquakes, educational policy, functionality, recovery, school systems
Key Points
A new framework is devised to estimate the resilience and functionality of K‐12 schools after earthquakes
The framework considers the role played by the society on maintaining the schools' functionality
A Markov chain stochastic model, coupled with dynamic optimization, is used to model the near‐optimal school recovery trajectory of the schools
1. Introduction
Earthquakes pose a potential threat to the social and economic stability of many communities. With children being among those most vulnerable to natural disasters (Fothergill, 2017; International Finance Corporation [IFC], 2010; Norris et al., 2002), the consequences of such extreme hazard events on schools and educational services are likely to be severe. Despite their importance to the community, especially in maintaining a sense of normalcy to children and their parents, schools often suffer significant physical damage and reduction in functionality after major earthquakes (Rodgers, 2011). In some cases, substantial injuries or loss of life has resulted from school building damage or collapse (Applied Technology Council, 2017; Fujieda et al., 2008). For instance, the 1989 Loma Prieta earthquake caused significant damage to three schools in San Francisco, Watsonville, and Los Gatos (EERI, 1990). The 1995 Kobe earthquake damaged approximately 4,500 schools, and even though no school‐related fatalities were recorded, full recovery of normal educational function required 10 years (Nakano, 2004). The impact of severe earthquakes on school systems in less‐developed countries can be even worse, with significant destruction, injuries, and loss of life in school systems, which are key institutions in social and economic development (Applied Technology Council, 2017; Asian Development Bank and World Bank, 2005; Government of Nepal [National Planning Commission], 2015; Green & Miles, 2011; Kabeyasawa et al., 2014).
A large number of schools are vulnerable to earthquakes in the United States (American Society of Civil Engineers, 2017; Applied Technology Council, 2017; Rodgers, 2011). There are approximately 56.6 million students attending K‐12 schools, employing around 3.7 million teachers (National Center for Education Statistics [NCES], 2019). Despite their importance to a community, schools typically are designed for Risk Category III, as per ASCE 7–16 (2016), with seismic importance factors of 1.25 as opposed to other essential facilities, such as hospitals, police stations, and fire stations, which are assigned a higher risk category (IV) (Hancilar et al., 2014). Various national plans and extensive retrofitting strategies have been introduced to enhance the safety of existing schools and reduce their vulnerability (Federal Emergency Management Agency, 2002; Fujieda et al., 2008; Nakano, 2004). For example, the Federal Emergency Management Agency (FEMA) has issued a series of reports to address the impact of different natural hazards on schools and provide strategies to enhance their performance during and following hazard occurrence (Applied Technology Council, 2017; Federal Emergency Management Agency, 2002, 2010, 2012). Furthermore, natural disasters impact not only school buildings but also the academic performance of students (Osofsky et al., 2009). Therefore, ensuring quick restoration of educational facilities and services is an essential component of the community recovery process. Reopening schools and restoring a sense of normalcy within the community can help schoolchildren recover from a major disaster and can minimize disruption to families as a whole (American Academy of Pediatrics, 2019).
Schools also play a crucial rule in societal stability before and after disasters especially for school children and their families (National Research Council (US) Panel to Review the Status of Basic Research on School‐Age Children, 1986; Ungar et al., 2019). Many studies have investigated the impact of natural disasters, including earthquakes, on the developmental and behavioral resilience of children (Masten et al., 2015; Masten & Narayan, 2012; Masten & Osofsky, 2010; Raccanello et al., 2017). These studies highlighted the fact that children's exposure to disastrous events will severely impact their adaptation to life following major events. Furthermore, measuring the impact of these events on individuals' behavior requires an understanding of the relationship between these individuals and other community systems that provide essential services including schools (Masten et al., 2015). Accordingly, including the cascading impact of earthquake disasters on physical infrastructure in communities is essential for quantifying this impact (Masten, 2018; Ungar, 2018). However, analytical methods geared toward quantifying this cascading impact are lacking, and more studies are needed to bridge the gap in linking children's developmental resilience and the functionality of school systems after disasters.
Elementary and secondary (K‐12) schools generally can be classified as either public or private schools. State regulations govern school operations, depending on the school type; these include the presence of qualified staff, proper space, and sufficient supplies and services. However, following extreme natural hazard events, many districts allow schools to run without supporting infrastructure for a limited time, provided that these schools are safe for students and staff (Balingit, 2017; Rundquist, 2012). Different options for delivering education also exist; one of these options is homeschooling, which allows parents to teach their children from home. Previous studies have focused on measuring the performance of schools during normal operating conditions (Mayer et al., 2000; National Research Council, 2012) while other studies pertained to performance during and after earthquakes (Augenti et al., 2004; Beaglehole et al., 2018; Oyguc & Guley, 2017). However, these studies did not introduce models that could be used to predict school functionality after extreme natural hazard events, such as earthquakes. Models that include quantitative representations of different components of a typical school, specifying a service component of functionality, and accounting for the mutual interaction between schools and their supporting lifelines are required for full functionality assessment.
This study presents a new framework to estimate the resilience and functionality of K‐12 schools after earthquakes and to assess how their performance impacts the social stability of communities. The framework considers the role played by parents, teachers, and administrative personnel on maintaining the functionality of schools while accounting for interdependence between schools and their supporting lifelines. The quantity and quality of educational services are quantified in terms of the schools' enrollment capacity at each grade and the class capacity combined with the student academic and social outcomes, respectively. A Markov chain stochastic model, coupled with dynamic optimization, is used to model the near‐optimal school recovery trajectory while considering limitations in repair resources and appropriate repair sequences. The framework is tested on a school network located in the Centerville virtual community (Ellingwood et al., 2016) subjected to two different earthquake scenarios.
2. Factors Affecting Educational Services
K‐12 education services are aimed at providing schoolchildren with appropriate academic and social experiences and training. A complex set of factors and their interactions influence the functionality and success of the educational system within a community in achieving these goals, as shown in Figure 1. School functionality represents the ability of a school to provide the desired level of educational services. School buildings provide essential space for teachers, administrative staff, and community volunteers to provide educational services to students. The continued availability of this space requires that damage to structural and nonstructural components, as well as building contents, be kept to an absolute minimum and those essential utilities, such as power, water, and sewer, be available. Since students in a typical community attend different school grades, the continued availability of all K‐12 grades in a school is crucial to reduce the potential for community outmigration for students and their families (Hinojosa et al., 2019). Finally, most students require transportation to reach school, which is provided by either school buses or private transportation. A set of national and local regulations must be followed in school management. These regulations differ based on the school type and require the availability of qualified staff, proper space and sufficient supplies and services. In the case of a school closure, different alternatives may be offered to students, which are determined based on the school policy and regulations.
Figure 1.
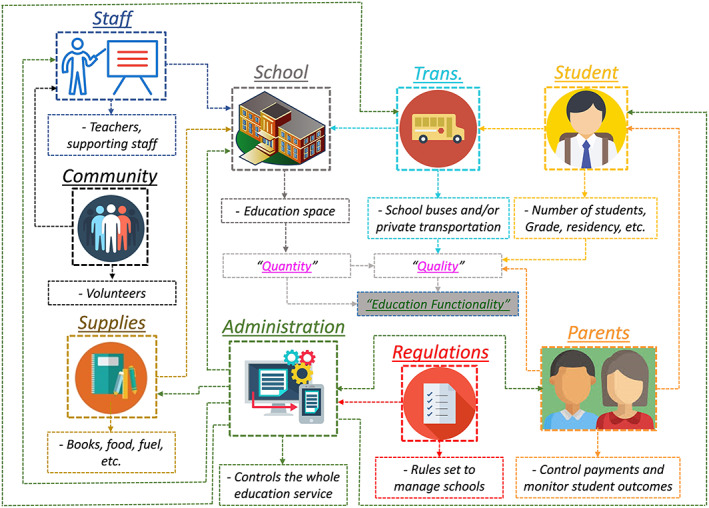
Components of educational services.
In normal conditions, student enrollment is based on the school zone. The selection of these zones depends on school capacity and the expected number of students within the zone. Some parents may select a different school for the students; however, school transportation is commonly limited to the students living in that zone. Following natural disasters such as earthquakes, some students might transfer to other schools as a consequence of school damage. In this situation, schools might increase class capacity or reduce the transportation service, or in some cases totally suspend it, due to damage to roads, shortage in staff, or damage to buses. Schools can also be used as temporary shelters, or as centers for community disaster relief (Singh, 2019) and recovery coordination (Applied Technology Council, 2017; Fujieda et al., 2008). Using schools as shelters is, however, a function of the disaster occurrence time, space availability, and school building safety. For instance, educational services are impacted by earthquakes differently during the academic year than when school is not normally in session.
In the following section, we build a model of postdisaster school functionality and recovery around the basic considerations introduced above. This model is focused on public schools, which enroll approximately 90% of K‐12 students in the United States.
3. Framework for School Functionality and Recovery
To measure the functionality of the educational services, two main indices are widely used: service availability (UNESCO, 2019) and quality of the education providers (Mayer et al., 2000). In this study, these two indices are combined to form a comprehensive measure of the educational service. The expected value of the total functionality of the education service, E[S], at any time, t, within a community can be mathematically calculated, including the correlation between quantity, S V, and quality, S S, of the service, or approximated using weighted geometric means, as shown in Equation 1. The weighted geometric mean is a common method to aggregate social indicators (U.S. Department of Education [Office of Innovation and Improvement], 2009).
| (1) |
in which α V and α S are weighting factors for quantity and quality. The short‐term functionality depends on the quantity of basic educational services that can be provided. Over the long term, however, the total functionality depends, in addition, on the quality of the service. The quantity can be measured by enrollment capacity and class size, which depend on the performance of schools' physical infrastructure, availability of staff, supplies, and supporting lifelines. On the other hand, the quality can be measured by combining different indices related to teachers' credentials and experience, classroom amenities, and school context (Mayer et al., 2000). Some of these parameters can be impacted significantly in the aftermath of an earthquake. For instance, outmigration or dislocation of professional staff might affect teachers' assignments, which could negatively impact the quantity and quality of the delivered education. Moreover, damage to structural and nonstructural components and to building contents, as well as the damage to the schools' supporting lifelines, might increase the class size.
3.1. Quantity Index
Staff, space, and supplies availability are the main components of the schools' post‐hazard quantity measure. The school staff includes teachers, supporting staff, and administrative staff as well as community volunteers. Appropriate space for students entails having a safe structure, reliable nonstructural components, and functioning contents (desks, computers, etc.). Schools also require various utilities (water, power, wastewater, and drinkable water), as well as infrastructure (transportation and telecommunication) to operate. Some schools are equipped with backup utilities. Books and other educational materials, food, fuel, and other supplies are also vital for operation. The probability of school seat availability for students can be estimated using the success tree shown in Figure 2. This success tree is composed of various events, each of which is assumed to be statistically independent. It describes the functionality of not only the school building itself but also the surrounding community's physical, economic, and social infrastructure. Similar to previous studies (Hassan & Mahmoud, 2019; Nozhati et al., 2019), the availability of each basic event is described by appropriate probabilistic mathematical functions. The basic events in the success tree analysis are connected using AND/OR gates to calculate the probability of top and intermediate events. Probabilities for these gates are calculated using Equation 2, where P OR and P AND denote AND and OR gate operations, respectively; P i refers to the basic event (i) probability; and n is the total number of considered basic events.
| (2) |
Figure 2.
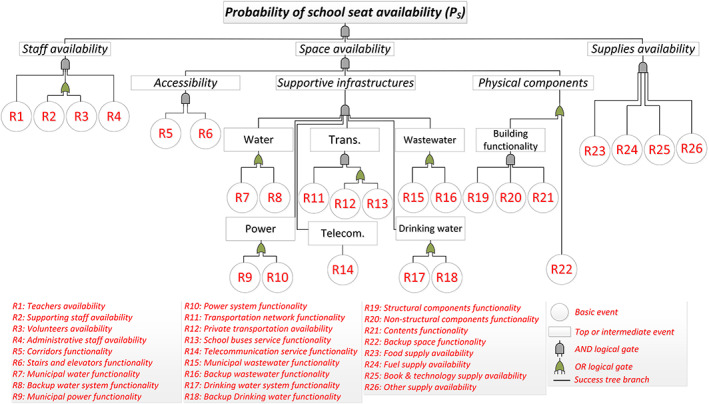
Success tree for determining the availability of seats in the school.
The probability of staff availability, P (ST i(t)), for each grade, i, at a time, t, after an earthquake occurrence is estimated as the union of events that the school staff is available, as given by:
| (3) |
where is the jth event for the ith grade considered and N is the total number of events. This equation is utilized to calculate the staff availability, R1, R2, and R4, which are related to staff casualties and trauma and are expected to be impacted immediately after an event as a result of the direct social losses, L DS. Other factors also can influence staff availability during the recovery time such as staff appointments (permanent and temporary), ST add; volunteer staff, ST vol; staff dislocation, ST dis; and staff personal responsibilities and commitments, ST dif. Volunteers from the community, R3, can temporarily fill the gap for the required supporting staff, R2. The availability of R3 is a function of the investigated community.
School space functionality considers school accessibility, the functionality of supporting infrastructure, and the availability of appropriate working space. Accessibility, R5 to R6, accounts for the corridor, stairs, and elevator functionality after the earthquake. School accessibility might be influenced by damage to structural and nonstructural components, which can block the corridors and impact the safety of stairs and elevators. School‐supporting infrastructure includes water, R7; power, R9; transportation, R10; telecommunication, R14; wastewater, R15; and drinking water, R17. School physical entities, commonly classified into structural, R19; nonstructural, R20; and content, R21, are taken into account as physical school building components. During the earthquake, damage can be quantified in these components based on building fragilities, which describe the probability of reaching a certain damage level for a given hazard intensity. The framework also considers the availability of backup space, R22, such as using a different building or turning other rooms in the school into classrooms.
School supplies include food for students, staff, and teachers, R23; fuel for heating, R24; books and technology supplies essential to a classroom, R25; and other supplies, R26. The availability of these supplies depends on the availability of suppliers, transportation, and storage.
The index of quantity functionality after an earthquake is given by the expected number of available seats for students at grade i in each school, which is calculated using the probability of school seat availability, P s. Equation 4 shows the expected value of education quantitative index, S V:
| (4) |
in which N i is the total number of seats at grade i and I g is the number of grades.
3.2. Quality Indices
The quality of the educational services that can be provided may be impacted after major disasters as a consequence of a shortage of teachers, staff, space, and supplies. The framework combines various quality measures including teacher assignment, T a, and experience, T e, as indicators of teacher quality; class size, C s, and technology, C t, as indicators of classroom quality; and leadership, S l, and professional community, S pc, as indicators of school quality as shown in Equation 5:
| (5) |
in which the α terms are weighting factors represent the importance of each quality measure. Combining these indicators can be used as a quality index, S S, of the education service mentioned in Equation 1.
Teacher quality, including teacher assignment and experience, can seriously be affected by staff shortages, difficulties in finding qualified staff, and a shortage of qualified community volunteers. Teacher assignment is evaluated as:
| (6) |
in which the required staff, ST i,req, varies with the number of students enrolled, N i(t), and the class capacity, R i(t):
| (7) |
The probability of finding alternative staff, P (ST alt), is shown in Equation 8 as a function of the required staff and available staff to hire, ST avl. However, it is probable that this replacement staff may be less qualified, P (ST unq), than the permanent staff, as shown in Equation 9.
| (8) |
| (9) |
Teacher experience is calculated as the ratio between the experienced staff and the total staff, ST i(t):
| (10) |
Teacher experience is mainly impacted by the percentage of teachers who are either appointed, transferred, or volunteered after the earthquake, and they have a lack of experience. The expected value of inexperienced teachers is calculated from the conditional probability of a new teacher joining the school staff, ST add, and does not have enough teaching experience, ST mis:
| (11) |
Larger class size and lack of technology can seriously impact class quality. The classroom size is measured as a ratio between existing, R(t), and normal, R(0), teacher‐to‐student ratios, considering maximum acceptable class capacity, R max as shown in Equation 12. The maximum acceptable capacity is assumed to be a function of the school regulations and community norms. The mean value of the classroom sizes for all grades is utilized to express the overall school's classroom quality as shown in Equation 13.
| (12) |
| (13) |
The ratio between the current technology availability, T(t), and the technology before earthquake occurrence, T(0), is used as an index for classroom technology, as shown in Equation 14. This technology will be impacted after an earthquake as a consequence of building contents damage, L C, and deficiencies in essential utilities, U, for classroom technology, such as power and telecommunication as shown in Equation 15.
| (14) |
| (15) |
The absence of effective leadership in the aftermath of an extreme natural event also impacts school quality. The leadership availability is represented before the earthquake, l(t), as well as following earthquake occurrence, l(0) as shown in Equation 16. In this study, school administration, ST admin, and experienced faculty, ST lp, control the quality of leadership, as defined by Equation 17. The appointment of less‐qualified teachers, as well as turnover in teaching staff, can negatively impact the relationship between teachers and their students and eventually reduce student outcomes.
| (16) |
| (17) |
The availability of the professional community is estimated as the ratio between the current professional community, p c(t), and its value before the earthquake, p c(0), as shown in Equation 18. Appointing unqualified teachers, ST unq, and the teacher change events, ST ch, are utilized as an indicator of the professional community as shown in Equation 19.
| (18) |
| (19) |
3.3. School Administration Model
The decisions that the school administration makes after disasters to maintain the school's functionality can make an enormous difference in the resilience of a school system. To mimic the role of school managers in the decision‐making process, decision support frameworks are introduced that model the main decision processes, including the students' admission and transfer, staff appointment, and community engagement. Figure 3 shows the framework for students' admission and transfer in which different schools and transportation options are considered. The framework also considers the role played by parents in terms of school selection, funding, transportation, and homeschooling.
Figure 3.
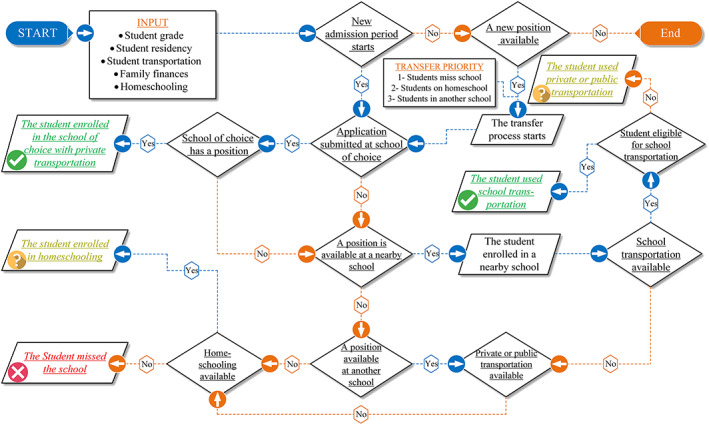
Students' enrollment and transfer process framework.
The decisions to reopen damaged schools after major disasters involve the school district, school administrators, the building and fire departments, office of public safety, and the community (U.S. Department of Education, 2007). In this study, we consider three cases. In the first, schools can be partially opened using backup spaces during the recovery stage to provide education for a limited number of students (Decision I) (Bounds, 2014). In the second, where schools are not provided with backup spaces, they can only reopen if they are repaired (Decision II). Finally, in the third, schools might stay closed until all buildings are fully functional (Decision III) (U.S. Department of Education, 2007). The first and second cases might reduce the total number of students who are in temporary classrooms, being homeschooled, or missing school, but they require high levels of coordination between the school administration, parents, and students to ensure equitable temporary student placement. School districts often work with the community to find temporary classrooms for students and professional staff after disasters (U.S. Department of Education, 2007).
A similar process simulates staff appointment (temporary, part‐time, and permanent) and transfer between schools, as shown in Equations 20–22.
| (20) |
| (21) |
| (22) |
Staff appointment or transfer is assumed to take place only where space and supplies are sufficient to accommodate additional staff and the existing staff, ST, are less than the required, ST req. Additionally, staff appointment is a function of having available human resources, E hr; the staff matching the school needs, E ma; and the funding availability, E fu. The probability of staff transfer between school m and n is calculated based on the willingness of the school district to transfer the staff between schools, E w, and the school m staff accepting a transfer, E tf, and the transferred staff will match the need of school n, E ma. The approach of an individual school to solve the staff shortage problem is shown in Figure 4, which starts with using the existing staff within the school, for instance, by assigning more teaching loads for teachers while assigning volunteers to substitute the supporting staff. In case the existing staff and volunteers are not enough (ST req > ST), schools could request staff transfer from other schools within the school district. If the school district cannot provide all required staff due to the fact that no staff is available to transfer (ΣST req > ΣST), schools can then appoint temporary and part‐time staff to close the gap in staff shortage. Later, those temporary and part‐time staff can be replaced with permanent, more qualified, and more experienced staff to increase the quality that is expected to be impacted by hiring temporary and part‐time staff with fewer qualifications.
Figure 4.
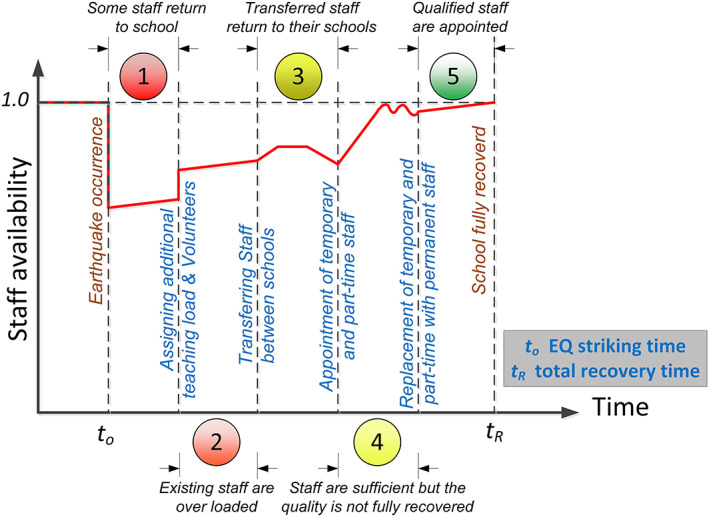
Staff shortage appointment approach.
Schools can also transfer supplies and resources to reduce the impact of the earthquake consequences on the school system. Equation 23 shows the expected amount of supplies that can be transferred.
| (23) |
in which
| (24) |
The probability that the supplies are transferred is assumed to be a function of an established agreement, E ag; availability of transportation between school m and school n, E tr; and the supplies matching the school need, E ma. For the public schools in the same school district, E ag can be considered 1.0, since public schools in a community typically are administrated centrally under the general supervision of an elected Board of Education, and in such cases “established agreements” are not relevant.
Community individuals can support education through supporting the school staff, providing donations, and encouraging students and staff to keep the school system as functional as possible. The effect of community individuals' behavior on school functionality following an earthquake is modeled by (a) calculating the number of available volunteers, R3, for each school; (b) tallying donations collected after the earthquake, which can be added to other recovery funding sources; and (c) considering the impact of the social vulnerability index (CVI) (Agency for Toxic Substances and Disease Registry, 2018) on the resilience of the school system. To estimate the total number of volunteers at each school, the probability that an individual responds to a request from the school depends on his/her gender, age, education, and income (Shi et al., 2018).
Schools can also play an important role as community shelters and as community centers for recovery management. The expected shelter capacity of each school, N sh, can be calculated as a product of the school capacity, N s, and the probability, P sh, that a school can serve as a shelter:
| (25) |
in which the probability is:
| (26) |
where E s is the event that the school structural is safe, E a is the event that the school is accessible, E u is the event that main supporting utilities or alternatives are available, and E m is the event that the school space can be used as a shelter, conditioned on the enrollment capacity of the school, N a, being more than the number of students attending the school, N t.
Different indices are used to quantify the quality of the educational service such as educational attainment (National Academies of Sciences, Engineering, 2019) and student outcomes (Patry & Ford, 2016). Student outcomes can be monitored using self‐reported or test‐based measures (Caspersen et al., 2017). Student outcomes have been found to depend on chronic absenteeism (Bruner et al., 2011), which typically increases after major natural hazard events as a consequence of school closure, population dislocation, and stress and trauma. In this study, student's chronic absenteeism is used as a resilience index of the educational service.
3.4. School System Recovery Model
To recover educational services, all school functions described above must be restored to or near their level prior to the disruption. Repair recovery time after major natural hazard events can be classified into two stages—(1) assessment and planning and (2) the repair process. The assessment and planning stage includes inspection of damage, review/redesign, procurement of funding, issuing of permits, and mobilization of contractors. The time required for each of the assessment and planning tasks can be estimated as a function of the building damage condition and other financial conditions (Almufti & Willford, 2013).
Repair or restoration of each school can be estimated using a semi‐Markov chain process, in which the restoration process is defined by discrete nondecreasing states. In the Markov chain process herein, the repair process at any time step can either improve the restoration state or will stay the same; the current restoration state depends on the previous state but is independent of other previous states (Kozin & Zhou, 1990). A school's quantity functionality is subcategorized into subcomponents based on the repair crew specialty: structural components, building envelope, permanent and movable partitions, mechanical equipment, and electrical systems. The discrete Markov chain modeling the recovery process is:
| (27) |
in which the functionality of subcomponent l, Q l, after time kΔt is assumed to be related to the initial functionality drop, Q l(0), due to seismic damage, the interaction between the repair process of each school, and other community lifelines, A l:
| (28) |
The interaction term A l is calculated based on factor β j, defined in terms of the interaction factor, e j , and the current functionality state of the lifeline j, Q j(t).
| (29) |
| (30) |
The transition probability matrix, P t, is shown in Equation 31 with components p s,r(t), defined in Equation 32.
| (31) |
in which
| (32) |
The transition probabilities, p s,r(t), are defined as the probability of the functionality state transitioning to the next (higher) level (Kozin & Zhou, 1990):
| (33) |
In which a and b are parameters referring to the geographical and structural properties of the investigated lifeline and accounts for the location of the building and how the building will be accessible for the repair crews as well as the building structural system and how easy it can be repaired (Kozin & Zhou, 1990). The transition probabilities are also calculated as a function of the assigned repair crews, x, and the current restoration stage, r.
The allocation of a limited number of repair crews with multiple specialties to repair the damage that is temporally changing in different schools has to be well managed to achieve the recovery objectives of the school system. In this study, the repair crews are distributed by dynamic optimization (Bellman, 1957) to achieve the predefined community objectives regarding the education service. While this process can maximize the quality or/and the quantity of school education, thus potentially minimizing population outmigration and enhancing community resilience, the impact of repair on the quantity of the education service can be immediately observed and measured. Therefore, we use the quantity of educational service delivered in illustrating the framework.
Suppose that the total available number of repair crews at each specialty, m, is X m(t), which changes as a function of the time after earthquake (Porter, 2016). The decision‐makers assumed in this study assign these crews, x m n(t), at any time, t, to repair the damaged components by crew's specialty, m, in each school, n, to achieve maximum quantity of the offered education service for the whole community as denoted by Equation 34. Distribution of the repair crews is subjected to the following constraints: (a) limitation of repair resources as shown in Equation 35, (b) predefined repair sequence based on engineering judgment (Almufti & Willford, 2013), and (c) work environment constraint that limits the total number of repair crews, x n,max, in any building, n, as a function of the building area, A t, as shown in Equation 36.
| (34) |
| (35) |
| (36) |
4. Case Study
4.1. Community and School System Characteristics
Centerville (shown in Figure 5) is a virtual midsize community in a Midwestern State, consisting of approximately 50,000 inhabitants; a mixture of residential, industrial, and commercial zones; and a diverse economy and including schools, fire stations, a hospital, and other public facilities (Ellingwood et al., 2016).
Figure 5.
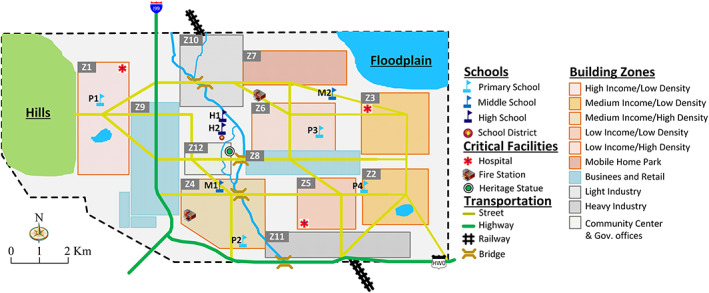
Centerville Community Testbed (after Ellingwood et al., 2016).
The Centerville school system consists of three primary schools, two middle schools, and two high schools, as well as a school district administrative office, which is attached to the high school building. To accommodate the number of students from K‐9 to K‐12, another high school is added to Centerville. Table 1 summarizes the characteristics of the Centerville schools, including grade, total area, building type, height, year of construction, and valuation of structural, nonstructural and contents prior to the earthquake. The values in Table 1 are obtained from a previous study (Ellingwood et al., 2016), except for the added high school and building type for all schools, which are assumed in this study. The school area is used to calculate the maximum number of repair crews allowed in the school building at any time based on (Almufti & Willford, 2013) and, if the school is used as an emergency shelter, the capacity of that shelter according to FEMA requirements (Federal Emergency Management Agency, 2015).
Table 1.
Centerville Schools and Their General Building Properties
| School | Grade | Type | A t (m2) | Building type | Height (stories) | Built year | Building components values (106 $) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Structural | Nonstructural (drift sensitive) | Nonstructural (accel. sensitive) | Content | |||||||
| P1–P4 | Elementary | Public | 9,290 | Reinforced masonry bearing walls | 1 | 1980 | 1.80 | 4.64 | 3.08 | 9.52 |
| M1 and M2 | Middle | Public | 9,290 | Concrete moment frame | 3 | 1990 | 1.71 | 4.39 | 2.92 | 9.02 |
| H1 and H2 | High | Public | 9,290 | Steel light frame | 3 | 1990 | 1.71 | 4.39 | 2.92 | 9.02 |
Table 2 shows the total number of classrooms for each grade, the number of students per grade, staff, and the backup utilities and supplies availability immediately prior to earthquake occurrence. The National Center for Education Statistics (NCES) (2017a), which provides an average total number of student enrollment per grade for public schools in the United States, is utilized to calculate the number of school students in Centerville as a function of the total population. Based on NCES for 2017, the total number of school‐age students is 7,754, which are distributed to the primary (pre‐K to Grade 5), middle (Grades 6–8), and high (Grades 9–12) schools as 3,702, 1,742, and 2,310, respectively. The elementary schools are assumed to have self‐contained classrooms, while both middle and high schools utilize instruction by topic (math, history, etc.), which impacts the number of students in each class. The resulting average class sizes, per the National Center for Education Statistics (2017b), are 22, 26, and 24 for the elementary, middle, and high school, respectively. The number of staff and administration are also estimated based on U.S. national averages (Glander, 2017). The experience of instructional staff is determined by years of teaching experience and the highest degree earned (National Center for Education Statistics, 2019). Based on the school's capacity and the expected travel time for students, the school district defines each school's zone as shown in Figure 6.
Table 2.
Staff, Space, and Supplies Availability for the Centerville School System Immediately Prior to the Earthquake
| School | Grades | # classroom per grade (National Center for Education Statistics, 2017b) | # student per class (National Center for Education Statistics, 2017b) | # staff per school (Glander, 2017) | Backup systems (%) | Supplies | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R1 | R2 | R4 | R8 | R10 | R13 | R16 | R18 | R22–R25% | ||||
| P1–P4 | P–K‐5 | 6 | 22 | 46 | 21 | 30 | 100 | 50 | 100 | 0 | 100 | 100 |
| M1 and M2 | 6–8 | 11 | 26 | 43 | 20 | 28 | 100 | 50 | 100 | 0 | 100 | 100 |
| H1 and H2 | 9–12 | 12 | 24 | 97 | 27 | 37 | 100 | 50 | 100 | 0 | 100 | 100 |
Figure 6.
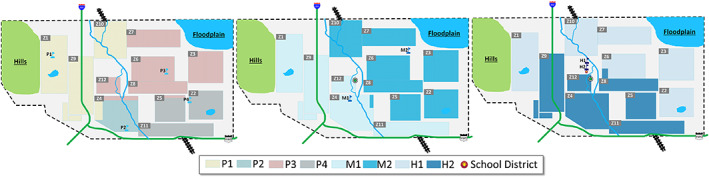
School zones before the earthquake occurrence.
Parameters for the school system recovery model are shown in Table 3 including the geographical and structural parameters (a and b in Equation 28), the total number of available repair crews for the school system, and the interaction values between schools and their supporting lifelines. Different specialties of repair crews are considered including structural, X1, plumbing, and HVAC systems, X2, interior partitions, ceiling tiles, and components of the exterior building envelope, X3; mechanical equipment, X4; electrical systems, X5; and elevators, X6. A building repair sequence starts with the repair of the structural components to guarantee the safety of the building, followed by corridors and stairs to ensure accessibility for the subsequent repair tasks. All other repair tasks can then be executed simultaneously. The total number of available repair crews is assumed to be changing with time since the impacted community may receive additional aid from the surrounding communities. It is assumed that each repair crew consists of 10 workers.
Table 3.
Input Parameters for the Recovery Model
| School | Geo and Structural data a | Repair crews (normal/with aid) a | Interaction values (Cimellaro, 2016) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | X1 | X2 | X3 | X4 | X5 | X6 | Power | Trans. | Telecom. | Water | W. water | Fuel | |
| P1 | 0.80 | 0.15 | 3/5 | 0/1 | 1/1 | 1/1 | 1/2 | 1/1 | 0.3 | 0.3 | 0.0 | 0.6 | 0.0 | 0.3 |
| P2 | 0.83 | 0.13 | ||||||||||||
| P3 | 0.89 | 0.17 | ||||||||||||
| P4 | 0.82 | 0.14 | ||||||||||||
| M1 | 0.88 | 0.18 | ||||||||||||
| M2 | 0.84 | 0.17 | ||||||||||||
| H1 | 0.81 | 0.15 | ||||||||||||
| H2 | 0.85 | 0.16 | ||||||||||||
Assumed data.
4.2. Damage and Recovery of Supporting Infrastructure
Two different earthquake scenarios are considered, both with moment magnitude, M w, equal to 7.9, epicenter approximately 40 km southwest of Centerville, and occurrence time 5:00 pm. In the first scenario, the earthquake is assumed to occur during the middle of the school year, while in the second, the earthquake occurs during the summer break. In both scenarios, the spatial distribution of the building damage is estimated from the earthquake intensity generated by IN‐CORE (Ellingwood et al., 2016) and damage states in Hazus MH 2.1 (2015), which is generated based on buildings characteristics shown in Table 1 including the building age and design code generation. Given the spatial distribution of the seismic demand in the community (Ellingwood et al., 2016), damage to buildings, transportation, power, telecommunication, water, wastewater, fuel, and education systems are calculated. As an example, the seismic fragilities of the school buildings in Centerville are summarized in Figure 7 including seismic fragility curves for structural components, nonstructural drift‐sensitive components, and nonstructural acceleration‐sensitive components.
Figure 7.
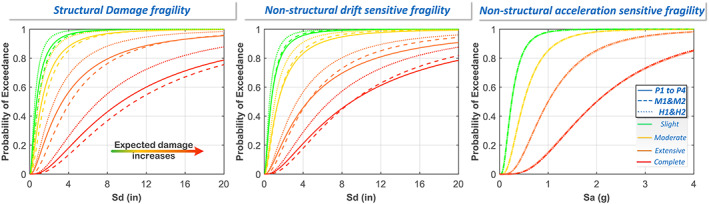
School buildings damage fragility curves (Hazus‐MH 2.1, 2015).
Economic and social losses at the different schools are estimated from FEMA P‐58 (2012), based on damage to the building components, expected occupancy at the time of the earthquake, and the building component values listed in Table 1. Figure 8 shows the immediate impact of the earthquake on Centerville buildings, schools, and main supporting infrastructure systems. Damage to infrastructure located on the west side of Centerville, which is closer to the epicenter and experienced higher earthquake intensities, is higher. The fact that most of the expected building damage is either slight or moderate reduces the population dislocation and the demand on the community shelters (Levine et al., 2007).
Figure 8.
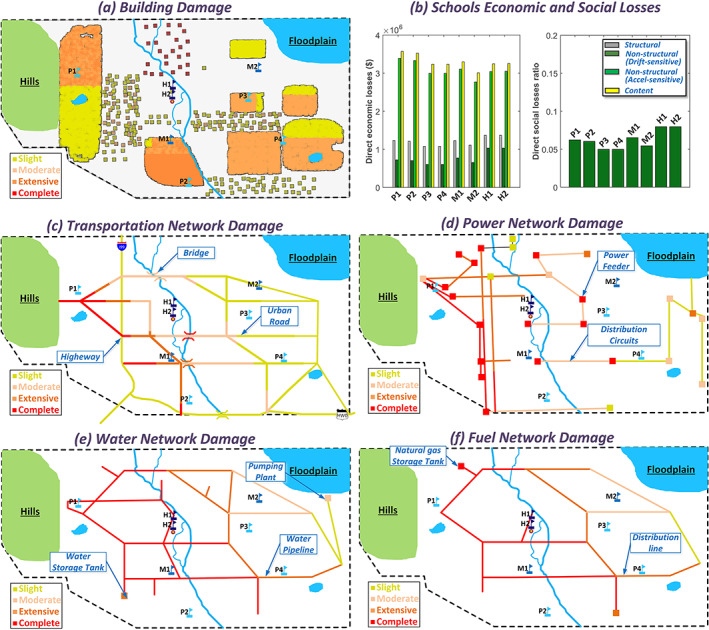
Buildings, schools, and schools supporting infrastructure damage.
Damages to school buildings and supporting infrastructure are utilized to estimate the recovery of educational services based on historical data and restoration curves from ATC‐13 (1985). Restoration of electricity, transportation, telecommunication, water, wastewater, and fuel supplies at each school is shown in Figure 9. These curves subsequently are utilized to calculate the functionality and recovery of the school buildings using the methods described in the previous section.
Figure 9.
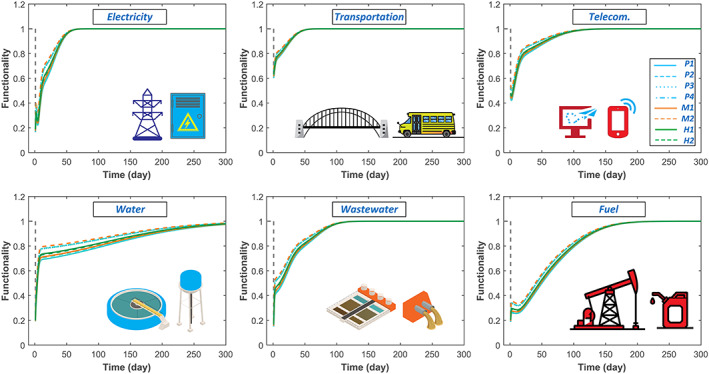
Recovery for schools' supporting infrastructure.
4.3. Recovery of School Functionality
Functionality, recovery, and resilience of the K‐12 school system in Centerville following the two earthquake scenarios are estimated using the methods described in section 3. The influence of school administrators on school reopening, cooperative interactions between schools during the recovery period, and resource optimization are investigated, as well as the different roles played by schools during community recovery such as providing community shelter.
In the first earthquake scenario when school is in session, students are directly impacted by any school closure. The semi‐Markov chain model, coupled with the dynamic optimization, estimates the near‐optimal repair progress of the school system that attains the predefined objectives of the education system of achieving the maximum quantity of the offered education service for the whole community, taking into account repair crew specialties and the possibility that repair crews from neighboring communities are available. Figure 10 shows the quantity and quality functionalities as well as the total functionality of each Centerville school. Substantial damage to the working space within the school system and supporting lifelines immediately after the earthquake leads to closure of all schools immediately following the earthquake. A week after the earthquake, the state of recovery of most supporting lifelines, coupled with the performance of operational backup utility systems and backup space in the schools, increases the supportive infrastructure availability and ends closure of schools. For middle schools (M1 and M2) one classroom is open while for all other schools, two classrooms are open. At this stage, proper backup space is required if schoolchildren, beyond the classroom capacities, are to return to school. However, backup spaces can be utilized only when transportation and utilities reach a sufficient functionality level, which is assumed to be 50%, based on decision‐makers' judgment (Decision I) as mentioned before. It is assumed that each school can be provided by temporary backup spaces (FEMA, 2011) that can be gradually increased as needed to 25% of the school capacity in 3 weeks. At 169 days after the earthquake, all classes in all the schools can reopen. To work towards full recovery of educational services, each school continues its efforts toward increasing the quality by replacing the unqualified staff, ending the staff internal and external transfer, and ensuring the adequacy of the class technology, which is achieved after 94 more days.
Figure 10.
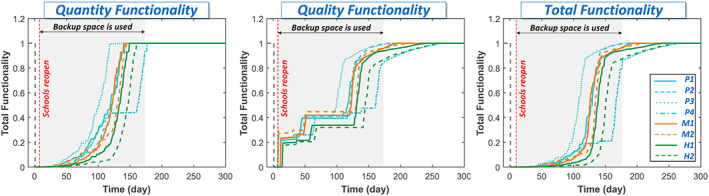
Restoration of school functionalities.
Due to damage to school facilities, schoolchildren can be enrolled in school (depending on damage level), transfer to homeschooling, or miss school. Figure 11a displays the change in total student enrollment in Centerville following the first earthquake occurrence scenario. Limitations in available student positions throughout the first month after the earthquake increase the number of schoolchildren who miss school. Even though permanent population dislocation is expected to be minimal overall, driven mainly by minor damage in buildings and the quick recovery of utilities, it is likely to be higher for families with children missing school for a longer time. If a nearby school district with schools that have suffered less damage can enroll these children, dislocation is less likely to occur. Figures 11b and 11c shows the percentage of student enrollment per census tract 30 and 100 days after the earthquake. The variation of student enrollment in each census tract is due to dissimilarity in damage at schools within Centerville, transportation availability, and ability of families in each census tract to provide alternatives for their schoolchildren, such as homeschooling and/or private transportation.
Figure 11.
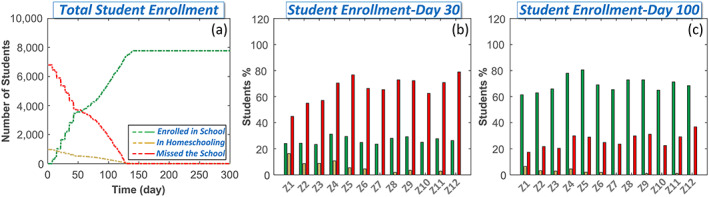
(a) Total student enrollment versus time, (b) the percentage of student enrollment per census tract at Day 30, and (c) percentage of student enrollment per census tract at Day 100.
To highlight the influence of school district administration on closing and reopening of schools, two other cases are considered, in which the schools do not have backup space (Decision II) or the schools remain closed after the earthquake by the school district until full recovery of all schools has been achieved (Decision III). Figure 12a displays the effect of backup space on the total number of students enrolled and the delay in reopening the schools (between 33 and 67 days). Figure 12b shows the impact of Decision III on student enrollment. A significant increase in school closures is apparent, in which it takes the school district 153 days to open all schools. However, Decision III provides the required time for the school district administration to arrange for school reopening and student return when most school infrastructure has restored to normal conditions. The average chronic absenteeism for three investigated decisions is shown in Figure 12c. It can be noted that Decisions II and III significantly increase chronic absenteeism, which is utilized here as a resilience index of the educational service provided by the Centerville community.
Figure 12.
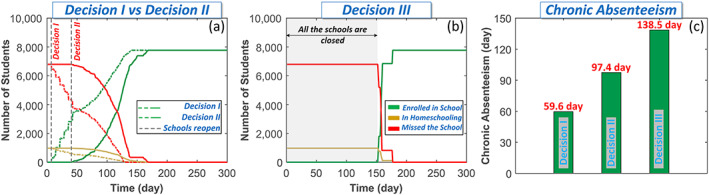
(a) The effect of Decisions I and II on the student enrollment, (b) student enrollment based on Decision III, and (c) chronic absenteeism comparison for Decisions I–III.
In the second earthquake scenario, in which the earthquake occurs when schools are in recess, the use of school buildings and backup space for community shelter does not interrupt the main services provided by the schools. On the other hand, shelters require emergency staff, including social workers, volunteers, transportation services, utilities, space (with different contents), fuel, and food supplies (Federal Emergency Management Agency, 2015). It is assumed that 2 days after the earthquake, the community can provide shelter in undamaged school buildings and backup spaces. The capacity of the backup spaces is assumed to gradually increase from 25% to 50% of the schools' capacities as a shelter within 18 days. Figure 13 shows the shelter capacities at each school. The shelter capacity can be increased by adding the classrooms, once they are repaired, to the number of accommodations as shown in Figure 13; after 142 days all the schools' area can be used as a shelter. Of course, if the school recess ends during this recovery period, the school utilization is likely to revert to its original intended purpose, creating social problems for community officials that are not addressed in this paper and would require modification to the framework presented in section 3.
Figure 13.
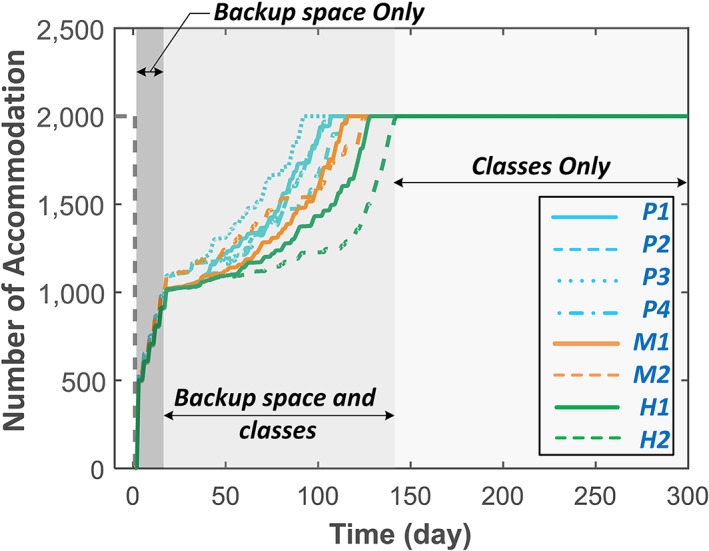
Shelter availability.
5. Summary and Conclusions
This article presents a new methodology to measure functionality, recovery, and resilience of a K‐12 school system exposed to a severe scenario earthquake. The methodology accounts for interdependencies between schools and their supporting lifelines, suppliers, parents, teachers, and administrative personnel, as well as relationships between the individuals involved in delivering quality education to a community. School functionalities are categorized into quantity functionality, measured in terms of the enrollment capacity for schoolchildren, and quality functionality estimated as a combination of different factors related to teacher quality, classroom quality, and school quality. Near‐optimal recovery trajectories of the school's buildings that attain the predefined objects of the school system are determined using a semi‐Markov chain stochastic model, coupled with dynamic optimization while considering limitations and specialties of the repair crews, change of the number of repair crews over time, and repair sequences. The role played by school administrators in managing school reopenings after the earthquake and finding alternatives for schoolchildren and staff to ensure the continuation of educational services is also considered. Two different earthquake scenarios are assumed to test the feasibility of the proposed approach as a planning tool. The first scenario focuses on the school system as a provider of education, while the second scenario considers the school system as a provider of emergency shelter.
The main conclusions drawn from this analysis can be summarized as follows:
Providing schools with reliable backup utilities and sufficient backup spaces is critical for keeping the schools open after the earthquake.
Recovering the schools' main supporting lifelines, especially transportation, is key for school reopening.
Providing alternative staff and using community volunteers can temporarily close the gap in staff shortage. However, it could also negatively impact the quality of educational services and student outcomes. However, staff swapping and appointing qualified staff sustain the leadership and professional community.
Establishing appropriate policies and decision‐making processes has a substantial impact on the school's recovery trajectory and students' enrollment state.
Using schools as shelters immediately after the earthquake is a function of the backup utility systems and backup spaces. However, it depends on the recovery progress of schools, supporting lifelines and suppliers.
The study also establishes the basis for defining the required parameters that need to be measured by communities after natural hazards, such as earthquakes, to assess the education system resilience, functionality, and recovery. Estimation of the presented model parameters can be modified to address the investigated communities' characteristics and hazard type. While the results obtained in this study highlight the importance of different school components in education system recovery, we acknowledge that factors related to the psychosocial and socioecological functioning of the human systems are found to be among the significant factors influencing resilience of schools, especially for the quality indices. Therefore, we recommend that these factors be included in future studies to provide a more holistic understanding of school system resilience.
Acknowledgments
Funding for this study was provided as part of Cooperative Agreement 70NANB15H044 between the National Institute of Standards and Technology (NIST) and Colorado State University and is gratefully acknowledged. The content expressed in this paper is the view of the authors and does not necessarily represent the opinions or views of CSU, NIST, or the U.S. Department of Commerce.
Hassan, E. M. , Mahmoud, H. N. , & Ellingwood, B. R. (2020). Resilience of school systems following severe earthquakes. Earth's Future, 8, e2020EF001518 10.1029/2020EF001518
Data Availability Statement
All data can be found online (at https://github.com/EmadShafik/Resilience‐of‐school‐systems‐following‐severe‐earthquakes).
References
- Agency for Toxic Substances and Disease Registry . (2018). CDC's social vulnerability index (SVI).
- Almufti, I. , & Willford, M. (2013). REDi ™ Rating System: Resilience‐based earthquake design initiative for the next generation of buildings. Retrieved from https://www.arup.com/perspectives/publications/research/section/redi‐rating‐system
- American Academy of Pediatrics (2019). Ensuring the health of children in disasters. Pediatrics, 136(5). 10.1542/peds.2015-3112 [DOI] [PubMed] [Google Scholar]
- American Society of Civil Engineers . (2017). Infrastructure report card. Reston, Virginia. [Google Scholar]
- Applied Technology Council . (2017). FEMA P‐1000, safer, stronger, smarter: A guide to improving school natural hazard safety.
- ASCE/SEI 7–16 . (2016). Minimum design loads and associated criteria for buildings and other structures.
- Asian Development Bank and World Bank . (2005). Pakistan 2005 earthquake preliminary damage and needs assessment. Pakistan: Islamabad. [Google Scholar]
- ATC‐13 . (1985). Earthquake damage evaluation data for California. Redwood City, California. [Google Scholar]
- Augenti, N. , Cosenza, E. , Dolce, M. , Manfredi, G. , Masi, A. , & Samela, L. (2004). Performance of school buildings during the 2002 Molise, Italy, earthquake. Earthquake Spectra, 20(1), 257–270. 10.1193/1.1769374 [DOI] [Google Scholar]
- Balingit, M. (2017). Some Puerto Rican schools reopen Tuesday without electricity. Retrieved January 16, 2020, from https://www.washingtonpost.com/local/education/some-puerto-rican-schools‐reopen‐tuesday‐without‐electricity/2017/10/23/cc35320a‐b82a‐11e7‐a908‐a3470754bbb9_story.html
- Beaglehole, B. , Bell, C. , Frampton, C. , & Moor, S. (2018). The impact of the Canterbury earthquakes on successful school leaving for adolescents. Australian and New Zealand Journal of Public Health, 41, 70–73. 10.1111/1753-6405.12625 [DOI] [PubMed] [Google Scholar]
- Bellman, R. (1957). Dynamic programming. Princeton: Princeton University Press. [Google Scholar]
- Bounds, A. (2014). Jamestown Elementary welcomes students for first time since September floods. Retrieved January 16, 2020, from https://www.dailycamera.com/2014/08/21/jamestown-elementary-welcomes-students-for-first-time-since-september-floods/#:~:text=JAMESTOWN — Fifteen students came back,giving the two kindergartners roses.
- Bruner, C. , Discher, A. , & Chang, H. (2011). Chronic elementary absenteeism: a problem hidden in plain sight. A research brief from attendance works and child & family policy center. Retrieved from https://www.edweek.org/media/chronicabsence‐15chang.pdf
- Caspersen, J. , Per, J. S. , & Aamodt, O. (2017). Measuring learning outcomes. European Journal of Education, 52, 20–30. 10.1111/ejed.12205 [DOI] [Google Scholar]
- Cimellaro, G. P. (2016). Urban resilience for emergency response and recovery. Switzerland: Springer International Publishing; 10.1007/978-3-319-30,656-8 [DOI] [Google Scholar]
- EERI (1990). Loma Prieta earthquake October 17, 1989, preliminary reconnaissance report. Earthquake Spectra, 6(S1), 127–149. 10.2208/jscej.1990.422_11 [DOI] [Google Scholar]
- Ellingwood, B. , Cutler, H. , Gardoni, P. , Peacock, W. G. , van de Lindt, J. W. , & Wang, N. (2016). The Centerville Virtual Community: A fully integrated decision model of interacting physical and social infrastructure systems. Journal of Sustainable and Resilient Infrastructure, 1(3–4), 95–107. 10.1080/23789689.2016.1255000 [DOI] [Google Scholar]
- Federal Emergency Management Agency (2002). Incremental seismic rehabilitation of school buildings, K‐12 (FEMA 395). Washington, D.C. [Google Scholar]
- Federal Emergency Management Agency (2010). Risk management series: Design guide for improving school safety in earthquakes, floods, and high winds (FEMA P‐424). Washington, D.C. [Google Scholar]
- Federal Emergency Management Agency (2012). Reducing the risks of nonstructural earthquake damage—A practical guide (FEMA E‐74). Washington, D.C. [Google Scholar]
- Federal Emergency Management Agency (2015). Shelter field guide (FEMA P‐785).
- FEMA (2011). Sample school emergency operations plan.
- FEMA P‐58‐1 . (2012). Seismic performance assessment of buildings. FEMA P‐58‐1. Applied Technology Council (ATC).
- Fothergill, A. (2017). Children, youth, and disaster Oxford research encyclopedia (pp. 1–28). 10.1093/acrefore/9780199389407.013.23 [DOI] [Google Scholar]
- Fujieda, A. , Pandey, B. H. , & Ando, S. (2008). Safe schools to reduce vulnerability of children to earthquakes. In The 14 World Conference on Earthquake Engineering. Beijing, China. [Google Scholar]
- Glander, M. (2017). Selected statistics from the public elementary and secondary education universe: school year 2015 ‐16 (NCES 2018‐052). Washington, DC: Retrieved from https://nces.ed.gov/pubsearch/ [Google Scholar]
- Government of Nepal (National Planning Commission) (2015). Nepal earthquake 2015 post disaster needs assessment executive summary. Kathmandu. [Google Scholar]
- Green, R. , & Miles, S. (2011). Social impacts of the 12 January 2010 Haiti earthquake. Earthquake Spectra, 27(S1), S447–S462. 10.1193/1.3637746 [DOI] [Google Scholar]
- Hancilar, U. , Çaktı, E. , Erdik, M. , Franco, G. E. , & Deodatis, G. (2014). Earthquake vulnerability of school buildings: Probabilistic structural fragility analyses. Soil Dynamics and Earthquake Engineering, 67, 169–178. 10.1016/j.soildyn.2014.09.005 [DOI] [Google Scholar]
- Hassan, E. M. , & Mahmoud, H. (2019). Full functionality and recovery assessment framework for a hospital subjected to a scenario earthquake event. Engineering Structures, 188, 165–177. 10.1016/j.engstruct.2019.03.008 [DOI] [Google Scholar]
- Hazus‐MH 2.1 . (2015). Multi‐hazard loss estimation methodology: Earthquake model. Washington, D.C. [Google Scholar]
- Hinojosa, J. , Meléndez, E. , & Pietri, K. S. (2019). Population decline and school closure in Puerto Rico (Centro RB2019‐01). Puerto Rico; Retrieved from https://centropr.hunter.cuny.edu/sites/default/files/PDF_Publications/centro_rb2019‐01_cor.pdf [Google Scholar]
- International Finance Corporation (IFC) . (2010). Disaster and emergency preparedness: guidance for schools. Washington, D.C. [Google Scholar]
- Kabeyasawa, T. , Kabeyasawa, T. , Kusunoki, K. , & Li, K. (2014). An outline of damage to school buildings in Dujiangyan by the Wenchuan earthquake on May 12, 2008. In the 14th World Conference on Earthquake Engineering. Beijing, China. [Google Scholar]
- Kozin, F. , & Zhou, H. (1990). System study of urban response and reconstruction due to earthquake. Journal of Engineering Mechanics, 116(9), 1959–1972. 10.1061/(asce)0733-9399(1990)116:9(1959) [DOI] [Google Scholar]
- Levine, J. N. , Esnard, A. , & Sapat, A. (2007). Population displacement and housing dilemmas due to catastrophic disasters. Journal of Planning Literature, 22(1), 4–15. 10.1177/0885412207302277 [DOI] [Google Scholar]
- Masten, A. S. (2018). Resilience theory and research on children and families: Past, present, and promise. Journal of Family Theory and Review, 10(1), 12–31. 10.1111/jftr.12255 [DOI] [Google Scholar]
- Masten, A. S. , & Narayan, A. J. (2012). Child development in the context of disaster, war, and terrorism: Pathways of risk and resilience. Annual Review of Psychology, 63(1), 227–257. 10.1146/annurev-psych-120,710-100,356 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masten, A. S. , Narayan, A. J. , Silverman, W. K. , & Osofsky, J. D. (2015). Children in war and disaster. Handbook of Child Psychology and Developmental Science, 1–42. 10.1002/9781118963418.childpsy418 [DOI] [Google Scholar]
- Masten, A. S. , & Osofsky, J. D. (2010). Disasters and their impact on child development: Introduction to the special section. Society for Research in Child Development, 81(4), 1029–1039. Retrieved from. https://www.jstor.org/stable/40801458 [DOI] [PubMed] [Google Scholar]
- Mayer, D. P. , Mullens, J. E. , Moore, M. T. , & Ralph, J. (2000). Monitoring school quality: An indicators report, NCES 2001‐030. Washington, D.C: Retrieved from https://nces.ed.gov/pubs2001/2001030.pdf [Google Scholar]
- Nakano, Y. (2004). Seismic rehabilitation of seismically vulnerable school buildings in Japan. Journal of Japan Association for Earthquake. Engineering, 4(3), 218–229. [Google Scholar]
- National Academies of Sciences, Engineering, and Medicine (2019). In Monitoring educational equity. Washington, DC: The National Academies Press; 10.17226/25389 [DOI] [Google Scholar]
- National Center for Education Statistics (2017a). Table 203.10. Enrollment in public elementary and secondary schools, by level and grade: Selected years, fall 1980 through fall 2027.
- National Center for Education Statistics (2017b). Table 7. Average class size in public primary schools, middle schools, high schools, and schools with combined grades, by classroom type and state.
- National Center for Education Statistics (2019). The condition of education 2019. Washington, D.C. [Google Scholar]
- National Center for Education Statistics (NCES) (2019). Back to school statistics.
- National Research Council (2012). In Beatty A. & Koenig J. A. (Eds.), Key national education indicators: Workshop summary. Washington, DC: The National Academies Press; 10.17226/13453 [DOI] [Google Scholar]
- National Research Council (US) Panel to Review the Status of Basic Research on School‐Age Children . (1986). In Collins W. A. (Ed.), Development during middle childhood: The years from six to twelve. Washington, DC: National Academy Press; 10.17226/56 [DOI] [PubMed] [Google Scholar]
- Norris, F. H. , Friedman, M. J. , & Watson, P. J. (2002). 60,000 disaster victims speak: Part II. summary and implications of the disaster mental health research. Psychiatry Interpersonal & Biological Processes, 65(3). 10.1521/psyc.65.3.240.20169 [DOI] [PubMed] [Google Scholar]
- Nozhati, S. , Ellingwood, B. R. , & Mahmoud, H. (2019). Understanding community resilience from a PRA perspective using binary decision diagrams. Risk Analysis, 39(10). 10.1111/risa.13321 [DOI] [PubMed] [Google Scholar]
- Osofsky, H. J. , Osofsky, J. D. , Kronenberg, M. , Brennan, A. , & Hansel, T. C. (2009). Posttraumatic stress symptoms in children after hurricane Katrina: predicting the need for mental health services. American Journal of Orthopsychiatry, 79(2), 212–220. 10.1037/a0016179 [DOI] [PubMed] [Google Scholar]
- Oyguc, R. , & Guley, E. (2017). Performance assessment of two aseismically designed RC school buildings after the October 23, 2011, Van, Turkey Earthquake. Journal of Performance of Constructed Facilities, 31(1), 1–19. 10.1061/(ASCE)CF.1943-5509.0000938 [DOI] [Google Scholar]
- Patry, D. , & Ford, R. (2016). Measuring resilience as an education outcome. Toronto, Canada. 10.13140/RG.2.1.1351.5769 [DOI]
- Porter, K. A. (2016). Damage and restoration of water supply systems in an earthquake sequence. Boulder, CO. [Google Scholar]
- Raccanello, D. , Burro, R. , & Hall, R. (2017). Children's emotional experience two years after an earthquake: An exploration of knowledge of earthquakes and associated emotions. PLoS ONE, 12(12), 1–21. 10.1371/journal.pone.0189633 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodgers, J. E. (2011). Why schools are vulnerable to earthquakes. In 15th World Conference on Earthquake Engineering. Lisbon, Portugal. [Google Scholar]
- Rundquist, J. (2012). Hurricane Sandy aftermath: Some N.J. schools reopen with no heat, no lunch. Retrieved January 16, 2020, from https://www.nj.com/news/2012/11/hurricane_sandy_aftermath_some.html
- Shi, M. , Xu, W. , Gao, L. , Kang, Z. , Ning, N. , Liu, C. , Liang, C. , Sun, H. , Jiao, M. , Liang, L. , Li, Y. , Cui, Y. , Zhao, X. , Fei, J. , Wei, Q. , Yi, M. , Hao, Y. , & Wu, Q. (2018). Emergency volunteering willingness and participation: A cross‐sectional survey of residents in northern China. BMJ Open, 1–11. 10.1136/bmjopen-2017-020218 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh, A. (2019). Puerto Ricans transform closed schools into community centers. Retrieved January 16, 2020, from https://truthout.org/articles/puerto-ricans-transform-closed-schools-into-community-centers/#:~:text=San Salvador isn't the,up the closed school building.
- U.S. Department of Education (2007). Lessons learned from school crises and emergencies. Emergency Response and Crisis Management Technical Assistance Center U.S., 2(5), 1–13. 10.4135/9781452219233.n12 [DOI] [Google Scholar]
- U.S. Department of Education (Office of Innovation and Improvement) (2009). State regulation of private schools. Washington, D.C. [Google Scholar]
- UNESCO (2019). Migration, displacement and education: Building bridges, not walls. Global Education Monitoring Report. Retrieved from https://unesdoc.unesco.org/ark:/48223/pf0000366946/PDF/366946eng.pdf.multi
- Ungar, M. (2018). Systemic resilience: Principles and processes for a science of change in contexts of adversity. Ecology and Society, 23(4). 10.5751/ES-10385-230,434 [DOI] [Google Scholar]
- Ungar, M. , Connelly, G. , Liebenberg, L. , & Theron, L. (2019). How Schools Enhance the Development of Young People's Resilience. Social Indicators Research, 145(2), 615–627. 10.1007/s11205-017-1728-8 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data can be found online (at https://github.com/EmadShafik/Resilience‐of‐school‐systems‐following‐severe‐earthquakes).


